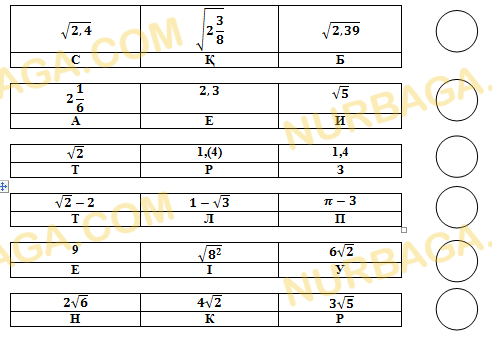
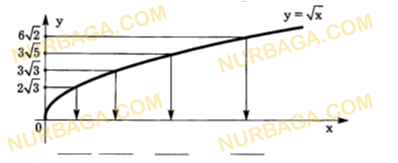
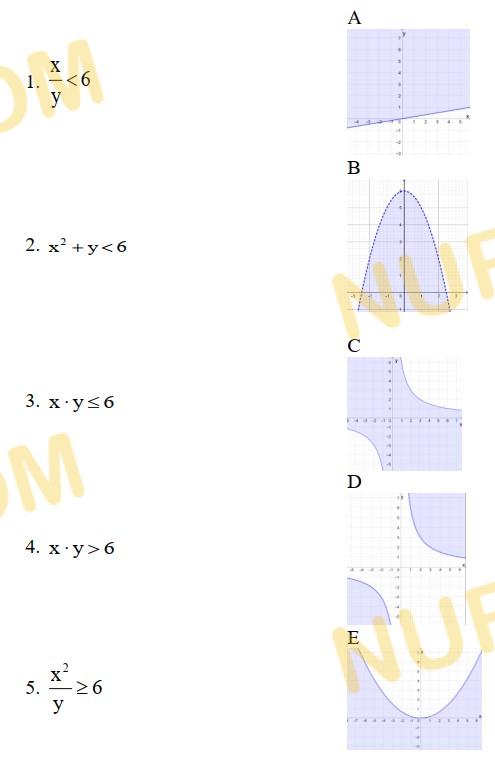
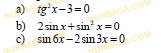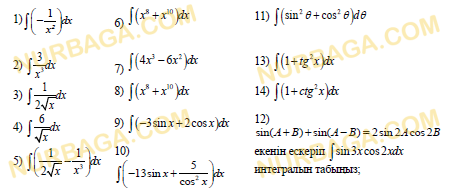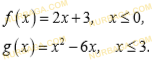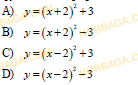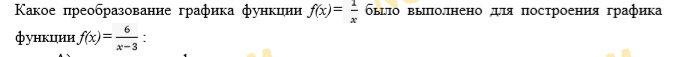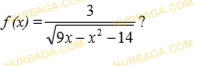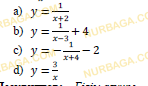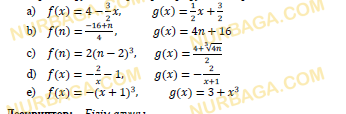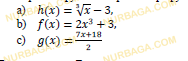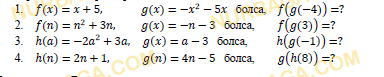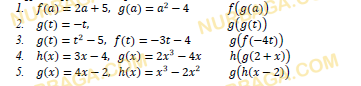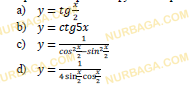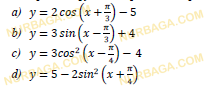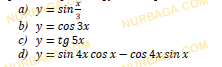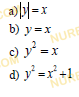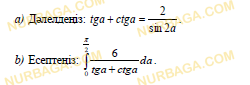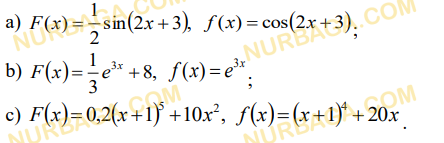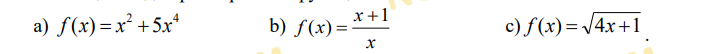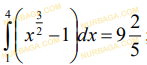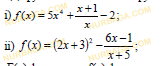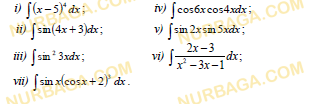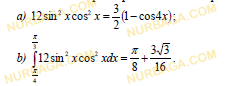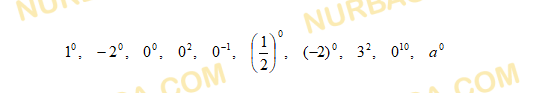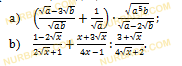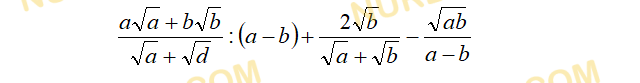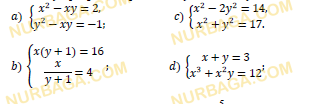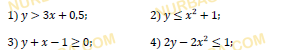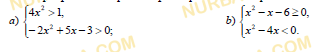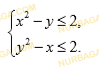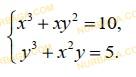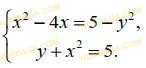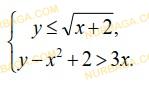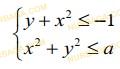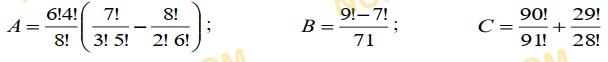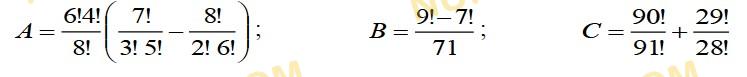Решение заданий СОР и СОЧ за 10 класс ЕМН
Записаться на онлайн-занятия
1 четверть
СОР 1 по алгебре, объясняет Дария:
СОР 2 по алгебре, объясняет Дария:
СОР 3 по алгебре, объясняет Дария:
СОР по геометрии, объясняет Айгерим:
СОЧ по алгебре:
СОЧ по геометрии, объясняет Айгерим:
2 четверть
СОР 1 по алгебре, объясняет Айгерим:
СОР 2 по алгебре, объясняет Айгерим:
СОР 3 по алгебре, объясняет Айгерим:
СОЧ по алгебре, объясняет Айгерим:
СОР по геометрии, объясняет Айгерим:
СОЧ по геометрии, объясняет Айгерим:
3 четверть
СОЧ по алгебре, объясняет Айгерим:
СОЧ по геометрии:
СОР 1 по алгебре:
СОР 2 по алгебре:
СОР 3 по алгебре:
СОР 1 по геометрии, объясняет Айгерим:
СОР 2 по геометрии:
4 четверть
СОЧ по алгебре, объясняет Айгерим:
СОЧ по геометрии, объясняет Айгерим:
СОР по геометрии, объясняет Айгерим:
Псст, есть ещё физика.
Методические рекомендации по суммативному оцениванию
по предмету «Алгебра и начала анализа»
10 класс
(естественно-математическое направление)
Нур-Султан 2019
2
Методические рекомендации составлены в помощь учителю при планировании,
организации и проведении суммативного оценивания за раздел по предмету «Алгебра» для
обучающихся 10 классов естественно-математического направления. Методические
рекомендации подготовлены на основе типовой учебной программы и учебного плана.
Задания для суммативного оценивания за раздел/сквозную тему позволят учителю
определить уровень достижения обучающимися целей обучения, запланированных на
четверть.
Для проведения суммативного оценивания за раздел/сквозную тему в методических
рекомендациях предлагаются задания, критерии оценивания с дескрипторами и баллами.
Также в сборнике описаны возможные уровни учебных достижений, обучающихся
(рубрики). Задания с дескрипторами и баллами носят рекомендательный характер.
Методические рекомендации предназначены для учителей, администрации школ,
методистов отделов образования, школьных и региональных координаторов по
критериальному оцениванию и других заинтересованных лиц.
При подготовке методических рекомендаций использованы ресурсы (рисунки,
фотографии, тексты, видео- и аудиоматериалы и др.), находящиеся в открытом доступе на
официальных интернет-сайтах.
3
СОДЕРЖАНИЕ
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ …………………………….. 4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции» ……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ …………………………… 14
Суммативное оценивание за раздел «Тригонометрические уравнения» …………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства» ………………………. 17
Суммативное оценивание за раздел «Вероятность» ………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ …………………………… 23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность» ……………………… 26
Суммативное оценивание за раздел «Производная» ……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ …………………………… 35
Суммативное оценивание за раздел «Применение производной» ………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые
характеристики» ………………………………………………………………………………………………………….. 39
4
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ
Суммативное оценивание за раздел «Функция, ее свойства и график»
Тема Свойства функции
Дробно-линейная функция
Понятия сложной и обратной функций
Цель обучения 10.4.1.4 Уметь описывать по заданному графику функции
её свойства:
1) область определения функции
2) область значений функции
3) нули функции
4) периодичность функции
5) промежутки монотонности функции
6) промежутки знакопостоянства функции
7) наибольшее и наименьшее значения функции

9) ограниченность функции
10) непрерывность функции
11) экстремумы функции
10.4.1.5 Определять свойства
0 ,
c
d cx
b ax
y
дробно-линейной функции и строить ее график
10.4.1.6 Знать определение обратной функции и находить
функцию, обратную заданной и знать свойство
расположения графиков взаимно обратных
функций
Критерий оценивания Обучающийся:
Исследует свойства функции по ее графику
Использует свойства и строит график дробно-линейной функции
Применяет алгоритм нахождения обратной
функции
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 25 минут
Задания
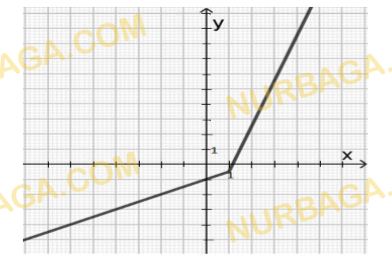
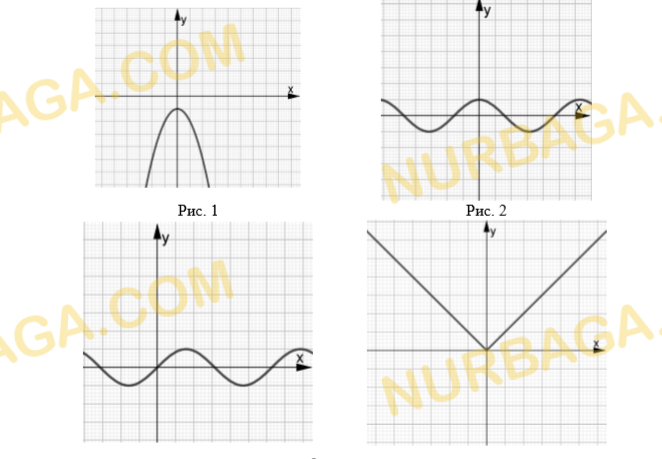
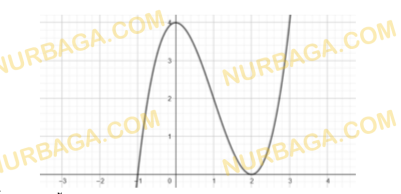
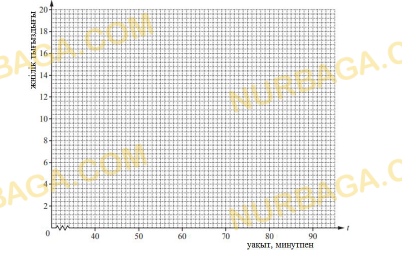
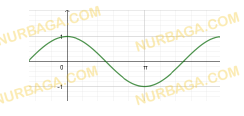
1. Дан график функции.
5
a) Запишите область определения функции.
b) Найдите множество значений функции.
c) Определите промежутки знакопостоянства функции;
d) Определите максимальное значение функции на области определения;
e) Определите четность функции.
2. Дробно-линейная функция задана уравнением: 𝑔(𝑦) =
𝑏𝑥−4
2𝑥−𝑐
.
a) Асимптоты функции имеют уравнения 𝑦 = 3 , 𝑧 = 1 . Найдите значение
переменных a и b.
b) Используя результаты предыдущего действия:
i) приведите функцию 𝑔(𝑦) =
𝑏𝑥−4
2𝑥−𝑐
к виду 𝑧 = 𝑜 +
𝑘
𝑥+𝑚
;
ii) найдите точки пересечения функции с осями координат;
iii) постройте график функции.
3.
a) Найдите обратную функцию для функции 𝑔(𝑦) =
𝑏𝑥−4
2𝑥−𝑐
с полученными
значениями переменных a и b.
b) Как будет расположен график обратной функции относительно первоначальной?
6
Критерий оценивания №
задания
Дескриптор Балл
Обучающийся
Определяет свойства
функции по ее графику
1
находит область определения функции; 1
находит область значений функции; 1
определяет промежутки знакопостоянства
функции;
1
находит максимальное значение функции; 1
определяет четность функции; 1
Использует свойства и
строит график дробно-линейной функции
2a
использует вертикальную асимптоту; 1
использует горизонтальную асимптоту; 1
2b
выбирает способ преобразования; 1
приводит функцию к заданному виду; 1
определяет точки пересечения функции с
осью Ох;
1
определяет точки пересечения функции с
осью Оу;
1
строит график функции; 1
Применяет алгоритм
нахождения обратной
функции 3
выполняет необходимые преобразования; 1
выражает одну переменную через другую; 1
находит обратную функцию; 1
определяет расположение графика
обратной функции.
1
Итого:
16
7
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Функция, ее свойства и график»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания Уровень учебных достижений
Низкий Средний Высокий
Исследует свойства функции
по ее графику
Затрудняется в определении
свойств функции по ее графику
Допускает ошибки при определении
области определения / промежутков
знакопостоянства / максимума /
минимума / четности функции
Oпределяет свойства функции по
ее графику
Использует свойства и строит
график дробно-линейной
функции
Затрудняется в использовании
свойств и построении графика
дробно-линейной функции
Допускает ошибки при определении
множества значений / области
определения / точек пересечения с
осями координат / построении
графика дробно-линейной функции
Определяет свойства и строит
график дробно-линейной
функции
Применяет алгоритм
нахождения обратной
функции
Затрудняется в нахождении
обратной функции
Допускает ошибки в преобразованиях
для нахождения обратной функции
Находит обратную функцию
8
Суммативное оценивание за раздел «Тригонометрические функции»
Тема Тригонометрические функции, их свойства и графики
Построение графиков тригонометрических функций с
помощью преобразований
Цель обучения 10.2.3.1 Знать определения, свойства тригонометрических
функций и уметь строить их графики
10.2.3.2 Уметь строить графики тригонометрических
функций с помощью преобразований
Критерий оценивания Обучающийся
Применяет свойства тригонометрических функций
Строит график тригонометрических функций
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 25 минут
Задания
1. Высота воды в пристани задается уравнением: ℎ(𝑢) = 3 − 2𝑡𝑖𝑜 (𝑢 −
𝜋
2
) , где h(t) –
высота воды (м), t – время (ч), 𝑢 ≥ 0.
a) Найдите максимальную и минимальную высоту воды в пристани.
b) Постройте график функции.
2. Расположите числа 1, 𝑐𝑢1, 𝑢1 в порядке возрастания.
3. Дана функция: у = 𝑢
𝑥
3
.
a) Найдите область определения функции.
b) Определите наименьший положительный период.
9
Критерий оценивания №
задания
Дескриптор Балл
Обучающийся
Использует свойства
тригонометрических
функций
1
находит максимальное значение
функции;
1
находит минимальное значение функции; 1
учитывает допустимые значения
абсциссы (начинает строить график от
начала координат);
1
строит график функции 1
Строит график
тригонометрических
функций 2
использует промежутки
возрастания/убывания тангенса;
1
использует промежутки
возрастания/убывания котангенса;
1
записывает числа в порядке возрастания; 1
3
использует область определения функции
у = 𝑢𝑦;
1
указывает область определения заданной
функции;
составляет выражение для нахождения
периода функции;
1
находит наименьший положительный
период.
1
Итого:
10
10
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Тригонометрические функции»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания Уровень учебных достижений
Низкий Средний Высокий
Применяет свойства
тригонометрических функций
Затрудняется в использовании
свойств тригонометрических
функции
Допускает ошибки при определении
четности/ нечетности,
использовании монотонности/
нахождении области определения/
периода/ максимального/
минимального значения
тригонометрических функций
Использует свойства
тригонометрических функций
Строит график
тригонометрических функций
Затрудняется в построении
графиков тригонометрических
функций
Допускает погрешности в
построении графиков синуса/
косинуса или тангенса/ котангенса
Выполняет построение
графиков тригонометрических
функций
11
Суммативное оценивание за раздел «Обратные тригонометрические функции»
Тема Обратные тригонометрические функции, их свойства и
графики.
Простейшие уравнения, содержащие обратные
тригонометрические функции.
Цель обучения 10.2.3.4 Знать определения и свойства обратных
тригонометрических функций
10.2.3.5 Строить графики обратных
тригонометрических функций
10.2.3.6 Выполнять преобразования выражений,
содержащих обратные тригонометрические
функции
10.2.3.7 Уметь решать простейшие уравнения,
содержащие обратные тригонометрические
функции
Критерий оценивания Обучающийся:
Вычисляет значения выражений, содержащих
обратные тригонометрические функции
Решает уравнения, содержащие обратные
тригонометрические функций
Строит график обратных тригонометрических
функций
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 20 минут
Задания
1. Дано: 𝑎𝑠𝑐𝑡𝑖𝑜
√3
2
+ 𝑎𝑠𝑐𝑢 (𝑢
6𝜋
7
) + 𝑎𝑠𝑐𝑐𝑢 (𝑐𝑢 (−
𝜋
3
)) = 𝑘𝜋. Найдите значение 𝑘.
2. Решите уравнение: 2𝑎𝑠𝑐𝑢𝑦 + 3𝑎𝑠𝑐𝑐𝑢𝑦 = 5
3. Постройте график функции: 𝑧 = 2arccos (𝑦 − 1)
12
Критерий оценивания №
задания
Дескриптор Балл
Обучающийся
Вычисляет значения
выражений, содержащих
обратные
тригонометрические
функции
1
находит значение арксинуса; 1
использует формулу приведения; 1
находит значение арктангенса; 1
использует нечетность котангенса; 1
находит значение арккотангенса; 1
находит значение неизвестной; 1
Решает уравнения,
содержащие обратные
тригонометрические
функции
2
использует сумму арктангенса и
арккотангенса;
1
переходит к уравнению, содержащему
арктангенс/арккотангенс;
1
находит корень уравнения; 1
Строит график обратных
тригонометрических
функций
3
определяет смещения графика функции; 1
использует график арккотангенса;
1
строит график заданной функции.
1
Итого:
12
13
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Обратные тригонометрические функции»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания Уровень учебных достижений
Низкий Средний Высокий
Вычисляет значения
выражений, содержащих
обратные
тригонометрические функции
Затрудняется в нахождении
значений выражений,
содержащих обратные
тригонометрические функции
Допускает ошибки при нахождении
значений арксинуса / арккосинуса /
арктангенса / арккотангенса
Hаходит значения выражений,
содержащих обратные
тригонометрические функции
Решает уравнения,
содержащие обратные
тригонометрические функции
Затрудняется в решении
уравнений, содержащих
обратные тригонометрические
функции
Допускает ошибки при
преобразованиях / вычислениях при
решении уравнений, содержащих
обратные тригонометрические
функции
Решает уравнения, содержащие
обратные тригонометрические
функции
Строит график обратных
тригонометрических функций
Затрудняется в построении
графиков обратных
тригонометрических функций
Допускает погрешности при
построении графиков обратных
тригонометрических функций
Выполняет построение
графиков обратных
тригонометрических функций
14
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ
Суммативное оценивание за раздел «Тригонометрические уравнения»
Тема Простейшие тригонометрические уравнения
Методы решения тригонометрических уравнений и их
систем.
Цель обучения 10.2.3.8 Уметь решать простейшие тригонометрические
уравнения
10.2.3.14 Уметь решать тригонометрические уравнения
методом введения вспомогательного аргумента
10.2.3.11 Уметь решать тригонометрические уравнения с
использованием тригонометрических формул
10.2.3.16 Уметь решать системы тригонометрических
уравнений
Критерий оценивания Обучающийся:
Находит решение простейших тригонометрических
уравнений
Решает тригонометрические уравнения с помощью
введения вспомогательного аргумента
Применяет формулы тригонометрии для решения
тригонометрических уравнений
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 25 минут
Задания
1. Решите уравнение sin (𝑦 +
𝜋
4
) =
√2
2
на промежутке (0; 2𝜋).
2. Используя метод вспомогательного аргумента покажите, что уравнение
sin 𝑦 + cos 𝑦 = 1 можно привести к виду sin (𝑦 +
𝜋
4
) =
√2
2
.
Запишите общее решение уравнения sin 𝑦 + cos 𝑦 = 1.
3. Решите уравнение 𝑢𝑦 = ±√3.
4. Найдите решение уравнения 𝑢𝑦𝑡𝑖𝑜𝑦 − 𝑐𝑝𝑡𝑦 =
1
2𝑑𝑜𝑠𝑥
на промежутке (0; 90°).
15
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Находит решение
простейших
тригонометрических
уравнений
1
использует формулу нахождения корней
уравнения;
1
выражает переменную;
1
находит корни на заданном промежутке
(обязательно в радианах);
1
3
использует формулу нахождения корней
уравнения;
1
находит общее решение уравнения;
1
Решает
тригонометрические
уравнения с помощью
введения
вспомогательного
аргумента
2
делит обе части уравнения на
необходимое число;
1
вводит вспомогательный аргумент; 1
использует формулу сложения
аргументов;
1
показывает равносильность уравнений; 1
записывает общее решение уравнения; 1
Применяет формулы
тригонометрии для
решения
тригонометрических
уравнений
4
делит обе части уравнения на 𝑐𝑝𝑡𝑦;
1
использует необходимую формулу
тригонометрии;
1
переходит к равносильному уравнению;
1
находит решение уравнения на заданном
промежутке (только в градусах).
1
Итого: 14
16
Рубрика для предоставления информации родителям по итогам суммативного оценивания
за раздел «Тригонометрические уравнения»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Находит решение
простейших
тригонометрических
уравнений
Затрудняется в нахождении
решения простейших
тригонометрических уравнений
Допускает ошибки при решении
простейших тригонометрических
уравнений, содержащих синус /
косинус / тангенс / котангенс
Pешает простейшие
тригонометрические уравнения
Решает тригонометрические
уравнения с помощью
введения вспомогательного
аргумента
Затрудняется в использовании
метода введения
вспомогательного аргумента
для решения
тригонометрических уравнений
Использует метод вспомогательного
аргумента, допускает ошибки при
выполнении преобразований
Использует метод
вспомогательного аргумента для
решения тригонометрических
уравнений
Применяет формулы
тригонометрии для решения
тригонометрических
уравнений
Затрудняется в использовании
необходимых формул для
решения тригонометрических
уравнений
Использует необходимые формулы,
допускает ошибки при выполнении
преобразований / нахождении
решения на заданном промежутке
Использует формулы для
решения тригонометрических
уравнений
17
Суммативное оценивание за раздел «Тригонометрические неравенства»
Тема Решение тригонометрических неравенств
Цель обучения 10.2.3.17 Уметь решать простейшие тригонометрические
неравенства
10.2.3.18 Уметь решать тригонометрические неравенства
Критерий оценивания Обучающийся:
Решает простейшие тригонометрические неравенства
Находит решение тригонометрических неравенств
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 25 минут
Задания
1.
a) Решите неравенство: 𝑡𝑖𝑜𝑧 < −
1
√2
.
b) Используя результаты предыдущего действия решите: 𝑡𝑖𝑜 (3𝑦 +
𝜋
6
) < −
√2
2
.
c) Найдите решение неравенства:
1
2
𝑐𝑝𝑡3𝑦 +
√3
2
𝑡𝑖𝑜3𝑦 < −
√2
2
.
2.
a) Докажите равносильность неравенств:
5𝑡𝑖𝑜
2
𝑦 − 3𝑡𝑖𝑜𝑦𝑐𝑝𝑡𝑦 − 36𝑐𝑝𝑡
2
𝑦 > 0 и 5𝑢
2
𝑦 − 3𝑢𝑦 − 36 > 0.
b) Используя результаты предыдущего пункта, решите неравенство:
5𝑡𝑖𝑜
2
𝑦 − 3𝑡𝑖𝑜𝑦𝑐𝑝𝑡𝑦 − 36𝑐𝑝𝑡
2
𝑦 > 0.
18
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Решает простейшие
тригонометрические
неравенства
1a
использует формулу /
тригонометрическую окружность;
1
находит решение неравенства; 1
1b
подставляет решение; 1
находит решение указанного
неравенства;
1
Находит решение
тригонометрических
неравенств 1c
использует введение вспомогательного
угла;
1
использует необходимые формулы; 1
выполняет преобразования и находит
решение неравенства;
1
2a
выполняет деление на косинус;
1
показывает равносильность;
1
2b
переходит к квадратному неравенству; 1
находит решение квадратного
неравенства;
1
возвращается к замене и переходит к
совокупности неравенств;
1
находит решение простейших
неравенств;
1
находит решение исходного неравенства. 1
Итого 14
19
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Тригонометрические неравенства»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Решает простейшие
тригонометрические
неравенства
Затрудняется в нахождении
решения простейших
тригонометрических неравенств
Допускает ошибки при решении
простейших тригонометрических
неравенств, содержащих синус /
косинус / тангенс / котангенс
Pешает простейшие
тригонометрические неравенства
Находит решение
тригонометрических
неравенств
Затрудняется в решении
тригонометрических неравенств
Допускает ошибки при выполнении
преобразований с помощью формул
тригонометрии / нахождении общего
решения
Решает тригонометрические
неравенства
20
Суммативное оценивание за раздел «Вероятность»
Тема Элементы комбинаторики и их применение для
нахождения вероятности событий.
Условная вероятность. Правила сложения и умножения
вероятностей
Формула Бернулли и ее следствия
Цель обучения 10.3.1.4 Решать задачи на нахождение вероятностей,
применяя формулы комбинаторики
10.3.2.8 Использовать формулу Бернулли и ее следствия
при решении задач
10.3.2.4 Понимать и применять правила умножения
вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A)
Критерий оценивания Обучающийся:
Применяет формулы комбинаторики при
решении задач на нахождение вероятности
Применяет формулу Бернулли для решения задач
на нахождение вероятностей
Применяет правило умножения вероятностей при
решении задач
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 25 минут
*Учащимся разрешается использовать калькулятор при
выполнении суммативной работы.
Задания
1. Школьный комитет, состоящий из 5 студентов, избирается из 8 мальчиков и 6
девочек.
a) Сколькими способами можно выбрать членов комитета?
b) Сколькими способами можно выбрать членов комитета так, чтобы в нем было
не менее 3 мальчиков?
c) Найдите вероятность того, что в комитете будет не менее трех мальчиков.
2. Производители деталей выявили, что на одной из сборочных линий 30%
производимых деталей имеют дефект. Во время очередной проверки инспектор
выбирает 6 деталей из этой сборочной линии. Найдите вероятность того, что
инспектору попадутся две детали с дефектом. Ответ округлите до тысячных.
3. Мешок А содержит 3 белых и 2 черных шара. Мешок В содержит 3 белых и 4 черных
шара. С каждого мешка вытаскивают по одному шару, затем возвращают.
a) Вычислите вероятность того, оба шара белые.
b) Из мешка В извлекают по очереди два шара, не возвращая их. Найдите
вероятность того, что оба шара будут черными.
21
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Применяет формулы
комбинаторики при
решении задач на
нахождение вероятности
1a находит число возможных способов; 1
1b
использует формулу числа сочетаний; 1
использует правило произведения; 1
использует правило суммы; 1
1с
находит число благоприятствующих
событий;
1
находит вероятность события; 1
Применяет формулу
Бернулли для решения
задач на нахождения
вероятностей 2
определяет все необходимые
компоненты;
1
применяет формулу Бернулли; 1
выполняет вычисления; 1
находит вероятность события (ответ
обязательно должен быть округлен до
тысячных);
1
Применяет правило
умножения вероятностей
при решении задач
3a
находит вероятность каждого события; 1
находит произведение вероятностей двух
независимых событий;
1
3b
находит вероятность каждого события; 1
находит произведение вероятностей двух
зависимых событий.
1
Итого: 14
22
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Вероятность»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Применяет формулы
комбинаторики при решении
задач на нахождение
вероятностей
Затрудняется в применении
формул комбинаторики для
решения задач на вероятность
Допускает ошибки в использованиии
правил произведения / суммы/ в
вычислениях
Использует формулы
комбинаторики при решении
задач на нахождение
вероятностей
Применяет формулу
Бернулли для решения задач
на нахождение вероятностей
Затрудняется в применении
формулы Бернулли при
решении задач
Допускает ошибки в применении
формулы Бернулли/ошибки в
вычислениях
Применяет формулу Бернулли
для решения задач на
нахождение вероятностей
Применяет правило
умножения вероятностей при
решении задач
Затрудняется в применении
правил произведения
вероятностей при решении
задач
Допускает ошибки в использовании
правила произведения независимых /
зависимых событий при решении
задач
Применяет правило
произведения вероятностей при
решении задач
23
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ
Суммативное оценивание за раздел «Многочлены»
Тема Общий вид многочлена с одной переменной
Деление «уголком» многочлена на многочлен
Теорема Безу, схема Горнера
Метод неопределенных коэффициентов
Цель обучения 10.2.1.3 Уметь распознавать многочлен с одной переменной и
приводить его к стандартному виду
10.2.1.4 Находить старший коэффициент, степень и
свободный член многочлена с одной переменной;
10.2.1.13 Знать метод неопределённых коэффициентов и
применять его при разложении многочлена на
множители
10.2.1.8 Применять теорему Безу и ее следствия при решении
задач
10.2.1.7 Выполнять деление «уголком» многочлена на
многочлен
Критерий оценивания Обучающийся:
Определяет многочлен с одной переменной и его
элементы
Раскладывает многочлен на множители с помощью
метода неопределенных коэффициентов
Применяет теорему Безу и ее следствия
Использует деление «уголком» для разложения
многочленов на множители
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 25 минут
Задания
1. Дано
6
5
2
3
1 3 4 2 x x x x
. Найдите:
a) степень многочлена;
b) старший коэффициент и свободный член;
c) сумму коэффициентов многочлена;
d) сумму коэффициентов при четных степенях.
2. Найдите значения А и В при которых данное тождество верное:
1 3 1 1 3 3
2 3 2 4 5 Вх Ах х х х х х
.
3. Многочлен 𝑦
3
+ 𝑘𝑦
2
− 𝑦 − 6 делится на двучлен 𝑦 − 3 без остатка. Используя теорему
Безу, найдите остаток при делении данного многочлена на двучлен𝑦 − 2.
4. Используя деление «уголком», запишите в каноническом виде частное при делении
многочлена ℎ(𝑦) = 𝑦
3
+ 𝑘𝑦
2
− 𝑦 − 6 на двучлен (𝑦 − 3). Найдите все корни многочлена и
разложите его на множители.
24
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Определяет многочлен с
одной переменной и его
элементы
1
находит степень многочлена; 1
находит старший коэффициент и
свободный член;
1
находит сумму коэффициентов
многочлена;
1
находит сумму коэффициентов при
четных степенях;
1
Раскладывает многочлен
на множители с помощью
метода неопределенных
коэффициентов
2
раскрывает скобки и приводит подобные
слагаемые;
1
находит значение первой переменной; 1
находит значение второй переменной; 1
Применяет теорему Безу и
ее следствия 3
использует теорему Безу; 1
находит значение параметра; 1
находит остаток; 1
Использует деление
«уголком» для
разложения многочленов
на множители
4
делит многочлен на двучлен;
1
записывает частное в каноническом
виде;
1
находит корни квадратного трехчлена; 1
раскладывает многочлен на множители. 1
Итого
14
25
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Многочлены»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Определяет многочлен с
одной переменной и его
элементы
Затрудняется в определении
многочлена с одной
переменной и его элементов
Допускает ошибки при определении
степени / старшего коэффициента /
свободного члена / нахождении
суммы коэффициентов многочлена с
одной переменной
Oпределяет многочлен с одной
переменной и указывает его
элементы
Раскладывает многочлен на
множители с помощью
метода неопределенных
коэффициентов
Затрудняется в применении
метода неопределенных
коэффициентов для разложения
многочленов на множители
Допускает ошибки в применении
метода неопределенных
коэффициентов/вычислительные
ошибки при нахождении неизвестных
Применяет метод
неопределенных коэффициентов
для разложения многочленов на
множители
Применяет теорему Безу и ее
следствия
Затрудняется в применении
теоремы Безу при решении
задач
Допускает вычислительные ошибки
при нахождении неизвестных
Применяет теорему Безу, при
решении задач
Использует деление
«уголком» для разложения
многочленов на множители
Затрудняется в делении
многочленов «уголком»
Допускает ошибки в делении
«уголком» /вычислительные ошибки
при разложении на множители
Делит многочлены «уголком»
для разложения многочлена на
множители
26
Суммативное оценивание за раздел «Предел функции и непрерывность»
Тема Предел функции в точке и на бесконечности
Асимптоты графика функции
Непрерывность функции в точке и на множестве
Первый замечательный предел
Цель обучения 10.4.1.14 Применять методы раскрытия
неопределенностей вида
,
0
0
и
при
вычислении пределов
10.4.1.15 Вычислять пределы, применяя первый
замечательный предел
10.4.1.10 Знать определение асимптоты к графику
функции и уметь составлять уравнения
асимптот
10.4.1.13 Знать свойства непрерывных функций и
применять их при доказательстве
непрерывности функции
Критерий оценивания Обучающийся:
Раскрывает неопределенности при вычислении
пределов функции
Применяет первый замечательный предел
Составляет уравнения асимптот функции
Доказывает непрерывность функций,
используя свойства непрерывных функций
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 20 минут
Задания
1. Найдите значение предела:
a) ;
b)
𝑥
3
+2𝑥−1
5𝑥
3
+4𝑥
2
+2
.
2. Вычислите значение предела:
x tg
x
x
5
8 sin
lim
0
.
3. Дана функция
2
2 5
2
х
х х
у
.
a) Запишите уравнение вертикальной асимптоты.
b) С помощью выделения целой части, найдите уравнение наклонной асимптоты.
c) Используя предел, покажите, что Вы верно нашли наклонную асимптоту.
9
27
lim
2
3
3
x
x
x x
lim
27
4. Известно, что lim
𝑥→2
𝑔(𝑦) = 3 и lim
𝑥→2
(𝑦) = −1 . Определите, будут ли следующие
функции непрерывными в точке 2:
a) 3𝑔(𝑦) + (𝑦);
b)
𝑔(𝑥)
(𝑥)+1
.
28
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Раскрывает
неопределенности при
вычислении пределов
1a
раскладывает выражения на множители; 1
находит значение предела; 1
1b
делит на старшую степень переменной; 1
находит значение предела; 1
Применяет первый
замечательный предел 2
выполняет преобразования; 1
использует первый замечательный предел; 1
находит значение предела; 1
Составляет уравнения
асимптот функции
3
находит вертикальную асимптоту;
1
выделяет целую часть (выполняет деление
многочленов с остатком);
1
находит наклонную асимптоту; 1
использует условие для нахождения
наклонной асимптоты;
1
Доказывает
непрерывность
функций, используя
свойства непрерывных
функций
4
определяет непрерывность суммы двух
функций;
1
определяет непрерывность частного двух
функций. 1
Итого:
14
29
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Предел функции и непрерывность»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Раскрывает
неопределенности при
вычислении пределов
Затрудняется в использовании
методов раскрытия
неопределенностей при
вычислении пределов
Допускает ошибки при
использовании методов раскрытия
неопределенностей / вычислении
пределов
Использует методы раскрытия
неопределенностей при
вычислении пределов
Применяет первый
замечательный предел
Затрудняется в применении
первого замечательного
предела
Допускает ошибки при выполнении
преобразований / вычислении
предела с помощью первого
замечательного предела
Выполняет преобразования и
применяет первый
замечательный предел
Составляет уравнения
асимптот функции
Затрудняется в нахождении
асимптот функций
Допускает ошибки при нахождении
вертикальных / горизонтальных /
наклонных асимптот функций
Находит асимптоты функций
Доказывает непрерывность
функций, используя свойства
непрерывных функций
Затрудняется в применении
свойств непрерывных функций
Допускает ошибки при
использовании свойств непрерывных
функций / определении
непрерывности функций
Применяет свойства
непрерывных функций,
доказывает непрерывность
функций
30
Суммативное оценивание за раздел «Производная»
Тема Определение производной
Правила нахождения производных
Производная сложной функции
Производные тригонометрических функций
Физический и геометрический смысл производной
Уравнение касательной к графику функции
Цель обучения 10.4.1.18 Находить производные постоянной функции и
степенной функции
10.4.3.1 Решать прикладные задачи, опираясь на
физический смысл производной
10.4.1.21 Знать и применять правила дифференцирования
10.4.1.25 Составлять уравнение касательной к графику
функции в заданной точке
10.4.1.23 Находить производные тригонометрических
функций
10.4.1.22 Находить производную сложной функции
Критерий оценивания Обучающийся:
Находит производную степенной функции
Применяет физический смысл производной при
решении задач
Применяет правила дифференцирования для
нахождения производной
Составляет уравнение касательной к графику
функции
Находит производную тригонометрической
функции и производную сложной функции
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 20 минут
Задания
1. Найдите производную функции: 𝑧(𝑦) =
5
𝑥
3
− 2√𝑦.
2. Два тела движутся прямолинейно: одно по закону
1 3
2
t s
, другое – по закону
t t t s
2 3
, где
) (t s
– путь в метрах,
t
– время в секундах. Определите момент
времени, когда скорости этих тел окажутся равными.
3. Дано уравнение кривой: 𝑔(𝑦) =
(𝑥+3)(𝑥−8)
𝑥
.
a) Не раскрывая скобок в числителе, найдите производную функции.
31
b) Используя результаты предыдущего действия, составьте уравнение касательной
к графику функции 𝑔(𝑦) =
(𝑥+3)(𝑥−8)
𝑥
при х=2.
4. Найдите производную функции: 2 sin(tg (3𝑦 + 𝜋)).
32
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Находит производную
степенной функции.
1
находит производную степени с
отрицательным показателем;
1
находит производную степени с
рациональным показателем;
1
Применяет физический
смысл производной
при решении задач.
2
находит производную функции; 1
использует физический смысл производной
и составляет уравнение;
1
решает уравнение; 1
определяет момент времени; 1
Применяет правила
дифференцирования
для нахождения
производной.
3a
использует правило дифференцирования
частного;
1
использует правило дифференцирования
произведения;
1
находит производную функции; 1
Составляет уравнение
касательной к графику
функции.
3b
находит значение производной в точке; 1
подставляет значения в формулу; 1
записывает уравнение касательной; 1
Находит производную
тригонометрической
функции и
производную сложной
функции.
4
использует правило нахождения
производной сложной функции;
1
находит производную синуса; 1
находит производную тангенса и
записывает ответ.
1
Итого:
15
33
Рубрика для предоставления информации родителям
по итогам суммативного оценивания за раздел «Производная»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Находит производную
степенной функции
Затрудняется в нахождении
производной степенной
функции
Допускает ошибки при нахождении
производной функции с
отрицательным / рациональным
показателем
Hаходит производную степенной
функции
Применяет физический
смысл производной при
решении задач
Затрудняется в применении
физического смысла
производной при решении
задач
Допускает ошибки при
использовании физического смысла
производной/ нахождении
производной функции/
вычислительные ошибки при
решении задач
Использует физический смысл
производной при решении задач
Применяет правила
дифференцирования для
нахождения производной
Затрудняется в применении
правил дифференцирования
Допускает ошибки в применении
правила дифференцирования
частного / произведения /
преобразовании выражений
Применяет правила
дифференцирования
Составляет уравнение
касательной к графику
функции
Затрудняется в составлении
уравнения касательной
Допускает ошибки в преобразованиях
/вычислениях при составлении
уравнения касательной
Применяет алгоритм
составления уравнения
касательной
34
Находит производную
тригонометрической функции
и производную сложной
функции
Затрудняется в нахождении
производной
тригонометрических функций,
сложной функции
Допускает ошибки при нахождении
производной тригонометрических
функций / преобразованиях при
нахождении производной сложной
функции
Находит производные
тригонометрических функций и
сложной функции
35
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ
Суммативное оценивание за раздел «Применение производной»
Тема Признаки возрастания и убывания функции
Критические точки и точки экстремума функции
Точки перегиба функции, выпуклость графика функции.
Исследование функции на выпуклость
Исследование функции с помощью производной и
построение графика
Наибольшее и наименьшие значения функции на отрезке
Цель обучения 10.4.1.26 Знать необходимое и достаточное условие
возрастания (убывания) функции на интервале
10.4.1.27 Находить промежутки возрастания (убывания)
функции
10.4.1.28 Знать определения критических точек и точек
экстремума функции, условие существования
экстремума функции
10.4.1.31 Знать определение точки перегиба графика
функции и необходимое и достаточное условие
выпуклости вверх (вниз) графика функции на
интервале
10.4.1.33 Исследовать свойства функции с помощью
производной и строить её график
10.4.3.3 Решать прикладные задачи, связанные с
нахождением наибольшего (наименьшего)
значения функции
Критерий оценивания Обучающийся:
Использует условие возрастания (убывания)
функции и находит промежутки монотонности
Использует определение точек экстремума
функции
Находит точки перегиба графика функции
Строит график функции
Решает задачи на нахождение наибольшего
(наименьшего) значения функции
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 30 минут
Задания
1. Функция
3
ax x x f
имеет минимальное значение, равное
3
2
, и максимальное
значение ,равное
3
2
на отрезке [-2;0].
(1) Найдите значение параметра a.
(2) Используя результаты предыдущего действия, найдите:
a) промежутки монотонности функции на отрезке [-3;3];
36
b) точки перегиба графика функции.
c) Изобразите точки пересечения графика функции с осями координат и
постройте эскиз графика функции на заданном промежутке.
2. На период распродаж меняется стоимость товара, соответственно и прибыль магазина.
Прибыль магазина может быть представлена как разность дохода и стоимости товара. На
период распродаж стоимость товара задается функцией 𝑔(𝑦) = 2,515𝑦 − 0,00015𝑦
2
, а
доход — = 7,390𝑦 − 0,0009𝑦
2
, где 0 ≤ 𝑦 ≤ 6500.
Какую максимальную прибыль может получить магазин в конце распродажи? Ответ
проверьте с помощью второй производной.
37
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Использует
определение точек
экстремума функции
1(1)
находит производную функции; 1
использует определение точек
экстремума для составления выражения;
1
находит значение параметра; 1
Использует условие
возрастания
(убывания) функции и
находит промежутки
монотонности
1(2a)
составляет выражение для определения
монотонности функции;
1
находит промежутки возрастания; 1
находит промежутки убывания; 1
Находит точки
перегиба графика
функции
1(2b)
находит вторую производную функции; 1
составляет и решает уравнение; 1
определяет точки перегиба; 1
Строит график
функции 1(2c)
изображает точки пересечения с осями
координат;
1
строит эскиз графика функции; 1
Решает задачи на
нахождение
наибольшего
(наименьшего)
значения функции
2
составляет функцию по условию задачи; 1
находит производную функции; 1
находит критические точки; 1
находит максимальное значение
функции;
1
использует вторую производную для
доказательства.
1
Итого
16
38
Рубрика для предоставления информации родителям
по итогам суммативного оценивания за раздел «Применение производной»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Использует условие
возрастания (убывания)
функции и находит
промежутки монотонности
Затрудняется в использовании
условия возрастания
(убывания) функции
Допускает ошибки при
использовании условий возрастания /
убывания функции / определении
промежутков возрастания / убывания
Использует условие возрастания
(убывания) функции
Использует определение
точек экстремума функции
Затрудняется в использовании
опредения точек экстремума
функции
Допускает вычислительные ошибки
при использовании определения
точек экстремума функции
Использует определение точек
экстремума функции
Находит точки перегиба
графика функции
Затрудняется в определении
точек перегиба графика
функции
Допускает ошибки при определении
точек перегиба графика функции
Определяет точки перегиба
графика функции
Строит график функции Затрудняется в построении
графика функции
Допускает погрешности в построении
графика функции
Строит график функции на
основании исследования
Решает задачи на нахождение
наибольшего (наименьшего)
значения функции
Затрудняется в решении задач
на определение максимума
(минимума)
Допускает ошибки при решении
задач на нахождение максимума
(минимума)/ вычислительные ошибки
Решает задачи на определение
максимума (минимума)
39
Суммативное оценивание за раздел «Случайные величины и их числовые
характеристики»
Тема Дискретные случайные величины
Числовые характеристики дискретных случайных
величин
Виды распределения дискретных случайных величин.
Закон больших чисел
Цель обучения 10.3.2.11 Составлять таблицу закона распределения
некоторых дискретных случайных величин
10.3.2.13 Вычислять математическое ожидание
дискретной случайной величины
10.3.2.14 Вычислять дисперсию и среднее квадратическое
(стандартное) отклонение дискретной
случайной величины
Критерий оценивания Обучающийся:
Использует закон распределения дискретных
случайных величин
Находит математическое ожидание дискретной
случайной величины
Вычисляет дисперсию и стандартное отклонение
дискретной случайной величины
Уровень мыслительных
навыков
Применение
Навыки высокого порядка
Время выполнения 20 минут
Задания
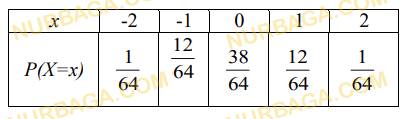
1. В результате опыта могут выпасть следующие значения: 1, 2, 3, 4, 5. Закон
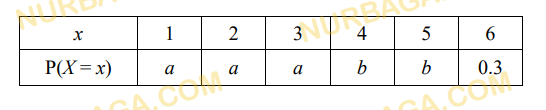
распределения вероятности этой случайно величины Х показан ниже в таблице.
x 1 2 3 4 5
P(X=x) 0.3 0.15 3p 2p 0.05
a) Найдите значение p.
b) Найдите вероятность P(x<3).
c) Вычислите математическое ожидание M(X.)
d) Вычислите значение 3∙M(X).
e) Вычислите дисперсию.
f) Вычислите стандартное отклонение случайной величины X.
2. Электронные устройства, работающие независимо друг от друга, на выходе производят
0, 1 или 3 вольт. Вероятность выхода каждого устройства равна
1
2
,
1
3
и
1
6
соответственно.
Случайная величина X обозначает сумму выходов, взятых двух любых устройств.
a) Постройте закон распределение вероятности случайной величины X.
[3]
b) В процессе 360 наблюдений найдите, в скольких случаях можно ожидать результат
в 1 вольт?
40
Критерий оценивания
№
задания
Дескриптор
Балл
Обучающийся
Использует закон
распределения
дискретных случайных
величин
1a
составляет выражение, используя закон
распределения;
1
находит значение параметра; 1
1b находит вероятность; 1
2a
определяет все значения случайно
величины;
1
находит вероятности минимум в трех
случаях;
1
находит вероятности во всех случаях; 1
Находит математическое
ожидание дискретной
случайной величины
1c
использует формулу математического
ожидания;
1
вычисляет математическое ожидание; 1
1d
использует свойства математического
ожидания;
1
2b
использует математическое ожидание; 1
находит ответ; 1
Вычисляет дисперсию и
стандартное отклонение
дискретной случайной
величины 1e
использует формулу дисперсии
(подставляет произведение суммы
квадратов значений случайных величин
на их вероятность);
1
использует формулу дисперсии
(подставляет математическое ожидание);
1
вычисляет дисперсию; 1
1f
находит стандартное отклонение. 1
Итого
15
*Учащимся разрешается использовать калькулятор при выполнении суммативной работы.
41
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Случайные величины и их числовые характеристики»
ФИ обучающегося _______________________________________________________________________________________________________
Критерий оценивания
Уровень учебных достижений
Низкий Средний Высокий
Использует закон
распределения дискретных
случайных величин
Затрудняется в составлении и
использовании закона
распределения дискретных
случайных величин
Допускает вычислительные ошибки
при составлении / использовании
закона распределения дискретных
случайных величин
Cоставляет и использует закон
распределения дискретных
случайных величин
Находит математическое
ожидание дискретной
случайной величины
Затрудняется в нахождении
математического ожидания
дискретной случайной
величины
Допускает вычислительные ошибки
при нахождении математического
ожидания дискретной случайной
величины
Находит математическое
ожидание дискретной случайной
величины
Вычисляет дисперсию и
стандартное отклонение
дискретной случайной
величины
Затрудняется в вычислении
дисперсии и стандартного
отклонения дискретной
случайной величины
Допускает вычислительные ошибки
при нахождении дисперсии /
стандартного отклонения дискретной
случайной величины
Вычисляет дисперсию и
стандартное отклонение
дискретной случайной величины
Подборка по базе: РП алгебра 8.doc, Программы для проведения инвестиционного анализа.pptx, Доклад на тему анализа Марса.docx, Pract. Теория экономического анализа.docx, Урок 3 марта 8 кл АЛГЕБРА.docx, Таблица сравнительного анализа по основным направлениям речевого, ЛИНЕЙНАЯ АЛГЕБРА.docx, ктп алгебра 9 3 часа.docx, Схема для анализа по посещению занятий.doc, курсовая работа 18.Роль финансового анализа в принятии управленч
Содержание
| Алгебра и начала анализа |
| Суммативное оценивание за раздел «Функция, ее свойства и график» |
| Суммативное оценивание за раздел «Тригонометрические функции» |
| Суммативное оценивание за раздел «Обратные тригонометрические функции» |
| Суммативное оценивание за раздел «Тригонометрические уравнения» |
| Суммативное оценивание за раздел «Тригонометрические неравенства» |
| Суммативное оценивание за раздел «Вероятность» |
| Суммативное оценивание за раздел «Многочлены» |
| Суммативное оценивание за раздел «Предел функции и непрерывность» |
| Суммативное оценивание за раздел «Производная» |
| Суммативное оценивание за раздел «Применение производной» |
| Суммативное оценивание за раздел «Случайные величины и их числовые характеристики» |
| Суммативное оценивание за 1 четверть |
| Суммативное оценивание за 2 четверть |
| Суммативное оценивание за 3 четверть |
| Суммативное оценивание за 4 четверть |
| Геометрия |
| Аксиомы стереометрии. Параллельность в пространстве |
| Перпендикулярность в пространстве |
| Перпендикулярность в пространстве |
| Прямоугольная система координат и векторы в пространстве |
| Прямоугольная система координат и векторы в пространстве |
| Суммативное оценивание за 1 четверть |
| Суммативное оценивание за 2 четверть |
| Суммативное оценивание за 3 четверть |
| Суммативное оценивание за 4 четверть |
| Форма анализа суммативного оценивание за учебный период (четверть) |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ФУНКЦИЯ, ЕЁ СВОЙСТВА И ГРАФИК»
| Тема | Функция и способы её задания. Преобразования графиков функций. Свойства функции. Дробно-линейная функция. Понятие сложной и обратной функции. |
| Цели обучения | 10.4.1.2 — уметь выполнять преобразования графика функции (параллельный перенос, сжатие и растяжение)
10.4.1.4 Уметь описывать по заданному графику функции её свойства: 1) область определения функции; 2) область значений функции; 3) нули функции; 4) периодичность функции; 5) промежутки монотонности функции; 6) промежутки знакопостоянства функции; 7) наибольшее и наименьшее значения функции; 9) ограниченность функции; 10) непрерывность функции; 11) экстремумы функции; 10.4.1.5 Определять свойства 10.4.1.6 Знать определение обратной функции и находить функцию, обратную заданной и знать свойство расположения графиков взаимно обратных функций; 10.4.1.7 — уметь распознавать сложную функцию f(g(x)) и составлять композицию функций. |
| Критерии оценивания | Обучающийся
Выполняет преобразования графика функции (параллельный перенос, сжатие и растяжение) Исследует свойства функции по ее графику Использует свойства и строит график дробно- линейной функции Применяет алгоритм нахождения обратной функции |
| Уровень мыслительных навыков | Применение
Навыки высокого порядка |
| Время выполнения | 35 минут |
ЗАДАНИЯ
| Оценивание заданий работы | ||||
| № задания | 1 | 2 | 3 | 4 |
| Количество баллов | 3 | 3 | 7 | 4 |
| Всего баллов | 17 баллов |
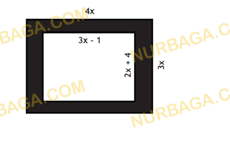
1 ВАРИАНТ
- Какие преобразования надо выполнить для построения графика функции
. Постройте график.
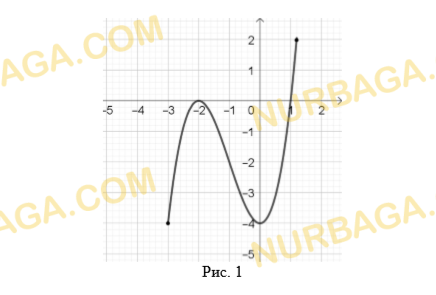
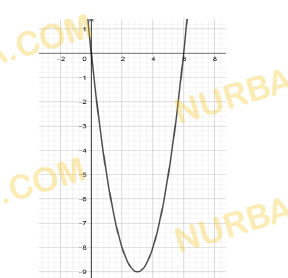
- Дан график функции.


a) Запишите область определения функции.
b) Найдите множество значений функции.
c) Определите максимальное значение функции на области определения;
d) Определите четность функции.
- Дробно-линейная функция задана уравнением: 𝑓(𝑥)=
.
a) Асимптоты функции имеют уравнения 𝑥=2,5, 𝑦=1,5. Найдите значение переменных a и b.
b) Используя результаты предыдущего действия:
- приведите функцию 𝑓(𝑥)=
к виду 𝑦=𝑛+
;
- найдите точки пересечения функции с осями координат;
- постройте график функции.
a) Найдите обратную функцию для функции 𝑓(𝑥)=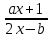
b) Как будет расположен график обратной функции относительно первоначальной?
2 ВАРИАНТ
- Какие преобразования надо выполнить для построения графика функции
. Постройте график.
- Дан график функции
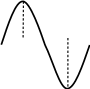

a) Запишите область определения функции.
b) Найдите множество значений функции.
c) Определите максимальное значение функции на области определения;
d) Определите четность функции.
- Дробно-линейная функция задана уравнением: 𝑓(𝑥)=
.
a) Асимптоты функции имеют уравнения 𝑥=-2, 𝑦=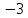
b) Используя результаты предыдущего действия:
- приведите функцию 𝑓(𝑥)=
к виду 𝑦=𝑛+
;
- найдите точки пересечения функции с осями координат;
- постройте график функции.
a) Найдите обратную функцию для функции 𝑓(𝑥)=
b) Как будет расположен график обратной функции относительно первоначальной?
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Выполняет преобразования графика функции (параллельный перенос, сжатие и растяжение) | 1 | Выполняет построение графика функции; | 1 |
| Записывает преобразования, применяемые при построении графика; | 2 | ||
| Определяет свойства функции по ее графику | 2 | находит область определения и область значения функции; | 1 |
| находит максимальное значение функции; | 1 | ||
| определяет четность (нечетность) функции; | 1 | ||
| Применяет свойства и строит график дробно-линейной функции | 3а | применяет вертикальную асимптоту; | 1 |
| применяет горизонтальную асимптоту; | 1 | ||
| 3b | выбирает способ преобразования; | 1 | |
| приводит функцию к заданному виду; | 1 | ||
| определяет точки пересечения функции с осью Ох; | 1 | ||
| определяет точки пересечения функции с осью Оу; | 1 | ||
| строит график функции; | 1 | ||
| Применяет алгоритм нахождения обратной функции | 4a | выполняет необходимые преобразования; | 1 |
| выражает одну переменную через другую; | 1 | ||
| находит обратную функцию; | 1 | ||
| 4b | определяет расположение графика обратной функции. | 1 | |
| Итого: | 17 |
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ФУНКЦИЯ, ЕЁ СВОЙСТВА И ГРАФИК»
ФИ ОБУЧАЮЩЕГОСЯ_______________________________________________________
| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Выполняет преобразования графика функции (параллельный перенос, сжатие и растяжение) | Затрудняется в преобразовании графика функции | Допускает ошибки при перечислении преобразований, применяемых при построении графика функции | Выполняет построение графика функции, применяя необходимые преобразования |
| Определяет свойства функции по ее графику | Затрудняется в
определении свойств функции по её графику |
Допускает ошибки при определении области значений /множества значений/нахождении максимального значения функции/четность(нечетность функции) | Определяет свойства функции по её графику |
| Применяет свойства и строит график дробно-линейной функции | Затрудняется в применении свойств и построении графика дробно-линейной функции | Допускает ошибки при определении области определения/ точек пересечения с осью Ох/ точек пересечения с осью Оу | Применяет свойства и строит график дробно-линейной функции |
| Применяет алгоритм нахождения обратной функции | Затрудняется при нахождении обратной функции | Допускает ошибки в преобразованиях при нахождении обратной функции | Находит обратную функцию и определяет расположение графика |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ»
| Тема | Тригонометрические функции, их свойства и графики. Построение графиков тригонометрических функций с помощью преобразований |
| Цели обучения | 10.2.3.1 — знать определения, свойства тригонометрических функций и уметь строить их графики;
10.2.3.2 — уметь строить графики тригонометрических функций с помощью преобразований; |
| Критерии оценивания | Обучающийся
Применяет свойства тригонометрических функций Строит график тригонометрических функций |
| Уровень мыслительных навыков | Применение
Навыки высокого порядка |
| Время выполнения | 30 минут |
ЗАДАНИЯ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 3 | 4 | 3 | 4 | 2 | 2 |
| Всего баллов | 18 баллов |
1 ВАРИАНТ
- Расположите данные числа
в порядке возрастания.
- Для функции
, найдите:
- область определения;
- область значений
- Не выполняя построений, найдите для функции
наименьший положительный период функции
- Постройте график тригонометрической функции
, определите:
- нули функции;
- асимптоты функции.
- Исследуйте функцию на четность
.
- Какое значение функция
принимает на
ровно один раз?
2 ВАРИАНТ
- Расположите данные числа
в порядке возрастания.
- Для функции
, найдите:
- область определения;
- область значений.
- Не выполняя построений, найдите для функции
наименьший положительный период функции
- Постройте график тригонометрической функции
определите:
- нули функции;
- асимптоты функции.
- Исследуйте функцию на четность
.
- Какое значение функция
принимает на
ровно один раз?
| Критерий оценивания | № задания | Дескриптор | Балл | |
| Обучающийся | ||||
| Использует свойства тригонометрических функций | 1 | использует формулы приведения; | 1 | |
| использует промежутки возрастания/ убывания синуса/ косинуса: тангенса/котангенса; | 1 | |||
| записывает числа в порядке возрастания; | 1 | |||
| Применяет свойства тригонометрических функций | 2 | использует область определения функции у=𝑡𝑔𝑥; |
1 | |
| указывает область определения заданной функции; | 1 | |||
| использует область значения функции у=𝑡𝑔𝑥; |
1 | |||
| указывает область значения заданной функции; | 1 | |||
| Использует свойства тригонометрических функций | 3 | указывает наименьший положительный период функции | 1 | |
| составляет выражение для нахождения периода функции; | 1 | |||
| находит наименьший положительный период заданной функции. | 1 | |||
| Строит график тригонометрической функции с помощью преобразований | 4 | строит график функции |
1 | |
| строит график заданной функции | 1 | |||
| находит нули функции | 1 | |||
| находит асимптоты функции | 1 | |||
| Использует свойства тригонометрических функций | 5 | использует свойства четности/нечетности функции | 1 | |
| исследует заданную функцию на четность | 1 | |||
| Применяет свойства тригонометрической функции | 6 | использует свойства монотонности | 1 | |
| находит значение для заданной функции на промежутке | 1 | |||
| Общий балл | 18 |
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ»
ФИ ОБУЧАЮЩЕГОСЯ ______________________________________________________
| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Использует свойства тригонометрических функций | Затрудняется в определении промежутков возрастания/ убывания функции, не точно записывает порядок убывания/ возрастания функции | Допускает ошибки при определении промежутков возрастания/убывания функции, не точно записывает порядок убывания/ возрастания функции | Использует промежутки возрастания/ убывания для функции;
записывает числа в порядке возрастания/убывания; |
| Применяет свойства тригонометрических функций | Затрудняется при определении области значения и определения заданной функции | Допускает ошибки при определении области значения и определения заданной функции | Находит область определения заданной функции; указывает область значения заданной функции; |
| Использует свойства тригонометрических функций | Затрудняется при составлении выражения для нахождения периода функции и нахождения наименьшего положительного периода заданной функции. | Допускает ошибки при составлении выражения для нахождения периода функции и нахождения наименьшего положительного периода заданной функции. | Составляет выражение для нахождения периода функции; находит наименьший положительный период заданной функции. |
| Строит график тригонометрической функции с помощью преобразований | Затрудняется при построении графика заданной функции, нахождении нули функции и при нахождении асимптоты функции | Допускает ошибки при построении графика заданной функции, нахождении нули функции и при нахождении асимптоты функции | Строит график заданной функции, находит нули функции, находит асимптоты функции |
| Использует свойства тригонометрических функций | Затрудняется при исследовании заданной функцию на четность | Допускает ошибки при исследовании заданной функцию на четность | Исследует заданную функцию на четность |
| Применяет свойства тригонометрической функции | Затрудняется при нахождении значения для заданной функции на промежутке | Допускает ошибки при нахождении значения для заданной функции на промежутке | Находит значение для заданной функции на промежутке |
Тригонометриялық функциялар
y =2+tgx функциясының графигін салыңыз
Смотреть ответ
Тригонометриялық теңдеулер
Тригонометриялық теңдеуді шешіңіз:
Смотреть ответ
Алғашқы функция және интеграл
Анықталмаған интегралдарды есептеңіз
Смотреть ответ
Функция және оның қасиеттері
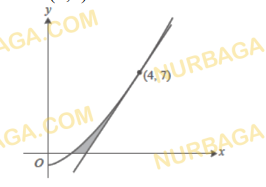
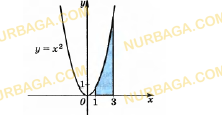
[-2;1]кесіндісінде f(x)= x² функциясы берілген 
Смотреть ответ
Тригонометриялық функциялар
Суреттегі мәліметтер бойынша анықтаңыз:
a) sin x
b) tgy
c) cos x*ctgy
d)tgx/siny
Смотреть ответ
Функция, ее свойства и график
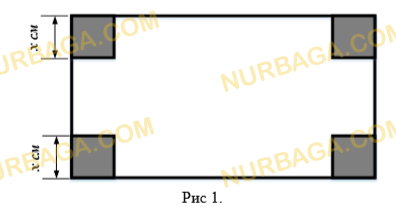
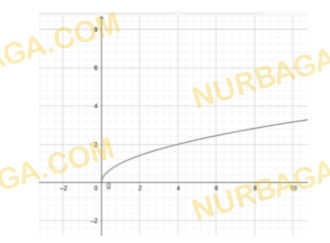
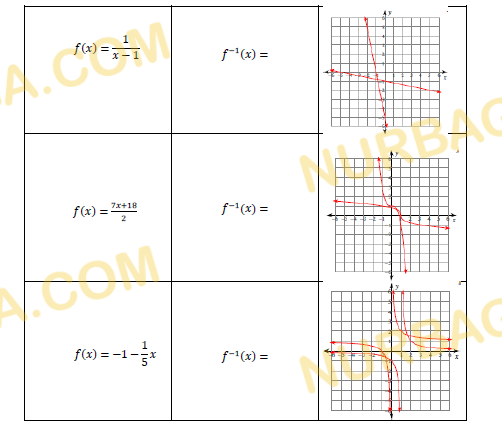
Выберите график той функции, которая обратима в своей области определения.
Смотреть ответ
Тригонометриялық функциялар
y = sin x +1 функциясының мәндер жиынын анықтаңыз
Смотреть ответ
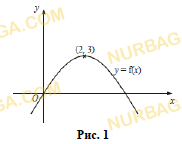
Функция, ее свойства и график
На рисунке изображен график функции y= f(x). Найдите значение выражения g (–2) + g (–4), если g (x) – функция, обратная для f(x).
Смотреть ответ
Функция, ее свойства и график
Для функций f(x)=3х +4 и g(x)= 2х– p, где p — постоянное число, найдите:
a) f(g(x));
b) g(f(x));
c) значение p, если f(g(x)) = g(f(x));
d) если p=3, найдите значение функции f(g(x)) для x= – 1.
Смотреть ответ
Кері тригонометриялық функциялар
Өрнекті ықшамдаңыз, жауабын инженерлік калькулятормен тексеріңіз
Смотреть ответ
Функция, ее свойства и график
a) g(f(x));
b) значение функции g(f(x)) при x=3;
Смотреть ответ
Кері тригонометриялық функциялар
y= arccos x функциясының графигін салыңыз
Смотреть ответ
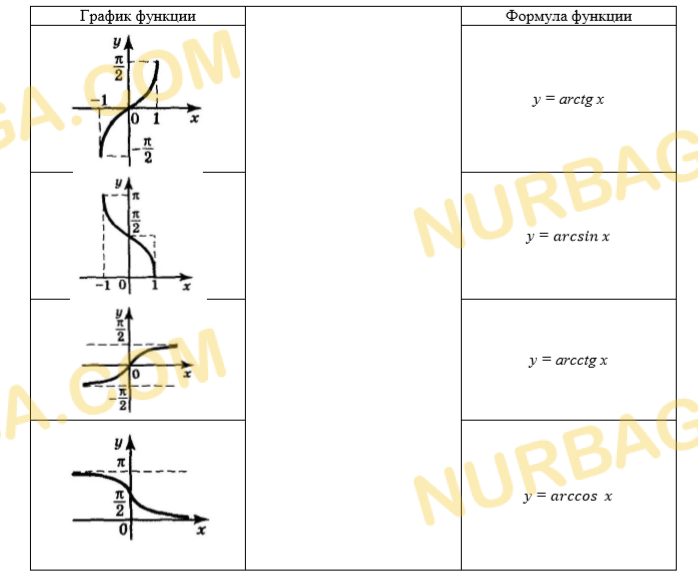
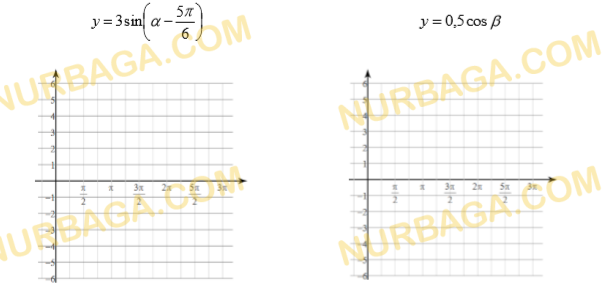
Тригонометрические функции
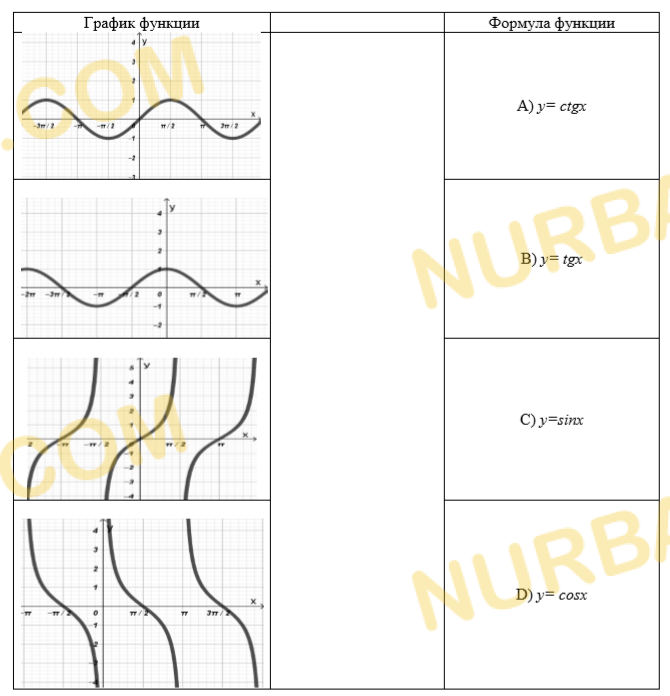
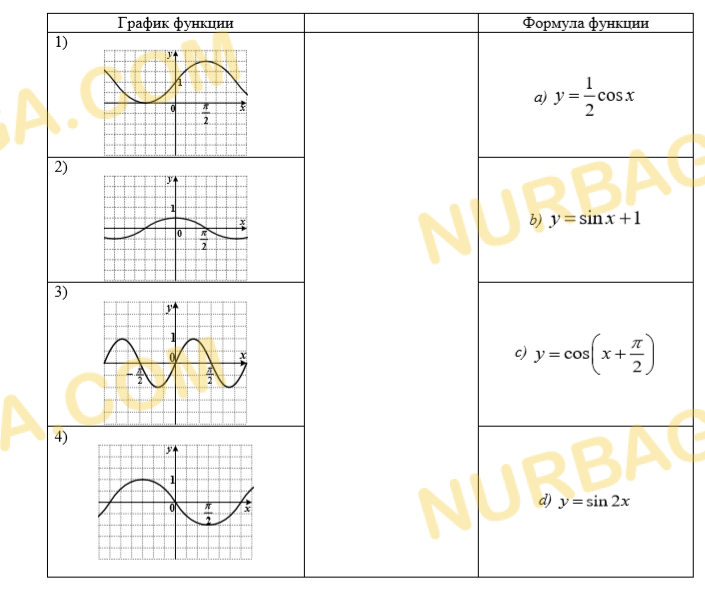
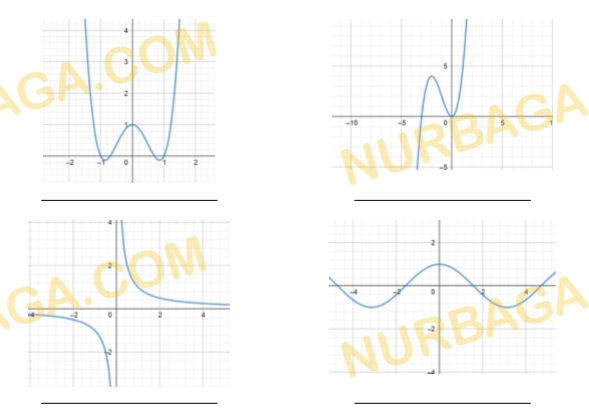
Установите соответствие между графиком функции и ее уравнением.
Смотреть ответ
Кері тригонометриялық функциялар
Қайық парасейлерді 300 метрлік арқанмен тартып келеді. Парасейлерсудың деңгейінен
100 метр биіктікте ұшып келеді. Арқан мен су деңгейінің арасындағы бұрыштың
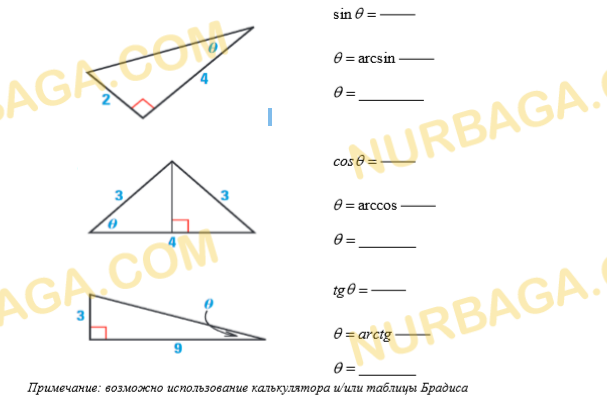
градустық өлшемін табыңыз. Жауабыңызды ондық үлеске дейін дөңгелектеңіз.
Смотреть ответ
Тригонометрические функции
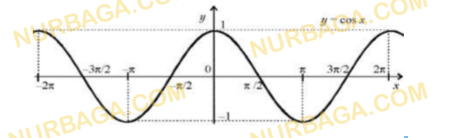
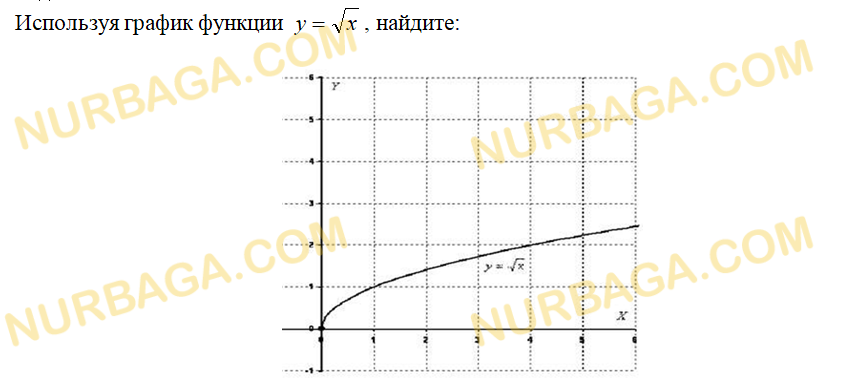
1) Используя график функции ? = cos?, укажите:
a) наибольшее значение функции;
b) нули функции;
c) монотонность на промежутке (0; π).
2) График данной функции:
a) симметричен относительно начала координат;
b) симметричен относительно оси ординат;
c) симметричен относительно оси абсцисс.
Смотреть ответ
Кері тригонометриялық функциялар
Төмендегі өрнектерді х-ке тәуелді алгебралық өрнек түрінде жазыңыз
a) sin(arccos x)
b) cos(2arccos x)
Смотреть ответ
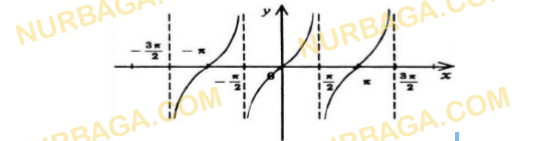
Тригонометрические функции
1) Используя график функции ? = tg?, определите:
a) значения х, при которых функция определена;
b) нули функции;
c) монотонность функции на промежутке (−π 2 ; π 2 ).
2) График данной функции:
a) симметричен относительно начала координат;
b) симметричен относительно оси ординат;
c) симметричен относительно оси абсцисс.
Смотреть ответ
Тригонометрические функции
Установите соответствие между графиком функции и ее уравнением.
Смотреть ответ
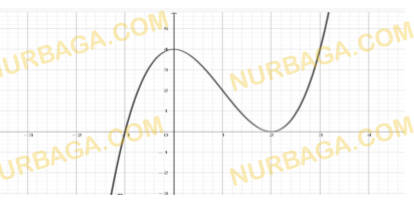
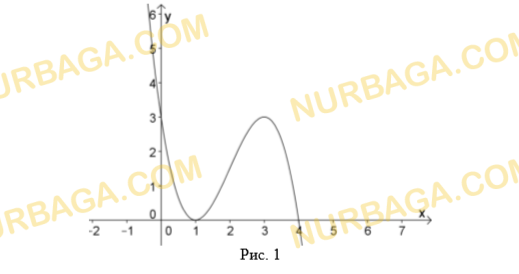
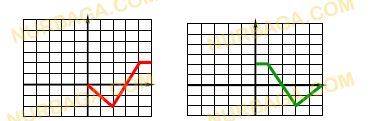
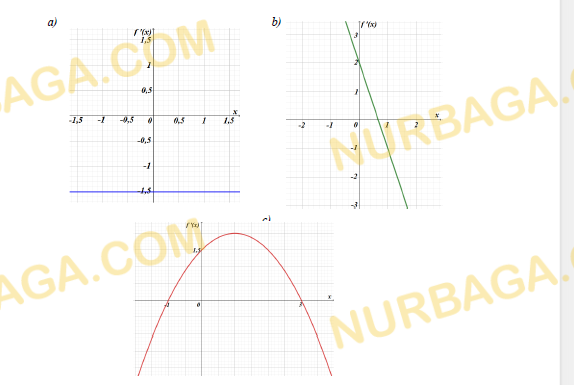
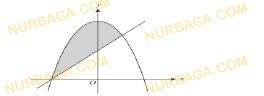
По заданному графику функции найдите:
а) промежутки убывания и возрастания функции;
b) нули функции.
Смотреть ответ
Тригонометриялық теңдеулер
Тригонометриялық теңдеуді шешіңіз:
Смотреть ответ
Тригонометрические функции
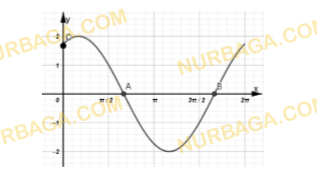
На рисунке показана часть графика функции ? = ?sin(? + ? /3), для 0 ≤ ? ≤ 2?, где k — постоянное число. Кривая пересекает ось ординат в точке C(0,√3),а ось абсцисс в точках ?(?,0) и ?(?,0).
a) Покажите, что k=2;
b) Найдите значения p и q.
Смотреть ответ
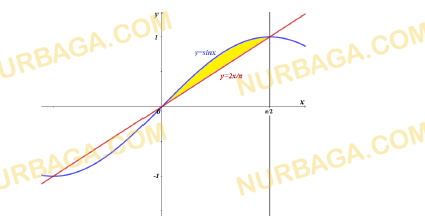
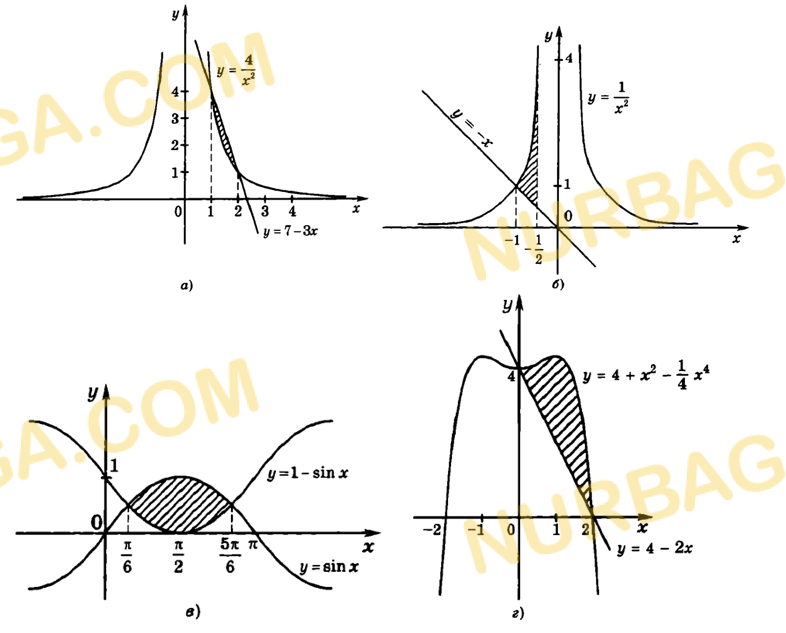
a) Постройте график функции y = sinx на промежутке
b) Постройте график функции
Смотреть ответ
Тригонометрические функции
Дана функция у=t??.
a) Запишите цепочку преобразований, с помощью которой из этого графика можно получить график функции у=−t?(2? − ?/ 3 ) .
b) Постройте график функции у=−t?(2? − ? /3 ) .
Смотреть ответ
Тригонометрические функции
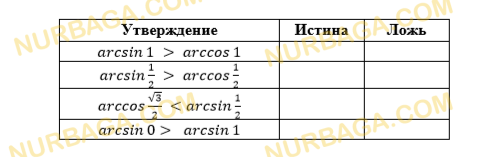
Установите истинность или ложность утверждений
Смотреть ответ
Тригонометриялық теңдеулер
a) cos2x +cos4x =0
b) sin 2xsin6x = cos xcos3x
Смотреть ответ
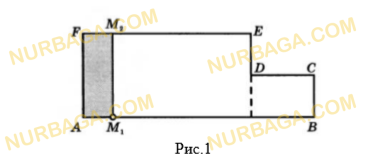
Прямые х = 3, у = 2 являются асимптотами дробно-линейной функции
Найдите значения a и d и постройте эскиз данного графика.
Смотреть ответ
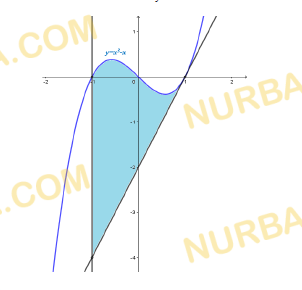
Даны функции:
Найдите множество значений x, удовлетворяющих неравенству:
Смотреть ответ
Тригонометриялық теңдеулер
a) Қосымша аргумент енгізу әдісі арқылытүріне келтіруге болатынын көрсетіңіз.
b) теңдеуін шешіңіз
Смотреть ответ
Обратные тригонометрические функции
Найдите значение выражения:
Смотреть ответ
Тригонометриялық теңдеулер
Теңдеуді универсал алмастыру әдісі арқылы шешіңіз:
Смотреть ответ
Обратные тригонометрические функции
Постройте график функции y = arctg 2x.
Смотреть ответ
Тригонометриялық теңдеулер
Тригонометриялық теңдеулер жүйесін шешіңіз:
Смотреть ответ
Обратные тригонометрические функции
Установите соответствие между графиком функции и ее уравнением.
Смотреть ответ
Обратные тригонометрические функции
a) Для каждой функции найдите область определения и множество значений:
b) Постройте графики данных функций.
Смотреть ответ
Тригонометриялық теңдеулер
ңсіздігі берілген.
a) берілген теңсіздіктікелтіруге болатынын көрсетіңіз;
b)теңсіздігін шешіңіз
Смотреть ответ
Обратные тригонометрические функции
Докажите тождество:
Смотреть ответ
Ықтималдық
a) Сыныптағы 12 оқушыны төрт-төрттен үш топқа бөлу керек. Мұны неше әртүрлі
тәсілмен жасауға болады?
b) Командадағы 20 адамнан басшы, оның оң қолы және хатшы болатын үш адамды
таңдау керек. Мұны неше әртүрлі тәсілмен жасауға болады?
c) Дөңгелек дастарханның бойына 6 адамды неше әртүрлі тәсілмен отырғызуға
болады?
Смотреть ответ
Ықтималдық
Компьютер құпиясөзі 5 әртүрлі латын әрпі және 3 әртүрлі цифрдан тұрады. Құпиясөзді
неше әртүрлі тәсілмен таңдауға болады?
Смотреть ответ
Ықтималдық
a) Дүкенде 3 ойыншық түрі сатылады. Осы дүкеннен 4 ойыншық алу керек болса, оны барлығы неше әртүрлі тәсілмен таңдауға болады?
b) Дүкенде 4 ойыншық түрі сатылады. Осы дүкеннен 3 ойыншық алып, оны Арман, Марат және Жанияға беру керек. Мұны барлығы неше әртүрлі тәсілмен жасауға болады?
c) 5 ақ және 3 қызыл бірдей шарларды бір қатарға қою керек. Мұны неші әртүрлі тәсілмен жасауға болады
Смотреть ответ
Ықтималдық
М А Н Д А Р И Н
a) сөзінің әріптерін ауыстыру арқылы неше әртүрлі сөз алуға болады?
б) сөзінің дауысты дыбысты әріптері бірге тұратындай неше әртүрлі сөз алуға болады?
с) сөзінің дауысты дыбысты әріптері де, дауыссыз дыбысты әріптері де бірге тұратындай неше әртүрлі сөз алуға болады?
Смотреть ответ
Ықтималдық
a) Ақтілек төрт таңбалы натурал сан жасырды. Оның жасырған санының құрамында 8 цифры бар болуының ықтималдығын табыңыз.
b) Мақсаттың ойлаған саны 4000-нан артық емес. Мақсаттың жасырған санының құрамында 8 және 9 цифрларының ең болмағанда біреуі болуының ықтималдығын табыңыз.
Смотреть ответ
Ықтималдық
Есептеңіз:
a) жауабын мыңдық үлеске дейін жуықтаңыз.
b) жауабын бүтінге дейін жуықтаңыз
Смотреть ответ
Ықтималдық
Келесі кездейсоқ шамалардың қайсысы дискретті кездейсоқ шама болып табылады?
a) Кездейсоқ шама кездейсоқ алынған оқушының бойы;
b) Кездейсоқ шама кездейсоқ алынған оқушының жасы;
c) Кездейсоқ шама кездейсоқ алынған оқушының салмағы;
d) Кездейсоқ шама кездейсоқ алынған оқушының 100 метр қашықтыққа жүгіру уақыты;
e) Кездейсоқ шама кездейсоқ алынған оқушының 100 метр қашықтыққа жүгіру уақытының нормативке сәйкес келуі;
f) Кездейсоқ шама кездейсоқ алынған оқушының 100 метр қашықтыққа жүгіру жарысынан алған орны.
Смотреть ответ
Вероятность
Шесть школьников случайным образом рассаживаются на скамейку.
Найдите:
a) количество всех возможных комбинаций.
b) количество комбинаций, когда Коля и Оля будут сидеть рядом.
c) вероятность того, что Коля и Оля будут сидеть рядом.
Смотреть ответ
Ықтималдық
Жәшікте 5 қара, 8 ақ және 7 қызыл орамал бар. Кездейсоқ алынған орамалдың:
a) ақ болуының ықтималдығын табыңыз;
b) қызыл болмауының ықтималдығын табыңыз;
c) сары болмауының ықтималдығын табыңыз
Смотреть ответ
Ықтималдық
0, 2, 3, 5, 6, 7 цифрлары жазылған алты карточка берілген. Кездейсоқ алынған үш карточка арқылы үш таңбалы сан жасалды. Жасалынған үштаңбалы санның жұп болуының ықтималдығын табыңыз.
Смотреть ответ
Ықтималдық
Жансұлтан, кездейсоқ алынған, екі таңбалы санды жасырды . Оның жасырған саны 2-ге де, 3-ке де бөлінбеуінің ықтималдығы қандай?
Смотреть ответ
Ықтималдық
Мергеннің 5 оғы бар. Әр атқанда, оның нысанаға тигізу ықтималдығы 0,6-ге тең. Мерген нысанаға бір рет тигізгенге дейін атады. Х кездейсоқ шамасы мергеннің атқан оғының саны деп алып, Х кездейсоқ шамасының үлестірім заңын жазыңыз.
Смотреть ответ
Ықтималдық
Екі атқыштың нысанаға дәл тигізуінің ықтималдығы 0,9 және 0,8. Екі атқыш бір-бірден оқ атты. Келесі оқиғалардың ықтималдығын табыңыз:
a) Нысанаға екі оқтың да тиуі;
b) Нысанаға тек қана бір оқтың тиуі;
c) Нысанаға оқтың тиуі;
d) Нысанаға бір ғана оқтың тигені белгілі болса, ол оқтың екінші атқыштың атуы.
Смотреть ответ
Ықтималдық
3 артилериялық қарудың көздеген нысанаға тигізуінің ықтималдықтары сәйкесінше 0,7; 0,8 және 0,9-ға тең. Жүріп келе жатқан танк, бір оқ тигенде тоқтауының ықтималдығы 0,3, ал екі оқ тигенде тоқтауының ықтималдығы 0,6, ал үш оқ тисе танк толығымен істен шығады. Егер артилериялық қарулар бір-бірден оқ атқан болса, олардың жүріп келе жатқан танкті тоқтатуының ықтималдығын табыңыз.
Смотреть ответ
Ықтималдық
Есеп: «Қорапта 10 ақ, 20 қара шарлар бар. Кездейсоқ кезекпен алынған екі шардың екеуі де ақ болуының ықтималдығын табыңыз».
Жоғарыдағы есепте Бернулли формуласын қолдануға болмайтынын түсіндіріңіз.
Смотреть ответ
Ықтималдық
Мергенның нысанаға тигізуінің ықтималдығы 0,8. Мергеннің 10 оқтың жетеуін тигізуінің ықтималдығын табыңыз
Смотреть ответ
Ықтималдық
Компанияда 8 адам жұмыс жасайды. Әр жұмыскер әртүрлі себептермен, орта есеппен айына 2 күн жұмысқа келмей қалады. Жұмыс күні сәтті өтуі үшін жұмыста кем дегенде 7 адам болуы керек. Бес жұмыс күнінің төртеуі сәтті өтуінің ықтималдығын табыңыз.
Смотреть ответ
Кездейсоқ шамалар және олардың сандық сипаттамалары
Төмендегі оқиғалардың қайсысы кездейсоқ шама болады?
A) Квадраттың қабырғаларының саны.
B) Берілген шеңбердің центрі болатын нүкте. C) x=3 санының 5x-15=0 теңдеуінің түбірі болуы. D) Қабырғалары 3, 4, 5 болатын үшбұрыштың ауданы.
Е) Қабырғалары 4, 5 болатын параллелограммның ауданы
Смотреть ответ
Дискретті кездейсоқ шамалар
Төмендегі оқиғалардың қайсысы дискретті кездейсоқ шама болады?
A) Қабырғасы 4-ке тең ромбтың ауданы.
B) Оқушының бүгін алған бағасының саны. C) Кітаптан алынған парақтағы әріптер саны. D) Оқушының журналдағы орны
Е) Оқушының бойы
Смотреть ответ
Дискретті кездейсоқ шамалар
Қорапта 10 ақ, 20 қара шарлар бар. Кездейсоқ екі шар алынды. Х – кездейсоқ шамасы алынған шардың ақ болу деп есептеп, Х кездейсоқ шамасының үлестірім заңын құрыңыз.
Смотреть ответ
Функция және оның қасиеттері
Келесі тұжырымдардың қайсысы дұрыс?
A) Кез-келген адам үшін оның атасын сәйкес қоятын бейнелеу – функция болады;
B) Кез-келген адам үшін оның әкесін сәйкес қоятын бейнелеу – функция болады;
C) Кез-келген адам үшін оның баласын сәйкес қоятын оператор – функция болады;
D) Кез-келген адам үшін оның сүйікті тамағын сәйкес қоятын оператор – функция болады
Смотреть ответ
Кездейсоқ шамалар
Тиын төрт рет лақтырылды. Х-кездейсоқ шамасы түскен гербтердің саны.
a) Х кездейсоқ шамасының математикалық күтімін табыңыз;
b) M(5X-7)мәнін табыңыз.
Смотреть ответ
Функция және оның қасиеттері
Келесі тәуелділіктердің қайсысы функция емес?
A) Қабырғаларының ұзындығы белгілі үшбұрыш үшін – оның периметрі;
B) Қабырғаларының ұзындығы белгілі үшбұрыш үшін – оның ауданы;
C) Қабырғаларының ұзындығы белгілі төртбұрыш үшін – оның периметрі;
D) Қабырғаларының ұзындығы белгілі төртбұрыш үшін – оның ауданы
Смотреть ответ
Дискретті кездейсоқ шамалардың сандық сипаттамалары
Ойын сүйегі үш рет лақтырылды. Х – кезедйсоқ шамасы түскен ұпайдың жай сан болуы.
a) Х-кездейсоқ шамасының математикалық күтімін табыңыз;
b) Х-кездейсоқ шамасының орташа квадраттық ауытқуын есептеңіз
Смотреть ответ
Функция, ее свойства и график
Среди зависимостей, предложенных ниже, найдите функциональные:
A) зависимость площади квадрата от его стороны;
B) зависимость периметра квадрата от его стороны;
C) зависимость количества купленных конфет от размера сумки;
D) зависимость расстояния, пройденного за одно и тоже время от длины ног
Смотреть ответ
Функция және оның қасиеттері
Арман, Көркем, Айша және Махаббат төртеуінің жастары өз есімдерінің әріптер санымен бірдей. Осы сәйкестік функция бола алатынын түсіндіріңіз және басқа түрде (аналитикалық, графиктік, таблица арқылы) көрсетіңіз
Смотреть ответ
Функция, ее свойства и график
На рисунке 1 изображен шестиугольник ABCDEF, составленный из двух прямоугольников, причем AB=10, BC=CD=3, DE=2
Используя условие задачи, выразите площадь S(x) закрашенной части многоугольника ABCDEF, как функцию от длины отрезка AM1= x
Смотреть ответ
Дискретті кездейсоқ шамалардың үлестірім түрлері. Үлкен сандар заңы
Мергеннің нысанаға тигізуінің ықтималдығы 0,5. Оның бес оғы бар және ол нысанаға тигізгенше атады. Х-кездейсоқ шамасы атылған оқтардың саны деп алып, Х-кездейсоқ шамасының геомериялық үлестірімінзаңын құрыңыз.
Смотреть ответ
Функция және оның қасиеттері
y =x ²функциясының графигін {2;3} векторына параллель көшіргенде қай
функцияның графигі шығады?
Смотреть ответ
Дискретті кездейсоқ шамалардың үлестірім түрлері. Үлкен сандар заңы
Тиын төрт рет лақтырылды. Х-кездейсоқ шамасы тиынның герб түсу саны. Х-кездейсоқ шамасының биномдық үлестірімін заңын құрыңыз.
Смотреть ответ
Функция, ее свойства и график
Открытая сверху коробка объемом 36 дм3 имеет форму прямоугольного параллелепипеда с отношением сторон основания 1:2. Выразите высоту этой коробки как функцию, зависящую от стороны основания.
Смотреть ответ
Функция және оның қасиеттері
A(4;2) нүктесі функциясының графигіне тиісті. Берілген функцияның графигін
функциясының графигіне түрлендіргенде A нүктесінің координатасы
қалай өзгереді?
A) (5;8)
B) (10;11)
C) (14;3)
D) (3;8)
Смотреть ответ
Дискретті кездейсоқ шамалардың үлестірім түрлері. Үлкен сандар заңы
Қорапта 6 ақ 14 қара шарлар бар. Қораптан кездейсоқ 5 шар алынды. Х-кездейсоқ шамасы шыққан шардың ақ шар болуы. Х-кездейсоқ шамасының гипергеомериялық үлестірімін заңын құрыңыз.
Смотреть ответ
Дискретті кездейсоқ шамалардың үлестірім түрлері. Үлкен сандар заңы
Компьютер 1, 2, 3, 4 цифрлары арқылы 1000 таңбалы сан алды. Үлкен сандар туралы заңды пайдаланып, осы санның цифрларының қосындысын табыңыз.
Смотреть ответ
Функция және оның қасиеттері
Үзіліссіз y = f(x)функциясының графигі Оу осьіне қатысты симметриялы екені
белгілі. Төмендегі тұжырымдардың ішінен берілген функцияға сәйкес келетінін
деп белгілеңіз:
A) функцияның анықталу облысы [-a;a] түрінде болады;
B) функцияның мәндер жиыны [-a;a] түрінде болады;
C) функцияның экстремумдар саны жұп болады;
D) функция жұп функция болады;
E) функция тақ функция болады;
F) функция бірсарынды бола алмайды.
Смотреть ответ
Функция, ее свойства и график
На рисунке 1 показан эскиз кривой y=f(x). Кривая пересекает ось Ох в точке (4;0), касается этой оси в точке (1;0) и пересекает ось Оу в точке (0;3).
Постройте график кривой:
a) ? = ?(? +1)
b) ? = 2?(?)
c) ? = ?(1 2 ?)
Запишите точки пересечения каждого графика с осями координат.
Смотреть ответ
Функция және оның қасиеттері
Суретте y=f (x) функциясының графигі берілген
Берілген функцияның:
A) анықталу облысын, мәндер жиынын анықтаңыз;
B) жұп-тақтығын және периодтылығын анықтаңыз;
C) нөлдерін және функцияның таңбатұрақтылық аралықтарын анықтаңыз;
D) бірсарындылық аралықтарын, экстремумдарын және ең үлкен және ең кіші мәндерін табыңыз.
Смотреть ответ
Функция, ее свойства и график
A) растяжение графика относительно оси ординат;
B) параллельный перенос графика вдоль оси абсцисс на 3 единицы влево;
C) растяжение графика относительно оси ординат, параллельный перенос графика вдоль оси абсцисс на 3 единицы влево;
D) сжатие графика относительно оси ординат, параллельный перенос графика вдоль оси абсцисс на 3 единицы влево;
E) растяжение графика относительно оси абсцисс, параллельный перенос графика вдоль оси абсцисс на 3 единицы влево.
Смотреть ответ
Функция және оның қасиеттері
функциясы берілген.
a) функцияның асимптоталарын, анықталу облысы мен мәндер жиынын анықтаңыз;
b) функция мәні 3-ке тең бола алмайтынын түсіндіріңіз;
c) функцияның графигін салыңыз.
Смотреть ответ
Функция, ее свойства и график
Сколько целых чисел входит в область определения функции
Смотреть ответ
Функция және оның қасиеттері
Берілген функциялардың кері функциясын табыңыз
Смотреть ответ
Функция, ее свойства и график
На рисунке 1 изображен график функции y=f(x). Область ее определения-отрезок [-3;1,2].
Найдите:
a) нули функции;
b) промежутки знакопостоянства функции;
c) экстремумы функции;
d) промежутки убывания и возрастания функции;
e) наибольшее и наименьшее значение функции;
f) область значений функции.
Смотреть ответ
Функция және оның қасиеттері
1функциясына кері функция табылмайтынын түсіндіріңіз
Смотреть ответ
Функция, ее свойства и график
Укажите графики четной функции, изображенные на рисунке:
Смотреть ответ
Функция, ее свойства и график
Для функции
a) асимптоты;
b) точки пересечения с осями координат;
c) любые две точки, принадлежащие графику функции. Используя эти данные, постройте график функции.
Смотреть ответ
Функция және оның қасиеттері
y = f (x) функциясы мен y =w(x) функциялары өзара кері функциялар және
f (0) = 2; f (1) =1; f (2) =3 . w(1),w(2) мәндерін табыңыз
Смотреть ответ
Функция және оның қасиеттері
функциялары берілген. Келесі күрделі
функцияларды табыңыз:
a) g f (x))
b) k (f (x))
c) f (k 9g(x)))
Смотреть ответ
Функция, ее свойства и график
Дробно-линейная функция задана уравнением: 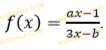
уравнения ? = 2, ? = 1.
a) Найдите значение переменных a и b;
c) Найдите точки пересечения функции с осями координат;
d) Постройте график функции.
Смотреть ответ
Функция және оның қасиеттері
y =f (s(x)) күрделі функциясы берілген. y = f (x), y = s(x)функцияларын табыңыз
Смотреть ответ
a) Постройте график функции
b) Применяя преобразования графика функции, постройте в той же системе координат
график функции y = 6 sin 2x + 3 на промежутке
Смотреть ответ
Найдите функцию, обратную функции 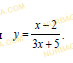
полученной функции.
Смотреть ответ
Функция, ее свойства и график
Среди зависимостей, предложенных ниже, найдите функциональные:
A) Зависимость площади квадрата от его стороны
B) Зависимость периметра квадрата от его стороны
C) Зависимость количества купленных конфет от размера сумки
D) Зависимость расстояния, пройденного за одно и тоже время от длины ног
Смотреть ответ
Функция, ее свойства и график
Из прямоугольного листа жести размером 3050 см по углам вырезали квадраты со стороной x см и из полученной заготовки в форме «креста» согнули коробку прямоугольной формы высотой, равной x см (Рис 1). Выразите объем полученной коробки как функцию от x.
Смотреть ответ
Функция, ее свойства и график
На рисунке 1 показан эскиз кривой y=f(x). a) Постройте график кривой ) 2( xfy . b) Запишите точки пересечения с осью Ох.
Смотреть ответ
Функция, ее свойства и график
Запишите цепочку преобразований для построения графика функции
Смотреть ответ
Функция, ее свойства и график
На рисунке изображен график функции
Укажите: a) область значений функции; b) нули функции; c) промежутки знакопостоянства функции; d) промежутки убывания и возрастания функции; e) наибольшее и наименьшее значение функции f) экстремумы функции;
Смотреть ответ
Функция, ее свойства и график
Укажите, какие из предложенных графиков будут являться графиками четных или нечетных функций:
Смотреть ответ
Функция, ее свойства и график
Используя определение, исследуйте на четность и нечетность следующие функции:
Смотреть ответ
Функция, ее свойства и график
Функции f и g определены следующим образом:
Смотреть ответ
Функция, ее свойства и график
Постройте график обратной функции для данной функции:
Смотреть ответ
Функция, оның қасиеттері және графигі
Бөліктеп берілген функцияның графигін салыңыз және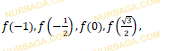
Смотреть ответ
Тригонометрические функции
Определите, какие из представленных ниже утверждений описывают график функции xy sin x/y cos x или оба графика одновременно. Поставьте в соответствующих столбцах. Утверждение
Смотреть ответ
Функция, оның қасиеттері және графигі
у=?² функциясының графигін пайдаланып, төмендегі түрлендірулерді орындаңыз
Смотреть ответ
Функция, оның қасиеттері және графигі
?=1/? функциясының графигін пайдаланып, төмендегі түрлендірулерді орындаңыз:
Смотреть ответ
Тригонометрические функции
Выберите функции, графики которых могут быть получены отражением графика функции
Постройте их в одной системе координат
Смотреть ответ
Функция, оның қасиеттері және графигі
Функцияның анықталу облысын табыңыздар:
Смотреть ответ
Тригонометрические функции
Найдите амплитуду, период в радианах, вертикальный сдвиг, минимальное и максимальное значение. Постройте график.
Смотреть ответ
Функция, оның қасиеттері және графигі
1. Функцияның жұп-тақтығын анықтаңыз
Берілген графиктерді 1) жұп функцияның графиктеріне дейін,
2) тақ функцияның графиктеріне дейін толықтырыңыз
Смотреть ответ
Тригонометрические функции
Заполните пропуски, используя определение тригонометрических функций. Вычислите угол Ө . Ответ округлите до трех значащих цифр.
Смотреть ответ
Функция, оның қасиеттері және графигі
?=?(?) функциясы тақ және периодты екені белгілі, периоды Т = 8. Егер ?(−5)=3,2 болса, онда ?(891) мәнін табыңыз
Смотреть ответ
Функция, оның қасиеттері және графигі
Берілген функциялар өзара кері функциялар бола алады ма? Тексеріңіз:
Смотреть ответ
Функция, оның қасиеттері және графигі
Берілген функциялардың кері функцияларын табыңыз
Смотреть ответ
Функция, оның қасиеттері және графигі
Берілген функциялардың кері функцияларын табыңыз және графиктерімен сәйкестендіріңіз
Смотреть ответ
Функция, оның қасиеттері және графигі
Берілген амалдарды орындаңыз
Смотреть ответ
Функция, оның қасиеттері және графигі
Күрделі функцияны өрнектеңіз
Смотреть ответ
Тригонометриялық функциялар
Тригонометриялық функциялардың анықталу облысын табыңдар
Смотреть ответ
Тригонометриялық функциялар
Тригонометриялық функциялардың мәндерінің жиынын табыңдар
Смотреть ответ
Тригонометриялық функциялар
Тригонометриялық функциялардың ең кіші оң периодтарын табыңдар
Смотреть ответ
Определите, какое из приведенных уравнений является функцией на множестве
действительных чисел.
Смотреть ответ
На рисунке 1 изображена часть графика функции y = f (x) . Наибольшее значение функция
достигает в точке с координатами (2;3).
Для заданных ниже функций, запишите координаты точек, в которых они достигают
наибольшего значения.
a) y = f (x -3)
b) y = 3 f (x)
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы

Смотреть ответ
Сила в 60 Н растягивает пружину на 3 см. Первоначальная длина пружины равна 16 см. Какую работу нужно совершить, чтобы растянуть её до 20 см?
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
теңдігі орындалатындай, k-ның натурал мәнін табыңыз
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
a) y = x ³-x 3 функция графигінің х =1 нүктесіне жүргізілген жанаманың теңдеуі
y =2x -2 болатынын көрсетіңіз.
b) Суретте бейнеленген боялған бөліктің ауданын табыңыз
Смотреть ответ
В ходе эксперимента с разведением морских свинок были получены следующие данные, представленные в таблице.
Найдите:
а) среднее значение.
b) моду и медиану.
c) дисперсию и стандартное отклонение
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
сызықтары және абсцисса осімен шектелген фигураның
ауданын табыңыз, жауабын жүздік үлеске дейінгі дәлдікпен жуықтаңыз
Смотреть ответ
Гистограмма и таблица дают информацию о возрасте людей, живущих в некоторой
местности.
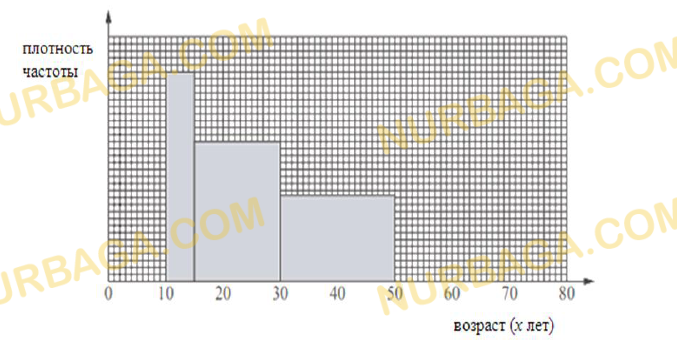
а) Используя гистограмму, дополните таблицу.
b) Используя таблицу, дополните гистограмму.
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
Суретте 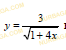
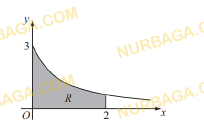
Смотреть ответ
На рисунке 1 показан график кривой, уравнение которой 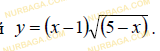
ограничена кривой, осью абсцисс и промежутком 1≤x≤5
а) Найдите 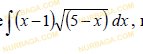
b) Вычислите точное значение площади фигуры R.
Закрашенная часть вращается вокруг оси ОХ на 360º, образуя тело вращения.
с) Найдите точное значение объёма тела вращения.
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
f(x)=x²-2x+1 функциясы берілген.
a) f ‘(x) табыңыз.
b) f (x) және f ‘(x) функция графиктерімен шектелген фигураның ауданын
табыңыз.
c) жауабын жүздік үлеске дейінгі дәлдікпен жуықтаңыз.
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
φ(x)= x + 2 , g(x) = 1 функциялары берілген.
i) f (x) =φ(x)- g(x) функциясын анықтаңыз;
ii) у = f (х), х = 0 және х = 2 сызықтарымен шектелген қисық сызықты трапецияны
абсцисса осімен айналдырғанда пайда болған дененің көлемін табыңыз
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
Суретте бейнеленген боялған бөлікті Ох осімен айналдырғанда пайда болған
дененің көлемін табыңыз.
b) жауабын жүздік үлеске дейінгі дәлдікпен жуықтаңыз
Смотреть ответ
Первообразная и интеграл
Покажите, что функция F(x) является первообразной функции f (x) на числовой прямой:
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
Смотреть ответ
Первообразная и интеграл
Напишите общий вид первообразных функции:
Смотреть ответ
Первообразная и интеграл
Непрерывная функция S(x) является первообразной для функции s(x) на множестве всех
действительных чисел. Найдите промежутки монотонности функции S(x), если
Смотреть ответ
Первообразная и интеграл
Найдите неопределенный интеграл, используя метод замены переменной:
Смотреть ответ
Первообразная и интеграл
Для заданного интеграла 
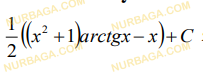
функций.
Смотреть ответ
Первообразная и интеграл
Найдите площадь криволинейной трапеции, ограниченной:
Смотреть ответ
Первообразная и интеграл
Вычислите интеграл, используя формулу Ньютона-Лейбница:
Смотреть ответ
Первообразная и интеграл
На рисунке показан график кривой 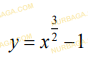
(1;0), и касательная к кривой в точке (4;7).
a) Покажите, что
b) Найдите площадь фигуры, ограниченной заданной кривой 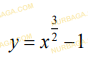
и осью Ох.
Смотреть ответ
Первообразная и интеграл
Найдите площадь фигуры, ограниченной линиями:
Смотреть ответ
Первообразная и интеграл
1.Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной
линиями
Смотреть ответ
Первообразная и интеграл
Определите объем твердого тела, полученного вращением области, ограниченной 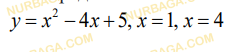
Смотреть ответ
Первообразная и интеграл
Два тела начали двигаться одновременно из одной точки в одном направлении по
прямой. Первое тело движется со скоростью второе — со скоростью
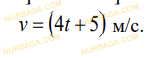
Смотреть ответ
Элементы математической статистики
1. Лидеру партии принесли следующую сводку данных о проголосовавших за его партию
по пяти избирательным участкам одного округа.
a) Найдите среднее значение процента проголосовавших за партию.
b) Подсчитайте общее количество голосовавших на этих пяти участках.
c) Подсчитайте количество проголосовавших за партию на каждом участке.
Смотреть ответ
Элементы математической статистики
Установите, в каких случаях будут полезны медиана, мода или среднее арифметическое:
a) Менеджер обувного магазина хотел бы иметь в наличии обувь различных
размеров.
b) Городской совет планирует построить школу в новом районе. Для оценки
количества учеников совет изучает численность детей в семьях в похожих районах.
c) Женщина часто путешествует на своем автомобиле, и каждый раз записывает
время, затраченное на поездку. Она хотела бы оценить время, которое затратит на
следующее путешествие.
Смотреть ответ
Элементы математической статистики
Случайная величина X задана следующей таблицей распределения
Найдите:
a) дисперсию случайной величины X;
b) стандартное отклонение случайной величины X.
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
Келесі бөлімдердің орындалатынын көрсетіңіз:
i) егер, серіппені 0,01 м-ге сығу үшін 10 Н күш қажет болса, онда k=1000;
ii) серіппені 0,04 м-ге сығу үшін жұмсалатын күш 40 Н.
iii) Күштің алғашқы функциясы жасалған жұмыс екені, яғни А(t) =∫ F(t)dt белгілі
болса, онда серіппені 0,04 м-ге сығу үшін жасалған жұмысты табыңыз.
Смотреть ответ
Элементы математической статистики
Количество спичек в коробке, взятых с упаковочной машины, было:
Найдите среднее значение и стандартное отклонение числа совпадений на ящик.
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
Поездың еңіспен жүріп келе жатқан (движущегося под уклон) жылдамдығы
v (t)=15 +0,2t теңдеуімен берілген.
a) жылдамдықтың алғашқы функциясы жүрілген жол екені, яғни s(t )=∫v(t)dt
белгілі болса, онда поездың жүрген жолын анықтаңыз.
b) егер, поезд 20 секундта жүріп өткен болса, онда еңістің ұзындығын метрмен
есептеңіз.
Смотреть ответ
Элементы математической статистики
Подбрасывается кубик. Дискретная случайная величина X — количество очков. Ниже
представлена таблица распределения случайной величины:
a) Известно, что M(X) = 4.2. Найдите значения a и b.
b) Покажите, что M(X2) = 20.4.
c) Вычислите D(5 – 3X)
Смотреть ответ
Бас жиын және таңдама
Қазақстандағы 9-сынып оқушыларының қазақ тілі пәні бойынша білімдерін тексеру үшін таңдама құралған.
Таңдама:
і) барлық қалалардағы қазақ тілін тереңдетіп оқытатын мектеп оқушыларынан кездейсоқ құралған;
іі) облыстар мен ауылды жерлердегі гимназиялар мен лицейлердің оқушыларынан кездейсоқ құралған;
ііі) әр облыс, ауылдар мен қалалардағы әртүрлі мектептер, гимназиялар мен лицейлердің оқушыларынан кездейсоқ құралған.
Тұжырымдардың қайсысы зерттелгелі отырған объектінің нақты көрсеткіші бола алатынын анықтап, жауабыңызды негіздеңіз
Смотреть ответ
Бас жиын және таңдама
Аудандағы жоғары деңгейлі кәсіби әншіні анықтау үшін, социолог мәдениет үйлерінде жұмыс жасайтын 150 адамнан сауалнама жүргізген.
і) бас жиынтық пен таңдаманы анықтаңыз;
іі) социологтың құрған таңдама нәтижесі сенімді ме?
ііі) таңдаманы сен қалай құрар едің?
Смотреть ответ
Бас жиын және таңдама
Шоколад фабрикасындағы 200 грамдық пакеттегі шоколад кәмпиттердің салмақтарын тексеру нәтижелері кестеде көрсетілген
і) таңдама көлемін;
іі) 200 грамнан ауытқыған пакеттер санын
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Қандай да бір полиграфиялық өнімнің сапасын бір-бірінен тәуелсіз алты инспектор
тексерген. Тексеру нәтижесі кестеде көрсетілген:
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
a) Математикадан он екі баланың бөлім бойынша жиынтық бағалау жұмысынан
жинаған ұпайларының саны мынадай: 18, 18, 20, 16, 13, 13, 15, 16, 18, 17, 14, 13.
b) Куръер дүкенге 30 аяқ киім әкелді, оның өлшемдері мынадай болды: 43, 38, 35, 45,
28, 38, 37, 41, 39, 38, 26, 25, 28, 26, 45, 41, 43, 37, 37, 39, 43, 28, 28, 37, 37, 38, 40,
40, 28, 38.
і) вариациялық қатар құрыңдар;
іі) таңдама жиілігінің үлестірімін анықтаңдар
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Таңдама жиілігінің үлестірім кестесі берілген
іі) салыстырмалы жиілік үлестірімін анықтаңыз
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Таңдаманың салыстырмалы жиілігінің үлестірім кестесі берілген
a) таңдалым көлемін;
b) жиілік үлестірімін
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Кестеде ерлер киімінің сапалық рейтингі көрсетілген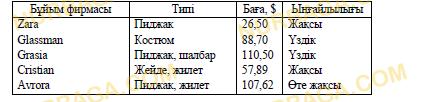
анықтаңыз;
b) қай айнымалылар сандық және қайсылары сапалық айнымалылар?
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
1. Кестеде белгілі бір мекемеде жұмыс жасайтын адамдардың салмақтары жайлы
мәліметтер келтірілген. Алайда, асығыс жазылғандықтан, кейбір ұяшықтар толмай
қалған:
a) кестедегі бос ұяшықтарды толтырыңыз;
b) абсолютті жиіліктер бойынша салынған гистограмманы толықтырыңыз.
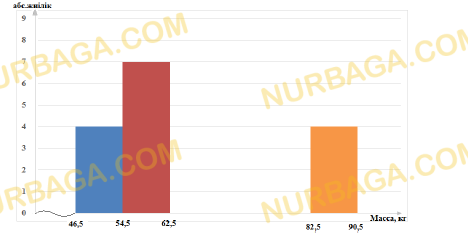
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Төменде таңдалынған 20 қауынның салмақтары кг-мен берілген:
3,0 6,9 9,5 13,6 19,0
4,4 7,2 10,2 14,3 21,2
5,3 7,8 11,1 15,7 22,4
6,1 8,6 12,1 16,4 23,0
a) деректерді 5 интервалға топтастырыңыз;
b) абсолютті және салыстырмалы жиіліктер кестесін құрыңыз;
c) абсолютті жиіліктер бойынша гистограмма (диаграмма) тұрғызыңыз;
d) салыстырмалы жиіліктер бойынша гистограмма (диаграмма) тұрғызыңыз;
e) қауындардың неше пайызының салмағы 10 кг-нан төмен екенін анықтаңыз
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Кестеде сауалнамаға қатысқан балалар жайлы мәліметтер берілген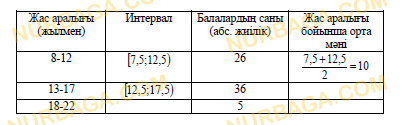
b) интервалдың орта мәнін табу арқылы кестедегі бос ұяшықтарды толтырыңыз;
c) орта мән мен абсолютті жиілікті қолданып, полигон тұрғызыңыз.
d) ең көп сауалнамаға қатысқан балалардың неше пайыз құрайтынын анықтаңыз.
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Жәшікте 2-уінің ақауы бар, ал 4-уі ақаусыз бұйымдар бар. Оның ішінен ақаусызы шыққанша бұйымдар алынып отырды.
a) алынған бұйымдар саны Х-дискретті кездейсоқ шамасының үлестірім заңын
жазыңыз;
b) үлестірім көпбұрышын (полигонды) салыңыз.
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
30 болат арқанның беріктігі туралы келесідей мәліметтер алынған (шартты белгілермен):
1800 1700 1740 1640 1780 1860 1600 1840 1880 1980
1540 1620 1860 1660 1840 1820 1840 1740 1780 1960
1940 1740 1800 1680 1800 1700 1640 1560 1740 1840
a) дискретті вариациялық қатар құрыңыз;
b) абсолютті және салыстырмалы жиіліктердің үлестірім заңын жазыңыз;
c) полигон салыңыз.
Смотреть ответ
Дискретті және интервалды вариациялық қатарлар
Стационардағы 45 емделушінің қан құрамындағы гемоглобиндері анықталды. Нәтижелері өспелі вариациялық қатар ретінде жазылды:
9,1
10,1
10,7
10,7
10,9
11,3
11,3
11,4
11,4
11,4
11,6
11,8
12,0
12,1
12,3
12,4
12,7
12,9
13,1
13,2
13,4
13,5
13,5
13,6
13,7
13,8
13,8
14,0
14,2
14,2
14,2
14,6
14,6
14,8
14,8
15,0
15,0
15,0
15,1
15,4
15,6
15,7
16,2
16,3
16,9
a) i) деректерді 8 интервалдарға топтастырыңыз;
іі) жиіліктер тығыздығын есептеңіз;
ііі) гистограмма тұрғызыңыз.
b) і) берілген вариациялық қатарды дискретті үлестірім кестесі түрінде жазуға бола ма?
іі) егер болса, онда сәйкес полигонды салып көрсетіңіз
Смотреть ответ
Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
1.
a) f(x) функцияның алғашқы функциясы F(x)-тің жалпы түрін жазыңыз
b) F(x) функциясы f(x) функцияның алғашқы функциясы болатынын көрсетіңіз.
c) графигі А(х;у) нүктесі арқылы өтетін f(x) функцияның алғашқы функциясын
табыңыз.
i) A(2;- 2); ii) A(0;0); iii) A(-1;1) .
Смотреть ответ
Кездейсоқ шаманың сандық сипаттамаларын таңдамалар бойынша бағалау
1.Маратта 200 хат бар.
Гистограмма хаттардың салмақтары (граммен) жайлы мәліметтерді көрсетеді.
a) 200 хат үшін жазылған жиіліктер кестесінің бос ұяшықтарын толтырыңыз;
Смотреть ответ
Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Туындының берілген графиктері бойынша F(x)-ті табыңыз
Смотреть ответ
Кездейсоқ шаманың сандық сипаттамаларын таңдамалар бойынша бағалау
Кестеде 200 күнде автотұрақ үшін төленген ақша құны жайлы мәліметтер көрсетілген
a) і) интервалдардың орта мәндерін есептеңіз;
іі) әрбір күні алынған ақшаның орта мәнін есептеңіз.
b) Гистограмма 200 автокөліктің уақыт ұзақтығы бойынша тұраққа қойылғанын
көрсетеді.
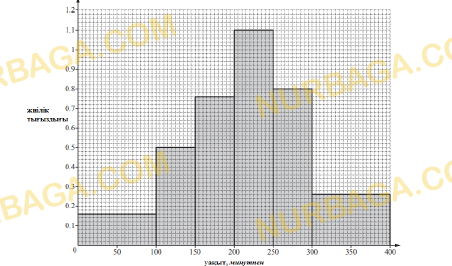
есептеңіз;
іі) 250 минуттан кейін тұраққа қойылған автокөліктердің неше пайызды
құрайтынын анықтаңыз.
Смотреть ответ
Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Смотреть ответ
Кездейсоқ шаманың сандық сипаттамаларын таңдамалар бойынша бағалау
Үш атқыш нысанаға бір реттен атты. Олардың нысанаға тию ықтималдықтары сәйкесінше
0,5, 0,6 және 0,8. Нысанаға тию саны Х кездейсоқ шамасының полигоны берілген.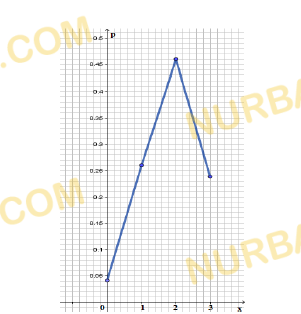
жазыңыз;
іі) полигон бойынша кестенің әрбір ұяшығындағы сандық мәліметтерді негіздеңіз.
Смотреть ответ
Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Анықталмаған интегралдарды есептеңіз
Смотреть ответ
Кездейсоқ шаманың сандық сипаттамаларын таңдамалар бойынша бағалау
Белгілі бір мәліметтерді тіркеу нәтижесі бойынша салынған полигон берілген:
і) абсолютті және салыстырмалы жиіліктердің үлестірім заңын жазыңыз;
іі) 5 ≤х ≤9 варианталар аралығына сәйкес жиіліктер берілген таңдаманың неше
пайызын құрайтынын анықтаңыз.
Смотреть ответ
Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Смотреть ответ
Кездейсоқ шаманың сандық сипаттамаларын таңдамалар бойынша бағалау
Кестеде 24 студенттің үй жануарларын асырайтындығы жайлы дерек берілгенa) үй жануарлар санының орта мәнін табыңыз;
b) Сәуле 24 студенттің қатарына қосылды. Сонда, жаңа орта мәні 3,44 болды.
Сәуленің қанша үй жануары болғанын есептеңіз
Смотреть ответ
Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттері
Смотреть ответ
Кездейсоқ шаманың сандық сипаттамаларын таңдамалар бойынша бағалау
Кесте 200 студенттің емтихан тапсыру уақыттары жайлы мәліметтерді көрсетедіa) интервалдардың орталарын анықтаңыз;
b) жиіліктер тығыздықтарын табыңыз;
c) төмендегі торға гистограмма салыңыз
Смотреть ответ
Кездейсоқ шаманың сандық сипаттамаларын таңдамалар бойынша бағалау
120 студенттің сұрақтарға жауап берулерін сұраған.
Әрбір студенттің жауап беру уақытын секундпен өлшеген.
Нәтижелері жиіліктер кестесінде көрсетілген
b) жиіліктер кестесіндегі мәліметтерді қолданып, жаңа кесте толтырыңыз c) жаңа кесте бойынша төмендегі гистограмманы толықтырыңыз
Смотреть ответ
Интегралдау тәсілдері
Айнымалыны алмастыру әдісін қолданып интегралдарды есептеңіз
Смотреть ответ
Интегралдау тәсілдері
Бөліктеп интегралдау әдісін қолданып, келесі интегралдарды есептеңіз
Смотреть ответ
Қисықсызықты трапеция және оның ауданы. Анықталған интеграл
[0;3] интервалында f (x)= x графигі мен Ох осінің арасындағы бөліктің ауданын
есептеңіз.
2.
a) [0;4] аралығында f (x)= 3х — 2 функциясының интегралы 16-ға тең болатынын
көрсетіңіз.
b) i) f (x) функциясы графигінің Ох осімен қиылысу нүктесін табыңыз.
іі) [0;4] аралығында f (x) -тің графигі мен Ох осі арасындағы бөліктің ауданын
есептеңіз.
3.
a) боялған бөліктің ауданын табыңыз;
b) [a;b] аралығында y = f (x) функциясының интегралын бағалаңыз
Смотреть ответ
Қисықсызықты трапеция және оның ауданы. Анықталған интеграл
Анықталған интегралдарды есептеңіз
Смотреть ответ
Анықталған интегралдың геометриялық және физикалық есептерді шығаруда қолданылуы
Келесі теңдіктердің орындалатынын көрсетіңіз
Смотреть ответ
Табиғатты пайдалануды реттеу
Қоршаған ортаны қорғаудың негiзгi принциптерiн берілген сілтеме арқылы оқып шығыңыз мұқият оқып шығыңыздар.
http://adilet.zan.kz/kaz/docs/K070000212_/k070212_.htm
Осы принцип негізінде жергілікті жерде (аймақта) болып жатқан экологиялық ахуалдың заңнамалық тәртіппен бекітілген нормаларға сәйкестігін анықтаңыз, қорытынды шығарыңыз
Смотреть ответ
Первообразная и интеграл
Покажите, что функция F является первообразной для функции f на указанном промежутке:
Смотреть ответ
Первообразная и интеграл
Для данной функции f найдите первообразную, график которой проходит через данную точку М:
Смотреть ответ
Первообразная и интеграл
Найдите площадь криволинейной трапеции, ограниченной:
Смотреть ответ
Первообразная и интеграл
На рисунке изображены график функции и прямые, параллельные оси ОУ, пересекающие график в точках А и В. Точка А является точкой максимума, а угловой коэффициент касательной в точке В равен 4.
- Найдите абсциссу точек А и В.
- Вычислите площадь криволинейной трапеции, изображенной на рисунке.
Смотреть ответ
Первообразная и интеграл
Вычислите определенный интеграл:
Смотреть ответ
Первообразная и интеграл
Вычислите площадь заштрихованной фигуры, изображенной на рисунке:
Смотреть ответ
Первообразная и интеграл
На рисунке изображены график функции и прямой
- найдите абсциссы точек А и В;
- вычислите площадь заштрихованной фигуры.
Смотреть ответ
Первообразная и интеграл
Найдите площадь фигуры, ограниченной:
Смотреть ответ
Первообразная и интеграл
Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной графиком функции:
Смотреть ответ
Первообразная и интеграл
Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
Смотреть ответ
Первообразная и интеграл
Найдите объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной графиками функции
Смотреть ответ
Покажите, что функция F(x) является первообразной функции f(x) на всей числовой прямой:
Смотреть ответ
Найдите площадь фигуры, ограниченной графиком, изображенном на рисунке, и осью абсцисс на промежутке [0;π]
Смотреть ответ
Фигура, ограничена линиями:
Вычислите:
a) площадь фигуры, ограниченной заданными линиями:
b) объѐм тела, образованного вращением вокруг оси Ох фигуры, ограниченной
заданными линиями.
Смотреть ответ
a) Покажите, что уравнение касательной к графику функции точке с абсциссой x= 2 принимaет вид y=6x- 3
b) Вычислите площадь фигуры, ограниченной графиком функции
касательной к этому графику в точке с абсциссой x = 2 и прямой x = 0 .
Смотреть ответ
Вычислите объeм тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями
Смотреть ответ
Алғашқы функция және интеграл
а) Төмендегі кестеде функция мен оның алғашқы функцияларының арасында
сәйкестікті орнатыңыз.
b) Алғашқы функцияны анықталмаған интеграл арқылы өрнектеп, кестені
толтырыңыз
Смотреть ответ
Алғашқы функция және интеграл
Функция туындысының графигі М нүктесінен өтетінін ескеріп, функцияны табыңыз:
Смотреть ответ
Алғашқы функция және интеграл
Анықталған интегралдарды есептеңіз
Смотреть ответ
Алғашқы функция және интеграл
1.Сызбада y = x² қисығымен және x =1, x = 3, y = 0 түзулерімен шектелген фигура
көрсетілген. Боялған бөліктің ауданын табыңыз.
2. y =sinх графигімен, Ох осінде [0;π⁄ 2]кесіндісімен және х =π/2 түзуімен шектелген фигура ауданын есептеңіз.
Смотреть ответ
Алғашқы функция және интеграл
Келесі сызбада y =4 — x² қисығы мен y = x + 2 түзуінің графигі көрсетілген.
a) қисық пен түзудің қиылысу нүктесінің х координатасын табыңыз;
b) интегралды қолдана отырып, түзу мен қисық арасындағы шектелген
фигура ауданын табыңыз.
Смотреть ответ
Алғашқы функция және интеграл
Сызбада y = -3x²-9x = 30 және y = 3x²+3x -10 қисықтарының графиктері берілген.
a) қисықтар A(-5;0) және B(2;0) нүктелерінде қиылысатынын көрсетіңіз;
b)екі қисықпен шектелетін фигураның ауданытабылатынын көрсетіңіз;
c) жоғарыдағы анықталған мәліметтерді қолдана отырып, боялған фигура ауданы 228 2/3(кв.бірлік) болатынын көрсетіңіз
Смотреть ответ
Алғашқы функция және интеграл
Сызбадақисығының графигі берілген. Боялған фигура осы қисықпен,
y =0, x = 3 және x = 6 түзулерімен шектелген. Осы фигураны Ох осінің айналасында
айналдырғаннан пайда болатын дененің көлемін табыңыз.
Смотреть ответ
Бүтін көрсеткішті дәреже
a) Егер шаршының қабырғасын 2 есеге, 5 есеге, n есеге арттырса, онда оның ауданы қалай
өзгеретінін анықтаңыз.
Дескриптор Білім алушы
− ауданды табу үшін өрнек кұрастырады;
− ауданның қалай өзгеретінін анықтайды.
b) Егер текшенің қырын 2 есеге, 5 есеге, n есеге арттырса, онда оның көлемі қалай
өзгеретінін анықтаңыз.
Смотреть ответ
Многочлены
Определите какие из алгебраических выражений, представленных в таблице являются многочленами.
Запишите их в стандартном виде, укажите степень и коэффициент.
Смотреть ответ
Бүтін көрсеткішті дәреже
а) Текшені бояуға 40 г бояу жұмсады. Қыры берілген текшеден 3 есе артық болатын текшені
бояуға 350 г бояу жете ме?
b) Текше түріндегі ыдыс құбыр арқылы суға 40 минутта толады. Қыры бастапқы ыдыс
қырынан екі есе үлкен болатын текше тәріздес ыдысты сол құбырмен 5 сағат ішінде суға
толтыра аламыз ба?
Смотреть ответ
Многочлены
Даны многочлены:
Найдите:
Запишите ответ в стандартном виде.
Смотреть ответ
Бүтін көрсеткішті дәреже
Сандарды негізі 3 болатын дәрежемен жазыңыз
Смотреть ответ
Бүтін көрсеткішті дәреже
Мысалдар мен олардың жауаптары арасында сәйкестікті орнатыңыз
Смотреть ответ
Бүтін көрсеткішті дәреже
Есептерді шешіңіз
a) Тринидад мемлекетінің халық саны адам, ал оның жер көлемі
Осы мемлекеттегі халықтың орналасу тығыздығын (адам/км2) есептеңіз. Жауапты бүтінге
бейін дөңгелектеңіз.
b) Жер массасы кг, ал Марс массасы
кг. Қайсысы артық: Жер массасы
ма әлде Марс массасы ма және қанша есе? Жауапты ондықтарға дейін дөңгелектеңіз.
c) Құлдар еңбегімен салынған Мысыр фараоны Хеопстың пирамидасының салмағы шамамен
алғанда 7,231∙106 т. Жүк тасымалдаушы вагон 64 т тасымалдай алады. Осындай салмақты
тасымалдау үшін мұндай вагондардан қанша қажет болар еді?
Смотреть ответ
Многочлены
Запишите математичекую модель следующих задач. Упростите полученные выражения.
i) На рисунке представлен план дачного участка. Найдите площадь закрашенной области.
ii) На парусной регате одна из яхт стартовала со скоростью a км/ч и плыла с этой скоростью t часов. Оставшееся время она плыла со скоростью на 7 км/ч большей. Сколько км проплыла яхта, если на прохождение дистанции она затратила 2t+3 часа?
Смотреть ответ
Многочлены
Покажите, что:
Указание: используйте разложение на множители исходных многочленов А и В.
Смотреть ответ
Бүтін көрсеткішті дәреже
Хабардың ақпараттық көлемі деп – хабардың ұзындығын, яғни хабарды жазу үшін
пайдаланылған символдар санын атайды. Есептеуіш техникада хабардың ең кіші өлшемі бір
екілік разрядқа немесе 1 битке тең болады. Ақпаратты өлшеу бірлігі 1 битке тең. Одан
қолайлырақ өлшем бірлігі — сегіз екілік разрядтың жиынтығы — 1 байт, ол символдарды
кодтауда жиі қолданылады.
Сұрақ: Кітапта 290 бет бар, бір бетте 39 жол, әр жолда 67 символ бар. Бұл кітаптың
сыйымдылығы 1,44 Мбайт дискіге сыйғызуға бола ма? Жауабыңызды есептеп, ондық үлеске
дейін дөңгелектеңіз.
Смотреть ответ
Бүтін көрсеткішті дәреже
a) Калькулятордың көмегімен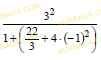
үлестерге дейін жуықтаңыз.
b) Калькулятордың көмегімен есептеп, жүздік үлестерге дейінгі жуық мәнін табыңыз
Смотреть ответ
Бүтін көрсеткішті дәреже
0,00030900 және 22,152348025 сандары берілген.
а) берілген сандарды жүзмыңдық үлестерге дейін жуықтап, нәтижені стандарт түрде
жазыңыз;
b) берілген сандарды жүздік үлестергее дейін артығымен жуықтап, нәтижені стандарт түрде
жазыңыз;
с) берілген сандарды мыңдық үлестерге дейін кемімен жуықтап, нәтижені стандарт түрде
жазыңыз
Смотреть ответ
Бүтін көрсеткішті дәреже
Шамаларды бір өлшем бірліктен екінші өлшем бірлікке айналдырып, стандарт түрде
жазыңыз және төменгі бөліктегі жауабымен сәйкестендіріңіз
Смотреть ответ
Бүтін көрсеткішті дәреже
Сандарды салыстырыңыз және неліктен үлкен немесе кіші екенін өз сөзіңізбен негіздеңіз.
Смотреть ответ
Бүтін көрсеткішті дәреже
Мұғалімге нұсқаулық: сұрақтарды слайд бетіне шығарып қоюңызға болады.
Математикалық диктант:
Келісетін болсаңыз 1 цифрын, ал келіспейтін болсаңыз 0 цифрын жазыңыз.
1. санынан кем
2. Стандарт түрде жазылған сандарды салыстыру үшін мәнді бөлігін салыстыру жеткілікті
3. Стандарт түрде жазылған сандарды салыстыру үшін санның ретін салыстыру жеткілікті
4. Санның реті үлкен болған сайын, санның өзі де үлкен болады
5. Егер санның реті теріс сан болса, санның өзі де теріс сан болады
6. Санның мәнді бөлігі үлкен болған сайын, санның өзі де үлкен болады
7. Егер санның реті оң сан болса, санның өзі де оң сан болады
8. Егер екі мәнді бөлігі теріс болатын стандарт түрдегі сандар берілсе, олардың үлкені сан
осінде координата басына жақынырақ орналасады
Смотреть ответ
Бүтін көрсеткішті дәреже
Есепті шығарыңыз:
а) Жер массасы ал Марстың массасы
Жер Марстан неше есе ауыр?
b)
— Сіздің жасыңыз нешеде?- деген сұраққа әкесі былай деп жауап берді:
— Менің жасымды табу үшін санын 600-ге көбейтіп, алынған көбейтіндіні
санына бөлу керек.Сонда менің жасымды табасың.
Әкесінің жасы нешеде?
Смотреть ответ
Бүтін көрсеткішті дәреже
Амалдарды орындаңыз және нәтижені стандарт түрде жазыңыз.
Смотреть ответ
Бүтін көрсеткішті дәреже
Кестеде Күн жүйесіндегі планеталардың диаметрлері берілген. Планеталар диаметрлерін
стандарт түрде жазыңыз және оның мәнді бөлігі мен ретін көрсетіңіз.
Смотреть ответ
Бүтін көрсеткішті дәреже
Мұғалімге нұсқаулық: Tarsia бағдарламасының көмегімен жасалған домино ойынын
ойнату. Санды оның стандарт түрдегі жазуымен сәйкестендіріңіз. Оқушыларға ұсыныс,
алдымен «Start» жазуы бар карточкадан бастаңыз.
Смотреть ответ
Степень с целым показателем
a) Заполните таблицу, указывая последнюю цифру значения степени:
b) Установите закономерность.
Смотреть ответ
Бүтін көрсеткішті дәреже
Тізбек аn = n³ формуласымен берілген.
а) тізбектің алғашқы бес мүшесін табыңыз _____; _____; ______; ______; ______
b) тізбектің оныншы мүшесін табыңыз ____________________________________
Смотреть ответ
Степень с целым показателем
Определите, какой цифрой оканчиваются следующие выражения:
Смотреть ответ
Бүтін көрсеткішті дәреже
Сан тізбегінің белгісіз екі мүшесін анықтаңыз және заңдылығын жазыңыз:
Смотреть ответ
Степень с целым показателем
В каком из случаев число 2 370000 записано в стандартном виде?
Смотреть ответ
Степень с целым показателем
При каком значении k верно равенство:
Смотреть ответ
Степень с целым показателем
Вычислите значение выражения:
Смотреть ответ
Степень с целым показателем
Вычислите рациональным способом:
Смотреть ответ
Бүтін көрсеткішті дәреже
і) Төмендегі теңдіктерді ақиқат, жалғандыққа тексеріңіз.
іі) Жұбыңызбен жауап парағын ауыстырып дайын жауаптармен тексеріңіз.
ііі) Жұптаса отырып жалған теңдіктердің дұрыс шешімін көрсетіңіз.
Смотреть ответ
Бүтін көрсеткішті дәреже
Айнымалының қандай мәнінде келесі өрнектердің мағынасы болмайды:
Смотреть ответ
Степень с целым показателем
- a) Сторона квадрата равна 1 см. Во сколько раз увеличится площадь квадрата, если увеличить сторону в 5 раз.
- b) Ребро куба равна 2 см. Во сколько раз увеличится объем куба, если ребро куба увеличить в 2 раза.
Смотреть ответ
Степень с целым показателем
Дайте развернутый ответ:
Площадь сказочного города . Запишите чему равна площадь города в м²‚км²
Смотреть ответ
Бүтін көрсеткішті дәреже
Өрнектің мәні болатындай айнымалылардың мүмкін мәндер жиынын табыңыз.
Смотреть ответ
Степень с целым показателем
Длина ребра первого куба равна 3 см, а длина ребра второго куба — 6 см.
а) Найдите площадь основания и объем каждого куба.
б) Определите, как отношение длины ребра повлияло на отношение площадей?
с) Определите, как отношение длины ребра повлияло на отношение объемов?
Смотреть ответ
Многочлены
Приведите одночлен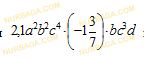
Смотреть ответ
Көпмүшелер
көпмүшелерінің қосындысы х+7 бөлінетіндігін;
көпмүшелерінің айырымы 4 – у³ бөлінетіндігін көрсетіңіз.
Нұсқау: Берілген А және В көпмүшелерін көбейткіштерге жіктеуді қолданыңыз.
Смотреть ответ
Степень с целым показателем
У Азата было 2 коробки по 15 кубиков в каждой. В первой коробке кубики с ребром 8 см, а во второй – с ребром 4 см. Азат построил 2 башни: одну — из кубиков, лежащих в первой коробке, другую — из кубиков второй коробки.
Определите:
a) какая башня имеет больший объём и на сколько кубических сантиметров?
b) как изменение длины ребра повлияло на изменение объема?
Смотреть ответ
Многочлены
Составьте выражение для нахождения объема параллелепипеда, ответ запишите в стандартном виде
Смотреть ответ
Многочлены
Найдите уменьшаемое, если вычитаемое равно 3х² — 2х, а разность двух двучленов равна 5х²-6х.
Смотреть ответ
Степень с целым показателем
Установите соответствие между примерами и их ответами
Смотреть ответ
Многочлены
Разложите на множители:
a)2х(а-b)+a(a-b)
b)3x+3y-bx-by
Смотреть ответ
Степень с целым показателем
Найдите при каких значениях переменных будут иметь смысл следующие выражения:
Смотреть ответ
Для каждого из предложенных ниже равенств запишите, какое выражение стоит на месте
Смотреть ответ
Многочлены
Напишите упрощенное выражение для определения площади закрашенной области
Смотреть ответ
Степень с целым показателем
Найдите значение выражений, если это возможно:
Смотреть ответ
Запишите выражение в виде одночлена в стандартном виде.
Смотреть ответ
Вирус А имеет диаметр 0,000000003 метра. Микроскоп позволяет увеличить объект в 4000 раз.
а) Запишите диаметр вируса А в стандартном виде.
b) Запишите увеличение микроскопа в стандартном виде.
с) Каким будет диаметр вируса А под микроскопом при максимальном увеличении? Ответ запишите в стандартном виде.
d) Вирус В имеет диаметр м. Во сколько раз диаметр вируса В больше диаметра вируса А?
Смотреть ответ
Көпмүшелер
Өрнектегі * таңбасын теңдік дұрыс болатындай бірмүшелермен алмастырыңыз:
Смотреть ответ
Көпмүшелер
Математикалық диктант: Берілген сөз тіркестерін тиісті ұяшықтарға орналастырыңыз.
— Жақшаны ашу;
— Көбейткіштерге жіктеу;
— Бірмүшені көпмүшеге көбейту;
— Көбейтіндіні көпмүше түрінде жазу;
— Ортақ көбейткішті жақша сыртына шығару;
— Көбейтінді түрінде жазу.
Смотреть ответ
Упростите выражение .
Результат запишите в стандартном виде.
Смотреть ответ
Степень с целым показателем
Заполните таблицу по образцу
Смотреть ответ
Көпмүшелер
Өлшемдері 40∙50 см² және 36∙52 см² болатын екі тіктөртбұрыш берілген. Осы
тіктөртбұрыштардың әр қабырғасын бірдей см-ге қысқарту арқылы аудандары тең болатын
тіктөртбұрыштар алуға бола ма? Жауабыңызды жазбаша шығару жолымен негіздеңіз
Смотреть ответ
При каком значении а произведение 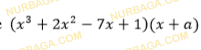
?
Смотреть ответ
Степень с целым показателем
Дана последовательность чисел: 1, 8, 27, 64…
a) Определите закономерность
b) Найдите десятый член последовательности
c) Является ли 216 членом данной последовательности?
Смотреть ответ
Көпмүшелер
Төмендегі көпмүшелердің қайсысы 2x³ − хy²− у³ үшмүшесімен тең мағыналы екендігін анықтаңыз:
Смотреть ответ
Көпмүшелер
Берілген фигуралардың боялған бөлігінің ауданын табыңыз:
Смотреть ответ
Степень с целым показателем
a) Запишите число в виде степени с основанием 10:
b) Запишите число в стандартном виде:
Смотреть ответ
Көпмүшелер
Ағайынды екі баланың бірі екіншісінен алты жасқа үлкен, оның жасы осыдан екі жыл
бұрын екі есе үлкен болатын. Балалардың жасы нешеде?
Смотреть ответ
Степень с целым показателем
a) Используя стандартный вид числа, запишите:
1) В сутках 86400 с
2) Атмосферное давление на высоте 100 км равно 0, 000024 мм ртутного столба
3) 1 ккал равна 0,00419 кДж
4) 1 сек составляет 0, 0002778 ч
b) Укажите значащую часть и порядок числа.
Смотреть ответ
Степень с целым показателем
В таблице даны диаметры планет Солнечной системы. Запишите диаметры планет в стандартном виде. Укажите их значащие части и порядки.
Смотреть ответ
Көпмүшелер
Жұптық жұмыс. Ой қозғау.
a) Тіктөртбұрыштардың аудандарын екі түрлі тәсілмен анықтаңыз:
b) Табылған тіктөртбұрыш аудандарының өрнектері бойынша қандай қорытынды жасауға
болады?
Смотреть ответ
Степень с целым показателем
Выполните действия над числами. Ответ запишите в стандартном виде.
Смотреть ответ
Көпмүшелер
Берілген екі таңбалы санның ондық цифры бірлігінен төрт есе үлкен. Берілген саннан
оның цифрларының орны ауысқанда шыққан санды азайтсақ, айырма 54-ке тең болады.
Берілген екі таңбалы санды табыңыз.
Смотреть ответ
Степень с целым показателем
Решите задачи:
a)
-Сколько тебе лет?- спросил Незнайка у отца.
Он ответил:
Смотреть ответ
Көпмүшелер
Боялған фигуралардың аудандарын табыңыз:
Мұғалімге нұсқау: деңгейлік топтарға бөлінген оқушыларға арналған тапсырмалар.
Смотреть ответ
теңдігіндегі М әріпін қандай бірмүшемен алмастырғанда теңбе-теңдік шығады.
Смотреть ответ
Көпмүшелер
1) Айталық, A = x² − 2xy + y² , B = 2x² − y² ,C = x² − 3xy болсын.
а) A + B − C ;
b) − A + B − C өрнектерін ықшамдаңыз.
Смотреть ответ
Көпмүшелер
Көпмүшені стандарт түрге келтіріп, 2a² + b көпмүшесіне тең немесе тең болмайтынын анықтап, сәйкесті символды қойыңыз.
Смотреть ответ
Көпмүшелер
Төмендегі алгебралық өрнектердің ішінен көпмүшелерді теріп жазыңыз және кестені
толтырыңыз:
Смотреть ответ
Степень с целым показателем
Переведите единицы измерения и ответ запишите в стандартном виде:
Смотреть ответ
Жердің массасы кг, ал Юпитердің массасы
кг.
а) Осы массаларды көбейтіңіз және жауабыңызды стандарт түрде жазыңыз
b) Жердің массасы мен Юпитердің массасының қайсысы үлкен және неше есе үлке екенін анықтаңыз және жауабыңызды стандарт түрде жазыңыз.
Смотреть ответ
Көпмүшелер
— өрнегін:
а) бірмүшенің квадраты түрінде;
b) бірмүшесінің біреуі болатын екі бірмүшенің көбейтіндісі түрінде;
с) бір бірмүшенің коэффициенті 2, ал екінші бірмүшенің дәрежесі 5 болатын екі бірмүшенің көбейтіндісі түрінде жазыңыз.
Смотреть ответ
Степень с целым показателем
За летний сезон улов рыбы на Балхаше составил 2 096 тонн.
а) запишите данное значение в стандартном виде
б) выразите вес пойманной рыбы в килограммах, центнерах
Смотреть ответ
Көпмүшелер
Төмендегі бірмүшелерді стандарт түрдегі бірмүшеге келтіріңіз:
Смотреть ответ
Степень с целым показателем
a) Выполните округление чисел по избытку до сотых, ответ запишите в стандартном виде:
i) 2,408005; ii) 0,3459; iii) 0,0888….
b) Выполните округление чисел по недостатку до тысячных, ответ запишите в стандартном виде:
i) 5,4231; ii) 0,67322; iii) 10, 1111….
Смотреть ответ
Бірмүшені көпмүшеге көбейтуді орындаңызЖауабыңызды
стандарт түрде жазыңыз.
Смотреть ответ
Көпмүшелер
Төмендегі алгебралық өрнектердің ішінен бірмүшелерді теріп жазыңыз және кестені толтырыңыз:
Смотреть ответ
Степень с целым показателем
Деталь, масса которой равна 54,12705 г была взвешена на весах. Весы имеют цену деления шкалы 0,1 г. Полученный результат взвешивания 54,1 г. Найдите абсолютную и относительную погрешности этого приближенного значения.
Смотреть ответ
Степень с целым показателем
а) Солнечный луч достигает Землю через 9 минут. Найдите растояние между Солнцем и Землей.
b) Расстояние, которое проходит солнечный луч за календарный год, называется Световым годом. Вычислите длину Светового года.
Смотреть ответ
Степень с целым показателем
Выразите в граммах массу одного атома водорода, гелия, алюминия и свинца, зная, что:
Масса атома водорода равна 1,008 а.е.м
Масса атома гелия равна 3, 016 а.е.м
Масса атома алюминия равна 29,99 а.е.м
Масса атома свинца равна 205,97 а.е.м
Смотреть ответ
Степень с целым показателем
В 2011 году численность населения Земли составила 7 млрд человек. Примерная численность населения через х лет после 2011 года или за х лет до этого времени может быть рассчитана по формуле
Запишите выражение для вычисления численности населения Земли и определите примерную численность населения: а) в 2017 г; б) в 2005 г.
Подсказка. Определите, какой знак должен иметь показатель степени х в каждом случае.
Смотреть ответ
Многочлены
Среди представленных в таблице алгебраических выражений найдите одночлены. Запишите их в стандартном виде, укажите степень и коэффициент.
Смотреть ответ
Элементы статистики
i) Для контрольной работы был создан тест из 7 заданий. Количество верных ответов, полученных каждым из 50 учащихся, было представлено в виде таблицы частот. Найдите пропущенное значение частоты.
ii) Для определения плана выпуска женской обуви фиксировалась относительная частота (в процентах) размеров проданной в течении месяца обуви. Найдите пропущенное значение относительной частоты.
iii) Ученики 7 класса решили выяснить какое количество времени они затрачивают на выполнение домашней работы по математике. В таблице фиксировалось время в минутах и относительная частота. Найдите пропущенное значение относительной частоты.
Смотреть ответ
Бүтін көрсеткішті дәреже
a) 7 санын дәрежеге шығарғанда пайда болатын сандар қандай цифрмен аяқталады? Кестені
толтырыңыз:
b) Заңдылықты құрастырып, жазыңыз.
c) Алынған мәліметтерді қолданып, 7521 саны қандай цифрмен аяқталатынын анықтаңыз.
Смотреть ответ
Многочлены
Представьте выражение в виде одночлена стандартного вида:
Смотреть ответ
Бүтін көрсеткішті дәреже
і) өрнегі берілген. Өрнектің мәні қандай цифрға
аяқталатынын табыңыз.
іі) 0, 1, 5 және 6 цифрларымен аяқталатын сандар дәрежелеріндегі заңдылықты жазыңыз.
Смотреть ответ
Многочлены
Выполните действие, запишите ответ в стандартном виде.
Смотреть ответ
Многочлены
i) Вместо «*» запишите такой одночлен, чтобы выполнялось равенство:
ii) Представьте заданное выражение в виде квадрата или куба некоторого одночлена:
iii)Вместо «*» запишите такие одночлены, чтобы получилось верное равенство:
Смотреть ответ
Дано выражение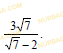
Смотреть ответ
Дана функция у=√х
a) Постройте график функции.
b) Укажите область определения и область значения функции.
c) График функции проходит через точку А (n; 8). Определите значение n.
Смотреть ответ
Квадратные корни и иррациональные выражения
Упростите выражение:
Смотреть ответ
Квадратные корни и иррациональные выражения
Представьте числа в виде и расположите их в порядке возрастания:
Смотреть ответ
Квадратные корни и иррациональные выражения
Выполните действия:
Смотреть ответ
Квадратные корни и иррациональные выражения
a) При каких значениях х имеет смысл выражение ?
b) Постройте график функции .
c) Покажите на графике значения х при у=2; 2,5. Запишите приближенные значения х.
Смотреть ответ
ХХ ғасырдың басында әлем бейнесі қандай болды?
Берілген мәтіндегі бос орынды төмендегі цифрлы сөздермен толықтырыңыз.
Ұлтшылдық. Нәсілшілдік. _____________. ХХ ғасырдың саяси ағымына айналды. Ұлттық мемлекеттердің орнығуы негізгі ұлттың маңызын арттырды. Ұлтшылдық өз ұлтының басқа ұлттан ____________айқындады. Ұлыдержавалық ұлтшылдық саны аз ұлыстардың, __________ ұлттардың мүдделеріне қысым жасауға барды. Еуропадағы ұлттық төзбеушіліктің бір түрі —___________(еврейлерге дұшпандықпен қарау) еді. ХIХ—ХХ ғасырлар тоғысында антисемитизм қуатты саяси әдіске айналды.
Жауап кестесі
Смотреть ответ
Квадратные корни и иррациональные выражения
Между какими соседними натуральными числами заключено число:
Смотреть ответ
Квадрат түбір және иррационал өрнек
a) Берілген сандардың қай жиынға жататындығын кестеде «+» таңбасын қою арқылы белгілеңіз
b) Бос орынды толтырыңыз.
Рационал және иррационал сандар жиыны бірігіп ____________ сандар жиынын құрайды. Диаграмманы N және Z жиындарымен толықтырыңыз
Смотреть ответ
Квадратные корни и иррациональные выражения
Отметьте галочкой во втором столбце числа, являющиеся иррациональными, а галочкой в третьем столбце – действительные числа.
Смотреть ответ
Кестені толтырыңыз:
Әр бағанға кемінде екі саннан жазыңыз
Смотреть ответ
Квадрат түбір және иррационал өрнек
Сандық өрнекті есептеңіз
Табылған жауаптарды ескере отырып төмендегі кестені сәйкес әріптермен және бос орындарды «Р» әрпімен толтырсаңыз, ежелгі грек мифологиясындағы 9 әйел құдайдың бірі – би құдайының есімін оқи аласыз
Смотреть ответ
Квадратные корни и иррациональные выражения
Найдите значение выражения:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Координаталық түзуде A, C, D нүктелері белгіленген. Олардың қайсысының координатасы
Смотреть ответ
Квадратные корни и иррациональные выражения
- a) n = 3;
- b) n = 7;
- c) n = 11.
Смотреть ответ
Квадрат түбір және иррационал өрнек
Көбейткішті квадрат түбір белгісінің астына алыңыз:
Смотреть ответ
Квадратные корни и иррациональные выражения
Вынесите множитель из-под знака корня:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Көбейткішті квадрат түбір белгісінің алдына шығарып, алынған өрнекті ықшамдаңыз:
Смотреть ответ
Квадратные корни и иррациональные выражения
Внесите множитель под знак корня:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Тіктөртбұрыш тәріздес бақшаның ені
есе артық. Бақшаның ауданын табыңыз.
Смотреть ответ
Квадратные корни и иррациональные выражения
Освободитесь от иррациональности в знаменателе:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Берілген сандардан өзара түйіндес сандар жұбын табыңыз:
Смотреть ответ
Қабырғасы y см , ауданы x см² болатын шаршы тәріздес мата берілген.
i) Шаршы қабырғасының ауданына тәуелділігін өрнектейтін формуланы жазыңыз;
іі) Алдыңғы пункттегі тәуелділік графигін тұрғызыңыз;
ііі) ?(100; 10) нүктесі функция графигіне тиісті ме?
iv) Функция графигі В (9;n) нүктесі арқылы өтетін болса, n санын анықтаңыз.
v) Егер мата ауданы [9; 100] аралығында өзгеретін болса, қабырға ұзындығының өзгеру
аралығын анықтаңыз
Смотреть ответ
Квадратные корни и иррациональные выражения
Упростите выражение:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Бөлшектің бөліміндегі иррационалдықтан арылыңыз:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Өрнекті ықшамдаңыз:
Смотреть ответ
Квадратные корни и иррациональные выражения
Упростите выражение:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Әр кестедегі үш саның ең үлкенін анықтап, оған сәйкес әріпті шеңбердің ішіне орналастырсаңыз, ұлы композитор-күйші, қазақтың аспапты музыка өнерінің классигі Құрманғазы Сағырбайұлының күйлерінің бірінің атын оқи аласыз.
Смотреть ответ
Квадратные корни и иррациональные выражения
Сравните значения выражений:
Смотреть ответ
Квадрат түбір және иррационал өрнек
a) y=a√x , a>0 функциясының қасиеттерін төмендегі схема бойынша сипаттаңыз:
1)
D(у)= ______________
E(у)= ______________
2) функция нөлдері;
3) өсу/кему аралығы;
4) функцияның ең үлкен және ең кіші мәні.
b) y=2√(x ) функциясының графигін салыңыз.
Смотреть ответ
Квадратные корни и иррациональные выражения
Расположите числа в порядке возрастания:
Смотреть ответ
Квадрат түбір және иррационал өрнек
Шаршының қабырғасын (a) оның ауданы (S) арқылы өрнектеп, a-ның S-тен тәуелді функциясын жазыңыз.
a) S=9; 4; 2 деп алып, шаршының қабырғасын анықтаңыз;
b) а= 1; 2; 4 деп алып, шаршының ауданын табыңыз.
Смотреть ответ
Квадратные корни и иррациональные выражения
1) D(у) = _____________
E(у) = _____________
2) нули функции;
3) промежутки возрастания, убывания;
4) наибольшее, наименьшее значения функции.
Смотреть ответ
Квадрат түбір және иррационал өрнек
Берілген сызбаға талдау жасаңыз.
a) Оу осіндегі сандардың Ох осіндегі қай сандарға сәйкес келетіндігін анықтаңыз;
b) Oх осіндегі 9 санына Оу осіндегі қай сан сәйкес келеді?
Смотреть ответ
Квадратные корни и иррациональные выражения
) у(2)= _________, у(0,5)= _________, у(5)= _________;
b) значение аргумента, когда значение функции равно 1,5;
c) наименьшее значение функции.
Смотреть ответ
Квадратные корни и иррациональные выражения
Кирпич падает на землю с высоты 1 м. Скорость свободного падения тела связана с высотой падения формулой 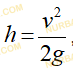
a) С какой скоростью кирпич упадет на землю с данной высоты в 1 м?
b) Во сколько раз увеличится скорость, если высота увеличится в 2, в 4, в 100 раз?
c) Какой должна быть высота расположения, чтобы скорость падения кирпича была равной 20 м/с?
Смотреть ответ
Даны числа:Запишите, сколько из них являются иррациональными
Смотреть ответ
Екі айнымалысы бар теңдеулер, теңсіздіктер, және олардың жүйелері
Берілген теңдеулерді:
қолданып, кестені толтырыңыз:
Смотреть ответ
Екі айнымалысы бар теңдеулер, теңсіздіктер, және олардың жүйелері
Графиктік әдіспен теңдеулер жүйесінің шешімінің санын көрсетіңіз
Смотреть ответ
Екі айнымалысы бар теңдеулер, теңсіздіктер, және олардың жүйелері
1) Теңдеулер жүйесін алмастыру әдісімен шешіңіз:
2) Теңдеулер жүйесін мүшелеп қосу немесе бөлу тәсілімен шығарыңыз
Смотреть ответ
Екі айнымалысы бар теңдеулер, теңсіздіктер, және олардың жүйелері
Есепті теңдеулер жүйесін құру арқылы шығарыңыз
1. Тік бұрышты үшбұрыштың гипотенузасы 20см-ге, ал оның катеттерінің қосындысы 28 см-ге тең. Қабырғаларының ұзындықтарын табыңыз.
2. Ара қашықтығы 80 км болатын Астана қаласы мен Шортанды елді мекенінен бір мезгілде біріне-бірі қарсы екі автомобиль жолға шықты. Кездескеннен кейін 20 мин өткенде автомобильдердің біреуі Шортанды елді мекеніне, ал 45 мин өткенде екіншісі Астана қаласына келеді. Әрбір автомобильдің жылдамдығын табыңыз.
Смотреть ответ
Екі айнымалысы бар теңдеулер, теңсіздіктер, және олардың жүйелері
пен у мәндерінің жұбы ?+3?+1<0 теңсіздігінің шешімі бола ма:
1) ?=0,?=0; 2) ?=0,?=−3;
3) ?=−3,?=0, 4) ?=1,?=2.
Смотреть ответ
Екі айнымалысы бар теңдеулер, теңсіздіктер, және олардың жүйелері
Екі айнымалысы бар теңсіздіктер берілген:
Теңсіздіктердің шешімін декарттық координаталық жазықтықта кескіндеңіз
Смотреть ответ
Екі айнымалысы бар теңдеулер, теңсіздіктер, және олардың жүйелері
Теңсіздіктер жүйесімен берілген нүктелер жиынын координаталық жазықтықта көрсетіңіз:
Смотреть ответ
Комбинаторика элементтері
Айгүлде алма, өрік, алша бар. Айгүл қанша тәсілмен жемістердің орнын алмастырып қоя
алады? Айгүл қанша тәсілмен жемістердің біреуін ғана таңдай алады?
Смотреть ответ
Комбинаторика элементтері
Егер n элементтен алынған 3 таңдау үшін қайталанбайтын орналастыру саны 240-қа тең
болса, элементтер саны нешеге тең?
Смотреть ответ
Комбинаторика элементтері
Мангышлақ-Астана жолаушылар поезында 11 вагон бар. Поезға 5 жолаушы отырды.
Жолаушылар әр түрлі вагонда болатындай қанша орналастыру жасауға болады?
Смотреть ответ
Комбинаторика элементтері
9 сыныпта 22 оқушы бар. Мектепішілік білім бәйгесіне қатысу үшін оқушылар пәндер
бойынша үш топқа бөлінді. Химия мен биология тобында 5 оқушы, физика мен математика
тобында 9 оқушы, тарих пен география тобында 8 оқушы болатындай қанша тәсілмен таңдап
алуға болады?
Смотреть ответ
Комбинаторика элементтері
Бином жіктелуіндегі төртінші мүшесін табыңыз
Смотреть ответ
Комбинаторика элементтері
өрнегінің жіктелуіндегі х-ке тәуелсіз мүшесін және ретін табыңыз
Смотреть ответ
Комбинаторика элементтері
бином жіктелуіндегі
мүшесінің коэффициентін табыңыз
Смотреть ответ
Комбинаторика элементтері
бином жіктелуіндегі коэффициенттерінің қосындысын табыңыз
Смотреть ответ
Найдите множество точек координатной плоскости, которое задано системой неравенств:
Смотреть ответ
Решите задачу с помощью системы уравнений. Один каменщик может выложить стену на 6 часов быстрее, чем другой. При совместной работе они за 2 часа выложат половину стены. За сколько часов каждый из них может выложить стену?
Смотреть ответ
Из цифр 2, 3, 5, 7, 8, 9 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые кратны 2?
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
1.Выпишите из предложенных уравнений нелинейные уравнения с двумя переменными:
Смотреть ответ
В роте пятнадцать солдат, три офицера и пять сержантов. На охрану объектов необходимо выделить восемь солдат, двух сержантов и одного офицера. Сколько существует вариантов составить наряд?
Смотреть ответ
Сколько существует различных семизначных телефонных номеров без повторения цифр и с учетом того, что нуль не может стоять на первом месте?
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Решите систему уравнений методом подстановки:
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Решите систему уравнений методом замены переменных:
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Решите систему уравнений:
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Решите систему уравнений методом алгебраических действий
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Решите систему уравнений с двумя переменными графически:
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Установите соответствие между условием задачи и системой уравнений.
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Башни «Темір жолы», называемые «Голубыми китами», в Нур-Султане посетили
две группы туристов. Они одновременно сели на соседние лифты, решив подняться на 27
этаж. Для этого им нужно проехать 120 м. Первый лифт поднялся на нужный этаж на 0,3
мин раньше. Туристы выяснили, что скорость второго лифта на 0,5 м/с меньше скорости
первого лифта. Какова скорость каждого из лифтов?
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Решите задачу с помощью системы уравнений.
Расстояние между городами А и В равно 120 км. Из города А в город В вышел автобус, а через
15 мин – легковая машина, скорость которой больше скорости автобуса на 12 км/ч. Легковая
машина пришла в город В на 5 мин раньше, чем туда прибыл автобус. Найдите скорости
автобуса и легковой машины.
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
В соревнованиях по бегу на дистанцию 120 м участвуют три спортсмена. Скорость
первого из них на 1 м/с больше скорости второго, а скорость второго бегуна равна
полусумме скоростей первого и третьего. Первый бегун пробежал дистанцию на 3 с
быстрее третьего. Определите скорость третьего бегуна.
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Изобразите на плоскости множество точек, заданных неравенством y > 3x -2 .
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
На ремонт участка трассы «Тараз – Шымкент» двум бригадам было отведено 18
дней. В действительности же, сначала работала только первая бригада, а заканчивала
ремонт участка дороги только вторая бригада, производительность труда которой выше,
чем у первой бригады. В результате ремонт участка дороги продолжался 40 дней, причем
первая бригада в свое рабочее время выполнила 2/3 всей работы. За сколько дней был бы
отремонтирован заданный участок трассы?
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
На рисунке изображен график функции, заданной уравнением y =x²- 6х 2 .
a) Покажите на координатной плоскости множество решений неравенства
y-x²+6x≤0
b) Какая из точек: А (3; 5) или В (–3; –2), принадлежит множеству решений
неравенства из пункта a?
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Соотнесите неравенства и их решения.
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Изобразите множество точек, заданных системой неравенств:
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Изобразите область, заданную на координатной плоскости системой:
Смотреть ответ
Элементы комбинаторики
a) Вычислите:
b) Упростите выражение:
Смотреть ответ
Элементы комбинаторики
a) Найдите первые три слагаемых в биномиальном разложении при возрастании
степени х и запишите коэффициент при х:
b) Используя результаты предыдущих действий, найдите коэффициент при х в
биномиальном разложении
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
При каком значении параметра а система неравенств имеет единственное решение?
Смотреть ответ
Элементы комбинаторики
Асель собрала цветы: 8 ромашек и 9 незабудок. Сколькими способами можно
составить букет из 7 цветов, если:
а) в букете 4 ромашки и 3 незабудки;
b) в букете как минимум должны быть 4 незабудки?
Смотреть ответ
Уравнения, неравенства с двумя переменными и их системы
Найдите все двузначные числа, удовлетворяющие следующим условиям:
а) сумма цифр числа не менее 7;
b) сумма квадратов цифр меньше 25.
Смотреть ответ
Элементы комбинаторики
Запишите выражения в порядке возрастания их числовых значений:
Смотреть ответ
Элементы комбинаторики
Запишите выражения в порядке возрастания их числовых значений:
Смотреть ответ
Элементы комбинаторики
Код от сейфа составлен из 5 букв латинского алфавита (в латинском алфавите 26 букв). Сколько существует вариантов кода, если буквы в коде не повторяются?
Смотреть ответ
Элементы комбинаторики
В магазин поступило 7 видов шампуней. Сколькими способами продавец может их расставить в ряд на полке?
Смотреть ответ
Элементы комбинаторики
Код от сейфа составлен из 5 букв латинского алфавита (в латинском алфавите 26 букв). Сколько существует вариантов кода, если буквы в коде не повторяются?
Смотреть ответ
Элементы комбинаторики
Ученикам на уроке литературы рекомендовано к прочтению 20 книг. Сколькими способами ученик может выбрать 9 книг из списка?
Смотреть ответ
Элементы комбинаторики
В городе Тараз открылась новая телефонная станция. Она предоставляет своим абонентам шестизначные телефонные номера, начинающиеся с 5. При этом последние пять цифр любые, но не повторяющиеся между собой. Сколько абонентов смогут получить телефонный номер?
Смотреть ответ
Элементы комбинаторики
В магазин поступило 7 видов шампуней. Сколькими способами продавец может их расставить в ряд на полке?
Смотреть ответ
Элементы комбинаторики
Команда из 7 учеников 9 класса участвуют в спaртакиаде.
а) Сколькими способами из них можно составить команду из 5 человек для игры в баскетбол?
b) Сколькими способами всех семeрых можно расставить для участия в эстафете?
c) Ведется статистика результативности каждого спортсмена. Сколько существует способов распределения 1, 2 и 3 мест внутри команды?
Смотреть ответ
Элементы комбинаторики
Ученикам на уроке литературы рекомендовано к прочтению 20 книг. Сколькими способами ученик может выбрать 9 книг из списка?
Смотреть ответ
Элементы комбинаторики
В классе учатся 12 девочек и 16 мальчиков. Сколько существует способов деления учеников класса поровну так, чтобы в каждой группе число мальчиков и девочек было одинаковым?
Смотреть ответ
Элементы комбинаторики
В городе Тараз открылась новая телефонная станция. Она предоставляет своим абонентам шестизначные телефонные номера, начинающиеся с 5. При этом последние пять цифр любые, но не повторяющиеся между собой. Сколько абонентов смогут получить телефонный номер?
Смотреть ответ
Элементы комбинаторики
Подбросили 8 монет. Сколько раз количество выпавших «орлов» превысит количество выпавших «решек»?
Смотреть ответ
Элементы комбинаторики
Команда из 7 учеников 9 класса участвуют в спaртакиаде. а) Сколькими способами из них можно составить команду из 5 человек для игры в баскетбол? b) Сколькими способами всех семeрых можно расставить для участия в эстафете? c) Ведется статистика результативности каждого спортсмена. Сколько существует способов распределения 1, 2 и 3 мест внутри команды?
Смотреть ответ
Элементы комбинаторики
У Алии в саду выросли 10 красных и 15 белых тюльпанов.
a) Сколькими способами можно сделать букет из 3 красных и 4 белых тюльпанов?
b) Мама Алии попросила сделать для нее букет из 7 цветов так, чтобы в нем было
хотя бы три красных тюльпана. Сколькими способами можно сделать такой букет?
Смотреть ответ
Элементы комбинаторики
Подбросили 8 монет. Сколько раз количество выпавших «орлов» превысит количество выпавших «решек»?
Смотреть ответ
Элементы комбинаторики
У Алии в саду выросли 10 красных и 15 белых тюльпанов. a) Сколькими способами можно сделать букет из 3 красных и 4 белых тюльпанов? b) Мама Алии попросила сделать для нее букет из 7 цветов так, чтобы в нем было хотя бы три красных тюльпана. Сколькими способами можно сделать такой букет?
Смотреть ответ
Элементы комбинаторики
Дан бином
a) Найдите коэффициент при х^3 в разложении бинома.
b) Найдите алгебраическую сумму коэффициентов многочлена.
Смотреть ответ
mowname
Модератор
-
#1
СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

ИНСТРУКЦИЯ:КАК СКАЧАТЬ ФАЙЛ
Последнее редактирование модератором: Фев 23, 2022
Галина Васильевна
Новичок
666555
Новичок
Afeliya
Новичок
-
#4
Методические рекомендации по суммативному оцениванию по предмету
«Алгебра и начала анализа»
10 класс
(естественно-математическое направление)СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

* Скрытый текст не может быть процитирован. *
Afeliya
Новичок
Надежда Касимова
Новичок
Куляш
Новичок
-
#7
Методические рекомендации по суммативному оцениванию по предмету
«Алгебра и начала анализа»
10 класс
(естественно-математическое направление)СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

* Скрытый текст не может быть процитирован. *
Здравствуйте. Спасибо
Нұрасыл
Новичок
Нұрасыл
Новичок
-
#9
Методические рекомендации по суммативному оцениванию по предмету
«Алгебра и начала анализа»
10 класс
(естественно-математическое направление)СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

* Скрытый текст не может быть процитирован. *
күшті
A.Z.Y_1011
Новичок
-
#10
Методические рекомендации по суммативному оцениванию по предмету
«Алгебра и начала анализа»
10 класс
(естественно-математическое направление)СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

* Скрытый текст не может быть процитирован. *
Керемет
НАми
Новичок
Еле
Новичок
ilkov1980
Новичок
ilkov1980
Новичок
катон
Новичок
-
#15
СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

* Скрытый текст не может быть процитирован. *
ИНСТРУКЦИЯ:КАК СКАЧАТЬ ФАЙЛ
катон
Новичок
Акмаралл
Новичок
-
#17
СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

* Скрытый текст не может быть процитирован. *
ИНСТРУКЦИЯ:КАК СКАЧАТЬ ФАЙЛ
Кумар
Новичок
-
#18
СОДЕРЖАНИЕ ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ……………………………..4
Суммативное оценивание за раздел «Функция, ее свойства и график» ……………………………. 4
Суммативное оценивание за раздел «Тригонометрические функции» …………………………….. 8
Суммативное оценивание за раздел «Обратные тригонометрические функции»……………. 11
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ……………………………14
Суммативное оценивание за раздел «Тригонометрические уравнения»…………………………. 14
Суммативное оценивание за раздел «Тригонометрические неравенства»………………………. 17
Суммативное оценивание за раздел «Вероятность»………………………………………………………. 20
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ……………………………23
Суммативное оценивание за раздел «Многочлены» ……………………………………………………… 23
Суммативное оценивание за раздел «Предел функции и непрерывность»……………………… 26
Суммативное оценивание за раздел «Производная»……………………………………………………… 30
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ……………………………35
Суммативное оценивание за раздел «Применение производной»………………………………….. 35
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики»………………………………………………………………………………………………………….. 39

* Скрытый текст не может быть процитирован. *
ИНСТРУКЦИЯ:КАК СКАЧАТЬ ФАЙЛ
Элмира Сабытжан
Новичок
Элмира Сабытжан
Новичок

 дробно-линейной функции и строить ее график;
дробно-линейной функции и строить ее график; . Постройте график.
. Постройте график. ;
; 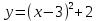 . Постройте график.
. Постройте график.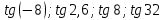 в порядке возрастания.
в порядке возрастания. , найдите:
, найдите: 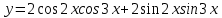 наименьший положительный период функции
наименьший положительный период функции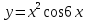 .
.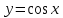 принимает на
принимает на  ровно один раз?
ровно один раз?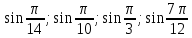 в порядке возрастания.
в порядке возрастания.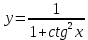 , найдите:
, найдите:  наименьший положительный период функции
наименьший положительный период функции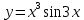 .
.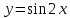 принимает на
принимает на  ровно один раз?
ровно один раз?