Алгоритм решения 9 задания егэ математика профиль 2022

В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы. Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике. 

Способы решения номера

9 задание по математике профильного уровня 2022 получится решить четырьмя методами. 

Первый вариант

Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом: 

Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки: 

Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты: 

16a — 4b + c = -3

Аналогичным образом записываем выражение, используя две остальные точки: 

9a — 3b + c = -2

4a — 2b + c = 1

Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем: 

b = 8;

c = 13. 

Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы: 

f(x) = x² + 8x + 13

f(-12) = 144 — 96 + 13 = 61

Второй вариант

Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы: 

Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x², сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x₀ = -b / 2a. По рисунку видно: x₀ = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще. 

Третий вариант

9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример: 

y = x²

Сдвиг влево записывается: 

y = (x + 4)²

Сдвиг вниз: 

y = (x + 4)² — 3

Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61. 

Четвертый вариант

Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат: 

Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!

В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum. 

Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации! 

Задание 9 Профильного ЕГЭ по математике – это несколько типов текстовых задач. Условия и «сюжеты» задач могут быть разными. При этом в каждой из них нужно построить математическую модель, то есть обозначить какие-либо величины за переменные, составить уравнение и решить его. И еще есть неочевидные секреты их решения. О них – в конце статьи.

Вот основные типы текстовых задач, которые могут вам встретиться на ЕГЭ под номером 9. Переходите по ссылкам, читайте краткую теорию и разбирайте вместе с нами решения задач!

1. Задачи на движение

2. Задачи на работу

3. Задачи на проценты

4. Задачи на сплавы, смеси, растворы

5. Задачи на движение по окружности

Формула работает и в этом случае. Здесь – расстояние,  – скорость, – время.

А секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в -ный раз.

6. Задачи на нахождение средней скорости

По определению, средняя скорость получается, если всё расстояние поделить на всё время. В общем случае она не равна среднему арифметическому скоростей, а находится по следующей формуле:

.

7. Задачи на движение протяженных тел, встречное движение и обгон

Да, это те самые задачи, где поезд проходит через туннель. Или проезжает мимо платформы. И нам нужно учитывать длину поезда.

Есть еще задачи на встречное движение или обгон. Например, два поезда движутся навстречу друг другу (конечно, по параллельным путям), или один поезд обгоняет другой. Такие задачи удобно решать в движущейся системе отсчета.

Но и это не все. Есть еще задачи ЕГЭ на арифметическую и геометрическую прогрессии.

8. Задачи на арифметическую прогрессию

Арифметическая прогрессия в задачах ЕГЭ по математике

9. Задачи на геометрическую прогрессии

Геометрическая прогрессия в задачах ЕГЭ по математике

И еще мы обещали секреты решения текстовых задач на движение и работу. Читайте и применяйте!

ЕГЭ по математике профиль

Инфоурок

›

Алгебра

›Презентации›Презентация «Решение задания №9 ЕГЭ 2022»

1. Алгоритмы решения задания № 9 «Графики функций»

Алгоритмы решения задания № 9
«Графики функций»
ЕГЭ по математике 2022, профильный уровень

2. Материалы по теме

• https://ege.sdamgia.ru/
• https://mat-ege.ru/ege-profile/profile-9-funkcii-i-ih-grafiki/
• https://ege-study.ru/ru/ege/podgotovka/matematika/zadanie-9-ege-pomatematike-grafiki-funkcij/
• https://mathematichka.ru/school/functions/Function_Graph_Table.html
• http://mathprofi.ru/grafiki_i_svoistva_funkcij.html
• https://ege314.ru/9-funktsii-i-ih-svoystva/

3. Парабола

Задание 9 № 562060
(6;
1) Координаты вершины: (6; 8), значит:
(2; 4)
2) Для поиска коэффициента k возьмем точку
на графике, например (2; 4):
3) Таким образом,
И

4. Парабола

Задание 9 № 562283
(5; 7)
1)
(3; 3)
2)
3) Таким образом,
И

5. Парабола

Задание 9 № 562161
1)
2)
(0; 2)
3) Таким образом,
И
(2; 0)

6. Парабола

Задание 9 № 564654
(-1; 6)
1) Возьмем координаты трех точек и запишем в виде
Вычтем из (1) (2) и из (2) (3):
(-2; 1)
(-3; -2)

7. Гипербола

Задание 9 № 564197
1) Точка пересечения асимптот
имеет координаты (3; 2), значит
(3; 2)
2) Коэффициент k найдем с помощью
координат точки на графике: (2; 1)
3) Таким образом,

8. Гипербола

Задание 9 № 564972
2) Коэффициент k найдем с помощью
координат точки на графике: (6; 0)
(5; -1)
3)
Ответ: -3

9. Гипербола

Задание 9 № 564960
2) Коэффициент k найдем с помощью
координат точки на графике: (3; -1)
(2; -4)
3) Приведем уравнение функции к нужному виду.
Для этого приведем к общему знаменателю:
Коэффициент

10. Гипербола

Задание 9 № 564970
(2; 5)
2) Коэффициент k найдем с помощью
координат точки на графике: (5; 4)
3) Приведем уравнение функции к нужному виду.
Для этого приведем к общему знаменателю:
Коэффициент

11. Гипербола

Задание 9 № 564966
(-2; 2)

12. Показательные функции

1. График нашей функции возрастает, значит
2. В общем виде график показательной функции проходит
через точку (0; 1).
3. Сдвиг на 3 единицы вниз, значит
4. По графику видим, что
Тогда найдем основание а:
5. Таким образом, функция:
Тогда
Сдвиг на 3 единицы вниз

13. Показательные функции

1. График нашей функции возрастает, значит
2. В общем виде график показательной функции проходит
через точку (0; 1).
3. Сдвиг на 3 единицы вниз, значит
4. По графику видим, что
Сдвиг на 3 единицы вниз
Тогда найдем основание а:
Тогда
5. Таким образом, функция:

14. Показательные функции

1. Возьмем координаты двух точек на графике: (1; 4) и (-3; 1)
(1; 4)
Рассмотрим отдельно
второе уравнение
Вернемся к системе и
найдем a
2. Значит
3. Тогда
(-3; 1)

15. Показательные функции

(1; 4)
1. Возьмем координаты двух точек на графике: (1; 4) и (-3; 1)
Рассмотрим отдельно
второе уравнение
(-3; 1)
Вернемся к системе и
найдем a
2. Значит
3. Тогда

16. Логарифмические функции

1. График нашей функции возрастает, значит
2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 3 единицы вниз, значит
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда
Сдвиг на 3 единицы вниз

17. Логарифмические функции

1. График нашей функции возрастает, значит
2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 3 единицы вниз, значит
Сдвиг на 3 единицы вниз
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда

18. Логарифмические функции

1. График нашей функции возрастает, значит
2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 5 единиц влево, значит
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда
Сдвиг на 5 единиц влево

19. Логарифмические функции

1. График нашей функции возрастает, значит
2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 5 единиц влево, значит
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда
Сдвиг на 5 единиц влево

20.

Линейная функция
Задание 9 № 508895
Задание 9 № 508903
1)
2)
(3; 4)
7
1)
2)
4

21.

Линейная функция
Найдите абсциссу точки пересечения графиков.
1)
f(x) = -x + 1
Задание 9 № 509229
1)
2)
(-2; 4)
2)
3
5
3
1

22.

Линейная функция
Задание 9 № 621771
Найдите абсциссу точки пересечения графиков.
2)
f(x) = x + 1
(-2; 4)
3
x + 1 = 1,5 x + 7
0,5x = -6
x = — 12
2
2
2
1)
2)

23.

Кусочно-линейная функция
Задание 9 № 564185
3

24.

Кусочно-линейная функция
Задание 9 № 56418

25.

k
Определим, что
m
k
m

26.

Кусочно-линейная функция
Задание 9 № 563824
1)
1) y = -1x + 3
k=-1; m=3
2) y = 3x — 5
k=3; m=-5
k
a+b = 3
a- b = -1
2a=2
a=1
2)
m
c+d = -5
-c+d = 3
2d=-2
d=-1
2
α
3
2
3
α
1
Справочно:
y = kx + m
k=tgα
1x — 1 = 0
x=1
y = 3x + m
(2;1) 3*2 + m = 1
m=-5

27.

Синусоиды
T = 2π
«горка» a > 0
«рост» 2
График симметричен
относительно Oy

28.

Синусоиды
Смещение по Ox
Задание 9 № 564531
«горка» a>0
Смещение по Оу
d =-1
а – изменение «роста»
функции
«рост» 4
-1
(стандартный «рост» = 2)
-3
а=4:2=2
с=0
График симметричен
относительно Oy

29.

T=2
f(x) = 2 cos (bπx) — 1
k = bπ;
|b| = 1
f(x) = 2 cos(πx) — 1

30.

Синусоиды
Задание 9 № 564589
T=1
а = -2 : 2 = -1
d =-1
|b| = 2
«рост» 2
f(x) = -cos (2πx) — 1
-2
с=0
«ямка»
а<0

31.

Синусоиды
На
рисунке
Задание 9 № 564556
изображён
график
функции
вида
где
«горка» a>0
T=4
числа a, b, c и d — целые. Найдите
4
а=4:2=2
|b| = 2
«рост» 4
2
с=0
d=2

32. Благодарим за внимание!

Белова Марина Александровна
[email protected]
Каратун Ольга Леонтьевна
[email protected]

Решение задач №8,

ЕГЭ профиль.

Выполнила: Лаврова И.В.,

учитель МБОУ «Поташкинская СОШ»

15 км/ч через 1ч II 14 км/ч через 2ч III х км/ч III II I 14 15 30 III догонит I v = х – 15 = — =3 III догонит II v = x – 14 = — = 3 3 — 103 х + 840 =0 = 40/3 = 13 не удовл. ограничению = 21 Ответ: 21 » width=»640″

Задачи с тремя участниками движения. Статград 16.02.2022

Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч.

Через час после него со скоростью 14 км/ч из того же посёлка в том же

направлении выехал второй велосипедист, а ещё через час после этого —третий. Найдите

скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа после этого догнал первого. Ответ дайте в км/ч.

I 15 км/ч ограничения: v 15 км/ч

через 1ч II 14 км/ч

через 2ч III х км/ч

III II I

14 15 30

III догонит I v = х – 15 = — =3

III догонит II v = x – 14 =

— = 3

3 — 103 х + 840 =0

= 40/3 = 13 не удовл. ограничению = 21

Ответ: 21

Мультиурок учитель математики Лаврова Ирина Васильевна

Блог

Видео –задача с тремя участниками движения

Метод рычага

8. Смешав 38-процентный и 52-процентный растворы кислоты и добавив

10 кг чистой воды, получили 36-процентный раствор

кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 38-процентного раствора использовали для получения смеси?

38х + 52у = 36(х+у+10) (I)

38х+52у + 50∙10 = 46(х + у+ 10) (II)

10(х + у + 10) = 500

х + у + 10 = 50

х + у = 40 у=40-х, подставим в (1) х=20, у=20

Задачи на концентрацию и сплавы есть статьи :

Журналы «Математика в школе» №4, 94

«Математика в школе» №1, 97

Журнал «Математика . Всё для учителя» №2 [62] ст.Л.В.Гориной «Как перестать бояться и начать.. решать задачи на смеси и сплавы»,

стр.26

Журнал «Математика для школьников», №2, 2006,, С.Н.Олехник,

«Старинный способ решения задач на смешение веществ», стр. 56

Метод креста

12. Задание 8 №  99576

Имеется два сплава. Первый содержит 10% никеля, второй  — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

10% 5 частей

25%

30% 15 частей

• 15 +5 = 20(частей)-всего
• 200 : 20 = 10 г- масса 1 части
• 10 ∙5 = 50 (г) – масса 1 сплава
• 10 ∙ 15 = 150 (г) –масса 2 сплава
• 150- 50 =100 (г)
• Ответ : 100

Задание 8 №  99576

Имеется два сплава. Первый сплав содержит 10% меди, второй  — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

10% 10 частей

30%

40% 20 частей

• 20 – 10 = на 10 ( частей) больше масса 2 сплава
• 3 : 10 = 0,3 (кг) – в одной части
• 0,3 ∙10 = 3 (кг)- масса 1 сплава
• 0,3 ∙ 20 = 6 ( кг) – масса 2 сплава
• 3 + 6 = 9 (кг)

Ответ: 9 кг

№ 8. Курага получается в процессе сушки абрикосов. Сколько

килограммов абрикосов потребуется для получения 21 килограмма

кураги, если абрикосы содержат 86 % воды, а курага содержит 18 % воды?

%воды % сух. масса масса

вещ-ва сух.вещ-ва

абрикосы 86 14 % х 0,14х

курага 18 82 % 21 кг 0,82∙ 21

0,14х = 0,82 ∙ 21 14х = 82 ∙ 21

0,14х = 17,22 2х =82 ∙ 3

х = 123 х = 246 : 2

х = 123

Ответ: 123

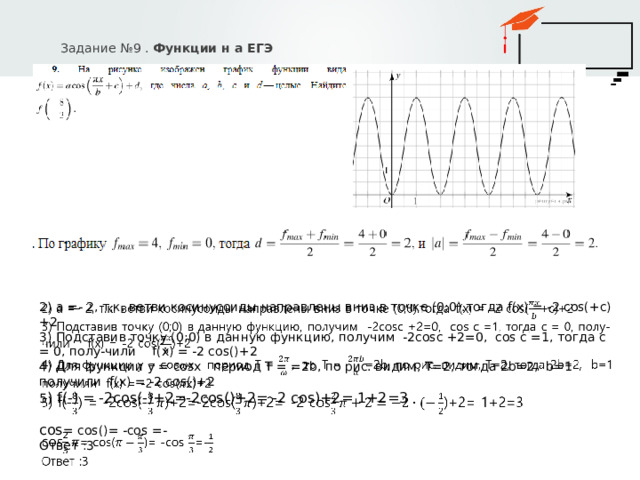
Задание №9 . Функции н а ЕГЭ

2) а =- 2, т.к. ветви косинусоиды направлены вниз в точке (0;0).тогда f(x) = -2 cos(+c)+2

3) Подставив точку (0;0) в данную функцию, получим -2cosc +2=0, сos c =1, тогда с = 0, полу-чили f(x) = -2 cos()+2

4) Для функции у = cosх период Т = =2b, по рис. видим, Т=2, тогда 2b=2, b=1

получили f(x) = -2 cos()+2

5 ) f(-) = -2cos(-)+2=-2cos()+2= -2 cos)+2= 1+2=3

cos = cos()= -cos =-

Ответ :3

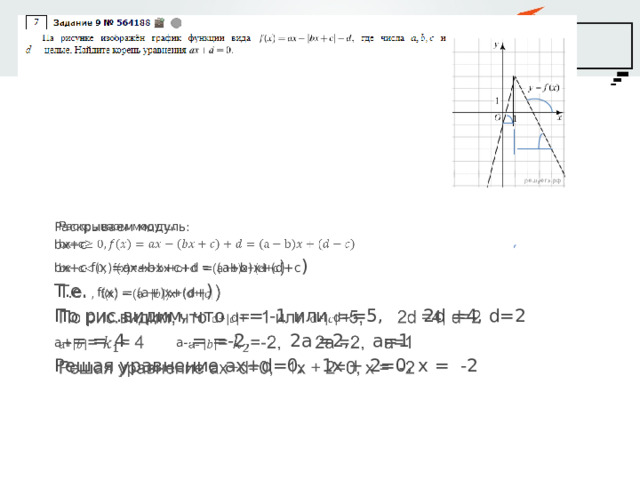
Раскрываем модуль:

bx+c

bx+c f(x)=ax+bx+c+d = (a+b)x+(d+c )

Т.е. f(x) = (a+)x+(d+ )

По рис.видим, что d+ = -1 или d+ =5, 2d =4, d=2

a+ = = 4 a- = =-2, 2a =2, a=1

Решая уравнение ax+d=0, 1x + 2=0, x = -2

Спасибо за внимание и понимание

23 октября 2021

В закладки

Обсудить

Жалоба

Четыре способа решить новую задачу из ЕГЭ

Задание №9 профильного ЕГЭ-2022.