Анализ экзамена по математике спо - Помощь в подготовке к экзаменам и поступлению

СОДЕРЖАНИЕ Введение	4
1. Общие положения	6
2. Рекомендации по составлению экзаменационных работ	7
3. Рекомендации по проведению и оцениванию экзамена	11
4. Примерные варианты экзаменационной работы для проведения письменного экзамена по математике	15
ПРИЛОЖЕНИЯ	24
Приложение 1. Инструкция для обучающихся по выполнению экзаменационной работы (примерная)	24
Приложение 2. Примерный перечень элементов содержания по математике для составления экзаменационных работ письменного экзамена в образовательных учреждениях НПО/СПО	25
Приложение 3. Примерный перечень требований к уровню подготовки обучающихся по математике для составления экзаменационных работ письменного экзамена в образовательных учреждениях НПО/СПО	31

Введение

При реализации основной профессиональной образовательной программы
(далее — ОПОП) по специальностям СПО с получением среднего (полного)
общего образования предусматривается итоговый контроль по освоению
образовательной программы среднего (полного) общего образования, который
согласно требованиям Федеральных государственных образовательных стандартов
начального и среднего профессионального образования (ФГОС СПО) проводится в
рамках промежуточной аттестации.

С одной стороны, в соответствии со ст. 15 п. 3 Закона РФ «Об
образовании» образовательное учреждение самостоятельно в выборе системы оценок,
формы, порядка и периодичности промежуточной аттестации обучающихся.

Для разработки
итогового контроля учебных достижений обучающихся по математике при реализации
образовательной программы среднего (полного) общего образования в пределах
основной профессиональной образовательной программы СПО использована следующая
нормативно-правовая база:

1)
Организация итогового контроля
учебных достижений обучающихся по математике при реализации образовательной
программы среднего (полного) общего образования в пределах основной
профессиональной образовательной программы НПО/СПО [Текст] : методические
рекомендации / авт.-сост.: М. А. Гуляева, Е. Г. Веклич, О. Е. Медведева, О. В.
Овсянникова, Т. П. Трушкина. – Кемерово: ГОУ «КРИРПО», 2012. – 32 с.

В итоговом контроле отражены требования к организации и проведению
экзамена, оценке результатов выполнения работ, даны рекомендации по подготовке
к проведению процедуры экзамена, по составлению и структурированию
экзаменационной работы, инструкция для обучающихся по выполнению заданий.

Варианты экзаменационной работы для проведения экзамена в одной группе
обучающихся составлены равноценны между собой. Приводятся варианты
экзаменационных работ по математике по разным профилям. Обозначены критерии
оценки заданий и шкалы перевода баллов в отметки по пятибалльной системе.

1. Общие положения

Освоение образовательной программы среднего общего
образования завершается обязательным итоговым контролем учебных достижений
обучающихся, который проводится в рамках промежуточной аттестации,
предусмотренной федеральными государственными образовательными стандартами
среднего профессионального образования (далее – ФГОС СПО).

Экзамен по математике за курс среднего (полного) общего образования в
учреждениях профессионального образования при реализации основной
профессиональной образовательной программы СПО с получением среднего (полного)
общего образования является обязательным.

Экзамен по математике за курс среднего (полного) общего образования в
учреждениях СПО проводится в зависимости от учебного плана профессии или
специальности. Дата проведения предусматривается образовательным учреждением.

Экзамен по математике проводится письменно за счет времени, выделяемого
ФГОС СПО на промежуточную аттестацию, с использованием экзаменационных
материалов в виде набора контрольных заданий, требующих краткого ответа и/или
полного решения. На выполнение письменной экзаменационной работы по математике
дается 4 астрономических часа (240 минут).

Обозначим основные Положения, касающиеся организации и порядка
проведения экзамена по математике в образовательных учреждениях СПО:

– содержание экзаменационных материалов должно отвечать требованиям к
уровню подготовки выпускников, предусмотренным стандартом среднего (полного)
общего образования по соответствующей общеобразовательной дисциплине (математике)
и зафиксированным в примерных программах общеобразовательных дисциплин (примерной
программе учебной дисциплины «математика») специальностей СПО

– экзаменационные материалы дополняются критериями оценки (в
рекомендациях используется шкала перевода баллов в отметки);

– содержание экзаменационных материалов и критерии разрабатываются
преподавателем соответствующей учебной дисциплины (математики), согласовываются
с предметной (цикловой) методической комиссией и утверждаются в установленном
порядке;

– экзаменационные материалы для проведения письменных экзаменов с
использованием набора контрольных заданий формируются из двух частей:
обязательной, включающей задания минимально обязательного уровня, правильное
выполнение которых достаточно для получения удовлетворительной оценки «3», и
дополнительной части с более сложными заданиями, выполнение которых позволяет
повысить удовлетворительную оценку до «4» или «5»;

– оценка результатов выполнения письменных экзаменов осуществляется
согласно утвержденным критериям (шкалой перевода баллов в отметки), которые
открыты для обучающихся до конца экзамена.

Для оценки выполнения каждого задания экзаменационной работы по
балльной системе используются критерии оценки заданий.

Для перевода количества набранных баллов в отметку используется шкала
перевода баллов в отметки по пятибалльной системе.

Результат экзамена (полученные отметки) сообщается обучающимся в сроки,
установленные образовательным учреждением в положении об итоговой и
промежуточной аттестации обучающихся (срок не должен превышать 3 дней после
сдачи экзамена).

2. Рекомендации по составлению экзаменационных работ

В каждом учебном году в образовательных учреждениях СПО для проведения
экзамена по математике не позднее 1 месяца до даты проведения экзамена
готовится новый комплект контрольных материалов не менее, чем из четырех
вариантов для группы обучающихся, которые сдают экзамен в образовательном
учреждении в один день и одно и то же время (если в образовательном учреждении
профессионального образования имеются группы обучающихся, сдающие экзамен в
другой срок, то для таких групп необходимо разработать новые комплекты
контрольных материалов).

В экзаменационную работу включаются задания, выполнение которых
свидетельствует о наличии общематематических навыков, необходимых человеку в
современном обществе. Эти задания должны проверять базовые вычислительные и
логические умения и навыки, умение анализировать информацию, представленную в
графиках, ориентироваться в простейших геометрических конструкциях.

При составлении заданий экзаменационной работы по математике необходимо
отразить в заданиях основные содержательные линии курса математики
(алгебраическую, уравнений и неравенств, теоретико-функциональную,
геометрическую), а также основные умения и виды деятельности, которые должны
быть сформированы при изучении курса математики:

– уметь использовать приобретенные знания и умения в практической
деятельности и повседневной жизни;

– уметь выполнять вычисления и преобразования;

– уметь решать уравнения и неравенства;

– уметь выполнять действия с функциями;

– уметь выполнять действия с геометрическими фигурами, координатами;

– уметь строить и исследовать математические модели.

При формировании содержания экзаменационной работы по математике
учитываются также следующие факты:

– ограниченность объема часов, выделяемого на выполнение экзаменационной
работы;

– невозможность отражения в одной экзаменационной работе всех элементов
содержания учебной дисциплины, которые были изучены;

– правильное выполнение ограниченного числа заданий (указано в шкале
перевода баллов в отметки) обязательной части отвечает минимально обязательному
уровню подготовки, подтверждающему удовлетворительное освоение программы по
математике как составной части программы среднего (полного) общего образования,
реализуемой в рамках основных профессиональных образовательных программ
НПО/СПО.

Письменная экзаменационная работа по математике составляется из 2-х
частей: обязательной и дополнительной. В обязательную часть включаются задания
минимально обязательного уровня, в дополнительную часть – более сложные.

В обязательную часть работы должны быть включены задания
базового уровня по всем основным разделам требований ФГОС – геометрия
(планиметрия и стереометрия), алгебра, начала математического анализа, теория
вероятностей, комбинаторика и статистика.

При выполнении заданий обязательной части обучающиеся должны
продемонстрировать базовую математическую компетентность. Задания этой группы
проверяют базовые вычислительные и логические умения и навыки, умение
анализировать информацию, представленную в графиках и таблицах, использовать
простейшие вероятностные и статистические модели, ориентироваться в простейших
геометрических конструкциях, владение основными алгоритмами, знание и понимание
ключевых элементов содержания (математических понятий, их свойств, приемов
решения задач и пр.), умение пользоваться математической записью, а также
применять математические знания в простейших практических ситуациях.

Обязательная часть содержит не менее 18 заданий.

Составителям экзаменационных работ следует предусматривать, чтобы в
формулировке каждого задания были обозначены конкретные виды деятельности, на
выполнение которых направлено соответствующее задание (определите, вычислите,
решите, найдите, обозначьте и др.).

При составлении экзаменационных работ по математике принципиально важно
предусмотреть, чтобы в большей части заданий обязательной части от обучающегося
требовалось представить ход решения задачи и полученный ответ.

Требование представить только ответ или ответ с кратким пояснением
допускается при выполнении отдельных (2–4) заданий обязательной части. (Например:
задания обязательной части могут содержать такие формы ответа: с выбором одного
ответа из четырех предложенных вариантов (2 задания), с кратким ответом (6
заданий), на установление соответствия между объектами двух множеств (1
задание) и с записью решения (5 заданий). В последнем типе заданий не
обязательно давать пояснения по ходу решения задачи, достаточно грамотно
применить требуемый алгоритм)

Дополнительная часть направлена
на проверку владения материалом на повышенном уровне и умение решать
математические задачи, не сводящиеся к прямому применению алгоритма. Эта часть
должна содержать не менее 4 заданий повышенного уровня сложности из различных
разделов курса математики (например: 1 задание по геометрии, 3 задания по алгебре).

При выполнении всех заданий дополнительной части необходимо от
обучающихся требовать представления описания хода решения задачи и полученный
ответ. Возможны различные способы решения в записи развернутого ответа. Главное
требование – решение должно быть математически грамотным, из него должен быть
понятен ход рассуждений автора работы. При этом оценивается продвижение
обучающегося в решении задачи, а не недочеты по сравнению с «эталонным»
решением. При решении задачи можно использовать любые математические факты без
доказательств и ссылок, содержащиеся в учебниках и учебных пособиях, допущенных
или рекомендованных Министерством образования и науки РФ.

При подборе задач прикладной и практической направленности для
вариантов экзаменационных работ по математике целесообразно учитывать и
отражать в содержании профиль получаемой профессии/специальности.

Ниже приводятся примерные варианты экзаменационных работ для проведения
письменного экзамена по математике. Предложенные варианты наглядно знакомят преподавателей
со структурой экзаменационной работы, примерным объемом заданий в обязательной
и дополнительной ее частях, с примерной шкалой перевода баллов в отметки по
пятибалльной системе.

Составителям экзаменационных работ для проведения экзамена по математике
в образовательных учреждениях НПО и СПО при ознакомлении с предложенным
примерным вариантом и составлении своих вариантов следует иметь в виду, что
включенные в них задания не могут отражать всех вопросов содержания изученного
материала. Полный перечень вопросов, которые могут контролироваться на экзамене
по математике и включаться в него, приведен в Перечне элементов содержания по
математике для составления экзаменационных работ письменного экзамена (приложение
2).

При составлении экзаменационных заданий следует учитывать требования к
уровню подготовки обучающихся по математике, которые предусмотрены при
составлении экзаменационных работ письменного экзамена (приложение 3).

При подборе заданий, следует учитывать, чтобы каждое из них
характеризовалось четырьмя параметрами: элемент содержания, проверяемое умение,
категория познавательной области, форма ответа.

Важно иметь в виду, что каждый год при подготовке экзаменационных
материалов в образовательном учреждении сначала формируется проект одного (базового)
варианта. Затем проект базового варианта анализируется и оценивается предметной
(цикловой) комиссией по выполнению соответствующих требований:

— к структуре (наличию
обязательной и дополнительной частей, к наполнению их заданиями соответствующих
уровней сложности);

— к содержанию (с
точки зрения представленности заданий разных содержательных линий курса
математики, соответствующих умений и видов деятельности, соответствия уровня
сложности заданий);

— к расположению заданий (по возрастающей степени сложности в обязательной и дополнительной
части),

— ко времени выполнения заданий.

По необходимости базовый вариант дорабатывается.

После того, как базовый вариант удовлетворит всем основным параметрам,
обозначенным выше, и будет принят соответствующей предметной (цикловой)
комиссией, на его основе формируются другие варианты, необходимые для
проведения письменного экзамена по математике одновременно во всех группах
образовательного учреждения, которые закончили в данный период освоение
учебного курса математики (не менее четырех вариантов).

При этом составители следят за тем, чтобы все варианты экзаменационной
работы, сформированные на основе базового, были равноценны между собой по
структуре, количеству заданий, представленности заданий разных содержательных
линий курса математики, по проверяемым элементам содержания, умениям и видам
деятельности, а также по уровню сложности заданий и критериям оценки. Задания,
включенные в разные варианты под одним и тем же номером, должны проверять одни
и те же элементы содержания одинакового уровня сложности.

Предложенная технология разработки экзаменационных работ позволит
учреждениям профессионального образования формировать на основе базового
варианта другие, равноценные ему по всем параметрам, что уравнивает условия для
всех обучающихся образовательного учреждения, сдающих экзамен в один и тот же
день, и использовать единую шкалу перевода баллов в отметки по пятибалльной
системе.

Предложенные ниже примерные варианты экзаменационной работы
рекомендуются образовательным учреждениям НПО и СПО использовать как основу для
структурирования, определения объема работы в целом, формирования содержания с
учетом разного уровня сложности заданий обязательной и дополнительной частей,
составления шкалы перевода баллов в отметки по пятибалльной системе при
самостоятельном составлении вариантов экзаменационных материалов письменного
экзамена по математике.

Заметим, что при составлении экзаменационных работ образовательное
учреждение с учетом уровня подготовки обучающихся вправе повышать уровень
сложности заданий, предложенных в примерном варианте (как в обязательной части,
так соответственно и в дополнительной части).

Обращаем также внимание преподавателей математики на следующее: в
обязательную часть экзаменационной работы включаются задания минимально
обязательного уровня и правильное выполнение определенной ее части считается
достаточным для удовлетворительной отметки (см. шкала перевода баллов в отметки
по пятибалльной системе). Снижать уровень обучения до уровня минимально
обязательных требований нельзя даже при невысоком уровне подготовки обучающихся
отдельных групп. Иначе не удастся достигнуть минимально обязательного уровня
подготовки обучающихся. Уровень обучения всегда должен быть выше, чем уровень
требований, предъявляемых к результатам обучения.

3. Рекомендации по проведению и оцениванию экзамена

Экзамен по математике в учреждении профессионального образования
проводится в один день для всех групп, завершивших обучение по математике за
курс среднего (полного) общего образования.

К проведению экзамена по математике для каждого обучающегося готовится:

— текст с вариантом экзаменационной работы;

— краткая инструкция для обучающихся;

— шкала перевода баллов в отметки;

— листы для чистового оформления работы и для черновика со штампом
образовательного учреждения.

При этом метод и форма описания решения задачи могут быть
произвольными.

Все листы подписываются и после завершения работы сдаются
экзаменационной комиссии.

Вместе с текстом экзаменационной работы обучающимся выдаются справочные
материалы, линейки, если они требуются.

Текст экзаменационных заданий сопровождается краткой инструкцией для
обучающихся, шкалой перевода баллов в отметки по пятибалльной системе для
получения каждой из положительных отметок («3», «4», «5»), которые остаются
открытыми для них в течение всего времени экзамена.

Перед началом выполнения письменной экзаменационной работы обучающиеся
должны быть ознакомлены с ее структурой, критериями оценки заданий, шкалой
перевода баллов в отметки.

Шкала перевода баллов в отметки должны оставаться открытыми для
обучающихся в течение всего времени, отведенного на экзамен, могут быть
представлены на доске или выданы обучающимся.

Обучающимся поясняется, что основные требования к выполнению заданий
состоят в том, чтобы:

– из представленного решения был понятен ход рассуждений обучающегося;

– ход решения был математически грамотным;

– представленный ответ был правильным;

метод и форма описания решения задачи могут быть произвольными;

– выполнение каждого из заданий оценивается в баллах.

За правильное выполнение любого задания из обязательной части обучающийся
получает один балл.

При выполнении задания из обязательной части, где необходимо привести
краткое решение, за неполное решение задания (вычислительная ошибка, описка)
можно выставить 0,5 балла.

Если обучающийся приводит неверное решение, неверный ответ или не
приводит никакого ответа он получает 0 баллов. За выполнение любого задания из дополнительной
части можно использовать следующие критерии оценки заданий:

Содержание критерия	Баллы
Приведено верное обоснованное решение, приведен правильный ответ	3
Приведено верное решение, но допущена вычислительная ошибка или описка, при этом может быть получен неверный ответ	2
Решение начато логически верно, но допущена ошибка, либо решение не доведено до конца, при этом ответ неверный или отсутствует	1
Неверное решение, неверный ответ или отсутствие решения	0

При формировании в образовательном учреждении дополнительной части
базового варианта экзаменационной работы в нее могут быть включены задания,
правильное выполнение которых будет оценено другим количеством баллов, также
может измениться количество заданий в дополнительной части (но не менее четырех
заданий), приведенные критерии оценки (другая балльная система). Например: в
дополнительной части может быть предусмотрено 6 заданий и оцениваться могут
максимально 2 баллами. В таком случае следует предусматривать соответствующий
уровень сложности заданий.

Число баллов, которое обучающийся может получить за правильное
выполнение того или иного задания, проставляется в скобках около его номера в
бланке экзаменационной работы. Баллы, полученные за все выполненные задания,
суммируются.

Особое внимание
обучающихся необходимо обратить на шкалу перевода баллов в отметки, в которой
указано, сколько баллов достаточно набрать, чтобы получить ту или иную
положительную оценку. Шкала перевода баллов в отметки разрабатывается
преподавателем к конкретному варианту заданий.

Так как обязательная часть состоит из 18 заданий, то
на отметку «3», обучающийся должен верно выполнить не менее 9 заданий.

Несколько вариантов шкалы перевода баллов в отметки, в
зависимости от уровня сложности, приведен ниже.

Шкала
перевода баллов в отметки по пятибалльной системе

Отметка	Число баллов, необходимое для получения отметки (социально-экономический профиль)	Число баллов, необходимое для получения отметки (технический профиль)
«3» (удовлетворительно)	9–14	9–16
«4» (хорошо)	15–20 (не менее одного задания из дополнительной части)	17–21
«5» (отлично)	более 21 (не менее двух заданий из дополнительной части)	более 21

Шкала перевода баллов в отметки может быть размещена в инструкции для
обучающегося.

Перед началом выполнения работы проводится инструктаж обучающихся. До
обучающихся доводятся требования по выполнению экзаменационной работы.

Обучающимся поясняется, что:

– начинать работу всем следует с выполнения заданий обязательной части;

– для получения удовлетворительной оценки не обязательно выполнять все
задания обязательной части;

– правильное выполнение определенной части заданий обязательной части,
во-первых, гарантирует получение отметки «3», а во-вторых, дает основу для
повышения отметки до «4» или «5» при правильном выполнении нескольких заданий
дополнительной части;

– при выполнении
заданий дополнительной части следует проследить по шкале перевода баллов в
отметки — сколько заданий достаточно правильно выполнить, чтобы получить 4 или
5;

— имеет право
выбрать, в первую очередь, те задания, при выполнении которых он будет
чувствовать себя более уверенным.

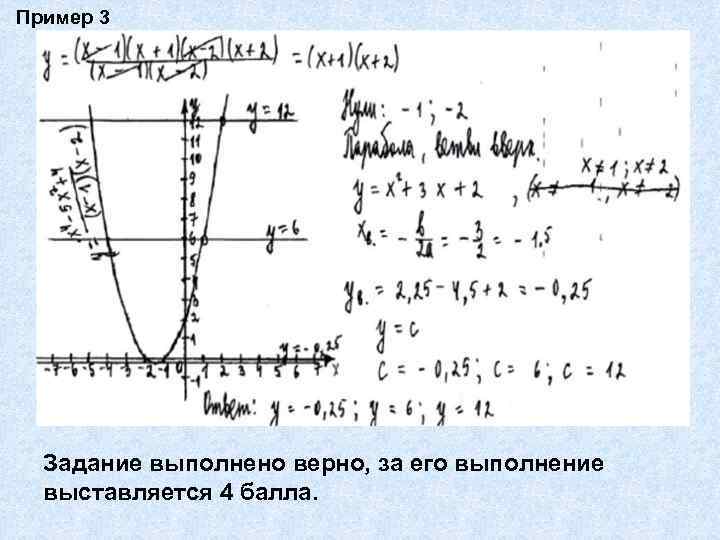
Примерный текст
краткой инструкции для обучающихся приводится в приложении 1, которая остается
на столах до завершения работы.

Примерный
вариант для экзаменационной работы

для проведения письменного экзамена по математике

*Обязательная часть* При выполнении заданий 1-6 запишите решение и полученный ответ. 1) (1 балл) Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны? 2) (1 балл) Вычислить значение выражения
3) (1 балл) Решить уравнение

4) (1 балл) Фабрика выпускает обувь. В среднем на 200 пар качественной обуви приходится две пары обуви со скрытыми дефектами. Найдите вероятность того, что купленная пара обуви окажется качественной. Результат округлите до сотых. 5) (1 балл) На рисунке изображен график функции, заданной на промежутке [-3; 7].

6)
(1 балл) Решите уравнение

При
выполнении заданий 7- 8 запишите правильный ответ из четырех предложенных
вариантов.

7)
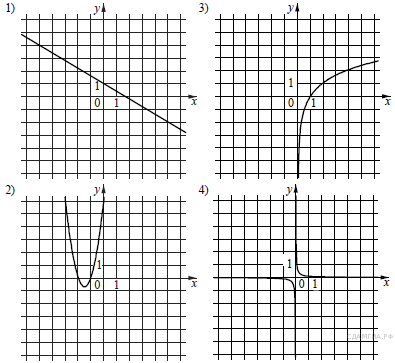
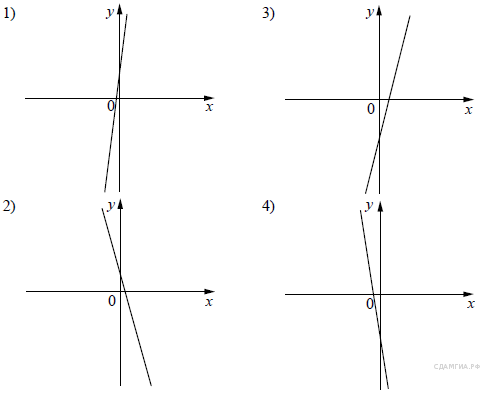
(1 балл) Укажите
график функции, заданной формулой

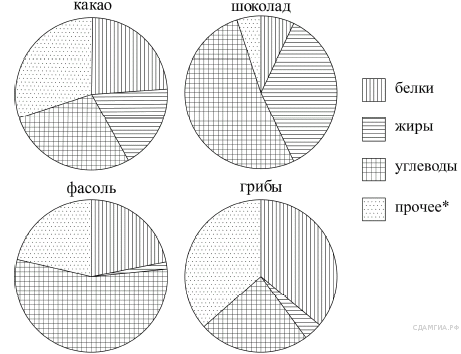
(1 балл) Определите, какие из
перечисленных точек принадлежат графику функции

В заданиях 9 — 12
найдите область определения функций, запишите ответ.

При выполнении
заданий 13- 18 запишите ход решения и полученный ответ.

15) (1 балл) Найдите наименьшее значение функции у = 7^х
на промежутке [-2; 4].

16) (1 балл) Тело движется по прямой так,
что расстояние S начальной точки изменяется по закону,
где – время движения в секундах. Найдите скорость тела через 2 секунды после
начала движения.

17) (1
балл) Найти объем параллелепипеда,

изображенного на
рисунке, при условии,

что все углы
прямые.

Дополнительная часть

При
выполнении заданий 15-18 запишите ход, обоснование решения и полученный ответ.

19) (3 балла) Решить неравенство

20) (3 балла)
Вычислить значение выражения

21) (3 балла)
Найдите точку минимума функции

22)
(3 балла) В правильной треугольной пирамиде

SABC
N – середина ребра BC, S –вершина.

Известно,
что SN=6, а площадь боковой поверхности равна 72.

Найдите
длину отрезка AB.

Примерный вариант для технического профиля

Обязательная
часть

При выполнении
заданий 1-3 запишите ход решения и полученный ответ.

1. (1 балл) Найдите корень уравнения 3^2-2х=81.

2. (1 балл) Найдите значение выражения

3. (1 балл) Флакон шампуня стоит 160 рублей. Какое наибольшее число
флаконов можно купить на 1000 рублей во время распродажи, когда скидка
составляет 25%?

При выполнении
заданий 4-7 запишите полученный ответ.

4.
(1 балл) На рисунке (см. ниже) изображен график функции y=f(x),
определенной на интервале (-6; 8). Определите количество целых точек, в которых
производная функции положительна.

5. (1 балл) Определите наименьшее и наибольшее значения
функции.

6. (1 балл) При каких значениях , f(х) ≥ 0.

7. (1 балл) При каких значениях х, f(x)≤0.

При выполнении
заданий 8-12 укажите ход решения и запишите полученный ответ.

8.
(1 балл) Найдите значение sinα, если известно, что cosα= и α I
четверти.

9. (1 балл) Решить уравнение

10. (1 балл) Решите уравнение

11. (1 балл) Строительной фирме нужно приобрести 50 кубометров
строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость
такой покупки с доставкой (в рублях)? Цены и условия указаны в таблице.

Поставщик	Цена бруса (руб.за 1м3)	Стоимость доставки	Дополнительные условия
А	3500	9900	—
Б	4500	7900	При заказе на сумму больше 150000 руб. доставка бесплатно
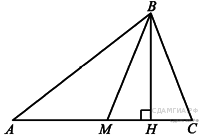
В	3600	7900	При заказе на сумму больше 200000 руб. доставка бесплатно

12. (1 балл) В равнобедренном треугольнике ABC с
основанием AC боковая сторона AB равна 8, а
Найдите высоту, проведенную к основанию.

При выполнении
заданий 13-18 запишите ход решения и полученный ответ.

13. Найдите значение
выражения:

14. Найдите корень уравнения

15. (1балл) Прямоугольный параллелепипед описан

около цилиндра, радиус основания которого

равен 4. Объем параллелепипеда равен 16.

Найдите высоту цилиндра.

16. (1 балл) Тело движется по закону: S(t) = х²–4х+3.
Определите, в какой момент времени скорость будет равна 4.

17. (1 балл) Решить
уравнение sin² x-2sinx-3=0.

18. (1 балл) Решите
неравенство

Дополнительная часть

При
выполнении заданий 19-22 запишите ход решения и полученный ответ.

19. (3 балла) Найдите наибольшее значение функции на отрезке

20. (3 балла) Решите систему уравнений:

21. (3 балла) В прямоугольном параллелепипеде АВСДА₁В₁С₁Д₁
известны ребра: AB=8 ,AD =6, СС₁= 5. Найдите угол между плоскостями
BDD₁ и AD₁B₁.

22. (3 балла) Найдите
решение уравнения: sin² x – 2sinx cosx – 3cos² x = 0.
Укажите корни, принадлежащие отрезку[-π; ].

Примерный вариант для социально-экономического профиля

Обязательная
часть

При выполнении
заданий 1-9 запишите ход решения и полученный ответ.

1. (1 балл) 1 метр ситца стоил 80 рублей. Сколько можно купить
ткани на 1000 рублей, если администрация магазина в честь праздника сделала
скидку 10%?

2. (1 балл) В группе 25 студентов. Необходимо выбрать старосту,
заместителя старосты и физорга. Сколько существует способов это сделать?

3. (1 балл) Проходит
ли график функции у = — 2 х² через
точки:

а) А (0,5; -0,5); б) В(-1,5; 1,1)

4. (1 балл) Сторона
квадрата равна 4 см. Точка, равноудаленная от всех вершин квадрата, находится
на расстоянии 6 см от этой точки пересечения его диагоналей. Найдите расстояние
от этой точки до вершин квадрата.

5. (1 балл) Найдите корень уравнения log₂ (4-х)
= 2.

6. (1 балл) Вычислите значение выражения:

7. (1 балл) Решите неравенство:

8. (1 балл) Является ли функция F(x)=x⁴ -3x²
+1 первообразной для функции f(x)=4x³
–x² +x ?

9. (1 балл) Даны векторы {5; -1; 2} и {3; 2; -4}. Найти координаты

10. (1 балл) Дорисуйте график четной функции.

При выполнении
задания 11-14, используя график функции у = f(х) (см. рис. ниже),
определите и запишите ответ:

11. (1 балл) Область определения функции.

12. (1 балл) Наименьшее
и наибольшее значения функции

13. (1 балл) Промежутки
возрастания и убывания функции.

14. (1 балл) При
каких значениях х, f(х) ≤0.

При
выполнении заданий 15-18 запишите ход решения и полученный ответ.

15. (1 балл) Найдите
площадь фигуры, ограниченной графиком функции

f(x) = х² — 6x + 10, прямыми х
= — 1, х = 3 и осью абсцисс.

16. (1 балл) Решите
уравнение: 4^х · 2^х =
12.

17. (1 балл) Найдите
производную функции f(x)=2x² +sinx.

18. (1 балл) Найдите корни уравнения tgx + 1 = 0, принадлежащие
отрезку [0;2π].

Дополнительная часть

При выполнении
заданий 19-22 запишите ход решения и полученный ответ.

19. (3 балла) Решите
уравнение:

20. (3 балла) Прямоугольная трапеция с
основаниями 6 см и 3 см и высотой 4 см вращается вокруг большого основания.
Найдите площадь поверхности полученного тела вращения.

21. (3 балла) Решите
систему уравнений:

22.
(3 балла) Решите уравнение: |4-5х|=5х-4.

ПРИЛОЖЕНИЯ

Приложение 1

Инструкция для обучающихся по выполнению экзаменационной работы
(примерная)

На выполнение письменной экзаменационной работы по математике дается 4
астрономических часа (240 минут).

Экзаменационная работа состоит из 2-х частей: обязательной и
дополнительной.

Обязательная часть содержат задания минимально обязательного уровня, а
дополнительная часть – более сложные задания.

При выполнении большинства заданий обязательной части требуется
представить ход решения и указать полученный ответ. Только в нескольких
заданиях достаточно представить ответ. За правильное выполнение любого задания
из обязательной части Вы получаете один балл. Если Вы приводите неверное
решение, неверный ответ или не приводите никакого ответа, получаете 0 баллов за
задание.

При выполнении любого задания дополнительной части необходимо подробно
описать ход решения и дать ответ.

Правильное выполнение заданий дополнительной части оценивается 3
баллами.

Баллы, полученные за все выполненные задания, суммируются.

Постарайтесь правильно выполнить как можно больше заданий и набрать как
можно больше баллов.

Перед началом работы внимательно ознакомьтесь со шкалой перевода баллов
в отметки и обратите внимание, что начинать работу следует с заданий
обязательной части.

Шкала перевода баллов в отметки по пятибалльной
системе

Отметка	*Число баллов,* *необходимое для получения отметки*
«3» (удов.)	9–14
«4» (хорошо)	15–21
«5» (отлично)	Более 21

Желаем
успехов!

Приложение
2

Примерный перечень
элементов содержания

по математике для
составления экзаменационных работ

письменного
итогового экзамена в образовательных учреждениях СПО

Коды разделов и
элементов содержания согласованы с кодами, представленными в Кодификаторе
элементов содержания к уровню подготовки выпускников общеобразовательных
учреждений для проведения ЕГЭ по математике, подготовленного ФГНУ «Федеральный
институт педагогических измерений», 2011.

Перечень элементов содержания составлен на основе Обязательного
минимума содержания основных образовательных программ по математике и
Требований к уровню подготовки выпускников средней (полной) школы (Приказ
Минобразования России от 05.03.2004 г. № 1089 «Об утверждении федерального
компонента государственных образовательных стандартов начального общего,
основного общего и среднего (полного) общего образования»).

Перечень элементов содержания по всем разделам учебного курса
математики включает в себя элементы содержания по программе среднего (полного)
общего образования (базовый уровень) и необходимые элементы содержания за
учебный курс математики основной общеобразовательной школы.

Код разде- ла	Код контролиру- емого элемента	Элементы содержания, проверяемые заданиями экзаменационной работы
1		Алгебра
1.1		Числа, корни и степени
	1.1.1	Целые числа
	1.1.2	Степень с натуральным показателем
	1.1.3	Дроби, проценты, рациональные числа
	1.1.4	Степень с целым показателем
	1.1.5	Корень степени n >1 и его свойства
	1.1.6	Степень с рациональным показателем и ее свойства
	1.1.7	Свойства степени с действительным показателем
1.2		Основы тригонометрии
	1.2.1	Синус, косинус, тангенс, котангенс произвольного угла
	1.2.2	Радианная мера угла
	1.2.3	Синус, косинус, тангенс и котангенс числа
	1.2.4	Основные тригонометрические тождества
	1.2.5	Формулы приведения
	1.2.6	Синус, косинус и тангенс суммы и разности двух углов
	1.2.7	Синус и косинус двойного угла
1.3		Логарифмы
	1.3.1	Логарифм числа
	1.3.2	Логарифм произведения, частного, степени
	1.3.3	Десятичный и натуральный логарифмы, число е
1.4		Преобразования выражений
	1.4.1	Преобразования выражений, включающих арифметические операции
	1.4.2	Преобразования выражений, включающих операцию возведения в степень
	1.4.3	Преобразования выражений, включающих корни натуральной степени
	1.4.4	Преобразования тригонометрических выражений
	1.4.5	Преобразование

		выражений, включающих операцию логарифмирования
	1.4.6	Модуль (абсолютная величина) числа
2		Уравнения и неравенства
2.1		*Уравнения*
	2.1.1	Квадратные уравнения
	2.1.2	Рациональные уравнения
	2.1.3	Иррациональные уравнения
	2.1.4	Тригонометрические уравнения
	2.1.5	Показательные уравнения
	2.1.6	Логарифмические уравнения
	2.1.7	Равносильность уравнений, систем уравнений
	2.1.8	Простейшие системы уравнений с двумя неизвестными
	2.1.9	Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных
	2.1.10	Использование свойств и графиков функций при решении уравнений
	2.1.11	Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем
	2.1.12	Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
2.2		*Неравенства*
	2.2.1	Квадратные неравенства

	2.2.2	Рациональные неравенства
	2.2.3	Показательные неравенства
	2.2.4	Логарифмические неравенства
	2.2.5	Системы линейных неравенств
	2.2.6	Системы неравенств с одной переменной
	2.2.7	Равносильность неравенств, систем неравенств
	2.2.8	Использование свойств и графиков функций при решении неравенств
	2.2.9	Метод интервалов
	2.2.10	Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем
3		Функции
3.1		Определение и график функции
	3.1.1	Функция, область определения функции
	3.1.2	Множество значений функции
	3.1.3	График функции. Примеры функциональных зависимостей в реальных процессах и явлениях
	3.1.4	Обратная функция. График обратной функции
	3.1.5	Преобразования графиков: параллельный перенос, симметрия относительно осей координат
3.2		Элементарное исследование функций
	3.2.1	Монотонность функций. Промежутки возрастания и убывания
	3.2.2	Четность и нечетность функций
	3.2.3	Периодичность функций
	3.2.4	Ограниченность функций
	3.2.5	Точки экстремума (локального максимума и минимума) функции
	3.2.6	Наибольшее и наименьшее значения функции
3.3		Основные элементарные функции
	3.3.1	Линейная функция, ее график
	3.3.2	Функция, описывающая обратную пропорциональную зависимость, ее график
	3.3.3	Квадратичная функция, ее график
	3.3.4	Степенная функция с натуральным показателем, ее график
	3.3.5	Тригонометрические функции, их графики
	3.3.6	Показательная функция, ее график
	3.3.7	Логарифмическая функция, ее график
4		Начала математического анализа
4.1		*Производная*
	4.1.1	Понятие о производной функции, геометрический смысл производной
	4.1.2	Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком
	4.1.3	Уравнение касательной к графику функции
	4.1.4	Производные суммы, разности, произведения, частного
	4.1.4	Производные основных элементарных функций
	4.1.5	Вторая производная и ее физический смысл
4.2		Исследование функций
	4.2.1.	Применение производной к исследованию функций и построению графиков
	4.2.2	Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах
4.3		Первообразная и интеграл
	4.3.1	Первообразные элементарных функций
	4.3.2	Примеры применения интеграла в физике и геометрии
5		Геометрия
5.1		*Планиметрия*
	5.1.1	Треугольник
	5.1.2	Параллелограмм, прямоугольник, ромб, квадрат
	5.1.3	Трапеция
	5.1.4	Окружность и круг
	5.1.5	Окружность, вписанная в треугольник, и окружность, описанная около треугольника
	5.1.6	Многоугольник. Сумма углов выпуклого многоугольника
	5.1.7	Правильные многоугольники. Вписанные и описанные окружности правильного многоугольника
5.2		Прямые и плоскости в пространстве
	5.2.1	Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
	5.2.2	Параллельность прямой и плоскости, признаки и свойства
	5.2.3	Параллельность плоскостей, признаки и свойства
	5.2.4	Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трех перпендикулярах
	5.2.5	Перпендикулярность плоскостей, признаки и свойства
	5.2.6	Параллельное проектирование. Изображение пространственных фигур
5.3		*Многогранники*
	5.3.1	Призма, ее основания, боковые ребра, высота, боковая поверхность; прямая призма; правильная призма
	5.3.2	Параллелепипед; куб; симметрии в кубе, в параллелепипеде
	5.3.3	Пирамида, ее основание, боковые ребра, высота, боковая поверхность; треугольная пирамида; правильная пирамида
	5.3.4	Сечения куба, призмы, пирамиды
	5.3.5	Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)
5.4		Тела и поверхности вращения
	5.4.1	Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
	5.4.2	Конус. Основание, высота, боковая поверхность, образующая, развертка
	5.4.3	Шар и сфера, их сечения
5.5		Измерение геометрических величин
	5.5.1	Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
	5.5.2	Угол между прямыми в пространстве; угол между прямой и плоскостью
	5.5.3	Длина отрезка, ломаной, окружности, периметр многоугольника
	5.5.4	Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными прямыми, параллельными плоскостями
	5.5.5	Площадь треугольника, параллелограмма, трапеции, круга, сектора
	5.5.6	Площадь поверхности конуса, цилиндра, сферы
	5.5.7	Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
5.6		Координаты и векторы
	5.6.1	Декартовы координаты на плоскости и в пространстве
	5.6.2	Формула расстояния между двумя точками; уравнение сферы
	5.6.3	Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
	5.6.4	Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам
	5.6.5	Компланарные векторы. Разложение по трем некомпланарным векторам
	5.6.6	Координаты вектора; скалярное произведение векторов; угол между векторами
6		Элементы комбинаторики, статистики и теории вероятностей
6.1		Элементы комбинаторики
	6.1.1	Поочередный и одновременный выбор
	6.1.2	Формулы числа сочетаний и перестановок. Бином Ньютона
6.2		6.2. Элементы статистики
	6.2.1	Табличное и графическое представление данных
	6.2.2	Числовые характеристики рядов данных
6.3		6.3. Элементы теории вероятностей
	6.3.1	Вероятности событий
	6.3.2	Примеры использования вероятностей и статистики при решении прикладных задач

Приложение 3.

Примерный перечень требований к уровню подготовки обучающихся

по математике для составления экзаменационных работ письменного
итогового экзамена в образовательных учреждениях СПО

Согласован с кодификатором требований к уровню подготовки выпускников
общеобразовательных учреждений для проведения ЕГЭ по математике,
подготовленного ФГНУ «Федеральный институт педагогических измерений», 2011.

Перечень требований к уровню подготовки по математике обучающихся
образовательных учреждений НПО/СПО составлен на основе Обязательного минимума
содержания основных образовательных программ и Требований к уровню подготовки
обучающихся в результате освоения учебной дисциплины «математики» на базовом
уровне (Об утверждении федерального компонента Государственных стандартов
начального общего, основного общего и среднего (полного) общего образования //
Приказ Минобрнауки РФ от 05.03.2004 № 1089).

Перечень требований по всем разделам включает в себя требования к
уровню подготовки обучающихся по математике, освоивших программу среднего
(полного) общего образования (базовый уровень).

Требования (умения и виды деятельности), проверяемые заданиями

письменной экзаменационной работы

Уметь выполнять вычисления и преобразования:

– выполнять арифметические действия, сочетая устные и письменные
приемы; находить значения корня натуральной степени, степени с рациональным
показателем, логарифма;

– вычислять значения числовых и буквенных выражений, осуществляя
необходимые подстановки и преобразования;

– проводить по известным формулам и правилам преобразования буквенных
выражений, включающих степени, радикалы, логарифмы и тригонометрические
функции.

Уметь решать уравнения и неравенства:

– решать рациональные, иррациональные, показательные,
тригонометрические и логарифмические уравнения, их системы;

– решать уравнения, простейшие системы уравнений, используя свойства
функций и их графиков; использовать для приближенного решения уравнений и
неравенств графический метод;

– решать рациональные, показательные и логарифмические неравенства. 32

Уметь выполнять действия с функциями:

– определять значение функции по значению аргумента при различных
способах задания функции; описывать по графику поведение и свойства функций,
находить по графику функции наибольшие и наименьшие значения; строить графики
изученных функций;

– вычислять производные и первообразные элементарных функций;

– исследовать в простейших случаях функции на монотонность, находить
наибольшие и наименьшие значения функций.

Уметь выполнять действия с геометрическими фигурами, координатами и
векторами:

– решать планиметрические задачи на нахождение геометрических величин
(длин, углов, площадей);

– решать простейшие стереометрические задачи на нахождение
геометрических величин (длин, углов, площадей, объемов); использовать при
решении стереометрических задач планиметрические факты и методы;

– определять координаты точки.

Уметь строить и исследовать простейшие математические модели:

– моделировать реальные ситуации на языке алгебры, составлять уравнения
и неравенства по условию задачи; исследовать построенные модели с
использованием аппарата алгебры;

– моделировать реальные ситуации на языке геометрии, исследовать
построенные модели с использованием геометрических понятий и теорем, аппарата
алгебры; решать практические задачи, связанные с нахождением геометрических
величин;

– проводить доказательные рассуждения при решении задач, оценивать
логическую правильность рассуждений, распознавать логически некорректные
рассуждения.

Уметь использовать приобретенные знания и умения в практической
деятельности и повседневной жизни:

– анализировать реальные числовые данные; осуществлять практические
расчеты по формулам, пользоваться оценкой и прикидкой при практических
расчетах;

– описывать с помощью функций различные реальные зависимости между
величинами и интерпретировать их графики; извлекать информацию, представленную
в таблицах, на диаграммах, графиках;

– решать
прикладные задачи, в том числе социально-экономического и физического
характера, на наибольшие и наименьшие значения, на нахождение скорости и
ускорения.

Источник

По теме: методические разработки, презентации и конспекты

Методические рекомендации по проведению экзамена (квалификационного) по освоению профессионального модуля «ПМ.03.Сборка, монтаж (демонтаж) элементов судовых конструкций, корпусов, устройств и систем металлических судов»

За это время в училище накоплен положительный опыт работы по внедрению ФГОС, проведению ГИА, а также промежуточной аттестации по каждому профессиональному модулю (далее ПМ) – экзамена (квалифика…

Методические рекомендации по проведению экзамена (квалификационного) по освоению профессионального модуля

С 1 сентября 2013 года мы приступили к внедрению ФГОС СПО по программе подготовки квалифицированных рабочих, служащих. Были скорректированы и обновлены учебные планы, определены формы конт…

Методические рекомендации по проведению итоговой аттестации по учебной дисциплине история в форме экзамена (устная форма)

Комплект экзаменационных материалов по истории для итоговой аттестации в устной форме состоит из 15 билетов, каждый которых содержит по два вопроса. Первый вопрос каждого билета проверяет знание выпус…

МЕТОДИЧЕСКАЯ РАЗРАБОТКА «МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ ЛЕТНЕЙ ПОЛЕВОЙ ПРАКТИКИ»

Главной формой подготовки молодежи к службе в армии является изучение студентами старших курсов учебных заведений СПО Российской Федерации раздела «Основы военной службы» в рамках курса &l…

Методические рекомендации по проведению комплексного экзамена по профессиональному модулю ПМ.04. Методическое обеспечение образовательного процесса в начальной школе

В сборнике представлены основные требования к результатам освоения профессионального модуля, форма проведения экзамена, регламент, критерии оценки для студентов очной форы обучения Государственного бю…

Краткие методические рекомендации Для демонстрационного экзамена | «Электромонтаж»

В компетенции «Электромонтаж» участник должен уметь планировать, проектировать системы электроснабжения, выбирать и устанавливать электрооборудование, сдавать в эксплуатацию электроустанов…

Методическая разработка «Методические рекомендации по проведению закаливания в ДОУ»

Методические рекомендации предназначены студентам колледжа для прохождения производственной практики по ПМ.01 «Организация мероприятий, направленных на укрепление здоровья ребенка и его фи…

Источник

«Анализ результатов экзамена по математике. Критерии проверки и оценивания выполнения заданий по алгебре с развернутым ответом»

Анализ выполнения первой части экзаменационной работы. Все результаты выполнения заданий Части 1 экзамена попадают в планируемый диапазон трудности от 40 % до 90%. Традиционно учащиеся наиболее успешно выполняют задания, формулировки которых носят стандартный характер, в основе решения которых лежит прямое применение математических терминов и понятий (планомерная отработка!) ü «Вычисления и преобразования» , ü «Сравнение чисел, изображенных точками на координатной прямой» , ü «Функции и их графики» , ü «Арифметическая прогрессия» , ü «Площадь параллелограмма» , ü «Прямоугольные треугольники» , ü «Проценты» , ü «Диаграммы» .

Анализ выполнения первой части экзаменационной работы. Значительно большие затруднения вызвали у выпускников задания, решение которых требовало осмысления важнейших понятий и их свойств, понимания содержания используемых приемов решения задач: ü «Линейные неравенства с одной переменной и их системы» , ü «Квадратное уравнение: формула корней квадратного уравнения» .

Анализ выполнения второй части экзаменационной работы Шесть заданий (3 задачи по алгебре, 3 – по геометрии), расположенных по нарастанию сложности. Задания позволяют проверить степень владения учащимися формально-оперативным аппаратом, способности к интеграции знаний из различных тем курса математики, умения найти и применить нестандартные приемы решения. Умение математически грамотно записать решение, из которого был бы понятен ход рассуждений учащегося. При этом никаких специальных требований к подробности и оформлению решения не выдвигалось.

Анализ выполнения второй части экзаменационной работы Сравнительный анализ заданий второй части позволил сделать вывод, что алгебраический материал второй части экзаменационной работы 2015 года не сложнее аналогичных заданий 2014 года. Усложнение второй части заданий произошло за счет геометрического материала.

Анализ выполнения второй части экзаменационной работы Близкие результаты выполнения заданий Части 2 экзамена к планируемому диапазону трудности учащиеся демонстрируют при выполнении № 21, № 22, № 23, № 24. Не попали в планируемый уровень трудности при выполнении заданий № 25, № 26, причём отклонения значительные.

Анализ выполнения второй части экзаменационной работы № 21 (50%) – «Cократить дробь» . При выполнении задания значительной частью учащихся приведено верное решение, однако за него выставлялось и 0 баллов Типичные ошибки ü Разложение на множители квадратного трехчлена со старшим коэффициентом, отличным от единицы ü вычислительные ошибки

Анализ выполнения второй части экзаменационной работы № 22 (21%) — Текстовая задача Основные трудности выпускники испытывают на всех этапах решения задач такого типа ü перевод содержания задачи на математический язык, ü составление уравнений, связывающих данные величины и переменные, которые вводит учащийся. Замечаний по решению и оформлению задачи: ü отсутствие этапа введения переменной и необходимых пояснений, ü ошибки при составлении уравнения, в том числе в выражении скорости против течения и по течению, ü вычислительные ошибки при решении уравнения, ü наличие неправильно сформированного ответа в части отсутствия именованных величин.

Анализ выполнения второй части экзаменационной работы № 23 (6, 04% ) –Построение и исследования функции, заданной кусочно. ü низкая графическая культура, ü отсутствие навыков исследовательской деятельности. Типичные ошибки: ü неправильно включены или не включены концы интервалов в окончательный ответ, ü неверный график ü отсутствуют единичный отрезок на координатных осях, направления координатных осей.

Анализ выполнения второй части экзаменационной работы ü Треть учащихся смогли справиться с решением планиметрической задачи на нахождение геометрических величин (углов), ü 6, 4 % довели до конца доказательные рассуждения при решении задач по теме «Четырёхугольник» , ü 1, 68% — по теме «Треугольник» , демонстрируя при этом умение оценивать логическую правильность рассуждений, распознавать ошибочные заключения, получив за задания максимально возможный балл.

Анализ выполнения второй части экзаменационной работы Слабая подготовка по разделу «Геометрия» у значительного числа учащихся, причем не только у «слабых» , но и у тех, кто продемонстрировал при выполнении всей работы хороший уровень математической подготовки. Основные недочёты подготовки по данному разделу: ü неумение работать с понятийным аппаратом в изменённой ситуации (формальное усвоение геометрического материала учащимися), ü отсутствие умения проанализировать предлагаемую в задаче фигуру, распознать в ней опорную конфигурацию и установить связи между ее элементами (их взаимное расположение, метрические соотношения и т. д. ), ü слабо сформированные практические навыки изображения геометрического чертежа согласно условию задачи (отсутствие чертежа!)

ОГЭ выпускников IX классов общеобразовательных учреждений 2016 год МАТЕМАТИКА по проверке заданий с развернутым ответом

Характеристика структуры и содержания экзаменационной работы • Работа состоит из трёх модулей: «Алгебра» , «Геометрия» , «Реальная математика» . Модули выполняются последовательно. Всего 26 заданий. • В модули «Алгебра» и «Геометрия» входит две части, соответствующие проверке на базовом и повышенном уровнях, в модуль «Реальная математика» — одна часть, соответствующая проверке на базовом уровне. • Общее время экзамена 235 минут

Характеристика структуры и содержания экзаменационной работы • Модуль «Алгебра» содержит 11 заданий: в части 1 — 8 заданий, в части 2 – 3 задания. • Модуль «Геометрия» содержит 8 заданий: в части 1 — 5 заданий, в части 2 – 3 задания. • Модуль «Реальная математика» содержит 7 заданий.

Характеристика структуры и содержания экзаменационной работы Распределение заданий по частям работы: 4 задания — с выбором ответа 16 заданий -с кратким ответом 6 заданий — с развёрнутым ответом

Система оценивания выполнения отдельных заданий и экзаменационной работы в целом • Задания, оцениваемые двумя и более баллами, считаются выполненными верно и в этом случае ему выставляется полный балл, соответствующий данному заданию, если: • учащийся выбрал правильный путь решения, • из письменной записи решения понятен ход его рассуждений, получен верный ответ.

Система оценивания выполнения отдельных заданий и экзаменационной работы в целом Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается балл, на 1 меньше указанного.

Назначение заданий с развернутым ответом и их особенности • Все задания второй части экзаменационной работы носят комплексный характер. • Они позволяют проверить владение формально-оперативным аппаратом, способность к интеграции знаний из различных тем школьного курса, владение достаточно широким набором приемов и способов рассуждений, а также умение математически грамотно записать решение.

Назначение заданий с развернутым ответом и их особенности • Задания части 2 относятся к двум модулям – «Алгебра» и «Геометрия» . • Фактически во второй части работы представлены три разных уровня

Назначение заданий с развернутым ответом и их особенности • Первые задания наиболее простые : № 21 – алгебраическое, № 24 – геометрическое • Они направлены на проверку владения формально-оперативными алгебраическими навыками: преобразование выражения, решение уравнения, неравенства, систем, построение графика, умению решить несложную геометрическую задачу на вычисление. • По уровню сложности эти задания немногим превышают обязательный уровень.

Назначение заданий с развернутым ответом и их особенности Задание 22 – алгебраическое, задание 25 – геометрическое более высокого уровня, они сложнее предыдущих и в техническом, и в логическом отношении. При хорошем выполнении первой части правильное выполнение этих заданий соответствует отметке « 5» . Последние два задания (№ 23 – алгебраическое, № 26 –геометрическое) наиболее сложные, они требуют довольно высокого уровня математического развития. Рассчитаны эти задачи на выпускников, изучавших математику более основательно, чем в рамках пятичасового курса

Критерии проверки и оценивания выполнения заданий с развернутым ответом Модуль алгебра.

Задание 21

Примеры выполнения заданий учащимися • Пример 1. За решение выставляется 1 балл, так как оно не содержит ошибок, но разложение на множители не доведено до конца.

• Пример 2. За решение выставляется 0 баллов; допущена ошибка в знаках при группировке слагаемых

Задание 21

• Решение. Корни квадратного трехчлена Замечание. Учащийся может разложить трехчлен на множители каким-либо иным способом.

Примеры выполнения заданий учащимися Пример 1 За решение выставляется 2 балла. Все шаги выполнены верно, получен правильный ответ.

Пример 2 Сокращение дроби выполнено верно. Но так как при указании ОДЗ допущена ошибка (хотя нахождение области определения дроби в данном случае не требуется), за решение выставляется 1 балл.

Задание 22 • 1. Решите неравенство Решение. 1) Определим знак разности

Задание 22 1. Решите неравенство

Примеры выполнения заданий учащимися Пример 1

Пример 2 Допущена ошибка принципиального характера в алгоритме решения неравенства. За решение выставляется 0 баллов.

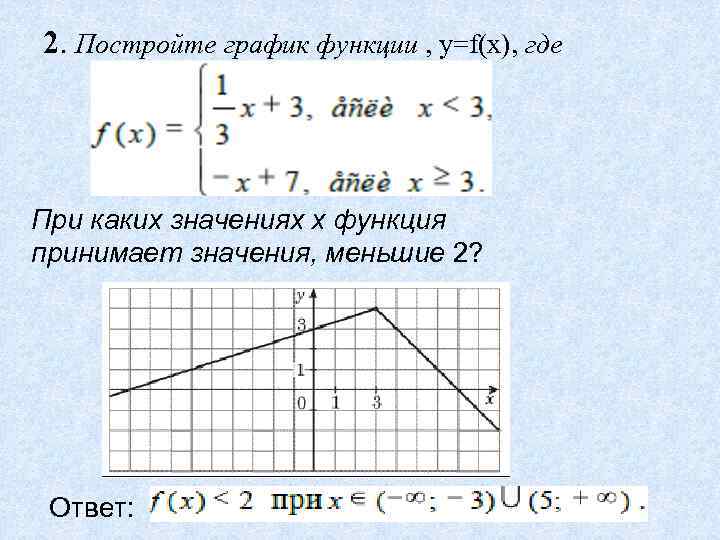
2. Постройте график функции , у=f(x), где При каких значениях х функция принимает значения, меньшие 2? Ответ:

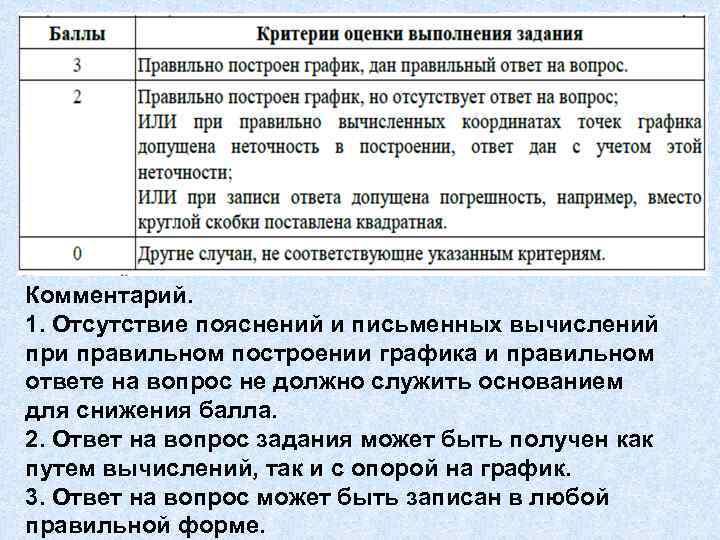
Комментарий. 1. Отсутствие пояснений и письменных вычислений при правильном построении графика и правильном ответе на вопрос не должно служить основанием для снижения балла. 2. Ответ на вопрос задания может быть получен как путем вычислений, так и с опорой на график. 3. Ответ на вопрос может быть записан в любой правильной форме.

Примеры выполнения заданий учащимися Пример 1 • За решение выставляется 0 баллов. Учащийся должен был выделить каким-либо способом (например, жирно) собственно график заданной функции.

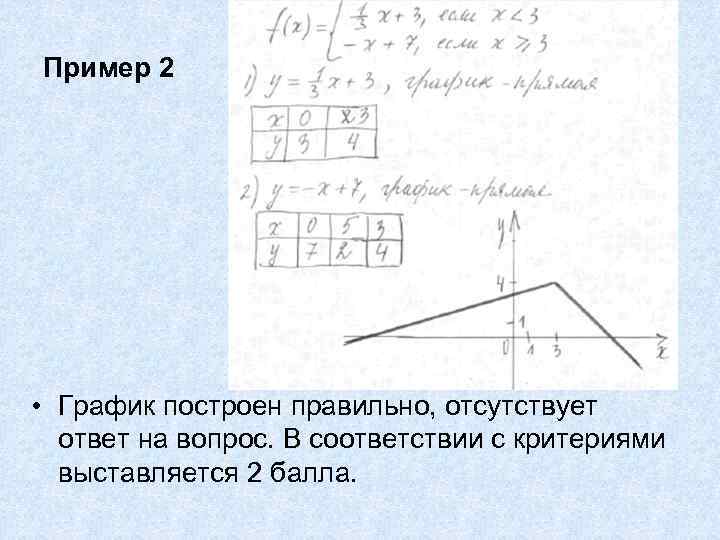
Пример 2 • График построен правильно, отсутствует ответ на вопрос. В соответствии с критериями выставляется 2 балла.

3. Найдите область определения выражения

• Решение. Область определения выражения задается условиями Решим неравенство Замечание. Ответ может быть представлен в форме:

Пример 1 За решение выставляется 2 балла. Ход рассуждений понятен, он правильный, получен верный ответ. Балл снижен за некорректное пояснение, приведенное в начале решения.

Пример 2

• За решение выставляется 0 баллов; в нем содержится более одной ошибки, поэтому оно соответствует графе «Другие случаи, не соответствующие указанным критериям» . Учащимся, во-первых, допущены две вычислительные ошибки при нахождении корней квадратного трехчлена; во-вторых, решив квадратное неравенство (с учетом найденных корней) и правильно наложив ограничение на знаменатель дроби, учащийся не сумел сделать на основе полученных результатов соответствующий вывод.

4. Найдите сумму всех отрицательных членов арифметической прогрессии – 8, 6; – 8, 4; … Ответ: -189, 2. Комментарий. 1. Учащийся имеет право воспользоваться другой формулой суммы первых n членов арифметической прогрессии. 2. Ошибки в применении формул, в том числе в подстановке числовых значений в формулы, считаются существенными, решение не засчитывается и оценивается 0 баллов.

• Решение. 1. Найдем разность прогрессии: d=-8, 4 +8, 6 =0, 2. • 2. Найдем число отрицательных членов прогрессии. • Составим формулу n-го члена:

Ход решения верный, но допущена вычислительная ошибка (при нахождении разности арифметической прогрессии), с ее учетом решение доведено до конца. Выставляется 2 балла.

Задание 23 • 1. Решите систему уравнений

Решение

Пример 1 • За решение можно выставить 3 балла: ход решения правильный, и, по сути, верный ответ получен. Но решение содержит логическую ошибку: выполнив проверку (которая в данном случае не является составной частью решения и может служить только цели самоконтроля), учащийся допустил вычислительную ошибку и сделал неправильный вывод о наличии постороннего решения, которого в принципе в данной ситуации быть не может.

• Замечание. За нерациональное решение баллы не снимаются. Хотя хотелось бы, чтобы для сильного учащегося наличие уравнения • (х+5)(2 у-1)=0 сразу же служило сигналом к попытке применить условие равенства нулю произведения. Приведенное решение показывает (и это не единичный случай), что не наработаны некоторые стандартные приемы, обязательные для подготовки сильного ученика.

Пример 2 За решение выставляется 3 балла; допущены ошибки в употреблении символики.

• 2. Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки? Ответ: плот пройдет всего пути.

Ход решения верный, введены нужные обозначения, приведены пояснения, но допущена вычислительная ошибка, с ее учетом решение доведено до конца. Можно выставить 3 балла.

При нахождении длины пути, который катер проплыл против течения, учащийся использует собственную скорость катера; решение оценивается 0 баллами.

3. Найдите все значения а, при которых неравенство х2 + (2 а + 4)х + 8 а + 1 ≤ 0 не имеет решений. Комментарий. Ошибки при составлении дискриминанта квадратного трехчлена или в применении алгоритма решения квадратного неравенства являются существенными, и при их наличии за решение выставляется 0 баллов.

Все шаги решения выполнены верно (хотя есть погрешность в терминологии), получен правильный ответ. За решение можно выставить 4 балла.

За решение выставляется 0 баллов. Учащийся не владеет приемом решения квадратного неравенства, допускает ошибки в применении формулы корней квадратного уравнения.

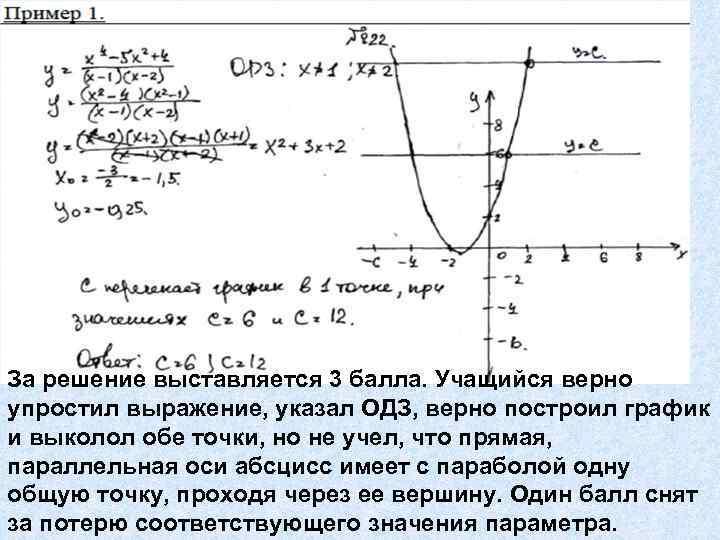
4. Постройте график функции и определите, при каких значениях с прямая у=с имеет с графиком ровно одну общую точку.

За решение выставляется 3 балла. Учащийся верно упростил выражение, указал ОДЗ, верно построил график и выколол обе точки, но не учел, что прямая, параллельная оси абсцисс имеет с параболой одну общую точку, проходя через ее вершину. Один балл снят за потерю соответствующего значения параметра.

За решение выставляется 3 балла. Один балл снят за то, что учащийся не указал еще два решения, соответствующих выколотым точкам параболы.

Пример 3 Задание выполнено верно, за его выполнение выставляется 4 балла.

СПАСИБО ЗА ВНИМАНИЕ!

Источник

Программа

итогового экзамена по математике

Раменское,

2013 г.

Пояснительная записка

Программа итогового экзамена по математике предназначена для студентов СПО.

Тест является основной формой проверки знаний за курс математики.

Объем теста – 20 заданий.

Продолжительность проведения экзамена – 5 часов.

Программа итогового экзамена по математике

Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем, согласно стандарта.

Тригонометрия:

Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.

Производная:

Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции.

Первообразная:

Основное свойство первообразной. Правила нахождения первообразных.

Понятие степени:

Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.

5. Показательная и логарифмическая функции:

Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций.

6. Стереометрия:

Многогранники. Тела вращения.

Критерии оценки контрольной работы

1 задание:

Степень с рациональным показателем – 1 балл

2 задание:

Степень с рациональным показателем – 1 балл

3 задание:

Свойства логарифмической функции – 1 балл

4 задание:

Основные тригонометрические формулы – 2 балла

5 задание:

Основные тригонометрические формулы–2 балла

6 задание:

Решение тригонометрических уравнений– 1 балл

7 задание:

Решение иррациональных уравнений – 2 балла

8 задание:

Решение показательных уравнений – 2 балла

9 задание:

Метод интервалов — Решение иррациональных уравнений – 1 балл

10 задание:

Свойства тригонометрических функций – 1 балл

11 задание:

Вычисление производных — 1 балл

12 задание:

Нахождение первообразной функции – 1 балл

13 задание:

Решение логарифмических уравнений – 1 балл

14 задание:

Нахождение максимального и минимального значений функции – 2 балла

15 задание:

Свойства тел в стереометрии – 1 балл

16 задание:

Площадь криволинейной трапеции – 3 балла

17 задание:

Построение графика логарифмической функции – 3 балла

18 задание:

Решение показательных неравенств — 3 балла

19 задание:

Многогранники — 3 балла

20 задание:

Тела вращения — 3 балла

Рекомендации для проверки (проведения) экзаменационного теста.

Тест состоит из 20 заданий.

Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и отметьте соответствующую ячейку в таблицу ответов.

Максимальный балл за тест – 35.

0 – 14 баллов — «2» («неудовлетворительно»)

15 – 19 баллов — «3» («удовлетворительно»)

21 – 29 баллов — «4» («хорошо»)

30 – 35 баллов — «5» («отлично» )

Ответы

Вариант 1

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1
2
3
4

Вариант 2

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1
2
3
4

Вариант 3

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1
2
3
4

Бланк ответов

экзаменационного теста

по математике

Ф.И.О.___________________________________________________

Группа № ________________________

Специальность ____________________

___ вариант.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1
2
3
4

Вариант 1

Вычислите 29 – 15.

2) 43 3) 73 4) 101.

Упростите выражение .

5 2) 1 3) 10 4) 0.

3) Упростите выражение – 2.

1) 2) 1 3) 8 4) 20.

4) Найдите значение , если = -0,8 и .

1) -0,6 2) 0,6 3) 0,2 4) 0,36

5) Упростите выражение 7cos²α – 5 + 7sin²α.

1) 1 + cos²α 2) 2 3) -12 4) 12.

6) Решите уравнение = 1.

1)2n, n 2) 3) +2n, n 4) n, n

7) Укажите промежуток, которому принадлежит корень уравнения = -х.

1) 2) (35;37) 3) (-2; 4) .

Укажите промежуток, которому принадлежит корень уравнения = 8.

1) [-4;0) 2) [0;1) 3) [-∞;-4) 4) [4;6).

9) Решите неравенство ≤0.

1) (-∞;-2) [) 2) [-2;) ( 1;+∞) 3) (-∞;-2) 4) (-∞;-5) (-2;.

10) Найдите множество значений функции у =– 2.

1) [3;1] 2) (-∞;+∞) 3) [-1;1] 4) [-3;-1].

11) Найдите производную функции f(x) = .

1) -4 2) -8 3) 8 4) .

12) Укажите первообразную функции f(x) = 2х + 4х³ – 1.

1) х² + х⁴ – х 2) 2х² + 4х⁴ 3) 2 + 12х² 4) х²+х⁴.

13) Решите равнение + = .

1) 0 2) 4 3) 9 4) 15.

14) Найдите точки максимума функции у = х³ – 3х² .

1) 0 2) 2 3) -2 4) 3.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1.

1) 5 2) 10 3) 3 4) 31.

16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х², у = 0, х = 0, х = 2.

1) 8 2) 2 3) 5 4) 6.

17) Укажите область определения функции у =.

1) (-∞;0)(2;+∞) 2) (-2;+∞) 3) (2;+∞) 4) (0;2).

18) Найдите наибольшее целое решение неравенства – 1 0.

1) 0 2) -1 3) 1 4) 2.

19) Площади двух граней прямоугольного параллелепипеда равны 56дм² и 192дм², а длина их общего ребра 8дм. Найдите объем параллелепипеда.

1) 840 2) 1029 3) 1344 4) 1210.

20) Образующая конуса равна 12см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 384 2) 192 3) 24 4) 648.

Вариант 2

Вычислите 7 — 3∙.

2) 8 3) -5 4) -17.

Упростите выражение .

1) 1,2 2) 5 3) 4) .

3) Упростите выражение + — .

1) 2 +2 2) 7 3) 3 — 6 4) 2.

4) Найдите значение, если = и 0.

1) — 2) 3) 4) .

5) Упростите выражение -3sin²α — 6 – 3cos²α.

1) 1 2) 2cosα 3) cosα + 4) -9 .

6) Укажите промежуток, которому принадлежит корень уравнения = -х.

1) 2) (-;-10) 3) 4) .

7) Решите уравнение = 1.

1) n, n 2) 3) +2n, n 4) n,n.

Укажите промежуток, которому принадлежит корень уравнения = 125.

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).

9) Решите неравенство ≤ 0.

1) (-2;) 2) [-2;2) (;+∞) 3) (-∞;3) 4) (-∞;-2) (].

10) Найдите множество значений функции у = + 4.

1) [3;5] 2) (-∞;+∞) 3) [-1;1] 4) [-5;-3].

11) Найдите производную функции f(x) = .

1) 3 2) 3) -3 4) —.

12) Укажите первообразную функции f(x) = 3х²+ 2х -4.

1) х³+ х² — 4х 2) 6х+ 2 3) х³+ х² 4) х²+ х – 4х.

13) Решите равнение + =

1) 0 2) 11 3) 3 4) 12.

14) Найдите точку минимума функции у = х² — 1.

1) -1 2) 1 3) -2 4) 0.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6.

1) 55 2) 7 3) 49 4) 11.

16) Вычислите площадь фигуры (S), ограниченной линиями у = х³+ 1, у = 0, х = 0, х = 2.

1) 8 2) 5 3) 6 4) 4.

17) Укажите область определения функции у =.

1) (-∞;0)(4;+∞) 2) (-4;+∞) 3) (4;+∞) 4) (0;4).

18) Найдите наименьшее целое решение неравенства – 1 0.

1) 0 2) 1 3) -1 4) 2.

19) Площади двух граней прямоугольного параллелепипеда равны 35см² и 42см², а длина их общего ребра 7см. Найдите объем параллелепипеда.

1) 840 2) 10290 3) 770 4) 210.

20) Образующая конуса равна 24см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 3840 2) 1092 3) 5184 4) 648.

Вариант 3

1) Вычислите 2∙ – 0,9⁰

1)10,9 2) 11 3) 9,1 4) 9.

2) Упростите выражение

2) 2 3) 0,7 4) 36.

3) Упростите выражение — +

1) -1 + 2) -2 3) 0 4) .

4) Найдите значение , если = — и

1) 2) 3) 4)

5) Упростите выражение -4sin²α +5 – 4cos²α

1) 1 2) 1 + 8sin²α 3) 1 + 8cos²α 4) 9.

6) Укажите промежуток, которому принадлежит корень уравнения = -х

1) 2) (-∞;-2) 3) 4) .

7) Решите уравнение = -1

1) 2)0 3) +2n, n 4) n, n

Укажите промежуток, которому принадлежит корень уравнения = 16

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).

9) Решите неравенство ≥0

1) (-∞;-8] (; 2) 2) [-8;) ( 2;+∞) 3) (-∞; 2) 4) (-∞;-8) (2; +∞.

10) Найдите множество значений функции у = – 1

1) [-1;1] 2) (-∞;+∞) 3) [-2;0] 4) [0;2].

11) Найдите производную функции f(x) =

1) -18 2) 6 3) 18 4) .

12) Укажите первообразную функции f(x) = 5х⁴ – 2х + 1

1) 5х⁵ – 2х² + 1 2) 20х³ – х 3) х⁴ – 2х + х 4) х⁵ – х² + х.

13) Решите равнение + =

1) 15 2) 5 3) 4 4) 10.

14) Найдите точку максимума функции у = 4х – х⁴

1) 4 2) 2 3) -4 4) 0.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7

1) 19 2) 11 3) 121 4) 36.

16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х³, у = 0, х = 0, х = 1.

1) 1 2) 3) 4) 1.

17) Укажите область определения функции у =.

1) (-3;+∞) 2) (-∞;0)(3;+∞) 3) (3;+∞) 4) (0;3).

18) Найдите наибольшее целое решение неравенства – 1 0.

1) 1 2) -1 3) 2 4) 0.

19) Площади двух граней прямоугольного параллелепипеда равны 20см² и 45см², а длина их общего ребра 5см. Найдите объем параллелепипеда.

1) 240 2) 120 3) 180 4) 4500.

20) Образующая конуса равна 18дм и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 3804 2) 2192 3) 2187 4) 6408.

Источник

ных повторов мысли, нарушения логики), качество речевого оформления текста.

При проверке творческого задания к тексту оценивается уровень сформированности следующих умений:

— создавать текст в соответствии с заданной темой;

— обрабатывать и интерпретировать информацию, заложенную в произведении, в прослушанном тексте, в иных источниках информации, привлекаемой для написания сочинения;

— подбирать убедительные аргументы, создавая аргументированное высказывание;

— выявлять отношение автора к поставленным проблемам, сопос-тавлять свою позицию с другой точкой зрения;

— осуществлять выбор языковых средств в соответствии с заданием;

— оформлять текст в соответствии с орфографическими, грамматичес-кими, пунктуационными и речевыми нормами русского литературного языка.

При проверке выполнения творческого задания следует учитывать, что их объем строго не лимитируется.

Преподавателю предлагается использовать следующие варианты оценивания изложения:

1) За изложение с творческим заданием выставляются три отметки: первая — за содержание изложения, вторая — за выполнение творческого задания третья — за орфографическую и пунктуационную грамотность (суммарно за изложение и выполнение творческого задания). Ито-

говая отметка определяется как среднее арифметическое трех оценок, выставленных за изложение с творческим заданием, и выставляется целым числом в соответствии с правилами математического округления.

2) За изложение с творческим заданием выставляются две отметки: первая — за изложение и выполнение творческого задания, вторая

— за орфографическую и пунктуационную грамотность. Итоговая отметка определяется как среднее арифметическое двух оценок и выставляется целым числом в соответствии с правилами математического округления.

Отметка выставляется по действующим Нормам оценки знаний, уме-ний и навыков учащихся по русскому языку (Оценка знаний, умений и навыков учащихся по русскому языку: пособие для учителя / авт.-сост.: В. И. Калинос, Т. А. Ко-стяева. — М. : Просвещение, 1986. — С. 134-143.)

Логично предположить, что в перспективе из двух предлагаемых форматов письменного экзамена по русскому языку большей популярностью будет пользоваться экзамен с использованием экзаменационных материалов в виде набора контрольных заданий. Контрольные задания проще выполнить обучающимся, и, соответственно, проще проверить преподавателям. Однако изложение с творческим заданием может оставаться приемлемым форматом для итогового контроля за курс среднего (полного) общего образования по русскому языку в учреждениях СПО, в которых русский язык изучается на профильном уровне.

ИТОГОВЫМ КОНТРОЛЬ УЧЕБНЫХ ДОСТИЖЕНИИ ОБУЧАЮЩИХСЯ ПО МАТЕМАТИКЕ ПРИ РЕАЛИЗАЦИИ ОБРАЗОВАТЕЛЬНОМ ПРОГРАММЫ СРЕДНЕГО (ПОЛНОГО) ОБЩЕГО ОБРАЗОВАНИЯ В ПРЕДЕЛАХ ОСНОВНОМ ПРОФЕССИОНАЛЬНОМ ОБРАЗОВАТЕЛЬНОМ ПРОГРАММЫ НПО/СПО

Гуляева М. А., методист лаборатории андрагогики ГОУ «КРИРПО», г. Кемерово

Богатый на перемены в образовательном процессе учреждений профессионального образования и сложный для педагогов 2011/2012 учебный год приближается к завершению. Изменения, которые затрагивают образовательный процесс, происходят не

только в организации профессиональной подготовки обучающихся учреждений профессионального образования, но и общеобразовательной. У педагогов возникает множество вопросов и затруднений, связанных с противоречиями в нормативной документации и в процессе своей профессиональной деятельности. Так, с одной стороны, в соответствии со ст. 15 п. 3 Закона РФ «Об образовании» образовательное учреждение самостоятельно в выборе системы оценок, формы,

порядка и периодичности промежуточной аттестации обучающихся. С другой стороны, образовательные учреждения профессионального образования испытывают определенные затруднения при организации и проведении итогового контроля по освоению обучающимися образовательной программы среднего (полного) общего образования в пределах ОПОП НПО/СПО.

Для четкой организации и проведения итогового контроля учебных достижений обучающихся, освоивших программу среднего (полного) общего образования по математике в пределах ОПОП НПО/СПО, на основании приказа Департамента образования и науки Кемеровской области № 788 от 06.04.2012 ГОУ «КРИРПО» были разработаны методические рекомендации «Организация итогового контроля учебных достижений обучающихся по математике при реализации образовательной программы среднего (полного) общего образования в пределах основной профессиональной образовательной программы НПО/СПО».

Рекомендации адресованы администрации, методистам и преподавателям образовательных учреждений НПО/СПО, которые готовят экзаменационные материалы для проведения письменного экзамена по математике по результатам освоения программы среднего (полного) общего образования в пределах ОПОП НПО/СПО.

В рекомендациях отражены требования к организации и проведению экзамена, оценке результатов выполнения работ, даны рекомендации по подготовке к проведению процедуры экзамена, по составлению и структурированию экзаменационной работы, инструкция для обучающихся по выполнению заданий.

Обозначены требования к подбору содержания экзаменационных заданий, в том числе минимально обязательного уровня требований и более высокого. Предлагается технология составления равноценных между собой вариантов экзаменационной работы для проведения экзамена в одной группе обучающихся. Приводятся примерные варианты экзаменационных работ по математике по разным профилям, которые служат наглядной основой для их самостоятельной разработки в образовательных учреждениях НПО и СПО, определения примерного объема экзаменационной работы. Обозначены критерии оценки заданий и шкалы перевода баллов в отметки по пятибалльной системе.

В данной статье обозначим основные требования к организации и проведению экзамена по математике по итогам образовательной программы среднего (полного) общего образования в пределах основной профессиональной обра-

зовательной программы НПО/СПО, обозначенных в указанных рекомендациях.

Освоение образовательной программы среднего (полного) общего образования завершается обязательным итоговым контролем учебных достижений обучающихся, который проводится в рамках промежуточной аттестации, предусмотренной федеральными государственными образовательными стандартами начального профессионального или среднего профессионального образования (далее — ФГОС НПО/СПО).

Экзамен по математике за курс среднего (полного) общего образования в учреждениях профессионального образования является обязательным.

Экзамен по математике проводится письменно с использованием экзаменационных материалов в виде набора контрольных заданий, требующих краткого ответа и/или полного решения. На выполнение письменной экзаменационной работы по математике дается 4 астрономических часа (240 минут).

Обозначим основные позиции, касающиеся организации и порядка проведения экзамена по математике:

— содержание экзаменационных материалов должно отвечать требованиям к уровню подготовки выпускников, предусмотренным стандартом среднего (полного) общего образования по соответствующей общеобразовательной дисциплине (математике) и зафиксированным в примерных программах общеобразовательных дисциплин (примерной программе учебной дисциплины «математика») для профессий НПО и специальностей СПО;

— экзаменационные материалы дополняются критериями оценки (в рекомендациях используется шкала перевода баллов в отметки);

— содержание экзаменационных материалов и критерии разрабатываются преподавателем соответствующей учебной дисциплины (математики), согласовываются с предметной (цикловой) методической комиссией и утверждаются в установленном порядке;

— экзаменационные материалы для проведения письменных экзаменов с использованием набора контрольных заданий формируются из двух частей: обязательной, включающей задания минимально обязательного уровня, правильное выполнение которых достаточно для получения удовлетворительной оценки «3», и дополнительной части с более сложными заданиями, выполнение которых позволяет повысить удовлетворительную оценку до «4» или «5»;

— оценка результатов выполнения письменных экзаменов осуществляется согласно ут-

вержденным критериям (шкалой перевода баллов в отметки), которые открыты для обучающихся до конца экзамена.

Для оценки выполнения каждого задания экзаменационной работы по балльной системе используются критерии оценки заданий.

Для перевода количества набранных баллов в отметку используется шкала перевода баллов в отметки по пятибалльной системе.

Результат экзамена (полученные отметки) сообщается обучающимся в сроки, установленные образовательным учреждением в положении об итоговой и промежуточной аттестации обучающихся (срок не должен превышать 3 дней после сдачи экзамена).

Рекомендации по составлению экзаменационных работ. В каждом учебном году в образовательных учреждениях НПО/СПО для проведения экзамена по математике не позднее чем за месяц до даты проведения экзамена готовится новый комплект контрольных материалов (не менее, четырех вариантов для группы обучающихся).

В экзаменационную работу включаются задания, выполнение которых свидетельствует о наличии общематематических навыков, необходимых человеку в современном обществе. Эти задания должны проверять базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную в графиках, ориентироваться в простейших геометрических конструкциях.

При составлении заданий экзаменационной работы по математике необходимо отразить в заданиях основные содержательные линии курса математики (алгебраическую, уравнений и неравенств, теоретико-функциональную, геометрическую), а также основные умения и виды деятельности, которые должны быть сформированы при изучении курса математики.

При формировании содержания экзаменационной работы по математике учитываются также следующие факты:

— ограниченность объема часов, выделяемого на выполнение экзаменационной работы;

— невозможность отражения в одной экзаменационной работе всех элементов содержания учебной дисциплины, которые были изучены;

— правильное выполнение ограниченного числа заданий (указано в шкале перевода баллов в отметки) обязательной части отвечает минимально обязательному уровню подготовки, подтверждающему удовлетворительное освоение программы по математике как составной части программы среднего (полного) общего образования, реализуемой в рамках основных про-

фессиональных образовательных программ НПО/СПО.

Письменная экзаменационная работа по математике составляется из 2-х частей: обязательной и дополнительной. В обязательную часть включаются задания минимально обязательного уровня, в дополнительную часть — более сложные.

В обязательную часть работы должны быть включены задания базового уровня по всем основным разделам требований ФГОС — геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей, комбинаторика и статистика.

При выполнении заданий обязательной части обучающиеся должны продемонстрировать базовую математическую компетентность. Задания этой группы проверяют базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную в графиках и таблицах, использовать простейшие вероятностные и статистические модели, ориентироваться в простейших геометрических конструкциях, владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и пр.), умение пользоваться математической записью, а также применять математические знания в простейших практических ситуациях.

Обязательная часть содержит не менее 18 заданий.

Составителям экзаменационных работ следует предусматривать, чтобы в формулировке каждого задания были обозначены конкретные виды деятельности, на выполнение которых направлено соответствующее задание (определите, вычислите, решите, найдите, обозначьте и др.).

При составлении экзаменационных работ по математике принципиально важно предусмотреть, чтобы в большей части заданий обязательной части от обучающегося требовалось представить ход решения задачи и полученный ответ.

Требование представить только ответ или ответ с кратким пояснением допускается при выполнении отдельных (2-4) заданий обязательной части. (Например: задания обязательной части могут содержать такие формы ответа: с выбором одного ответа из четырех предложенных вариантов (2 задания), с кратким ответом (6 заданий), на установление соответствия между объектами двух множеств (1 задание) и с записью решения (5 заданий). В последнем типе заданий не обязательно давать пояснения по ходу решения задачи, достаточно грамотно применить требуемый алгоритм).

Дополнительная часть направлена на проверку владения материалом на повышенном уровне и умение решать математические задачи, не сводящиеся к прямому применению алгоритма. Эта часть должна содержать не менее 4 заданий повышенного уровня сложности из различных разделов курса математики (например: 1 задание по геометрии, 3 задания по алгебре).

При выполнении всех заданий дополнительной части необходимо от обучающихся требовать представления описания хода решения задачи и полученный ответ. Возможны различные способы решения в записи развернутого ответа. Главное требование — решение должно быть математически грамотным, из него должен быть понятен ход рассуждений автора работы. При этом оценивается продвижение обучающегося в решении задачи, а не недочеты по сравнению с «эталонным» решением. При решении задачи можно использовать любые математические факты без доказательств и ссылок, содержащиеся в учебниках и учебных пособиях, допущенных или рекомендованных Министерством образования и науки РФ.

При подборе задач прикладной и практической направленности для вариантов экзаменационных работ по математике целесообразно учитывать и отражать в содержании профиль получаемой профессии/специальности.

Составителям экзаменационных работ для проведения экзамена по математике в образовательных учреждениях НПО и СПО при составлении своих вариантов следует иметь в виду, что включенные в них задания не могут отражать всех вопросов содержания изученного материала.

При составлении экзаменационных заданий следует учитывать требования к уровню подготовки обучающихся по математике, которые предусмотрены при составлении экзаменационных работ письменного экзамена.

Важно иметь в виду, что каждый год при подготовке экзаменационных материалов в образовательном учреждении сначала формируется проект одного (базового) варианта. Затем проект базового варианта анализируется и оценивается предметной (цикловой) комиссией по выполнению соответствующих требований:

— к структуре (наличию обязательной и дополнительной частей, к наполнению ихзадания-ми соответствующих уровней сложности);

— к содержанию (с точки зрения представленности заданий разных содержательных линий курса математики, соответствующих умений и видов деятельности, соответствия уровня сложности заданий);

— к расположению заданий (по возрастающей степени сложности в обязательной и дополнительной части),

— ко времени выполнения заданий.

По необходимости базовый вариант дорабатывается.

После того, как базовый вариант удовлетворит всем основным параметрам, обозначенным выше, и будет принят соответствующей предметной (цикловой) комиссией, на его основе формируются другие варианты, необходимые для проведения письменного экзамена по математике одновременно во всех группах образовательного учреждения, которые закончили в данный период освоение учебного курса математики.

При этом составители следят за тем, чтобы все варианты экзаменационной работы, сформированные на основе базового, были равноценны между собой по структуре, количеству заданий, представленности заданий разных содержательных линий курса математики, по проверяемым элементам содержания, умениям и видам деятельности, а также по уровню сложности заданий и критериям оценки. Задания, включенные в разные варианты под одним и тем же номером, должны проверять одни и те же элементы содержания одинакового уровня сложности.

Предложенная технология разработки экзаменационных работ позволит учреждениям профессионального образования формировать на основе базового варианта другие, равноценные ему по всем параметрам, что уравнивает условия для всех обучающихся образовательного учреждения, сдающих экзамен в один и тот же день, и использовать единую шкалу перевода баллов в отметки по пятибалльной системе.

Заметим, что при составлении экзаменационных работ образовательное учреждение с учетом уровня подготовки обучающихся вправе повышать уровень сложности заданий, предложенных в примерном варианте методических рекомендаций (как в обязательной части, так соответственно и в дополнительной части).

Обращаем также внимание преподавателей математики на следующее: в обязательную часть экзаменационной работы включаются задания минимально обязательного уровня и правильное выполнение определенной ее части считается достаточным для удовлетворительной отметки (см. шкала перевода баллов в отметки по пятибалльной системе). Снижать уровень обучения до уровня минимально обязательных требований нельзя даже при невысоком уровне подготовки обучающихся отдельных групп. Ина-

че не удастся достигнуть минимально обязательного уровня подготовки обучающихся. Уровень обучения всегда должен быть выше, чем уровень требований, предъявляемых к результатам обучения.

Рекомендации по проведению и оцениванию экзамена. Экзамен по математике в учреждении профессионального образования проводится в один день для всех групп, завершивших обучение по математике за курс среднего (полного) общего образования.

К проведению экзамена по математике для каждого обучающегося готовится:

— текст с вариантом экзаменационной работы;

— краткая инструкция для обучающихся;

— шкала перевода баллов в отметки;

— листы для чистового оформления работы и для черновика со штампом образовательного учреждения.

При этом метод и форма описания решения задачи могут быть произвольными.

Все листы подписываются и после завершения работы сдаются экзаменационной комиссии.

Текст экзаменационных заданий сопровождается краткой инструкцией для обучающихся, шкалой перевода баллов в отметки по пятибалльной системе для получения каждой из положительных отметок («3», «4», «5»), которые остаются открытыми для них в течение всего времени экзамена.

При формировании в образовательном учреждении дополнительной части базового варианта экзаменационной работы в нее могут быть включены задания, правильное выполнение которых будет оценено другим количеством баллов, также может измениться количество заданий в дополнительной части (но не менее четырех заданий), приведенные критерии оценки (другая балльная система). Например: в дополнительной части может быть предусмотрено 6 заданий и оцениваться могут максимально 2 баллами. В таком случае следует предусматривать соответствующий уровень сложности заданий.

Перед началом выполнения письменной экзаменационной работы обучающиеся должны быть ознакомлены с ее структурой, критериями оценки заданий, шкалой перевода баллов в отметки.

Обучающимся поясняется, что основные требования к выполнению заданий состоят в том, чтобы:

— из представленного решения был понятен ход рассуждений обучающегося;

— ход решения был математически грамотным;

— представленный ответ был правильным;

— метод и форма описания решения задачи могут быть произвольными;

— выполнение каждого из заданий оценивается в баллах.

За правильное выполнение любого задания из обязательной части обучающийся получает один балл.

При выполнении задания из обязательной части, где необходимо привести краткое решение, за неполное решение задания (вычислительная ошибка, описка) можно выставить 0,5 балла.

Если обучающийся приводит неверное решение, неверный ответ или не приводит никакого ответа он получает 0 баллов.

За выполнение любого задания из дополнительной части можно использовать следующие критерии оценки заданий:

Таблица 1

Число баллов, которое обучающийся может получить за правильное выполнение того или иного задания, проставляется в скобках около его номера в бланке экзаменационной работы. Баллы, полученные за все выполненные задания, суммируются.

Особое внимание обучающихся необходимо обратить на шкалу перевода баллов в отметки, в которой указано, сколько баллов достаточно набрать, чтобы получить ту или иную положительную оценку. Шкала перевода баллов в отметки разрабатывается преподавателем к конкретному варианту заданий.

Содержание критерия Баллы

Приведено верное обоснованное решение, приведен правильный ответ 3

Приведено верное решение, но допущена вычислительная ошибка или описка, при этом может быть получен неверный ответ 2

Решение начато логически верно, но допущена ошибка, либо решение не доведено до конца, при этом ответ неверный или отсутствует 1

Неверное решение, неверный ответ или отсутствие решения 0

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Так как обязательная часть состоит из 18 заданий, то на отметку «3», обучающийся должен верно выполнить не менее 9 заданий.

Несколько вариантов шкалы перевода баллов в отметки, в зависимости от уровня сложности, приведен ниже.

Таблица 2

Шкала перевода баллов в отметки по пятибалльной системе

Отметка Число баллов, необходимое для получения отметки (социально-экономический профиль) Число баллов, необходимое для получения отметки (технический профиль) Число баллов, необходимое для получения отметки (гуманитарный профиль)

«3» (удовлетворительно) 9-14 9-16 9-13

«4» (хорошо) 15-20 (не менее одного задания из дополнительной части) 17-21 14-19

«5» (отлично) более 21 (не менее двух заданий из дополнительной части) более 21 более 20

Шкала перевода баллов в отметки может быть размещена в инструкции для обучающегося.

Перед началом выполнения работы проводится инструктаж обучающихся. До обучающихся доводятся требования по выполнению экзаменационной работы.

Обучающимся поясняется, что:

— начинать работу всем следует с выполнения заданий обязательной части;

— для получения удовлетворительной оценки не обязательно выполнять все задания обязательной части;

— правильное выполнение определенной части заданий обязательной части, во-первых, га-

рантирует получение отметки «3», а во-вторых, дает основу для повышения отметки до «4» или «5» при правильном выполнении нескольких заданий дополнительной части;

— при выполнении заданий дополнительной части следует проследить по шкале перевода баллов в отметки — сколько заданий достаточно правильно выполнить, чтобы получить 4 или 5;

— имеет право выбрать, в первую очередь, те задания, при выполнении которых он будет чувствовать себя более уверенным.

Приведенный в статье материал более подробно представлен в методических рекомендациях, представленных на сайте ГОУ «КРИРПО».

АКТИВИЗАЦИЯ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ ВО ВНЕУРОЧНОЙ РАБОТЕ: ИЗ ОПЫТА ПРЕПОДАВАНИЯ ФИЗИКИ

Т. Е. Тарасенко, преподаватель физики ГОУ НПО «Профессиональное училище № 14», г. Ленинск-Кузнецкий

Традиции школы и современные тенденции развития образовательных стандартов по физике выдвигают в качестве приоритетных цели физического образования: формирование научного мышления и мировоззрения учащихся; развитие у учащихся качеств: наблюдательность, любознательность, образное и аналитическое мышление и др.; развитие творческих способностей учащихся, умение преобразовывать информацию, делать на этой основе выводы; формирование и поддержание познавательного интереса к физике.

Необходимость одновременного усвоения учащимися учреждений НПО учебного материала, определяемого двумя стандартами (общего среднего и профессионального), приводит к перегрузкам и снижению качества как общего образования, так и профессиональной подготовки.

В 90-е годы появилась тенденция к отставанию уровня знаний и умений по физике учащихся российских школ от сверстников других развитых стран.

Низкий престиж школьной физики, отсутствие интереса к ней, а отсюда неудовлетворительное

Источник

КОМИТЕТ ОБРАЗОВАНИЯ И НАУКИ КУРСКОЙ ОБЛАСТИ

ОБЛАСТНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РЫЛЬСКИЙ АГРАРНЫЙ ТЕХНИКУМ»

А.В. Дягилева

Методические указания

по проведению экзамена

____ОДП. 01________МАТЕМАТИКА___________

(код, название дисциплины /модуля)

ДЛЯ СПЕЦИАЛЬНОСТИ

_080214 «Операционная деятельность в логистике»

Рыльск 2014 г.

УДК 373

ББК 74

С 87

Печатается по решению редакционно-издательского совета ОБОУ СПО «Рыльский аграрный техникум»

Автор – составитель: А.В. Дягилева, преподаватель ОБОУ СПО «Рыльский аграрный техникум».

Рецензент: Н.И. Шатилина, методист ОБОУ СПО «Рыльский аграрный техникум».

Методические указания по проведению экзамена по «Математике» для специальности 080214 «Операционная деятельность в логистике»

Учебно-методическое пособие/сост.: А.В. Дягилева. Рыльск, 2014.15с

В данном пособии представлены методические указания по проведению экзамена по «Математике» для специальности 080214 «Операционная деятельность в логистике», содержатся примерные варианты экзамена с ответами. Методические указания по проведению экзамена предназначены студентам, обучающимся на 1 курсе ОБОУ СПО «Рыльский аграрный техникум».

Дягилева А.В., 2014г.

ОБОУ СПО «Рыльский аграрный техникум», 2014г.

Основные требования к содержанию письменной экзаменационной работы по математике

1 Содержание экзаменационных материалов должно отвечать требованьям к уровню подготовки выпускников, предусмотренный стандартом среднего (полного) общего образования по математике (Федеральный компонент государственного стандарта общее образования. Часть II среднее (полное) общее образование.) и зафиксированным в примерной программе по математике для профессий НПО и специальностей СПО (одобрены Департаментом государственной политики и нормативно-правового регулирования в сфере образования Минобрнауки России ото 16.04.2008 г.)

Экзаменационные варианты дополняются критериями оценок их выполнения.

2. Содержание экзаменационных материалов и критерии оценок их выполнения разрабатываются преподавателем математики образовательного учреждения, согласовываются с цикловой (предметной) методической комиссией и утверждаются заместителем директора по общеобразовательным дисциплинам.

3. Экзаменационные материалы для проведения письменного экзамена по математике с использованием набора контрольных заданий формируются из двух частей: обязательной, включающей задания минимально обязательного уровня, правильное выполнение которых достаточно для получения отметки «3» (удовлетворительно) и дополнительной части с более сложными заданиями, правильное выполнение которых позволяет повысить отметку до «4» (хорошо) или «5» (отлично)

4. Оценка результатов выполнения письменного экзамена по математике осуществляется согласно утвержденным критериям, которые открыты для обучающихся до конца экзамена.

5. Результаты экзамена признаются удовлетворительными в случае если обучающийся при их сдаче получил отметку не ниже «3» (удовлетворительно)

Инструкция для студентов

На выполнение письменной экзаменационной работы дается 4 астрономических часа (240 минут).

В посменной экзаменационной работе по математике включено 23 задания. Работа состоит из 2-х частей: обязательной и дополнительной. Обязательная часть содержит задания минимально обязательного уровня, а дополнительная часть — более сложные задания.

Обязательная часть содержат 19 заданий. Из них задания с 1 по 15 требуют краткого ответа. После их выполнения полученный ответ надо написать около номера соответствующего задания. Задание считается выполненным верно, если экзаменуемый дал верный ответ .

Остальные задания (16 — 19) обязательной части требуют решение и ответа.

При выполнении заданий дополнительной части задания с 20 по 23 обучающийся должен представить полное решение и ответ.

Правильное выполнение заданий оценивается баллами. За правильное выполнение заданий обязательной части обучающийся получает 1 балл. за правильное выполнение заданий дополнительной части по 3 балла. Баллы указываются в скобках около номера задания. Если приводится неверный ответ или ответ отсутствует, ставится 0 баллов. Баллы, полученные за выполнения заданий суммируются. Постарайтесь выполнить как можно больше заданий и набрать как можно больше баллов.

Перед началом работы внимательно изучите критерии оценивания обратите внимание, что начинать работу следует с заданий обязательной части. И только после того, как Вы наберете необходимое количество баллов до удовлетворительной оценки, можно переходить к заданиям дополнительной части , чтобы повысить оценку до четырёх или пяти .

Желаем успехов!

Требования к оформлению посменной экзаменационной работы по математике

Каждый обучающийся получает пакет документов, вложенный в файл:

текст с вариантом посменной экзаменационной работы и критериями оценки:
титульный лист посменной экзаменационной работы:
лист для ответов:
два тетрадных листа в клетку для выполнения решения заданий с 16 по 23:
тетрадные листы в клетку для черновиков
оценочный лист письменной экзаменационной работы/

Все выданные обучающимся листы должны иметь штамп образовательного учреждения, фамилию, имя, отчество обучающегося и номер варианта экзаменационной работы.

РАССМОТРЕНО

на заседании ПЦК

Протокол №__ от «__»_____2014г

Председатель

_________ __ И. В. Кузьменко

УТВЕРЖДАЮ

Зам. директора по учебной работе

___________И.Н. Добрынина

Вариант 1

Обязательная часть

Выполните задание 1-23 и запишите полученный ответ

(1 балл) Вычислите значение производной функции в данной точке:

f(x) = x² — 3x + 7, х = 2

(1 балл) Решите уравнение:

(1 балл) Вычислите

(1 балл) Назовите взаимное расположение прямых в пространстве.

(1 балл) ,Найдите площадь сферы, радиус которой равен 6см .

(1 балл) Вычислите:

(1 балл) В урне 3 белых и 9 черных шаров. Из урны наугад вынимают один шар. Какова вероятность того, что вынутый шар окажется черным?

(1 балл) Решите уравнение: 3^{х — 3}= 27

(1 балл) На рисунке изображен график функции y=f(x). Прямая, проходящая через точку (-1;1), касается этого графика в точке с абсциссой 3. Найдите f(3).



1
	0	2	х

(1 балл) Решите уравнение: х²-6х+9=0

(1 балл) Даны точки А(3; -7; и В(-5; 4; 1). Найти координаты вектора .

(1 балл) Найдите наибольшее значение функции у=12tgx – 12x + 3π – 13 на отрезке

(1 балл) Найдите объем прямоугольного параллелепипеда, стороны основания которого равны11см и 12см, а высота равна15см.

(1 балл) Решите уравнение:

(1 балл) Решите неравенство: х² – 5х + 4 0

16. (1 балл) Решите систему уравнений:

17.(1 (балл) Найдите все первообразные для функции: у = 2 – х³ + 3х

18. (1 балл) Вычислите значение выражения:

19 (1 балл) Найдите область определения функции:

Дополнительная часть

20. (3 балла) Решите уравнение:

21. (3 балла) Решите систему уравнений:

22. (3 балла) Решите неравенство:

23. (3 балла) Вычислите площадь фигуры (предварительно сделав рисунок), ограниченной линиями:

y = х² – 4х + 5, у = 0, х = 0, х = 4

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	15 – 17 баллов
«4» (хорошо)	18 – 24 балла (не менее 1 задания из дополнительной части)
«5» (отлично)	25 – 31 балл

РАССМОТРЕНО

на заседании ПЦК

Протокол №__ от «__»_____2014г

Председатель

_________ __ И. В. Кузьменко

УТВЕРЖДАЮ

Зам. директора по учебной работе

___________И.Н. Добрынина

Вариант 2

Обязательная часть

Выполните задание 1-23 и запишите полученный ответ

(1 балл) Вычислите значение производной функции в данной точке:

f(x) = 2x + x³– 4, х = 4

(1 балл) Решите уравнение:

(1 балл) Вычислите

(1 балл) Назовите взаимное расположение прямых в пространстве.

(1 балл) Диаметр основания цилиндра равен 1м, высота цилиндра равна 3м. Найдите площадь боковой поверхности цилиндра.

(1 балл) Вычислите:

(1 балл) В партии из 8 деталей имеется 6 стандартных. Найти вероятность того, что взятая наугад деталь окажется нестандартной?

(1 балл) Решите уравнение: 5^{х +5}= 0,04

(1 балл) На рисунке изображен график функции y=f(x). Прямая, проходящая через точку (-6;-1), касается этого графика в точке с абсциссой 6. Найдите f(6).



1
	0	2	х

(1 балл) Решите уравнение: х²+10х+25=0

(1 балл) Даны точки А(7; -2; 3) и В(-1; 5; 6). Найти координаты вектора

12/ (1 балл) Найдите наибольшее значение функции у=11х + cos x + 10 на отрезке

13. (1 балл) Найдите объем правильной 4-х угольной призмы, у которой каждое ребро равно 4см.

14/(1 балл) Решите уравнение:

15. (1 балл) Решите неравенство: х² – 3х — 4

(1 балл) Решите систему уравнений:

17.(1 (балл) Найдите все первообразные для функции: у = 5х² — 1 + 2х

18. (1 балл) Вычислите значение выражения:

19 (1 балл) Найдите область определения функции:

Дополнительная часть

20. (3 балла) Решите уравнение:

21. (3 балла) Решите систему уравнений:

22. (3 балла) Решите неравенство:

23. (3 балла) Вычислите площадь фигуры (предварительно сделав рисунок), ограниченной линиями:

y = х⁴, y = 0, х = — 1, х = 1

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	15 – 17 баллов
«4» (хорошо)	18 – 24 балла (не менее 1 задания из дополнительной части)
«5» (отлично)	25 – 31 балл

Лист для ответов

Вариант №1

(Фамилия Имя Отчество)

Обязательная часть

Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________

Дополнительная часть

Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________

Лист для ответов

Вариант №2

(Фамилия Имя Отчество)

Обязательная часть

Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________

Дополнительная часть

Ответ: _________
Ответ: _________
Ответ: _________
Ответ: _________

Письменная экзаменационная работа

по математике

студент__ группы 1¹ лог

(Фамилия Имя Отчество)

Вариант № 1

Письменная экзаменационная работа

по математике

студент__ группы 1¹ лог

(Фамилия Имя Отчество)

Вариант № 2

Оценочный лист

Вариант №1

(Фамилия Имя Отчество)

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	15 – 17 баллов
«4» (хорошо)	18 – 24 балла (не менее 1 задания из дополнительной части)
«5» (отлично)	25 – 31 балл

Оценочная таблица

Количество баллов обязательной части	Количество баллов дополнительной части	Общее количество баллов	Итоговая оценка	Подпись преподавателя	Подпись ассистента	Подпись председателя экзаменационной комиссии

Оценочный лист

Вариант №2

(Фамилия Имя Отчество)

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	15 – 17 баллов
«4» (хорошо)	18 – 24 балла (не менее 1 задания из дополнительной части)
«5» (отлично)	25 – 31 балл

Оценочная таблица

Количество баллов обязательной части	Количество баллов дополнительной части	Общее количество баллов	Итоговая оценка	Подпись преподавателя	Подпись ассистента	Подпись председателя экзаменационной комиссии

Решение: 1 вариант

№ п/п	Решение	Ответ
1		1
2	7 – x = 16 х = 7 – 16 х = — 9	— 9
3		2
4	Пересекающиеся
5	S = 4πR² S = 4∙π∙6 ² = 144π = 452,16(см²)	144π
6		3
7	9 + 3 = 12 = 0,75	0,75
8	3^{х — 3} = 3³ x – 3 = 3 x = 6	6
9	f(3) = = — 0.5	— 0,5
10	(x – 3)² = 0 x = 3	3
11	= ( — 5 – 3; 4 – (-7); 1 – = ( — 8; 11; — 7)	( — 8; 11; — 7)
12	y^I = = 0 cos²x = 1 x = 2πn y(+ 6π y( y(	— 1
13	V = abh V = 11 ∙ 12 ∙ 15 = 1980 см³	1980
14	2cosx = — cosx = — x = ±+ 2πn	x = ±+ 2πn
15	D(f) = R х² – 5х + 4 = 0 (x – 1)(x – 4) 0	(-∞;1)U(4;+∞)
16		R
17	F = 2x –	F = 2x –
18	=	2
19	D(f) 16x – x³≥ 0 x (4 – x) (4 + x) ≥ 0	(-∞;

Дополнительная часть

20. (3 балла) Решите уравнение:

Пусть , тогда уравнение примет вид:

а² = 4 – 3а

Решая его получим а₁ = 1 и а₂ = -4

Обратная замена: и

х₁ = 3 и х₂ = 3^-4 =

Ответ: 3 и

21. (3 балла) Решите систему уравнений:

Ответ: (3: 0)

22. (3 балла) Решите неравенство:

-cos2.5x

cos2,5x-

+2πn

+0,8πn

23. (3 балла) Вычислите площадь фигуры (предварительно сделав рисунок), ограниченной линиями:

y = х² – 4х + 5, у = 0, х = 0, х = 4

S =

Ответ:

Решение: 2 вариант

№ п/п

Решение

Ответ

1

50

2

x + 4 = 49,

x = 49 – 4

х= 45

45

3

2

4

Параллельные

5

S =2 πRh

S = 2π0,5∙3 = 3π = 9,42м²

3π

6

0

7

Нестандартных 8 – 6 = 2, тогда

0,25

8

5^{х + 5} = 5^-2

х + 5 = -2

х = -7

-7

9

f(6) = = 0.25

0,25

10

(х + 5)² = 0

х = -5

-5

11

(- 1 – 7; 5 – (-2); 6 – 3) = ( — 8; 7; 3)

( — 8; 7; 3)

12

y^[=11 – sinx

11 – sinx = 0

Sinx = 11 – нет решения

y( = 11(-∙ + cos( + 10

y(0) = 11

11

13

V = abh

V = 4 ∙ 4 ∙ 4 =64 см³

64

14

sin x=

х =

х =

15

D(f) = R

х² – 3х — 4 = 0

(x + 1)(x – 4)

( — 1; 4)

16

(1; -1)

17

F =

F =

18

=

3

19

D(f) x³ + 8 0

x³ -8

x -2

(-2; +∞)

Дополнительная часть

20. (3 балла) Решите уравнение:

Введем замену переменной: lg(x – 1) = a, тогда уравнение примет вид:

3а² – 10а + 3 = 0

Решая его получим: а₁ = 3 и а₂ =

Обратная замена: lg(x – 1) = 3 и lg(x – 1) =

х – 1 = 1000 и х – 1 =

Ответ: х = 1001 и х = + 1

21. (3 балла) Решите систему уравнений:

Пусть 2^у = а, тогда уравнение примет вид а² + 16а – 512 = 0

Решая уравнение получим: а₁ = 16 и а₂ = -32

Обратная замена: 2^у = 16 и 2^у = -32(решения нет)

у = 4 , тогда х = 5

Ответ: (5: 4)

22. (3 балла) Решите неравенство:

Sin 4x ≤

23. (3 балла) Вычислите площадь фигуры (предварительно сделав рисунок), ограниченной линиями: y = х⁴, y = 0, х = — 1, х = 1

S =

Ответ: 0,4

Источник

Государственное бюджетное профессиональное образовательное учреждение

Иркутской области

«Черемховский техникум промышленной индустрии и сервиса»

Рассмотрены и одобрены на

заседании методической комиссии

преподавателей общеобразовательных

дисциплин «_____»___сентября____2015 г.

Протокол № ____1______

Председатель МК

___________________ Богданова В.А.

Утверждаю

Зам. директора ГБПОУ ИО ЧТПиС

_______________С.Н. Дроботенко

«_____»_____________2015 г

КОНТРОЛЬНО-ОЦЕНОЧНЫЕ МАТЕРИАЛЫ

для проведения промежуточной и итоговой аттестации

по УД «Математика»

за период 2015-2016 учебного года

в группах 1 курса

профиля:

Разработчик:

Стефанцева Наталья Геннадьевна, преподаватель общественных дисциплин

ГБПОУ ИО ЧТПиС

Черемхово

2015

Содержание

I. Общие положения.

II. Паспорт комплекта контрольно-оценочных средств

III. Контрольно-измерительные материалы для проведения письменного экзамена в виде набора контрольных заданий

I. Общие положения

1. Пояснительная записка

1.1 Нормативная база

Комплект контрольно-оценочных средств для проведения промежуточной аттестации в форме экзамена по УД «Математика» разработан на основании нормативных документов:

ФГОС среднего (полного) общего образования в пределах ОПОП НПО/СПО с учетом профиля получаемого профессионального образования в соответствии с федеральными базисными учебными планами и примерными учебными планами для образовательных учреждений РФ, реализующих программы общего образования (приказ Минобразования России от 09.03.2004 г. № 1 312)
Рабочая программа учебной дисциплины Математика
Положение о текущем контроле знаний и промежуточной аттестации студентов НПО/СПО ГБПОУ ИО «Черемховский техникум промышленной индустрии и сервиса»

1.2 Общие положения

Экзамен по математике проводится за счет времени, выделяемого ФГОС НПО/СПО на промежуточную аттестацию.

Содержание экзаменационных материалов отвечает требованиям к уровню подготовки выпускников, предусмотренным государственным образовательным стандартом среднего (полного) общего образования и зафиксированным в примерной программе учебной дисциплины «Математика» для профессий НПО и специальностей СПО.

Экзамен по математике проводится с использованием экзаменационных материалов в виде набора контрольных заданий.

II. Паспорт комплекта контрольно-оценочных средств

2.1 Область применения

Комплект контрольно-оценочных средств предназначен для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины ОУД 03 Математика в рамках реализации федерального государственного образовательного стандарта по программам подготовки квалифицированных рабочих (служащих)

Профессия: Электро-газосварщик

Машинист локомотива

Технология продукции общественного питания

2.2. 2.Сводные данные об объектах оценивания, основных показателях оценки

Таблица№1

Результаты освоения учебных достижений (объекты оценивания)	Основные показатели оценки результата
У1. Решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;	Выполнение: решения неравенств методом интервалов; решение тригонометрического уравнения; решение показательного уравнения; решения квадратных уравнений анализировать решение уравнений, неравенств при выборе ответа выбор правильного ответа на числовой прямой использование свойств логарифмических функций; преобразование тригонометрических выражений
У2. Умение находить производные элементарных функций; находить первообразную функции; вычислять в простейших случаях площади и объемы с использованием определенного интеграла; находить производные элементарных функций; использовать производную для изучения свойств функций и построения графиков;	Применение правил вычисления производных элементарных функций; правил нахождения первообразных элементарных функций; проверка правильности нахождения первообразной функции
У3. Решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); проводить доказательные рассуждения в ходе решения задач; описывать взаимное расположение прямых и плоскостей в пространстве.	Выполнение правильного построения чертежа; применение теоремы Пифагора; вычисление геометрических измерений
У4. Находить наименьшее и наибольшее значения функций; умение находить производную функции	правила вычисления производных элементарных функций; алгоритм нахождения наименьшего (наибольшего) значения функции
У5. Уметь решать иррациональные уравнения и логарифмические неравенства	умение правильно выбирать решение; находить область определения функции; умение решать дробно — рациональные неравенства
У6. Уметь выполнять арифметические действия над числами; находить значения корня, степени, логарифма, тригонометрических функций; находить число по проценту	уметь проводит арифметические вычисления над числами, нахождение значений корня, степени, логарифмов, тригонометрических функций нахождение числа по проценту
У7. Уметь выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций;	выполнять преобразования выражений, содержащих степени, корни, логарифмы, дроби
У8. Уметь вычислять значение функции по заданному значению аргумента при различных способах задания функции; определять основные свойства числовых функций, строить графики функций, иллюстрировать по графику свойства элементарных функций;	уметь применять основные свойства числовых функций; уметь находить значения функции; уметь «читать» графики / диаграммы
У9. Уметь описывать взаимное расположение прямых и плоскостей в пространстве, изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;	уметь строить параллельные и перпендикулярные прямые и плоскости в пространстве; нахождение недостающих элементов многогранников и круглых тел по условию задачи
У10. Уметь находить вероятности событий и элементы комбинаторики	уметь применять формулы комбинаторики и теории вероятностей к задачам практического содержания, оценивать логическую правильность рассуждений, анализировать реальные числовые данные
З 1.Знание свойства показательной и логарифмической функции	— применение свойств степени, показательной функции, равносильности уравнений
З 2.Знание теоретических основ начал математического анализа	знание формулы уравнение касательной к графику функции; алгоритма нахождения уравнения касательной к графику функции; знание определения первообразной функции; основного свойства первообразной функции
З 3. Знание формулировок аксиом и основных теорем и их следствий; понятия тела вращения: цилиндр, конус и шар; свойств перпендикуляра и наклонной; основных теорем планиметрии и стереометрии понятия объема тела	свойств прямоугольного треугольника; знание основных теорем и их следствия; знание основных формул планиметрии – свойства прямоугольного, равнобедренного треугольника. свойств параллелограмма, трапеции; знание формул площадей многоугольников; знание формул поверхности и объема многогранников и круглых тел
З4. Знание понятия о числовых функциях и их основных свойствах, графиках функций. свойств и графиков степенной, показательной, логарифмической функций;	знание определения функции, области определения и области значений числовых функций; знание свойств числовых функций: возрастание/убывание, четность/нечетность, периодичность, ограниченность и т.д.
З 5. Знание свойств иррациональных. показательных, логарифмических, тригонометрических уравнений и неравенств; Основных приемов решения уравнений и неравенств с одной и двумя переменными;	знание формул сокращенного умножения; знание алгоритма решения квадратного уравнения; знание метода интервалов при решении неравенств; знание свойств логарифмической функции при решении данного вида неравенств
З6. Знание обобщенного понятия о степени числа, корня n-степени из числа; преобразований степенных выражений; преобразований выражений, содержащих логарифмы;	знание основных свойств степени с натуральным, целым, дробным, действительным показателем; выполнение действий со степенями, корнями п-ой степени; преобразование выражений. Содержащих степени, корни и логарифмы
З7. Знание о производной функции, ее геометрическом и физическом смысле. правила вычисления производные элементарных функций;. уравнение касательной к графику функции исследования функций с помощью производной	знание определения производной функции; вычисление производных функций; уравнения касательной к графику функции; алгоритма исследования функции с помощью производной
З8. Знание первообразной функции и определенного интеграла, формулы Ньютона — Лейбница;	знание определения первообразной функции, основного свойства первообразных, правил нахождения первообразных; знание формулы Ньютона -Лейбница
З8. Знание основ комбинаторики и теории вероятностей	знание основных формул комбинаторики: подсчет числа элементов сочетаний, размещений, перестановок; знание понятий «событие», «вероятность события», знание формул для вычисления вероятности события

2.3 Содержание и структура экзаменационной работы

Письменная экзаменационная работа по учебной дисциплине ОУД 03. Математика состоит из 2-х частей: обязательной и дополнительной.

В обязательную часть включаются задания минимально обязательного уровня, в дополнительную часть – более сложные.

В обязательную часть работы включены задания базового уровня по всем основным разделам требований ФГОС – геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей, комбинаторика .

Обязательная часть содержит 19 заданий.

К каждому типу заданий прилагается инструкция по форме представления ответа.

При выполнении всех заданий дополнительной части необходимо представить описание хода решения задачи и полученный ответ. Возможны различные способы решения в записи развернутого ответа. Главное требование – решение должно быть математически грамотным, из него должен быть понятен ход рассуждений автора работы. При этом оценивается продвижение обучающегося в решении задачи, а не недочеты по сравнению с «эталонным» решением. При решении задачи можно использовать любые математические факты без доказательств и ссылок, содержащиеся в учебниках и учебных пособиях, допущенных или рекомендованных Министерством образования и науки РФ.

Распределение заданий по частям экзаменационной работы с указанием первичных баллов представлено в таблице 2.

Таблица 2

Части работы	Число заданий	Максимальный первичный балл	Тип заданий
Часть 1 (обязательная)	8	8	С выбором ответа С кратким ответом
11	11
Часть 2 (дополнительная)	7	14	С развёрнутым ответом
Итого	26	33

При подборе контрольных заданий для проведения экзамена использован перечень элементов содержания по математике.

Предлагаемый перечень элементов содержания и требований к уровню подготовки обучающихся составлен на основе Федерального компонента государственных стандартов основного общего и среднего (полного) общего образования по математике базового/профильного уровня (Приказ Минобразования России от 05.03.2004 г. № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования» (в ред. Приказов Минобрнауки РФ от 03.06.2008 № 164 от 31.08.2009 № 320, от 19.10.2009 № 427).

Проверяемые элементы содержания

Таблица 3

Введение	Математика в науке, технике, экономике, информационных технологиях и практической деятельности.
Развитие понятия о числе	Целые и рациональные числа. Действительные числа.
Корни, степени и логарифмы	Корни и степени. Корни натуральной степени из числа и их свойства. Степени с рациональными показателями, их свойства. Степени с действительными показателями. Логарифм. Логарифм числа. Основное логарифмическое тождество. Десятичные и натуральные логарифмы. Правила действий с логарифмами. Преобразование алгебраических, рациональных, иррациональных степенных, показательных и логарифмических выражений.
Прямые и плоскости в пространстве	Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей. Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей.
Элементы комбинаторики	Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля.
Координаты и векторы	Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов.
Основы тригонометрии	Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества, формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Преобразования простейших тригонометрических выражений. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений.
Функции, их свойства и графики. Степенные, показательные, логарифмические и тригонометрические функции	Функции. Область определения и множество значений; график функции, построение графиков функций, заданных различными способами. Свойства функции: монотонность, четность, нечетность, ограниченность, периодичность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума. Графики
Многогранники	Вершины, ребра, грани многогранника. Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида. Правильная пирамида. Тетраэдр. Симметрии в кубе, в параллелепипеде. Сечения куба, призмы и пирамиды. Представление о правильных многогранниках.
Тела и поверхности вращения	Цилиндр и конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию. Шар и сфера, их сечения.
Начала математического анализа	Последовательности. Способы задания и свойства числовых последовательностей. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Применение производной к исследованию функций и построению графиков. Нахождение скорости для процесса, заданного формулой и графиком. Первообразная и интеграл. Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница. Примеры применения интеграла в физике и геометрии.
Измерения в геометрии	Объем и его измерение. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы. Подобие тел. Отношения площадей поверхностей и объемов подобных тел.
Элементы теории вероятностей. Элементы математической статистики	Событие, вероятность события, сложение и умножение вероятностей. Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана.
Уравнения и неравенства	Равносильность уравнений, неравенств, систем. Рациональные, иррациональные, показательные и тригонометрические уравнения, неравенства и их системы. Основные приемы их решения. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов.

2.3.Процедура проведения экзамена.

На выполнение письменной экзаменационной работы отводится 240 минут.

Для проведения экзамена по математике с использованием экзаменационных материалов в виде набора контрольных заданий каждому обучающемуся выдаётся:

— текст с одним из четырех вариантов письменной экзаменационной работы;

— инструкция по выполнению экзаменационной работы;

— лист для черновика.

Все задания обучающийся выполняет на листах с печатной основой

Перед началом выполнения письменной экзаменационной работы (время не входит в 4 астрономических часа) преподаватель контролирует заполнение личных данных обучающихся, знакомит обучающихся со структурой экзаменационной работы, с критериями оценивания еѐ результатов.

Обучающимся поясняется, что экзаменационная работа состоит из двух частей: обязательной и дополнительной. В обязательную часть включены задания минимально обязательного уровня, а в дополнительную часть – более сложные. Выполнение каждого из заданий оценивается в баллах. Количество баллов, которое можно получить за правильное выполнение того или иного задания, проставлено в скобках рядом с его номером. Баллы, полученные за все выполненные задания, суммируются.

Шкала перевода баллов в отметки по пятибалльной системе показывает, сколько баллов необходимо набрать, чтобы получить отметку «3», «4» или «5». Шкала остаётся открытой для обучающихся в течение всего экзамена, они могут ориентироваться на неё в ходе выполнения экзаменационной работы. Обучающиеся могут просчитать при помощи шкалы, сколько и какие задания необходимо выполнить правильно, чтобы получить определённую отметку.

Обучающиеся должны начинать выполнение экзаменационной работы с заданий обязательной части. Для получения удовлетворительной отметки необязательно выполнять минимум 15 заданий обязательной части, но только после выполнения достаточного для получения удовлетворительной отметки количества заданий обязательной части обучающийся может переходить к заданиям дополнительной части, чтобы повысить оценку до «4» или «5». Обучающийся может начинать выполнение работы с любого задания с нужным количеством баллов, учитывая при этом степень своей уверенности в ответе.

Шкала перевода баллов в отметки по пятибалльной системе

Отметка	Число баллов, необходимое для получения отметки
«2» (неудовлетворительно)	Менее 15
«3» (удовлетворительно)	15-19
«4» (хорошо)	20-23
«5» (отлично)	Более 23

III. Контрольно-измерительные материалы для проведения письменного экзамена в виде набора контрольных заданий

3.1 Краткая инструкция для обучающихся по выполнению экзаменационной работы

На письменный экзамен учащиеся приходят за 20 мин до начала экзамена. При себе иметь шариковую, гелиевую или капиллярную ручку с черными чернилами;

К экзамену по математике при себе также иметь чертежные инструменты и справочные материалы, которые можно использовать.

Во время проведения экзаменов запрещается иметь при себе и использовать средства связи и электронно-вычислительную технику, за исключением случаев, установленных нормативно-правовыми актами РФ.

Получить от преподавателя и ассистента черновики и экзаменационный комплект с вложенными в них контрольно-измерительными материалами (КИМ), бланками ответов № 1 и № 2.

Внимательно прослушать инструктаж, проводимый преподавателем, информирующий экзаменующих о порядке проведения экзамена,

правилах заполнения бланков, продолжительности экзамена

Заполнить регистрационные части бланков: бланка регистрации, бланков ответов № 1 и 2.

На выполнение экзаменационной работы дается 4 часа (240 минут).

Работа состоит из двух частей и содержит 26 заданий.

Часть 1 содержит 19 заданий с выбором ответа и с кратким ответом. Задания части 1 считаются выполненными, если экзаменующий выбрал верные ответы.

Часть 2 содержит 7 более сложных заданий ( А20-А26) по материалу курса математики. При их выполнении надо записать полное решение и ответ.

Совет: для экономии времени пропускать задание, которое не удается выполнить сразу и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.

– начинать работу всем следует с выполнения заданий обязательной части;

– для получения удовлетворительной оценки не обязательно выполнять все задания обязательной части;

– правильное выполнение определенной части заданий обязательной части, во-первых, гарантирует получение отметки «3», а во-вторых, дает основу для повышения отметки до «4» или «5» при правильном выполнении нескольких заданий дополнительной части;

– при выполнении заданий дополнительной части следует проследить по шкале перевода баллов в отметки — сколько заданий достаточно правильно выполнить, чтобы получить 4 или 5; После объявления о времени начала экзамена, которое фиксируется на доске, приступить к выполнению экзаменационной работы.

Во время экзамена учащиеся должны соблюдать установленный порядок проведения экзамена и следовать указаниям организаторов.

Во время экзамена учащиеся не вправе общаться друг с другом, свободно перемещаться по кабинету, пользоваться справочными материалами, иметь при себе и использовать средства связи и электронно-вычислительной техники.

Учащиеся могут выходить из кабинета в случае необходимости (в туалет, в медицинскую комнату), предварительно сдав бланки.

По окончании экзамена необходимо:

сдать экзаменационный материал КИМ, черновики, бланки ответов № 1 и № 2;

Допускается досрочная сдача экзаменационных материалов, которая прекращается за пятнадцать минут до окончания экзамена.

Желаем успеха!

3.2. Контрольная работа по математике

По профессиям: электрогазосварщик,

машинист локомотива

ВАРИАНТ № 1

Часть 1.

1. Найдите значение выражения

2. Одна из точек, отмеченных на координатной прямой, соответствует числу

Какая это точка?

1) точка M

2) точка N

3) точка P

4) точка Q

3. Сравните числа и 10.

В ответе укажите номер правильного варианта.

4. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. Установите соответствие между функциями и их графиками.

Графики

Функции

А)

Б)

В)

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б	В

6. Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?

1) 83	2) 95	3) 100	4) 102

7. Найдите значение выражения при

8. На каком рисунке изображено множество решений неравенства

В ответе укажите номер правильного варианта.

В выпуклом четырехугольнике ABCD , , , . Найдите угол A. Ответ дайте в градусах.

Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.

11. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.

12. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

13. Укажите номера верных утверждений.

1) Любые три прямые имеют не более одной общей точки.

2) Если угол равен 120°, то смежный с ним равен 120°.

3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из данной точки к прямой, больше 3.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

14. Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 35,5 г.

Категория	Масса одного яйца, г
Высшая	75,0 и выше
Отборная	65,0 − 74,9
Первая	55,0 − 64,9
Вторая	45,0 — 54,9
Третья	35,0 — 44,9

В ответе укажите номер правильного варианта.

1) отборная

2) первая

3) вторая

4) третья

15. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наибольшее значение температуры. Ответ дайте в градусах Цельсия.

16. Расстояние от Солнца до Нептуна свет проходит примерно за 252,95 минуты. Найдите приблизительно расстояние от Солнца до Нептуна, ответ округлите до миллионов км. Скорость света равна 300 000 км/с.

17. На сколько градусов повернется Земля вокруг своей оси за 7 часов?

18. На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание жиров находится в пределах от 15% до 25%.

*К прочему относятся вода, витамины и минеральные вещества.

1) какао

2) шоколад

3) фасоль

4) грибы

19. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.

Часть 2.

20. Центростремительное ускорение при движении по окружности (в м/c²) можно вычислить по формуле где — угловая скорость (в с⁻¹), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с⁻¹, а центростремительное ускорение равно 45 м/c².

21. Решите уравнение

22. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

23. Постройте график функции

и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

24. Основания трапеции равны 9 и 15. Найдите отрезок, соединяющий середины диагоналей трапеции.

25. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.

26. В трапеции ABCD боковая сторона AB перпендикулярна основаниюBC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 6, BC = 5.

ВАРИАНТ № 2.

ЧАСТЬ 1.

1. Найдите значение выражения

2. На координатной прямой отмечено число

В ответе укажите номер правильного варианта.

Какое из утверждений относительно этого числа является верным?

3. Найдите значение выражения (1,7 · 10^− 5)(2 · 10^− 2).

В ответе укажите номер правильного варианта.

1) 0,0000034

2) 34000000000

3) 0,000000034

4) 0,00000034

4. Решите уравнение (x − 9)² = (x − 3)².

5. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.

Графики

Коэффициенты

А) k 0, b 0

Б) k 0, b

В) k 0

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А	Б	В

6. Выписаны первые несколько членов геометрической прогрессии: 1; −5; 25; … Найдите сумму первых 5 её членов.

7. Упростите выражение и найдите его значение при .

В ответе запишите найденное значение.

8. Решение какого из данных неравенств изображено на рисунке?

В ответе укажите номер правильного варианта.

9. В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 15 и BC = BM. Найдите AH.

10. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.

11. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на .

12. Найдите площадь трапеции, изображённой на рисунке.

13. Укажите номера верных утверждений.

1) В любую равнобедренную трапецию можно вписать окружность.

2) Диагональ параллелограмма делит его углы пополам.

3) Площадь прямоугольного треугольника равна половине произведения его катетов.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

14. В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет ближе всех к Солнцу?

Планета	Нептун	Юпитер	Уран	Венера
Расстояние (в км)	4,497 · 10⁹	7,781 · 10⁸	2,871 · 10⁹	1,082 · 10⁸

В ответе укажите номер правильного варианта.

1) Нептун

2) Юпитер

3) Уран

4) Венера

15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.

16. В начале 2010 г. в поселке было 730 жителей, а в начале 2011 г. их стало 803. На сколько процентов увеличилось число жителей поселка за год?

17. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

18. На диаграмме представлены семь крупнейших по площади территории (в млн км²) стран мира. Какое из следующих утверждений неверно?

1) По площади территории второе место в мире занимает Канада.

2) Площадь территории Австралии составляет 7,7 млн км².

3) Площадь Китая больше площади Канады.

4) Площадь США больше площади Бразилии на 1 млн км².

19. В магазине канцтоваров продаётся 200 ручек, из них 31 красная, 25 зелёных, 38 фиолетовых, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или чёрная ручка.

ЧАСТЬ 2.

20. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 70 см, n =1400 ? Ответ выразите в километрах.

21. Решите неравенство

22. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.

23.. Постройте график функции и определите, при каких значениях прямая имеет с графиком не менее одной, но не более трёх общих точек.

24. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.

25. В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.

26. Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

ВАРИАНТ № 3.

ЧАСТЬ 1.

1. Вычислите:

2. Какому из данных промежутков принадлежит число

В ответе укажите номер правильного варианта.

1) [0,5;0,6]

2) [0,6;0,7]

3) [0,7;0,8]

4) [0,8;0,9]

3. Укажите наибольшее из следующих чисел.

В ответе укажите номер правильного варианта.

4. Решите уравнение

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. Найдите значение по графику функции , изображенному на рисунке.

6. Геометрическая прогрессия задана условием b₁ = −7, b_n_{+ 1} = 3b_n. Найдите сумму первых 5 её членов.

7. Упростите выражение и найдите его значение при . В ответ запишите полученное число.

8. На каком рисунке изображено множество решений неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

9. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.

10. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.

11. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.

12. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

13. Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2) Если угол равен 60°, то смежный с ним равен 120°.

3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4) Через любые три точки проходит не более одной прямой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

14. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.

Превышение скорости, км/ч	11 − 20	21 − 40	41 − 60	61 и более
Размер штрафа, руб.	100	300	1000	2500

Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 175 км/ч на участке дороги с максимальной разрешённой скоростью 110 км/ч?

В ответе укажите номер правильного варианта.

1) 100 рублей

2) 300 рублей

3) 1000 рублей

4) 2500 рублей

15.. В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Вещество	Дети от 1 года до 14 лет	Мужчины	Женщины
Жиры	40—97	70—154	60—102
Белки	36—87	65—117	58—87
Углеводы	170—420	257—586

Какой вывод о суточном потреблении жиров, белков и углеводов 13-летним мальчиком можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров, 90 г белков и 359 г углеводов? В ответе укажите номера верных утверждений.

1) Потребление жиров в норме.

2) Потребление белков в норме.

3) Потребление углеводов в норме.

16. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?

17. Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?

18. а диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание белков превышает 30%.

*К прочему относятся вода, витамины и минеральные вещества.

1) какао 2) шоколад 3) фасоль 4) грибы

19. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.

ЧАСТЬ 2.

20. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле , где n — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 5 колец.

21. Решите уравнение:

22. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Через полчаса навстречу ему из В в А выехал велосипедист, который ехал со скоростью, на 11 км/ч большей скорости пешехода. Найдите скорость велосипедиста, если известно, что они встретились в 5 км от пункта А.

23. Постройте график функции и определите, при каких значениях построенный график не будет иметь общих точек с прямой .

24. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

25. Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.

26. В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

ВАРИАНТ № 4.

ЧАСТЬ 1.

1. Вычислите:

2. На координатной прямой отмечено число Расположите в порядке возрастания числа и

В ответе укажите номер правильного варианта.

3. Расстояние от Земли до Солнца равно 147,1 млн км. В каком случае записана эта же величина?

В ответе укажите номер правильного варианта.

1) 1,471⋅10¹⁰ км

2) 1,471⋅10⁸ км

3) 1,471⋅10⁷ км

4) 1,471⋅10⁶ км

4. Найдите корни уравнения

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. Задание 5 № 193101. Найдите значение по графику функции изображенному на рисунке.

6. Дана геометрическая прогрессия (b_n), знаменатель которой равен 2, аb₁ = 16. Найдите b₄.

7. Сократите дробь

8. На каком рисунке изображено множество решений неравенства ?

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

9. В треугольнике угол равен 90°, . Найдите .

10. Центральный угол AOB опирается на хорду ABдлиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

Найдите площадь трапеции, изображённой на рисунке.

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

13. Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

4) В любом параллелограмме диагонали равны.

14. Для квартиры площадью 135 м² заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.

Цвет потолка	Цена в рублях за 1 м² (в зависмости от площали помещения)
	до 10 м²	от 11 до 30 м²	от 31 до 60 м²	свыше 60 м²
белый	1200	1000	800	600
цветной	1350	1150	950	750

Какова стоимость заказа, если действует сезонная скидка в 20%?

В ответе укажите номер правильного варианта.

1) 81 000 рублей

2) 64 800 рублей

3) 6480 рублей

4) 80 980 рублей

15. На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?

16. Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?

17. крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.

18. На диаграмме показаны религиозные составы населения Германии, США, Австрии и Великобритании. Определите по диаграмме, в какой стране доля католиков превышает 50%.

1) Германия

2) США

3) Австрия

4) Великобритания

ЧАСТЬ 2.

20. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6000 + 4100 · n , где n — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 20 колец.

21. Решите систему уравнений

22. Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

23. Постройте график функции и определите, при каких значениях параметра прямая имеет с графиком три общие точки.

24. Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 39°, 78° и 63°.

25. Основания BC и AD трапеции ABCD равны соответственно 5 и 20,BD = 10. Докажите, что треугольники CBD и ADB подобны.

3.3 Критерии оценки экзаменационной работы в виде набора контрольных заданий

Оценка 5 (отлично) ставится за работу, выполненную полностью без ошибок и недочётов; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Оценка 4 (хорошо) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Оценка 3 (удовлетворительно) ставится, если обучающийся правильно выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки и двух недочётов, не более одной грубой и одной не грубой ошибки, не более трёх негрубых ошибок, одной негрубой ошибки и трёх недочётов, при наличии четырёх-пяти недочётов.

Оценка 2 (неудовлетворительно) ставится, если число ошибок и недочётов превысило норму для оценки 3 или правильно выполнено не менее 2/3 всей работы; допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере

КЛЮЧ

№	1 вариант	2 вариант	3 вариант	4 вариант
	-3786,7	20	1,03	1,55
	1	1	1	2
	1	4	2	2
	-5;3	6	0,5;1	3;6
	412	132	4	1
	4	521	-847	128
	31	1,5	0,4	84
	4	3	1	2
	95	11,25	80	33
	144	30	4	6
	2688	50	156	270
	2	28	52	58
	1;3	3	2;3;4	13\|31\|1;3\|1,3
	4	4	4	2
	16	756	1;3\|13\|1; 3	50000
	4553000000	10	16000000	9
	105	3,5	1440	15
	1	3	4	3
	0,6	0,42	0,0625	0,0625
	5	0,98	26500	88000
	-8:-5		-1;0;5	(3; −4)
	61,6	5	16 км/ч	220
	2,6		2/3;1;2	(0;5)
	3	8	16	102°, 24°, 54°

		3,2	9

25. 1 вариант.

Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.

Решение.

Поскольку четырёхугольник ABCD вписанный, сумма углов BAD и BCD равна 180°.

Следовательно,

∠MCB = 180° − ∠BCD = ∠BAD.

Получаем, что в треугольниках MBC и MDA углы MCB и MAD равны, угол M общий, следовательно, эти треугольники подобны.

25. 2 вариант.

В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.

Решение.

Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,

Площадь параллелограмм равна а площадь треугольника

25. 3 вариант.

Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.

Решение.

Точка I равноудалена от A и B, поэтому она лежит на серединном перпендикуляре к отрезку AB. То же можно сказать и о J . Значит IJ — серединный перпендикуляр к AB.

25. 4 вариант.

Основания BC и AD трапеции ABCD равны соответственно 5 и 20,BD = 10. Докажите, что треугольники CBD и ADB подобны.

Решение.

Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках и следовательно, эти треугольники подобны по двум парам подобных сторон и углу между ними.

Контрольная работа по математике

по профессии среднего профессионального образования

Технология продукции общественного питания

Вычислить предел:

1). Ответ:

2). Ответ:

3) Ответ

4). Ответ

5). Ответ :

6) Ответ:

7). Ответ:

8). Ответ:

9). Ответ:

10). Ответ:

11). Ответ:

12). Ответ:

13). Ответ:

2. Пользуясь определением производной, найти производную функции у, если:

,
,
у = 5 − 6x ,
у= 4 − 7x,
,
,
у = 2х²— 13х +3,
у=-3x²-13x,
у=7x²+3x,
у =4 – 5х + 2х²,
у = 3х²— 2х – 8,
у=х³— 9х – 4,
у=3х³ — 4х²— 8х – 4,
у =-2х³ -4х²-4х

Решить задачи по теории вероятностей.

№ 1. В кармане у Миши 4 конфеты – «Грильяж», «Маска», «Белочка», «Красная шапочка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Маска»

№ 2. Оля, Денис, Витя, Артур и Рита бросали жребий – кому начать игру. Найдите

вероятность того, что начинать игру будет Рита?

№ 3. Катя, Настя, Игорь, Даша и Андрей бросали жребий – кому начать игру.

Найдите вероятность того, что начинать игру будет мальчик?

№ 4. Игральную кость бросают один раз. Найдите вероятность того, что выпало

число очков не меньше, чем 3?

№ 5. Бабушка решила дать внуку Илье на дорогу какой-нибудь случайно

выбранный фрукт. У неё было 3 зелёных яблока, 3 зеленых груши и 2 желтых

банана. Найдите вероятность того, что Илья получит фрукт зеленого цвета?

№ 6. Игральную кость бросают два раза. Найдите вероятность того, что оба раза

выпало число большее 3?

№ 7. Игральную кость бросают два раза. Найдите вероятность того, что один раз

выпало число большее 3, а другой раз — меньшее 3?

№ 8. В случайном эксперименте симметричную монету бросают дважды. Найдите

вероятность того, что орёл выпадет ровно один раз?

№ 9. В случайном эксперименте симметричную монету бросают три раза. Найдите

вероятность того, что решка выпадет ровно два раза?

№ 10. В случайном эксперименте бросают две игральные кости. Найдите

вероятность того, что в сумме выпадет 7 очков?

№ 11. В соревнованиях по керлингу выступают 20 команд из 5 стран: Швеция,

Норвегия, Финляндия, Канада, Дания. Причем каждая страна выставила по 4

команды. Порядок выступления команд определяется жеребьевкой. Найдите

вероятность того, что 17-ой по счету будет выступать одна из команд Канады?

№ 12. В соревнованиях по керлингу выступают 20 команд из 5 стран: Швеция,

Норвегия, Финляндия, Канада, Дания. Причем каждая страна выставила по 4

команды. Порядок выступления команд определяется жеребьевкой. Найдите

вероятность того, что 17-ойп по счету будет выступать одна из команд

Швеции, Норвегии или Дании?

№ 13. В коробке находятся 7 красных шаров, 13 белых шаров и 6 голубых шаров.

Определите вероятность того, что наудачу взятый из коробки шар окажется

белым.

№ 14. В копилке находятся монеты достоинством 2 рубля – 14 штук, 5 рублей – 10

штук и 10 рублей – 6 штук. Какова вероятность того, что первая монета,

выпавшая из копилки, будет достоинством 10 рублей?

№ 15. В корзине лежат 7 помидоров, 6 огурцов, 12 перцев. Найдите вероятность того,

что первый наугад взятый овощ из корзины будет перцем.

КЛЮЧ

№	№	ответ
1	1	(-1/3) – неопределённость -раскрывать путём разложения на множители
2	(-1/3) — неопределённость -раскрывать путём домножения на сопряжённое выражение
3	:(-1/2) — неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем
4	:(0) — неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем
5	— неопределённость -раскрывать путём вынесения за скобки x с наибольшим показателем
6	— –неопределённость — раскрывать с помощью метода приведения ко второму замечательному пределу — сначала преобразовать скобку следующим образом
7	-–неопределённость — раскрывать с помощью метода приведения ко второму замечательному пределу — сначала преобразовать скобку следующим образом
8	— неопределённость — раскрывать с помощью метода приведения ко второму замечательному пределу — сначала преобразовать скобку следующим образом
9	– неопределённость — раскрывать с помощью метода приведения к первому замечательному пределу
	10	– неопределённость — раскрывать с помощью метода приведения к первому замечательному пределу=1
11	-–неопределённость — раскрывать с помощью метода приведения к первому замечательному пределу=1
12	(6). –воспользоваться свойством вычисления предела непрерывной функции
13	). –воспользоваться свойством вычисления предела непрерывной функции
2	1	-2
2	8
3	-6
4	-7
5	2х-1
6	2а+в
7	4х-13
8	6х-13
9	14х+3
10	-5+4х
11	6х-2
12	3х2-9
13	9х2-8х-8
14	-6х2-8х-4
3	1	0,25
2	0,2
3	0,4
4	2/3
5	0,75
6	0,25
7	1/3
8	0,5
9	3/8
10	1/6
11	0,2
12	0,6
13	0,5
14	0,2
15	0,48

Критерии оценивания заданий

Оценка в пятибалльной шкале	Критерии оценки	Количество правильно данных вопросов
«2»	Выполнено менее 50% заданий	Даны верные ответы менее, чем на 21 вопросов
«3»	Выполнено 51-74 % заданий	Даны верные ответы на 21-30 вопроса
«4»	Выполнено 75-89% заданий	Даны верные ответы на 31-37 вопросов
«5»	Выполнено более 90% заданий	Данные верные ответы на 38-42 вопросов

Критерии оценивания заданий:

За каждое правильно выполненное тестовое задание (верный ответ) ставится 1 балл, за

Критерии оценивания выполнения практического задания

Своевременность выполнения практической работы.

Выполнение работы в полном объеме с соблюдением необходимой последовательности

вычислений.

Источник