Анализ информационных моделей егэ информатика теория - Помощь в подготовке к экзаменам и поступлению

Урок посвящен тому, как решать 1 задание ЕГЭ по информатике

Содержание:

Объяснение заданий 1 ЕГЭ по информатике
- Структурирование информации и информационные модели
- Поиск кратчайшего пути (перебор)
Решение заданий 1 ЕГЭ по информатике

1-я тема характеризуется, как:
— задания базового уровня сложности,
— требуется использование специализированного программного обеспечения — нет,
— время выполнения – примерно 3 минуты,
— максимальный балл — 1

Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)

До ЕГЭ 2021 года — это было задание № 3 и задание № 7 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Как и в большинстве простых заданий, основные ошибки происходят из-за торопливости и невнимательности»

ФГБНУ «Федеральный институт педагогических измерений»

* Некоторые изображения страницы взяты из материалов презентации К. Полякова

Структурирование информации и информационные модели

Рассмотрим кратко необходимые для решения 1 задания ЕГЭ понятия.

Структурирование информации — это установление главных элементов в информационных сообщениях и установление связей между ними.

Структурирование выполняется с целью облегчения восприятия и поиска информации.

Структурирование возможно при помощи следующих структур (информационных моделей):

множество:

перечисление элементов, собранных по характерному признаку;

Вася, Петя, Коля
1, 17, 22, 55

В множестве упорядочивание элементов не обязательно, т.е. порядок следования не важен.

линейный список

Важна упорядоченность следования элементов.

таблица

В таблицах выделяются объекты (отдельные записи таблиц) и свойства (названия столбцов или названия строк):

дерево или иерархия объектов

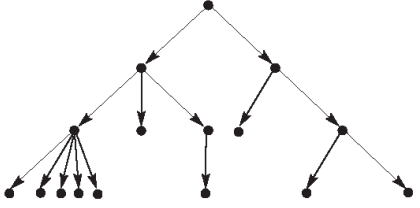
Уровни в дереве

Рассмотрим родственные отношения в дереве:

«Сыновья» А: B, C.

«Родитель» B: A.

«Потомки» А: B, C, D, E, F, G.

«Предки» F: A, C.

Корень – узел без предков (A).
Лист – узел без потомков (D, E, F, G).
Высота – наибольшее расстояние от корня до листа (количество уровней).

файловая система (иерархия)

Допустим, на жестком диске компьютера имеются следующие папки (каталоги) с файлами:

Получим дерево:

графы

Иногда очень трудно структурировать информацию описанными структурами из-за сложных «взаимоотношений» между объектами. Тогда можно использовать графы:

Граф – это набор вершин и связей между ними, называющихся рёбрами:

Граф, отображающий дороги между поселками

матрица и список смежности

Связный граф – это граф, между любыми вершинами которого существует путь.

Связный граф

Дерево – это связный граф без циклов (замкнутых участков).

Дерево — связный граф без циклов

взвешенные графы и весовая матрица

У взвешенных графов указан «вес ребра»:

Из взвешенных графов получается весовая матрица, обратное преобразование тоже возможно.

Весовая матрица

Поиск кратчайшего пути (перебор)

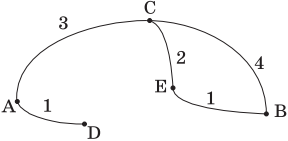
Определение кратчайшего пути между пунктами A и D

В заданиях ЕГЭ этой темы чаще всего используются две информационные модели — таблицы и схемы.
Информация в таблице строится по следующим правилам: на пересечении строки и столбца находится информация, характеризующая комбинацию этой строки и столбца.
На схеме информация строится по следующему правилу: если между объектами схемы имеется связь, то она отображается линией, соединяющей названия этих объектов на схеме.

Егифка ©:

Решение заданий 1 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Задание демонстрационного варианта 2022 года ФИПИ

1_3: Решение 1 задания ЕГЭ по информатике:

Между населенными пунктами A, B, C, D, E, F построены дороги, протяженность которых приведена в таблице (если ячейка пуста — дороги нет).

	A	B	C	D	E	F
A		7	3
B	7		2	4	1
C	3	2		7	5	9
D		4	7		2	3
E		1	5	2		7
F			9	3	7

Определите длину кратчайшего пути между пунктами A и F.

Подобные задания для тренировки

✍ Решение:

Для решения задачи используем построение дерева с подсчетом значений для каждой ветви (протяженности дорог).
При движении от корня дерева (А) вниз будем иметь в виду, что:
рассматривать вершины, которые уже есть в текущей «ветви», — не нужно,
если получаемое число (суммарная протяженность дорог) превышает какое-либо из найденных вариантов от A до F, то дальше эту ветвь можно не рассматривать.
В итоге получим дерево:

Самый короткий путь: A -> C -> B -> E -> D -> F = 11

Результат: 11

Видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

1_4: Решение 1 задания ЕГЭ по информатике:

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

	A	B	C	D	E	F
A		3	7		6
B	3			4	4
C	7			5		9
D		4	5			5
E	6	4				8
F			9	5	8

Определите длину кратчайшего пути между пунктами A и F при условии, что передвигаться можно только по указанным в таблице дорогам.

✍ Решение:

Решим задание при помощи построения дерева, вершиной которого является отправной пункт — A. На ребрах дерева будем записывать числа — результат протяженности пути до конкретной вершины.

Кратчайший путь: A -> B -> D -> F = 12

Результат: 12

1_5: Решение 1 задания ЕГЭ по информатике:

Между населенными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяженность каждой дороги (отсутствие числа в таблице означает, что прямой дороги между пунктами нет).

	A	B	C	D	E	F	Z
A		3		5			14
B			2				8
C		2					7
D					1	4	4
E						1	5
F			12		1		9
Z

Сколько существует таких маршрутов из A в Z, которые проходят через пять и более населенных пунктов? Пункты A и Z при подсчете учитывайте. Два раза проходить через один пункт нельзя.

* в учебниках 2018 года задания 2 и 3 поменяли местами: теперь 2 — Поиск кратчайшего пути, а 3 — Алгебра логики

✍ Решение:

Для решения будем использовать дерево:

Розовым отмечены неподходящие маршруты, а голубым — подходящие.
Заметим, что после 4-го уровня сверху, все варианты будут подходить.

Результат: 6

1_2: 1 задание:

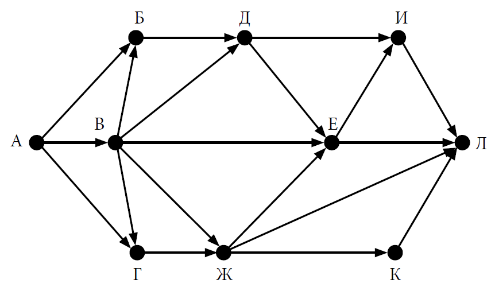
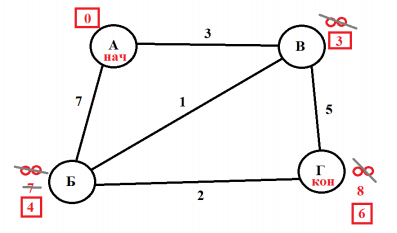
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта А в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.

Подобные задания для тренировки

✍ Решение:

Посчитаем сколько ребер у каждой вершины:

A -> 3 (В Г Д)
Б -> 1 (В)
В -> 4 (А Б Г Е)
Г -> 4 (А В Д К)
Д -> 2 (А Г)
Е -> 1 (В)
К -> 1 (Г)

Три ребра имеет только одна вершина — А, поэтому только А может соответствовать П3.
Уникальное значение количества ребер имеет также вершина Д, — два ребра. В таблице вершине Д будет соответствовать П4.
Вершины Г и В имеют по 4 ребра. Рассмотрим матрицу, в ней 4 числа соответствуют пунктам П2 и П5.
С пунктом Д пересекается только вершина Г (Г -> 4 (А В Д К)). В весовой матрице с вершиной Д пресекается П5. Значит вершина Г соответствует П5.
В П5 на пересечении с П3 находится число 6.

Результат: 6

Подробное решение данного 1 задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

1_1: ЕГЭ по информатике:

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова длина дороги из пункта Д в пункт К. В ответе запишите целое число — так, как оно указано в таблице.

✍ Решение:

Рассмотрим граф и посчитаем количество ребер из каждой вершины:

А - > 2 ребра (Г, В)
В - > 4 ребра (А, Г, К, Д)
Г - > 4 ребра (А, В, К, Д)
Б - > 2 ребра (Г, К)
К - > 5 ребер (Б, Г, В, Д, Е)
Е - > 2 ребра (К, Д)
Д - > 3 ребра (В, К, Е)

Мы выделили вершины, с уникальным числом ребер: 3 ребра соответствует только вершине Д, а 5 ребер соответствует только вершине К.
Рассмотрим таблицу и найдем те строки или столбцы, в которых 5 значений и 3 значения: Это П2 и П4.
Получаем П2 соответствует Д, а П4 соответствует К. На пересечении находится цифра 20.

Результат: 20

Кроме того, Вы можете посмотреть видео решения этого задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

1_6: Разбор 1 задания ЕГЭ:

На рисунке изображена схема дорог Н-ского района, в таблице звездочкой обозначено наличие дороги из одного населенного пункта в другой, отсутствие звездочки означает, что такой дороги нет. Каждому населенному пункту на схеме соответствует его номер в таблице, но неизвестно, какой именно номер.

	1	2	3	4	5	6	7	8
1			*	*			*
2			*	*				*
3	*	*
4	*	*			*	*	*	*
5				*		*	*
6				*	*			*
7	*			*	*
8		*		*		*

Определите, какие номера населенных пунктов в таблице могут соответствовать населенным пунктам D и E на схеме? В ответе запишите эти два номера в возрастающем порядке без пробелов и знаков препинания.

Подобные задания для тренировки

✍ Решение:

Для начала найдем уникальные вершины — у которых уникальное число ребер: это A (2 ребра) и H (6 ребер). В таблице им соответствуют номера 3 и 4:

	1	2	A	H	5	6	7	8
1			*	*			*
2			*	*				*
A	*	*
H	*	*			*	*	*	*
5				*		*	*
6				*	*			*
7	*			*	*
8		*		*		*

По схеме находим, что смежными вершинами для A являются B и G. В таблице определяем соответствующие им цифры — 1 и 2. Поскольку по заданию они нас не интересуют, обозначим их вместе:

	B,G	B,G	A	H	5	6	7	8
B,G			*	*			*
B,G			*	*				*
A	*	*
H	*	*			*	*	*	*
5				*		*	*
6				*	*			*
7	*			*	*
8		*		*		*

У обеих вершин B и G смежными являются уже известные A и H и, кроме того, вершины F и C. По первому столбцу или первой строке находим, что F или C будет соответствовать цифра 7, а по второй строке — цифра 8. Обозначим их в таблице:

	B,G	B,G	A	H	5	6	F,C	F,C
B,G			*	*			*
B,G			*	*				*
A	*	*
H	*	*			*	*	*	*
5				*		*	*
6				*	*			*
F,C	*			*	*
F,C		*		*		*

В результате получаем, что искомым вершинам — D и E — соответствуют цифры 5 и 6. Поскольку не имеет значения, какой именно цифре должна соответствовать та или иная вершина, то в ответе просто запишем эти цифры в порядке возрастания.

Результат: 56

Источник

Представление и считывание данных в разных типах информационных моделей
(схемы, карты, таблицы, графики и формулы)

Многообразие объектов предполагает использование огромного количества инструментов для реализации и описания этих моделей. Для исследования большинства объектов не обязательно создавать материальные модели. Если ясно представлять цель исследования, то часто достаточно иметь нужную информацию и представить ее в оптимальной форме. В этом случае речь идет о создании информационной модели. Информационные модели — это абстрактные модели, поскольку, как известно, информация — это нематериальная категория.

Информационная модель — это целенаправленно отобранная информация об объекте, представленная в некоторой форме.

Простейшими примерами информационных моделей являются различные загадки, в которых описываются свойства, по которым нужно угадать название объекта («Летом серый, зимой белый»; «Зимой и летом одним цветом»). К информационным моделям можно отнести тексты справочных изданий, энциклопедий.

Формы представления информационных моделей могут быть различными. Наиболее известны следующие формы:

в виде сигналов;
устная, словесная;
символьная (числа, текст, символы);
табличная;
схемы, карты;
графики.

Один и тот же объект, в зависимости от поставленной цели, можно представить несколькими информационными моделями, отличающимися набором параметров и способом их представления. Рассмотрим примеры анализа информации для модели, представленной в табличной форме.

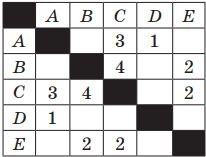
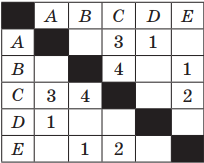
Пример 1. Таблица стоимости перевозок между станциями A, B, C, D, E построена следующим образом: числа, стоящие в ячейках на пересечении строк и столбцов, означают стоимость проезда между соответствующими соседними станциями. Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями. Если на пересечении строки и столбца пусто, то станции не являются соседними. Выбрать таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6».

Решение. Прежде всего, нужно отметить, что данные в таблицах симметричны относительно главной диагонали, т. е. проезд из А в В стоит столько же, сколько и из В в А.

Рассмотрим первую таблицу. Выберем все возможные варианты проезда из А в В и соответственно подсчитаем стоимости: AC(3) + CB(4); AC(3) + CE(2) + EB(2)

Примечание. В скобках указана стоимость проезда.

Стоимость, как первого, так и второго варианта маршрута равна 7.

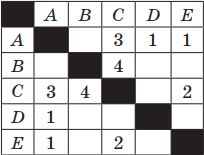
Аналогично поступим для второй таблицы: AC(3) + CB(4); AE(1) + EC(2) + CB(4).

Как и в случае с предыдущей таблицей, стоимость как первого, так и второго варианта маршрута равна 7.

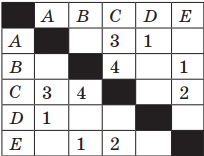
Выписываем все варианты для третьей таблицы: AC(3) + CB(4); AC(3) + CE(2) + EB(1).

Стоимость последнего варианта маршрута равна 6.

Ответ: таблица номер 3 содержит маршрут из А в В, стоимость которого не превышает 6.

Пример 2. Для заданной информационной модели, записанной в форме таблицы, построить модель в виде схемы. В ячейках на пересечении строк и столбцов таблицы указана стоимость проезда между соседними станциями. Пустые ячейки означают, что станции не являются соседними.

Решение. Отметим точку A, она должна быть соединена с C и D. Отмечаем точки C и D и соединяем их с точкой А дугами; над каждой дугой указываем стоимость проезда. Точка С должна быть соединена, кроме А, с точками В и Е. Точка D является соседней только с А. Точка В должна быть соединена, кроме С, с точкой Е. В результате можно получить следующую схему:

Источник

ЕГЭ-2015 задание 5.

Анализ информационных моделей

При решении задач данного вида используется знания информационных моделей (таблицы, диаграммы, графики) и перебор вариантов, выбор лучшего по какому-то признаку

Теория

особых знаний, кроме умения перебирать варианты (не пропустив ни одного!) здесь, как правило, не требуется
полезно знать, что такое граф (это набор вершин и соединяющих их ребер) и как он описывается в виде таблицы, хотя, как правило, все необходимые объяснения даны в формулировке задания
чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки
рассмотрим граф (рисунок слева), в котором 5 вершин (A, B, C, D и E); он описывается таблицей, расположенной в центре; в ней, например, число 5 на пересечении строки В и столбца С означает, что, во-первых, есть ребро, соединяющее В и С, и во-вторых, вес этого ребра равен 5; пустая клетка на пересечении строки А и столбца В означает, что ребра из А в В нет

обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее
в приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так)
желательно научиться быстро (и правильно) строить граф по весовой матрице и наоборот

Задача

Между населенными пунктами A, B, C, D, E, F, G построены дороги, протяженность которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

	A	B	C	D	E	F	G
A		2		6
B	2		5	3
C		5		1			8
D	6	3	1		9	7
E				9			5
F				7			7
G			8		5	7

Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).

Решение

Из пункта A за 1 шаг можно попасть в пункты B и D. AB(2) и AD(6) — в скобках указана длина маршрута.
Из пункта B можно попасть в пункты C и D. ABC(2+5=7) и ABD(2+3=5).
Из пункта C можно попасть в пункты D и G. ABCD(2+5+1=8) (этот путь длиннее прямого AD и его можно не рассматривать дальше) и ABCG(2+5+8=15) — первый способ добраться в конечный пункт длиной 15.
Из пункта D можно попасть в пункты E и F, причем будем учитывать только кратчайший маршрут ABD длиной 5. Соответственно ABDE (2+3+9=14) и ABDF (2+3+7=11).
Из пункта E попадаем в G и общая длина пути ABDEG (2+3+9+5=19) равна 19.
Из пункта F попадаем в G и общая длина пути ABDFG (2+3+7+7=19) тоже равна 19.

Правильный ответ: 15.

Подробности: Опубликовано: 29 Апрель 2015; Просмотров: 15133

Источник

Анализ информационных моделей

Разбор заданий № 3 ЕГЭ (11 кл)

Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных
моделей (схемы, карты, таблицы, графики и формулы).

(базовый уровень, время – 3 мин)

Что нужно знать:

Модель^{^[1]}
(в науке и технике) — упрощённый объект, сохраняющий лишь

важнейшие свойства настоящего
существующего объекта или системы, и

предназначенный для их изучения; упрощённое
представление действительного

объекта и/или
протекающих в нём процессов.

Модель
(информатика) — система, исследование которой служит средством для

получения информации о
другой системе.

Всё многообразие моделей можно условно разделить на три
класса: материальные,

знаковые и умозрительные. Знаковые модели
можно поделить еще на три типа:

описательные,
математические и информационные^{^[2]}.

Информационные модели^{^[3]}
формируются с помощью языка информатики —

цифрового двоичного кода, в который
переводятся сведения (данные), представленные

в любой форме, в том
числе мультимедийной.

Информационная модель^{^[4]}
— это знаковая (цифровая) модель, описывающая

информационные процессы
и информационные системы разной природы.

Информационные модели можно разделить на два типа: модели объектов и

процессов и модели знаний. Модели этих типов
различаются по технологии

моделирования: в первом случае в основу
закладывается формирование базы данных,

во втором — базы знаний. в свою очередь модели объектов и процессов
можно

разбить на пять групп: вербальные,
математические, кибернетические, табличные,

графические.

В группу табличных
информационных моделей попадают электронные таблицы

видов «объект — свойство», «объект —
объект» и «двоичная матрица». В заданиях

представлены таблицы типа «объект — объект», в
которых отображаются взаимосвязи

между разными объектами.

В группе графических
информационных моделей выделяют четыре вида моделей:

схемы, чертежи, карты, графы. Графы, в свою
очередь, разбиты на две категории —

иерархические системы и
сети.

	Граф — это информация о составе и структуре системы, представленная в
	графической форме. Элементы системы называются вершинами, связи между ними
	— отношениями. Симметричные связи называются рёбрами, несимметричные —
	дугами.
Сеть — это граф, в котором вершины различных уровней связаны между собой по
принципу «многие-ко-многим».

Информационные ресурсы:

1.
Теория: Информационные модели, Классификация
информационных моделей

2.
Задания для тренировки: ЕГЭ−2020, информатика: задания, ответы,
решения. Обучающая система «РЕШУ ЕГЭ» Дмитрия Гущина.

3.
Онлайн-тест Константина Полякова для подготовки к ЕГЭ:

B3 — Информационные модели

Задание № 3 (ДЕМО ЕГЭ 2020)

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о протяжённости каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите, какова *протяжённость* дороги из пункта Д в пункт Е. В ответе
запишите целое число – так, как оно указано в таблице.
Решение:

1. По схеме только
из п.Д выходит 5 дорог, в таблице это №4.

2. На схеме из п.А
только одна дорога – в п.Б. В таблице п.А соответствует №3, следовательно п.Б –
№6.

3. По схеме из п.Е
выходит 2 дороги. В таблице п.Д связан с двумя пунктами, имеющими два выхода –
это №1 и №2. но т.к. №2 связан с №6 (п.Б), то №1 – п.Е

4. №4 (п.Д) связан
с №1 (п.Е) дорогой, протяженностью 9 км. Ответ:
9

Задание № 3 (ДЕМО ЕГЭ 2019)

На рисунке слева изображена схема дорог Н-ского района, в таблице звёздочкой
обозначено наличие дороги из одного населённого пункта в другой. Отсутствие
звёздочки означает, что такой дороги нет.

Каждому населённому пункту на схеме соответствует его номер в таблице, но
неизвестно, какой именно номер. Определите, какие *номера* населённых пунктов в
таблице могут соответствовать населённым пунктам B и C на схеме. В ответе
запишите эти два номера в возрастающем порядке без пробелов и знаков препинания.
Решение:

1.
На схеме из пунктов B, C, G и F выходят три дороги. В таблице это
номера 2, 3, 5 и 6.

2.
на схеме пункты B и C связаны только через п.D:

a. №1
связывает №5 и №6, но эти номера связаны еще напрямую дорогой;

b. №7
связывает №2 и №3, но эти номера связаны еще напрямую дорогой;

c. №4
связывает №2 и №6, дороги напрямую между этими номерами не существует.

Следовательно пункты B и C могут иметь номера 2 и 6.

Ответ:
26

Задание № 3 (ДЕМО ЕГЭ 2018)

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о протяжённости каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите, какова *протяжённость* дороги из пункта А в пункт Г. В ответе
запишите целое число – так, как оно указано в таблице.
Решение:

1.
На схеме только из п.А выходят три дороги. В таблице п.А соответствует №3.

2. По схеме пункты
В и Г связаны с п.А и имеют 4 дороги. В таблице им соответствуют №2 и №5.

3. По схеме только
п.Г связан единственной дорогой с п.К, а п.В единственными дорогами с п.Б и с
п.Е:

a. в
таблице №1 и №6 связаны единственными дорогами с №2 ⇒ №2 – п.В;

b. в
таблице №7 связан единственной дорогой с №5 ⇒
№5 – п.Г.

4. В таблице
№3(п.А) и №5(п.Г) единственной дорогой протяжённостью 6 км. Ответ: 6

Разбор заданий № 3. СтатГрад. Подготовка к ЕГЭ 2019^{^[5]}

Вариант 1

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о
длине этих дорог в километрах.

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите *длину* дороги из пункта Б в пункт Г. В ответе запишите целое
число.
ВНИМАНИЕ. Длины отрезков на схеме не отражают длины дорог.
Решение:

п.Г – №7 –
только из п.Г выходят четыре дороги;

п.В – №1 (№4 и №8 – А или Е) –
только из п.В выходят две дороги;

п.К – №2 (№6 и №8
– Д или Е) – не связан с п.Г;

методом исключения имеем №5 – п.Б

БГ (5-7) – 28 км

Ответ:
28

Вариант 2

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о
длине этих дорог в километрах.

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите *длину* дороги из пункта Б в пункт Г. В ответе запишите целое
число.
ВНИМАНИЕ. Длины отрезков на схеме не отражают длины дорог.
Решение:

п.Г – №1 –
только из п.Г выходят четыре дороги;

п.В – №3 (№2 и №6 – А или Е) –
только из п.В выходят две дороги;

п.К – №4 (№2 и №8
– Д или Е) – не связан с п.Г;

методом исключения имеем №7 – п.Б

БГ (7-1) – 56 км

Ответ:
56

Вариант 3

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о
длине этих дорог в километрах.

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите *длину* *кратчайшего* пути из пункта А в пункт Д, если
передвигаться можно только по указанным дорогам. В ответе укажите целое число –
длину дороги в километрах.
Решение:

1.
На схеме из п.Д выходит 4 дороги. В таблице п.Д соответствует №5.

2.
По схеме из пунктов Б и В выходит по три дороги, в таблице им
соответствуют №1 и №4.

3.
По таблице №1 и №4 имеют еще один общий узел – №3,
а на схеме это п.А.

4.
Длина маршрута 3-1-5 = 3+7 = 10, длина маршрута 3-4-5 = 6+8 = 14.
Длина кратчайшего маршрута равна 10 км.

Ответ:
10

Вариант 4

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о
длине этих дорог в километрах.

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите *длину* *кратчайшего* пути из пункта Г в пункт Д, если
передвигаться можно только по указанным дорогам. В ответе укажите целое число –
длину дороги в километрах.
Решение:

1.
На схеме из п.Д выходит 4 дороги. В таблице п.Д соответствует №6.

2.
По схеме из пунктов Б и В выходит по три дороги, в таблице им
соответствуют №4 и №7.

3.
По таблице №1 и №4 имеют еще один общий узел – №2,
а на схеме это п.А.

4.
Не связаны прямыми дорогами с п.Д (№6) – №2 и №3 ⇒ №3 – п.Г

5.
Длина маршрута 3-1-6 = 4+5 = 9, длина маршрута 3-7-6 = 3+7 = 10.
Длина кратчайшего маршрута равна 9 км. Ответ:
9

Вариант 5

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о
длине этих дорог в километрах.

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Известно, что длина кратчайшего пути из пункта A в пункт К не превышает 30
километров. Определите длину кратчайшего пути из пункта Г в пункт Е. В ответе
укажите целое число – длину пути в километрах.
Решение:

п.Г и п.А – №3 или №5 ⇒
п.В и п.Б – №2 или №4 ⇒ №1 – Д ⇒ №7 и №6 – Е или К маршруты:

№3-№2-№7 = 29 ⇒
АВК

№3-№4-№6 = 32

№5-№2-№7 = 31

№5-№4-№6 = 31

№5 – Г №4 – Б №6 –Е

ГБЕ =
31

ГБДЕ =№5-№4-№1-№6 = 17+14+19 = 50 Ответ: 31

Вариант 6

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о
длине этих дорог в километрах.

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Известно, что длина кратчайшего пути из пункта A в пункт Е не превышает 30
километров. Определите длину кратчайшего пути из пункта Г в пункт К. В ответе
укажите целое число – длину пути в километрах.
Решение:

На схеме

1) п.А и п.Г
– №4 или №5 ⇒ п.Б и п.В – №1 или
№6

2) №4-№1-№3
= 32+17 = 49 -ГВК

№4-№6-№2 = 16+15 = 31

№5-№1-№3 = 22+17 = 39

№5-№6-№2 = 12+15 = 27

3) min{49,
31, 39, 27} = 27 ⇒ №5-№6-№2 – АБЕ;
4) п.Г – №4, п.В – №1, п.К – №3:

№4-№1-№3 = 32+17 = 49 → ГВК

Ответ:
49

Разбор заданий № 18. ЕГЭ 2020. Ушаков Д.М. 10 тренировочных
вариантов^{^[6]}

Вариант 1

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о длине этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите, какова длина дороги из пункта Д в пункт К. В ответе запишите
целое число – так, как оно указано в таблице.
Решение:

1.
На схеме только из п.Д выходят 3 дороги ⇒ п.Д – П2;

2.
На схеме только из п.К выходят 5 дорог ⇒ п.К – П4;

3.
ДК = 20 км Ответ:
20

Вариант 2

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о длине этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите, какова длина дороги из пункта Г в пункт Е. В ответе запишите
целое число – так, как оно указано в таблице.
Решение:

1.
На схеме из п.Е и п.Б выходят по 3 дороги, в таблице им
соответствуют П5 и П6.

2. На
схеме только п.Е связан с двумя вершинами из которых выходят по 2 дороги ⇒ п.Е – П5, а П2 и П7 могут быть п.Г и п.К; тогда
п.А – П3.

3. п.Г
и п.К связаны с п.Б и п.Д соответственно, из которых выходит по 4 дороги (в
таблице это П1 и П4).

4. Но
только п.Б связан с двумя пунктами, имеющими по 2 дороги – п.Г и п.А.

5. Из
таблицы видно, что П2 (п.А) связан с П4, имеющем 4 дороги ⇒ П4 – п.Б.

6. Из
таблицы видно, что П4 (п.Б) связан с П7, имеющими по 2 дороги ⇒ П7
– п.Г.

7. ГЕ
= 8 км. Ответ:
8

Вариант 3

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о дорогах между населёнными пунктами(* означает, что дорога
между соответствующими городами есть).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите, *номера* населенных пунктов Д и Е в таблице. В ответе напишите
числа в порядке возрастания без разделителей. Например, если бы ответом являлись
пункты П9 и П8, в ответе нужно было бы написать 89.
Решение:

1.
На схеме видно, что п.Д и п.Е и имеют по 2 дороги. Этим пунктам в
таблице не могут соответствовать П6 и П7, а также П1 и П3 имеющие по 3 дороги.

2.
Из оставшихся П2, П4, П5 и П8 связаны с П1и П3 – П2 и П1⇒ П5
и П8 – населенные пункты Д и Е. Ответ:
58

Вариант 4

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость
которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой
дороги между пунктами нет).
		A	B	C	D	E	F
A		3	8		4
B	3		5	9	2	13
C	8	5		4	3
D		9	4			3
E	4	2	3			11
F		13		3	11
Определите, *длину* кратчайшего пути между пунктами A и F (при условии, что
передвигаться можно только по построенным дорогам).
Решение:

Рассмотрим возможные маршруты из п.А в п.F:

1.
L_AEF = 4 + 11 = 15; L_ABF
= 3 + 13 = 16 ⇒ длина
кратчайшего пути может быть меньше или равна 15;

2.
LABC = L AC = 8;

3.
L_AEC
= 4 + 3 = 7 ⇒ начало маршрута;

4.
L_CDF = 4 + 3 = 7 – min
участок
оставшегося пути.

L_AECDF
= 4 + 3 + 4 + 3 = 14;

Самый кратчайший
путь – L_AECDF
= 14

Ответ:
14

Вариант 5

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость
которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой
дороги между пунктами нет).
		A	B	C	D	E	F
A		3	8			16
B	3		4	7
C	8	4		2	6
D		7	2		5	4
E			6	5		2
F	16			4	2
Определите, *длину* кратчайшего пути между пунктами A и F (при условии, что
передвигаться можно только по построенным дорогам).
Решение:

Рассмотрим возможные маршруты из п.А в п.F:

1.
L_AF = 16 ⇒ длина
кратчайшего пути может быть меньше или равна 16;

2.
L_ABC < L_AC
на 8 — (3 + 4) = 1 ⇒ ABC – первая часть пути;

3.
Из C в F можно попасть следующими способами:

a. L_CDF
= 2 + 4 = 6 – min участок
пути;

b. остальные
пути из C в F больше 6.

4.
L_ABCDF
=
3 + 4 + 2 + 4 = 13.

Самый кратчайший
путь – L_ABCDF
= 13.

Ответ:
13

Вариант 6

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о длине этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите, какова длина дороги из пункта Б в пункт Д. В ответе запишите
целое число – так, как оно указано в таблице.
Решение:

1. На
схеме видно, что п.Б и п.Д связаны
между собой, и, из них выходят по 3 дороги, в таблице им соответствуют П5 и
П7;

2. Из
п.К тоже выходит по 3 дороги, ему соответствует П6.

3. БД
= 35 км. Ответ:
35

Вариант 7

На рисунке справа схема дорог Н-ского района изображена в
виде графа, в таблице

содержатся сведения о
длине этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга,
то нумерация

населённых пунктов в таблице никак не
связана с буквенными обозначениями на

графе. Определите,
какова длина
дороги из пункта А в пункт Г.
В ответе запишите

целое число – так, как
оно указано в таблице.

Решение:

1.
На схеме видно, что п.А и п.Б связаны с двумя пунктами, имеющими
по 3 дороги; это могут быть П2 и П6.

2.
п. Е и п.Ж связаны с двумя пунктами, один из которых имеет по 3
дороги, а другой – по 2; это могут быть П4 и П5. Эти пункты связаны между собой
и с П3, П8 ⇒ П3, П8 – п.К и п.Д.

3.
П3 связан с П2 (2 дороги) и с П4, П8 ⇒ П3 – п.К и П2 – п.Б. ⇒
п.А – П6.

4.
П2 связан с П3 и с П7 (3 дороги) ⇒
П7 – п.Г.

5.
АГ = 19 Ответ:
19

Вариант 8

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о дорогах между населёнными пунктами(* означает, что дорога
между соответствующими городами есть).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными обозначениями на
графе. Определите, *номера* населенных пунктов D и G в таблице. В ответе напишите
два числа без разделителей. Сначала для пункта D, затем для пункта G.
Решение:

1.
По схеме:

	D(3)			G(4)
C(3)	E(3)	H (4)	B(4)	A(3)	F(4)

2.
Рассмотрим в таблице вершины, имеющие по 3 дороги

П2	П3	П4	П6
П4(3), П6(3), П7(4)	П1(4), П5(4), П8(4)	П1(4), П2(3), П7(4)	П1(4), П2(3), П8(4)

3.
Из п.1 и п.2 можно сделать вывод, что D – П2. И
общая вершина – H (П7)

4.
Рассмотрим в таблице вершины, имеющие по 4 дороги

П1	П5	П7 – H	П8
П3(3), П4(3), П5(4), П6(3)	П1(4), П3(3), П7(4), П8(4)	П2(3), П4(3), П5(4), П8(4)	П3(3), П5(4), П6(3), П7(4)

5.
Из п.1 и п.4 можно сделать вывод, что G – П5.

Ответ:
25

Вариант 9

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость
которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой
дороги между пунктами нет).
		A	B	C	D	E	F
A		9	6	3
B	9		3		2
C	6	3		2	7	8
D	3		2			10
E		2	7			2
F			8	10	2
Определите, *длину* кратчайшего пути между пунктами A и F (при условии, что
передвигаться можно только по построенным дорогам).
Решение:

Рассмотрим возможные маршруты из п.А в п.F:

1.
LACF = 6 + 8 = 14; L_ADF =
3 + 10 = 13 ⇒ длина
кратчайшего пути может быть меньше или равна 13;

2.
L_ADC
= 3 + 2 = 5 ⇒ min
участок
начала маршрута; 3. L_CBEF = 3 + 2 + 2 = 7 –
min участок
оставшегося пути.

4. L_ADCBEF
= (3 + 2) + (3 + 2 + 2) = 5 + 7 = 12; ADCBEF – самый кратчайший путь. Ответ: 12

Вариант 10

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость
которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой
дороги между пунктами нет).
		A	B	C	D	E	F
A		3	8
B	3		6		8
C	8	6		3		4
D			3		1	3
E		8		1		2
F			4	3	2
Определите, *длину* кратчайшего пути между пунктами A и F (при условии, что
передвигаться можно только по построенным дорогам).
Решение:

Рассмотрим возможные маршруты из п.А в п.F:

1.
L_ACF = 8 + 4 = 12 ⇒
длина
кратчайшего пути может быть меньше или равна 12;

2.
L_ABC > L_AC
на (3 + 6) — 8 = 1 ⇒ ABC – не
является кратчайшей частью
пути;

3.
LABEF > L_ACF
на (3 + 8 + 2) — 12 = 1 ⇒ ABEF – не
является кратчайшим
маршрутом. Ответ:
12

Источник

Анализ информационных моделей

Вокруг нас очень много информации, которую необходимо запомнить. Для того, чтобы с информацией было проще работать, её структурируют и представляют в виде понятных и простых образов. Вот эти образы и называются информационными моделями. Формулы в учебнике по физике, таблицы с расписанием рейсов в аэропорту, схема эвакуации в торговом центре — это все информационные модели. По способу передачи информации модели делят на образные (это рисунки, чертежи) и знаковые (формулы, программы на языке программирования). В целом в ЕГЭ информационным моделям посвящено аж пять заданий — №1, №3, №9, №13, №18.

В экзамене в первую очередь встречаются смешанные модели. В них входят таблицы, графики, диаграммы и схемы. Среди схем самыми важными для экзамена являются графы (ориентированные и не ориентированные), деревья и блок-схемы (умение работать с последними существенно для понимания конструкций языков программирования).

Граф — это упрощенная схема, которая состоит из вершин и ребер.

С помощью графа удобно описать, например, схему дорог с указанием расстояния между всеми пунктами. На примере ниже приведена карта (слева) и построенный по ней граф (справа):

Граф, нарисованный справа, называется неориентированным. В неориентированном графе ребра не имеют направления — они показывают только связь между двумя вершинами. В противопоставление неориентированному графу существует ориентированный — такой, по которому четко видно, откуда и куда мы можем двигаться. Ниже приведен ориентированный граф из задания №13 в ЕГЭ:

Дерево — это граф, между любыми двумя вершинами которого существует ровно один путь.

Данный вид графа имеет ветвистую структуру, поэтому и получил такое название:

Таблица — еще одна важная с точки зрения ЕГЭ информационная модель.

Например, задание №3 проверяет ваше умение находить соответствие между графами и таблицами, а также строить дерево по таблице. Последний случай особенно распространен в данном задании, поэтому его стоит разобрать отдельно. Кроме того, в экзамене особое внимание уделено электронным таблицам — важному инструменту анализа данных. Теме обработки электронных таблиц посвящено задание №9 и №18 в ЕГЭ (подробнее см. соответствующий раздел теории).

Построение дерева по таблице и алгоритм Дейкстры

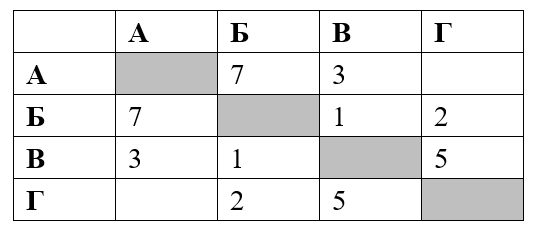
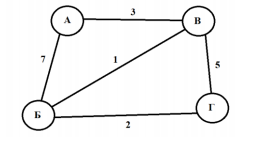
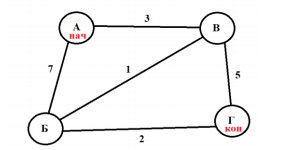
Классический прототип задания №1 выглядит следующим образом: дана таблица с населенными пунктами, в ячейках которой – расстояния между ними. Вам надо найти кратчайший путь между какими-то двумя пунктами (обычно между первым и последним) Пусть есть таблица, и необходимо найти кратчайший путь из пункта А в пункт Г:

Есть 2 способа решения данного задания:

1) Построить граф по заданной таблице.

2) Применить алгоритм Дейкстры, который назван в честь голландского ученого в области информатики и информационных технологий.

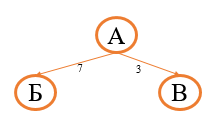
Начнем с первого способа. Нам необходимо построить граф, соответствующий заданной таблице. Из всех видов графов для этой задачи подойдет дерево, его мы и будем строить. Из вершины А можно проехать в вершину Б и В (длины путей соответственно 7 и 3):

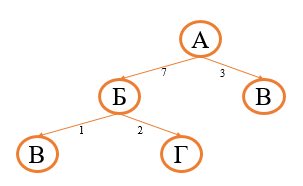
Из вершины Б можно проехать в вершины В и Г (длины путей соответственно 1 и 2):

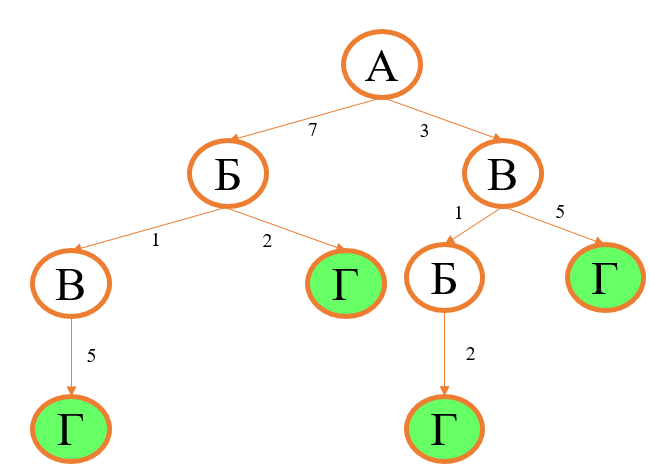
Новые маршруты из В – в Г (длина пути 5) и т.д.:

Получаем, что кратчайший путь – это путь А-В-Б-Г, длина которого равна 6.

Рассмотрим алгоритм Дейкстры для решения этой же задачи. Суть алгоритма заключается в том, что возле каждой вершины будут стоять временные метки, которые будут обновляться в соответствии с найденными минимальными путями. Метка возле финального пункта назначения будет ответом на задачу.

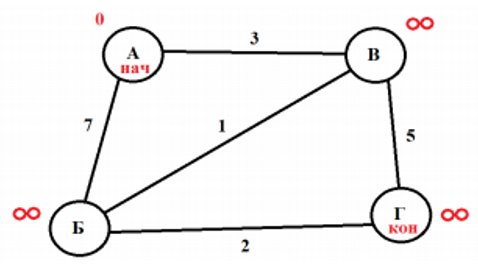
Первое, и самое важное, — правильно нарисовать граф.

Отметим начало и конец.

Около каждой из вершины, кроме начальной оставим временную метку – бесконечности, а около начальной вершины – метку 0, ведь нахождение кратчайшего пути начинаем с нее. Именно с временными метками мы будем сравнивать, является ли маршрут минимальным или нет.

Начинаем со стартовой вершины. Рассматриваем возможные передвижения из нее. То есть в

вершину В и вершину Б. Рассчитываем новую временную вершину следующим образом:

складываем временную метку у исходной вершины с весом ребра, проходящего к необходимой

вершине:

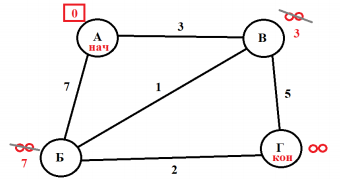
Для вершины В: 0 + 3 = 3

Для вершины Б: 0 + 7 = 7

Далее определяем, является ли новая метка, меньше чем предыдущая?

Для вершины В: 3 меньше чем бесконечность, поэтому бесконечность зачеркиваем и пишем

новую временную метку – 3.

Для вершины Б: аналогично. Зачеркиваем предыдущую временную метку, и ставим новую – 7.

Так как мы рассмотрели вершину А, ее временная метка становится постоянной и не может быть

изменена.

Таким образом, мы должны рассмотреть все вершины. Причем нельзя рассматривать уже

пройденные вершины. Только те, что имеют врЕменные метки.

Для того, чтобы определить, какую следующую вершину необходимо рассматривать, пользуемся

правилом: «У кого меньше значение временной метки, тот наш герой!».

В нашем случае этот герой вершина В!

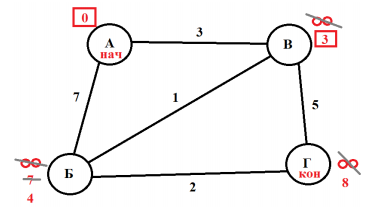
В–Б: 3 + 1 = 4. Четверка меньше семи, поэтому зачеркиваем 7, и ставим новую метку – 4.

В–Г: 3 + 5 = 8. Восемь меньше бесконечности, поэтому зачеркиваем бесконечность, и ставим

новую метку – 8.

Делаем временную метку 3 у вершины В постоянной, тем самым показывая, что эта вершина

рассмотрена.

Следующая вершина – Б.

Б–Г: 4 + 2 = 6. Шесть меньше чем 8, поэтому зачеркиваем 8, и ставим новую временную метку – 6.

Временная метка у Б теперь постоянная.

Остается последняя вершина Г, которая является конечной. И ее временная метка становится

постоянной и является ответом на нашу задачу. Кратчайший путь между вершинами А и Г – 6.

Ответ сошелся с предыдущим способом!

Теперь вы знаете два возможных способа найти кратчайший путь в графе!

Стоит отметить, что с помощью обоих алгоритмов можно находить как самый короткий, так и самый длинный путь. При построении дерева достаточно просто выбрать ветку с максимальным итоговым значением. При применении алгоритма Дейкстры, при перезаписи временной метки вершины, вместо выбора наименьшего значения, мы будем выбирать наибольшее.

Источник

Модель — представление реально существующего объекта, процесса или явления, содержащее свойства, действия или признаки, необходимые для изучения самого объекта или его взаимодействия с другими объектами.

Построение сложных моделей, о которых часто упоминают средства массовой информации, таких, например, как цифровые двойники в промышленности, градостроительстве и космосе, модели морских транспортных потоков, моделирование поведения вирусов и создание полимерных материалов неосуществимы без помощи компьютеров и даже современных суперкомпьютеров.

Компьютерное моделирование — реализация информационной модели средствами компьютерных приложений или специализированных пакетов программ.

Компьютерное моделирование даёт исследователям возможность уточнения модели в том случае, если в процессе исследования выясняется, что не все необходимые признаки объекта были собраны для построения адекватной модели.

Как это происходит
1. На первом этапе построения компьютерной модели формулируется основная задача исследования.
2. На втором этапе выстраивается информационная модель.
3. По созданной модели разрабатывается компьютерная модель исследования, алгоритм.
4. Далее проводится компьютерный эксперимент.
5. Анализируются результаты эксперимента, и в зависимости от них уточняется либо задача (возвращение к этапу (1)), либо информационная модель (возвращение к этапу (2)), либо алгоритм исследования (возвращение к этапу (3)) или же проводится заново компьютерный эксперимент (возвращение к этапу (4)).

6. В завершение компьютерного моделирования делаются выводы об объекте моделирования. Можно считать, что объект изучен всесторонне.

Информационная модель — совокупность информации об объекте, представленная одним из языков кодирования информации.

Наиболее известными формами представления информационных моделей являются сигналы, речь (устная и письменная), символы (числа, текст), таблицы, схемы, карты, графики, графы.

Граф — это конечное множество точек, некоторые из которых соединены линиями, т. е. рёбрами.

Количество рёбер, выходящих из вершины графа, называют степенью вершины.

Взвешенный граф — граф, в котором каждое ребро имеет вес.

Цепь — путь по вершинам и рёбрам, включающий любое ребро графа не более одного раза.

Таблица — это совокупность однотипных данных, хранящихся в виде структурированной базы данных.

Источник

Васильева Ю.С.¹, Гусева Е.Н.¹
¹ФГБОУ ВО «Магнитогорский государственный технический университет им. Г. И. Носова»

Аннотация
В данной статье рассматривается раздел из ЕГЭ по информатике «Моделирование и компьютерный эксперимент». Разбираются типовые задачи в области моделирования с использованием таблиц, графов, диаграмм.

Vasylieva Yu.S.¹, Guseva E.N.¹
¹Mаgnitogorsk Stаte Technicаl University named after G.I. Nosov

Abstract
In this article, a section from the Unified State Exam on Informatics «Modeling and Computer Experiment» is considered. Typical modeling problems are analyzed using tables, graphs, and diagrams.

Библиографическая ссылка на статью:
Васильева Ю.С., Гусева Е.Н. Анализ информационных моделей из материалов ЕГЭ по информатике // Современные научные исследования и инновации. 2017. № 4 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2017/04/80527 (дата обращения: 24.02.2023).

Одним из разделов в ЕГЭ по информатике является «Моделирование и компьютерный эксперимент». Основное понятие в данном разделе – это модель. Модель — это объект, который создается искусственно и дает упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования. Следовательно, моделирование — это создание моделей, которые предназначены для изучения и исследования объектов, процессов или явлений.[2]

Данный раздел в школьной программе по учебно-методическому комплексу автора Л.Л. Босовой начинают изучать с 6 класса. Учащихся знакомят с понятиями информационного моделирования, а так же с его разнообразием. В учебниках представлены знаковые (словесные, математические модели), табличные информационные модели, графики, диаграммы, схемы. С каждым классом объем знаний по разделу добавляется и усложняется, например, в 6 классе изучаются информационные модели в виде таблиц «объект – свойства», «объект – объект», то есть рассматриваются типы связи «один к одному» и «один ко многим». В 7 классе в раздел моделирование добавляются информационные модели, описывающие связи «многие ко многим», например «объекты – объекты», «объекты – свойства – объекты». Для подготовки учеников к ГИА и ЕГЭ, начиная с 8 класса, после каждой главы учебника расположены тестовые задания для самоконтроля.

При решении задач по информатике в области моделировании школьникам приходится сталкиваться с различными видами информационных моделей. В данной статье рассмотрим задачу по моделированию, которая связана с анализом графиков и диаграмм в электронных таблицах, а также разберем особенности решения задачи построения кратчайшего пути в таблице смежности для формирования навыков учащихся исследования графов.

Граф — совокупность непустого множества вершин и наборов пар вершин (связей между вершинами)[1]. Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра[3]. Графы применяются в разных областях, для каждой области применяется определенные, которые имеют свою направленность, ограничения, а так же дополнительные данные о вершинах и ребрах.

Графы можно представить различными способами:

1) графический способ – изображение графа;

2) список ребер – перечисление всех ребер графа как пар обозначений связываемых этими ребрами вершин;

3) матрица смежности – квадратная симметричная таблица, в которой столбцы и строки соответствуют вершинам графа, а на пересечении ячеек записываются числа, обозначающие наличие или отсутствие связей между соответствующими парами вершин;

4) матрица инцидентности – таблица, строки которой соответствуют ребрам, а столбцы – вершинам, на пересечении ячеек указывается связь между инцидентными элементами графа (ребро и вершина).

Таблица – это систематизированный перечень цифровых данных или каких-либо иных сведений, расположенных в определенном порядке по графам.

Диаграмма – это графическое представление данных. Они используются для анализа и сравнения данных, представления их в наглядном виде.

Существуют различные виды диаграмм:

1) гистограмма – графическое представление в виде прямоугольников одинаковой ширины, расположенных вертикально, одиночные прямоугольники либо сгруппированные по определенному признаку. применяются для распределения числовых значений какого-либо показателя во времени или по составным частям;

2) линейчатые диаграммы – графическое представление в виде прямоугольников, расположенных горизонтально. высота прямоугольников соответствует числовым значениям сравниваемых величин;

3) круговая диаграмма – графическое представление в виде окружности, круга. применяется для изображения удельного веса составных частей какого-либо целого (в долях или процентах).

Рассмотрим типовые задачи по моделированию.

Пример 1.

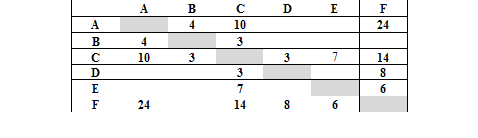
Между городами A, B, C, D, E, F проложены дороги, протяженность которых приведена в таблице (отсутствие числа в таблице означает, что дороги нет). Определите длину кратчайшего пути между городами А и F (при условии, что передвигаться можно только по построенным дорогам).

Решение:

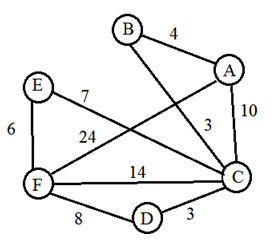
Нам дана таблица смежности, следовательно, эта задача на построение графа. Вершинами графа являются названия городов, от A до F, а ребра определяются наличием в таблице чисел, указывающих вес этих ребер. Расставляем вершины и соединяем линиями, только те на пересечении столбца и строки имеются непустые ячейки. Число, в соответствующих ячейках, записываем над ребрами.

В условии задачи не говорится, что движение в одном направлении, следовательно, граф не является ориентированным. Матрица смежности зеркально симметрична (т.е. ячейки над главной диагональю и под симметричны).

Граф для данной таблицы смежности:

Методом перебора, перечислим все возможные пути от A к F и определим самый короткий путь.

AF – длина пути: 24;

ABCDF – длина пути: 4+3+3+8=18;

ABCF – длина пути: 4+3+14=21;

ABCEF – длина пути: 4+3+7+6=20;

ACDF – длина пути: 10+3+8=21;

ACF –длина пути: 10+14=24;

ACEF –длина пути: 10+7+6+23.

Самый короткий путь – ABCDF длиной 18 единиц.

Пример 2.

Дан фрагмент электронной таблицы.

№	A	B	C	D
1		1	2
2	=C1/2	=(A2+B1)/2	=C1–B1	*=2B2**

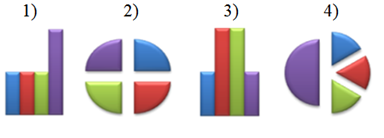
После выполнения вычислений была построена диаграмма по значениям диапазона ячеек A2:D2. Укажите получившуюся диаграмму.

Решение

Вычисляем значения формул и вписываем их в таблицу:

№	A	B	C	D
1		1	2
2	1	1	1	2

Анализируем ответ:

2-й вариант не подходит, т.к. все доли равны.
3-й не соответствует, т.к. A2 и D2 равны и меньше B2 и C2.
4-й является не верным, т.к. D2=A2+B2+C2, а согласно таблице: 2=1+1+1 – равенство не верное, значит ответ не правильный.

Ответ: диаграмма № 1 (поскольку A2,B2,C2 равны между собой и каждая из этих долей вдвое меньше D2).

Навыки анализа информационных моделей, умение конструировать оптимальные маршруты в графах способствуют развитию логического мышления детей. Задачи компьютерного моделирования учат школьников не только выполнять вычисления, использовать математические формулы и логику, но и дают возможность самостоятельно исследовать законы и явления из разных научных областей, сравнивать и давать анализ объектам.

Библиографический список

Karmanova E.V., EfimovaI.Yu., Guseva E.N., Kostina N.N., Saveleva L.A., Bobrova I.I.//Modeling of students’ competency development in the higher education distant learning system. –В сборнике: Proceedings of the 2016 Conference on Information Technologies in Science, Management, Social Sphere and Medicine (ITSMSSM 2016) 2016. С. 308-315.
Гусева Е. Н. Информатика: [электронный ресурс] учеб.пособие/ Е. Н. Гусева, И.Ю. Ефимова, Р.И. Коробков, К.В. Коробкова, И.Н. Мовчан, Л.А. Савельева. – 3-е изд., стереотип. – М.: Флинта, 2011.– 260 с.–Режим доступа: http://www.knigafund.ru/books/116085
Гусева Е.Н. Анализ результатов имитационного моделирования в среде Rockwell Software Arena /В сборнике: Теплотехника и информатика в образовании, науке и производстве сборник докладов V Всероссийской научно-практической конференции студентов, аспирантов и молодых учёных (TИМ’2016) с международным участием. Министерство образования и науки Российской Федерации, Уральский федеральный университет имени первого Президента России Б. Н. Ельцина, Институт материаловедения и металлургии, Кафедра «Теплофизика и информатика в металлургии». 2016. С. 194-198.
Гусева Е.Н. Дидактические условия использования педагогических программных средств в процессе профессиональной подготовки будущих учителей: дис. канд. пед. наук.– Магнитогорск, 1999, – 168 с.
Гусева Е.Н. Задачи на измерение количества информации с использованием понятия вероятности// Информатика и образование. – М.: № 2, 2008. –С. 61-64.
Гусева Е.Н. Имитационное моделирование как среда компьютерной визуализации знаний/ В книге: Новые информационные технологии в образовании/ Материалы VII международной научно-практической конференции. Российский государственный профессионально-педагогический университет. 2014. С. 395-399.
Гусева Е.Н. Математические основы информатики/ Е.Н. Гусева, И.И. Боброва, И.Ю. Ефимова, И.Н. Мовчан, С.А. Повитухин, Л.А. Савельева. – Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016.- 234 с.
Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2007. – 140с.
Ермакова Т.А., Гусева Е.Н. Использование компьютерного моделирования в преподавании геометрии // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/06/68886 (дата обращения: 24.06.2016).
Информатика и информационные технологии. Тема 9. Информационное моделирование. Электронный ресурс: http://www.ido.rudn.ru/nfpk/inf/inf9.html.
Казачков И.А., Гусева Е.Н. Компьютерная модель «Хищник-Жертва» // Современные научные исследования и инновации. 2017. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/01/77530
Никулина Н.М., Гусева Е.Н. Задачи компьютерного моделирования в школьном курсе информатики // Современные научные исследования и инновации. 2017. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/01/76147
Саралашвили А.А., Гусева Е.Н. Компьютерное моделирование демографических процессов // Современные научные исследования и инновации. 2017. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/01/77136
Татарникова В.В., Гусева Е.Н. Использование компьютерного моделирования в решении задач о системах массового обслуживания // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/06/69373 (дата обращения: 07.07.2016).

Количество просмотров публикации: Please wait

Все статьи автора «Васильева Ю.С.»

Источник

Структурирование информации и информационные модели

Поиск кратчайшего пути (перебор)

Решение заданий 1 ЕГЭ по информатике

Представление и считывание данных в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)

ЕГЭ-2015 задание 5.

Анализ информационных моделей

Теория

Задача

Решение

За​да​ние № 3 (​ДЕМО ЕГЭ 2020​)

За​да​ние № 3 (​ДЕМО ЕГЭ 2019​)

За​да​ние № 3 (​ДЕМО ЕГЭ 2018​)

Разбор заданий № 3. ​СтатГрад. Подготовка к ЕГЭ 2019[5]

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Разбор заданий № 18. ​ЕГЭ 2020. Ушаков Д.М. 10 тренировочных вариантов[6]

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9

Вариант 10

Анализ информационных моделей

Представление и считывание данных в разных типах информационных моделей
(схемы, карты, таблицы, графики и формулы)

Задание № 3 (ДЕМО ЕГЭ 2020)

Задание № 3 (ДЕМО ЕГЭ 2019)

Задание № 3 (ДЕМО ЕГЭ 2018)

Разбор заданий № 3. СтатГрад. Подготовка к ЕГЭ 2019^{^[5]}

Разбор заданий № 18. ЕГЭ 2020. Ушаков Д.М. 10 тренировочных
вариантов^{^[6]}