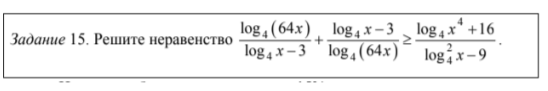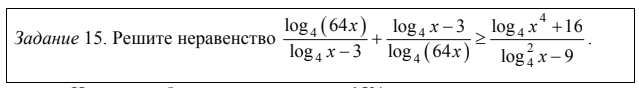Анализ ошибок по егэ по математике - Помощь в подготовке к экзаменам и поступлению

Чтобы успешно сдать экзамен, подготовку нужно начинать заранее. И если вы не можете самостоятельно определить свои слабые места и проблемы, рекомендуем начать с разбора типичных ошибок ЕГЭ и ОГЭ по математике.

Здесь мы приведем анализ типичных ошибок 2023 и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.

Базовый уровень математики

Ошибки в задачах на проценты

Чаще всего их допускают, так как не разбираются в сути процента.

Возьмем пример задачи, когда нужно сначала снизить цену на 25%, а потом повысить ее на 25%. Самая частая ошибка – полагать, что эти проценты будут равны одной и той же сумме. На самом же деле база их зачисления будет совершенно разной.

В этом примере 6% участников допустили вариант, что новую цену нужно понизить на 25%. На самом же деле новая цена – это 125% от старой. И вопрос в этой задаче – узнать, сколько будет 100% от старой цены.

Совет: повторить основы расчета процентов, повторить взаимосвязи величин, подумать над способом решения таких задач.

Невнимательное прочтение условия задания

Волнение и психологическое напряжение приводят к тому, что участники часто неправильно понимают условие задания. В итоге – снижение итогового балла по невнимательности, а не по незнанию.

Например:

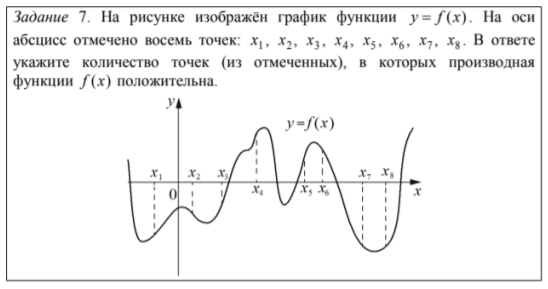
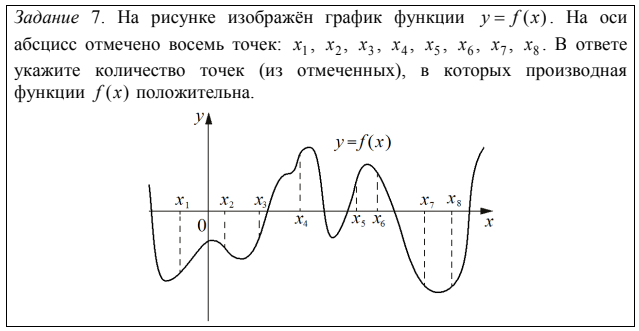
В 24% участников упомянули те точки, где значение функции (а не производной) положительное. Еще 2% указали номера точек, где производная принимает положительное значение.

Совет: вдумчиво, медленно и несколько раз читайте задание.

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Учащиеся могут не только неправильно понять, но и вовсе не понять условия. Иногда это происходит из-за незнания величин, единиц их измерения или плохой работы с формулами. Многие просто пропускают эту часть тестирования.

Вот пример задачи:

Её выполнило только 57% участников тестирования. 8% вообще не дали ответа, 6% дали ответ «чем ближе, тем лучше», 4% – «лампочку необходимо поместить в середину разрешенного интервала», еще 4,5% приняли фокус за основной параметр.

Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.

Ошибки в вычислениях

Школьная привычка использовать даже в самых легких примерах калькулятор приводит к плачевному результату на экзамене. Если учащийся не научиться быстро считать в уме или хотя бы на бумаге, во время тестирования он может ошибиться даже в самых простых заданиях.

Особенно сложно участникам тестирования даются дроби, отрицательные числа, элементарные преобразования выражений и другие проблемы, копившиеся еще с 5 класса.

Совет: если в чем-то не разбираетесь, обязательно отработайте эту тему до автоматизма перед экзаменом, потому что она обязательно попадется.

Ошибки теоретического характера

Это касается фактов по геометрии и алгебре, незнание которых приводит к снижению процента выполнения заданий и базового, и профильного уровней.

Например:

В этой задаче около 8% участников вообще не ответили на поставленное условие, 38% дали ответ с ошибками относительно боковой поверхности конуса, а 12% совершили ошибки в расчёте объёма.

Статистика показывает, что в таких заданиях ошибок гораздо больше, чем в гораздо более сложных профильных заданиях.

Совет: потренируйтесь перед тестированием. Если ответы не сходятся с ключами, обратитесь за помощью к стороннему специалисту (репетитору или сервису студенческой помощи), чтобы они указали, где вы ошибаетесь.

Ошибки в алгоритмах и методах решения

Этот тип ошибок встречается во всех заданиях.

Например:

Около 15% участников получили нулевые баллы из-за проблем с невнимательным чтением неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств.

Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.

Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.

Ошибки в чтении и построении чертежа

Такое случается, когда ученик не понимает взаимосвязь элементов геометрических конструкций, а также не обладает основными пространственными представлениями.

Например:

Около 10% участников экзамена сделали ошибки в вычислении углов по их записи, просто перепутав буквы или не понимая, где расположены вершины всех углов. Еще 5% решили, что угол ACD прямой. А 3% увидели в угле ABD равносторонний треугольник.

Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.

Неумение обосновывать и доказывать

14 и 16 задания по стереометрии и планиметрии отличаются повышенным уровнем сложности и требуют развернутого ответа. В каждом по 2 пункта: в первом нужно доказать, во втором – произвести вычисления.

Самые распространенные ошибки касаются первого пункта, так как у участников выявились проблемы с умением доказывать.

Есть проблемы и в оформлении доказательств. Например:

Основная трудность в отсутствии понимания логики построения доказательства.

Совет: тренируйтесь в доказательной базе, повышайте математическую культуру, учитесь обосновывать выбранные методы и способы их решения.

Ошибки в заданиях по тригонометрии

Из-за невнимательности и неаккуратности, а также отсутствия знаний по большому количеству теоретических фактов и способности их применять на практике, участники совершают частые ошибки в решении тригонометрических заданий.

Например:

Только 34% участников выполнили его. Самые частые ошибки (около 12%) связаны в первую очередь с нахождением тригонометрического знака – чаще всего потеря знака «минус». Еще 22% ждут «красивого» ответа, равного 1 или 2.

Ошибки математического моделирования

В 11 и 17 заданиях проверяют способность учащихся к построению и исследованию простейших математических моделей.

В текстовых задачах основную роль играет сюжетная часть – она имеет практическую ориентацию. И часто из-за непонимания взаимосвязи величин в этих заданиях допускают ошибки.

Например, в задачах на движение примерно 10% не понимают принципы движения по реке – они умножают собственную скорость на время движения.

Совет: тренируйте текстовые задачи, внимательно читайте условие задачи.

Профильный уровень

Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:

Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей.
Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры).
Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже.
Задание 8 – ошибаются в наглядном решении.
Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики.
Задание 12 – ошибаются в задачах с нулями производной.

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

Есть несколько рекомендаций, чтобы избежать ошибок из-за невнимательного прочтения задания. Это и будет алгоритмом решения задачи:

прочтите условие;
выпишите данные величины, сделайте рисунок в геометрическом задании;
установите и запишите отношения и взаимосвязи между известными данными;
выпишите что найти, ответ на какой вопрос нужно дать;
определите тип задания;
сформулируйте содержание и последовательность действий.

Это будет ваш своеобразный чек-лист, который обязательно нужно соблюдать при решении любой задачи, чтобы не допустить обидных ошибок.

Данные условия важно именно выписывать, а не иметь в виду. Фиксация их в уме чаще всего приводит к записи неправильного ответа.

И еще момент: не приступайте к решению задачи сразу же после ее прочтения. Психологи утверждают, что важно выдержать паузу между стимулом и реакцией – именно при этом условии удастся добиться оптимальных результатов:

сориентироваться в условии,
обдумать и спланировать ее решение,
понять уровень ее сложности и решить, откладывать ли ее решение напоследок.

Кроме сложности задачи оцените, сколько баллов она принесет и насколько она утомительна. Важно оставить энергию для решения других заданий при сдаче единого государственного экзамена.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Знание типичных ошибок ЕГЭ и ОГЭ по математике даст вам полную картину того, к каким заданиями нужно готовиться с большим усилием. А чтобы не отвлекаться на другие учебные дела, не забывайте: рядом есть сервис студенческой помощи, который подставит плечо в трудную минуту.

Источник

О.А. Горшков

АННОТАЦИЯ

В данной статье говориться об ошибках учащихся, которые наиболее часто допускаются на ЕГЭ по математике. Так же рассматриваются пути решения данной проблемы для успешной сдачи экзамена.

Ключевые слова: ЕГЭ, математика, ошибки.

АНАЛИЗ ОШИБОК ЕГЭ ПО МАТЕМАТИКЕ И ПУТИ РЕШЕНИЯ

ЕГЭ по математике – серьёзное испытание в жизни каждого выпускника школы. Каждый год в процедуру проведения экзамена вносятся изменения. В 2015 году новшеством является разделение экзамена по математике на два отдельных испытания: базовый и профильный уровень. Базовый уровень ЕГЭ — это совсем новый экзамен. Он предназначен для тех, кому математика не потребуется в дальнейшем обучении. Либо обучение не предполагается вообще, либо предполагается в вузах, где предмет «Математика» отсутствует в перечне вступительных испытаний. Профильный экзамен, по сути, не отличается от того ЕГЭ по математике, что сдаётся уже много лет. Новшества заключаются в незначительном изменении количества заданий. В любом случае в заданиях обоих экзаменов присутствует и геометрия, и тригонометрия, и логарифмы, и производные, и теория вероятностей, и прочие премудрости… В этом смысле, задания базового уровня не сильно отличаются от аналогичных заданий профильного ЕГЭ.

Единый государственный экзамен базового и профильного уровня составлен таким образом, что без специальной подготовки выполнить все задания, основываясь на базе знаний, полученных в ходе изучения школьной программы невозможно. Часто случаются примеры, когда даже отличные оценки в школе не являются гарантией успешного прохождения этого барьера. Необходима совместная серьезная, кропотливая работа учителя, ученика и родителей для успешной сдачи экзамена. В данной работе будут рассмотрены основные ошибки 2013-2015 года, которые встают на пути к успешной сдаче ЕГЭ.

Самые частые ошибки в ЕГЭ по математике связаны с дробями и отрицательными числами — такие результаты из года в год отмечают специалисты из федеральной группы разработчиков ЕГЭ по математике. То есть «слабым местом» оказались темы, которые ученики проходят в 5-7 классах. В «топ» также входит: невнимательная работа с вероятностью, неправильное чтение графиков, незнание основных планиметрических утверждений, неумение работать с формулами стереометрии.

Экзаменаторы отмечают, что ученики не понимают условие задания, допускают простейшие арифметические ошибки и не умеют себя проверить — все это, естественно, очень негативно влияет на результат. Выяснилось также, что геометрию школьники знают хуже алгебры. По наблюдениям экзаменаторов, больше половины учеников не умеют доказывать, — а ведь даже правильно решенный пример без доказательства не засчитывали.

Рассмотренные нами показатели ошибок учащихся 2013-2015 года, можно выделить следующие причины не успешности на ЕГЭ по математике:

наличие только отдельных фрагментарных знаний по предмету; отсутствие систематической базовой подготовки обучающимися, не освоено даже и половины планируемых результатов, которые осваивает большинство обучающихся, имеются значительные пробелы в знаниях;

обучающийся может выполнять отдельные задания базового уровня; слабая способность запоминать материал, полученную информацию, необходимую для сдачи экзамена;

непонимание логической связи в заданиях, отсутствие умения концентрироваться на задаче при работе с цифрами и текстами;

тревожность ребенка, не помогает уделять больше внимания решению задач и принятию решений; неумение концентрироваться на задаче при отсутствии умения четко планировать свое время, расставлять приоритеты, успешно распределять усилия, все делать вовремя.

Привычка считать все на калькуляторе, вплоть да таблицы умножения доставляет много проблем. Отсутствие навыков быстрого счета, непривычка считать самостоятельно — в уме или на бумаге, приводит к тому, что ученики подчас совершают грубые ошибки в элементарных примерах. Типичные ошибки повторяются из года в год, и выпускники допускают одни и те же ошибки.

Незнание многими выпускниками критериев оценивания решений в части С, где требуется полное обоснованное решение и ответ для каждой задачи. Главным критерием является математическая правильность решения.

Для того чтобы успешно сдать экзамен по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.

Таким образом, подготовка к успешному написанию ЕГЭ требует от учителя и учащихся особого подхода.

Учителям математики, начинающим работу в 10-м классе и готовящим выпускников к итоговой аттестации, необходимо в начале учебного года получить достоверную информацию об уровне подготовки десятиклассников по основным разделам курса алгебры основной школы и своевременно организовать работу по ликвидации пробелов в знаниях учащихся. Одной из особенностей организации проведения итогового повторения по математике является проведение мониторинга результатов обучения в классах независимо от профиля. Это эффективно реализуется в форме тестов учебных достижений, что позволяет провести диагностику проблемных зон в знаниях и умениях выпускников и провести последующую коррекцию, а также поощрять индивидуальные учебные достижения. Оперативная проверка может быть проведена при решении устных упражнений, математических диктантов и решении задач на готовых чертежах.

Решить проблему ликвидации пробелов в знаниях десятиклассников по курсу алгебры основной школы только с помощью организации вводного повторения не удастся. Поэтому целесообразно организовать еще и индивидуальное повторение, учитывающее пробелы в знаниях и умениях конкретного ученика, и с помощью диагностических работ систематически фиксировать продвижение старшеклассника по пути достижения уровня запланированных требований.

При подготовке к экзамену особое внимание должно уделяться «западающим» темам.

Необходимо проводить тренировочные тесты по каждой теме с жёстким ограничением времени, поэтому занятия нужно всегда проводить в форсированном режиме с подчёркнутым акцентированием контроля времени. Этот режим очень тяжёл школьникам на первых порах, но привыкнув к этому, они затем чувствуют себя намного спокойнее и собраннее. Одним из недостатков современной математической подготовки учащихся является отсутствие навыков работы с задачами минимальной практической направленности. Большая часть упражнений в учебниках направлены на проверку умений «вычислять, упрощать, решать». Но доля текстовых, практико-ориентированных задач на ЕГЭ возрастает.

В преддверии экзаменов практически все выпускники начинают ощущать психологическое напряжение. Оно и понятно – наступает ответственный момент в их жизни. Даже самые подготовленные ученики могут на экзамене переволноваться, растеряться и в самый ответственный момент появляются обидные и совершенно ненужные ошибки. Чтобы помочь старшеклассникам справится с психологическими проблемами, нужно знакомить их с процедурой и спецификой экзамена. Необходимо, чтобы старшеклассники привыкли к специфике экзамена, умели правильно распределить время на все задания, занимались систематически, чтобы появилась отработанная техника решений. Одним из существенных аспектов психолого-педагогического сопровождения выпускников является ознакомление родителей со способами правильного общения со своими детьми, оказания им психологической поддержки, создания в семье благоприятного психологического климата.

Чем ученики больше знают — тем меньше стресс и больше уверенность в себе и своих силах. Очень важна аксиома: Больше знаешь – меньше боишься, меньше боишься — больше веришь в победу, веришь в победу — значит победишь. Задача педагогов и родителей заставить поверить в это учеников.

В целом результативность сдачи ЕГЭ во многом определяется тем, насколько эффектно организован процесс подготовки на всех ступенях обучения, со всеми категориями обучающихся. Главное организовать правильный подход для подготовки учащихся к успешной сдаче экзамена.

Список литературы

1.http://www.fipi.ru/ web-сайт Федерального института педагогических измерений.

2. Ященко И. В., Шестаков С. А., Трепалин А.С. Подготовка к ЕГЭ по математике в 2015 году. Методические указания. – М.: МЦНМО, 2015.

3. Курганский С.М. Технология метода обучения в сотрудничестве. Завуч. 2006, №4.

4.edu.ru- Центральный образовательный портал.

5. ctege.info/- сайт информационной поддержки ЕГЭ.

6. http://ege-pro100.ru/wp-content/uploads/2016/02/Metodicheskie_rekomendatsii_na_osnove_oshibok_EGE2015_goda.pdf

Источник

10 основных ошибок, допускаемых в ЕГЭ по математике

Совет учиться на ошибках других бесполезен; научиться чему-либо можно только на собственных ошибках.

Б. Шоу

Обзор основных ошибок

Обзор составлен на основе материалов ФИПИ за 2016, 2017 гг.

https://drive.google.com/file/d/0B8MkXVdvfYcrZUdvcmk0TEpia1k/view

http://www.fipi.ru/sites/default/files/document/1476454097/matematika.pdf

Профильный уровень

Задание	Процент выполнения	Типичные ошибки
1	90%	Неумение читать условие и непонимание процентов
2	95%	Невнимательное чтение условия и непонимание единиц измерения
3	88%	Невнимательное чтение условия
4	89%	Невнимательное чтение условия
5	91%	Ошибки в свойствах степеней
6	65%	Непонимание математической записи угла и неверное чтение чертежа
7	54%	Невнимательное чтение условия
8	57%	Отсутствие базовых пространственных представлений и знаний соотношений
9	47%	Ошибки в определении знака тригонометрической функции
10	65%	Невнимательное чтение условия или непонимание текста
11	36%	Невнимательное чтение условия
12	38%	Непонимание алгоритма исследования функции с помощью производной
13	36%	Неумение и небрежность отбора корней тригонометрического уравнения с помощью единичной окружности
14	6%	Неумение доказывать, непонимание взаимосвязи элементов геометрической конструкции, ошибки в теоретических фактах
15	15%	Невнимательное чтение математической записи неравенства, непонимание алгоритма решения совокупностей и систем логарифмических неравенств, забыт знаменатель при решении дробно-рационального неравенства, небрежность при изображении множества решений на координатной прямой
16	3%	Неверное понимание логики построения доказательства, ошибки в построении чертежа
17	11%	Неверное составление модели задачи (непонимание взаимосвязи величин) и вычислительные ошибки
18	3,5%	Недостаточная сформированность графического метода решения – отсутствие объяснений и обоснований, отсутствие ответа на поставленный вопрос
19	3,5%	Непонимание того, что на вопрос «Может ли…?» нужно давать аргументированное решение, а не ответ «да» или «нет»

Базовый уровень

Основные факторы, вызывающие ошибки:

недостаточный уровень понимания условия при чтении задания,
вычислительные ошибки,
недостаточная развитость наглядных геометрических представлений.

Анализ 10 типичных ошибок на примерах заданий ЕГЭ

Задачи на проценты – непонимание механизма начисления процентов.

В большинстве случаев причина ошибок – непонимание сущности процента. Например, если в условии сказано, что цена товара сначала была повышена на 25%, а затем понижена на 25%, то эти проценты не будут одной и той же суммой денег, т.к. база начисления этих процентов разная.

Пример:

При решении этого задания 6% участников экзамена посчитали, что если цена была повышена на 25%, то для нахождения старой цены нужно новую цену понизить на 25%. В действительности же новая цена составляет 125% от старой цены, а узнать нужно, сколько рублей соответствуют 100%.

В более сложной экономической задаче требуется понимание механизма начисления простых и сложных процентов, обоснованное применение формул, выбор правильного способа решения. Типичные ошибки здесь связаны с неверным составлением модели задачи, непониманием взаимосвязи величин, непониманием того, что важен не только ответ, но и способ решения задачи.

Невнимательное чтение условия.

К сожалению, это самая распространенная ошибка согласно анализу типичных ошибок ЕГЭ, проведенному ФИПИ.

Конечно, многое здесь можно списать на волнение и психологическое напряжение. Даже самые подготовленные ученики на экзамене могут растеряться, переволноваться или поспешить в решении более простых заданий. Однако факт остается фактом, и при подготовке к экзаменам на него нужно обратить внимание.

Примеры:

Почти 24% участников экзамена указали количество точек, в которых значение функции (а не ее производной) положительно, а еще около 2% участников пытались перечислить номера точек, в которых производная принимает положительное значение.

Около 2,5% участников экзамена нашли вероятность выбора подтекающего насоса, не обратив внимания на частицу «не» в условии.

Практико-ориентированные задания базового и повышенного уровня – непонимание текста задачи.

Кроме ошибок, связанных с невнимательным чтением условия, на первое место здесь выходит непонимание текста задачи, незнание единиц измерения величин, неумение работать с формулами. Многие выпускники даже не приступают к технически не сложным практико-ориентированным задачам повышенного уровня.

Пример:

Выполнение задания – около 57%. Отмечается, что 8% участников не дали никакого ответа; 6% решили, что чем ближе, тем лучше; 4% решили, что лампочку нужно поместить в середину разрешенного интервала, а еще 4,5% решили, что самый главный параметр – это фокус.

Вычислительные ошибки.

Привычка вычислять все с помощью калькулятора, вплоть до таблицы умножения и действий с круглыми числами доставляет учащимся немало проблем на экзамене. Отсутствие навыков быстрого счета в уме или на бумаге часто приводит к тому, что участники экзамена допускают грубые ошибки в элементарных примерах. «Слабые» места многих старшеклассников – это дроби, отрицательные числа, элементарные преобразования выражений, т.е. проблемы, накопившиеся с 5 класса.

Ошибки в теоретических фактах.

Незнание необходимых для решения задач теоретических фактов, как по алгебре, так и по геометрии, существенно снижает процент выполнения большинства заданий как базового, так и повышенного уровня сложности.

Примеры:

Около 8% выпускников не дали никакого ответа; 38% ошиблись в формуле боковой поверхности конуса, а еще 12% в формуле его объема. Отмечается, что процент выполнения этого задания существенно ниже, чем, например, формально гораздо более сложного задания с полным решением на решение уравнения и осуществление отбора корней. Это означает, что низкий процент выполнения заданий по стереометрии вызван именно существенными проблемами в ее преподавании.

В задании 5 проверялось умение решать показательные и логарифмические уравнения. Из семи процентов выпускников, не справившихся с заданием, 2% ошиблись в свойствах степеней.

Незнание алгоритмов и методов решения.

Знание алгоритмов и методов решения проверялось во многих заданиях экзаменационной работы. Например, в задании 12 требовалось продемонстрировать понимание алгоритма исследования функции с помощью производной, а в заданиях 5,13,15 знание общих и частных методов решения уравнений и неравенств.

Пример:

Ненулевые баллы получило около 15% участников экзамена. Типичные ошибки связаны с невнимательным чтением математической записи неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств. Очень много ошибок при решении дробно-рационального неравенства (забыт знаменатель).

Неверное чтение чертежей, непонимание взаимосвязи элементов геометрической конструкции, отсутствие базовых пространственных представлений, ошибки в построении чертежа.

В преподавании геометрии очень важным является не только умение решать вычислительные задачи с геометрическим содержанием (по формулам), но и формировать геометрические представления о фигурах (телах). При отсутствии базовых пространственных представлений сложно ожидать высокого процента выполнения стереометрического задания с полным решением.

Пример:

Отмечается, что около 10% участников экзамена при решении этой задачи неверно определили углы по их записи (перепутали буквы или не понимают, какая из букв в записи угла соответствует его вершине). Около 5% участников «увидели» прямоугольный треугольник ACD, а еще 3% — равносторонний треугольник ABD.

Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. В целом при решении геометрических задач более половины выпускников продемонстрировали отсутствие знания взаимосвязей элементов геометрической конструкции и соотношений между величинами пространственных фигур.

Неумение доказывать, обосновывать.

К заданиям повышенного уровня относились задания второй части 14 (стереометрия) и 16 (планиметрия) с развернутым ответом. Оба задания содержали два пункта. В первом пункте задание доказать, а во втором пункте вычислить. Основной проблемой оказалось выполнение первого пункта. Участники экзамена продемонстрировали неумение доказывать. При этом много встречается различного рода логических ошибок. Наибольшие затруднения участники испытывали при оформлении доказательства.

Пример:

Типичные ошибки связаны с непониманием логики построения доказательства. Например, доказательство начинается так: «Пусть точка О является серединой отрезка СК…». Т.е. в начале доказательства уже допускается факт, который и требуется доказать.

Задания 18 и 19 высокого уровня сложности предназначены для конкурсного отбора в ВУЗы с повышенными требованиями к математической подготовке абитуриентов. Это задания на комбинацию различных методов. Для успешного их выполнения, кроме прочих математических знаний, необходим высокий уровень математической культуры, который предполагает, в частности, умение обосновывать выбранные методы и способы решения.

Примеры:

Ненулевые баллы при решении этого задания получило около 17% участников экзамена. Многие выпускники попробовали исследовать несколько примеров, а потом обобщить полученный результат. Типичным заблуждением для многих оказалось, что на вопрос «Может ли?» нужно давать аргументированное решение, а не качественный ответ «да» или «нет».

Ненулевые баллы при решении этого задания получило около 3% участников экзамена. Основной проблемой оказалось применение графического метода, который, как показали работы участников экзамена, не достаточно сформирован. Без объяснений и обоснований на координатной плоскости отмечаются графики, и считывается множество значений параметра. Во многих случаях на координатной плоскости обозначено много верных объектов, а ответа на поставленный вопрос так и не последовало.

Задания по тригонометрии требуют тщательности решения.

Представленные в экзаменационной работе задания по тригонометрии не относятся к числу самых сложных, однако их выполнение требует тщательности решения, аккуратности, внимания, знания большого количества теоретических фактов и умения их применять на практике.

Примеры:

Выполнение задания – около 34%. Типичные ошибки связаны в первую очередь с определением знака тригонометрической функции – почти 12% участников экзамена потеряли знак «минус». Еще 22% решили, что ответ ожидается «хорошим» — 1 или 2.

Задание 13 проверяло умение решать тригонометрические уравнения и производить отбор корней. Основной проблемой первого пункта оказалось неумение вводить новую переменную (ошибки в свойствах степеней), незнание формул решения простейшего тригонометрического уравнения. При выполнении второго пункта участники продемонстрировали неумение или небрежность отбора корней.

Отсутствие навыков математического моделирования.

Способность к построению и исследованию простейших математических моделей проверяется в заданиях 11 (текстовая задача) и 17 (текстовая задача с экономическим содержанием). Текстовые задачи, как правило, являются стандартными задачами на составление уравнений курса алгебры 8 класса. В экономической задаче требуется верно построить математическую модель и исследовать ее. Важную роль при этом играет сюжетная, практико-ориентированная часть условия. При составлении математических моделей основные ошибки являются следствием непонимания взаимосвязи величин. Так, например, в задачах на движение около 10% участников экзамена продемонстрировали непонимание движения по реке – собственную скорость умножили на время движения.

Задачи с ошибками как форма работы на уроке.

Одной из форм работы на уроках является поиск и исправление ошибок. «Задачи с ошибками» являются заданиями творческого типа, они приучают обращать внимание на особо тонкие места в логических рассуждениях, помогают различать во многом сходные понятия, приучают к точности суждений и математической строгости и т. д.

Мой опыт преподавания показывает, что такие задания нравятся учащимся и являются достаточно эффективным способом совершенствования навыков решения задач.

Методика работы с задачами с ошибками может быть следующей:

1 этап: Индивидуальная, парная или групповая работа, в зависимости от уровня подготовленности учащихся, по поиску и исправлению ошибок. Задачи с ошибками могут быть представлены в раздаточном материале (карточки) или на слайдах презентации.

2 этап: Совместное обсуждение ошибок.

3 этап: Снова индивидуальная или парная работа – составление памятки «Советы ученику, решающему задачу».

4 этап: Проверка результатов и подведение итогов учителем.

Примеры заданий с ошибками по многим темам можно составить самим или найти в литературных и интернет-источниках.

Мои рекомендации:

Черкасов О.Ю., Якушев А.Г. Математика для поступающих в ВУЗы.

У меня старое издание 1996 года, но есть и более поздние издания этой книги.

Раздел 7 этого пособия так и называется: «Учимся на чужих ошибках».

http://math4school.ru/rabota_nad_oshibkami.html

Раздел сайта «Мath4school» называется «Работа над ошибками», содержит большое количество примеров с решениями и подробным анализом ошибок.

Источник

Егэ математика частые ошибки

Типичные ошибки ЕГЭ по базовой математике

Математику базового уровня часто недооценивают, пренебрегая подготовкой к ней. Однако от нее зависит судьба аттестата: без «отлично» за математику отличник не получит красный аттестат, а без порогового балла выпускники в принципе рискуют уйти из школы со справкой! Типичные ошибки на ЕГЭ по математике помогут избежать этой участи.

Типичные ошибки ЕГЭ по математике в задачах на проценты

Проблемы возникают из-за неумения рассчитывать процент от суммы. Так, стоит обратить внимание, что процент повышения или понижения стоимости вычисляется от старой, а не новой цены, поэтому принимать новую цену за 100% и исходить из нее станет причиной ошибки на ЕГЭ по математике. Новая цена — это 100% ± процент повышения (+) или понижения (-).

Частые ошибки в вычислениях

Вычислительные ошибки на ЕГЭ по математике не редкость, но от этого они не перестают быть опасными и обидными. Стоит следить за наличием минуса (и его сокращением), а также помнить правила преобразования выражений, действий с дробями. Не стоит полагаться исключительно на умение считать в уме: лучше выполнять свои вычисления на бумаге и обязательно производить проверку (подставляя значение на место неизвестной в уравнениях и производя смежные действия (сложение-вычитание, деление-умножение) в простых примерах).

Основные ошибки теоретического характера

Ошибки на ЕГЭ по математике часто возникают из-за неумение работать с чертежами и терминологией. Большинство выпускников пытается найти заданную в номере величину с помощью инструментов или на глаз, часть из них не знает терминологии и находит не ту величину. Чтобы не допустить этого, стоит научиться работать с объемными фигурами: находить площадь их поверхности (всей или боковой), объемы и их части.

Также стоит обратить внимание на важные аспекты теории: основные теоремы, аксиомы, свойства.

Распространенные ошибки в алгоритмах и методах решения

Последовательность выполнения действий проходится еще во втором классе, однако даже такие ошибки на ЕГЭ по математике встречаются. Стоит помнить как простейшие алгоритмы решения примеров: сначала действия в скобках, а потом остальные; первыми идут умножение и деление, потом сложение и вычитание, — так и более сложные. Так, в дробях ни в коем случае нельзя забывать про знаменатель, а сокращаться из числителя и знаменателя могут только множители (простые числа и выражения в скобках).

Ошибки при чтении и построении чертежа

Ошибки на ЕГЭ по математике, касающиеся чертежа, возникают при работе как с объемными фигурами, так и с расположенными в одной плоскости. Они связаны с отсутствием пространственного представления и невнимательностью, вызванной неправильным прочтением буквенной записи (угол АВС — это не то же самое, что углы АСВ и САВ). Также сложности могут возникнуть при неумении ориентироваться в основных обозначениях на чертеже (равные стороны, равные углы, прямые углы).

Типовые ошибки в заданиях по тригонометрии

Раздел тригонометрии построен на знании тригонометрических тождеств и свойств тригонометрических функций, поэтому ошибки на ЕГЭ по математике могут быть допущены из-за недостаточного владения теорией. В КИМ-е базовой математике даны основные формулы, которые могут быть полезны выпускникам, однако стоит также научиться выводить из них остальные.

Ошибки математического моделирования

Трудности, связанные с математическими моделями, вызваны неумением решать практические текстовые задачи. Для их решения необходимо понимать принцип работы действия (чаще всего, один из видов движения). Сложности возникают с подстановкой в формулу неверных данных, из-за чего искажается ответ.

Таким образом, базовая математика не так проста, как может показаться на первый взгляд. Она не займет так много времени, как профильная, но все равно требует подготовки.

Типичные ошибки ЕГЭ по математике в задачах на проценты

Сложности возникают с подстановкой в формулу неверных данных, из-за чего искажается ответ.

Umschool. net

08.11.2020 16:01:26

2020-11-08 16:01:26

Источники:

Https://umschool. net/journal/ege/tipichnye-oshibki-ege-po-bazovoj-matematike/

Типичные ошибки ЕГЭ по математике, анализ ошибок 2022 » /> » /> .keyword { color: red; } Егэ математика частые ошибки

Топ-10 ошибок в ЕГЭ по математике

Здесь мы приведем анализ типичных ошибок 2022 и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.

Базовый уровень математики

Ошибки в задачах на проценты

Чаще всего их допускают, так как не разбираются в сути процента.

Невнимательное прочтение условия задания

Совет: вдумчиво, медленно и несколько раз читайте задание.

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Вот пример задачи:

Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.

Ошибки в вычислениях

Ошибки теоретического характера

Ошибки в алгоритмах и методах решения

Этот тип ошибок встречается во всех заданиях.

Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.

Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.

Ошибки в чтении и построении чертежа

Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.

Неумение обосновывать и доказывать

Есть проблемы и в оформлении доказательств. Например:

Основная трудность в отсутствии понимания логики построения доказательства.

Ошибки в заданиях по тригонометрии

Ошибки математического моделирования

Совет: тренируйте текстовые задачи, внимательно читайте условие задачи.

Профильный уровень

Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:

Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей. Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры). Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже. Задание 8 – ошибаются в наглядном решении. Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики. Задание 12 – ошибаются в задачах с нулями производной.

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

прочтите условие; выпишите данные величины, сделайте рисунок в геометрическом задании; установите и запишите отношения и взаимосвязи между известными данными; выпишите что найти, ответ на какой вопрос нужно дать; определите тип задания; сформулируйте содержание и последовательность действий.

сориентироваться в условии, обдумать и спланировать ее решение, понять уровень ее сложности и решить, откладывать ли ее решение напоследок.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Контрольная работа от 1 дня / от 120 р. Узнать стоимость Дипломная работа от 7 дней / от 9540 р. Узнать стоимость Курсовая работа 5 дней / от 2160 р. Узнать стоимость Реферат от 1 дня / от 840 р. Узнать стоимость

Наталья – контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нейрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Узнать стоимость.

Zaochnik. ru

12.11.2019 23:27:19

2019-11-12 23:27:19

Источники:

Https://zaochnik. ru/blog/top-10-oshibok-v-ege-po-matematike/

Десять типичных ошибок в ЕГЭ по профильной математике — Без Сменки » /> » /> .keyword { color: red; } Егэ математика частые ошибки

Десять типичных ошибок в ЕГЭ по профильной математике

Мы попросили наставников онлайн-школы Вебиума проанализировать работы школьников по профильной математике, чтобы выделить самые частые причины, из-за которых теряются баллы на ЕГЭ.

Среди таких ошибок:

отсутствие ограничений; неправильное составление формул приведения; непонимание тригонометрии; оформление; невнимательность.

Отсутствие ограничений

Эту ошибку ребята допускают как и в первой, так и во второй части. Ограничения необходимо прописывать в ходе решения задачи, иначе большая вероятность, что вы забудете это сделать.

Как избежать ошибку: выучить, что корни, логарифмы, тангенсы, котангенсы вызывают ОДЗ (область допустимых значений).

Неправильное составление формул приведения

Самая распространённая ошибки в формуле — sin(3pi/2 + A) = — cosA. Знак у косинуса смотрится по синусу, а не наоборот.

Как избежать ошибку: выучить формулы приведения. Как их запомнить, рассказываем в видео.

Непонимание тригонометрии

В школах курсу тригонометрии уделяют мало времени, поэтому ребята не умеют работать с окружностью и не понимают её в целом. Все знаки преобразования обычно выбирают на окружности без определения четвертей и чётности — а это неправильно.

Как избежать ошибку: научиться самостоятельно чертить тригонометрическую окружность, запомни все оси (тангенс, котангенс) и углы, чтобы не путаться со знаками и аргументами.

Оформление

Чаще всего на ЕГЭ по профильной математике снижают баллы за оформление задания.

Роман Махмутов, наставник по профильной математике в команде Вебиума, рассказал, как избежать эту ошибку: «Если говорить про недочёты в оформлении, то для большинства важно дойти до правильного ответа, поэтому не все реагируют на мои комментарии по этому поводу. Чтобы это исправить, могу дать несколько советов:

Чаще обсуждайте решения заданий с наставником;

Не только смотреть на правильность/неправильность ответа, но и на советы по оформлению, так как это тоже играет очень важную роль.

Я часто сталкивался со студентами, у которых такая логика мышления: «Самое главное — получить правильный ответ, а красиво оформлять на экзамене буду». Если вы не хотите потерять баллы на экзамене, научитесь учитывать все критерии оценивания работы как можно раньше».

Невнимательность

Наставники команды Вебиума отмечают, что школьники часто невнимательно читают условие задачи. Из-за этого ход решения сразу становится неверным: приходится переделывать задание полностью.

Чтобы сдать ЕГЭ по профильной математике на высокий балл, нужно ознакомиться с Темами, которые попадутся на экзамене. А также познакомиться со всеми изменениями в Демоверсии — демонстрационном варианте ЕГЭ, по которому составляются реальные варианты экзамена.

Частые ошибки в ЕГЭ по профильной математике

Научиться решать все виды уравнений — Рациональные, показательные, логарифмические, тригонометрические, смешанные — Можно на курсе «Задание 12 — уравнения». Также курс можно взять с Проверкой Задач от наставника.

Чтобы разобрать метод интервалов и рационализации, можно записаться на курс «Задание 14 — решение неравенств». Также есть возможность взять Проверку Наставника.

А если вы допускаете ошибки в других заданиях, например, в Теории вероятности, Текстовых задачах Или Параметрах, то наши спецкурсы помогут это исправить.

Не ошибаться — это навык, который можно проработать путём многочисленной практики. Рассмотренные нами ошибки в большей степени зависят от внимательности и ответственного подхода к заданию. Рекомендуем несколько раз проверять домашнюю работу перед сдачей и выписывать, в каких заданиях были допущены ошибки, чтобы их проанализировать.

Теорию, которая нужна для ЕГЭ по профильной математике, объясняем на Наших курсах. А практику можно отработать на Бесплатных пробниках.

А если вы готовитесь к ЕГЭ по базовой математике, то Набрать нужные баллы и сэкономить время для подготовки к другим предметам Наш спецкурс.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Как избежать ошибку выучить, что корни, логарифмы, тангенсы, котангенсы вызывают ОДЗ область допустимых значений.

Bez-smenki. ru

16.04.2020 16:24:39

2020-04-16 16:24:39

Источники:

Https://bez-smenki. ru/desyat-tipichnyh-oshibok-v-ege-po-profilnoj-matematike/

Источник