Анализ репетиционного экзамена по математике 11 класс - Помощь в подготовке к экзаменам и поступлению

                                                             Анализ пробного
экзамена по математике

(базовый уровень)

11 класс

Всего
в классе:
8 уч-ся

Выполняли
работу: 8
учащихся

Успеваемость: 100%

Качество
знаний:
62,5%

Средний
балл:3,63

Максимальный балл—
«16» -1 чел. (Симонян Н.)

Минимальный балл
– «8»- 1 чел. (Сафронова Д.)

Результаты выполнения заданий

№

задания

справились

100%

62,5%

87,5%

62,5%

75%

87,5%

75%

100%

50%

25%

50%

37,5%

50%

25%

87,5%

12,5%

не справились

37,5%

12,5%

37,5%

25%

12,5%

25%

50%

75%

50%

62,5%

50%

75%

12,5%

87,5%

Анализ результатов показывает, что
успешнее всего учащиеся 11 класса справились с заданиями:

№1(100%
справились) – найти значение выражения

№3(87,5%
справились) — решение задач на проценты

№8
(87,5% справились) – решение геометрической задачи на соотношения между
величинами в треугольнике

№11(100%
справились) – решение задач с помощью графика

№19
(71% справились) – решение логической задачи

Трудности при выполнении работы вызвали
задания:

№13(25%
справились) – решение задачи на свойства многогранника

№14(25%
справились) – установление соответствия между графиками функций и формулами

№16(37,5%
справились) – решение геометрической задачи

№18(25%
справились) – решение логической задачи

№20(12,5%
справились) – решение логической задачи

Учащиеся Симонян Н., Кукош А.
Джанунц Ю. , Марянян Н.допустили вычислительные ошибки из-за
невнимательности, а у учащихся Канифольской К., Сафроновой Д., Шляхова Д. трудности
при выполнении работы связаны с недостаточными знаниями за курс основной
школы.

Все задания из пробных КИМов и
допущенные ошибки проанализированы с каждым учащимся. Подобные задания
включаются в ежедневную работу на уроке, разбираются на дополнительных
индивидуальных консультациях во внеурочное время.

15.12.2018г.

Учитель математики:
Г.Н.Шигаева

Источник

Анализ пробного экзамена по математике в 11 классе в форме ЕГЭ

Дата проведения:

Всего в классе –чел.

Присутствовало –чел.

Работа состоит из 20 заданий базового уровня сложности с кратким ответом. Ответы к данным заданиям вносятся в бланки № 1.

«5»
«4»
«3»
«2»

Написали на оценку

Таблица распределения баллов в классе

Большинство учащихся справились с работой.

Справились по зданиям:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	итого
	1	1	1	1	1	1	1	1	1	1	1	0	1	1	1	1	1	1	1	0	Баллов – 18 Оценка — 5
	1	1	1	1	1	1	1	1	0	1	1	1	0	1	1	0	1	1	0	1	Баллов – 16 Оценка — 4
	0	х	х	х	х	0	х	х	1	0	1	х	0	0	0	х	х	х	х	0	Баллов – 2 Оценка — 2
	х	х	0	х	х	х	х	х	0	0	1	х	х	0	х	0	0	0	х	х	Баллов – 1 Оценка — 2
	1	1	1	1	х	1	0	0	1	х	1	0	х	0	х	0	х	1	0	1	Баллов – 7 Оценка — 3
	х	1	0	1	х	1	0	1	0	1	1	1	0	1	х	х	1	1	х	0	Баллов – 10 Оценка — 3
	0	0	0	0	х	1	0	1	1	0	1	1	1	0	х	х	0	0	1	х	Баллов – 7 Оценка — 3
Не выполнили задания (не приступали)	4	3	4	3	5	2	5	3	3	4	0	4	5	4	5	6	5	3	5	5

Самыми сложными заданиями оказались:

Задание 16 – геометрическая задача (на поверхности тел)

Задание 5 – нахождение значения выражения

Задание 7 – решение уравнения

Задание 13 – геометрическая задача (на поверхности тел)

Задание 15 – геометрическая задача (на плоские фигуры)

Задание 17 – соотнесение неравенств и их решений

Задание 19 – задача на теорию вероятности и статистику

Задание 20 – задача на логику

Вывод: уделить особое внимание на уроках, на неаудиторной занятости данным задания

Источник

Анализ ТТ по математике (профильный уровень) МБОУ «СОШ № 2 с.Чермен» в 2021-2022 учебном году

В МБОУ «СОШ № 2 с.Чермен» в 2021-2022 учебном году в 11 классе обучается 10 учащихся, из них ЕГЭ по математике (профильный уровень) выбрали 3 ученика. В тренировочном тестировании (далее – ТТ), проведенном 21.01.2022 года приняло участие 2 обучающихся 11 класса, 1 ученик по состоянию здоровья не смог принять участие.

Все учащиеся преодолели минимальный порог для получения аттестата, так же ими преодолен порог для поступления в ВУЗы и подведомственные ОУ Минобрнауки. Для оценки результатов ТТ использовался показатель «первичный балл», а не «тестовый балл» (по 100 балльной шкале) поскольку, в связи с изменениями в содержании КИМ 2022 г. по сравнению с экзаменационными материалами предыдущих лет, во всех учебных предметах планируется изменение шкалы перевода первичных баллов ЕГЭ в тестовые баллы на основе реальных результатов экзамена 2022 года для обеспечения сопоставимости ЕГЭ 2022 года с экзаменами прошлых лет (Объявление ФИПИ).

Средний балл по школе составил 9,5.

ТТ по математике профильной проведено с использованием материалов тестирования аналогичным по структуре КИМ ЕГЭ 2022 г.

КИМ ЕГЭ 2022 г. по данному предмету имеет ряд отличий от КИМ 2021 г., в частности уменьшено количество заданий (с 19 до 18). Изменился, но незначительно, максимальный первичный балл с 32 до 31 балла, удалены некоторые задания и добавлены другие (№ 9 и 10).

В таблицах представлены результаты ТТ по математике профильного уровня.

Всего уч-ся	Сдавали ТТ	Преодолели мин.порог	Не преодолели мин.порог
Кол-во	%	Кол-во	%
3	2	2	100	0	0

№	Ф.И.О	Задания с кратким ответом	Задания с развернутым ответом	Перв.б.	% выполн.
1	2	3	4	5	6	7	8	9	10	11	12 (2)	13 (3)	14 (2)	15 (2)	16 (3)	17 (4)	18 (4)
1	Ученик 1	+	+	–	+	+	+	+	+	+	+	–	0	0	0	0	0	0	0	9	29
2	Ученик 2	+	+	+	+	+	+	+	+	–	–	–	0	0	2	0	0	0	0	10	32
	средний балл	9,5

№ задания	Задания с кратким ответом	Задания с развернутым ответом
1	2	3	4	5	6	7	8	9	10	11	12 (2)	13 (3)	14 (2)	15 (2)	16 (3)	17 (4)	18 (4)
справились	2	2	1	2	2	2	2	2	1	1	0	0	0	1	0	0	0	0
% выполнения	100	100	50	100	100	100	100	100	50	50	0	0	0	50	0	0	0	0

О тличный уровень знаний учащиеся показали при решении уравнений и неравенств, умении строить и исследовать простейшие математические модели, при выполнении вычислений и преобразований, действий с функциями, геометрическими фигурами, координатами и векторами, а так же умение использовать приобретенные знания и умения в практической деятельности и повседневной жизни (задания 1,2,4,5,6,7,8). Процент выполнения этих заданий составил 100 %.

Средний уровень знаний выпускники показали при решении задач на измерение геометрических величин, действий с функциями повышенного уровня сложности, решение задач с использованием элементов теории вероятности, а так же решение неравенства из второй части повышенного уровня сложности (задания 3,9,10,14). Процент выполнения составил 50 %.

Наибольшую сложность для экзаменуемых составило задание 11 из 1 части на знание производной и исследование функций, а так же задания второй части (№ 12,13,15-18). С этими заданиями никто не справился. Задания из 2 части 12-16 повышенного уровня сложности, 17-18 высокого уровня сложности выполняют те учащиеся, которые имеют более высокие математические способности. К решению заданий второй части приступили оба выпускника, но справился только 1 ученик и только с одним 14 заданием.

№ зада-ния КИМ	Проверяемые требования (умения)	Элементы содержания, проверяемые заданиями	Уровень сложности задания/ макс. балл	Кол-во сдававших	Кол-во справившихся	% выполнения заданий
Часть 1. Задания с кратким ответом
1	Уметь решать уравнения и неравенства	Уравнения	Б 1	2	2	100
2	Уметь строить и исследовать простейшие математические модели	Элементы теории вероятности	Б 1	2	2	100
3	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Планиметрия Измерение геометрических величин	Б 1	2	1	50
4	Уметь выполнять вычисления и преобразования	Числа, корни, степени Основы тригонометрии Логарифмы Преобразование выражений	Б 1	2	2	100
5	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Прямые и плоскости в пространстве Многогранники Тела и поверхности вращения Измерение геометрических величин	Б 1	2	2	100
6	Уметь выполнять действия с функциями	Производная Исследование функций Первообразная и интеграл	Б 1	2	2	100
7	Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни	Уравнения Неравенства	П 1	2	2	100
8	Уметь строить и исследовать простейшие математические модели	Уравнения Неравенства	П 1	2	2	100
9	Уметь выполнять действия с функциями	Уравнения Неравенства Определение и график функции Элементарное исследование функции Основные элементарные функции	П 1	2	1	50
10	Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни	Элементы теории вероятности	П 1	2	1	50
11	Уметь выполнять действия с функциями	Производная Исследование функций	П 1	2	0	0
Часть 2 Задания с развернутым ответом
12	Уметь решать уравнения и неравенства	Уравнения Неравенства	П 2	2	0	0
13	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Прямые и плоскости в пространстве Многогранники Тела и поверхности вращения Измерение геометрических величин Координаты и векторы	П 3	2	0	0
14	Уметь решать уравнения и неравенства	Уравнения Неравенства	П 2	2	1	50
15	Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни	Числа, корни, степени Уравнения Применение мат.методов для решения задач из различных областей науки и практики. Интерпретация результата, учёт реальных ограничений	П 2	2	0	0
16	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Планиметрия Измерение геометрических величин	П 3	2	0	0
17	Уметь решать уравнения и неравенства	Уравнения Неравенства	В 4	2	0	0
18	Уметь строить и исследовать простейшие математические модели	Числа, корни, степени Основы тригонометрии Логарифмы Преобразование выражений Уравнения Неравенства Определение и график функции Элементарное исследование функции Основные элементарные функции	В 4	2	0	0

По результатам тренировочного тестирования подведен итог по каждому заданию, и отмечены те задания, которые вызвали наибольшие затруднения.

Как следует из таблицы и диаграммы наиболее сложными для выполнения оказались задание № 11 повышенного уровня сложности, проверяющее умение выполнять действие с функциями, задания № 12-13, 15-16 повышенного уровня сложности, 17-18 высокого уровня сложности. В этих заданиях поверяется умение решать уравнения и неравенства, выполнять действия с геометрическими фигурами, координатами и векторами, использование приобретенных знаний и умений в практической деятельности и повседневной жизни, так же умение строить и исследовать математические модели.

Результаты ТТ по математике профильного уровня были обсуждены на МО учителей математики и было вынесено решение:

1. Всем учителям уделять внимание отработкам соответствующих навыков не только при подготовке к экзаменам, но и во время их изучения.

2. Келехсаевой А.С. составить план работы по отработке западающих тем каждого учащегося, проанализировав полученные результаты. Так же необходимо обращать внимание на сам подход к выполнению некоторых из них, чтобы не возникало психологического барьера, как, к примеру, дети избегают задач с большим текстом.

3. На дополнительных занятиях особое внимание уделять учащимся с высокими математическими способностями с целью повышения решаемости заданий повышенного и высокого уровней сложности.

Планируемые меры по корректировке знаний

1. Данное представление результатов позволяет выявить наиболее критичные разделы дисциплины, по которым наблюдается пониженный уровень освоения материала и, следовательно, составить дорожную карту на каждого учащегося по западающим темам.

2. По итогам индивидуальной работы с учащимися провести внутришкольный срез знаний по математике профильного уровня с целью выявления результата индивидуальной работы с выпускниками.

Заместитель директора по УВР, учитель математики /Келехсаева А.С./

Источник

Тарасова Галина Алексеевна

МКОУ №Журавлевская средняя общеобразовательная школа»

Учитель математики

Анализ пробного ЕГЭ по математике (профильный уровень)

(14.03.2018 года)

Класс: 11

Количество учащихся: 4

ЕГЭ по математике профильного уровня состоит из двух частей, включающих 19 заданий. Минимальный порог – 27 баллов.

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.

Определяющим признаком каждой части работы является форма заданий:

часть 1 содержит 8 заданий (задания 1–8) с кратким ответом в виде целого числа или конечной десятичной дроби;

часть 2 содержит 4 задания (задания 9–12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).

Цель: анализ и оценка результативности обучения, оценка эффективности учебного процесса с точки зрения образовательных стандартов.

Проверяемые требования:

Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни (Простейшие текстовые задачи (округление с избытком и недостатком, проценты).

Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни (Чтение графиков и диаграмм).

Уметь выполнять действия с геометрическими фигурами, координатами и векторами (Планиметрия: вычисление длин и площадей. Вектора, координатная плоскость).

Уметь строить и исследовать простейшие математические модели (Начала теории вероятностей).

Уметь решать уравнения и неравенства (Простейшие уравнения (линейные, квадратные, кубические, рациональные, иррациональные, показательные, логарифмические, тригонометрические).

Уметь выполнять действия с геометрическими фигурами, координатами и векторами (Планиметрия: задачи, связанные с углами в различных фигурах планиметрии).

Уметь выполнять действия с функциями (Производная: физический, геометрический смысл производной, касательная, применение производной к исследованию функций, первообразная).

Уметь выполнять действия с геометрическими фигурами, координатами и векторами (Стереометрия: задачи на вычисление основных элементов геометрических тел).

Уметь выполнять вычисления и преобразования (Вычисление значений и преобразования выражений, дробей различного вида: алгебраических, тригонометрических, показательных, логарифмических).

Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни (Задачи с прикладным содержанием).

Уметь строить и исследовать простейшие математические модели (Текстовые задачи: на движение по прямой и окружности, по воде, на совместную работу, проценты, сплавы, смеси, прогрессии).

Уметь выполнять действия с функциями (Наибольшее и наименьшее значение основных функций: с помощью производной и на основе свойств функции).

Уметь решать уравнения и неравенства (Уравнения, системы уравнений: тригонометрические, показательные, логарифмические, смешанные).

Уметь выполнять действия с геометрическими фигурами, координатами и векторами (Стереометрия: углы и расстояния в пространстве).

Уметь решать уравнения и неравенства (Неравенства и системы неравенств).

Уметь выполнять действия с геометрическими фигурами, координатами и векторами (Планиметрическая задача).

Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни (Задачи на проценты).

Уметь решать уравнения и неравенства (Уравнения, неравенства, системы с параметром).

Уметь строить и исследовать простейшие математические модели.

Оценка выполнения заданий с кратким ответом.

№ п/п	Фамилия, имя	1	2	3	4	5	6	7	8	9 (1б)	10 (1б)	11 (1б)	12 (1б)	Кол-во выполненных заданий
1.	Лутков Н.С.	+	+	—	+	+	—	+	—	—	—	—	—	5
2.	Мезенцев Р.С.	+	+	+	+	+	+	—	+	+	+	+	+	11
3.	Нурписова Г.К.	+	+	+	+	+	—	+	+	—	+	—	—	8
4.	Самокрутов А.Н.	+	+	+	+	+	—	—	—	—	+	—	—	6
Количество верно выполненных заданий	4	4	3	4	4	1	2	2	1	3	1	1
% верно выполненных заданий	100%	100%	75%	100%	100%	25%	50%	50%	25%	75%	25%	25%

Из приведенной выше таблицы видно, что учащиеся испытывают трудности при выполнении задания № 12 на нахождение наибольшего (наименьшего) значений функции, заданий № 7 и 8 (геометрический смысл производной и стереометрическая задача), при решении текстовых задач (№ 11). 25% решили текстовую и 50% задачу на геометрический смысл производной. 50% учащихся выполнили стереометрическую задачу. 25% учащихся не испытывают трудностей при выполнении планиметрической задачи, 100% безошибочно выполнили простейшую текстовую задачу, простейшее уравнение.

Оценка выполнения заданий с развернутым ответом.

№ п/п	Фамилия, имя	13 (2б)	14 (2б)	15 (2б)	16 (3б)	17 (3б)	18 (4б)	19 (4б)	Всего баллов за 2 часть
1.	Лутков Н.С.	0	0	0	0	0	0	0	0
2.	Мезенцев Р.С.	0	0	0	0	0	0	0	0
3.	Нурписова Г.К.	0	0	0	0	0	0	0	0
4.	Самокрутов А.Н.	0	0	0	0	0	0	0	0

Анализируя результаты пробного репетиционного экзамена по математике в форме ЕГЭ можно сделать вывод, что 9 выпускников из 15, набравшие 50 баллов и выше, имеют не только базовый уровень подготовки по математике средней школы, но и профильный. Лутков Николай — ученик 11 класса не преодолел минимальный порог в 27 баллов установленный Рособрнадзором на 2018 год.

На основании вышеизложенного, учителю математики рекомендуется:

1.Проанализировать результаты выполнения заданий КИМ, обратив внимание на выявленные типичные ошибки и пути их устранения.

2.Организовать систему повторения с поурочным контролем и проверкой.

3.Использовать на уроках задания, включенные в КИМ.

4.Обратить внимание на формирование у учащихся общеучебных и простейших математических навыков, находящих непосредственное применение на практике.

5.При организации повторения уделить необходимое внимание вопросам, вызвавшим наибольшие затруднения у школьников на пробном экзамене.

6.Систематически проводить работу с учащимися, отрабатывая с ними задания базового уровня сложности.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/306368-analiz-probnogo-egje-po-matematike-profilnyj-

Источник

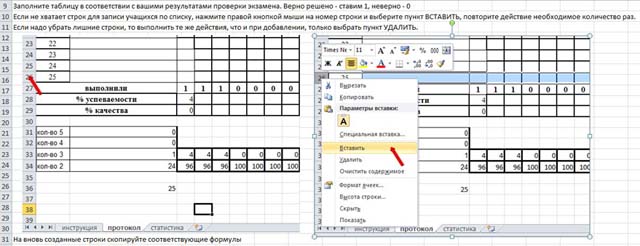
Анализ диагностической работы (пробного экзамена) по математике в 10-11 классе в формате ЕГЭ составлен в Excel и предназначен для облегчения подготовки и сдачи отчетности по проведенной(ым) работе(ам) в формате ЕГЭ.

В таблицу протокола вписываются фамилия, имя учащегося и его результаты (если задание решено верно ставим 1, если неверно, то ставим 0). После того как данные занесены в таблицу мы автоматически получаем подсчет баллов, % выполнения заданий, итоговый результат по каждому учащемуся, результаты по классу (успеваемость, качество), а также диаграммы наглядно показывающие результаты выполнения заданий.

Файл содержит инструкцию, протокол и диаграммы. Все просто и удобно.

Источник