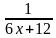Самоанализ урока математики по теме:
«ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ ПРИ РЕШЕНИИ ЗАДАЧ ЕГЭ»
Учитель математики МБОУ «Бухоловская СОШ» Севостьянова Н.Р.
Урок проводился в 11 классе. С этими детьми работаю с 8 класса. В классе обучаются всего 4 ученика. Хорошими математическими способностями обладает одна ученица. Еще одна девочка пришла в нашу школу в 9 класс и испытывает большие трудности в изучении математики. Одним словом класс «слабый». Но тем не менее в результате анкетирования выяснилось, что всем учащимся класса при поступлении в ВУЗ нужна математика. Поэтому подготовку к ЕГЭ веду по двум направлениям: базовому и профильному. Тематику базового уровня мы уже отработали и ребята уже самостоятельно решают задания базового уровня на сайте «ФИПИ», а на элективных занятиях мы разбираем возникающие при решении вопросы. С февраля мы начали подготовку к ЕГЭ профильного уровня.
Как показывает анализ результатов ЕГЭ, задания по теме «Производная» вызывают наибольшее затруднение у учеников. Поэтому этой теме уделяю большое внимание.
Мы изучили «Кодификатор элементов содержания по МАТЕМАТИКЕ для составления контрольных измерительных материалов для проведения ЕГЭ», «Кодификатор требований к уровню подготовки выпускников», «Спецификацию контрольных измерительных материалов», «Демонстрационный вариант контрольных измерительных материалов ЕГЭ 2015» и выяснили, что знания и умения о функции и её производной нужны для успешного решения задач В8 и В14. Поэтому сегодня на уроке мы отрабатывали навыки решения задач этого типа.
Урок по теме «Применение производной при решении задач ЕГЭ» очень хорошо вписывается в раздел «Производная показательной, логарифмической и степенной функций», изучение которого приходится как раз на февраль, в соответствии с календарно-тематическим планированием. Урок является предпоследним по данной теме, это урок обобщения и систематизации знаний. В рамках изучаемого раздела мы уже повторили все теоретические и практические знания и умения по теме «Производная»:
- правила дифференцирования;
- производные основных элементарных функций;
- геометрический и физический смысл производной;
- необходимый признак возрастания и убывания функции;
- понятия экстремумов;
- алгоритм отыскания наибольшего и наименьшего значения функции на отрезке;
- алгоритм исследования функции на экстремумы.
На примере февральских вариантов сайта «Решу ЕГЭ» мы отработали навыки применения физического смысла производной и начали работу с геометрическим смыслом производной. Сегодня на уроке мы продолжили работу над этой темой тестированием, результаты которого подведем на следующем уроке и будем работать над ошибками. На уроке мы приступили к решению задач типа В14, в которых необходимо с помощью производной исследовать функции на экстремумы и уметь находить наибольшее и наименьшее значения функции.
Цель урока состояла в том, чтобы подвести учащихся к понимаю важности производной в курсе математики.
Для достижения цели были определены задачи:
образовательные:
обобщить и систематизировать теоретические знания по теме; отработать умения и навыки при решении упражнений, предлагаемых на ЕГЭ; раскрыть прикладное значение производной;
развивающие:
развивать самостоятельность, потребность к самообразованию, к активной творческой деятельности; уметь применять знания, умения и навыки в нестандартной ситуации; формировать навыки самоконтроля;
воспитательные:
воспитывать чувство ответственности, культуры общения, уважения друг к другу, уверенности в себе.
На сегодняшний день современный урок немыслим без «тактики сотрудничества»: ученик-учитель-ученик. Чтобы вовлечь ребят в учебу, необходимы все новые и новые формы урока. Считаю, что предложенная вашему вниманию форма проведения урока существенно повысила мотивацию, эффективность и продуктивность учебной деятельности; обеспечила работу всего класса, позволила учащимся раскрыть свои способности.
Были определены следующие этапы урока:
- Организационный момент, который был нацелен на снятие эмоционального напряжения и мотивацию на успех.
- В ходе проверки домашнего задания были решены образовательные задачи: раскрыто прикладное значение производной и систематизированы знания по теме.
- Фронтальная устная работа с тренажером по решению задач типа В8 ЕГЭ, которая была нацелена на подготовку к последующему контрольному тестированию по теме «Геометрический смысл производной».
- Тестирование в режиме оn-line с подведением итогов.
- Отработка алгоритмов исследования функции на экстремум и нахождение наибольшего и наименьшего значений функции на примере решения задач типа В14 ЕГЭ.
- При подведении итогов ученики обозначили, что нужно знать и уметь для успешного решения задач типа В8 и В14 на ЕГЭ.
- Домашнее задание состоит из двух частей:
1 часть нацелена на обобщение и систематизацию знаний по теме и в то же время является творческим, т.к. предложено оформить обозначенные знания и умения по теме в виде справочного пособия для подготовки к ЕГЭ;
2 часть нацелена на отработку практических навыков по теме при решении заданий типа В14 из вариантов открытого банка заданий ЕГЭ.
- На заключительном этапе внимание учащихся опять было направлено на понимание того, что знания и умения по теме «Производная» нужны не только для успешной сдачи ЕГЭ, но также и для дальнейшей учебы, а кому-то возможно пригодятся и в профессиональной деятельности.
Все этапы урока выполнены. На каждом этапе стремилась построить работу таким образом, чтобы каждый ученик чувствовал себя полноценным участником образовательного процесса. Деятельность учащихся была направлена на решение поставленных задач и развитие самого себя. Свою задачу видела в том, чтобы вовлечь каждого в работу, создать условия для самореализации и уверенности в себе.
Отзыв на урок алгебры в 11 классе
по теме: «Исследование функций с помощью производных»
Дата проведения: 17 февраля 2018 г. Класс: 11
Цель урока: Образовательная – провести повторение тем алгебры с целью подготовки учащихся к ГИА, ЕГЭ; отработать умения систематизировать, обобщать при исследовании функции ее свойства, применять знания производной при построении графиков функции.
Развивающая – развитие мыслительных операций посредством наблюдений, сравнений, сопоставлений, обобщений, развитие зрительной памяти, математической речи учащихся. Воспитательные – воспитание познавательной активности, чувства ответственности, уважения друг другу, взаимопонимания, воспитание культуры общения
Предмет: алгебра.
Тип урока: урок закрепления полученных знаний.
Вид: комбинированный.
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Муниципальное общеобразовательное учреждение лицей №5
им. Ю.А.Гагарина Центрального района Волгограда
Урок подготовки к ЕГЭ по математике в 11 классе
« Решение задач по теории вероятностей »
Подготовила
Таболаева Марина Васильевна-
учитель математики
2016г
Урок подготовки к ЕГЭ по математике в 11 классе
« Решение задач по теории вероятностей »
Тема: «Решение задач по теории вероятностей »
Цели урока:
-
обобщить материал по теме «Элементы комбинаторики, статистики и теории вероятностей в ЕГЭ по математике»;
-
развивать вероятностное мышление учащихся;
-
повысить положительную мотивацию к учению.
Задачи урока:
-
образовательные:
-
обобщить и систематизировать основные понятия изучаемой темы;
-
отработать и закрепить практические навыки решения ключевых задач;
-
продолжить подготовку учащихся к ЕГЭ по математике;
-
-
развивающие:
-
продолжить формирование аналитического и логического мышления учащихся;
-
продолжить формирование у учащихся навыков самостоятельной деятельности при подготовке к ЕГЭ;
-
воспитательные:
-
воспитывать коммуникативные компетенции;
-
продолжить формирование общей и математической культуры учащихся;
-
воспитывать понимание значимости ведущей роли математики в развитии современного научно-технического общества.
Тип урока: комбинированный.
Форма работы учащихся: индивидуальная и групповая.
Оборудование:
-
компьютер;
-
проектор;
-
экран.
Дидактический материал: компьютерная презентация «Решение задач по теории вероятностей » (, Microsoft Office Power Point 2003).
Литература, использованная при подготовке к уроку:
-
Мордкович А.Г. Семенов П.В. События. Вероятности, Статистическая обработка данных: Доп. параграфы к курсы алгебры 7-9 кл. общеобразоват. учреждений. – 3-е изд. – М.: Мнемозина, 2005. – 112 с.
-
Математика. 10-11 классы: элективный курс «В мире случайных закономерностей» / ав.-сост. В.Н. Студенецкая и др. – Волгоград: Учитель, 2007. – 126 с.
-
Задачник-практикум по теории вероятностей с элементами комбинаторики и математической статистики: Учебное пособие для студентов-заочников IV курса физико-математических факультетов педагогических институтов / Н.Я. Виленкин, В.Г. Потапов. – Москва: Просвещение, 1979. – 112 с.
-
Демоверсии ЕГЭ по математике – 2015, 2016.
-
http://mathege.ru/ — открытый банк заданий по математике.
План урока:
-
Вводное слово учителя. Постановка цели урока – 1 мин.
-
Теоретический материал – повторение основных понятий, формул и правил по теме «Элементы комбинаторики, статистики и теории вероятностей» — 10 мин.
-
Практикум: решение ключевых типов задач В-4 ЕГЭ по математике – 15 мин.
-
Самостоятельная работа учащихся — решение задач по теме «Элементы комбинаторики, статистики и теории вероятностей в ЕГЭ» – 15 мин. (см. ПРИЛОЖЕНИЕ 1)
-
Проверка результатов самостоятельной работы – 2 мин.
-
Домашнее задание – 1 мин.
-
Подведение итогов урока. – 1 мин.
Ход урока:
-
Вводное слово учителя. Постановка цели урока.
Учитель: Великий французский ученый Блез Паскаль писал об этой чудесной науке так: «Сочетая строгость научных доказательств с неопределенностью случая и примиряя казалось бы противоположные вещи, и, извлекая ее [новой науки имя] из того и другого, можно по праву присвоить ей ошеломляющее название геометрия случая».
С 2012 года в контрольно-измерительные материалы ЕГЭ по математике включена задача с прошлого года это В4 по теме «Элементы комбинаторики, статистики и теории вероятностей». Практика показала, что ряд учащихся испытывает затруднения при решении задач данной тематики, поэтому для успешного решения таких задач на экзамене нам предстоит серьезная работа. Сегодня на уроке мы вспомним и повторим материал по этой теме, решим ключевые типы задач В4, входящие в ЕГЭ.
2) Теоретический материал – повторение основных понятий, формул и правил по теме «Элементы комбинаторики, статистики и теории вероятностей».
Учитель: Первым делом нам необходимо заложить теоретические основы, без которых невозможно успешное решение задач на «Элементы комбинаторики, статистики и теории вероятностей». Для этого давайте все вместе вспомним и повторим основные понятия, формулы и правила. (Демонстрация слайдов презентации. Учитель акцентирует внимание учащихся на теоретических аспектах темы).
Слайд 1.
Определение: Событие, которое может произойти, а может и не произойти, называют случайным событием.
Пример: Попадание или промах при стрельбе по мишени.
Определение: Элементарные события – простейшие события (исходы), которыми может окончиться случайный опыт.
Слайд 2.
Определение: Событие Ā называется противоположным событию А,
если состоит из тех и только тех элементарных исходов, которые не входят в А.
Слайд 3.
Определение: Два случайных события называются несовместными,
если они не могут произойти одновременно при одном и том же исходе испытания.
Учитель: Иными словами: несовместные события не могут наступить в одном опыте.
Слайд 4.
Определение (классическое определение вероятности):
Вероятностью события называется отношение числа
благоприятных для него исходов к числу всех равновозможных исходов.
Обозначение: P(A) – вероятность события А
Формула Лапласа (классическое определение вероятности):
P(A) = , где
ma — число благоприятных исходов события А,
n – число всех равновозможных исходов.
Замечание: Часто в специальной литературе формула классической вероятности
записывается в таком виде: P = , где P — вероятность,
k — число благоприятных исходов,
n — общее число возможных исходов.
Слайд 5
Пример.
Андрей, Роман, Максим и Сергей бросили жребий, кому быть вратарем.
Найти вероятность того, что вратарем стал Роман.
Решение:
Пусть событие А = {вратарем стал Роман}.
Число благоприятных исходов k = 1.
Общее число возможных исходов n = 4.
По формуле классической вероятности получаем:
P(A) = = 0, 25.
Ответ: 0,25
Слайд 6
Определение: Вероятность события А равна сумме вероятностей элементарных событий, благоприятствующих этому событию.
Сумма вероятностей всех элементарных событий равна 1.
Учитель: Ребята, обратите особое внимание: в задании В4 ЕГЭ по математике ответ всегда записывается в виде положительной десятичной дроби, значение которой всегда меньше 1.
Слайд 7
Определение: Вероятность противоположных событий:
Р(А) + Р(Ā) = 1
Р(А) = 1 — Р(Ā)
Слайд 8
Определение:AU B (объединение) – событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий А, В.
Определение:А ∩ В (пересечение) – событие, состоящее из элементарных исходов, благоприятствующих обоим событиям А и В.
Формула сложения вероятностей для совместных событий:
Р(A U B) = Р(А) + Р(В) – Р(А ∩ В)
Формула сложения для несовместных событий:
Р(A U B) = Р(А) + Р(В)
Слайд 9
Формула умножения вероятностей для независимых событий:
Р( A ∩ B) = Р(А)*Р(В)
Формула умножения вероятностей для зависимых событий:
Р( A ∩ B) = Р(А)*Р(ВА) = Р(В)*Р(АВ)
Учитель: Обратите внимание: Р(ВА) – это вероятность события B при условии, что произошло событие A (аналогично для Р(АВ).
Слайд 10
Определение: Факториалом числа n называется произведение первых натуральных n чисел от 1 до n.
Обозначение: n!
Формула: n! = 1*2*3*….*n
Пример: 4! = 1*2*3*4 = 24
Запомните: 0! = 1 (по определению)
Слайд 11
Определение: Сочетанием из n элементов по k называется любое множество составленное из k элементов, выбранных из данных n элементов.
Обозначение: Сnk — число сочетаний из n элементов по k
Формула:
Сnk =
Слайд 12
Пример.
Иван Петрович купил билет спортлото. Он должен зачеркнуть 6 номеров из 49. Сколько существует способов это сделать?
Решение:
С496 = =
= = 13 983 816.
(Красным цветом отмечены множители, которые автоматически сокращаются).
Ответ: 13 983 816 способов
Учитель: Рассмотрим случай повторных независимых испытаний с двумя исходами. Вероятность того, что событие А наступит ровно раз m при проведении n независимых испытаний, каждое из которых имеет два исхода, обозначается Рn(m) и вычисляется по формуле Бернулли.
Слайд 13
Формула Бернулли:
Рn(m) = Сnm * pm *(1 – p) n – m , где
р – вероятность наступления события А в каждом испытании,
m= 0, 2, 3, …, n.
3)Практикум – решение ключевых типов задач В4 ЕГЭ по математике.
Учитель: Переходим от теории к практике. Рассмотрим, как теоретические знания основных понятий, законов и формул помогут нам в решении ключевых типов задач В4 ЕГЭ по математике.
(Демонстрация слайдов презентации. Учитель акцентирует внимание учащихся на приемах решения ключевых задач В4 ЕГЭ по данной теме. Наименование типов задач составлено таким образом, чтобы сформировать у детей ассоциативные связи между типом задачи и алгоритмом ее решения. Учащиеся, испытывающие затруднения при решении задач по данной теме, делают краткие записи в своих рабочих тетрадях. Остальные работают устно по слайдам презентации вместе с учителем).
Слайд14
Тип 1. Самая простая задача.
Задание B4 (№ 283483) открытого банка заданий по математике
В чемпионате по гимнастике участвуют 64 спортсменки: 20 из Японии, 28 из Китая, остальные — из Кореи. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Кореи.
Решение: Из Кореи выступают 64 – (20 + 28) = 16 спортсменок.
По формуле классической вероятности получим: P = = = 0, 25.
Ответ: 0,25
Слайд 15
Тип 2. Задача с бросанием монет
Задание B4 (№ 283473) открытого банка заданий по математике
В случайном эксперименте симметричную монету бросают дважды.
Найдите вероятность того, что орел не выпадет ни разу.
Способ I. Метод перебора комбинаций:
Нужно выписать все возможные комбинации орлов и решек,
а затем выбрать нужные и применить формулу классической вероятности.
Решение:
-
Выписываем все возможные комбинации: ОО, ОР, РО, РР. Значит, n = 4.
-
Среди полученных комбинаций выбираем те,
которые требуются по условию задачи: РР. Значит, ma = 1.
-
По формуле классической вероятности получим: P = = 0, 25.
Ответ: 0,25
Учитель: Метод перебора комбинаций крайне неудобен для большого количества бросков, т.к. занимает много времени. Поэтому мы можем пойти другим путем.
Слайд 16
Способ II. Специальная формула вероятности,
адаптированная для решения задач с монетами.
Пусть в случайном эксперименте монету бросают n раз, тогда вероятность того,
что орел выпадет ровно k раз, можно найти по формуле: P = , где
2n – число всех возможных исходов, Сnk — число сочетаний из n элементов по k,
которое вычисляется по формуле Сnk =
Учитель: В задаче с монетами нужно знать два числа: число бросков и число орлов (решек). В большинстве задач эти числа заданы непосредственно в тексте задачи. Аналогично решаются задачи для решек. Имеем:
Слайд 17
Задача. В случайном эксперименте симметричную монету бросают трижды.
Найдите вероятность того, что орел не выпадет ни разу.
Решение (Способ II):
С30 = = 1 P = = = 0,125
Ответ: 0,125
Слайд 18
Тип 3. Задача с игральным кубиком
Игральный кубик бросили один раз.
Какова вероятность того, что выпадет не менее 4 очков?
Решение:
-
Бросаем игральный кубик один раз — 6 исходов.
Значит, у данного действия (бросание одного игрального кубика 1 раз)
всего имеется n = 6 возможных исходов.
-
Выписываем все благоприятные исходы: 4; 5; 6.
Значит, k = 3 – число благоприятных исходов.
-
По формуле классической вероятности имеем: P = = 0,5.
Ответ: 0,5
Слайд 19
Тип 4. Задача с игральными костями
Задание B4 (№ 283441) открытого банка заданий по математике
В случайном эксперименте бросают две игральные кости.
Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Решение:
-
Бросаем первую игральную кость — 6 исходов, для каждого из которых
возможны еще 6 исходов (когда мы бросаем вторую кость).
Значит, у данного действия (бросание двух игральных костей)
всего имеется n = 6² = 36 возможных исходов.
-
Выписываем все благоприятные исходы в виде пар чисел:
(1;4), (2;3), (3;2), (4;1).
Значит, k = 4 – число благоприятных исходов.
-
По формуле классической вероятности имеем: P = = ≈ 0,11.
Ответ: 0,11
Учитель: Практика показала, что следующий тип задач вызывает у школьников наибольшие затруднения. Однако здесь нечего бояться. Такие задачи решаются просто.
Слайд 20
Тип 5. Задача с перекладыванием монет
В кармане у Андрея было 4 монеты по 2 рубля и 2 монеты по 5 рублей.
Он, не глядя, переложил 3 монеты в другой карман.
Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане.
Решение:
-
Всего у Андрея было: 4 + 2 = 6 монет.
-
3 (переложенные) монеты можно выбрать из 6 (имеющихся) монет:
n = С63 = = = = 20 способами.
(Красным цветом отмечены множители, которые автоматически сокращаются).
-
2 монеты по 5 рублей выбираем из двух пятирублевых монет: 2! = 2 способами.
-
3 монеты из 4-х монет по 2 рубля выбираем:
n = С43 = = = 4 способами.
(Красным цветом отмечены множители, которые автоматически сокращаются).
-
По формуле классической вероятности и правилу произведения получим:
P = = 0,4.
Ответ: 0,4
Слайд 21
Тип 6. Задача с экзаменационными билетами
Задание B4 (№ 320385) открытого банка заданий по математике
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
-
А = {вопрос на тему «Вписанная окружность»}
В = {вопрос на тему «Тригонометрия»}
С = {вопрос по одной из этих двух тем}
-
События А и В несовместны, т.к. по смыслу задачи нет вопросов, относящихся к двум темам одновременно. Значит, С = A U B.
-
По правилу сложения для несовместных событий имеем:
Р (С) = Р(A U B) = Р(А) + Р(В)
Р(С) = 0,1 + 0,35 = 0,45.
Ответ: 0,45
Слайд 21
Тип 7. Задача с кофейными автоматами
Задание B10 (№ 320435) открытого банка заданий по математике
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение:
-
А = {кофе закончится в первом автомате}
В = {кофе закончится во втором автомате}
С = A U B = {кофе закончится хотя бы в одном автомате}
-
По условию: Р(А) = Р(В) = 0,2, Р(А ∩ В) = 0,16
-
По смыслу задачи события А и В являются совместными. По формуле сложения вероятностей совместных событий имеем:
Р(С) = Р(A U B) = Р(А) + Р(В) – Р(А ∩ В) = 0,2 + 0,2 – 0,16 = 0,24.
-
Р( A U B) = 1 – 0,24 = 0,76.
Ответ: 0,76
Слайд 22
Тип 8. Задача о стрельбе по мишеням
Задание B4 (№ 320477) открытого банка заданий по математике
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,85. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение:
Вероятность попадания = 0,85.
Вероятность промаха = 1 – 0,85 = 0,15.
А = {попадание, попадание, промах, промах}
События независимые. По формуле умножения вероятностей:
Р(А) = 0,85*0,85*0,15*0,15 = 0,7225*0,0225 = 0,01625625 ≈ 0,02.
Ответ: 0,02
-
Самостоятельная работа учащихся — решение задач по теме «Элементы комбинаторики, статистики и теории вероятностей в ЕГЭ».
Учащиеся получают индивидуальные задания самостоятельной работы (см. ПРИЛОЖЕНИЕ 1) и выполняют их любым удобным способом на двойных листах в течение 15 минут. Учащиеся, справившиеся со своими заданиями раньше указанного времени, получают новое задание (на дополнительную оценку).
-
Проверка результатов самостоятельной работы.
Каждый учащийся обменивается работой со своим соседом по парте. Учащиеся проверяют работу своего товарища, сверяя его ответы с верными ответами, представленными учителем на слайде.
Слайд 22
|
№ варианта |
№ задачи |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0,05 |
0,07 |
0,35 |
0,5 |
0,4 |
|
2 |
0,3 |
0,03 |
0,6 |
0,56 |
0,43 |
|
3 |
0,04 |
0,17 |
0,6 |
0,78 |
0,4 |
|
4 |
0,25 |
0,14 |
0,3 |
0,66 |
0,43 |
|
5 |
0,28 |
0,07 |
0,55 |
0,4 |
0,4 |
|
6 |
0,1 |
0,14 |
0,35 |
0,34 |
0,43 |
|
7 |
0,14 |
0,14 |
0,55 |
0,42 |
0,4 |
|
8 |
0,25 |
0,08 |
0,5 |
0,74 |
0,4 |
|
9 |
0,1 |
0,02 |
0,6 |
0,4 |
0,4 |
|
10 |
0,1 |
0,06 |
0,45 |
0,58 |
0,43 |
|
11 |
0,12 |
0,08 |
0,25 |
0,64 |
0,43 |
|
12 |
0,24 |
0,375 |
0,5 |
0,76 |
0,4 |
|
13 |
0,15 |
0,5 |
0,3 |
0,8 |
0,43 |
|
14 |
0,12 |
0,0625 |
0,4 |
0,54 |
0,4 |
|
15 |
0,2 |
0,125 |
0,45 |
0,52 |
0,43 |
Учитель: Ребята, а теперь оцените результаты работы соседа по парте по следующим критериям:
«5» — за 5 верных задач
«4» — за 4 верные задачи
«3» — за 3 верные задачи
«2» — если верно выполнено менее 3-х задач
Поставьте полученную оценку в работу своего соседа по парте
-
Домашнее задание.
Учитель: Ребята, для закрепления успехов, достигнутых вами на уроке, а также для устранения допущенных ошибок и пробелов в ваших знаниях по данной теме, на дом вы получаете следующие задания:
Слайд 23
Домашнее задание:
-
Повторить всю теорию по теме.
-
Проанализировать алгоритмы решения всех ключевых задач.
-
Решить в рабочих тетрадях задачи:
-
В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что орел выпадет ровно 4 раза.
-
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,75. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
-
В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,03 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
-
Подобрать из открытого банка задач такие типы задач, которые не были рассмотрены сегодня науроке
-
Подведение итогов урока.
Учитель: Молодцы! Сегодня вы все активно работали на уроке, решили много задач. Но не следует забывать, что для получения глубоких и прочных знаний по предмету и успешной сдачи ЕГЭ по математике каждому из вас необходима систематическая ежедневная учебная работа.
Спасибо за урок!
ПРИЛОЖЕНИЕ 1
Задания для самостоятельной работы учащихся
Вариант 1
-
На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 6 прыгунов из Голландии и 2 прыгуна из Аргентины. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что четырнадцатым будет выступать прыгун из Аргентины.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Павла было 4 монеты по 2 рубля и 2 монеты по 5 рублей. Он, не глядя, переложил 3 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане.
Вариант 2
-
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 6 прыгунов из Германии и 10 прыгунов из США. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что одиннадцатым будет выступать прыгун из Германии.
-
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Ольги было 6 монет по 1 рублю и 2 монеты по 5 рублей. Она, не глядя, переложила 4 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане. Ответ округлите до сотых.
Вариант 3
-
На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 5 прыгунов из Италии и 2 прыгуна из Парагвая. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что двадцать девятым будет выступать прыгун из Парагвая.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Инны было 4 монеты по 1 рублю и 2 монеты по 2 рубля. Она, не глядя, переложила 3 монеты в другой карман. Найти вероятность того, что обе монеты по 2 рубля лежат в одном кармане.
Вариант 4
-
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 5 прыгунов из Голландии и 7 прыгунов из Венесуэлы. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что седьмым будет выступать прыгун из Голландии.
-
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,25. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.
-
В кармане у Татьяны было 6 монет по 1 рублю и 2 монеты по 5 рублей. Она, не глядя, переложила 4 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане. Ответ округлите до сотых.
Вариант 5
-
На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 7 прыгунов из России и 10 прыгунов из Парагвая. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что четырнадцатым будет выступать прыгун из России.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 13 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,3. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,4. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.
-
В кармане у Артура было 4 монеты по 2 рубля и 2 монеты по 5 рублей. Он, не глядя, переложил 3 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане.
Вариант 6
-
На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 4 прыгуна из Италии и 10 прыгунов из Аргентины. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что первым будет выступать прыгун из Италии.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,25. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,1. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,4. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.
-
В кармане у Маргариты было 6 монет по 1 рублю и 2 монеты по 5 рублей. Она, не глядя, переложила 4 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане. Ответ округлите до сотых.
Вариант 7
-
На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 7 прыгунов из Италии и 10 прыгунов из Канады. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что двадцать вторым будет выступать прыгун из Италии.
-
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Антона было 4 монеты по 2 рубля и 2 монеты по 5 рублей. Он, не глядя, переложил 3 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане.
Вариант 8
-
На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 9 прыгунов из Великобритании и 10 прыгунов из Венесуэлы. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что двенадцатым будет выступать прыгун из Венесуэлы.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,2. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Ангелины было 4 монеты по 1 рублю и 2 монеты по 2 рубля. Она, не глядя, переложила 3 монеты в другой карман. Найти вероятность того, что обе монеты по 2 рубля лежат в одном кармане.
Вариант 9
-
На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Украины и 4 прыгуна из США. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что четвертым будет выступать прыгун из Украины.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,35. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Владимира было 4 монеты по 2 рубля и 2 монеты по 5 рублей. Он, не глядя, переложил 3 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане.
Вариант 10
-
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 5 прыгунов из Польши и 2 прыгуна из Венесуэлы. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что шестнадцатым будет выступать прыгун из Венесуэлы.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 14 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Полины было 6 монет по 1 рублю и 2 монеты по 5 рублей. Она, не глядя, переложила 4 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане. Ответ округлите до сотых.
Вариант 11
-
На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 4 прыгуна из Украины и 6 прыгунов из Канады. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что тридцатым будет выступать прыгун из Канады.
-
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,1. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Элины было 6 монет по 1 рублю и 2 монеты по 5 рублей. Она, не глядя, переложила 4 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане. Ответ округлите до сотых.
Вариант 12
-
На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 6 прыгунов из Великобритании и 5 прыгунов из Бразилии. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что третьим будет выступать прыгун из Великобритании.
-
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,3. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,2. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.
-
В кармане у Анатолия было 4 монеты по 2 рубля и 2 монеты по 5 рублей. Он, не глядя, переложил 3 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане.
Вариант 13
-
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 3 прыгуна из Голландии и 4 прыгуна из Колумбии. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что восьмым будет выступать прыгун из Голландии.
-
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,1. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Дмитрия было 6 монет по 2 рубля и 2 монеты по 5 рублей. Он, не глядя, переложил 4 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане. Ответ округлите до сотых.
Вариант 14
-
На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 6 прыгунов из России и 7 прыгунов из Аргентины. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что четвертым будет выступать прыгун из России.
-
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,25. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Ивана было 4 монеты по 2 рубля и 2 монеты по 5 рублей. Он, не глядя, переложил 3 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане.
Вариант 15
-
На чемпионате по прыжкам в воду выступают 45 спортсменов, среди них 2 прыгуна из Испании и 9 прыгунов из Боливии. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что девятнадцатым будет выступать прыгун из Боливии.
-
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка не выпадет ни разу.
-
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,2. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
-
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
-
В кармане у Елены было 6 монет по 1 рублю и 2 монеты по 5 рублей. Она, не глядя, переложила 4 монеты в другой карман. Найти вероятность того, что обе монеты по 5 рублей лежат в одном кармане. Ответ округлите до сотых.
Цель: повторение и закрепление, практическое
применение усвоенных теоретических знаний.
Задачи:
Образовательные:
- Сформировать у учащихся умение использовать
приобретенные знания в практической
деятельности и повседневной жизни; - Отрабатывать навыки решения задач
практического значения, - Отработать навыки решения уравнений различного
типа.
Развивающие:
- Развивать и совершенствовать умения применять
накопленные знания в измененной ситуации, делать
выводы и обобщения.
Воспитательные:
- Подготовка к ЕГЭ, воспитывать настойчивость в
достижении поставленной цели.
Оборудование: мультимедийная установка,
презентация.
Ход занятия
1. Организационный этап.
Задача: подготовить учащихся к работе на
занятии.
2. Вводный этап.
Учитель: Прежде чем вы узнаете тему
сегодняшнего урока, я хотела бы
продемонстрировать вам видео сюжет.http://www.youtube.com/watch?v=NgGGcuB2lrM
(Ученики смотрят фильм о значении витаминов в
жизни людей). Как вы думаете, почему наш урок
начался с этого видеофрагмента?
Ученики отвечают.
Учитель: Действительно, мы заговорили о
витаминах потому, что их названия точно такие же,
как названия заданий на экзамене по математике в
форме ЕГЭ.
Ваша задача на уроке сегодня отработать и
закрепить навыки решения некоторых заданий из
экзаменационного материала. Для этого в
предложенной презентации каждый отвечающий
должен выбрать задание определённого номера
различной сложности и решить его.
3. Основная часть.
Учитель: показывает презентацию “Витаминный
коктейль”.
Ученики:Выбирают задания, щёлкнув мышью в
определённую ячейку таблицы и перейдя по
гиперссылке на соответствующий слайд. Затем
решают эти задания. Чтобы вернуться к номерам
заданий, необходимо навести мышью на название
задания, щёлкнуть на него и вернуться к таблице
заданий.
4. Подведение итогов.
5. Постановка домашнего задания.
Подобрать на сайте www.mathege.ru открытого банка
заданий ЕГЭ по математике заданий В1-В9 и
выполнить не менее 10.
ПЛАН-КОНСПЕКТ УРОКА ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА В 11 «А» КЛАССЕ
Учитель: Багаева Анна Мухаровна
ТЕМА: «Наибольшее и наименьшее значение функции»
Урок проводится с целью изучения и первичного закрепления материала по теме “ Наибольшее и наименьшее значения функции на промежутке”, как одной из основных тем по исследованию функций. Это первый урок из четырёх по теме “Применение производной для нахождения наибольших и наименьших значений величин” и рассчитан на 1 час учебного времени. По ходу урока акцент делается на изучение и отработку как общих методов решения задач (по известному алгоритму), так и перевод задачи на другой язык (использование свойств функций).
Тип урока: урок изучения нового материала с использованием ИКТ.
Методы урока: репродуктивный, частично-поисковый.
Внутрипредметные связи: с темами: «Свойства непрерывных функций», «Исследование функции с помощью производной».
Вид занятия: Применение знаний, умений и навыков.
Виды контроля знаний и умений: предварительный, текущий, тематический.
Оборудование и материалы для урока: ПК, проектор, доска, презентация для сопровождения урока, карточки.
Цель: познакомить учащихся с приемами нахождения наибольшего и наименьшего значения функции на промежутке.
Задачи.
Образовательная — повторить необходимые и достаточные условия существования точек экстремума, понятия: стационарная и критическая точка; вывести алгоритм нахождения наименьшего и наибольшего значений функции, формировать умения решать задачи на отыскание наибольших и наименьших значений функции.
Развивающая – развивать познавательный интерес обучающихся, умение исследовать, выделять главное, сравнивать, анализировать, делать выводы.
Воспитательная – воспитывать умения работать в сотрудничестве в парах и группе, оценивать работу товарища.
Знания, умения, навыки и качества, которые актуализируют, приобретут, закрепят ученики в ходе урока:
— овладение практическими умениями и навыками по теме “Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке”
— умение устанавливать причинно-следственные связи, выделять главное, обобщать, систематизировать;
— формирование навыков самостоятельной работы с учебным материалом;
— формирование навыков самоконтроля.
Структура урока.
Орг. момент.(1-2 мин)
Актуализация знаний ( 5-6 мин)
Мотивационно-целевой этап.(5-6 мин)
Изучение нового материала. Первичное осмысление (7-8 мин).
Закрепление изученного материала.( 15-17 мин)
Рефлексия. Определение домашнего задания (5 мин)
Ход урока
« В мире не происходит ничего,
в чем бы ни был виден смысл
какого-нибудь максимума или минимума!»
Леонард Эйлер
1. Орг. момент.
Приветствие. Эпиграф к уроку (слайд 1).
2. Актуализация знаний.
Устная работа (слайды 2-6). Повторение материала, изученного на предыдущих уроках. Фронтальная работа. Учитель обращает внимание обучающихся на существенное различие понятий максимума (минимума) функций и наибольшего (наименьшего) значений.
3. Мотивация.
Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач на нахождение наилучших, оптимальных решений при наименьших затратах труда, так называемые задачи на оптимизацию.
С некоторыми из таких задач мы познакомимся на следующих уроках. Чтоб успешно решать такие задачи необходимо уметь находить наибольшее и наименьшее значения заданных функций на заданном промежутке.
Постановка обучающимися темы и целей урока (слайды 7-10 ).
4. Изучение нового материала.
Давайте рассмотрим различные варианты поведения непрерывной на отрезке функции, и попытаемся определить, в каких точках она достигает своего наибольшего и наименьшего значений.
Обсуждение в группах по предложенному плану. Обмен мнениями. Фиксация выводов.
План обсуждения слайдов.
Что можно сказать о монотонности функции на отрезке [a;b]?
В какой точке функция достигает своего наибольшего значения?
В какой точке функция достигает своего наименьшего значения?
Чем можно сказать о данных точках отрезка [a;b]?
Какой вывод можно сделать?
А) Функция возрастает (убывает) на отрезке.
(слайд 11 )
Б) Функция имеет на отрезке [a;b] единственную точку экстремума.
(слайд 12)
В) Функция имеет несколько точек экстремума на отрезке [a;b].
( слайд 13)
Г) Анализ всех рассмотренных случаев, установление закономерности нахождения наибольшего и наименьшего значения функции на отрезке.
Беседа по слайду:
Где функция может достигать своего наибольшего (наименьшего) значения на отрезке?
Какой общий подход к нахождению наибольшего и наименьшего значений функции на отрезке можно применить?
(слайд 14)
Выводы:
1. Если функция у = f(х) на отрезке [а; b] имеет лишь одну точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
2. Если функция у = f(х) на отрезке [а; b] не имеет критических , то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает одном конце отрезка, а наименьшее – на другом.
3. Если на отрезке [а; b] функция имеет несколько критических точек, то своего наибольшего (наименьшего) значения она достигает либо на концах этого отрезка, либо в критических точках, лежащих на данном отрезке.
3) Составление алгоритма.
(слайды 15-16 )
5. Закрепление изученного материала.
А) Решение упражнения. Ученики у доски с комментированием.
Подведение мини-итога, повторение алгоритма.
Проверка через мультимедийный проектор. (слайды 17-19.)
Б) Применение алгоритма нахождения наибольшего наименьшего значения функции при решении задач ЕГЭ ( 12 задания из профильной математики)
Вводное слово учителя: Сегодня мы уже говорили о большой практической значимости данной темы. Традиционно задачи, связанные с нахождением наибольшего и наименьшего значения функции на отрезке включаются в ЕГЭ. Давайте попробуем применить полученные знания при решении задач .
З
на отрезке [3; 10].
З
Задача 3. Найти наименьшее значение функции:
Задача 4. Найти наибольшее значение функции:
Проверка через мультимедийный проектор. (слайды 20-23).
В) Математическое моделирование.
( слайды 23-28)
Задача 1. Рекламный щит имеет форму прямоугольника S=9 м2. Изготовьте щит в виде прямоугольника с наименьшим периметром.
Задача 2. Кусок проволоки 48 метров сгибают так, чтобы получился прямоугольник. Какую длину должны иметь стороны прямоугольника, чтобы его площадь была наибольшей?
Решение: Пусть длина- а см. ширина –в см. Тогда периметр 2(а+в) а по условию 48 см. Площадь а*в полупериметр а+в=24 см Чтобы перейти к функции , вводим новое обозначение : длина х см, ширина 24-х см, тогда площадь х(24-х)=24х-х2 должна быть наибольшей. Применяем заданный алгоритм ( 24х-х2)1=24-2х 24-2х=0 х=12 критическая точка
Находим значения функции при х=0 х=12 и х=48 ( на концах промежутка 0,48) f(0)=0 f(12)=144 f(48)= -1152: площадь будет наибольшей , если стороны равны по 12 см данный прямоугольник -квадрат.
Рефлексия. Определение домашнего задания.
(слайды 29-30)
Учитель предлагает учащимся обсудить урок и свою деятельность при постановке учебной задачи, планировании, изучении нового материала, обращая внимания на следующие моменты:
1.Каковы ваши главные результаты, что вы поняли, чему научились?
2.Способы, которые использовались в ходе вашей учебной деятельности для достижения цели урока?
3.Какие чувства испытывали во время урока?
4.Пережили ли вы чувство радости, успеха?
5.С каким настроением вы уходите с урока?
Дома предлагается выполнить задания:
Уровень «А»: № 938 , № 940
Уровень «В»: № 944
Уровень «С»: № 947
Анализ урока математики в 11 «А» классе в соответствии с ФГОС
Ф. И. О. учителя — Багаева А.М.
Дата посещения урока 09.11.2021.
Предмет – алгебра и начала анализа
Класс 11 А
Тема урока «Наименьшее и наибольшее значение функции».
Тип урока: урок изучения нового материала с использованием ИКТ.
Методы урока: репродуктивный, частично-поисковый.
Вид занятия: Применение знаний, умений и навыков.
Виды контроля знаний и умений: предварительный, текущий, тематический.
Оборудование и материалы для урока: ПК, проектор, доска, презентация для сопровождения урока, карточки
Цель: познакомить учащихся с приемами нахождения наибольшего и наименьшего значения функции на промежутке
Все этапы урока были направлены на то, чтобы повысить мотивацию
обучения. Структура урока соответствовала его целям и содержанию.
При проведении организационного момента визуально проверена подготовка класса и каждого обучающегося к уроку.
Проверка домашнего задания и устная работа способствовала актуализации знаний, связи данной темы с ранее изученным материалом и развитию математической речи. Применён фронтальный метод работы со всем классом, так как все обучающиеся страдают недостаточно развитой математической речью.
На уроке использовалась и устная работа, и работа на доске, и самостоятельная работа в тетрадях.
В ходе урока применялась как индивидуальная работа с обучающимися, так и коллективная. Использование различных видов работы в течение урока поддерживает внимание обучающихся на высоком уровне, что позволяет говорить об эффективности урока. Такие уроки снимают утомляемость, перенапряжение обучающихся за счёт переключения на разнообразные виды деятельности.
Объём изученного материала соответствовал программе и уровню знаний
обучающихся. Задачи, которые они решали на уроке, были различны по содержанию.
На протяжении всего урока обучающиеся активно работали и показали хорошие знания по изученной теме. Самостоятельная индивидуальная деятельность каждого обучающегося поощрялась получением оценок, что в свою очередь стимулировало их работу на протяжении всего урока и показывало на уровень усвоения ЗУН.
Использование такой формы проведения урока стимулировало восприятие учебного материала, усилило интерес, позволило сделать математику более доступной и увлекательной, привлечь интерес всех обучающихся, привлечь их к деятельности, в процессе которой приобретаются необходимые знания, умения и навыки, способствовало возникновению положительных эмоций.
Этап подведения итогов урока включал в себя оценку деятельности обучающихся на уроке. Исходя из открытости требований, они смогли объективно оценить свою работу.
Последний этап имел задачу нацелить на осознанное выполнение домашнего задания.
Цель урока была достигнута, план реализован, расчётное время этапов урока совпало с реальным.
Директор школы —————— Медоев А.М.
Система подготовки учащихся к ЕГЭ по математике
Мастер-класс
Учитель математики МБОУ «Завьяловска средняя общеобразовательная школа №1»
Юдакова Ольга Витальевна
Система подготовки к ЕГЭ
- С чего начать?
- Как помочь школьнику при подготовке к ЕГЭ и успешно его сдать?
- Что мешает?
- Что помогает в подготовке к ЕГЭ?
Система подготовки к ЕГЭ
Главная заповедь при подготовке к ЕГЭ по математике
«Чтобы научиться решать
задачи, надо их решать»
Система подготовки к ЕГЭ
Задачи учителя:
- изучение программного материала в формах, используемых при итоговой аттестации
- системный характер подготовки
Система подготовки к ЕГЭ
Задачи ученика:
- уметь выполнять предложенные задания
- выбирать задания, которые решить под силу
- способность к самоконтролю
- уметь правильно распорядиться отведенным
временем
- психологический настрой и концентрация
Система подготовки к ЕГЭ
Этапы подготовки к ЕГЭ:
- работа с демоверсией
- входной контроль
и анализ результатов
- скрупулезная работа с каждым
заданием
Система подготовки к ЕГЭ
Проблемы:
- слабые знания некоторых учащихся за курс основной
школы
- низкий уровень вычислительных навыков
- завышенное самомнение или заниженная
самооценка учащихся
- отсутствие мотивации к обучению
- безразличие к результатам учебной деятельности
Система подготовки к ЕГЭ
Задачи по подготовке учащихся к ЕГЭ
1. Восстанавливать пробелы в знаниях учащихся за курс основной школы.
2. Готовить учащихся к ЕГЭ на каждом уроке .
3. Создать учебный материал по типу ЕГЭ :
тематические тесты, мини – тесты, математические диктанты, зачеты, самостоятельные и контрольные домашние работы.
4. Использовать готовые печатные и электронные пособия .
5. Учить школьников «технике сдачи теста» .
6. Повышать интерес к предмету и личную ответственность учащегося за результаты обучения через систему дополнительных занятий.
7. Психологически настраивать учащихся на атмосферу экзамена.
Система подготовки к ЕГЭ
Каждый учащийся должен иметь:
- маршрутный лист по решению заданий ЕГЭ
- «шпаргалку» по математике
- «тематическую тетрадь»
(решение прототипов всех заданий ЕГЭ)
- «папку тренировочных вариантов ЕГЭ»
с подробным решением некоторых заданий «В» части ЕГЭ и «С» части
Система подготовки к ЕГЭ
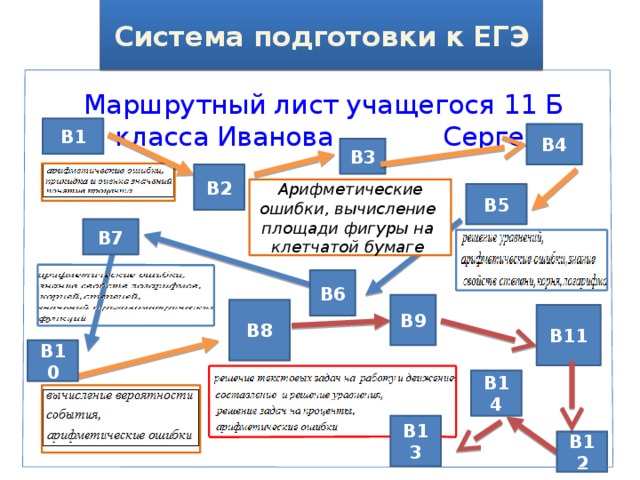
Маршрутный лист учащегося 11 Б класса Иванова Сергея
В1
В4
В3
В2
Арифметические ошибки, вычисление площади фигуры на клетчатой бумаге
В5
В7
В6
В9
В8
В11
В10
В14
В13
В12
10
Система подготовки к ЕГЭ
Центральное место
в подготовке к ЕГЭ
работа по повышению
качества
и оперативности
вычислительных навыков
учащихся
Система подготовки к ЕГЭ
Важный этап в подготовке к ЕГЭ – обучение «технике сдачи теста»
- строгий самоконтроль времени
- определение трудности заданий
- приемы «прикидки» результата
подстановкой
- приемы «спирального движения по тесту»
- нестандартные способы и методы решения заданий для «чайников»
Система подготовки к ЕГЭ
- На каждое задание первой части надо затрачивать не более
двух — трех минут .
- За 12 минут необходимо
решить 4 — 6 заданий теста .
- За урок можно решить все 14 заданий базового уровня
Система подготовки к ЕГЭ
Принцип «спирального движения» :
- просмотр теста от начала до конца
- выполнение простых в режиме скорости
- выполнение 2- 3 заданий , понятных, но требующих большего времени
- размышление над остальными заданиями теста
- движение по тесту по нарастанию сложности заданий
Максимальное количество баллов за 1часть — 60 , это хороший результат!
Система подготовки к ЕГЭ
Виды учебных занятий:
- Уроки теории – лекции
- Практические занятия (ПРЗ )
- Зачеты
- Консультации
- Уроки обобщающего повторения и систематизации знаний по наиболее проблемным заданиям ЕГЭ
Система подготовки к ЕГЭ
«Шпаргалка»
«Шпаргалка» — справочник с кратким изложением основных
теоретических положений
и с индивидуальными дополнениями в виде формул,
схем, таблиц, чертежей,
определений
Система подготовки к ЕГЭ
Карточка для устного счета
- Книга стоит 70 рублей. Сколько книг можно купить на 500 рублей?
- Билет на автобус стоит 110 рублей. Ожидается повышение на 10%. Сколько будет стоить билет после повышения?
- Поезд Екатеринбург-Москва отправляется в 7:23, а прибывает в 9: 23 на следующий день (время московское). Сколько часов поезд находился в пути?
- Грузоподъемность автомобиля 3,5 тонн. Сколько автомобилей потребуется для перевозки 40 тонн груза?
17
Система подготовки к ЕГЭ
Вычислить: Карточка для устного счета 1час 45 мин выразить в часах 20 мин + 1 час 5 мин выразить в минутах 15 кг 5 г выразить в граммах 80 кг выразить в тоннах Вычислить:
18
Система подготовки к ЕГЭ
Мини — тест
В школе есть трехместные туристические палатки. Какое наименьшее
число палаток нужно взять в поход, в котором участвуют 20 человек.
Решите уравнение
Найдите значение выражения при с = 0,5.
Бетонный шар весит 0,5 тонн. Сколько тонн будет весить шар вдвое
большего радиуса, сделанный из такого же бетона?
Смешали 14 литров 30% раствора некоторого вещества с 10 литрами
18% раствора этого же вещества. Сколько процентов составляет
Концентрация получившегося раствора? Знак % в ответе не писать.
Найдите наименьшее значение функции на отрезке [-4,5; 5].
В1
В5
В7
В11
В13
В14
Мастер-класс
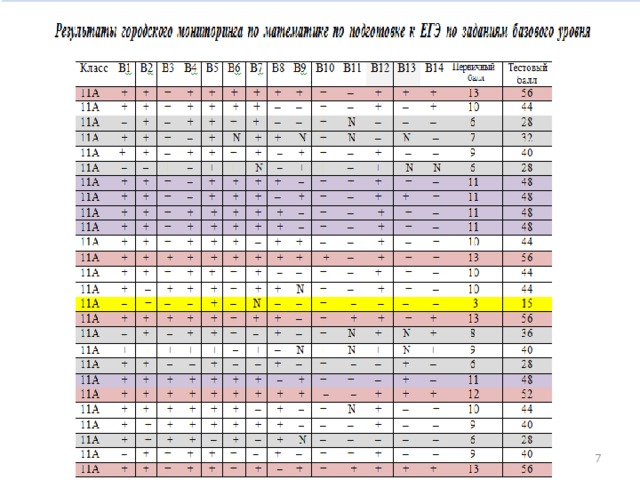
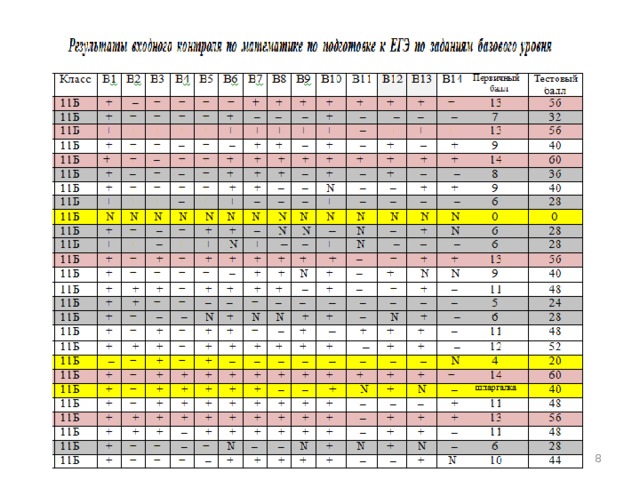
Применение производной Решение заданий В14 ЕГЭ
Мастер-класс
- 30% выпускников на городском
мониторинге по заданиям базового уровня допустили ошибки при решении
В 8 задания
- 60% выпускников допустили ошибки
в В14 задании или не приступили к его
выполнению
- С 2014 года В 14 задание включено
во 2 часть ЕГЭ
Готовимся к ЕГЭ. Повторение.
1. Хорошо знать теорию производной функции 2. Хорошо знать алгоритм решения заданий 3 . Применять при выполнении задания нестандартные способы решения 4. Чтобы научиться решать эти задания, надо их решать 5. Иметь желание и быть ответственным за свои результаты
Я хочу и могу
Готовимся к ЕГЭ. Повторение.
Проблемы, которые необходимо решать Нахождение производных Преобразование выражений: действия с многочленами, раскрытие скобок, применение формул тригонометрии Решение уравнений: квадратных, дробно-рациональных, тригонометрических Определение точек экстремума и промежутков монотонности функции Вычисление значений функции
Готовимся к ЕГЭ. Повторение.
Формулы дифференцирования
- Найдите производную
функции
Готовимся к ЕГЭ. Повторение.
Правила дифференцирования
Найдите производную функции
Готовимся к ЕГЭ. Повторение.
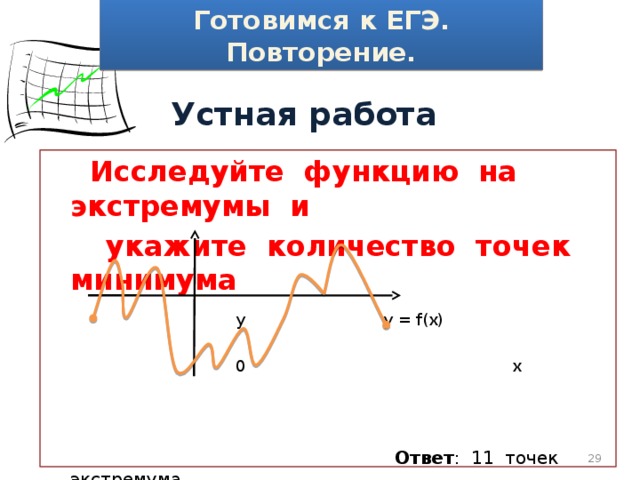
Устная работа
Исследуйте функцию на экстремумы и
укажите количество точек минимума
y y = f(x)
0 x
Ответ : 11 точек экстремума
5 точек минимума
Готовимся к ЕГЭ. Повторение.
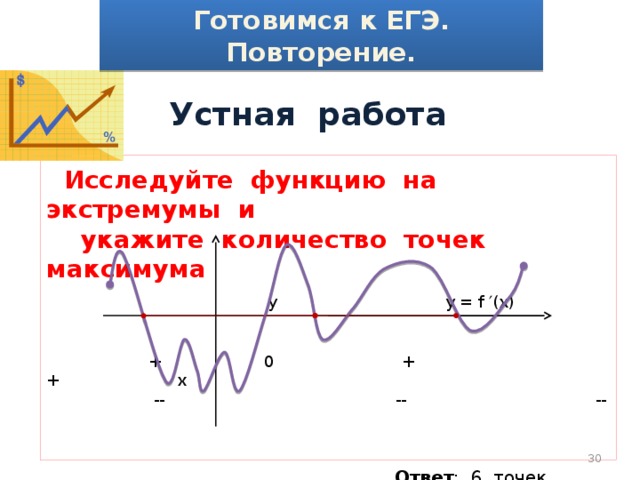
Устная работа
Исследуйте функцию на экстремумы и
укажите количество точек максимума
y у = f ′(x)
+ 0 + + x
— — —
Ответ : 6 точек экстремума
3 точки максимума
Готовимся к ЕГЭ. Повторение.
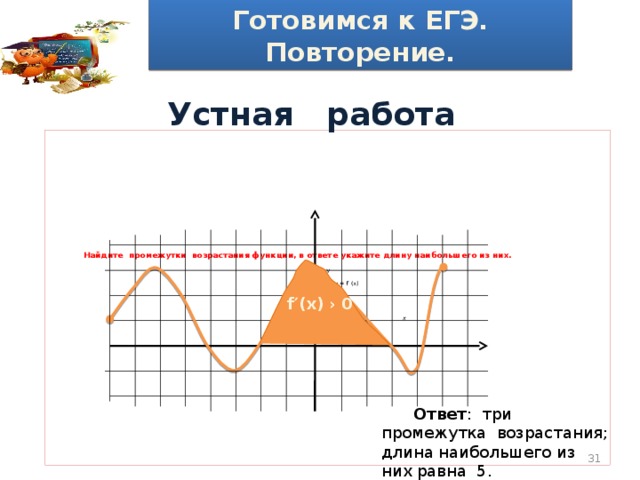
Устная работа
Найдите промежутки возрастания функции, в ответе укажите длину наибольшего из них. у y = f′ (x) 0 х
f′(x) › 0
Ответ : три промежутка возрастания; длина наибольшего из них равна 5.
Готовимся к ЕГЭ. Повторение.
- Проверяемые умения и виды деятельности
по кодификатору
Уметь строить и исследовать простейшие
математические модели:
- Вычислять производные элементарных функций
- Исследовать функции на монотонность
- Находить точки экстремума
- Находить наибольшее и наименьшее
значения функции на указанном отрезке
Готовимся к ЕГЭ. Повторение.
Нахождение наибольшего и наименьшего значений функции на отрезке
Вычисление точек экстремума
В14
Наименьшее или наибольшее значение на отрезке непрерывная функция имеет либо в критической точке, либо в конце отрезка. Практически во всех заданиях в критических точках производная равна нулю. Поэтому сначала находим производную данной функции, приравниваем
ее к нулю и находим критические точки на данном отрезке, затем сравниваем значения функции в найденных точках и
на концах отрезка.
Полезно помнить, что, если функция имеет единственную критическую точку, то минимум в ней является наименьшим, а максимум – наибольшим значением на данном отрезке.
Готовимся к ЕГЭ. Повторение.
- Найдите точку минимума функции
Решение . 1 способ
+ — min +
Ответ: 1
Готовимся к ЕГЭ. Повторение.
Найдите точку максимума функции
Решение . 2 способ
+ max — +
Ответ : — 5
Готовимся к ЕГЭ. Повторение.
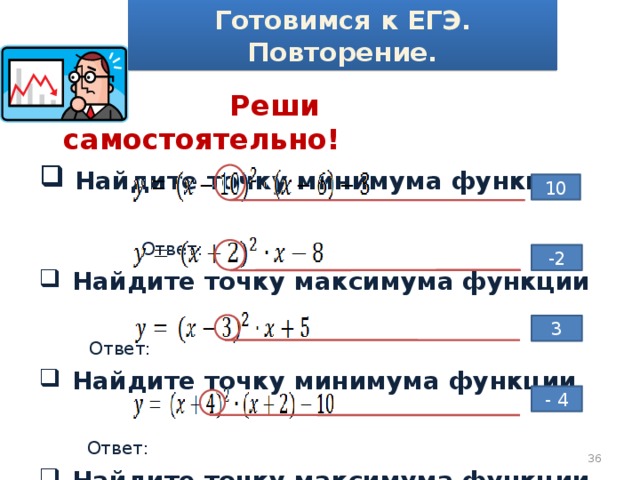
Реши самостоятельно!
- Найдите точку минимума функции
Ответ:
- Найдите точку максимума функции
Ответ:
- Найдите точку минимума функции
Ответ:
- Найдите точку максимума функции
Ответ:
10
-2
3
— 4
Готовимся к ЕГЭ. Повторение.
- Найдите наибольшее значение функции
на отрезке [-12;-6].
Решение.
+ max –
-12 -8 -6
Ответ: — 6
Готовимся к ЕГЭ. Повторение.
- Найдите наименьшее значение функции
на отрезке .
Решение .
— min +
— 4,5 — 4 0
Ответ: — 26
Готовимся к ЕГЭ. Повторение.
Короткий способ решения
- Найдите наименьшее значение функции
на отрезке .
Решение .
Ответ: — 9
- Найдите наибольшее значение функции
на отрезке .
Решение .
+
Ответ: 4
Готовимся к ЕГЭ. Повторение.
- Найдите наибольшее значение функции
на отрезке .
Решение.
Значит, функция убывает на отрезке .
Ответ: — 9
Готовимся к ЕГЭ. Повторение.
- Найдите наименьшее значение функции
на отрезке .
Решение .
Значит, функция возрастает на отрезке .
Ответ: — 7
Готовимся к ЕГЭ. Повторение.
Реши самостоятельно!
- Найдите наименьшее значение функции
на отрезке .
- Найдите наибольшее значение функции
на отрезке .
- Найдите наименьшее значение функции
на отрезке .
- Найдите наибольшее значение функции
на отрезке .
Ответ:
0
Ответ:
9
Ответ:
5
Ответ:
-10
Мастер-класс
Найди производную функции
Проверь себя !
Я могу!
Я понял!
Я попробую!
Найди наибольшее значение функции на отрезке
Найди точку максимума функции
Спасибо за внимание!
Сайт МБНОУ «Лицей г. Полысаево»
polysaevolyceum.ucoz.ru
Сайт ИМЦ г. Полысаево
b23.ru/l0kp
Полысаево WWW.schoolup.ru/ Школа/77615/ Информационно-Методический_Центр,_
Адреса сайтов в сети Интернет
- www.fipi.ru — Федеральный институт педагогических измерений(ФИПИ). Раздел «Открытый сегмент ФБТЗ» – это система для подготовки к ЕГЭ – в режиме on-line.
- http : //mathege.ru – Открытый банк задач ЕГЭ по математике. Здесь можно найти все пробные ЕГЭ по математике.
- http : //egetrener.ru/ — увлекательная и эффективная подготовка к ЕГЭ по математике. Зарегистрируйтесь и попытайтесь попасть в 30 лучших.
- http://uztest.ru – бесплатные материалы для подготовки к ЕГЭ по математике: интерактивные тематические тренажеры, возможность записи на бесплатные on-line курсы по подготовке к ЕГЭ.
- http : //www.alexlarin.narod.ru/ege.html — материалы для подготовки к ЕГЭ по математике (сайт Ларина Александра Александровича).
- http : //www.diary.ru/~eek/ — сообщество по оказанию помощи в решении задач по математике, здесь много полезных книг по математике и для подготовки к ЕГЭ.
- http : //4ege.ru/ — ЕГЭ портал, все последнее к ЕГЭ. Вся информация о ЕГЭ. ЕГЭ 2014.
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
пос. Мизур Алагирского района РСО-Алания
Открытый урок по теме
«Решение заданий ЕГЭ»
Учитель математики Агузарова Л.Д.
п. Мизур
2021г
Тема: Решение заданий ЕГЭ
(задачи с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения, логарифмические неравенства )
Цели занятия:
Образовательные:
-
Повторить материал по данной теме;
Развивающие:
-
Развитие познавательного интереса учащихся к уроку математики;
-
Развитие логического мышления;
-
Развитие скорости и аккуратности;
-
Развитие навыков коллективной работы в сочетании с индивидуальной.
Воспитательные:
-
Воспитание трудолюбия ;
-
Воспитание уважения к окружающим;
Тип урока: урок актуализации знаний и умений (урок повторения).
Ход урока
I. Организационный этап.
Приветствие. Открыли тетради, записали на полях число, классная работа.
I I. Проверка домашней работы
Как у вас обстоят дела с домашней работой? Для того чтобы урок прошел успешно, я должна знать какие затруднения у вас были в домашней работе. Поднимите руки у кого они были.
I I I. Постановка цели и задач урока.
У вас на столах лежат листы, посмотрите на заголовок и попробуйте сформулировать тему нашего урока. «Решение заданий ЕГЭ». Посмотрите на содержание и попробуйте сформулировать цели урока. Сегодня у нас необычный урок, на котором мы будем повторять почти все виды уравнений. Перед вами стоит задача – показать свои знания и умения по решению задач с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения. А так же задание 15 из второй части профильного уровня.
Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сегодня работать самостоятельно.
IV. Актуализация знаний
-
Что такое процент? Какие три типа задач на % существуют? (% от числа, целого по части процента, сколько % составляет одна величина от другой)
-
Что такое корень уравнения? Что значить решить уравнение?
V. Повторение
Прототип задания 1 Задания с практическим содержанием
-
Шариковая ручка стоит 30 рублей. Какое наибольшее количество таких ручек можно будет купить на 300 рублей после повышения цены на 25%?
-
Цена на электрический чайник была повышена на 14% и составила 1596 рублей. Сколько рублей стоил чайник до повышения цены?
-
Для приготовления маринада для огурцов на 1 литр воды требуется 10 г лимонной кислоты. Лимонная кислота продается в пакетиках по 15 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 8 литров маринада?
-
В летнем лагере 152 ребенка и 21 воспитатель. Автобус рассчитан не более чем на 30 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Прототип задания 5
Рациональные уравнения
-
=
Показательные уравнения
-
(
)х+4=49
-
2х-3=
-
(0,2)5+4х=125
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде степени с одним и тем же основанием
-
Переходим к линейному уравнению и решаем уравнение.
-
Записываем ответ.
Логарифмические уравнения
-
log3(x+6)=log3(10-x)-1
-
log2(8-x)=2 log2(4+x)
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде логарифма с одним и тем же основанием.
-
Потенцируем и решаем уравнение.
-
Проверяем корни.
-
Записываем ответ.
Иррациональные уравнения
-
√2х-3=х-3
VI. Применение знаний и умений в новой ситуации
Решить рациональное уравнение
(2х-11)2=(2х-1)2
(х-11)4=(х+3)4
Решить логарифмическое неравенство
х2log243(4-x)≤ log3(x2-8x+16)
VII.. Контроль усвоения, обсуждение допущенных ошибок
Самостоятельная работа в парах
Решите уравнения
Вариант 1
Решите уравнение
-
25-х=64
-
42х-17=
-
√4х+16=10
-
log8(x+4)=log8(5x-16)
-
=
Вариант 2
Решите уравнение
-
21-х=32
-
35х-12=
-
√14-5х=3
-
log2(x+3)=log2(3x-15)
-
=
VIII .Домашнее задание варианты 11-14 задания 7
IX. Рефлексия
Продолжи предложение
Сегодня на уроке я научился…
Сегодня на уроке мне понравилось…
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…























![Система подготовки к ЕГЭ Мини - тест В школе есть трехместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвуют 20 человек. Решите уравнение Найдите значение выражения при с = 0,5. Бетонный шар весит 0,5 тонн. Сколько тонн будет весить шар вдвое большего радиуса, сделанный из такого же бетона? Смешали 14 литров 30% раствора некоторого вещества с 10 литрами 18% раствора этого же вещества. Сколько процентов составляет Концентрация получившегося раствора? Знак % в ответе не писать. Найдите наименьшее значение функции на отрезке [-4,5; 5]. В1 В5 В7 В11 В13 В14](https://fsd.videouroki.net/html/2019/01/06/v_5c32183211949/img21.jpg)










![Готовимся к ЕГЭ. Повторение. Найдите наибольшее значение функции на отрезке [-12;-6]. Решение. + max – -12 -8 -6 Ответ: - 6](https://fsd.videouroki.net/html/2019/01/06/v_5c32183211949/img36.jpg)








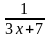 =
=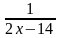
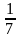 )х+4=49
)х+4=49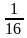
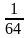
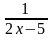 =
=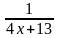
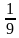
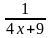 =
=