Анализ устного экзамена по геометрии 8 класс

Аналитическая
справка по результатам регионального публичного зачета по геометрии обучающихся
8 классов

Публичный
зачет по геометрии проходит по билетам, разработанным РЦРО.

Дата проведения:_15-19 мая

Цель: определение уровня знаний обучающихся по геометрии
за курс 8 класса.

 
На основном этапе в зачете приняли участие 844 обучающихся, что составило
96,3%. Не приняли участие в основной этап в зачете 32 человека, из которых дети
с ограниченными возможностями здоровья, не явившиеся на зачет по болезни, по
причине участия в соревнованиях.

С
учетом дополнительных сроков для пересдачи в зачете приняли участие 871
обучающийся (99,4%).

Результаты
публичного зачета по геометрии в 8-х классах:

«2»

«3»

«4»

«5»

Успеваемость

Качество

Гимназия№1

8

31

22

24

90,59

53.49

СОШ №1

0

56

19

33

100,0

46,02

СОШ №3

20

34

21

23

79,59

44,0

СОШ №4

0

30

4

7

100,0

25,0

ООШ №5

0

21

8

11

100,0

47,5

СОШ №6

6

34

19

26

92,94

51,72

СОШ №8

8

58

18

26

92,73

37,93

ООШ №9

0

15

0

5

100,0

22,73

СОШ №10

32

23

10

21

62,79

32,98

СОШ №12

45

25

13

18

55,45

30,39

СОШ №13

9

33

11

17

87,14

38,89

Итого в основной этап:

128

360

145

211

84,83

40,64

Результаты с учетом пересдачи:

0

498

154

219

100,0

42,7

На
основном этапе зачета успеваемость составила 84,8%, с учетом сдачи зачета в
дополнительный срок успеваемость по городу повысилась и составила 100%.

Результаты
публичного зачета показали, что более 50% обучающихся получили оценку «3», то
есть их знания учебного материала по геометрии на низком базовом уровне. А это
значит, что у большинства обучающихся знание материала по геометрии за курс 8
класса на уровне заучивания теоретического материала, без наличия твердых
практических навыков, что подтверждается низким качеством (42,7%) и
недостаточной сформированностью навыков решения задач.

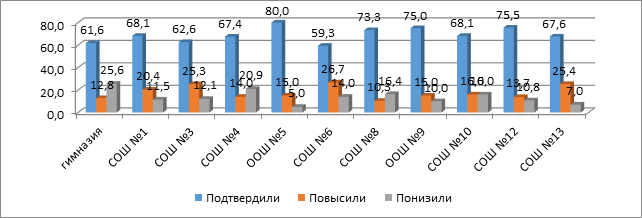
Сравнение результатов
публичного зачета по геометрии с оценкой за последнюю контрольную работу (по
КТП)

Сравнение результатов
публичного зачета с результатами последней контрольной работы так же показало,
что 51% обучающихся на публичном зачете получили оценку,  соответствующую
оценке последней контрольной работы (по школам от 35% до 70%). 33,6%
обучающихся, получили на зачете оценку выше, чем за последнюю контрольную
работу (по школам от 20% до 55% школьников), что объясняется тем, что к зачету
в школах была хорошо организована подготовка к публичному зачету. Однако, наличие
 обучающихся (15,4%), получивших на зачете оценку ниже, чем на последней
контрольной работе (по школам от 7% до 32%) говорит о  возможном необъективном оценивании
(завышении) учителями текущих знаний по геометрии.

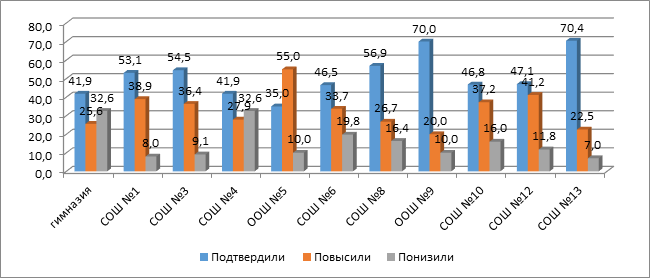
Сравнение
результатов публичного зачета по геометрии с оценкой за 3 четверть текущего
учебного года

Сравнение результатов
публичного зачета с оценкой за 3 четверть текущего учебного года показало, что в
среднем по городу 51% обучающихся (по школам от 46% до 76%) на зачете подтвердили
оценку, выставленную за 3 четверть. 33,6% обучающихся, получили оценки выше
того, что выставлено за 3 четверть (по школам от 10% до 36%), что может
объясняться планомерной подготовкой к зачету, однако 15,4% обучающихся (по
школам от 10% до 23%) на зачете получили оценку ниже, чем оценка за 3 четверть,
что так же указывает на проблему объективности оценивания ответов и письменных работ
обучающихся на уроках.

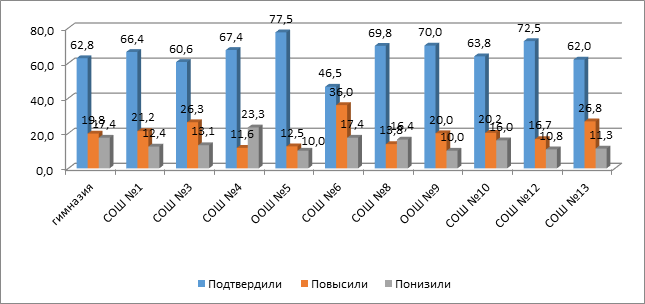
Сравнение
результатов публичного зачета по геометрии с оценкой за год

Сравнение результатов
публичного зачета и годовой оценки по геометрии  показывает, что в среднем по
городу у 68,1% обучающихся годовая оценка по геометрии совпадает с  оценкой,
полученной на зачете (по школам от 59% до 80% обучающихся). 17,9% обучающихся
на зачете получили оценку выше, чем за оценка за год (по школам от 10% до 27%),
значит у этой группы обучающихся и у учителей, работающих с ними появился стимул
для повышения качества знаний по предмету в новом учебном году. 14% обучающихся
(по школам от 7% до 26%) на публичном зачете получили оценку ниже, чем годовая,
и это повод еще раз обратить внимание на объективность оценивания учителями
знания обучающихся в течении учебного года.

Максимально на публичном зачете по геометрии можно было набрать 6
баллов, минимально – 3 балла.   

14% обучающихся получили на зачете максимальный балл.

В основной период успешно
(без двоек) сдали зачет все обучающиеся СОШ №1, СОШ №4, ООШ №5, ООШ №9.

В 7% школ города доля
обучающихся, не справившихся с зачетом в основные сроки составила от 7% (СОШ
№6, СОШ №8) до 45% (СОШ №12).

Сравнение успешности
выполнения геометрических заданий на региональном экзамене текущего учебного
года и прошлого учебного года позволяет отметить, что планомерная подготовка к
публичному зачету позволила увеличить долю обучающихся, которые стали
приступать к выполнению геометрических заданий и справляться с ними.

Однако, несмотря на
удовлетворительные результаты публичного зачета, у 46% обучающихся на
региональном экзамене вызвало затруднение геометрическое задание №7 первой
части, у 43% обучающихся геометрическое задание №9 первой части. Обучающиеся
школ № 4,9 при 100% сдаче публичного зачета по геометрии в основной этап на
региональном экзамене не смогли применить теоретические знания и не справились
с геометрическими заданиями №7 и №9 первой части (СОШ 4 – около 50 %
обучающихся, ООШ №9 –более 70% обучающихся), так как у них недостаточно
отработаны практические навыки применения теоретических знаний.  Это должно
найти отражение в анализе работы школьных методических объединений и в
планировании работы на 2018-2019 учебный год.

 

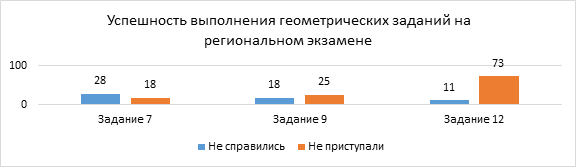
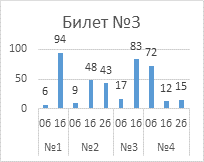
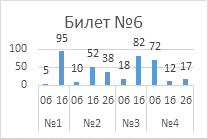
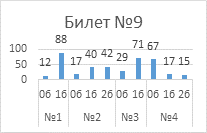
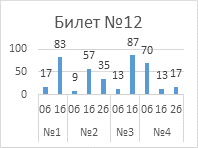
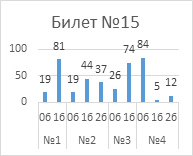
Выполнение
заданий публичного зачета в разрезе заданий, билетов (%)

  

  

  

  

  

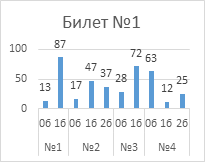
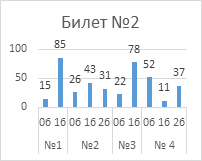
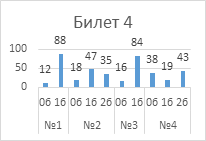
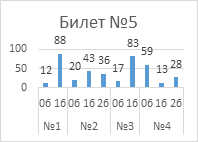
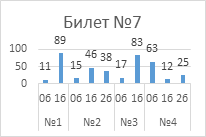
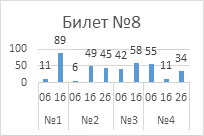
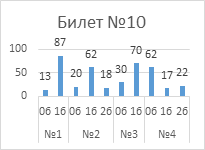
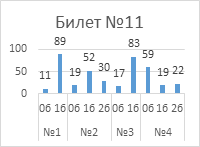
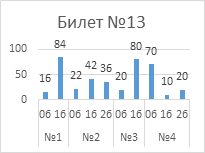
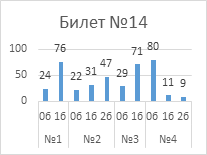
Анализ успешности
выполнения заданий указывает на то, что с первым заданием каждого билета справились
от 76% обучающиеся до 95%.

Первое задание – это
теоретический вопрос, в котором требовалось дать определение. Верные ответ
оценивался в 1 балл. Наибольшие проблемы в теоретическом вопросе вызвало
определение окружности, вписанной в треугольник,
описанной около треугольника, нахождение центра этих окружностей (билет
14, 24% обучающихся не ответили на вопрос). Тема
наиболее сложная, изучается в 3 четверти 8 класса.

При ответе на
второе задание каждого билета необходимо было привести доказательство теоремы.
От 31% обучающихся до 47% обучающихся получили максимальные 2 балла за второе
задание, верно сформулировав теорему и представив ее доказательство. В билете
№10 (признак параллелограмма по двум противоположным сторонам) только 18%
обучающихся получили по 2 балла.  От 6% до 26% обучающихся со вторым заданием
на публичном зачете не справились. Наибольшая доля обучающихся при ответе на
второе задание билета сформулировали теорему, но не смогли доказать или не
приступили к доказательству теорем, тем самым получив только по 1 баллу. Наиболее
сложным для обучающихся стало доказательство теоремы о медиане треугольника
(билет №2). 26% не справились с заданием, получив «0» баллов.

Задание №3
оценивалось в 1 балл и требовало решения простой геометрической задачи. От 71% обучающихся
до 87% с заданием успешно справились. Наибольшее затруднение вызвало задание из
билета №8 на нахождение высоты треугольника с использованием формулы площади
треугольника.

В задании№ 4
каждого билета было предложена более сложная задача, для решения которой требовалось не только применение теоретических знаний но и умение логически
рассуждать, делать умозаключения. 2 балла
обучающийся получал, если выбирал правильный путь
решения, понятный путь рассуждения, давал верный ответ. Только от 15% до 43%
обучающихся школ за ответ на 4 задание получили по 2 максимальных балла. От 38%
до 84% обучающихся школ с заданием не справились.

Максимальный
балл за данное задание чаще получали обучающиеся гимназии, школ №1,3,6,8.
Обучающиеся школ №4, 9 за 4 задание в основном получало по «0» баллов.

Вывод.

Анализ
результатов публичного зачета по геометрии показал удовлетворительный уровень
знаний обучающихся 8-х классов по геометрии. Анализ успешности
решения заданий №2, 4 выявил проблему неумения большинства обучающихся
применять теоретические знания на практике. Так
как менее половины обучающихся успешно справились с заданием №2 и не приступили
(или не справились) с заданием №4, то можно утверждать, что
основная доля обучающихся владеют теорией на уровне понятий, однако в
большинстве случаев понятий аппарат обучающихся не сформирован на уровне осознанного
применения при решении задач. У обучающихся вызывает трудность выделение
условия задачи, заключения, построение чертежа по условию задачи, составление плана
решения, описание решения.

Наибольшее
затруднение вызвали задания на отработку умения решать задач на
применение вписанной и описанной окружности, на нахождение медианы треугольника.

Рекомендации:

МКУ ЦРО:

1.      Запланировать
на 2018-2019 учебный год посещение уроков геометрии учителей, требующих
методической помощи при отработке с обучающимися навыков применения
теоретических знаний при решении задач по геометрии, в том числе при работе с
чертежами.

2.      Организовать
серию открытых уроков для учителей, которым требуется методическая помощь при
отработке навыков решения геометрических задач, в том числе при обучении
обучающихся работать с чертежами.

ГМО

1.      Рассмотреть
на заседании ГМО тему «Методика решения задач на применение вписанной и
описанной окружности» с формированием банка заданий, направленных на отработку
умения решать эти задачи.

Руководителям ОО:

1.      Включить
во внутришкольный контроль на 2018-2019 учебный год следующие вопросы

—       
объективность
оценивания знаний обучающихся по геометрии;

—       
качественная
подготовка обучающихся к публичному зачету.

—       
Скачано с www.znanio.ru

Источник

АНАЛИТИЧЕСКИЙ ОТЧЕТ

по результатам промежуточной аттестации по
геометрии в 8 классе

Промежуточная аттестация по геометрии 
прошла в форме контрольной работы.

Экзаменационная работа по
геометрии, включала основные элементы содержания курса 8 класса, изученные к
моменту проведения работы, а также материал 8 класса, необходимый для успешного
освоения программы курса математике  основной школы.

Структура экзаменационной
работы максимально приближена к структуре демоверсии по количеству заданий и
уровням их сложности (или свой вариант). Основные
контролируемые дидактические единицы:

1) Четырёхугольники

2) Площади

3) Подобные треугольники

4) Окружность

 Варианты
носят характер «парного подобия». Они представляют собой как текстовые задания
с выбором ответа (часть А), задания с кратким ответом (часть В), а также
содержится по одной задаче (часть С), к которой надо дать развернутый ответ.

Часть
А направлена на проверку достижения уровня обязательной подготовки. Она
содержит 10 заданий, соответствующих минимуму содержания курса «Геометрия 7».
Предусмотрены задания с выбором ответа из четырёх предложенных.

Часть
В направлена на дифференцируемую проверку повышенного уровня владения
программным материалом. Она содержит 2 заданий. При выполнении этой части
проверяется способность учащихся интегрировать различные темы, владеть навыками
исследования, а также применять нестандартные приёмы рассуждений.

Часть
С направлена на выявление учащихся, проявляющих повышенный интерес к предмету.
Она содержит 1 задание повышенной трудности, при выполнении которого требуется
проанализировать условие, разработать математическую модель, реализовать её и
грамотно обосновать. Решение задания предполагает свободное владение изученными
тематическими модулями и высокий уровень подготовки.

Максимальное количество баллов
за экзаменационную работу – 18

В экзамене приняли участие – 1 чел.

Количество баллов, соответствующее отметке
«5», набрали 0 ученик (0%), отметке «4» — 1 ученик (100%), отметке «3» — 
ученик (0%).

Из них:

•        
1чел.
(100%) — подтвердили годовую оценку,

•        
0
чел. (100  %) – получили оценку выше годовой оценки,

•        
0
чел. (0 %) – получили оценку ниже годовой.

1 обучающийся показали максимальный
результат, получив за экзаменационную работу 13 баллов.

О-бучающихся показали неудовлетворительный
результат, получив за экзаменационную работу  баллов.

№ задания

Проверяемые элементы содержания

% выполнения заданий

Проверяемые виды деятельности

Вар-т 1

Вар-т 2

Предметные умения

Общеучебные умения

1

Площадь
прямоугольника

100

Уметь находить
сторону через формулу площади

Умение выделять общий
признак двух или нескольких предметов или явлений и объяснять их сходство

2

Площадь
параллелограмма

100

Уметь применять
фомулу площади

Умение выделять общий
признак двух или нескольких предметов или явлений и объяснять их сходство

3

Свойства ромба

100

Уметь, используя
свойства ромба, находить неизветные элементы

Умение выдвигать
гипотезы при решении задачи

4

Подобие треугольников

100

Уметь применять 
признаки подобия

Умение устанавливать
причинно-следственные связи, строить логические рассуждения, умозаключения и
делать выводы

5

Центральные и
вписанные углы

100

Умение применять
свойства центральных и вписанных углов

Умение выделять общий
признак двух или нескольких предметов или явлений и объяснять их сходство

6

Четырёхуольники

100

Уметь применять
свойства четырёхугольников

Умение выделять общий
признак двух или нескольких предметов или явлений и объяснять их сходство

7

Площадь ромба

100

Умение применять
формулы площадей

Умение выделять общий
признак двух или нескольких предметов или явлений и объяснять их сходство

8

Площадь квадрата

100

Умение применять
формулы площадей

Умение выделять общий
признак двух или нескольких предметов или явлений и объяснять их сходство

9

Синус, косинус и
тангенс острого угла прямоугольного треугольника.

100

Умение использовать
определения и осноного тригометрического тождества

Умение выделять общий
признак двух или нескольких предметов или явлений и объяснять их сходство

10

Вписнные
четырёхугольники

100

Умение использовать
теорему о вписанном четырёхугольнике

Умение оценивать
правильность выполнения учебной задачи, собственные возможности ее решения.

11

Подобие теугольников

0

Уметь применять 
признаки подобия

Умение устанавливать
причинно-следственные связи, строить логические рассуждения, умозаключения и
делать выводы

12

Отрезки
пересекающихся хорд

100

Умение применять
теорему об отрезках хорд

Умение определять
понятия, создавать обобщения, устанавливать аналогии, классифицировать,
самостоятельно выбирать основания и критерии для классификации

13

Теорема Пифагора.

50

Умение использовать
теорему

Умение устанавливать
причинно-следственные связи, строить логические рассуждения, умозаключения и
делать выводы

По результатам экзамена выяснилось, что
обучающиеся 8 класса  усвоили материал по геометрии и показали хороший
 уровень качества обученности.

Лучше всего обучаемые справились с
заданиями части А

Рассмотрим наиболее проблемные задания

1. Признаки подобия треугольников

2. Задачи в несколько этапов.

Анализ показал, что учебный материал за
курс 8 класса  освоен, уделить внимание задачам, которые решаются в несколько
действий,  умению применять теоремы и аксиомы при решении, умению составлять
уравнения по условию задачи, выполнять преобразования выражений, строить и
исследовать простейшие математические модели. 

Недостаточно освоенными следует считать
такие метапредметные умения, как умение понимать и использовать математические
средства наглядности для иллюстрации, интерпретации, аргументации.

Источник

Билеты по геометрии

для промежуточной аттестации

обучающихся 8 класса

по УМК Л.С. Атанасян и др.

Составила: Южалина Лариса Николаевна,

учитель первой категории

2020 – 2021 уч.год

Пояснительная записка

Спецификация контрольных измерительных материалов

для проведения промежуточной аттестации по геометрии (устно) в 8 классе

  1. Назначение КИМ:

  • оценить уровень общеобразовательной подготовки по геометрии учащихся 8 классов;

  • итоговый контроль.

  1. Документы, определяющие содержание КИМ.

Содержание и уровень требований устного экзамена определяются следующими

документами:

  • Авторской программы: Бурмистрова Т.А. Геометрия 7 — 9 классы. Программы общеобразовательных учреждений. М., «Просвещение», 2009. рекомендованной Минобразования РФ к использованию в образовательном процессе; Бурмистрова Т.А. Геометрия 7 — 9 классы. Программы общеобразовательных учреждений. М., «Просвещение», 2012.

  • Учебник «Геометрия 7-9 класс» автор Атанасян Л.Н. издательство «Просвещение» 2017 год. Итоговый контроль проводится по экзаменационным билетам

Подходы к отбору содержания, разработке структуры КИМ

Структура КИМ отвечает цели построения системы дифференцированного

обучения математике в современной школе. Целью устного экзамена является проверка уровня предметной компетентности учащихся за курс 8 класса по геометрии в рамках проведения переводной аттестации.

Отличие геометрии от всех других общеобразовательных предметов состоит в том, что ее содержание практически не меняется в течение многих веков и основные цели ее изучения остаются неизменными:

1. Развитие пространственных представлений, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как умение:

  • читать и делать чертежи, необходимые для решения;

  • выделять необходимую конфигурацию при чтении чертежа;

  • определять необходимость дополнительных построений при решении задач и выполнять их;

  • различать взаимное расположение геометрических фигур.

Формирование и развитие логического мышления, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как владение методами доказательств, применяемыми при обосновании геометрических утверждений (теорем, следствий и т. д.), а также при проведении аргументации и доказательных рассуждений в ходе решения задач.

Характеристика структуры и содержания КИМ

Количество билетов: 17

Билет содержит в себе 2 вопроса

Первый вопрос предполагает, что учащийся должен сформулировать теорему, свойство, определение, привести пример или выполнить необходимый рисунок.

Второй вопрос предполагает решение задачи.

Задания в экзаменационных билетах соответствуют темам, изучаемым в 8 классе, а именно:

1.Четырехугольники

2.Площадь

3.Подобные треугольники

4.Окружность

Распределение заданий КИМ по содержанию, проверяемым умениям и

способам деятельности.

Включенные в работу задания проверяют следующие виды познавательной

деятельности:

  • умение пользоваться языком геометрии для описания предметов окружающего мира;

  • умение распознавать геометрические фигуры, различать их взаимное расположение;

  • умение изображать геометрические фигуры;

  • умение выполнять чертежи по условию задач; осуществлять преобразования фигур;

  • умение проводить доказательные рассуждения, используя известные теоремы, обнаруживая возможности для их использования;

Распределение заданий КИМ по уровню сложности

Общее число билетов промежуточной аттестации – 17. В каждом билете представлены вопросы базового уровня сложности

Продолжительность выполнения работы.

Учащиеся производят выбор билета и готовятся к ответу в течение 20 минут. Остальные экзаменуемые заходят в аудиторию по мере того, как из кабинета выйдет ответивший ученик.

Каждому ученику дается на подготовку не менее 20 минут.

Досрочный ответ возможен.

Дополнительные материалы.

Разрешается использовать линейку, циркуль и карандаш.

Система оценивания выполнения отдельных заданий и работы в целом.

Оценка складывается из следующих компонентов:

Оценивание устных ответов:

Отметка 5 (отлично) – ставится за полный, логически обоснованный ответ на все вопросы билета.

Отметка 4 (хорошо) – выставляется за изложенный вопрос с небольшими недочетами и решение задачи, но возможны, допустимы вычислительные ошибки или неточности в доказательстве теоремы.

Отметка 3 (удовлетворительно) – ставится за решение задачи и правильно сформулированные теоремы, свойства, определения (без доказательства).

Отметка 2 (неудовлетворительно) – выставляется во всех остальных случаях.

Кодификатор элементов содержания контрольных измерительных материалов

для проведения промежуточной аттестации (устно) по геометрии в 8 классе.

Кодификатор элементов содержания для проведения аттестационной работы по геометрии является одним из документов, определяющих структуру и содержание контрольных измерительных материалов (КИМ). Кодификатор является систематизированным перечнем требований к уровню подготовки учащихся и проверяемых элементов содержания, в котором каждому объекту соответствует определенный код.

Код

Код

Элементы содержания, проверяемые заданиями

раздела

контролируе

аттестационной работы

мого

элемента

1

Четырехугольники

1.1

Многоугольники

1.1.1

Многоугольник

1.1.2

Выпуклый многоугольник

1.1.3

Четырехугольник

1.2

Параллелограмм и трапеция

1.2.1

Параллелограмм

1.2.2

Признаки параллелограмма

1.2.3

Трапеция

1.3

Прямоугольник, ромб, квадрат

1.3.1

Прямоугольник

1.3.2

Ромб и квадрат

1.3.3

Осевая и центральная симметрии

2

Площадь

2.1

Площадь многоугольника

2.1.1

Понятие площади многоугольника

2.1.2

Площадь квадрата

2.1.3

Площадь прямоугольника

2.2

Площади параллелограмма, треугольника, трапеции

2.2.1

Площадь параллелограмма

2.2.2

Площадь треугольника

2.2.3

Площадь трапеции

2.3.

Теорема Пифагора

2.3.1

Теорема Пифагора

2.3.2

Теорема, обратная теореме Пифагора

2.3.3

Формула Герона

3.1

Определение подобных треугольников

3.1.1

Пропорциональные отрезки

3.1.2

Определение подобных треугольников

3.1.3

Отношение площадей подобных треугольников

3.2

Признаки подобия треугольников

3.2.1

Первый признак подобия треугольников

3.2.2

Второй признак подобия треугольников

3.2.3

Третий признак подобия треугольников

3.3

Применение подобия к доказательству теорем и решению

задач

3.3.1

Средняя линия треугольника

3.3.2

Пропорциональные отрезки в прямоугольном треугольнике

3.3.3

Практические приложения подобия треугольников

3.3.4

О подобии произвольных фигур

3.4

Соотношения между сторонами и углами прямоугольного

треугольника

3.4.1

Синус, косинус и тангенс острого угла прямоугольного

треугольника

3.4.2

Значения синуса, косинуса и тангенса для углов 300, 450, 600

4

Окружность

4.1

Касательная к окружности

4.1.1

Взаимное расположение прямой и окружности

4.1.2

Касательная к окружности

4.2

Центральные и вписанные углы

4.2.1

Градусная мера дуги окружности

4.2.2

Теорема о вписанном угле

4.3

Четыре замечательные точки треугольника

Свойство биссектрисы угла

4.3.1

Свойство серединного перпендикуляра к отрезку

4.3.2

Теорема о пересечении высот треугольника

4.4

Вписанная и описанная окружность

4.2.1

Вписанная окружность

4.2.2

Описанная окружность

Билеты по геометрии за курс 8 класса (Атанасян Л.С.)

Билет № 1

1.Определение выпуклого многоугольника. Сумма углов выпуклого многоугольника. Понятие площади многоугольника. Свойства площадей многоугольников. 2.Най­ди­те тан­генс угла А тре­уголь­ни­ка ABC, изоб­ражённого на ри­сун­ке.

Рис. 2.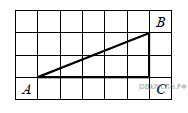

Билет № 2

1.Определение четырехугольника, параллелограмма. Свойства параллелограмма. Площадь параллелограмма.

2.Отрезки и  — диаметры окружности с центром . Угол равен . Найдите угол . Ответ дайте в градусах.

Рис.2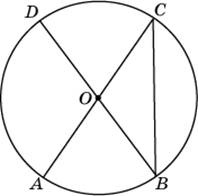

Билет № 3

1.Определение четырехугольника, параллелограмма. Признаки параллелограмма. Площадь параллелограмма.

2.В 60 м одна от дру­гой рас­тут две сосны. Вы­со­та одной 31 м, а дру­гой — 6 м. Най­ди­те рас­сто­я­ние (в мет­рах) между их вер­хуш­ка

Рис.2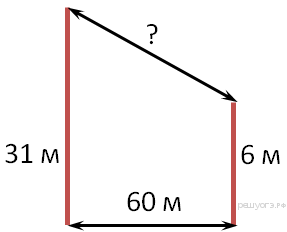

Билет № 4

1.Определение трапеции, её виды. Свойства равнобедренной трапеции. Площадь трапеции.

2.. На ри­сун­ке изоб­ра­жен ромб АВСD. Ис­поль­зуя ри­су­нок, най­ди­те tg ОВС.

Рис.2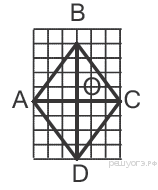

Билет № 5

1. Определение прямоугольника. Свойства прямоугольника. Площадь прямоугольника.

2.На ри­сун­ке изоб­ра­жен па­рал­ле­ло­грамм  ABCD. Ис­поль­зуя ри­су­нок, най­ди­те  sin HBA.

Рис. 2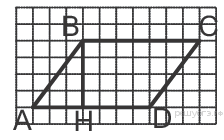

Билет № 6

1. Определение ромба. Свойства диагоналей ромба. Площадь ромба.

2. Отрезки и  — диаметры окружности с центром . Угол равен . Найдите вписанный угол . Ответ дайте в градусах.

Рис. 2

Билет № 7

1. Определение ромба. Признаки ромба. Площадь ромба.

2. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.2). Ответ дайте в квадратных сантиметрах.

рис.2

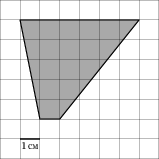
Билет № 8

1.Определение средней линии треугольника. Свойства средней линии треугольника.Площадь треугольника. Формула Герона.

2. Касательные к окружности с центром в точках и пересекаются под углом . Найдите угол . Ответ дайте в градусах.

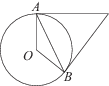
Билет № 9

1.Определение квадрата. Свойства квадрата и признаки квадрата. Площадь квадрата.

2. Прямая касается окружности в точке . Точка  — центр окружности. Хорда образует с касательной угол, равный . Найдите величину угла . Ответ дайте в градусах.

Рис. 2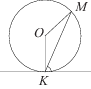

Билет № 10

1. Определение прямоугольного треугольника. Теорема Пифагора. Пифагоровы тройки. Площадь треугольника.

2. Точка  — центр окружности, на которой лежат точки , и . Известно, что и . Найдите угол . Ответ дайте в градусах.

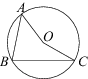
Билет № 11

1. Определение прямоугольника. Признаки прямоугольника. Площадь прямоугольника.

2. От­ре­зок AB = 40 ка­са­ет­ся окруж­но­сти ра­ди­у­са 75 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

Рис. 2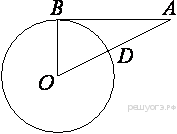

Билет № 12

1.Определение трапеции, её виды. Признаки равнобедренной трапеции. Площадь трапеции.

2.В тре­уголь­ни­ке ABC от­ре­зок DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 97. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

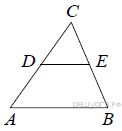
рис. 2

Билет № 13

1.Определение подобных треугольников. Признаки подобия треугольников. Свойство биссектрисы угла.

2.Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

Билет № 14

1. Определение центрального и вписанного угла. Свойства углов, вписанных в окружность.

2. Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

Рис. 2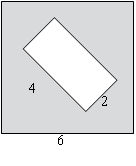

Билет № 15

1. Определение центрального и вписанного угла; следствия.

2. Бис­сек­три­са угла A па­рал­ле­ло­грам­ма ABCD пе­ре­се­ка­ет сто­ро­ну BC в точке K. Най­ди­те пе­ри­метр па­рал­ле­ло­грам­ма, если BK = 7, CK = 12.

Билет № 16

1. Определение касательной; свойство касательной к окружности.

2.Сто­ро­на квад­ра­та равна 10. Най­ди­те его пло­щадь. 

Билет № 17

1. Определение синуса, косинуса, тангенса. Основное тригонометрическое тождество.

2.Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

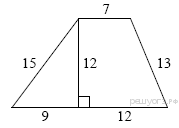
Ответы к билетам по геометрии 8 класс

№ билета

/вопроса

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

2

0,4

104

65

0,75

0,8

35

17,5

36

7

32

10

388

176

28

52

100

168
Источник

Пояснительная записка.

В 2020 -2021учебном году промежуточную аттестацию по геометрии в 8 классе рекомендуем организовать в форме устного экзамена.

Целью устного экзамена является проверка уровня предметной компетентности учащихся 8 классов по геометрии за курс 8 класса.

Основные цели изучения геометрии:

  1. Развитие пространственных представлений, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как умение:

  • читать и делать чертежи, необходимые для решения;

  • выделять необходимую конфигурацию при чтении чертежа;

  • определять необходимость дополнительных построений при решении задач и выполнять их;

  • различать взаимное расположение геометрических фигур.

  1. Формирование и развитие логического мышления, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как владение методами доказательств, применяемыми при обосновании геометрических утверждений (теорем, лемм, следствий и т.д.), а также при проведении аргументации и доказательных рассуждений в ходе решения задач.

Структура экзаменационного билета.

Билеты содержат три вопроса по различным темам курса геометрии за 8 класс (два теоретических вопроса и одна задача).

Первый вопрос. Базовый уровень.

В первом вопросе от учащихся требуется выполнить одно из трех возможных заданий: первое – дать определение фигуры; второе – воспроизвести одну из формул для вычисления длин отрезков, градусных мер углов, площадей; третье – воспроизвести формулировку одной из теорем о свойствах или признаках фигур, их элементов, отношениях фигур.

При ответе на первый вопрос учащиеся должны:

— дать четкое определение фигуры, включающее в себя как вербальное определение, так и графическое – чертеж, а также привести пример применения этого определения, верно иллюстрирующий его смысл.

-правильно воспроизвести одну из формул для вычисления значений геометрических величин (площадей), при этом, кроме записи формулы, необходимо выполнить чертеж и объяснить смысл формулы. Привести пример применения этой формулы, позволяющий сделать вывод об уровне сформированности умения применять эту формулу.

— воспроизвести формулировку теоремы, проиллюстрировав содержание теоремы выполнением чертежа; привести пример применения этой теоремы, верно отражающий ее содержание и смысл.

Второй вопрос. Продвинутый уровень.

Во втором вопросе учащиеся должны, как правило, дать определение фигуры, сформулировать ее свойство или признак, указанный в теореме, и доказать эту теорему.

При ответе на второй вопрос учащиеся должны:

  • дать определение фигуры, включающее в себя как вербальное определение, так и графическое – чертеж;

  • правильно воспроизвести формулировку теоремы, проиллюстрировав ее выполнением чертежа по условию теоремы;

  • привести доказательство теоремы, при этом доказательство считается выполненным верно, если учащийся правильно привел схему доказательства, обосновал все логические шаги, выполнил чертежи, которые правильно отражают, кроме условия, еще и ход доказательства.

Практическая часть. Третий вопрос билета – задача. Цель включения этих заданий – проверка овладения учащимися основными практическими умениями, полученными в ходе изучения курса, эти задачи соответствуют уровню базовой подготовки.

С помощью заданий третьих вопросов проверяются знание и понимание важных элементов содержания (геометрических понятий, свойств основных фигур, отношений между фигурами, методов доказательств и пр.), владение основными формулами, умение применять полученные знания к решению геометрических задач. При выполнении этих заданий учащиеся также должны продемонстрировать определенную системность знаний и широту представлений, узнавать стандартные задачи в разнообразных формулировках.

Время подготовки выпускника. Система оценивания ответа.

Примерное время, отводимое на подготовку выпускника к ответу, – 20–30 минут.

Оценивание ответа осуществляется по традиционной пятибалльной шкале. Ученик у доски отвечает на теоритические вопросы, дополняя свой ответ необходимыми чертежами и записями. Далее на доске рассматривается подробное решение задач, с ссылками на все используемые факты.

Критерии оценивания:

Отметка 5 (отлично) – ставится за полный, логически обоснованный ответ на все три вопроса билета.

Отметка 4 (хорошо) – выставляется за обоснованный полный ответ, но с допущением 1-2 негрубых недочетов на 1-2 вопросы с доказательством и решение задачи;

Отметка 3 (удовлетворительно) – ставится за решение задачи и правильно сформулированные теоремы, свойства, определения первого и второго вопросов (без доказательства).

Отметка 2 (неудовлетворительно) – выставляется во всех остальных случаях.

  1. Вопросы без доказательства:

  1. Сформулируйте определение многоугольника. Элементы многоугольника. Виды многоугольников. Сформулировать теорему о сумме углов выпуклого многоугольника.

  2. Сформулируйте определение трапеции. Виды трапеции.Сформулируйте свойства равнобедренной трапеции.

  3. Сформулировать определение квадрата и перечислить все его свойства.

  4. Приведите формулы площадей ромба, квадрата, параллелограмма, трапеции. Для ромба приведите несколько формул.

  5. Сформулируйте определение подобных треугольников. Сформулируйте признаки подобия треугольников.

  6. Сформулируйте теорему Фалеса. Начертите чертеж.

  7. Сформулируйте утверждения о пропорциональных отрезках в прямоугольном треугольнике.

  8. Сформулируйте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Запишите основное тригонометрическое тождество.

  9. Сформулируйте определение окружности. Взаимное расположение прямой и окружности. Сформулируйте определение касательная к окружности и свойство касательной.

  10. Сформулируйте свойство отрезков касательных, проведенных из одной точки.

  11. С формулируйте формулу нахождения величины угла между пересекающимися хордами через дуги окружности.

С формулируйте формулу нахождения величины угла между секущими, пересекающимися вне окружности 

  1. Назовите формулу Герона. В каких случаях данную формулу применяют?

  2. Назовите значение синуса, косинуса и тангенса для углов 30 , 45 , 60 .

  3. Сформулируйте определения центрального угла окружности и угла, вписанного в окружность. Сформулируйте теорему об измерении вписанного угла и следствия из нее.

  4. Сформулируйте условия, когда в четырехугольник можно вписать окружность и условие, когда около четырехугольника можно описать окружность.

  1. Вопросы с доказательством

  1. Сформулируйте определение параллелограмма. Сформулируйте признаки параллелограмма и докажите один признак по выбору.

  2. Сформулируйте определение параллелограмма. Сформулируйте и докажите свойства углов и сторон параллелограмма.

  3. Сформулируйте определение параллелограмма. Сформулируйте и докажите свойство диагоналей параллелограмма.

  4. Сформулируйте определение ромба. Сформулируйте и докажите свойство диагоналей ромба.

  5. Сформулируйте определение прямоугольника. Сформулируйте и докажите свойство диагоналей прямоугольника.

  6. Приведите формулы площади прямоугольника и площади параллелограмма. Выведите одну из формул по выбору.

  7. Запишите формулу площади треугольника и докажите теорему площади треугольника. Сформулируйте теорему об отношении площадей двух треугольников, имеющих по равному углу.

  8. Выведите формулу площади трапеции.

  9. Сформулируйте определение прямоугольного треугольника. Сформулируйте и докажите теорему Пифагора.

  10. Сформулируйте определение подобных треугольников. Докажите теорему об отношении площадей подобных треугольников.

  11. Сформулируйте определение средней линии треугольника. Сформулируйте и докажите теорему о средней линии треугольника.

  12. Сформулируйте определение касательной к окружности. Сформулируйте и докажите свойство касательной к окружности.

  13. Сформулируйте и докажите теорему об отрезках пересекающихся хорд.

  14. Сформулируйте определение окружности, вписанной в многоугольник. Сформулируйте и докажите теорему об окружности, вписанной треугольник. Каким свойством обладают стороны четырехугольника, описанного около окружности?

  15. Сформулируйте определение окружности, описанной около многоугольника. Сформулируйте и докажите теорему об окружности, описанной около треугольника. Каким свойством обладают углы четырехугольника, вписанного в окружность?

  1. Задача.

Задачи из образовательного портала по подготовке к экзаменам «РЕШУ ОГЭ»:

16.Треугольники, четырехугольники, многоугольники и их элементы

  • Многоугольники

  • Параллелограмм

  • Ромб

  • Трапеция

17.Окружность, круг и их элементы

  • Касательная, хорда, секущая, радиус

  • Окружность, описанная вокруг многоугольника

  • Центральные и вписанные углы

18.Площади фигур

  • Квадрат

  • Прямоугольник

  • Трапеция

  • Параллелограмм

 19.Фигуры на квадратной решётке

  • Многоугольники

  • Параллелограмм

  • Ромб

  • Трапеция

5

Источник

Сведения

об анализе по итогам проведения диагностической контрольной работы

за 20-21 учебный год

по предмету геометрия

8 классы

            Педагог: Штарк М.В. Дата: 17.09.21.

      Цель: анализ результатов дистанционного обучения в 7 классе, планирование работы по восполнению пробелов в течение 21-22 учебного года

 
Предмет

Писал

Макс балл

Процентное содержание баллов суммативного оценивания

% качества

% успеваемости

низкий

средний

высокий

0-39%

40-84%

85-100%

1

2

3

4

5

6

7

8

Количество учеников

8 а

25

20

5

11

7

28

80

8 б

19

20

3

11

4

21

84

8 в

17

20

2

11

4

24

88

8 г

21

20

3

11

6

29

86

8 д

15

20

3

8

4

27

80

Проверяемые ц проверяемые цели обучения

Цели, вызвавшие затруднения

7.1.2.1. знать и применять аксиомы расположения точек на прямой и на плоскости (аксиома порядка);

7.1.1.10. доказывать и применять свойства вертикальных и смежных углов;

7.1.1.12. знать определение медианы, биссектрисы, высоты, треугольника и изображать их;

7.1.1.22. применять признаки равенства треугольников при решении задач на вычисление и на доказательство;

7.1.2.5. применять признаки параллельности прямых при решении задач;

7.1.1.17. применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач;

7.1.1.20. знать соотношение между сторонами и углами треугольника и применять его при решении задач;

7.1.2.14. знать определения окружностей, вписанной в треугольник и описанной около треугольника;

7.1.2.7. применять свойства параллельных прямых при решении задач;

7.1.1.27. применять свойства прямоугольного треугольника;

7.1.1.19. применять теорему о внешнем угле треугольника.

7.1.1.17. применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач;

7.1.1.20. знать соотношение между сторонами и углами треугольника и применять его при решении задач;

7.1.2.7. применять свойства параллельных прямых при решении задач;

7.1.1.27. применять свойства прямоугольного треугольника;

7.1.1.19. применять теорему о внешнем угле треугольника.

1. Анализ результатов СОР и СОЧ показал следующий уровень знаний
у обучающихся:

      высокий (В): 85-100%:

8 «А»: Азизова Дильназ, Видякина Ирина, Лезина Анастасия, Ингамджанова Мадина, Жумабек Айым, Ержан СамИр, Саимова Амина;

8 «б»: Асанхан Темирлан, Иминжанова Анель, Матыкеева Әйгірим, Сарсенбек Еркебулан;

8 «В»: Бегалиев Алан, Лобкова Мария, , Ильясов Турсунжан, Исраилова Медина;

8 «Г»: Скворцова Лидия, Тохтахунова Марьям, Алаев Ибрахим, Бычкова Ольга, Мансуров Джалил, Ячменев Руслан;

8 «Д»: Ганиев Муслим, Ахунбаев Абдурасул, Махмутов Алымжан, Спесивцев Денис.

              низкий (Н): 0-39%:

8 «А»: Ниязов Махир, Нариков Нуралы, Прудаев Артем,Пильгук Матвей.

8 «Б»:Ахметжанова Ильзира, Семетова Амира , Джумаш Ерасыл;

8 «В»: Исламов Ислам, Мираев Ильхам;

8 «Г»: Бурова Александра, Кошкаров Константин, Бычкова Ольга;

8 «Д»: Исламова Зарина, Ниязов Муса, Сеитова Азиза.

средний (С): 40-84%: остальные ученики.

—

      2. Перечень затруднений, которые возникли у обучающихся при выполнении заданий:

учащиеся затрудняются в выборе алгоритма действий, сокращают дроби, не выполняя разложения на множители, допускают ошибки при вычислениях

      3. Причины, указанных выше затруднений у обучающихся при выполнении заданий: учащиеся затрудняются в применении свойств центральных, вписанных углов; затрудняются в применении специфических и общих свойств треугольников при решении задач.

Учащиеся не уделяют достаточного внимания на сознательное заучивание теоретического материала, формул и правил, самые слабые ученики не понимают материал или не распознают правило, которое необходимо применить, не могут выполнять задания самостоятельно, допускают ошибки при выполнении задания по образцу. Отдельные учащиеся недостаточно тщательно анализируют условие задачи, знают геометрические понятия, но необоснованно применяют их при решении задач.

      4. Планируемая коррекционная работа: рассмотреть теорию с помощью наглядных, практических и занимательных задач показать применение геометрии в жизни человека на уроках до 21.05.22 года.

Рассмотреть достаточное число устных задач, задач на готовых чертежах во время 5-тиминутного повторения на уроках, использовать индивидуальные задания для слабых учащихся, организовать способы помощи и поддержки слабых учеников со стороны учителя и других учеников, осуществлять дифференцированный подход к сильным учащимся.

Проверяемые цели

Хорошо

усвоили классы

Необходимо

повторить со всем классом

7.1.2.1. знать и применять аксиомы расположения точек на прямой и на плоскости (аксиома порядка);

8а, 8б, 8г, 8д

8в

7.1.1.10. доказывать и применять свойства вертикальных и смежных углов;

8а, 8б, 8в, 8г

8д

7.1.1.12. знать определение медианы, биссектрисы, высоты, треугольника и изображать их;

8а, 8б, 8в, 8г

8д

7.1.1.22. применять признаки равенства треугольников при решении задач на вычисление и на доказательство;

8а, 8б, 8в, 8г, 8д

—

7.1.2.5. применять признаки параллельности прямых при решении задач;

8а, 8в, 8г

8д, 8б

7.1.1.17. применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач;

8а, 8б

8д, 8г, 8в

7.1.1.20. знать соотношение между сторонами и углами треугольника и применять его при решении задач;

8в

8д, 8б, 8в, 8г

7.1.2.14. знать определения окружностей, вписанной в треугольник и описанной около треугольника;

7.1.2.7. применять свойства параллельных прямых при решении задач;

8б, 8в, 8г

8д, 8а

7.1.1.27. применять свойства прямоугольного треугольника;

—

8а, 8б, 8в, 8г

7.1.1.19. применять теорему о внешнем угле треугольника

—

8а,8д, 8б, 8в, 8г

Использованы методические рекомендации для учителя математики «Организация работы по восполнению пробелов в званиях учащихся» ведущих учителей РК

Источник

Совершенствование учебного процесса породило в последние годы новую форму проверки знаний обучающихся – зачеты по предметам. Зачёт – это форма контроля знаний, умений и навыков. Любой контроль должен быть направлен на проверку планируемых результатов обучения, тех знаний и умений, которые учащиеся должны усвоить в рамках данной темы (раздела или курса), а также уровня усвоения этих знаний и умений.

Зачеты составляют главное в зачетной системе, её ядро, но не исчерпывают её. Зачетная система характеризуется следующими признаками:

  • программный материал по предмету делится на определённое число зачетных разделов;
  • каждый зачетный раздел представляет собой этап в формировании знаний и умений учащихся;
  • проверка знаний и умений, учащихся по зачетному разделу осуществляется путём проведения зачетов, которые сочетаются с текущим учетом знаний на уроке;
  • каждому зачету предшествует специальная, целенаправленная подготовка учащихся на уроках, консультациях и в процессе самостоятельной домашней работы;

Материал для зачёта может быть представлен в следующих формах:

  • в виде математического диктанта;
  • теста;
  • контрольной работы;
  • решения практических задач;
  • собеседования по вопросам и т. д.

На протяжении последних 3-х лет своей педагогической деятельности использую зачетный метод. Ввожу его уже в конце первого полугодия в седьмом классе, когда геометрия только начинает изучаться как учебный предмет. Зачетная система представляет сочетание текущей проверки знаний, умений и навыков каждого ученика с зачетом по основным темам курса геометрии.

Я выбрала такой вид зачёта как тематический. Он проводится в конце изучения темы и направлен на проверку усвоения материала в целом. В начале изучения темы я вывешиваю в классе список задач, отвечающих уровню обязательной подготовки по данной теме, подчёркивая, что подобные им необходимо будет решать на зачёте. Объем зачёта рассчитан, чаще всего, на один урок.

Зачётная система предполагает трехбалльную систему оценки: “отлично”, “хорошо”, “удовлетворительно” (при неудовлетворительной отметке обучающиеся допускаются к повторной сдаче зачёта). Зачёт, не сданный по уважительной причине, может быть сдан в удобное для учителя и учащихся время. Оценки, полученные за зачёты, выставляются в классный журнал и в “Зачётную книжку учащегося”.

Однако зачётная система не отменяет использования и текущих оценок за различные виды контроля знаний. В зачётный материал должны быть включены все три элемента контроля: вопросы для проверки теоретических знаний, типовые задачи и практические задания.

В зачёте две части: обязательная (базовая) и дополнительная. Обязательная часть предусматривает применение знаний в знакомой ситуации, выполнение простых вычислений и решение задач по известному образцу. Дополнительная часть включает в себя набор из нескольких задач различного уровня сложности. В зависимости от своего уровня подготовки ученик сам выбирает, какие задачи ему решать. Причем сам ребенок решает: решить ему простую задачу или сложную. Возможно, среди предложенных задач он встретит подобные тем, что были решены на уроках ранее. Итоги проверки позволяют сделать анализ успешности усвоения основных элементов знаний и приобретения умений всеми учащимися класса.

Главный результат введения зачетной системы — её влияние на усвоение учащимися программного материала: более глубокое, осознанное усвоение учебного материала; объективность проверки знаний, т. к. итоговые оценки становятся более весомыми, точнее отражают действительный уровень знаний учащихся.

Работа в “зачетной системе” предъявляет повышенные требования к уровню знаний учащихся и к их самостоятельности. Учащиеся должны уметь систематизировать довольно значительный по объёму материал зачетного раздела, вычленять в нём главное, уметь использовать при подготовке к зачету, помимо учебника, и другие источники знаний — всё это создаёт необходимые условия для повышения качества знаний, изменить структуру урока.

Анализ результатов зачётной системы выявил её достоинства и недостатки. Зачётная система применялась на уроках геометрии в качестве контроля знаний по отдельным темам. Учитывая специфику предмета можно назвать следующие достоинства:

  1. Большая самостоятельная работа учащихся при подготовке к зачётам.
  2. Вырабатываются навыки работы с учебной литературой.
  3. Индивидуальный подход к каждому учащемуся. Проверка знаний, умений и навыков каждого ученика.
  4. Стремление учеников получить наиболее высокую оценку за зачёт, так как она сильно влияет на четвертную оценку.
  5. Качество знаний увеличивается постепенно.
  6. Проведение зачетов даёт возможность оценить конкретные знания и умения ученика по каждой теме, указать на пробелы, дать возможность их устранить.
  7. Работа на зачетах в строго регламентированных временных рамках, заставляет учеников ценить предоставленное время, сразу включаться в работу. На зачетах нет времени на раскачку, на разговоры, на подсказки. Зачеты составлены таким образом, что для того, что бы получить максимальный бал, ученик должен выложиться полностью, показав тем самым, что его предварительная работа была очень серьёзной.
  8. Списанных работ намного меньше, чем при обычной проверке, когда в контрольной работе только два варианта.

После проведения зачета и анализа результатов на следующем уроке разбираются вопросы, вызвавшие максимальное затруднение, решаются задачи. Через урок проводится контрольная работа. Надо отметить, что после сдачи зачета и проведения его анализа результаты контрольной работы начинают радовать. Ведь уже сами ученики знают, на что надо обратить внимание еще раз, а какие моменты уже отработаны до автоматизма.

Ниже приведу примеры зачетов, проведенных мною в 8 классах по геометрии.

Зачёт в 8 классе по теме «Площади»

Учащиеся вытягивают билеты с вопросами. Время на письменный ответ – 15 мин.

  • Площадь прямоугольника.
  • Площадь параллелограмма.
  • Площадь треугольника.
  • Площадь ромба.
  • Площадь трапеции.
  • Теорема Пифагора.

Ответ должен содержать: чертеж, формулы для нахождения площади указанной фигуры и доказательство теоремы.

I уровень сложности

1) В треугольнике ABC A = 30°, АВ = 10 см, АС = 12 см. Найти Sabc.

2) Найти S ромба, если d1 = 12 cм, d2 =16 cм. Найти его высоту, если сторона равна 10 см.

3) Стороны параллелограмма равны 6 см и 15 см, высота, проведенная к меньшей стороне – 10 см. Найти вторую высоту.

4) В прямоугольнике диагональ равна 13 см, одна из сторон 12 см. Найти Sпр.

5) Найти S равнобедренного треугольника, если его боковая сторона равна 6см, а угол при основании – 30°.

6) Основания трапеции относится как 2 : 3, высота – 6см, Sтр = 60 см2. Найти основания.

7) Одна из боковых сторон трапеции перпендикулярна основаниям, длины которых 6 см и 8 см. Найти S трапеции, если один из её углов равен 45°.

8) Найти наименьшую высоту треугольника со сторонами 17 см, 65 см, 80 см.

II уровень сложности.

1) Стороны двух квадратов 8 см и 16 см. Найти сторону и диагональ квадрата, площадь которого равна сумме площадей двух квадратов.

2) В треугольнике ABC A = 45°, АВ = 10 см, высота AD делит СВ на СВ = 8 см и DB = 6 см. Найти SАВС и высоту, проведенную к АВ.

3) Найти hc если а = 30 см, b = 25 см, с = 11 см.

4) Равнобокая трапеция, тупой угол равен 135°, меньшее основание 4 см, а высота 2 см. Найти S трапеции.

5)Найти наибольшую высоту треугольника со сторонами 13 см, 14 см, 15 см.

III уровень сложности.

1) Найти S треугольника, если его высота равна 36 см, а боковые стороны 85 см и 60 см.

2) Найти Sтр, если её основания 6 см и 18 см, боковая сторона, образующая с большим основанием угол, равный 60°, равна 6 см.

3) Найти S ромба, если его сторона 5 см, а большая диагональ 8 см.

4) Найти наименьшую высоту треугольника со сторонами 5 см, 5 см, 6 см.

Зачёт в 8 классе по теме «Четырёхугольники»

  1. Доказать свойство параллелограмма о диагоналях
  2. Доказать свойство параллелограмма об углах и сторонах.
  3. Доказать признак параллелограмма о сторонах.
  4. Доказать признак параллелограмма о сторонах и углах.
  5. Доказать признак параллелограмма о диагоналях.
  6. Доказать теорему об углах равнобедренной трапеции.
  7. Доказать теорему о диагоналях равнобедренной трапеции
  8. Доказать свойство диагоналей прямоугольника.
  9. Доказать признак прямоугольника о диагоналях.
  10. Доказать признак ромба о диагоналях.
  11. Доказать признак квадрата о диагоналях.
  12. Доказать свойство ромба о диагоналях
  13. Доказать признак квадрата о диагоналях.

Задачи:

  1. В параллелограмме АВСД точка О- точка пересечения диагоналей. ВД =12 см, АД=8 см, АО= 7 см. Найдите периметр треугольника ВОС.
  2. Дано: АВСД – параллелограмм; ВЕ – биссектриса угла АВС;
    Найти: углы параллелограмма.
  3. Угол ромба равен 32°. Найдите углы, которые образует его сторона с диагоналями.
  4. Сторона ромба в 2 раза больше перпендикуляра, проведённого к ней из вершины тупого угла. Найдите углы ромба.
  5. Дано: АВСД – прямоугольник; АС и ВД – диагонали, т. О – точка пересечения диагоналей. Найти: САД, ВДС.
  6. Дано: АВСД – прямоугольник. АС и ВД – диагонали, т. О- точка пересечения диагоналей. АДВ : СДВ=4 : 5. Найти: углы треугольника АОВ.
  7. Сторона ромба образует с его диагоналями углы, один из которых в 4 раза больше другого. Найдите углы ромба.
  8. Диагонали ромба образуют с его стороной углы, один из которых на 50° меньше другого. Найдите углы ромба.
  9. В прямоугольнике АВСД биссектриса угла А образует с диагональю АС угол 20°. Найдите угол между диагоналями прямоугольника.
  10. Дано: АВСД – параллелограмм. АС и ВД – диагонали пересекаются в точке О. Периметр АОВ равен 17 см, ВС= 9 см, СД =6 см. Найти периметр АОД.
  11. Дано: АВСД – параллелограмм. АС и ВД – диагонали пересекаются в точке О. Периметр СОД равен 24 см, ВС= 12 см, периметр АОД равен 28 см. Найти периметр АВСД.
  12. Биссектриса одного из углов прямоугольника делит большую сторону пополам. Найдите периметр прямоугольника, если его меньшая сторона 12 см.
  13. Найдите периметр ромба, если один из углов ромба равен 60°, а меньшая диагональ 18 см.
  14. Периметр прямоугольника 96 см. Найдите его стороны, если они относятся, как 1 : 3.
  15. Сторона ромба равна 12 см, а угол 150° . Найдите расстояние между его противолежащими сторонами.
  16. В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках M и N. Найдите угол АNВ, если угол АМС равен 120°.
  17. Через точку пересечения диагоналей квадрата проведены две взаимно перпендикулярные прямые. Докажите, что точка пересечения этих прямых со сторонами квадрата являются вершинами еще одного квадрата.
Источник

Муниципальное общеобразовательное бюджетное учреждение

«Якутская городская национальная гимназия им. А.Г. и Н.К. Чиряевых»

ГО «город Якутск»

Методическое пособие для проведения устного экзамена по геометрии

Автор: Габышевой Ольги Ксенофонтовны

                 2021 г.

Предисловие

Данное методическое пособие предназначено для учителей математики как общеобразовательных школ, так и в школах с углубленным изучением математики при работе с любым учебником.

О проведении экзамена по геометрии в 7-11 классах

Цель: проверка уровня предметной компетентности учащихся за курс 7-11 класса по геометрии в рамках проведения переводной аттестации.

Отличие геометрии от всех других общеобразовательных предметов состоит в том, что ее содержание практически не меняется в течение многих веков и основные цели ее изучения остаются неизменными:

1. Развитие пространственных представлении, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как умение:

  • читать и делать чертежи, необходимые для решения;
  •  выделять необходимую конфигурацию при чтении чертежа;
  • определять необходимость дополнительных построений при решении задач и выполнять их;
  •  различать взаимное расположение геометрических фигур.

2. Формирование и развитие логического мышления, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как владение методами
доказательств, применяемыми при обосновании геометрических утверждений (теорем, лемм, следствий и т. д.), а также при проведении аргументации и доказательных рассуждений в ходе решения задач.

Билеты по геометрии составлены на основе Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования.

В билетах представлен материал, изучаемый в курсе геометрии 7-11класса. Практические задания составлены аналогично заданиям ГИА по математике. Устная форма проведения экзамена выбрана не случайно, именно она позволяет более правильно и глубоко оценить предметные знания и все виды умений (практические, теоретические, интеллектуальные, организационно – коммуникативные), которыми должен владеть учащийся, охватить все изучаемые темы.

Структура экзаменационного билета.

Билеты содержат два вопроса по различным темам курса геометрии 7-11 класса (один теоретический и один практический).

Теоретическая часть. В первом вопросе обучающиеся должны, как правило, дать определение фигуры, сформулировать её свойство или признак, указанный в теореме, и доказать эту теорему.

При ответе на первый вопрос обучающиеся должны:

  • дать определение фигуры, включающее в себя как вербальное определение, так и графическое – чертёж;
  • правильно воспроизвести формулировку теоремы, проиллюстрировав её выполнением чертежа по условию теоремы;
  • привести доказательство теоремы, при этом доказательство считается выполненным верно, если обучающийся правильно привел схему доказательства, обосновал все логические шаги, выполнил чертежи, которые правильно отражают, кроме условия, ещё и ход доказательства.

Практическая часть. Второй  вопрос билета – задача. Цель включения этих заданий – проверка овладения обучающимися основными практическими умениями, полученными в ходе изучения курса.

Целью является проверка уровня сформированности логического мышления или логической интуиции. При выполнении второй части работы обучающиеся должны продемонстрировать умение геометрически грамотно записывать условие (что дано) и заключение (что требуется найти или доказать) задачи, её решение, сопровождая само решение необходимой аргументацией и доказательными рассуждениями. Кроме того, обучающиеся должны показывать умение геометрически грамотно выполнять чертежи.

Ответы на два практических задания билета позволяют судить об уровне сформированности предметной компетентности обучающегося.

Время подготовки учащегося. Система оценивания ответа.

Примерное время, отводимое на подготовку обучающегося к ответу, ‒ 20-25 минут. Оценивание ответа осуществляется по традиционной пятибалльной шкале. В одних случаях устный опрос производится по вопросам теории, а решения задач предъявляются комиссии без комментариев в письменной форме, в других случаях у доски рассматривается подробное решение задач со ссылками на все используемые факты, а теория оценивается по представленным записям. Поэтому и даны общие рекомендации по оцениванию ответов обучающихся.

Отметка «5» ставится, если обучающийся ответил на теоретический вопрос и решил  задачу.

Отметка «4» ставится, если обучающийся ответил на теоретический вопрос не достаточно хорошо и  решил задачу.

Отметка «3» ставится, если обучающийся ответил на теоретический вопрос и ли решил задачу

Во всех остальных случаях ставится отметка «2».

Билеты устного экзамена по геометрии

7 класс

Билет № 1

1. Первый признак равенства треугольников.

2. Отрезок АК – биссектриса треугольника САЕ. Через точку К проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если угол .

Билет № 2

1. Второй признак равенства треугольника.

2. В прямоугольном треугольнике АВС (уголС=90°) биссектрисы CD  и AE пересекаются в точке О. Угол АОС равен 105°. Найдите острые углы треугольника АВС.

Билет № 3

  1. Смежные углы (определение). Теорема о сумме смежных углов.

  2. В треугольнике АВС угол А равен 90°, а угол С на 40° больше угла В. Найдите углы В и С.

Билет № 4

1. Параллельные прямые (определение). Признаки параллельности двух прямых (доказательство одного из них).

2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.

Билет № 5

 1. Теорема о соотношении между сторонами и углами треугольника

 2. Один из углов прямоугольного треугольника равен 60°, а разность                                        гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу.

Билет № 6

          1.Вертикальные углы (определение).  Свойства вертикальных углов.

          2. В треугольнике АВС угол а угол . Высота ВВ1 равна 2 см.

 Найдите АВ.

Билет № 7

1.Третий признак равенства треугольника

2. В треугольнике АВС угол С равен 90°, а угол В равен 35°,CD – высота. Найдите углы треугольника ACD.

Билет № 8

          1. Неравенство треугольника.

2.  В треугольнике АВС угол С равен 90°,  – высота,                             . Найдите угол САВ.

Билет № 9

1. Свойства равнобедренного треугольника (доказательство одного из них).

2. Периметр равнобедренного треугольника равен 50 см, а один из его сторон на 13 см меньше другой. Найдите стороны треугольника.

Билет № 10

1. Внешний угол треугольника (определение). Теорема о внешнем угле  треугольника.

2. В треугольнике АВС угол А равен 50°, а угол В в 12 раз меньше угла С. Найдите углы В и С.

Билет № 11

1. Теорема о свойстве катета, лежащего против угла в 30º.

2. Отрезок AD – биссектриса треугольника АВС. Через точку Dпроведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если угол ВАС равен 72°.

Билет № 12

1. Треугольник (определение). Теорема о сумме углов треугольника.

2. В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5:2. Найдите стороны треугольника.

Билет № 13

1. Признаки равенства прямоугольных треугольников

2. Один из углов, образовавшихся при пересечении двух прямых, на 70° больше другого. Найдите эти углы.

Билеты устного экзамена по геометрии

 8 класс

Билет №1

1. Параллелограмм. Определение, свойства, признаки.

2. В прямоугольном треугольнике гипотенуза равна 24 см, угол А равен 35о. Найдите второй острый угол. Выразите катеты через гипотенузу и угол А.

Билет№2

1. Трапеция. Определение, виды, средняя линия.

2. Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите ВС, если угол ОАВ равен 30о, АВ=5см.

Билет №3

1. Прямоугольник. Определение, свойства, признак.

2. Прямые МА и МВ касаются окружности с центром О в точках А и В. Точка С симметрична точке О относительно точки В. Докажите, что угол АМС равен трем углам ВМС.

Билет№4

1. Ромб. Определение, свойства, признак.

2. Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равна 2,5 м. Найдите высоту дерева.

Билет№5

1. Квадрат. Определение, свойства, признак.

2. Зная , что , найдите косинус и тангенс данного угла.

Билет№6

1. Теорема Пифагора.

2. Через точку А проведены касательные АВ (В — точка касания) и секущая, которая пересекает окружность в точках С и Д. Найдите СД, если АВ = 4см и  АС = 2см.

Билет№7

1. Средняя линия треугольника.

2. Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

Билет№8

1. Свойство медиан треугольника.

2. Меньшая сторона параллелограмма равна 29 см. Перпендикуляр, проведенный из точки пересечения диагоналей к большой стороне, делит ее на отрезки, равные 33 см и 12 см. Найдите площадь параллелограмма.

Билет№9

1. Синус, косинус, тангенс в прямоугольном треугольнике.

2. В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, угол ВАС равен углу САД. Найдите АД, если периметр трапеции равен 20 см, а угол Д равен 60о.

Билет№10

1. Касательная к окружности.

2. Найдите острый угол, образованный двумя секущими, проведенными из точки, лежащей вне окружности, если дуги, заключенные между секущими, равны 140о и 52о.

Билет№11

1. Центральные и вписанные углы.

2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.

Билет№12

1. Вписанная окружность.

2. Диагонали прямоугольной трапеции АВСД с прямым углом А взаимно перпендикулярны. Основание АВ равно 6 см, а боковая сторона АД равна 4см. Найдите ДС, ДВ и СВ.

Билет№13

1. Описанная окружность.

2. Диагональ АС квадрата АВСД равна 18,4 см. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и СД соответственно в точках М и N. Найдите MN.

Билеты устного экзамена по геометрии

9 класс

Билет № 1

1. Первый признак равенства треугольников.

2. Найдите координаты точки  А(х; у), если она симметрична точке В(–20; 11) относительно точки М (0; –5).

Билет № 2

1. Второй признак равенства треугольников.

2. В прямоугольном треугольнике АВС угол  В равен 30°. Вершина прямого угла С соединена отрезком с точкой М, принадлежащей гипотенузе. Угол АМС равен 60°. Докажите, что СМ является медианой треугольника.

Билет № 3

1. Третий признак равенства треугольников.

2. Постройте фигуру, в которую перейдет квадрат АВСD при повороте вокруг точки D по часовой стрелке на угол 45°.

Билет № 4

1. Теорема о сумме внутренних углов треугольника.

2. В треугольнике АВС углы А и С равны. На стороне АС взяты точки D и Е такие, что АD = СЕ. Докажите, что треугольник DВЕ — равнобедренный.

Билет № 5

1. Теорема о сумме углов выпуклого n-угольника.  

2.  В прямоугольных треугольниках АВС и А1В1С1 из вершин прямых углов С и С1 проведены высоты СН и С1Н1; СН = С1Н1, АН = А1Н1. Докажите, что треугольники АВС и А1В1С1 равны.

Билет № 6

1. Теорема о средней линии треугольника.

2. Точки М и М1 симметричны относительно точки А. Точки М1 и М2 симметричны относительно точки В. Докажите, что отрезок ММ2 = 2АВ.

Билет № 7

1. Теорема о средней линии трапеции.

2. Окружность разделена тремя точками на части, которые относятся между собой как 2:3:5. Через точки деления проведены хорды. Определите вид получившегося треугольника.

Билет № 8

1. Теорема Фалеса.

2. В параллелограмме АВСD биссектриса угла А пересекает продолжение ВС в точке Е. Найдите периметр параллелограмма, если ВЕ = 16 см, СЕ = 5 см.

Билет № 9

1. Теорема Пифагора.

2. На отрезке АВ взята произвольная точка С. Через точки А и В проведены по одну сторону от данного отрезка параллельные лучи. На них соответственно взяты точки D и Е таким образом, что АD = АС и ВЕ = ВС. Найдите угол DСЕ.

Билет № 10

1. Теорема синусов.

2. Хорда окружности пересекает ее диаметр под углом 30° и делится им на части, равные 12 см и 6 см. Найдите расстояние от середины хорды до диаметра.

Билет № 11

1. Теорема косинусов.

2.  Даны точки М(–2; 6), К(1; 2) и L(4; –2). Определите, принадлежат ли данные точки одной прямой.

Билеты устного экзамена по геометрии

10 класс

Билет №1.

  1. Сформулируйте аксиомы стереометрии и их следствия. Сделайте чертежи и пояснения.
  2. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 
    10 см. Найдите площадь боковой и полной поверхности призмы.

Билет №2.

  1. Сформулируйте определение параллельности прямой и плоскости. Сформулируйте признак параллельности прямой и плоскости. Сделайте чертежи и пояснения.
  2. В правильной треугольной пирамиде апофема образует с плоскостью основания угол 30º. Сторона основания равна 12 см. Найдите площадь поверхности пирамиды.

Билет №3.

  1. Сформулируйте определение скрещивающихся прямых. Сформулируйте признак скрещивающихся прямых. Сделайте чертежи и пояснения.
  2. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы

Билет №4.

  1. Опишите взаимное расположение прямых в пространстве. Как определяется угол между двумя прямыми в пространстве? Сделайте пояснения и чертежи.
  2. В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 60º. Высота пирамиды равна 6 см. Найдите площадь боковой поверхности пирамиды.

Билет №5.

  1. Перпендикулярность прямой и плоскости. Сформулируйте признак перпендикулярности прямой и плоскости. Сделайте чертежи и пояснения.
  2. Высота правильной четырехугольной пирамиды равна 6 см и образует с боковой гранью угол 30º. Найдите площадь боковой поверхности пирамиды.

Билет №6.

  1. Сформулируйте лемму о параллельных прямых, перпендикулярных третьей. Сделайте чертежи и пояснения.
  2. Через вершину прямого угла К треугольника DKF проведена прямая КМ, перпендикулярная к плоскости этого треугольника. Известно, что КМ = 15 см, 
    FK = DK = 10 см. Найдите расстояние от точки М до прямой DF.

Билет №7.

  1. Сформулируйте лемму о параллельных прямых, пересекающих плоскость. Сделайте пояснения и чертежи.
  2. В правильной треугольной пирамиде боковое ребро образует с плоскостью основания угол 60º. Сторона основания пирамиды равна 8 см. Найдите площадь боковой поверхности пирамиды.

Билет №8.

  1. Сформулируйте определение параллельных плоскостей. Сформулируйте признак параллельности двух плоскостей.
  2. Дан куб ABCDA1B1C1D1. Точки К, М и Т – середины ребер СС1, В1С1 и С1D1соответственно. Найдите АС1, если периметр сечения куба плоскостью КМТ равенhello_html_23d1b532.gifсм.

Билет №9.

  1. Тетраэдр и его элементы. Сделайте чертеж и пояснения..
  2. В правильной треугольной пирамиде сторона основания равна высоте и равна 12 см. Найдите площадь поверхности пирамиды.

Билет №10.

  1. Параллелепипед и его элементы. Сделайте чертеж и пояснения.
  2. Дан куб ABCDA1B1C1D1. Диагональ АС1 равна hello_html_7a22eef.gif.Найдите периметр сечения куба плоскостью РТН, где точки Р, Т и Н – середины ребер ВС, ВВ1 и АВ соответственно.

Билет №11.

  1. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.
  2. Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь полной и боковой поверхности призмы.

Билет №12.

  1. Признак перпендикулярности прямой и плоскости.
  2. Через вершину угла Е прямоугольного треугольника НРЕ с гипотенузой НЕ проведена прямая МЕ, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки М до плоскости ЕРН, если ЕР = 5 см, а расстояние от точки М до прямой РН равно 10.

Билет №13.

  1. Угол между прямой и плоскостью. Приведите примеры величины угла между прямой и плоскостью. Сделайте чертежи и пояснения.
  2. Через вершину прямого угла С равнобедренного треугольника DСЕ проведена прямая СК, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки К до прямой DЕ, если СК = 35 см, CD = hello_html_ma04135b.gif см.

Билет №14.

  1. Признак перпендикулярности двух плоскостей.
  2. Основание прямой призмы – прямоугольный треугольник с гипотенузой 25 см и катетом 20 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.

Билет №15.

  1. Призма и его элементы. Сделайте чертеж и пояснения..
  2. Высота правильной четырехугольной пирамиды равна 16 см, а боковое ребро пирамиды равно 20 см. Найдите площадь боковой поверхности пирамиды.

Билеты устного экзамена по геометрии

11 класс

Билет № 1

1. Перпендикуляр и наклонная. Расстояние от точки до плоскости. Теорема о трех перпендикулярах.

2. Каждый из четырех равных шаров радиуса 6 касается двух других шаров и касается некоторой плоскости. Найдите радиус пятого шара, который касается той же плоскости и каждого из данных четырех шаров.

Билет № 2

1. Цилиндр. Боковая и полная поверхности цилиндра. Объем цилиндра.

2. В прямоугольном параллелепипеде АВСDА1В1С1D1 сечение BDD1B1 – квадрат и образует с сечением ACC1A1 угол 60°. Диагональ параллелепипеда равна  . Найдите объем параллелепипеда.

Билет № 3

1. Параллелепипед. Виды параллелепипеда. Формулы для вычисления объема прямоугольного параллелепипеда и объема наклонного параллелепипеда. Площадь полной поверхности.

2. Ребро правильного тетраэдра равно 1. Первый шар вписан в этот тетраэдр. Второй шар касается вписанного шара и трех граней тетраэдра. Найдите объем второго шара.

Билет № 4

1. Призма. Виды призм. Формулы для вычисления объема прямой призмы и объема наклонной призмы.

2. Высота правильной треугольной пирамиды равна  см, а боковая грань наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности пирамиды.

Билет № 5

1. Пирамида. Виды пирамид. Формула для вычисления объема пирамиды.

2. Найдите угол развертки конуса, осевое сечение которого правильный треугольник.

Билет № 6

1. Цилиндр и его элементы. Объем цилиндра. Формула для вычисления объема цилиндра.

2. Основания наклонной призмы АВСА1В1С1 – правильные треугольники ABC и A1B1C1. Боковое ребро призмы вдвое больше ребра ее основания, а основанием высоты призмы, опущенной из вершины А1 на плоскость АВС, является точка В. Найдите косинус угла между скрещивающимися прямыми АВ и СС1.

Билет № 7

1. Конус и его элементы. Объем конуса. Формула для вычисления объема конуса.

2. Дана правильная треугольная призма АВСА1В1С1. Вершина А1 удалена от прямой ВС на расстояние 5 и от плоскости ВСС1 на расстояние 3. Найдите площадь полной поверхности призмы.

2. Найдите отношение ребра правильного тетраэдра к радиусу шара, описанного около этого тетраэдра.

Билет № 8

1. Векторы в пространстве. Задание вектора. Модуль вектора. Равенство векторов. Определение суммы двух векторов в пространстве.

2. Найдите отношение ребра правильного тетраэдра к радиусу шара, вписанного в этот тетраэдр.

Билет № 9

1. Усеченный конус и его элементы. Площадь боковой поверхности усеченного конуса.

2. Через образующую АВ цилиндра проведены осевое сечение ABCD и сечение ABFH, образующее с плоскостью АВС угол в 30°. Радиус цилиндра равен 5. Найдите расстояние между прямыми AF и CD.

Билет № 10

1. Правильный тетраэдр. Объем правильного тетраэдра.

2. Точка М, равноудаленная от вершин А1, В1, С правильной треугольной призмы АВСА1В1С1, лежит в плоскости АВС. Высота призмы равна ребру ее основания и равна . Найдите объем пирамиды МА1В1С.

Билет № 11

1 . Усеченный конус и его элементы. Объем усеченного конуса.

2. Дан прямоугольный параллелепипед АВСDА1В1С1D1, АВ = 1, AD = 2, AA1 = 3. Точка М лежит на диагонали параллелепипеда и не совпадает ни с одной вершиной параллелепипеда. Докажите, что сумма расстояний от точки М до всех граней параллелепипеда не зависит от ее расположения на диагонали. Найдите эту сумму.

Билет № 12

1. Усеченная пирамида. Виды усеченных пирамид. Формула для вычисления объема усеченной пирамиды.

2. Точки А и В лежат в различных гранях двугранного угла, равного 60°, на расстояниях а и b от ребра t двугранного угла соответственно (а < b). Расстояние между ортогональными проекциями этих точек на ребро t равно d. Найдите АВ.

Источник

Понравилась статья? Поделить с друзьями:
  • Анализ произведения экзамен шукшин
  • Анализ произведения судьба человека шолохова для итогового сочинения
  • Анализ произведения история одного города сочинение
  • Анализ произведений для итогового сочинения 2022
  • Анализ проведенного экзамена