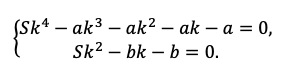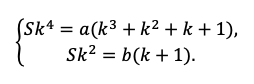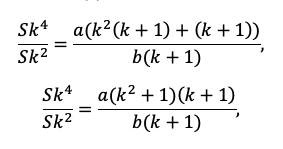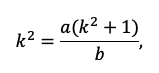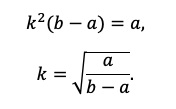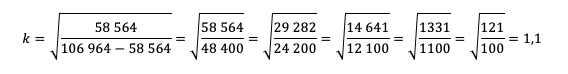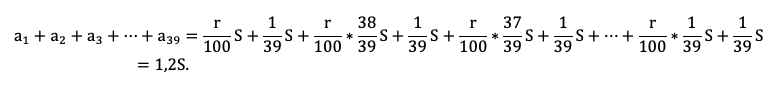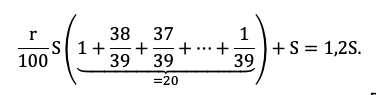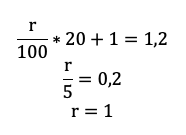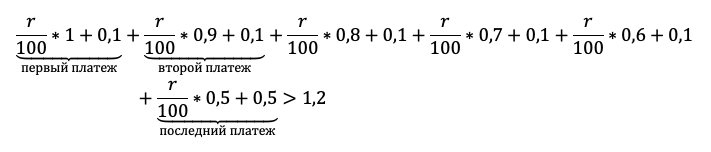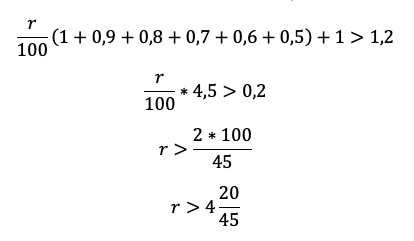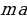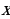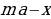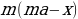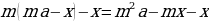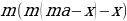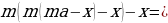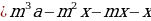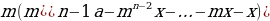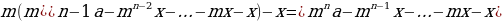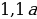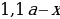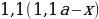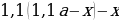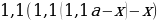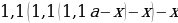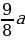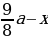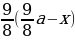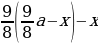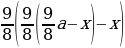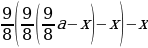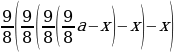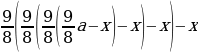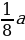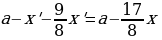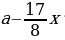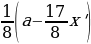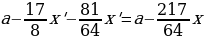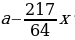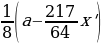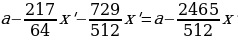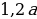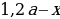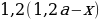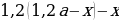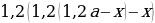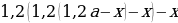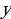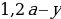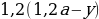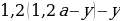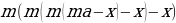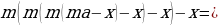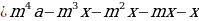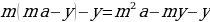Аннуитет егэ математика

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

ГОТОВИМСЯ
К ЕГЭ ПО МАТЕМАТИКЕ                         ЭКОНОМИЧЕСКИЕ ЗАДАЧИ

                                                                                                         
I.           
АННУИТЕТНЫЕ ПЛАТЕЖИ

Определение.

Аннуитетный платёж –
вариант ежемесячного (ежегодного) платежа по кредиту, когда размер ежемесячного
(ежегодного) платежа остается постоянным на всем периоде кредитования..

         При решении экономических задач на
аннуитетные платежи примем следующие обозначения величин:

         Решение задач на аннуитетные платежи удобно оформлять в
виде таблицы. Рассмотрим примеры решения задач.

Задача 1.

В июле 2021 года
планируется взять кредит в банке на некоторую сумму. Условия его возврата
таковы:

§  каждый
январь долг увеличивается на 20% по сравнению с концом предыдущего года;

§  с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Сколько рублей будет
выплачено банку, если известно, что кредит будет полностью погашен тремя
равными платежами (то есть за три года) и общая сумма выплат после полного
погашения кредита на 96500 рублей больше суммы, взятой в кредит?

Решение.

         Пусть S
рублей – сумма кредита,

r = 20 %, тогда p
= 1 + 20/100 = 1,2.

n = 3
года.

х – годовой
платёж,

тогда 3х
– общая сумма платежа за 3 года,

3х – S = 96500.

Заполним таблицу:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	х	р S – х
2	р S – х	p2 S –p х	х	p2 S –p х – х
3	p2 S –p х – х	p3 S –p2 х – pх	x	p3 S –p2 х – pх – x = 0

         В
последней ячейке таблицы мы получили уравнение:

p³
S – p² х – pх – x = 0.

Подставим вместо S выражение 3х – 96500.

p³
∙ (3х –
96500) – p² х – pх – x = 0.

3p³∙ х – 96500 p³–
p² х – pх – x = 0.

Теперь выразим из этого уравнения переменную х:

х
∙ (3p³
– p² – p – 1) = 96500 p³,

х =  = .

3х = .

         Подставив p = 1,2,
получим общую сумму выплат за три года:

3х = 324000
рублей.

Ответ:
324000 рублей.

Задача 2.

В июле планируется
взять кредит в банке на сумму 1 000 000 рублей. Условия его возврата таковы:

§  каждый
январь долг увеличивается на 10% по сравнению с концом предыдущего года;

§  с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

§  ежегодные
выплаты не превышают 300 000 рублей.

На какое минимальное
число рублей сумма выплат может превышать размер кредита?

Решение.

S =
1 000 000 рублей – сумма кредита,

r = 10 %, тогда p
= 1 + 10/100 = 1,1.

Для того, чтобы переплаты были минимальными, нужно,
чтобы сумма ежегодных выплат принимала наибольшую возможную сумму. Поэтому
примем х = 300 000 рублей, за исключением последнего
платежа, сумма которого может быть меньше предыдущих платежей.

Заполним таблицу:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	1        000 000	1,1 ∙ 1 000 000 = =  1 100 000	300 000	1 100 000 – 300 000 = = 800 000
2	800 000	1,1 ∙ 800 000 = =  880 000	300 000	880 000 – 300 000 = = 580 000
3	580 000	1,1 ∙ 580 000 = =  638 000	300 000	638 000 – 300 000 = = 338 000
4	338 000	1,1 ∙ 338 000 = =  371 800	300 000	371 800 – 300 000 = = 71800
5	71 800	1,1 ∙ 71 800 = =  78 980	78 980	78 980 – 78 980 = 0.

         Общая сумма выплат равна:

4 ∙
300 000 + 78 980 = 1 278 980 (рублей).

Наименьшее значение переплат за весь срок кредитования:

1 278 980
– 1 000 000 = 278 980 (рублей).

Ответ:
278 980 рублей

Задача 3 (для самостоятельного решения).

В июле планируется
взять кредит в банке на сумму 1 000 000 рублей. Условия его возврата таковы:

§  каждый
январь долг увеличивается на 20% по сравнению с концом предыдущего года;

§  с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

§  ежегодные
выплаты не превышают 400 000 рублей.

На какое минимальное
число рублей сумма выплат может превышать размер кредита?

Ответ:
526 400 рублей.

Задача 4.

31 декабря 2020 года
Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5 % годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (т.е. увеличивает долг на 14,5 %), затем
Дмитрий переводит в банк х рублей. Какой должна быть сумма х,
чтобы Дмитрий выплатил долг двумя равными платежами (т.е. за два года)?

Решение.

S =
4 290 000 рублей,

r = 14,5%, тогда p
= 1,145.

n = 2 года.

х – годовой
платёж,

Заполним таблицу:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	х	р S – х
2	р S – х	p2 S –p х	х	p2 S –p х – х = 0

В
последней ячейке таблицы мы получили уравнение:

p² S – pх –
x = 0.

Выразим
из этого уравнения х:

p² S – х ∙ (p + 1) = 0,

p² S = х ∙ (p + 1),

х = ,

Подставим
числа, данные в условии задачи, вместо букв S и p:

х =  = 2 622 050.

Ответ:
2 622 050 рублей.

Задача 5 (для самостоятельного решения).

31 декабря 2020 года Алексей
взял в банке 6 902 000 рублей в кредит под 12,5 % годовых. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (т.е. увеличивает долг на 12,5 %), затем Алексей
переводит в банк х рублей. Какой должна быть сумма х,
чтобы Алексей выплатил долг четырьмя равными платежами (т.е. за четыре года)?

Ответ:
2 296 350 рублей.

Задача 6.

31 декабря 2020 года Ярослав
взял в банке некоторую сумму в кредит под 12,5 % годовых. Схема выплаты кредита
следующая: 31 декабря каждого следующего года банк начисляет проценты на
оставшуюся сумму долга (т.е. увеличивает долг на 12,5 %), затем Ярослав
переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав
в банке, если он выплатил долг четырьмя равными платежами (т.е. за четыре
года)?

Решение.

Пусть S рублей
– сумма, взятая в кредит,

r = 12,5%, тогда p
= 1,125.

n = 4 года.

х =
2 132 325 рублей – ежегодные платежи,

Заполним таблицу:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	х	р S – х
2	р S – х	p2 S –p х	х	p2 S –p х – х = 0
3	p2 S –p х – х	p3 S –p2 х – pх	x	p3 S –p2 х – pх – x = 0
4	p3 S –p2 х – pх – x	p4 S –p3 х – p2 х –px	х	p4 S –p3 х – p2 х –px – x = 0

В
последней ячейке таблицы мы получили уравнение:

p⁴ S –p³ х – p² х –px – x = 0.

Выразим
из этого уравнения S:

p⁴
S – х ∙ (p³ + p²
+ p + 1) = 0,

p⁴
S = х ∙ (p³ + p²
+ p + 1),

S = ,

Подставим
числа, данные в условии задачи, вместо букв x и p:

х =  = 6 409 000.

Ответ:
6 409 000 рублей.

Задача 7 (для самостоятельного решения).

В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:

§  каждый
январь долг увеличивается на 10% по сравнению с концом предыдущего года;

§  с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга,
равную 399 300 рублей.

Сколько рублей было
взято в банке, если известно, что кредит был полностью погашен тремя равными
платежами (т.е. за три года)?

Ответ:
993 000 рублей.

Задача 8 (для самостоятельного решения).

В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:

§  каждый
январь долг увеличивается на 20% по сравнению с концом предыдущего года;

§  с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга,
равную 207 360 рублей.

Сколько рублей было
взято в банке, если известно, что кредит был полностью погашен четырьмя равными
платежами (т.е. за четыре года)?

Ответ:
536 800 рублей.

Задача 9.

31 декабря 2020 года
Тимофей взял в банке 7 007 000 рублей в кредит под 20 % годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (т.е. увеличивает долг на 20 %), затем
Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных
платежа. На сколько рублей меньше он бы отдал банку, сели бы смог выплатить
долг за 2 равных платежа?

Решение.

S =
7 007 000 рублей,

r = 20%, тогда p
= 1,2.

n₁ = 3 года,

n₂ = 2 года.

х рублей –
ежегодные платежи.

1)    Заполним
таблицу для n₁ = 3:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	х	р S – х
2	р S – х	p2 S –p х	х	p2 S –p х – х = 0
3	p2 S –p х – х	p3 S –p2 х – pх	x	p3 S –p2 х – pх – x = 0

В последней ячейке таблицы мы получили уравнение:

p³ S – p² х –px – x = 0.

Выразим из этого уравнения переменную х:

p³ S – х ∙ (p²
+ p + 1) = 0,

p³ S = х ∙ (p²
+ p + 1),

х = ,

3х = =  = 9 979 200.

2)    Заполним
таблицу для n₂ = 2:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	х	р S – х
2	р S – х	p2 S –p х	х	p2 S –p х – х = 0

В последней ячейке таблицы мы получили уравнение:

p² S – px – x = 0.

Выразим из этого уравнения переменную х:

p² S – х ∙ (p + 1) = 0,

p² S = х ∙ (p + 1),

х = ,

2х = =  = 9 172 800.

3)    9 979 200
– 9 172 800 = 806 400 (рублей).

Ответ:
806 400 рублей.

Задача 10 (для самостоятельного решения).

31 декабря 2020 года Савелий
взял в банке 7 378 000 рублей в кредит под 12,5 % годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (т.е. увеличивает долг на 12,5 %), затем Савелий
переводит в банк платёж. Весь долг Савелий выплатил за 3 равных платежа. На
сколько рублей меньше он бы отдал банку, сели бы смог выплатить долг за 2
равных платежа?

Ответ:
506 250 рублей.

Задача 11.

В июле планируется
взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:

§  каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;

§  с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Известно, что кредит
был полностью погашен за два года, причём в первый год было переведено
75 000 рублей, а во второй год – 46 000 рублей. Найдите число r.

Решение.

Заполним таблицу:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	75 000	р S – 75 000
2	р S – 75 000	p2 S – 75 000 p	46 000	p2 S – 75 000 p – 46 000 = 0

В последней ячейке таблицы мы получили уравнение:

p²
S – 75 000 p
– 46 000 = 0.

Поскольку
S
= 100 000, то получаем квадратное уравнение:

100 000
p²
– 75 000 p
– 46 000 = 0,

100
p²
– 75 p – 46 = 0,

Положительный
корень этого уравнения равен:

p
= 1,15,

откуда
r
= 15 %.

Ответ:
15 %.

Задача 12 (для самостоятельного решения).

В июле планируется
взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:

§  каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;

§  с февраля
по июнь каждого года необходимо выплатить одним платежом часть долга.

Известно, что кредит
был полностью погашен за два года, причём в первый год было переведено
68 000 рублей, а во второй год – 59 000 рублей. Найдите число r.

Ответ:
18 %.

Задача 13.

Дмитрий взял кредит в
банке на сумму 270 200 рублей. Схема выплаты кредита такова: в конце
каждого года банк увеличивает на 10 % оставшуюся сумму долга, а затем Дмитрий
переводит в банк свой очередной платёж. Известно, что Дмитрий погасил кредит за
три года, причём каждый его следующий платёж был ровно втрое больше
предыдущего. Какую сумму Дмитрий заплатил в первый раз? Ответ дайте в рублях.

Решение.

Заполним таблицу:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	х	р S – х
2	р S – х	p2 S –p х	3х	p2 S –p х – 3х = 0
3	p2 S –p х –3 х	p3 S –p2 х – 3pх	9x	p3 S –p2 х – 3pх – 9x = 0

В последней ячейке таблицы мы получили уравнение:

p³
S –p²
х – 3pх
– 9x = 0.

Выразим из этого уравнения переменную х:

p³
S – х ∙ (p² +
3p + 9) = 0,

p³
S = х ∙ (p² +
3p + 9),

х = ,

х =  = 26 620.

Ответ:
26 620 рублей.

Задача 14 (для самостоятельного решения).

Георгий взял кредит в
банке на сумму 270 200 рублей. Схема выплаты кредита такова: в конце
каждого года банк увеличивает на 10 % оставшуюся сумму долга, а затем Георгий
переводит в банк свой очередной платёж. Известно, что Георгий погасил кредит за
три года, причём каждый его следующий платёж был ровно вдвое меньше
предыдущего. Какую сумму Георгий заплатил в третий раз? Ответ дайте в рублях.

Ответ:
133 100 рублей.

Задача 15.

В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:

§  каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;

§  с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Известно, что если
каждый год выплачивать по 292 820 рублей, то кредит будет  полностью
погашен за четыре года, а если ежегодно выплачивать по 534 820 рублей, то
кредит будет полностью погашен за два года. Найдите число r.

Решение.

Пусть S рублей –
сумма кредита,

n₁ = 4 года, при этом
х = 292 820 рублей – ежегодные платежи,

n₂ = 2 года,
при
этом у = 534 820 рублей – ежегодные платежи.

1)    Заполним
таблицу для n₁ = 4:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	х	р S – х
2	р S – х	p2 S –p х	х	p2 S –p х – х = 0
3	p2 S –p х – х	p3 S –p2 х – pх	x	p3 S –p2 х – pх – x
4	p3 S –p2 х – pх – x	p4 S –p3 х – p2х – px	x	p4 S –p3 х – p2х – px – x = 0

2)    Заполним
таблицу для n₂ = 2:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	р S	у	р S – у
2	р S – у	p2 S –p у	у	p2 S –p у – у = 0

В последних ячейках таблиц мы получили два уравнения:

p⁴ S –p³ х – p²х – px – x = 0       и      p² S –p у – у = 0.

Умножим второе уравнение на p², а затем
вычтем из него первое уравнение:

(p³ у – p³ х) + (p² у – p² х) – (pх + х) =
0,

p³ (у – х) +
p² (у – х) –
х (p + 1) = 0,

p² (у – х) (p + 1) = х
(p + 1).

Поскольку p – число
положительное, то число (p + 1) – также
является положительным числом. Поэтому обе части уравнения можно разделить на
(p + 1).

p² (у – х) =
х,

p² = ,

p² = = 1,21.

p = 1,1.

Значит,
r
= 10 %.

Ответ:
10 %.

Задача 16 (для самостоятельного решения).

В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:

§  каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;

§  с февраля
по июнь каждого года необходимо выплатить одним платежом часть долга.

Известно, что если
каждый год выплачивать по 216 000 рублей, то кредит будет  полностью
погашен за четыре года, а если ежегодно выплачивать по 366 000 рублей, то
кредит будет полностью погашен за два года. Найдите число r.

Ответ:
20 %.

Задача 17.

Планируется выдать
льготный кредит на целое число миллионов рублей на пять лет. В середине каждого
года действия кредита долг заёмщика возрастает на 10 % по сравнению с началом
года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по
кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го
годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью.
Найдите наибольший размер кредита (в млн. рублей), при котором общая сумма
выплат заёмщика будет меньше 8 млн. рублей.

Решение.

r = 10%, тогда p
= 1,1.

Заполним
таблицу:

Год	Долг до начисления процентов (млн. руб.)	Долг после начисления процентов (млн. руб.)	Выплаты (млн. руб.)	Долг после выплаты (млн. руб.)
1	S	р S	р S — S	S
2	S	р S	р S — S	S
3	S	р S	р S — S	S
4	S	р S	x	р S – x
5	р S – x	p2х – px	x	p2х – px – x = 0

1)    Рассмотрим
уравнение в последней ячейке таблицы:

p²х
– px – x = 0.

         Выразим
из этого уравнения х:

p²х
– х (p +1) = 0,

p²х
= х (p +1),

х
=  =
 = .

2)   
Общая сумма выплат равна:

3
∙
(р S – S) + 2х
= 3 ∙ (р
S – S) + 2S ∙  = S ∙
(3p – 3 + 2 ∙ ) = … = S ∙ .

         По
условию, эта сумма меньше 8 млн. рублей, тогда

S
∙  < 8,

S
 < ≈ 5,508…

         При
этом S – целое
число миллионов рублей. Значит, S = 5 (млн. рублей).

Ответ:
5 млн. рублей.

Задача 18 (для самостоятельного решения).

Планируется выдать
льготный кредит на целое число миллионов рублей на пять лет. В середине каждого
года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом
года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по
кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го
годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью.
Найдите наименьший размер кредита (в млн. рублей), при котором общая сумма
выплат заёмщика превысит 10 млн. рублей.

Ответ:
6 млн. рублей.

Задача 19.

Гражданин Гусев взял
кредит в банке, рассчитывая погасить долг равными ежегодными платежами, каждый
из которых (кроме, возможно, последнего) составляет половину суммы S,
взятой в кредит. Схема выплаты кредита следующая: в конце каждого года банк
увеличивает на 25 % оставшуюся сумму долга, а затем гражданин Гусев переводит в
банк очередной платёж. После двух лет выплат банк снизил процентную ставку до
20 % годовых, и гражданин Гусев внёс третий платёж. Четвёртым платежом долг был
полностью погашен. Сколько процентов от первоначальной суммы S
составлял четвёртый платёж по кредиту гражданина Гусева?

Решение.

r₁ = 25%, тогда p₁ = 1,25.

r₂ = 20%, тогда p₂ = 1,2.

Заполним
таблицу:

Год	Долг до начисления процентов (руб.)	Долг после начисления процентов (руб.)	Выплаты (руб.)	Долг после выплаты (руб.)
1	S	1,25 S	0,5 S	1,25 S – 0,5 S = 0,75 S
2	0,75 S	1,25 ∙ 0,75 ∙ S = = 0,9375 ∙ S	0,5 S	0,9375 ∙ S – 0,5 ∙ S = = 0,4375 ∙ S
3	0,4375 ∙ S	1,2 ∙ 0,4375 ∙ S = 0,525 ∙ S	0,5 S	0,525 S — 0,5 S = = 0,025 S
4	0,025 S	1,2 ∙ 0,025 ∙ S = = 0,03 ∙ S	0,03 ∙ S	0,03 ∙ S – 0,03 ∙ S = 0

 = 0,03 = 3 %.

Ответ:
3 %.

Я – репетитор по информатике и математике! Давайте знакомиться

Приветствую вас на своем персональном сайте! Меня зовут Александр Георгиевич. Уже более (10) лет я являюсь профессиональным репетитор по информатике, математике, программированию, базам данных и алгоритмам.

Хочу познакомить вас с основными направлениями своей профессиональной деятельности:

1. Подготовка школьников (9-11) классов для успешной сдачи ОГЭ и ЕГЭ по математике и информатике.

2. Обучение студентов из всех вузов России востребованным и актуальным языкам программирования, таким как С («чистый» СИ), С++, C#, Pascal.

3. Реализация под заказ всевозможных проектов по информатике: рефератов, контрольных, лабораторных, курсовых и дипломных работ.

4. Подготовка к олимпиадам различного уровня сложности наиболее подкованных школьников и студентов.

5. Консультирование школьников (11) класса, у которых появляются сомнения относительно вуза, куда они хотят поступить, чтобы получить наиболее качественные знания за приемлемые деньги.

Я прекрасно понимаю, что вы предельно занятой человек, но, несмотря на это, я настоятельно рекомендую вам потратить (2-3) минуты собственного времени и внимательно ознакомиться с отзывами клиентов, прошедших под моим контролем фундаментальную подготовку. Все они достигли поставленных целей! Чем вы хуже? Думаю, что ничем!

Все люди по-своему уникальны, у каждого сформировано собственное мировоззрение, поэтому специально для своих потенциальных учеников-клиентов я разработал мощную параметрическую систему, которая предлагает вам на выбор (144) варианта стоимости моих услуг. Обещаю, что вы (100%) сумеете подобрать для себя вариант, полностью отвечающий всем вашим текущим запросам.

Хотите научиться решать задачи из раздела «Финансовая математика»? Хотите фундаментально понять квинтэссенцию модели аннуитетного платежа? Тогда берите сотовый телефон, набирайте мой контактный номер и записывайтесь на первый пробный урок.

И не забывайте, что я достаточно востребованный репетитор, у которого плотное расписание. Поэтому в обязательном порядке загляните на страницу моего графика проведения индивидуальных уроков.

Не откладывайте решение в долгий ящик – записывайтесь ко мне на частную подготовку прямо сейчас! Еще осталось несколько вакантных мест для учеников. Завтра эти места уже могут быть заняты.

Минимальные знания про банковский кредит

Чтобы не было привязки к конкретному моменту времени, я не буду сейчас, в момент создания данной статьи, сообщать, какой на дворе стоит год. Но достоверным фактом является то, что раньше официальный экзамен – ЕГЭ по математике не содержал категории, ориентированной на «Финансовую математику».

Школьная образовательная система диктует (11)-классникам, что просто необходимо на качественном уровне разбираться с такими понятиями, как кредит, вклад, схема платежа.

Банковский кредит – сумма денег, получаемая заемщиком от банка на временное пользование под определенный процент.

Количество банков на территории РФ исчисляется тысячами, причем ежеквартально банкротятся десятки банков, а место разорившихся занимают новые, свежеиспеченные финансовые структуры.

Абсолютно любые кредитные деньги характеризуется процентным начислением. Это называется процентная ставка банка. В современном мире средневзвешенное значение процентных ставок на выдаваемые кредиты колеблется в диапазоне от (12) до (20%).

Также любая ссуда/кредит должна быть полностью погашена за определенный период времени. Это называется срок погашения кредита. Выплаты заемщиком проводятся еженедельно, ежемесячно, ежеквартально, ежегодно и т. п.

Неискушенный потребитель легко может неправильно посчитать, что обращаться в банк за кредитными деньгами достаточно выгодно, но на самом деле любая закредитованность – малоприятное жизненное положение. Повышайте финансовую грамотность и избегайте взятия кредитных денег у финансовых институтов!

Понятие аннуитетного платежа

Как показывает практика и мой богатый репетиторский опыт, превалирующее большинство всех (11)-классников, сдающих ЕГЭ по математике, в процессе решения экономической задачи не могут правильно провести ее классификацию. То есть они не замечают, что в данном упражнении необходимо прибегнуть к схеме аннуитетного платежа.

Модель аннуитетного платежа связана на (100%) с банковским кредитом, так как эта модель платежа подразумевает погашение взятой ссуды особым образом.

На территории нашей страны, если сравнивать две схемы: дифференцированных и аннуитетных платежей, то однозначно господствует аннуитетная модель.

Каждый функционирующий банк предлагает потребителям финансовых услуг погашение кредита аннуитетными платежами, и лишь единичные банки дают возможность своим клиентам прибегнуть к схеме дифференцированных платежей. А ведь неспроста все это!

В чем же квинтэссенция аннуитетного платежа? Все предельно просто! Ежемесячные выплаты по кредиту для заемщика получаются одинаковыми в течение всего срока кредитования независимо от того, какую сумму он еще остался должен банку.

Легко запомнить: размер каждого платежа идентичен любому другому. Они все равны. Именно в этом проявляется главная особенность схемы аннуитетных платежей. Запомните ее! Она не раз вам пригодится в процессе решения егэшных задач по математике из раздела «Финансовая математика».

Существуют некоторые многоэтажные формулы, которые якобы призваны упростить вычисления размера выплат по модели аннуитетных платежей. Но их не стоит зазубривать! Я даже не собираюсь их здесь приводить. Нужно учиться строить математическую модель аннуитета с нуля, используя собственные знания и понимание.

Давайте смоделируем ситуацию: мы взяли кредит на сумму (1) миллион рублей, сроком на (8) лет с ежегодной выплатой, процентная ставка банка равна (16%). Конечная цель – узнать, какую сумму мы в итоге заплатим банку после погашения всего кредита.

Кстати, приведенная ситуация является достаточно повседневной, так как многие граждане нашей страны обращаются за кредитными деньгами именно на подобных условиях.

Для упрощения демонстрации решения задачи давайте договоримся, что кредит был получен (1) января. Банк начисляет проценты на тело кредита (15) декабря соответствующего года. Мы, будучи заемщиками, проводим платеж в последний день календарного года, то есть (31) декабря.

Итак, идет первый год кредитного периода. Наступило (15) декабря. Банк проводит начисление процентов на текущий объем кредита. Чему равняется добавочная сумма? Давайте посчитаем!

<Процентное начисление> = <Сумма долга> • <Процентная ставка банка, выраженная в долях>
<Процентное начисление> = 1000000 • 0.16 = 160 000 рублей

Сейчас наша задолженность составляет 1 миллион плюс 160 000 рублей, то есть 1 160 000 рублей.

Наступает 31 декабря первого года кредитного периода. Сейчас мы должны провести первый транш, чтобы выплатить часть взятой ссуды. А сколько рублей составляет наш платеж? Чтобы квалифицированно ответить на этот вопрос, требуется провести ряд вычислений.

То есть в данный момент неизвестен размер нашей выплаты. Требуется составлять математическую модель схемы аннуитетного платежа. Детальное построение такой схемы я разбираю на своих частных уроках. Поэтому если вы хотите научиться безошибочно вычислять размер аннуитетного платежа, то записывайтесь ко мне на пробный урок.

Я уже провел все выкладки у себя на черновике и могу сообщить, что сумма ежегодного платежа составляет 230 224.26 рубля. Хочу заметить, что появились сотые доли рубля, то есть копейки. Зачастую банки округляют подобные величины до целых, то есть с точностью до рублей. Я оставлю копейки, чтобы показать максимальную точность расчета.

Сейчас я приведу процессинговую таблицу, в которую сведу все необходимые вычисления. Ваша задача постараться разобраться с числами, представленными в этой таблице. Если возникнут какие-либо уточняющие вопросы, то публикуйте их как комментарии к данной статье.

№ платежа	Текущий долг перед банком, рублей	Сумма начисленных процентов, рублей	Сумма платежа, рублей	«Новый» долг перед банком, рублей
1	1 000 000	160 000.00	230 224.26	929 775.74
2	929 775.74	148 764.12	230 224.26	848 315.60
3	848 315.60	135 730.50	230 224.26	753 821.83
4	753 821.83	120 611.49	230 224.26	644 209.07
5	644 209.07	103 073.45	230 224.26	517 058.26
6	517 058.26	82 729.32	230 224.26	369 563.33
7	369 563.33	59 130.13	230 224.26	198 469.19
8	198 469.19	31 755.07	230 224.26	0

Обратите внимание на четвертую колонку «Сумма платежа, рублей». Она имеет неизменное значение на протяжении всех выплат по схеме аннуитетных платежей. В самой нижней правой ячейке фигурирует число 0 – это означает, что кредит полностью выплачен/погашен.

Но вернемся к вопросу, поставленному в условии задачи! Вопрос был сформулирован так: какую сумму мы в итоге заплатим банку после погашения всего кредита?

Чтобы финансово грамотно ответить на данный вопрос, необходимо просуммировать значения из колонки «Сумма начисленных процентов, рублей» и затем к полученной величине приплюсовать первоначальный кредит.

<Общая сумма всех платежей> = 160 000.00 + 148 764.12 + … + 59 130.13 + 31 755.07 + 1 000 000
<Общая сумма всех платежей> = 841 794.08 + 1 000 000 = 1 841 794.08 рубля

Рассчитанное значение – ответ на поставленный вопрос.

Краткое резюме: общая сумма переплат по взятой ссуде — 841 794.08 рубля, что составляет приблизительно 84.1% от первоначального тела кредита. Примерно такие ситуации и возникают у заемщиков, которые прибегают к услугам финансовых учреждений.

Но я все-таки особенно хочу подчеркнуть тот факт, что в данном решении я привел практически готовый ответ. Откуда я взял величину разового платежа в размере 230 224.26 рубля? Да, я построил специализированную модель аннуитетного платежа, вывел закономерность и рассчитал данное значение. В данном примере этих выкладок нет. Будьте внимательны!

Характеристики аннуитетного платежа

Сейчас я вам предлагаю на рассмотрение ключевые маркеры, которые подскажут, что перед вами «стоит» модель аннуитетного платежа.

1. Тело первоначального кредита уменьшается неравными частями.

2. Разовый платеж является постоянным, то есть заемщик выплачивает каждый отчетный период одну и ту же сумму денег. Это, пожалуй, самое главное свойство аннуитетного платежа.

3. При построении математической модели аннуитетного платежа нужно выявить закономерность, включающую геометрическую прогрессию (в разобранном примере это не прослеживается, так как я по факту сразу предоставил ответ).

4. Банковская система очень лояльна к данному виду платежей, поэтому она старается «навязать» своим клиентам именно эту модель взаиморасчетов.

Примеры условий реальных задач, встречающихся на ЕГЭ по математике

В данном разделе я приведу лишь условия некоторого количества задач, которые наиболее часто встречаются на официальном экзамене ЕГЭ по математике. Каждая из задач акцентирована на модели аннуитетного платежа, и только на нем.

А ведь существует масса комбинированных финансовых задач, в процессе решения которых аннуитетный платеж занимает лишь какую-то часть решения. Все подобные задачи я разбираю со своими учениками на индивидуальных занятиях.

Пример №1 В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы: Каждый январь долг возрастает на 20% по сравнению с концом предыдущего года. С февраля по июнь каждого года необходимо выплатить некоторую часть долга. Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?

Пример №2 В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: Каждый январь долг возрастает на 20% по сравнению с концом предыдущего года. С февраля по июнь каждого года необходимо выплатить часть долга, равную 2.16 миллиона рублей. Сколько миллионов рублей было взято в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за 3 года)?

Пример №3 В июле планируется взять кредит на сумму 4 026 000 рублей. Условия его возврата таковы: Каждый январь долг возрастает на 20% по сравнению с концом прошлого года. С февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придется отдать, в случае если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года) по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?

Пример №4 В июле планируется взять кредит в банке на сумму 1 300 000 рублей. Условия его возврата таковы: Каждый январь долг возрастает на 10% по сравнению с концом предыдущего года. С февраля по июнь каждого года необходимо выплатить часть долга. На какое минимальное количество лет можно взять кредит при условии, чтобы ежегодные выплаты были не более 350 000 рублей?

Пример №5 Анна хочет взять в кредит 100 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента — 10% годовых. На какое минимальное количество лет может Анна взять кредит, чтобы ежегодные выплаты были не более 24000 рублей?

Пример №6 31 декабря 2033 года Сергей будет брать в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредит следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Пример №7 1 января 2033 года Иван Павлович будет брать в банке 1.1 миллиона рублей в кредит. Схема выплаты кредита следующая: 1-го числа каждого следующего месяца банк начисляет 2% на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Иван Павлович переводит платеж в банк. На какое минимальное количество месяцев Иван Павлович может взять кредит, чтобы ежемесячные выплаты были не более 220 тысяч рублей?

Пример №8 1 ян­ва­ря 2045 года Анна Сергеевна планирует взять в банке 1 миллион руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 1-го числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 1% на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 1%), затем Анна Сергеевна пе­ре­во­дит в банк платеж. На какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Анна Сергеевна может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 125 тысяч руб­лей?

Пример №9 31 де­каб­ря 2018 года Андрей взял в банке 6 902 000 руб­лей в кре­дит под 12.5% го­до­вых. Схема вы­плат кре­ди­та сле­ду­ю­щая: 31 декаб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 12.5%), затем Андрей пе­ре­во­дит в банк Z руб­лей. Какой долж­на быть сумма Z, чтобы Андрей вы­пла­тил долг че­тырь­мя рав­ны­ми пла­те­жа­ми (то есть за 4 года)?

Пример №10 31 де­каб­ря 2000 года Александр взял в банке 7 007 000 руб­лей в кре­дит под 20% го­до­вых. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 31 де­каб­ря каж­до­го сле­ду­ю­ще­го года банк на­чис­ля­ет про­цен­ты на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 20%), затем Александр пе­ре­во­дит в банк платеж. Весь долг Александр вы­пла­тил за 3 рав­ных пла­те­жа. На сколь­ко руб­лей мень­ше он бы отдал банку, если бы смог вы­пла­тить долг за 2 рав­ных пла­те­жа?

Не все понятно относительно схемы аннуитетных платежей? Звоните мне и задавайте интересующие вопросы!

Само собой разумеется, что, прочитав от корки до корки данную статью, вы не научитесь безошибочно решать задачи финансовой направленности, ориентированные на аннуитетные платежи. Необходимо учиться строить модель, описывающую схему аннуитета.

Также хочу отметить, что схема дифференцированных платежей проще схемы аннуитетных платежей, так как в первом случае фигурирует арифметическая прогрессия, а во втором случае – геометрическая. Как правило, математические расчеты, связанные с геометрической прогрессией, более трудоемки.

На своих частных уроках я с подопечными рассматриваю колоссальное количество задач, так или иначе связанных с моделью аннуитетных платежей. Начинаем с обзора достаточно тривиальных заданий и заканчиваем разбором задач олимпиадной сложности.

Да-да, среди упражнений из категории «Финансовая математика» иногда попадаются задачи неимоверно высокого уровня сложности. Подобные задачи нужны тем школьникам, которые стремятся получить от 93 баллов на официальном экзамене – ЕГЭ по математике.

Если вы имеете громадные проблемы, связанные с экономическими задачами, то немедленно берите мобильный телефон, набирайте мой контактный номер и записывайтесь на первое пробное занятие.

И не забывайте о том, что на рубежном экзамене – ЕГЭ по математике вам непременно попадется задача либо на вклады, либо на кредиты, либо на акции, и крайне высока вероятность того, что в процессе решения вам придется обратиться к схеме аннуитетных платежей!

Увидимся и «услышимся» на индивидуальном уроке!

В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!

Прототипы для 17-го номера делятся на три большие группы: 

• банковские задачи, 
• на ценные бумаги,
• задачи на оптимальный выбор. 

В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

• Как работает процент по кредиту?
• На какую сумму начисляется?
• Из каких частей состоит платеж?
• Как уменьшается долг?

На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс! 

Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.

С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике

Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:

• Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
• Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
• Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг. 

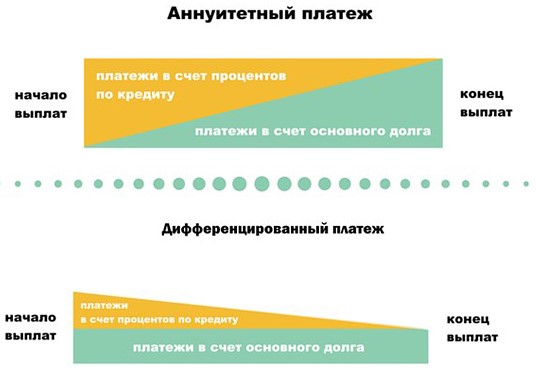
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.

Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.

Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.

Тип 1. Равные платежи

Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

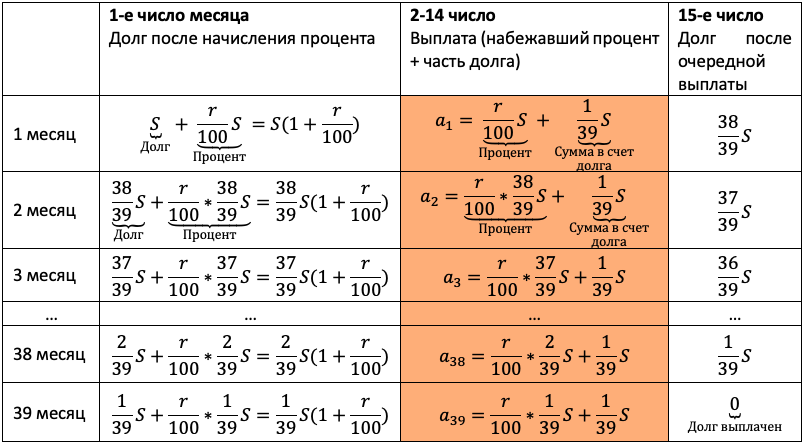
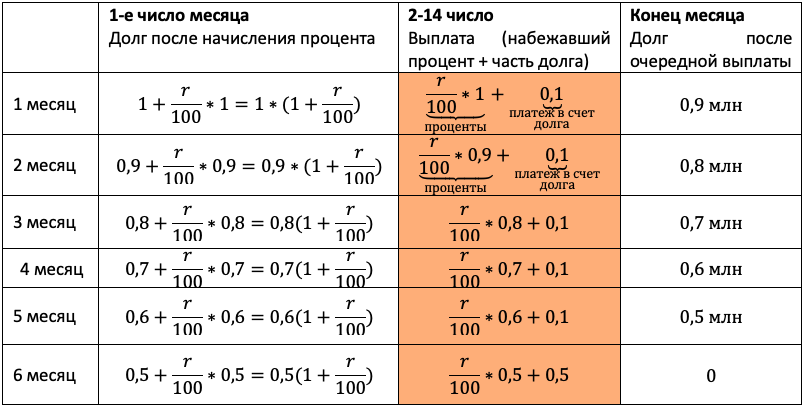
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!

Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.

Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.

Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!

Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.

Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:

Наше решение не зависит от суммы кредита, S сокращается. 

По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:

Пожалуй, все, проще уже некуда. Подставляем значения!   

Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.

Вспоминаем, что k=1+r/100, а найти нам надо r.

Ответ: 10%.

Не забудьте после решения расставить акценты в задаче:

Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.

Тип 2. Равномерно убывающий долг

В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.  

15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)

Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.

Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:

Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:

Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:

Приведем подобные, вынесем общий множитель за скобку:

Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:

Ответ: 1%.

И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.

Тип 3. Долг, убывающий согласно табличке

Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг(в млн рублей)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.

Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.

Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:

Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.

Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.

«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:

Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.

Приведем подобные и вынесем общие множители за скобку:

Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.

Ответ: 5%.

Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.

Тип 4. Погашение кредита в два этапа.

По сути, это та же прошлая задача, но месяцев больше

В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!

15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?

И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.

Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.

Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.

Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:

Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:

Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.

Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:

Посчитаем эту сумму:

Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!

Ответ: 700 тысяч.

Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.

Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике

Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:

• Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
• Повторите типы задач и механизм распределения платежа на проценты и долг;
• Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
• Проговорите, что математическая модель должна точно отражать условие задачи.

Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.

За что дают баллы?

Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.

17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.

Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа. 

Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:

А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.

Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.

Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги. 

Задание № 17. Финансовые задачи. Аннуитетные платежи

Аннуитетный платеж – это такая система выплат, при которой кредит выплачивается раз в год (месяц) равными платежами. При этом каждый год (месяц) до внесения платежа банк начисляет на оставшуюся часть долга некоторый процент, то есть оставшаяся сумма долга увеличивается на это количество процентов.

Пусть а руб. – сумма кредита

р – процентная ставка

коэффициент наращивания

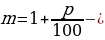
n – период кредитования

х руб. – ежегодный платеж

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2
3
…
n

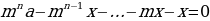
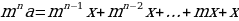
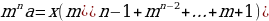
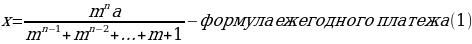
Выведем еще одну формулу для вычисления суммы ежегодного платежа:

После первой выплаты сумма долга равна

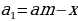
После второй выплаты

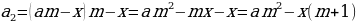
После третьей выплаты

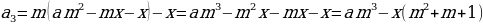
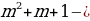
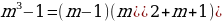
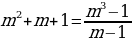
Так как это кусочек формулы , то

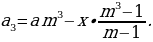
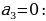
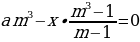
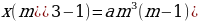
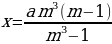
Значит, Если три года кредитования, то

Для четырех лет кредитования:

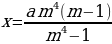
Для n лет кредитования

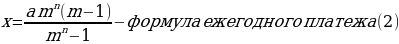
Задача 1.

31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Решение:

Пусть а руб. – сумма кредита (а = 9 930 000 руб.)

р = 10 % – процентная ставка

коэффициент наращивания

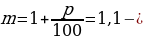
n = 3 года – период кредитования

х руб. – ежегодный платеж

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2
3

После третьего платежа долг равен нулю:

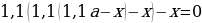
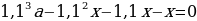
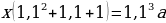
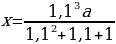
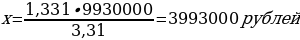
Ответ: 3993000 рублей.

Задача 2.

31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк х рублей. Какой должна быть сумма х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

Решение:

Пусть а руб. – сумма кредита (а = 6 902 000 руб.)

р = 12,5 % – процентная ставка

коэффициент наращивания

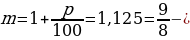
n = 4 года – период кредитования

х руб. – ежегодный платеж

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2
3
4		x

После четвертого платежа долг равен нулю:

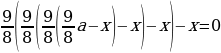
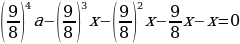
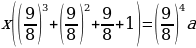
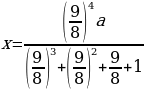
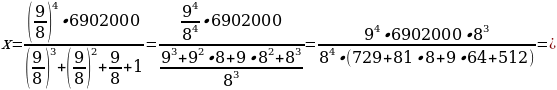
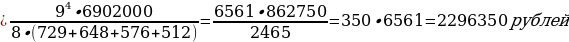
Ответ: 2296350 рублей.

Примечание. Можно было найти сумму ежегодного платежа по формуле (2):

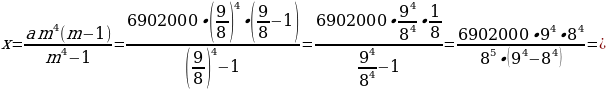
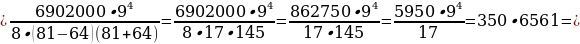
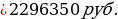
Рассмотрим еще один способ решения задачи.

Год	Долг (руб.)	Платеж (руб.)	Остаток
Проценты (p %)	Основная сумма
1
2			?
3			?
4			?

Покажем, как вычислять основную сумму платежа, то есть на что заменять знак «?».

1-й год: платеж составляет .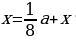

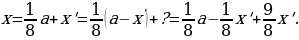
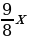
2-й год: Значит, основная сумма платежа составляет рублей.

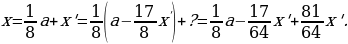
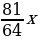
3-й год: Значит, основная сумма платежа составляет рублей.

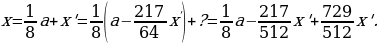
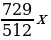
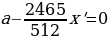
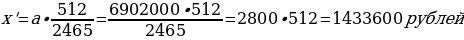
4-й год: Значит, основная сумма платежа составляет рублей.

Тогда ежегодные платежи составляют:

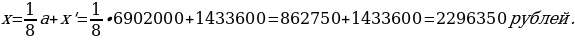
Ответ: 2296350 рублей.

Задача 3.

31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

Решение:

Пусть а руб. – сумма кредита (а = 7 007 000 руб.)

р = 20 % – процентная ставка

коэффициент наращивания

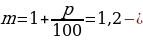
х руб. – ежегодный платеж, если n = 3 года; у руб. – ежегодный платеж, если n = 2 года.

Если Тимофей выплатил за три года, то имеем:

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2
3

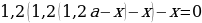
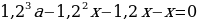
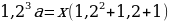
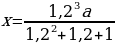
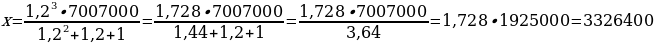
Значит, за 3 года Тимофей выплатил: 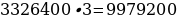рублей.

Если бы Тимофей смог выплатить долг за два года, то имеем:

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2

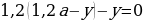
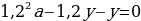
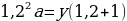
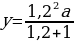
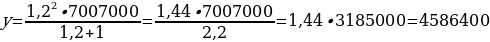
Значит, за 2 года Тимофей выплатил бы: 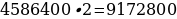рублей.

Тогда переплата составляет: 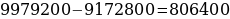рублей.

Ответ: на 806400 рублей.

Примечание. Рассмотрим другой способ решения:

Если выплатил за 3 года, то:

После первой выплаты сумма долга равна

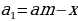
После второй выплаты

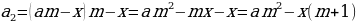
После третьей выплаты

рублей – выплаты за три года.

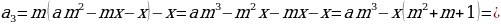
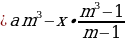
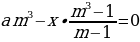
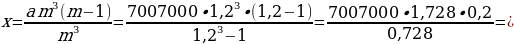
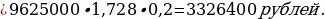
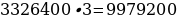
Если выплатил за 2 года, то:

После первой выплаты сумма долга равна

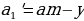
После второй выплаты

рублей – выплаты за два года.

рублей – переплата.

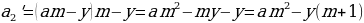
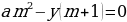
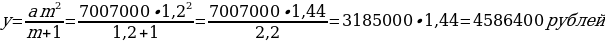
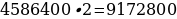
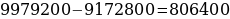
Задача 4.

31 декабря 2014 года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Ярослав переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?

Решение:

Пусть а руб. – сумма кредита

р = 12,5 % – процентная ставка

коэффициент наращивания

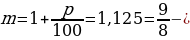
n = 4 года – период кредитования

х руб. – ежегодный платеж (х = 2 132 325 рублей)

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2
3
4

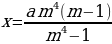
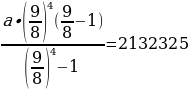
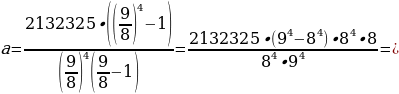
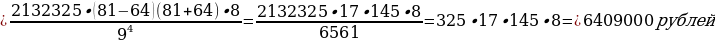
Ответ: 6 409 000 рублей.

Задача 5.

31 декабря 2014 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на р%), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?

Решение:

Пусть а руб. – сумма кредита

р % – процентная ставка

коэффициент наращивания

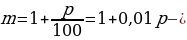
n – период кредитования

х руб. – ежегодный платеж, если n = 4 года; у руб. – ежегодный платеж, если n = 2 года.

Если за 4 года, то:

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2
3
4

Если за 2 года, то:

Год	Долг (руб.)	Платеж (руб.)	Остаток
1
2

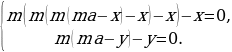
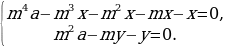
Из второго уравнения выразим :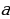

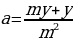
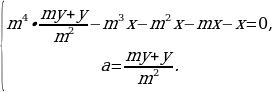
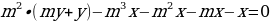
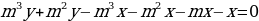
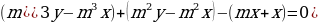
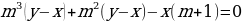
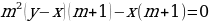
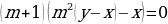
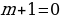
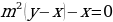
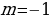
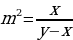
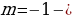
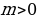
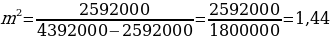
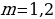
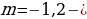
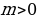
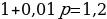
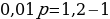
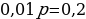
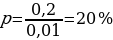
и подставим в первое уравнение.

или

не удовлетворяет условию задачи .

или не удовлетворяет условию задачи .

Ответ: 20%.

Задания для самостоятельного решения:

1. (вариант 23 из сборника ЕГЭ 2020, Ященко И.В., 50 вариантов)

31 декабря 2016 года Василий взял в банке 5 460 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Василий переводит в банк х рублей. Какой должна быть сумма х, чтобы Василий выплатил долг тремя равными платежами (то есть за три года)?

Ответ: 2 592 000 рублей.

2. (вариант 24)

31 декабря 2016 года Виктор взял в банке 3 972 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Виктор переводит в банк х рублей. Какой должна быть сумма х, чтобы Виктор выплатил долг тремя равными платежами (то есть за три года)?

Ответ: 1 597 200 рублей.

3. (вариант 39)

31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Василий выплатил долг двумя равными платежами (то есть за два года)?

Ответ: 2 622 050 рублей.

4. (вариант 18)

31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 11% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 11%), затем Василий переводит в банк 3 696 300 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (то есть за два года)?

Ответ: 6 330 000 рублей.

5.  № (511283)

В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга, равную
69 690 821 рубль.

Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами (то есть за три года)?

Ответ: 124 809 100 рублей.

6. (508217)

31 декабря 2014 года Савелий взял в банке 7 378 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Савелий переводит в банк платёж. Весь долг Савелий выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

Ответ: 506 250 рублей.

7. (507218)

31 декабря 2014 года Никита взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на р%), затем Никита переводит очередной транш. Если он будет платить каждый год по
2 073 600 рублей, то выплатит долг за 4 года. Если по 3 513 600 рублей, то за 2 года. Под какой процент Никита взял деньги в банке?

Ответ: 20%.