- Треугольник
- Четырехугольники
- Окружность и круг
- Призма
- Пирамида
- Усеченная пирамида
- Цилиндр
- Конус
- Усеченный конус
- Сфера и шар
1. Формулы сокращённого умножения
Наверх
2. Модуль числа
Определение:
Основные свойства модуля:
Наверх
3. Степень с действительным показателем
Свойства степени с действительным показателем
Пусть Тогда верны следующие соотношения:
Наверх
4. Корень n-ой степени из числа
Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
Основные свойства арифметического корня:
Наверх
5. Логарифмы
Определение логарифма:
Основное логарифмическое тождество:
Основные свойства логарифмов
Пусть
Тогда верны следующие соотношения:
Наверх
6. Арифметическая прогрессия
Формула n-го члена арифметической прогрессии:
Характеристическое свойство арифметической прогрессии:
Сумма n первых членов арифметической прогрессии:
При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
7. Геометрическая прогрессия
Формула n-го члена геометрической прогрессии:
Характеристическое свойство геометрической прогрессии:
Сумма n первых членов геометрической прогрессии:
При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
8. Бесконечно убывающая геометрическая прогрессия
Сумма бесконечно убывающей геометрической прогрессии:
Наверх
9. Основные формулы тригонометрии
Зависимость между тригонометрическими функциями одного аргумента:
Формулы сложения:
Формулы тригонометрических функций двойного аргумента:
Формулы понижения степени:
Формулы приведения
Все формулы приведения получаются из соответствующих формул сложения. Например:
Применение формул приведения укладывается в следующую схему:
— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;
— определяется знак приводимой функции;
— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или
, то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид
, то функция названия не меняет.
Например, получим формулу :
— — IV четверть;
— в IV четверти тангенс отрицательный;
— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,
Формулы преобразования суммы тригонометрических функций в произведение:
Формулы преобразования произведения тригонометрических функций в сумму:
Наверх
10. Производная и интеграл
Таблица производных некоторых элементарных функций
Правила дифференцирования:
1.
2.
3.
4.
5.
Уравнение касательной к графику функции в его точке
:
Таблица первообразных для некоторых элементарных функций
Правила нахождения первообразных
Пусть ― первообразные для функций
и
соответственно, a, b, k ― постоянные,
Тогда:
— ― первообразная для функции
— ― первообразная для функции
— ― первообразная для функции
— Формула Ньютона-Лейбница:
1. Треугольник
Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно;
― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно;
― длины высот AA2, BB2, CC2 треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC;
― площадь треугольника ABC. Тогда имеют место следующие соотношения:
(теорема синусов);
(теорема косинусов);
Наверх
2. Четырёхугольники
Параллелограмм
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.
Площадь четырехугольника
Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Наверх
3. Окружность и круг
Соотношения между элементами окружности и круга
Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга, — длина дуги в
градусов,
— длина дуги в
радиан,
— площадь сектора, ограниченного дугой в n градусов,
— площадь сектора, ограниченного дугой в
радиан. Тогда имеют место следующие соотношения:
Вписанный угол
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, — прямой.
Вписанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Описанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.
Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны
Наверх
4. Призма
Пусть H ― высота призмы, AA1 ― боковое ребро призмы, ― периметр основания призмы,
― площадь основания призмы,
― площадь боковой поверхности призмы,
― площадь полной поверхности призмы, V ― объем призмы,
― периметр перпендикулярного сечения призмы,
― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
Свойства параллелепипеда:
— противоположные грани параллелепипеда равны и параллельны;
— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;
— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Наверх
5. Пирамида
Пусть H ― высота пирамиды, ― периметр основания пирамиды,
― площадь основания пирамиды,
― площадь боковой поверхности пирамиды,
― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:
;
.
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то
Наверх
6. Усечённая пирамида
Пусть H ― высота усеченной пирамиды, и
― периметры оснований усеченной пирамиды,
и
― площади оснований усеченной пирамиды,
― площадь боковой поверхности усеченной пирамиды,
― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.
Тогда имеют место следующие соотношения:
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то:
Наверх
7. Цилиндр
Пусть h ― высота цилиндра, r ― радиус цилиндра, ― площадь боковой поверхности цилиндра,
― площадь полной поверхности цилиндра, V ― объем цилиндра.
Тогда имеют место следующие соотношения:
Наверх
8. Конус
Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса, ― площадь боковой поверхности конуса,
― площадь полной поверхности конуса, V ― объем конуса.
Тогда имеют место следующие соотношения:
Наверх
9. Усечённый конус
Пусть h ― высота усеченного конуса, r и ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,
― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:
Наверх
10. Сфера и шар
Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы, ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,
― объем сегмента, высота которого равна h,
― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:
Наверх
Материалы, выдаваемые на экзамене, смотрите здесь
- Полный краткий справочник
- Формулы сокращенного умножения
- Модуль числа, модуль выражения
- Степень с действительным показателем
- Корень n-ой степени из числа
- Логарифмы
- Арифметическая прогрессия
- Геометрическая прогрессия
- Бесконечно убывающая геометрическая прогрессия
- Основные формулы тригонометрии
- Производная и интеграл
- Треугольник
- Четырехугольники
- Окружность и круг
- Призма
- Пирамида
- Усеченная пирамида
- Цилиндр
- Конус
- Усеченный конус
- Сфера и шар
- Векторы и координаты
- Особенности экзаменационных заданий профильной математики
- Задания 1: округление величин, проценты
- Особенности экзаменационных заданий на округление
- Округление величин с избытком и недостатком
- Проценты
- Особенности экзаменационных заданий на проценты
- Задания 2: анализ графических зависимостей
- Анализ графических зависимостей
- Особенности экзаменационных заданий на чтение графиков и диаграмм
- Задания 3 и 6: планиметрия
- Треугольник
- Равносторонний треугольник
- Равнобедренный треугольник
- Прямоугольный треугольник
- Тригонометрические функции дополнительных углов
- Основное тригонометрическое тождество и следствия из него
- Смежные углы
- Средняя линия треугольника
- Медиана треугольника
- Биссектриса треугольника
- Высота треугольника
- Серединный перпендикуляр
- Теорема косинусов
- Параллелограмм
- Прямоугольник
- Ромб
- Параллелограмм Вариньона
- Трапеция
- Правильный шестиугольник
- Теоремы о площадях многоугольников
- Окружность
- Вписанный угол
- Хорда
- Касательная к окружности
- Секущая
- Круг и его элементы
- Соотношения между элементами окружности и круга
- Вписанная окружность
- Описанная окружность
- Вектор
- Сумма и разность векторов
- Координаты вектора
- Скалярное произведение векторов
- Расстояния от точки до координатных осей
- Расстояние между точками
- Треугольник
- Задания 4: вероятности событий
- Определение вероятности
- Теоремы о вероятностях событий
- Особенности экзаменационных заданий на начала теории вероятности
- Задания 5: простейшие уравнения
- Простейшие уравнения
- Линейные уравнения
- Квадратные уравнения
- Рациональные уравнения
- Иррациональные уравнения
- Показательные уравнения
- Логарифмические уравнения
- Особенности решения экзаменационных заданий на простейшие уравнения
- Задания 7: производные, первообразные
- Правила дифференцирования
- Производная числа, линейной и степенной функции
- Производная многочлена
- Уравнение прямой
- Уравнение касательной
- Физический смысл производной
- Монотонность и экстремумы функции
- Первообразная
- Криволинейная трапеция и ее площадь
- Задания 8: стереометрия
- Особенности экзаменационных заданий по стереометрии
- Куб
- Призма. Прямоугольный параллелепипед
- Прямая призма
- Прямоугольный параллелепипед и его свойства
- Особенности правильной шестиугольной призмы
- Пирамида
- Сечения
- Цилиндр и его соотношения
- Конус и его соотношения
- Сфера и шар
- Комбинации круглых тел. Вписанные сферы
- Комбинации круглых тел. Описанные сферы
- Комбинации конуса и цилиндра
- Комбинации многогранников и круглых тел. Описанные сферы
- Комбинации многогранников и круглых тел. Вписанные сферы
- Комбинации конуса, цилиндра и многогранников
- Задания 9: тождественные преобразования выражений
- Действия с дробями
- Формулы сокращенного умножения
- Степень и её свойства
- Свойства степени
- Степень с дробным показателем
- Арифметический корень
- Свойства арифметического корня
- Определение логарифма и его свойства
- Основные тригонометрические формулы
- Правило для запоминания формул приведения
- Свойства четности и нечетности функций
- Задания 10: задачи с прикладным содержанием
- Задачи с прикладным содержанием
- Задания 11: текстовые задачи
- Определение процента
- Правило креста для решения задач на смеси
- Движение по прямой
- Движение по окружности
- Алгоритм решения задач на совместную работу
- Задания 12: исследование функций при помощи производной
- Производная некоторых элементарных функций
- Правила дифференцирования
- Монотонность и экстремумы функции
- Наибольшее и наименьшее значение функции
- Задания 1: округление величин, проценты
Выражения, содержащие знак радикала (корень), называются иррациональными.
Арифметическим корнем натуральной степени $n$ из неотрицательного числа а называется некоторое неотрицательное число, при возведении которого в степень $n$ получается число $а$.
$(√^n{a})^n=a$
В записи $√^n{a}$, «а» называется подкоренным числом, $n$ — показателем корня или радикала.
Свойства корней $n$-ой степени при $а≥0$ и $b≥0$:
1. Корень произведения равен произведению корней
$√^n{a∙b}=√^n{a}∙√^n{b}$
Пример:
Вычислить $√^5{5}∙√^5{625}$
Решение:
Корень произведения равен произведению корней и наоборот: произведение корней с одинаковым показателем корня равно корню из произведения подкоренных выражений
$√^n{a}∙√^n{b}=√^n{a∙b}$
$√^5{5}∙√^5{625}=√^5{5∙625}=√^5{5∙5^4}=√^5{5^5}=5$
Ответ: $5$
2. Корень из дроби – это отдельно корень из числителя, отдельно из знаменателя
$√^n{{a}/{b}}={√^n{a}}/{√^n{b}}$, при $b≠0$
3. При возведении корня в степень, в эту степень возводится подкоренное выражение
$(√^n{a})^k=√^n{a^k}$
4. Если $а≥0$ и $n,k$ — натуральные числа, больше $1$, то справедливо равенство.
$√^n{√^k{a}}=√^{n∙k}a$
5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
$√^{n∙m}a^{k∙m}=√^n{a^k}$
6. Корень нечетной степени можно извлекать из положительных и отрицательных чисел, а корень четной степени – только из положительных.
7. Любой корень можно представить в виде степени с дробным (рациональным) показателем.
$√^n{a^k}=a^{{k}/{n}}$
Пример:
Найдите значение выражения ${√{9∙√^11{с}}}/{√^11{2048∙√с}}$ при $с>0$
Решение:
Корень произведения равен произведению корней
${√{9∙√^11{с}}}/{√^11{2048∙√с}}={√9∙√{√^11{с}}}/{√^11{2048}∙√^11{√с}}$
Корни из чисел мы можем извлечь сразу
${√9∙√{√^11{с}}}/{√^11{2048}∙√^11{√с}}={3∙√{√^11{с}}}/{2∙√^11{√с}}$
Далее применим формулу
$√^n{√^k{a}}=√^{n∙k}a$
${3∙√{√^11{с}}}/{2∙√^11{√с}}={3∙√^22{с}}/{2∙√^22{с}}$
Корни $22$ степени из $с$ мы сокращаем и получаем ${3}/{2}=1,5$
Ответ: $1,5$
Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.
Пример:
Найдите значение выражения $√{(с-7)^2}+√{(с-9)^2}$ при $7 < c < 9$
Решение:
Если над корнем не стоит показатель, то это означает, что мы работаем с квадратным корнем. Его показатель равен двум, т.е. четный. Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.
$√{(с-7)^2}+√{(с-9)^2}=|c-7|+|c-9|$
Определим знак выражения, стоящего под знаком модуля, исходя из условия $7 < c < 9$
Для проверки возьмем любое число из заданного промежутка, например, $8$
Проверим знак каждого модуля
$8-7>0$
$8-9<0$, при раскрытии модуля пользуемся правилом: модуль положительного числа равен самому себе, отрицательного числа — равен противоположному значению. Так как у второго модуля знак отрицательный, при раскрытии меняем знак перед модулем на противоположный.
$|c-7|+|c-9|=(с-7)-(с-9)=с-7-с+9=2$
Ответ: $2$
Свойства степеней с рациональным показателем:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n∙a^m=a^{n+m}$
2. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n∙m}$
3. При возведении в степень произведения в эту степень возводится каждый множитель
$(a∙b)^n=a^n∙b^n$
4. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
Дроби
Практика: решай 6 задание и тренировочные варианты ЕГЭ по математике (профиль)
Арифметический корень натуральной степени
Предлагаю систему заданий, предназначенных для подготовки к ЕГЭ на уроках математики по теме «Арифметический корень натуральной степени»
Свойства арифметического корня натуральной степени:
1)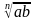
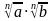
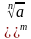
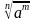
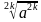
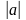
4) 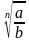
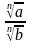
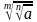
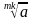
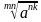
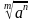
гдеa ≥ 0, b ≥ 0, m ≥ 2, n ≥ 2, m 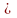
Реши самостоятельно.
-
2)
;
3)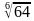
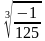
5) 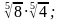
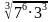
7) 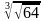

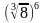
9)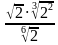
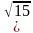
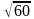
;
11) ; 12) ;
13) ( —
)(
+
); 14) (
—
)(
+ 4
).
Банк заданий ЕГЭ.
Найти значение выражения:
-
; 2)
; 3)
; 4)
;
5) ; 6)
; 7) )
;

; 9)
; 10)
;
11) ; 12) ; 13) ; 14) ; 15) ;
16) ; 17) ;
18) ; 19) ;
20)
21) ( ):
; 22)(
):
;
23)( ): ; 24)(
):
;
25);( ):
;
26) ; 27)
; 28)
; 29)
; 30)
;
31) ; 32)
; 33)
; 34)
; 35)
;
36) 9 ; 37)3
; 38)8
;
39) 7 ; 40) 8
;
41) 42) 43) 44)
45) ; 46) ; 47)
;
48) ; 49)
; 50)
.
Скачать материал

Скачать материал


- Сейчас обучается 76 человек из 33 регионов


- Сейчас обучается 28 человек из 12 регионов


- Сейчас обучается 1079 человек из 83 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Выражения: степени, корни. Яковлева Татьяна Петровна, доцент кафедры математики и физики Камчатского государственного университета имени Витуса Беринга, кандидат педагогических наук, доцент, г. Петропавловск — Камчатский
-
2 слайд
Теоретические сведения
-
3 слайд
Формулы сокращенного умножения
-
4 слайд
Преобразование степеней и корней
-
5 слайд
Примеры вычислений со степенями и корнями
-
-
-
-
-
-
11 слайд
20 21 22 23 24 25
-
-
-
-
-
-
-
-
-
-
-
22 слайд
Различные виды заданий со степенями и корнями
-
-
-
-
-
-
-
-
-
-
32 слайд
Решите самостоятельно!
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
56 слайд
Благодарим за внимание!
-
57 слайд
Список используемой литературы: Андреева А.О. ЕГЭ по математике. Практическая подготовка. – СПб.: БХВ-Петербург, 2014. – 256 с. Гайкова И.И. ЕГЭ по математике. Оптимальный результат. – СПб.: БХВ-Петербург, 2054. – 304 с. Глазков Ю.А. ОГЭ. Математика. Задачник. Сборник заданий и методических рекомендаций/ Ю.А. Глазков, М.Я. Гаиашвили. – М.: Издательство «Экзамен», 2017. – 376 с. ГИА по математике. 9 класс: учебное пособие / Л.О. Денищева (и др.). – М.: БИНОМ. Лаборатория знаний, 2011. – 246 с. Математика: ЕГЭ: учебно-справочные материалы (Серия «Итоговый контроль: ЕГЭ») / Ю.М. Нейман, Т.М. Королева, Е.Г. Маркарян. – М., СПб: «Просвещение», 2011. – 287 с. Математика. ЕГЭ-2016. Тематический тренинг. 10-11 классы: учебно-методическое пособие / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2015. – 400 с. Мордкович А.Г. Математика: Полный справочник / А.Г. Мордкович, В.И. Глизбург, Н.Ю. Лаврентьева. – М.: АСТ: Астрель, 2016. – 351 с. Семенов А.В. Основной государственный экзамен. Математика. Комплекс материалов для подготовки учащихся. Учебное пособие. / А.В. Семенов, А.С. Трепалин, И.В. Ященко, П.И. Захарова, И.Р. Высоцкий; под ред. И.В. Ященко; Московский Центр непрерывного образования. – М.: Интеллект-Центр, 2017. – 248 с. Третьяк И.В. ОГЭ. Математика : универсальный справочник / И.В. Третьяк. — Москва : Эксмо, 2016. — 352 с. Шестаков С.А. ЕГЭ 2017. Математика. Значения выражений. Задача 9 (профильный уровень). Задачи 2 и 5 (базовый уровень). Рабочая тетрадь / Под ред. И.В. Ященко. – М.: МЦНМО, 2017. – 64 с. Ященко И.В. ОГЭ: 3000 задач с ответами по математике / Под ред. И.В. Ященко. – М. Издательство «Экзамен». МЦНМО, 2017. – 479 с.
Краткое описание документа:
Презентация предназначена для систематизации и обобщения знаний по нахождению значений выражений, содержащих степени и корни. Материал полезен для подготовки к ЕГЭ по математике. Рассматриваются теоретические сведения, образцы выполнения заданий (58 заданий), различные задания со степенями и корнями (18 зданий), задания для самостоятельного решения (43 заданий).
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 185 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни)», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
Больше материалов по этому УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни)», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.
Больше материалов по этому УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Пратусевич М.Я., Столбов К.М., Головин А.Н.
Больше материалов по этому УМК
-
-
-
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни)», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.
Больше материалов по этому УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Пратусевич М.Я., Столбов К.М., Головин А.Н.
Больше материалов по этому УМК
-
-
Другие материалы
Контрольная работа по теме «Степени»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
- Тема: § 35. Свойства корня n-й степени
- 10.05.2018
- 1124
- 2





Электив Подготовка к ЕГЭ
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
- 07.05.2018
- 410
- 1

Рабочая программа по алгебре 10 класс
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
- 07.05.2018
- 376
- 0

Презентация по алгебре для 11 класса по теме «Площадь криволинейной трапеции»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
- Тема: Глава 8. Первообразная и интеграл
Рейтинг:
5 из 5
- 05.05.2018
- 875
- 7

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС медицинских направлений подготовки»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Разработка эффективной стратегии развития современного вуза»
-
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
-
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика музейного дела и охраны исторических памятников»
-
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
Алгебра и начала математического анализа, 10 класс
Урок №16 Название темы: Арифметический корень натуральной степени.
Перечень тем, рассматриваемых на уроке:
- преобразование и вычисление арифметических корней,
- свойства арифметического корня натуральной степени,
- корень нечетной степени из отрицательного числа,
- какими свойствами обладает арифметический корень натуральной степени.
Глоссарий
- Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
- Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
- Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
- Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
- Арифметическим корнем натуральной степени, где n ≥ 2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл.– М.: Просвещение, 2014.
- Сканави М. И., Зайцев В. В., Рыжков В. В. «Элементарная математика». – Книга по требованию, 2012.
- Семенова А.Л., Ященко И.В. ЕГЭ 3000 задач с ответами, математика под редакцией Москва, 2017.
- Ященко И. В. ЕГЭ 3300 задач с ответами, математика профильный уровень под редакцией Москва, 2017.
Объяснение темы «Арифметический корень натуральной степени»
Решим задачу.
Площадь квадрата S=16 м².
Обозначим сторону квадрата а, м.
Тогда, а² = 16.
Решим данное уравнение:
a=4 и а= –4.
Проверим решение:
4² = 16;
(–4)² = 16.
Ответ: длина стороны квадрата равна 4 м.
Определение:
Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
Определение:
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
Обозначение: 
Определение:
Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
Обозначение: 
Например:



На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.
Определение:
Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
Определение:
Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Обозначение: 
n–степень арифметического корня;
а– подкоренное выражение.
Давайте рассмотрим такой пример: 
Мы знаем, что (–4)³ = –64, следовательно, 
Еще один пример: 
Мы знаем, что (–3)5 = –243, следовательно, 
На основании этих примеров, можно сделать вывод:

Свойства арифметического корня натуральной степени:
Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:
.
Примеры:


.
Примеры:


.
Пример:

.
Пример:

- Для любогоа справедливо равенство:
Пример:
Найдите значение выражения 
Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:


Получаем: х – 3 + 6 – х= 3.
Примеры заданий.
Первый пример.
Задача:
Выберите верные утверждения:
Разбор задания.
Применим определение арифметического корня: Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Следовательно, верными могут быть только неотрицательные выражения.
Ответ: 

Второй пример.
Задача:
Выделите самое маленькое число:
Разбор задания:
Корень из отрицательного числа будет отрицательным числом, следовательно, наименьшее число –
Ответ: 4.

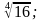 2)
2) 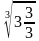 ;
; 



































































 .
. .
. .
. .
.












