Поиск
Всего: 11 1–11
Добавить в вариант
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Китая будет выступать после группы из Канады и после группы из Англии? Результат округлите до сотых.
За круглый стол на 101 стул в случайном порядке рассаживаются 99 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.
За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.
В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
Всего: 11 1–11
Бином Ньютона и треугольник Паскаля
18 декабря 2021
Сегодня мы детально разберём Бином Ньютона. Это формула, по которой можно раскрыть скобки ${{left( a+b right)}^{n}}$ и получить готовый многочлен. Сама формула выглядит так:
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $C_{n}^{k}$ — биноминальные коэффициенты (они же — «число сочетаний из $n$ по $k$»), которые считаются по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
Вот и всё. На этом можно было бы закончить, но есть одно но: большинство начинающих учеников не понимают эту формулу, не умеют пользоваться её, а уж чтобы доказать её — об этом даже речи не идёт.
Сегодня мы всё это исправим. Вы узнаете буквально всё, что нужно знать про Бином Ньютона:
- Постановка задачи — в чём вообще проблема?
- Формула бинома Ньютона — что значат все эти значки?
- Знак суммы — чрезвычайно полезный материал для всех, кто хочет понять математику.
- Биноминальные коэффициенты — минутка комбинаторики.
- Треугольник Паскаля — лайфхак для быстрых вычислений.
- Доказательство Бинома Ньютона — для тех, кто хочет познать Истину.:)
Материала много, но всё будет максимально понятно и — главное — чрезвычайно полезно. Погнали!
1. Постановка задачи
Итак, мы хотим быстро раскрывать скобки в конструкциях вида ${{left( a+b right)}^{n}}$. Начнём с того, что мы и так знаем. Например:
[{{left( a+b right)}^{1}}=a+b]
Спасибо, кэп. Теперь вспомним формулы сокращённого умножения. Квадрат суммы:
[{{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]
И куб суммы:
[{{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}]
Видим, что с ростом степени растёт и количество слагаемых-одночленов: их всегда на одно больше, чем степень. Но это не проблема. Проблема в другом: у этих одночленов появляются некие коэффициенты, принцип вычисления которых не ясен. Пока не ясен…
Именно для нахождения этих коэффициентов придумали бином Ньютона.
2. Бином Ньютона
Пусть $nin mathbb{N}$. Тогда верно равенство
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $sum{left( … right)}$ — краткая запись суммы, $C_{n}^{k}$ — биноминальный коэффициент, который считается по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
В этой формуле прекрасно всё. Одних пугает знак суммы. Другие не понимают, что за $C_{n}^{k}$ такое (ещё раз: это объект из мира комбинаторики, читается «число сочетаний из $n$ по $k$»). Третьи более-менее понимают, о чём речь, но применить эту формулу на практике не могут.
Сегодня мы решим все эти проблемы. Начнём со знака суммы.
3. Знак суммы
Знак суммы — это краткая запись суммы нескольких однотипных слагаемых:
[sumlimits_{k=a}^{k=b}{fleft( k right)}]
Формула $fleft( k right)$ задаёт общий вид однотипных слагаемых, а нижний и верхний индексы $k=a$ и $k=b$ (сверху вместо $k=b$ обычно пишут просто $b$) определяют диапазон значений, которые «пробегает» $k$ и которые нужно подставить в $fleft( k right)$. Например:
[sumlimits_{k=3}^{5}{2k}=2cdot 3+2cdot 4+2cdot 5]
Более привычный формат:
[sumlimits_{k=1}^{n}{fleft( k right)=fleft( 1 right)+fleft( 2 right)+…+fleft( n right)}]
То же самое с индексами:
[sumlimits_{k=1}^{n}{{{a}_{k}}={{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}]
Обратите внимание: если $k$ пробегает значения от $k=a$ до $k=b$, то всего таких слагаемых будет ровно $b-a+1$:
[sumlimits_{k=a}^{b}{fleft( k right)=underbrace{fleft( a right)+fleft( a+1 right)+ldots +fleft( b right)}_{b-a+1text{ слагаемых!}}}]
Кроме того, полезно потренироваться и с обратным переходом — от полной записи к краткой:
[frac{1}{1}+frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}=sumlimits_{n=1}^{5}{frac{1}{2n-1}}]
[frac{2}{3}+frac{4}{9}+frac{6}{27}+frac{8}{81}=sumlimits_{n=1}^{4}{frac{2n}{{{3}^{n}}}}]
В приложении к уроку — куча задач для самостоятельной тренировки.
Но вернёмся к биному Ньютона. Распишем его без знака суммы:
[begin{align} {{left( a+b right)}^{n}} & =C_{n}^{0}cdot {{a}^{n}}{{b}^{0}}+C_{n}^{1}cdot {{a}^{n-1}}{{b}^{1}}+ \ & +ldots +C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}+ldots + \ & +C_{n}^{n-1}cdot {{a}^{1}}{{b}^{n-1}}+C_{n}^{n}cdot {{a}^{0}}{{b}^{n}} end{align}]
В целом, всё понятно: степени буквы $a$ уменьшаются с ${{a}^{n}}$ до ${{a}^{0}}$; одновременно степени буквы $b$ растут с ${{b}^{0}}$ до ${{b}^{n}}$. Сумма степеней этих букв в каждом одночлене равна $n$. Но что такое $C_{n}^{k}$?
4. Биноминальные коэффициенты
Немного комбинаторики.
Определение. Число сочетаний из $n$ по $k$ — это число способов, которыми можно выбрать $k$ элементов среди $n$ элементов, если порядок выбора не имеет значения. Обозначается $C_{n}^{k}$ и считается по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
Обратите внимание: в числителе и знаменателе стоят факториалы. Стандартное определение: $n!$ — это произведение всех чисел от единицы до $n$:
[n!=1cdot 2cdot 3cdot …cdot n]
У факториалов много интересных свойств. Чуть позже мы рассмотрим их и даже введём более корректное определение самого факториала. А пока просто потренируемся считать биноминальные коэффициенты.
Пример. На пруду плавают 5 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Очевидно, порядок кормления уток неважен. Покормить сначала утку №1, а затем №2 — это то же самое, что покормить сначала утку №2, затем №1. Результат один и тот же: накормлены лишь эти две утки, а остальные три — нет. Поэтому считаем $C_{5}^{2}$:
[begin{align} C_{5}^{2} & =frac{5!}{2!cdot 3!} \ & =frac{5cdot 4cdot 3cdot 2cdot 1}{2cdot 1cdot 3cdot 2cdot 1}= \ & =10 end{align}]
Вот и всё. Однако при больших $n$ и $k$ посчитать число сочетаний напрямую становится затруднительно. Тут на помощь приходит сокращение дробей.
Пример. На пруду 150 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Порядок вновь неважен, просто уток стало больше. Поэтому считаем $C_{150}^{2}$:
[begin{align} C_{150}^{2} & =frac{150!}{2!cdot 148!}= \ & =frac{150cdot 149cdot 148cdot …cdot 1}{2cdot 1cdot 148cdot …cdot 1}= \ & =frac{150cdot 149}{2cdot 1}= \ & =11175 end{align}]
Видим, что факториалы образуют «длинные хвосты» в числителе и знаменателе, которые легко сокращаются. Однако для корректной работы с биномом Ньютона нам потребуется расширить определение факториала.
4.1. Новое определение факториала
Стандартное определение мы уже привели выше:
[n!=1cdot 2cdot 3cdot …cdot n,quad nin mathbb{N}]
Но как посчитать, например, факториал нуля? И как сокращать «длинные хвосты», не расписывая факториалы? Здесь нам поможет более грамотное определение.
Определение. Пусть $nin mathbb{N}bigcup left{ 0 right}$ — целое неотрицательное число. Тогда факториал считается по формуле:
[n!=left{ begin{align} & 1,quad n=0 \ & ncdot left( n-1 right)!,quad n gt 0 \ end{align} right.]
В частности, $0!=1$ по определению.
Простейшие коэффициенты:
[begin{align} C_{n}^{0} & =frac{n!}{0!left( n-0 right)!}=frac{n!}{1cdot n!}=1; \ C_{n}^{1} & =frac{n!}{1!left( n-1 right)!}=frac{ncdot left( n-1 right)!}{1cdot left( n-1 right)!}=n; \ end{align}]
А вот ещё парочка весёлых примеров:
[begin{align} C_{7}^{3} & =frac{7cdot 6cdot 5cdot 4cdot ldots cdot 1}{3cdot 2cdot 1cdot 4cdot ldots cdot 1}=35 \ C_{8}^{2} & =frac{8cdot 7cdot 6cdot ldots cdot 1}{2cdot 1cdot 6cdot ldots cdot 1}=28 \ C_{64}^{3} & =frac{64cdot 63cdot 62cdot 61cdot ldots cdot 1}{3cdot 2cdot 1cdot 61cdot ldots cdot 1}= \ & =41664 end{align}]
5. Треугольник Паскаля
Посчитаем бином Ньютона для $n=0$, $n=1$, $n=2$, $n=3$:
[begin{align} & {{left( a+b right)}^{0}}=1 \ & {{left( a+b right)}^{1}}=1cdot a+1cdot b \ & {{left( a+b right)}^{2}}=1cdot {{a}^{2}}+2cdot ab+1cdot {{b}^{2}} \ & {{left( a+b right)}^{3}}=1cdot {{a}^{3}}+3cdot {{a}^{2}}b+3cdot a{{b}^{2}}+1cdot {{b}^{3}} \ end{align}]
Составим таблицу:
[begin{matrix} 1 \ 1quad 1 \ 1quad 2quad 1 \ 1quad 3quad 3quad 1 \ 1quad 4quad 6quad 4quad 1 \ end{matrix}]
Получили треугольник, который в народе называют «Треугольник Паскаля»: по бокам единицы, а внутри каждое число равно сумме двух ближайших, стоящих этажом выше:
[begin{align} & 3=1+2 \ & 4=1+3 \ & 6=3+3 \ end{align}]
И это не случайность. Перед нами важнейшее свойство биноминальных коэффициентов, которое мы оформим в виде теоремы и докажем.
Теорема. Биноминальные коэффициенты вычисляются по формуле
[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]
Доказывается напролом.
Распишем доказательство детально:
[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!}]
[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!} \ end{align}]
Заметим, что по определению факториала
[begin{align} & left( k+1 right)!=left( k+1 right)cdot k! \ & left( n-k right)!=left( n-k right)cdot left( n-k-1 right)! end{align}]
Поэтому знаменатели биноминальных коэффициентов можно переписать:
[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)left( n-k-1 right)!}+frac{n!}{left( k+1 right)k!left( n-k-1 right)!}]
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{n!}{k!left( n-k right)left( n-k-1 right)!}+ \ & +frac{n!}{left( k+1 right)k!left( n-k-1 right)!} end{align}]
Приведём к общему знаменателю:
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} end{align}]
[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ = & frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}=frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} \ end{align}]
Окончательно получим:
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( n+1 right)!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)!}{left( k+1 right)!left( n+1-left( k+1 right) right)!}= \ & = C_{n+1}^{k+1} end{align}]
Теорема доказана. Теперь мы знаем, как формируется треугольник Паскаля. Осталось доказать сам Бином Ньютона.
6. Доказательство Бинома Ньютона
Итак, нужно доказать, что
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $C_{n}^{k}$ — биноминальные коэффициенты с теми чудесными свойствами, которые мы рассмотрели и доказали выше.
Будем доказывать по индукции.
6.1. База индукции
Рассмотрим $n=1$. Формула Бинома Ньютона для него:
[begin{align} {{left( a+b right)}^{1}} & =sumlimits_{k=0}^{1}{C_{1}^{k}{{a}^{1-k}}{{b}^{k}}}= \ & =C_{1}^{0}{{a}^{1}}{{b}^{0}}+C_{1}^{1}{{a}^{0}}{{b}^{1}}= \ & =a+bend{align}]
Очевидно, для $n=1$ формула верна. Переходим к индуктивному предположению.
6.2. Индуктивное предположение
Пусть Бином Ньютона верен для некоторого $n=t$:
[{{left( a+b right)}^{t}}=sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}]
Используя этот факт, докажем верность и для $n=t+1$, т.е. выполним индуктивный переход.
6.3. Индуктивный переход
Докажем, что бином Ньютона верен для $n=t+1$:
[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
Для этого сначала заметим, что
[{{left( a+b right)}^{t+1}}={{left( a+b right)}^{t}}cdot left( a+b right)]
Однако согласно индуктивному предположению, ${{left( a+b right)}^{t}}$ допускает разложение по Биному Ньютона, поэтому
[begin{align} left( a+b right)cdot {{left( a+b right)}^{t}} & =left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} end{align}]
[begin{align} & left( a+b right)cdot {{left( a+b right)}^{t}}= \ = & left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} \ end{align}]
Запишем отдельно первое слагаемое первой суммы и учтём, что $C_{t}^{0}=C_{t+1}^{0}=1$:
[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} & = C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ & = C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}= \ = & C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]
И последнее слагаемое последней второй суммы и учтём, что $C_{t}^{t}=C_{t+1}^{t+1}=1$:
[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Сейчас будет самая нетривиальная операция. Меняем индекс суммирования в последней сумме: выполняем подстановку $k=m-1$. При этом меняются и пределы суммирования:
[left[ begin{align} k & =m-1 \ k & =0Rightarrow m=1 \ k & =t-1Rightarrow m=t \ k+1 & =m \ t-k & =t+1-m \ end{align} right]]
В итоге последняя сумма перепишется так:
[sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]
[begin{align} & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ = & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Объединяем суммы вместе:
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+ \ + & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Заметим, что два знака суммы различаются лишь названием индекса и биноминальными коэффициентами. Всё остальное — диапазоны суммирования, степени буквы $a$ и буквы $b$ — всё идеально совпадает и никак не меняется, если написать вместо $k$ индекс $m$ или наоборот.
Такие суммы можно записать под единым знаком:
[C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]
[begin{align} & C_{t+1}^{0}cdot {{a}^{t+1}}+ \ + & sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+ \ + & C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Выражение под знаком суммы легко раскладывается на множители:
[begin{align} C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} & =left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ & =C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} end{align}]
[begin{align} & C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} \ end{align}]
Здесь в последнем шаге мы использовали свойство биноминальных коэффициентов, доказанное выше:
[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]
Или, что то же самое
[C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k}]
Таким образом, всю сумму можно переписать более компактно, а затем внести под знак суммы первое и последнее слагаемое:
[ C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
[begin{align} C_{t+1}^{0}cdot {{a}^{t+1}} & +sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ & =sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]
Сопоставляя исходное выражение и конечное, получим
[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
Именно это и требовалось доказать. Следовательно, исходная формула Бинома Ньютона верна.
Смотрите также:
- Схема Горнера
- Теорема Безу и корни многочленов
- Знаки тригонометрических функций
- Уравнение касательной к графику функции
- Как представить обычную дробь в виде десятичной
- Сложные задачи B2 на проценты: вычисление полной стоимости
Видеоурок 1: Сочетания
Видеоурок 2: Перестановки
Видеоурок 3: Бином Ньютона
Лекция: Формулы числа сочетаний и перестановок. Бином Ньютона

Существует основные формулы для сочетаний и перестановок:
В данной таблице важно внимательно смотреть на условие задачи: по горизонтали происходит разделение формул в зависимости от возможности повторения элементов. По вертикали сверху описаны случаи задач, в которых важен или не важен порядок элементов. А снизу Вы можете наблюдать задания, которые следует выполнить над элементами.

С частным случаем Бинома Ньютона мы уже сталкивались при использовании формул сокращенного умножения, а именно при возведении суммы или разности чисел во вторую и в третью степень. Сейчас же мы рассмотрим формулу, которая позволит возвести сумму некоторых двух чисел в любую степень.
Формула Бинома Ньютона:
Чтобы найти коэффициенты, следует воспользоваться сочетательным законом комбинаторики без повторений:
Давайте для начала рассмотрим знакомую нам формулу и как она получилась:

Для более простого подсчета коэффициентов Бинома Ньютона для невысоких степеней удобно пользоваться треугольником Паскаля:
Данный треугольник несложно вычислить и самостоятельно. По бокам в каждой строчке имеется коэффициент, равный единице. Все средние коэффициенты считаются, как сумма верхних, которые находятся над ними.
Существует очень важное свойство коэффициентов для Бинома Ньютона, которое позволит проверить правильность их расставления. Для этого необходимо сложить все коэффициенты на четных местах, затем сложить коэффициенты на нечетных местах, после чего сравнить полученные значения. Они должны получиться равными.
Материалы для подготовки к ЕГЭ. Онлайн-Справочник по математике.
Раздел 6 «Элементы комбинаторики» (§§ 19-20): Размещения, перестановки, сочетания. Формула бинома Ньютона.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Раздел VI. Элементы комбинаторики
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
§ 19. Размещения, перестановки, сочетания.
200. Размещения.
201. Перестановки.
202. Сочетания и их свойства. Треугольник Паскаля.
§ 20. Формула бинома Ньютона.
203. Бином Ньютона.
204. Свойства формулы бинома Ньютона.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Материалы для подготовки к ЕГЭ. Онлайн справочник по математике.
Раздел 6 «Элементы комбинаторики» (§§ 19-20): Размещения, перестановки, сочетания. Формула бинома Ньютона.
Просмотров:
2 190
«Бином Ньютона. Свойства биноминальных коэффициентов».
Цели урока:
— обучающие:
познакомить с формулой бинома Ньютона, научить применять формулу бинома Ньютона при возведении в степень двучлена;
— развивающие:
способствовать развитию памяти, алгоритмического и логического мышления, внимания;
— воспитательные:
продолжить воспитание чувства ответственности, самостоятельности, добросовестности.)
Оборудование:
карточки с теоретическим материалом.
Тип урока – комбинированный;
Формы работы учащихся – фронтальная, индивидуальная.
Ход урока:
1.Организационный момент:
Сообщение темы, целей урока, практической значимости рассматриваемой темы.
2. Актуализация знаний
I. Фронтальный опрос:
1)Что изучает комбинаторика?
2)Какие виды соединений или выборок вам известны?
3) Отгадать кроссворд «Комбинаторика».
II. Устный счет:
-
5!=….(120), А52 =…(20)., С42=….(8)
-
Сколькими способами можно разместить 5 человек на скамейке?
-
Изложение нового материала.
-
Работа с карточками.
I) История комбинаторики.
На прошлом уроке мы познакомились с основами комбинаторики.
-
Какие же ученые внесли вклад в развитие комбинаторики как науки?
-
Одним из выдающихся умов того времени был английский ученый Исаак Ньютон.
II) Исаак Ньютон- великий математик.
Вы услышали из доклада, сколько гениальных идей и открытий принадлежит великому математику Исааку Ньютону. Одним из его открытий является формула Бином Ньютона.
III)Бином Ньютона.
Именно этому открытию мы посвятим наш сегодняшний урок. Запишем тему урока.
Цели нашего урока:
познакомиться с формулой бинома Ньютона, научиться применять формулу бинома Ньютона при возведении в степень двучлена.
Слово бином означает «Два числа» В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.
Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
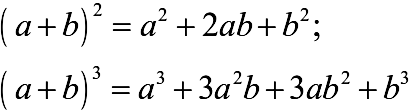
Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах
Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?
Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
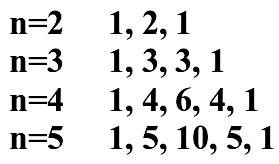
Возможно, вы уже догадались, что «рояль в кустах» – это треугольник Паскаля на предыдущей странице. Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):
Окончательно получим:
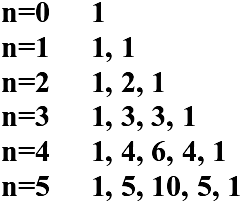
Это утверждение было известно задолго до Паскаля — его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло). Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел (биномиальных коэффициентов) до
включительно.
Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.
IV) Блез Паскаль.
Теперь понятно, как возвести бином в любую степень n. В левой части записываем (а+b)n. А в правой части записываем сумму аn + аn-1b + … + bn, оставляя в каждом слагаемом место для коэффициента. И эти места заполняем числами из n–ой строчки треугольника Паскаля, которую, конечно, нужно заранее выписать.
Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:
(a + b)n = an + C1n an — 1 b + C2n an — 2 b2 +…+Ckn an — kbk +… + Cn — 1nabn — 1 + Cnnbn
где Ckn —все возможные сочетания, которые можно образовать из n элементов по k.
Пример:
(a + b)5 = a5 + C15 a4b + C25 a3b2 + C35 a2b3 + C45 ab4 + C55 b5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
Таким образом можно записать формулу для возведения двучлена в любую степень. Давайте заметим некоторые свойства у слагаемых в разложении двучлена по формуле Бинома Ньютона.
V)Свойства бинома Ньютона.
-
Число слагаемых на 1 больше степени бинома.
-
Коэффициенты находятся по треугольнику Паскаля или равны числу сочетаний С
, где n – степень двучлена , m – переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.
-
Коэффициенты симметричны.
-
Если в скобке знак минус, то знаки + и – чередуются.
-
Сумма степеней каждого слагаемого равна степени бинома.
-
Сумма коэффициентов разложения ( a + b) n равна 2 n .
VI) Закрепление нового материала.

Мы знакомились с вами с применением бинома Ньютона при изучении формул сокращенного умножения: Где же ещё применяется Бином Ньютона?
VII) Применение Бинома Ньютона.
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Пример.
Доказать, что значение выражения , где n – натуральное число, делится на 16 без остатка.
Решение.
Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:
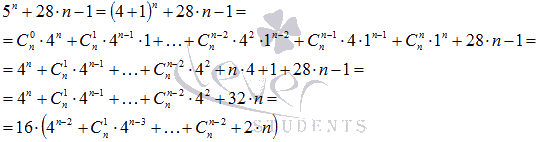
-
Полученное произведение доказывает делимость исходного выражения на 16. Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница
VIII) Что означает фразеологизм «Бином Ньютона»?
Шутливая фраза, применяется по отношению к плевому делу, простой задаче, которую некоторые ошибочно считают непосильной для выполнения или архисложной.
Возникновение фразы: из романа Михаила Булгакова (1891 — 1940 гг.) «Мастер и Маргарита» (1940 г.).
Слова Коровьева, которые решил прокомментировать разговор Воланда с буфетчиком Соковым. Буфетчик жалуется на зрителей, которые расплатились с ним фальшивыми деньгами, чем «на сто девять рублей наказали буфет».
« — Ну, конечно, это не сумма, — снисходительно сказал Воланд своему гостю, — хотя, впрочем, и она, собственно, вам не нужна. Вы когда умрете?
Тут уж буфетчик возмутился.
— Это никому не известно и никого не касается, — ответил он.
— Ну да, неизвестно, — послышался все тот же дрянной голос (Коровьева) из кабинета, — подумаешь, бином Ньютона! Умрет он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвертой палате».
IX) Итоги урока. Рефлексия
Подумаешь, Бином Ньютона
Оскар Хуторянский
«Подумаешь, Бином Ньютона»
Кот промяукал Бегемот
(Он Воланда слуга покорный),
Предсказывая жизни ход.
Все это только подтверждает
Ньютона гений, но давно
Бином известен был в Китае,
Арабы знали про него.
Но обобщил Ньютон решение,
Возвёл он в степень многочлен…
Избавил нас от всех сомнений
Других же нет у нас проблем.
Скажите нам совсем без прений
Зачем нам нужен тот бином?
Комбинаторику явлений
Мы без бинома не найдём.
— Что нового вы узнали на уроке? Важна ли эта формула для математики? Трудно ли вам было усваивать новый материал?
Дополнительное задание.
1.Из 12 членов команды нужно выбрать капитана и заместителя. Сколькими способами можно это сделать?
2.Вычислите: 4Р3+3А210-С25
-
Выпускники экономического института работают в трех различных организациях: 17 человек в банке,23- в фирме и 19-в налоговой инспекции. Найдите вероятность того, что случайно встреченный выпускник работает в банке?
-
Имеется 8 различных книг 2 из которых сборники стихов. Сколькими способами можно расставить эти книги на полке так, чтобы справочники оказались рядом?
-
Для игры в КВН нужно выбрать команду из 6 человек, Сколькими способами можно это сделать, если в команде должно быть мальчиков и девочек поровну,и в классе 12 девочек и 10 мальчиков?
-
Сколько трехзначных чисел с разными цифрами можно составить из цифр , 0,1,3,6,7,9?
-
Разложите на множители: (a-b)9 и (3x+y)10
В данной статье мы рассмотрим темы раздела элементов комбинаторики по математике, задания этого раздела наиболее часто встречаются на ЕГЭ по математике базового уровня, итак, перейдём к рассмотрению темы.
Комбинаторика и выборка. Определения и вид
Комбинаторикой называют науку, которая изучает способы составления.
Выборкой называют подмножество, которое составлено из элементов конечного подмножества.
Упорядоченным подмножеством называют множество, в котором определено, какой элемент следует либо какому предшествует. Если поменять место элементов, то получится совсем другое множество.
Также выборкой называют результат отбора, а также извлечение предпочитаемого из наличного.
Как правило, комбинаторная задача включает в себя подсчёт числа выборок из основных элементов М (а1, а2, а3, …). Выборки бывают разного объёма (то есть с разным количеством выбираемых элементов), порядка (то есть неупорядоченные и упорядоченные), повторения (наличие элементов, которые встречаются несколько раз).
Различают три вида соединений для выборок:
– Размещение;
– Перестановка;
– Сочетание.
Размещением из n элементов по k называют выборку, каждая из которых содержит элементы из множества n. Размещения различают по порядку элементов. Определённые элементы в множестве могут находиться повторно, их называют кортежами или повторяющимися размещениями. Длиной элементов называют их число в размещении. Размещения с повторениями – выборка, которая состоит из n не всегда отличающихся элементов.
Перестановкой с повторением называют размещения, составляющие не всегда разные элементы из основного множества n. Pn – количество перестановок, содержащих повторения.
Размещения без повторений – k-элементы, из разных элементов множества. Ak – количество размещений, состоящих из n элементов по k.
Неупорядоченные выборки (одновременный выбор). Сочетания, не имеющие повторений.
Сочетания, состоящие из n элементов по k называют соединениями, которые содержат k-элементы. Их отличие состоят из одного элемента.
Для нас важны только сами элементы множества, порядок не имеет большого значения. Нужно определять, элементы, которые содержаться в соединении. Cn^k – количество сочетаний (число подмножеств) k из множества, которое содержит n элементы. Видно, что при рассмотрении сочетаний из n по k и их упорядочении различными способами мы получим: An^k = Cn^k * Pk.
Сочетаниями с повторениями называют неупорядоченную выборку, которая состоит из n не всегда разных элементов. Сочетания с обозначениями обозначают следующим образом: Ckn.
Таким образом, мы рассмотрели основные понятия, встречающиеся в комбинаторике, виды соединений, а также их характеристики.
Итак, перейдём к рассмотрению темы формул числа сочетаний и перестановок. Рассмотрим данные формулы, для складывания чёткого понимания их следует рассматривать в виде таблицы:
| Порядок важен | Порядок неважен | ||
| Без повторений | A nk = n! / ( n – k )! | Pn = A nn = n! | С kn = n! / ( n – k ) ! k! |
| С повторениями | A nk = n^k | Pn = A nn = n^n P ( k1, k2, …kn ) = ( k1, k2,…kn )! / k1!k2,…, kn! | Ckn = ( n + k – 1)! / ( n – 1! )k! |
| Размещения | Перестановки | Сочетания |
В этой таблице нужно внимательно читать условия задач, то есть по горизонтали распределены формулы в соответствии с зависимостью от повторения элементов, а по вертикали указаны примеры задач, в которых порядок элементов может быть, как важен, так и не важен. В конце таблицы указаны действия, которые можно выполнять по отношению к элементам.
Таким образом, рассматривая формулы в виде таблицы не сложно запомнить и в случае надобности применить при решении заданий ЕГЭ по математике, следует учитывать, что формулы делят на две группы: формулы, где важен порядок, а также, где неважен.
Бином Ньютона
С темой Бинома можно столкнуться при применении формул сокращённого умножения, а конкретно при возведении сложения либо вычитания чисел в различных степенях. Рассмотрим формулы, позволяющую возвести сумму разных двух чисел в определённую степень: ( a + b )^n = С 0n * a^n + С 1n * a^( n – 1 ) * b + С 2n * a^( n – 2 ) * b^2 + …+ С n-1 n * a * b^( n – 1 ) + С nn * b^n.
Для нахождения коэффициентов воспользуемся сочетательным законом комбинаторики, не содержащего повторения: С kn = ( n )! / ( k )! * ( n – k )! = n ( n -1 ) ( n – 2 ) * …( n – ( k – 1 )) / ( k )! – биномиальные коэффициенты.
Рассмотрим ранее встречающуюся формулу и разберём её получение: ( a + b )^2 = С 02 * ф:2 + С 1 2 * a^1 * b + С 2 2 * b^2 = a^2 + 2ab + b^2.
Также существуют коэффициенты Бинома Ньютона. Для их подсчёта принято использовать треугольник Паскаля.
Этот треугольник не составляет труда вычислить самостоятельно. В боковых строках расположены коэффициенты, которые равны единицы. Коэффициенты, расположенные посередине считают в виде суммы верхних. Существует важное свойство коэффициентов для Бинома Ньютона, они помогают проверять правильность их расстановки. Для этого нужно складывать все имеющиеся коэффициенты, расположенные на чётных местах и выполнить сложение коэффициентов на нечётных местах. Далее следует сравнить полученные значения. Они должны быть одинаковым.
Распределение заданий в экзаменационной работе
У многих выпускников при подготовке к ЕГЭ возникают вопросы к содержанию КИМов. Поэтому уделим небольшое количество времени этому вопросу.
Задания, содержащиеся в КИМах определяются в соответствии с кодификатором, содержащим требования к проведению ЕГЭ. Кодификатор составлен в соответствии с содержанием программ обучения, то есть их минимумом, являющимся обязательным. Кодификатор включает в себя код раздела и умений, а также основные требования к проверяемым заданиям на экзамене.
Сама работа включает в себя часть, состоящую из двадцати заданий, которые требуют краткие ответы. Ответами являются целые числа либо десятичные дроби, также ответом может быть определённая последовательность чисел. Как правило, ответы вписывают в бланки формы №, она предусматривается инструкцией к выполнению заданий.
Рассмотрим структуру заданий, содержащихся в КИМах ЕГЭ по математике, а также их подразделы:
– Задания из раздела алгебры (числа, степени, тригонометрия, логарифмы, преобразование выражений);
– Задания, содержащие уравнения и неравенства;
– Задания с функциями, а также их определения (графики, монотонность, чётность / нечётность);
– Задания, содержащие начала математического анализа (производные, исследования функций, интегралы, первообразные);
– Задания раздела геометрии (планиметрия, прямые и плоскости, многогранники, геометрические величины и их измерения);
– Задания раздела комбинаторики (теории вероятностей и так далее).
Система оценивания заданий следующая: один правильный ответ = один балл. Максимальное количество баллов, которые можно набрать – двадцать.
Также у выпускников часто возникает вопрос о времени, которое даётся на выполнение заданий, итак, продолжительность ЕГЭ по математике составляет три часа, то есть сто восемьдесят минут.
Таким образом, при подготовке к экзамену рекомендуем использовать данный в статье материал, а также изучить дополнительный, включающий в себя методические материалы, просмотреть и решить демонстрационные варианты экзамена, их вы можете найти на нашем сайте.
Алгебра и начала математического анализа, 11 класс
Урок №31. Сочетания без повторений. Бином Ньютона
Перечень вопросов, рассматриваемых в теме
1) понятие сочетания без повторения и их свойства;
2) правила подсчета числа сочетаний из n-элементов по m без повторений;
3) бином Ньютона;
4) треугольник Паскаля.
Глоссарий по теме
Сочетаниями из n элементов по m в каждом (m ≤ n) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.
Число всевозможных сочетаний из n различных элементов по m элементов обозначают
Формула для подсчёта числа сочетаний:
Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.
Числа 
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Общим термином «соединения» в комбинаторике называют три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству. Ранее уже рассматривались два вида комбинаций. Это перестановки и размещения. В данных соединениях важен порядок размещения элементов. В случае, когда этот порядок не важен, то мы имеем дело с сочетаниями.
Сочетаниями из n элементов по m в каждом (m ≤ n ) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.
Иногда такие сочетания называют сочетаниями без повторений.
Число всевозможных сочетаний из из n элементов по m элементов обозначают
Формула для подсчёта числа сочетаний:
Используя данную формулу можно отметить основные свойства сочетаний.
Простейшие свойства сочетаний:
1)
2)
3)
Доказательства свойства сочетаний
1)
2)
3)
При возведении суммы или разности двух чисел во вторую или третью степень мы пользовались формулами сокращенного умножения, которые являются частным случаем бинома Ньютона.
Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.
Числа 
Для более простого подсчета коэффициентов Бинома Ньютона для невысоких степеней удобно пользоваться треугольником Паскаля:
По бокам в каждой строчки имеется коэффициент, равный единице. Все средние коэффициенты считаются, как сумма верхних, которые находятся над ними.
Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.
Не трудно заметить, что строки треугольника симметричны относительно вертикальной оси. Это еще одно замечательное свойство треугольника Паскаля
Историческая справка
Исаак Ньютон (1642-1727 гг.) – выдающийся английский ученый, один из создателей классической физики. Биография Ньютона богата во всех смыслах этого слова. Он сделал немало открытий в области физики, астрономии, механике и математике. Ньютон является автором фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета, заложил основы современной физической оптики, создал многие другие математические и физические теории.
А при чем же здесь бином Ньютона и биномиальные коэффициенты? Формула
была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени произвольное рациональное число (возможно, отрицательное).
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
В вазе лежат двенадцать конфет, четыре из которых шоколадные, а остальные карамель. Вы хотите угоститься, выбрав две шоколадные и три карамельные конфеты. Сколькими способами вы можете это сделать?
Решение :
Мы имеем два события. Это выбор шоколадных и выбор карамельных конфет. Порядок конфет не важен. Поэтому мы можем использовать формулу сочетания для каждого из событий. Так, как шоколадных конфет всего четыре, а выбрать мы хотим две, то это можно сделать способами 
1)
Теперь посчитаем количество выбора карамельных конфет. Их общее количество в вазе 12-4=8, а выбрать мы хотим три. Рассчитаем сочетание из восьми по три.
2)
События выбора разных видов конфет между собой независимы, поэтому по правилу умножения получаем
3)
Ответ: 336
Пример 2.
Представить разложение двучлена в n степени в виде многочлена, где n=0, 1, 2, …,5
Решение:
Первые четыре разложения мы хорошо умеем делать, используя формулы квадрата и куба разности.
А для представления бинома четвертой и пятой степени воспользуемся треугольником Паскаля.



















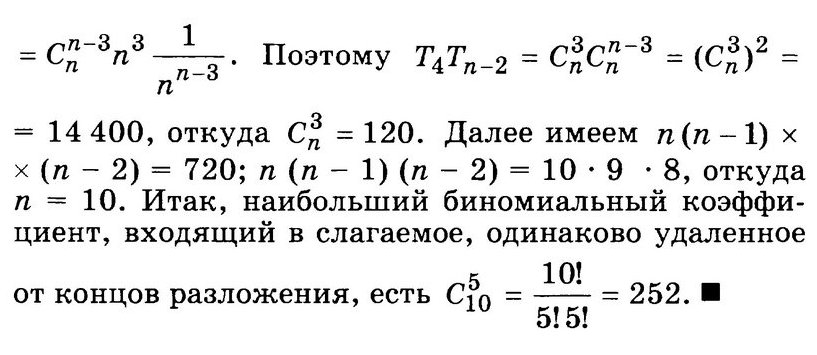
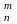 , где n – степень двучлена , m – переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.
, где n – степень двучлена , m – переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.





























