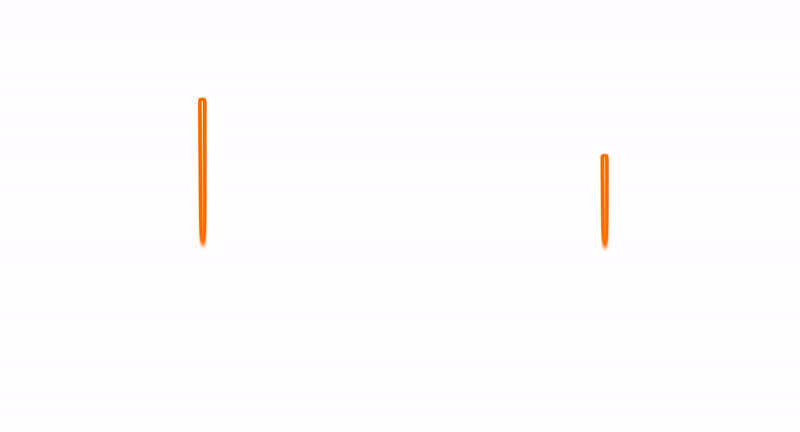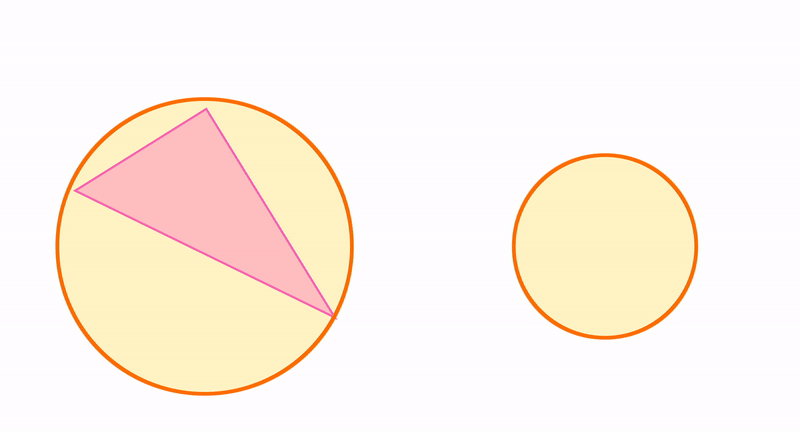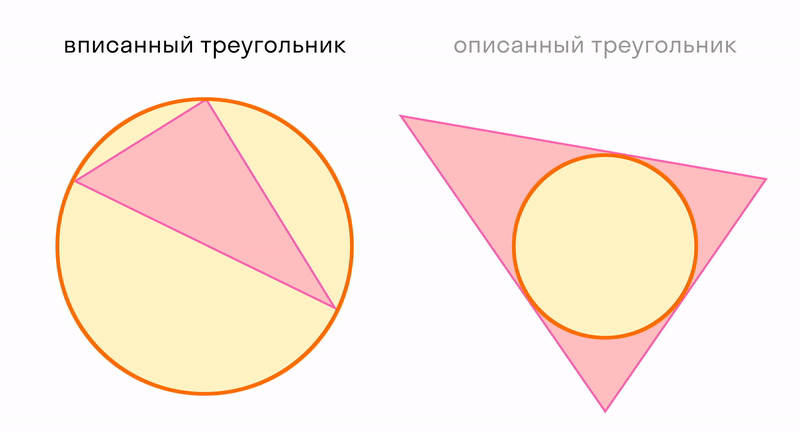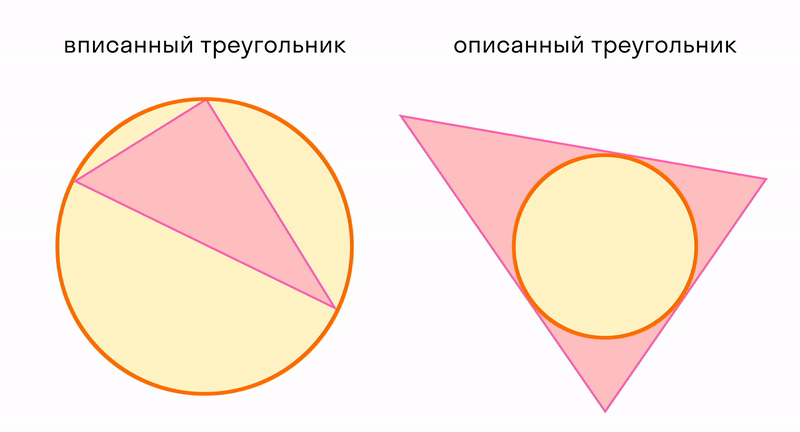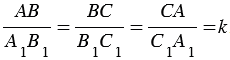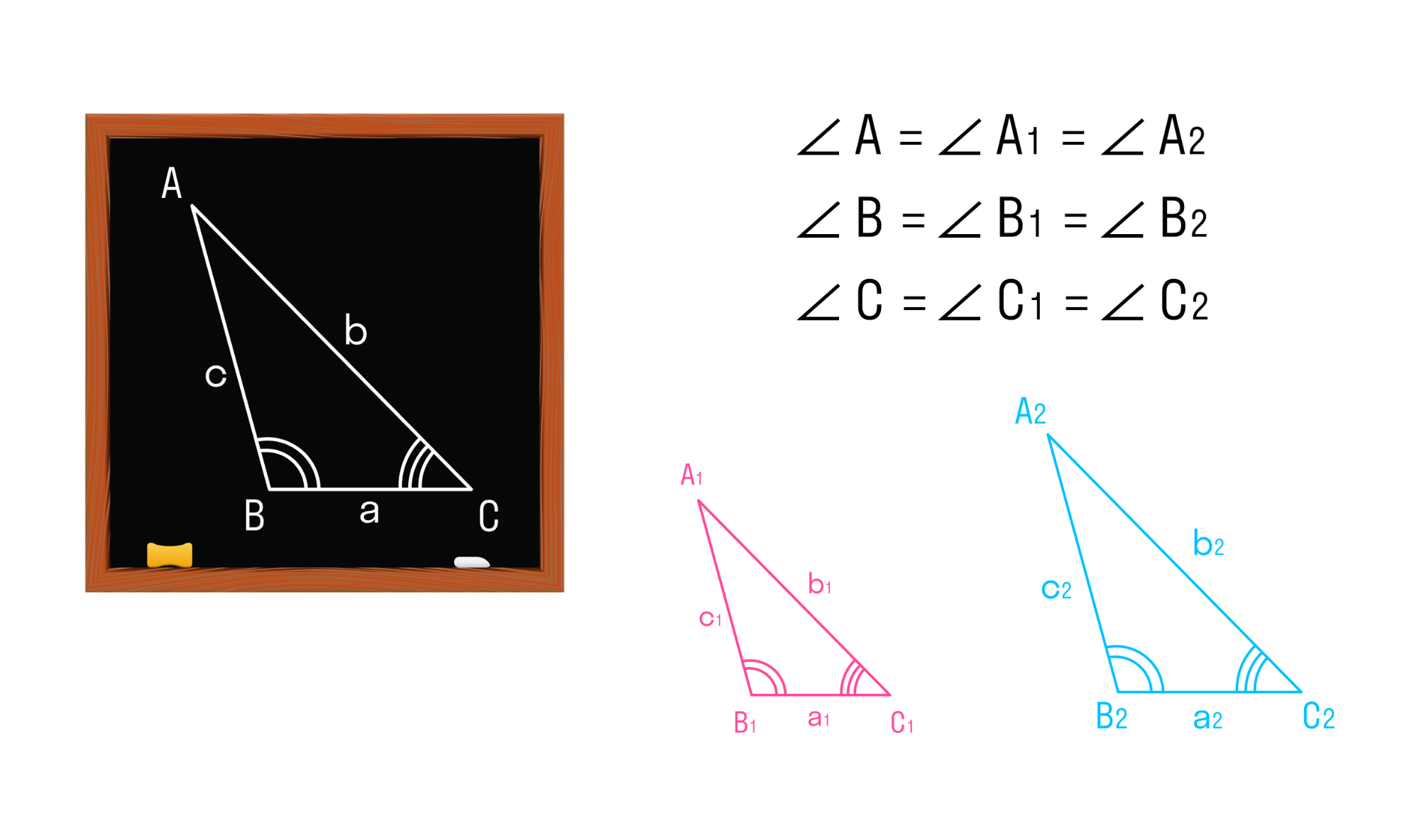Ученики, для которых на ЕГЭ геометрия — это что-то страшное, часто через силу пытаются выучить предмет и получают посредственные баллы. Вместо этого можно просто поменять свою подготовку. В этой статье мы расскажем, с помощью каких учебников изучать теорию, где решать задачи и как оформлять ответы правильно.
Учебники для подготовки
Многое решает то, по каким пособиям вы готовитесь к ЕГЭ. Геометрия могла быть легкой в 2020-м году, но какой от этого толк, если в 2021-м все поменяли?
Бывает и другая ситуация: ученик по десять раз читает одну страницу теории, чтобы понять хоть одно слово. А в другом учебнике такая информация уложена в две строчки и объяснена понятнее.
Вот учебники, с которыми на ЕГЭ геометрия будет легко решаема:
- Шарыгин И.Ф. «Наглядная геометрия»;
- Золотарева Н.Д. «Геометрия. Базовый курс с решениями и указаниями»;
- Золотарева Н.Д. «Геометрия. Углубленный курс с решениями и указаниями»;
- Акопян А.В. «Геометрия в картинках».
Некоторые из них простым языком объясняют, почему на ЕГЭ геометрия такая сложная. Книга Акопяна же для людей с опытом — в ней нет ни одного слова (кроме заголовков), сплошные чертежи.
Что и где решать?
После изучения теории нужно обязательно закрепить материал решением задач. Где это делать, чтобы на ЕГЭ геометрия не казалось страшной? Давайте разбираться.
- РешуЕГЭ. Этот сервис можно использовать для отработки своих знаний, так как на нем удобно выбирать конкретные задачи для закрепления и составлять свой собственный вариант. Однако, на нем можно встретить задания с ошибками, версии задач прошлого года, поэтому нужно тщательно фильтровать все, что попадается там. Если не хотите тратить на это время, а сосредоточиться на ЕГЭ — геометрия есть и на других сервисах.
- Открытый банк заданий ФИПИ. На сайте официального составителя ЕГЭ геометрия не покажется сложной. А еще можно не волноваться за ошибки в заданиях.
- Незнайка. Это сайт для отработки всех предметов на ЕГЭ. Геометрия тоже там есть. На сайте собрано много вариантов для решения любого предмета — нужно просто выбрать, что необходимо подтянуть. Теории там нет, но есть возможность посмотреть решение задач других пользователей и почерпнуть для себя что-то новое.
- Варианты Алекса Ларина. Про них и говорить не нужно — они сложные, но после них на ЕГЭ геометрия будет решаться на «ура».
Помимо этого нужно учиться правильно оформлять ответы. Об этом поговорим ниже.
Как правильно оформлять ответы
Представьте, что вы объясняете, почему на ЕГЭ геометрия такая сложная, человеку, который вообще не знает предмет. Вы будете описывать каждое действие, чтобы он понял последовательность и мог отследить ход мыслей. Также и здесь.
Оформление должно быть:
- Четким;
- Структурированным;
- Понятным;
- Развернутым.
Это не значит, что эксперты не разбираются в предмете. Как раз таки наоборот, им нужно знать, что на ЕГЭ геометрия не была для вас непонятной. И всегда стоит держать в голове мысль, что не всё очевидное для вас является таким для всех остальных. Кстати, не только во время экзамена.
Что делать, если совсем не понимаешь геометрию
В таком случае есть два пути:
- Сосредоточиться на ней. Но в таком случае вы можете испортить свои «отношения» с алгеброй, а еще потерять кучу нервов, так как на ЕГЭ геометрия — это отдельный мир с кучей формул, схем, теорем и так далее.
- Забыть о ней и сосредоточиться на алгебре. Если вы будете полностью уверены в том, что справитесь с алгеброй на ЕГЭ, геометрия заберет у вас всего 5-10 баллов.
Стоит исходить из своих целей и уровня знания. Если есть хоть какое-то понимание, можно предпринять попытку. Но если до знания геометрии еще далеко, лучше ее не трогать вообще.
Что будет, если пропустить задания по геометрии
Ничего страшного не произойдет. Развитий событий несколько, но все хорошие:
- Если вы полностью решите только алгебру на ЕГЭ, геометрия заберет только 10 баллов, что равно 90 баллам за экзамен.
- Если решите еще и геометрию B части, то получите 95-96 баллов.
Но для этого нужно хорошо знать алгебру.
Итог
В этой статье мы разобрали, как сделать так, чтобы на ЕГЭ геометрия не оказалась сложной и стоит ли готовиться к ней вообще. Выбор всегда остается за вами, но нужно учитывать все факторы: пригодится ли она вам в дальнейшем, сколько времени у вас есть на подготовку и готовы ли вы тратить нервы, силы и здоровье на изучение этого сложного блока. Только помните, что изучить ее можно и после экзамена, а нервы и здоровье вам еще пригодятся.
Что делать, если я совершенно не понимаю геометрию
Мудрость форума:
Подростки
37 ответов
Последний —
09 декабря 2022, 07:49
Перейти

05 сентября 2021, 14:01
#2
05 сентября 2021, 14:02
#3
05 сентября 2021, 14:03
#4
Аматерасу-Хатшепсут
Я тоже такая и вуаля — все прекрасно!😺
05 сентября 2021, 14:05
#5

05 сентября 2021, 14:05
#6
Гость
но как вы сдали экзамены?
05 сентября 2021, 14:12
#7
05 сентября 2021, 14:13
#8
05 сентября 2021, 14:17
#9
05 сентября 2021, 14:18
#10
05 сентября 2021, 14:25
#11

05 сентября 2021, 14:27
#12

05 сентября 2021, 14:35
#13
05 сентября 2021, 14:37
#14
05 сентября 2021, 14:46
#15
Гость
Просто тупая. Будешь в магазине работать, там геометрия не понадобится.
05 сентября 2021, 14:48
#16
Гость
Как можно понимать алгебру и не понимать геометрию???
05 сентября 2021, 15:02
#17
05 сентября 2021, 15:54
#18
05 сентября 2021, 18:45
#19
Гость
Как можно понимать алгебру и не понимать геометрию???
05 сентября 2021, 18:50
#20
Гость
Я тоже в недоумении, я вот гуманитарий от и до, но геометрию знала на отлично, она же прикладная и наглядная наука. Вот с алгеброй я уже страдала, потому что там всё гораздо сложней.
05 сентября 2021, 19:09
#21
05 сентября 2021, 19:10
#22
Гость
Такая же была ситуация. Математика явно не мое. Огэ сдала на 4, 9 класс там не сложно сдать математику. В 11 не сдавала, пошла в медицинский и проблема исчезла.
05 сентября 2021, 19:15
#23
Гость
Как можно понимать алгебру и не понимать геометрию???
Эксперты Woman.ru
-
Владимир Титаренко
Фитнес-нутрициолог
188 ответов
-
Алёшина Мария
Психолог
116 ответов
-
Иванова Светлана
Коуч
86 ответов
-
Анна Антончик
Женский психолог
163 ответа
-
Максим Сорокин
Практикующий психолог
1 056
-
Международный Институт
Психология, психотерапия,…
20 ответов
-
Токарь Дарья Анатольевна
Фитнес-тренер
53 ответа
-
Мария Бурлакова
Психолог
335 ответов
-
Мария Синяпкина
Психолог-Сексолог
92 ответа
-
Кременецкая Мария
Логопед — дефектолог
44 ответа
06 сентября 2021, 00:15
#24
Гость
Как можно понимать алгебру и не понимать геометрию???
06 сентября 2021, 00:23
#25
Гость
Просто тупая. Будешь в магазине работать, там геометрия не понадобится.
06 сентября 2021, 10:28
#26
07 сентября 2021, 00:15
#27
14 октября 2021, 10:07
#28
Гость
Как можно понимать алгебру и не понимать геометрию???
01 ноября 2021, 20:52
#29
Гость
Просто тупая. Будешь в магазине работать, там геометрия не понадобится.
10 ноября 2021, 19:05
#30
Гость
Как можно понимать алгебру и не понимать геометрию???
01 февраля 2022, 17:51
#31
Гость
Как можно понимать алгебру и не понимать геометрию???
01 февраля 2022, 17:55
#32
Гость
Я тоже в недоумении, я вот гуманитарий от и до, но геометрию знала на отлично, она же прикладная и наглядная наука. Вот с алгеброй я уже страдала, потому что там всё гораздо сложней.
Гость
Как можно понимать алгебру и не понимать геометрию???
20 сентября 2022, 14:37
#35
18 ноября 2022, 21:17
#36
Гость
Как можно понимать алгебру и не понимать геометрию???
09 декабря 2022, 07:49
#37
Загрузить PDF
Загрузить PDF
Геометрия — это наука о фигурах и углах, она может оказаться сложной для многих учащихся. При первом ознакомлении многие идеи геометрии кажутся абсолютно новыми, что может вызвать замешательство. Для геометрии характерно большое количество аксиом, теорем, определений и символов, которые необходимо выучить, прежде чем у вас начнет формироваться стройная картина. Тем не менее правильные привычки в учебе и несколько полезных правил помогут вам преуспеть в изучении геометрии.
-
1
Посещайте все занятия. В классе вы сможете усвоить новый материал и закрепить то, что изучали на предыдущих уроках. Если вы не будете посещать занятия, вам будет намного сложнее вовремя усваивать весь изучаемый материал.
- Задавайте на уроках вопросы. Учитель присутствует в классе для того, чтобы помочь вам как следует разобраться в изучаемом материале. Если у вас возник какой-либо вопрос, не стесняйтесь задать его. Возможно, некоторых присутствующих интересует тот же вопрос.
- Готовьтесь к занятиям: заранее читайте соответствующие разделы и разбирайтесь в формулах, теоремах и аксиомах.
- Внимательно слушайте учителя во время уроков. У вас будет время поговорить с одноклассниками на перемене или после занятий.
-
2
Рисуйте схемы. Геометрия изучает фигуры и углы.[1]
Чтобы легче понять материал, представьте задачу, а затем нарисуйте схему или чертеж. Если речь идет об углах, нарисуйте их. Например, свойства вертикальных углов намного легче понять с помощью рисунка. Если в задаче не приведен рисунок, сделайте его самостоятельно.- Чтобы продвинуться в изучении геометрии и понять свойства фигур, представляйте их на схемах и рисунках.
- Потренируйтесь распознавать фигуры в различных ориентациях на основании их геометрических свойств (величин углов, количества параллельных и перпендикулярных линий и тому подобного).
-
3
Организуйте учебную группу. Объединитесь с некоторыми другими одноклассниками в группу — это хороший способ изучить новую информацию и выяснить неясные моменты. Регулярно собирайтесь вместе, чтобы вовремя усваивать пройденный материал и как можно лучше понимать его. Совместные занятия с одноклассниками помогут вам, когда вы перейдете к изучению более сложных разделов. Вы сможете вместе прорабатывать их.
- Скорее всего, кто-нибудь из ваших одноклассников понимает то, в чем вы не разобрались, и поможет вам. Вы также сможете объяснить своим друзьям какой-то материал и при этом лучше усвоите его сами.
-
4
Научитесь пользоваться транспортиром. Транспортир представляет собой полукруглый инструмент для измерения углов. Кроме того, с его помощью можно чертить углы. Узнайте, как пользоваться транспортиром — это необходимый навык при изучении геометрии. Чтобы измерить угол, поступите следующим образом:
- совместите центральное отверстие транспортира с вершиной (острием) угла;
- покрутите транспортир до тех пор, пока его основание (прямая часть) не совпадет с одной из сторон угла;
- продолжите вторую сторону угла до дуги транспортира и запишите угол, при котором они пересекаются. Это будет величина измеряемого угла.
-
5
Выполняйте все домашние задания. Домашняя работа помогает как следует закрепить пройденный материал. Если вы будете выполнять домашние задания, то действительно поймете то, что изучали в классе и узнаете, каким разделам следует уделить больше внимания.
- Во время домашней работы вы сможете неспешно повторить пройденный материал и обратить особое внимание на трудные моменты, чтобы лучше понять их. Если у вас возникнут вопросы, попросите о помощи одноклассников или учителя.
-
6
Объясняйте пройденный материал кому-то другому. Если вы как следует усвоите какую-то тему или идею, то сможете рассказать о ней непосвященному человеку. Если же вы не в состоянии ясно объяснить материал, так чтобы другой человек понял его, возможно, вы недостаточно усвоили его сами. Кроме того, когда вы объясняете какой-либо вопрос, то лучше запоминаете его.[2]
- Попробуйте обучать геометрии своего брата, сестру или одного из родителей.
- Объясняйте в учебной группе темы, в которых вы хорошо разобрались.
-
7
Решайте побольше задач. Геометрия — это не только область знаний, но и своего рода искусство. Простого изучения правил и теорем геометрии недостаточно для того, чтобы получить высокую оценку, для этого необходимо уметь решать задачи. Решайте все задачи, которые учитель задает на дом, а также дополнительные задачи по темам, которые трудно даются.
- Старайтесь решать как можно больше задач из других источников. Помните о том, что схожие задачи могут по-разному формулироваться.
- Чем больше задач вы решите, тем легче сможете решать их в будущем.
-
8
Поищите дополнительную помощь. Иногда посещений занятий и общения с учителем бывает недостаточно. Не исключено, что вам потребуется репетитор, который сможет уделить больше внимания трудным для вас темам. Индивидуальные занятия очень полезны при изучении сложного материала.
- Спросите у своего учителя, нет ли у него знакомых репетиторов.
- Посещайте дополнительные занятия и спрашивайте о том, что вы не до конца поняли.
Реклама
-
1
Запомните пять аксиом евклидовой геометрии. Геометрия основывается на системе постулатов, или аксиом, которые были собраны вместе древнегреческим математиком Евклидом.[3]
Знание и понимание этих аксиом поможет вам усвоить множество различных идей и концепций.- 1. Между любыми двумя точками можно провести прямую линию.
- 2. Ограниченный прямой отрезок можно бесконечно продолжать по прямой.
- 3. Из всякого центра любым размахом циркуля может быть описан круг, причем размах циркуля будет составлять его радиус.
- 4. Все прямые углы равны между собой.
- 5. Если даны прямая и не лежащая на ней точка, то через эту точку можно провести единственную прямую, параллельную данной.
-
2
Изучите используемые в геометрии символы. Когда вы приступите к изучению геометрии, вам покажется, что в ней используется слишком большое количество символов. Однако со временем вы с легкостью сможете распознавать их, что облегчит дальнейшую учебу. Ниже перечислены некоторые из символов, которые наиболее часто используются в геометрии:[4]
- небольшой треугольник обозначает треугольник;
- небольшой угол обозначает угол;
- буквы с линией над ними обозначают конечный отрезок;
- буквы с линией над ними, которая с обеих сторон заканчивается стрелками, обозначают прямую линию;
- горизонтальный отрезок и проведенный из его центра вертикальный отрезок обозначают две взаимно перпендикулярные прямые линии;
- два вертикальных отрезка обозначают две взаимно параллельные линии;
- знак равенства с волнистой линией поверх него означает, что две фигуры конгруэнтны;
- волнистая линия означает, что две фигуры подобны;
- три точки в форме треугольника означают “следовательно”.
-
3
Изучите свойства прямых линий. Прямая линия продолжается бесконечно в обоих направлениях. На концах такой линии ставятся стрелки, чтобы обозначить, что линию можно продолжить дальше. Отрезок имеет начало и конец. Еще один вид прямых линий называется лучом: луч имеет только начало и бесконечно продолжается во втором направлении. Прямые линии, отрезки и лучи могут быть параллельными, перпендикулярными или пересекающимися.[5]
- Параллельные линии никогда не пересекаются друг с другом.
- Перпендикулярными называются линии, которые пересекаются под углом 90°.
- Пересекающимися называются линии, которые пересекаются друг с другом. Пересекающиеся линии могут быть перпендикулярными, но они никогда не могут быть параллельны друг другу.
-
4
Узнайте о разных видах углов. Существует три типа углов: тупые, острые и прямые. Тупыми называются углы, величина которых превышает 90°. Величина острых углов меньше 90°, а прямые углы в точности равны 90°.[6]
При изучении геометрии необходимо знать разницу между различными видами углов.- Угол 90° называют также прямым, или говорят, что образующие его линии пересекаются под прямым углом.
-
5
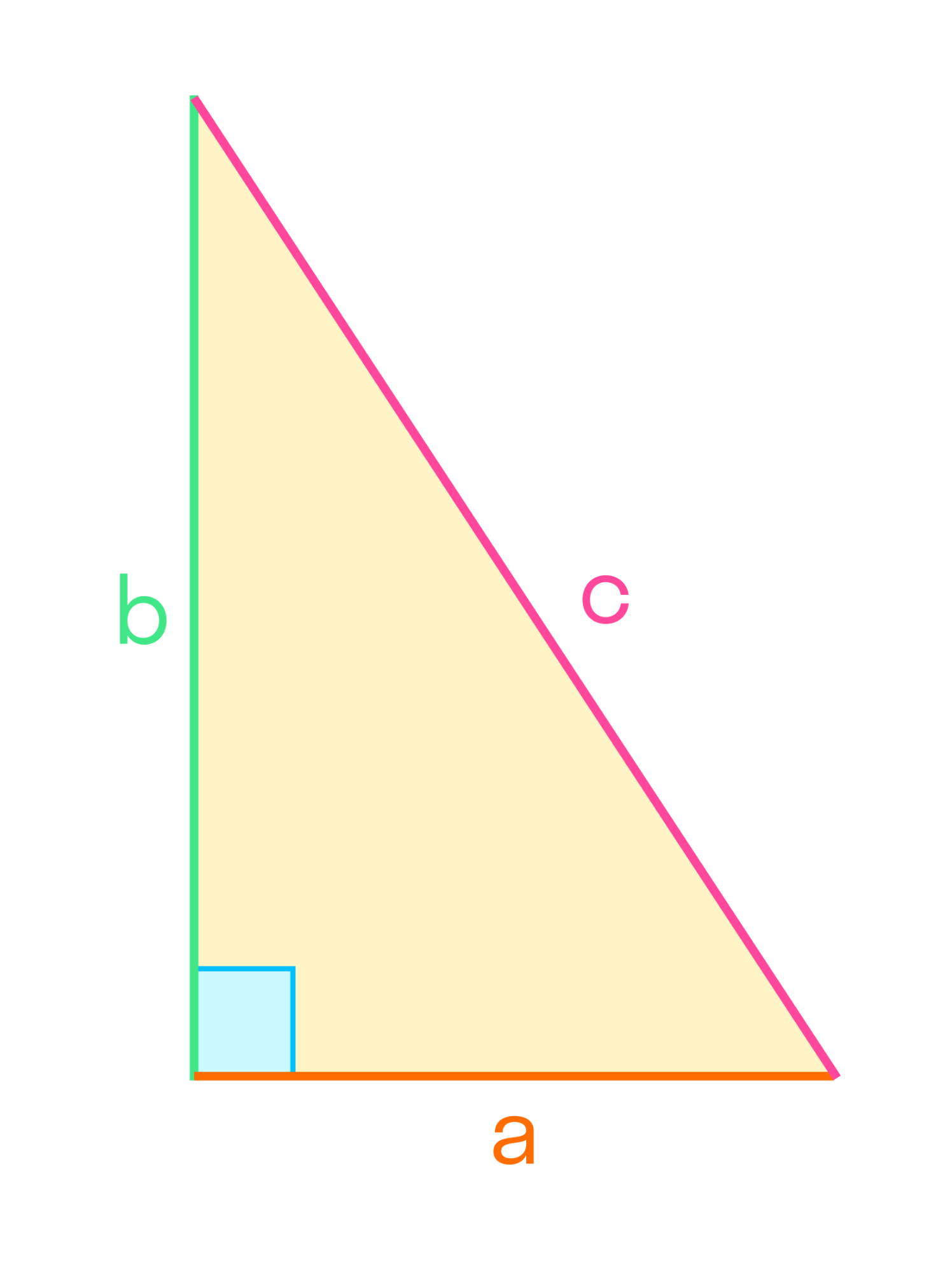
Изучите теорему Пифагора. Согласно теореме Пифагора, a2 + b2 = c2.[7]
Это соотношение позволяет рассчитать длину стороны прямоугольного треугольника, если известны длины двух других сторон. Прямоугольным называется треугольник, один из углов которого равен 90°. В приведенной выше формуле a и b обозначают две прилежащие к прямому углу стороны (катеты), а c соответствует противолежащей стороне (гипотенузе).- Предположим, необходимо найти длину гипотенузы прямоугольного треугольника, если даны длины катетов a = 2 и b =3.
- a2 + b2 = c2
- 22 + 32 = c2
- 4 + 9 = c2
- 13 = c2
- c = √13
- c = 3,6
-
6
Научитесь распознавать типы треугольников. Треугольники бывают трех видов: разносторонние, равнобедренные и равносторонние. У разностороннего треугольника нет конгруэнтных (равных) сторон или углов. В равнобедренных треугольниках конгруэнтны по крайней мере две стороны и два угла. Равносторонний треугольник имеет три равных стороны и три равных угла. Зная различные типы треугольников, вы сможете определять их свойства и правильно использовать аксиомы и теоремы.[8]
- Помните, что равносторонний треугольник обязательно является и равнобедренным, поскольку в нем есть две равных стороны. Все равносторонние треугольники являются равнобедренными, однако не все равнобедренные треугольники являются равносторонними.
- Треугольники можно классифицировать по их углам: остроугольные, прямоугольные и тупоугольные. В остроугольных треугольниках каждый из трех углов меньше 90°; в прямоугольных треугольниках один из углов равен 90°; в тупоугольных треугольниках величина одного из углов превышает 90°.
-
7
Узнайте о разнице между подобными и конгруэнтными фигурами. Фигуры называются подобными, если их соответствующие углы равны, а стороны одной фигуры пропорционально больше или меньше, чем соответствующие стороны второй фигуры. Иными словами, один многоугольник может иметь такие же углы, что и второй, но длина его сторон будет другой. Конгруэнтные фигуры идентичны, их соответствующие стороны и углы равны.[9]
- Соответствующими углами называются равные углы в двух фигурах. Например, два прямоугольных треугольника имеют соответствующие прямые углы. Чтобы фигуры имели соответствующие углы, их стороны не обязательно должны быть равными.
-
8
Изучите понятия дополнительных и смежных углов. Дополнительными углами называются такие углы, сумма которых составляет 90 градусов. Сумма смежных углов составляет 180 градусов. Помните, что вертикальные углы всегда конгруэнтны. Схожим образом, внутренний накрест лежащий и внешний накрест лежащий углы также всегда конгруэнтны. Прямые углы равны 90 градусов, а развернутые — 180 градусов.
- Вертикальные углы — эта пара углов с общей вершиной, которые образованы двумя пересекающимися прямыми, причем стороны одного угла являются продолжением сторон другого.[10]
- Внутренние накрест лежащие углы образуются в том случае, когда две прямые линии пересекают третью. Они находятся на противоположных сторонах пересекаемой линии, но с внутренней стороны двух пересекающих ее линий.[11]
- Внешние накрест лежащие углы также образуются, когда две прямые линии пересекают третью. Они находятся на противоположных сторонах пересекаемой линии и с внешней стороны двух пересекающих ее линий.[12]
- Вертикальные углы — эта пара углов с общей вершиной, которые образованы двумя пересекающимися прямыми, причем стороны одного угла являются продолжением сторон другого.[10]
-
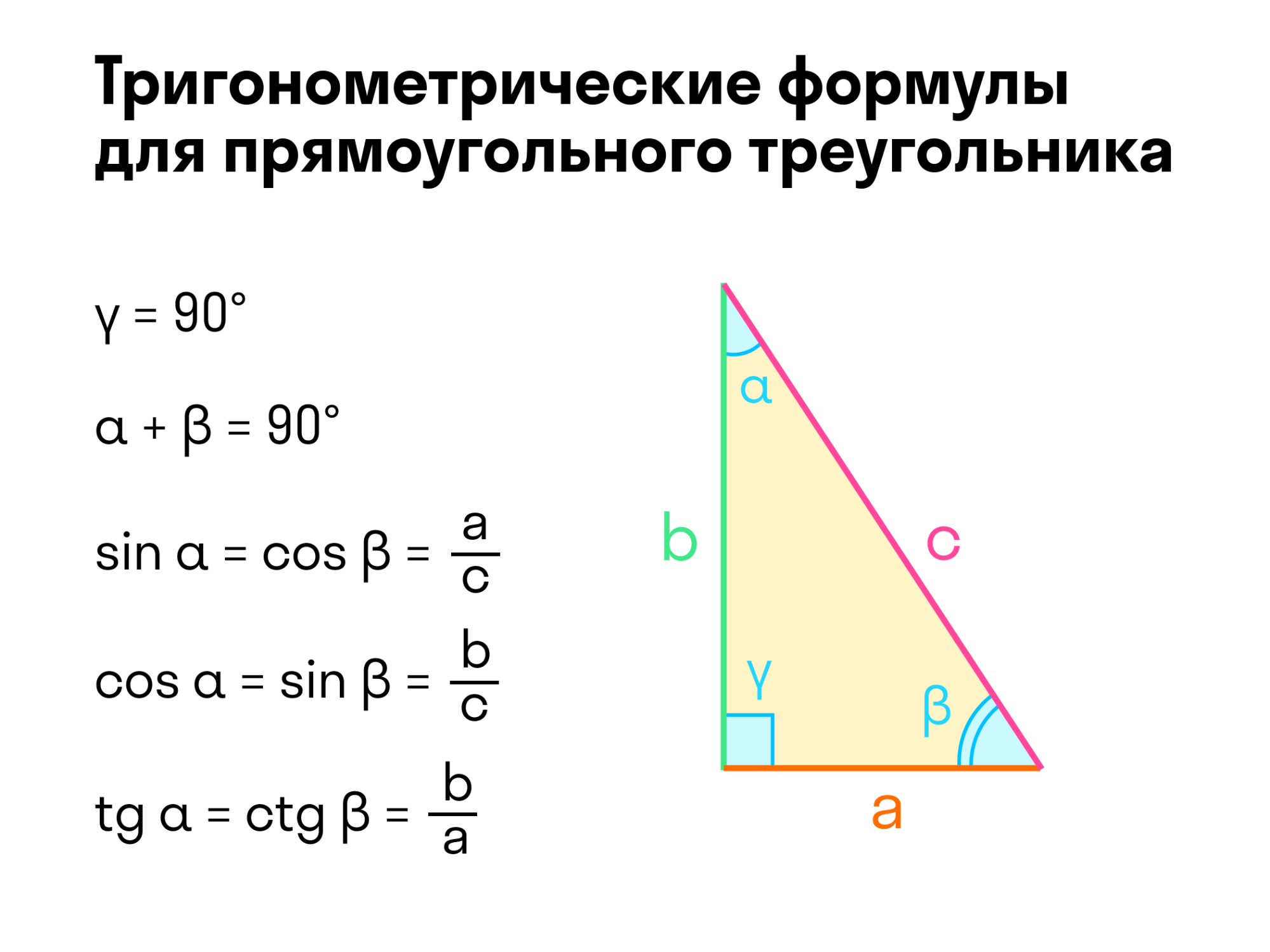
9
Запомните формулы для синуса, косинуса и тангенса в прямоугольном треугольнике. Синус, косинус и тангенс угла можно определить по следующим формулам: Синус = Противолежащий катет/Гипотенуза, Косинус = Прилежащий катет/Гипотенуза, Тангенс = Противолежащий катет/Прилежащий катет.[13]
- Предположим, необходимо найти синус, косинус и тангенс угла 39° в прямоугольном треугольнике со сторонами AB = 3, BC = 5 и AC = 4.
- sin(39°) = противолежащий катет/гипотенуза = 3/5 = 0,6
- cos(39°) = прилежащий катет/гипотенуза = 4/5 = 0,8
- tg(39°) = противолежащий катет/прилежащий катет = 3/4 = 0,75
Реклама
-
1
После того, как вы прочитаете условие задачи, сделайте чертеж. Иногда задача не сопровождается рисунком, и в этом случае следует сделать чертеж, чтобы лучше понять условие. Сначала можно сделать примерный эскиз, а затем нарисовать более точный чертеж, который более или менее правильно отображает все линии и углы.
- Ясно укажите на рисунке все, что дано в задаче и что требуется найти.
- Чем понятнее получится рисунок, тем легче вам будет решить задачу.
-
2
Рассмотрите получившийся рисунок. Обозначьте на нем прямые углы и равные отрезки. Если есть параллельные линии, также обозначьте их на чертеже. Если в условии не указано явно, что два отрезка равны, можно ли доказать это? Не забывайте доказывать все свои предположения.
- Запишите соотношения между длинами различных отрезков и величинами углов, которые можно получить из сделанного рисунка и ваших предположений.
- Запишите, что дано в задаче. Условие любой задачи по геометрии содержит исходные данные. Запишите все исходные данные, чтобы иметь их перед глазами при решении задачи.
-
3
Попробуйте при доказательстве двигаться в обратном направлении. В задачах по геометрии приводятся какие-то исходные данные, и на их основании необходимо доказать определенные утверждения о свойствах фигур и углов. Иногда наиболее простой способ заключается в том, чтобы начать решать задачу с конца.
- Подумайте, каким образом исходные данные могут привести к конечному результату?
- Есть ли очевидные предположения, доказательство которых позволяет получить конечный результат?
-
4
Составьте таблицу из двух колонок: в одну колонку записывайте утверждения, а во вторую — их обоснования. Чтобы получить строгое доказательство, необходимо сделать ряд промежуточных предположений и доказать их истинность. Ниже колонки с предположениями вы запишете конечное утверждение, например, угол ABC = углу DEF. Колонка обоснований будет содержать доказательства соответствующих утверждений и предположений. Если какое-то утверждение дано в условии задачи, просто напишите в соответствующей ячейке колонки обоснований “дано”, в противном случае запишите доказательство данного утверждения (например, укажите использованную теорему).
-
5
Определите, какие теоремы подходят для решения данной задачи. В геометрии существует масса отдельных теорем, которые можно использовать при решении задач. В этих теоремах доказываются различные свойства треугольников, пересекающихся и параллельных линий, окружностей и так далее. Определите, с какими геометрическими фигурами вы имеете дело в данной задаче, и найдите подходящие теоремы. Посмотрите, не решали ли вы подобные задачи ранее. Для треугольников есть множество теорем, и среди них наиболее важными являются следующие:[14]
- соответствующие части конгруэнтных треугольников конгруэнтны между собой;
- если три стороны одного треугольника равны трем сторонам другого треугольника, то эти треугольники конгруэнтны;
- если два треугольника имеют две равные стороны и угол между ними, то эти треугольники конгруэнтны;
- если одна сторона одного треугольника и два прилежащих к ней угла равны соответствующим стороне и двум углам второго треугольника, то эти треугольники конгруэнтны;
- треугольники с тремя равными углами подобны, но не обязательно конгруэнтны.
-
6
На пути к конечному результату не пропускайте промежуточные шаги. Запишите краткую схему доказательства. Напишите обоснование для каждого шага. При этом добавляйте приведенные в условии данные там, где они используются, а не пишите их все в начале таблицы. Если необходимо, поменяйте шаги местами.
- Чем подробнее вы запишете доказательство, тем легче вам будет разместить отдельные шаги в правильном порядке.
-
7
В последней строке запишите выводы. Хотя последний шаг должен завершать доказательство, его также следует обосновать. Когда вы завершите доказательство, просмотрите его еще раз и убедитесь в том, что в нем нет пробелов. Удостоверьтесь, что ваше решение правильно, после чего запишите в нижней правой ячейке “что и требовалось доказать”. Таким образом вы укажете, что задача решена.
Реклама
Советы
- УЧИТЕСЬ КАЖДЫЙ ДЕНЬ. Просматривайте свои записи за текущий и предыдущий дни и всегда повторяйте пройденный материал, пока вы не забыли изученные накануне аксиомы, теоремы, определения, символы и обозначения.
- Если вы чего-то не понимаете, поищите дополнительную информацию и учебные ролики в интернете.
- Заведите карточки и записывайте на них формулы. Почаще просматривайте карточки, чтобы запомнить изученные формулы.
- Запишите номера мобильных телефонов и адреса электронной почты своих одноклассников, чтобы в случае необходимости вы могли обратиться к ним за помощью.
- Занимайтесь на летних каникулах. Это облегчит вашу работу в течение учебного года.
- Медитируйте. Это помогает.
Реклама
Предупреждения
- Не откладывайте все на последний момент.
- Не занимайтесь зубрежкой.
Реклама
Что вам понадобится
- Линейка-треугольник
- Циркуль
- Научный калькулятор
- Тетрадь в клетку
- Транспортир
- Простые карандаши (записи и чертежи необходимо делать карандашами)
- Маркер
- Цветные карандаши
Об этой статье
Эту страницу просматривали 38 838 раз.
Была ли эта статья полезной?
Как научиться хорошо и быстро решать задачи по геометрии
Как подружиться с геометрией, если предмет кроме страха, других эмоций не вызывает? Этим вопросом с одинаковой частотой задаются как сами ученики, так и их родители. Многим, сложно преодолеть психологический барьер и начать просто вникать в тему. О том, как правильно подойти к изучению, этого, действительно сложного предмета, в нашей статье.
Распространенная причина страха
На 90% отношение к предмету формирует преподаватель. Если он сумеет пробудить в детях живой интерес – в геометрии начнут разбираться даже самые закоренелые троечники. Дети будут готовы оставаться на перемене в классе, только чтобы рассмотреть еще один вариант решения задачи.
Если же, предмет объясняется скучно, непонятно, вникнуть в тему будет сложно. В таких случаях, рекомендуем воспользоваться нижеописанными советами.
С чего начать изучение
Первое, что нужно сделать, перед тем, как погрузиться в изучение предмета – осознать, за один день ничего не произойдет. Процесс обучения займет определенное количество времени. Сколько конкретно, зависит от поставленной цели. Если в планах просто хорошая оценка на экзамене, или нужно написать контрольную, достаточно изучить конкретную тему и немного попрактиковаться.
Вникнуть в предмет: рабочие приемы
Пролистайте в учебнике несколько последних параграфов. Спешить не нужно, старайтесь вникнуть в написанное. После, попытайтесь решить несколько задач. Постоянно возвращайтесь к тексту в учебнике, постарайтесь самостоятельно «увидеть» алгоритм решения задачи.
Если первое время, испытываете какие-либо затруднения, ничего страшного. Главное, не опускать руки, и проявить упорство. Загляните в выпущенный к учебнику, решебник, но не просто списывайте готовые решения, а попытайтесь ухватить логику алгоритма. Если подобную задачу рассматривали на уроке, попробуйте вспомнить, что говорил учитель по этой теме. Возможно, что-то из озвученного им, пригодится.
Не пренебрегайте помощью сверстников. Иногда, одноклассники, друзья, сестры или братья, могут донести суть изучаемой темы гораздо быстрее, чем это сделал бы взрослый человек.
Другое дело, если перед учеником стоит задача более глубокого погружения в предмет. Усилий потребуется гораздо больше, и опять, на первом месте будет стоять мотивация и осознание, того, что придется потрудиться. Помните! Решить одну задачу самостоятельно, а потом скатиться к систематическому списыванию из интернета готовых решений, не поможет. Упражняться в решении следует систематически и довольно часто. Прекрасно, если полчаса или даже час в день, вы будете посвящать исключительно геометрии.
Достичь поставленной цели и овладеть предметом на должном уровне поможет только практика. Пусть решение 1-2 задачек в день, станет привычкой. Со временем, вы отметите про себя, что процесс решения идет все легче, а находить правильные ответы становится интереснее.
Если на уроке рассматривается задача и учитель предлагает желающим попробовать решить ее у доски, отзывайтесь, даже пока не видите, как ее осилить. Начните рассуждать. Преподавателям всегда приятно, когда ученик искренне интересуется предметом. Учитель обязательно включится в ваши рассуждения. Там, где нужно, поможет. Направит ход мыслей в нужном направлении. Вы запомните алгоритм, и в следующий раз с блеском справитесь самостоятельно.
Использовать по желанию
Если геометрия не дается ни в какую или требуется понимание предмета, выше школьного уровня, можно провести несколько занятий с репетитором. Индивидуальные занятия с преподавателем практически всегда дают хороший результат. Репетитору даже не обязательно посещать лично. Организовать уроки, при современных технологиях, возможно по скайпу или через другие подобные приложения.
Вот и все рекомендации. Ничего сложного, а польза огромная. Просто выполняйте их, и вы даже не заметите, как серьезно продвинетесь в геометрии.
Источник
Как выучить геометрию с нуля с 7 по 11 класс
Можно ли выучить всю геометрию самостоятельно
Как освоить школьный предмет с нуля
Есть два эффективных способа, с помощью которых можно с нуля понять геометрию или подтянуть уже изученный материал:
На нашем сайте есть детский раздел, где вы сможете выбрать подходящую программу обучения под свои требования.
Подобрать онлайн-курс по геометрии можно через наш сервис. У нас собраны обучающие программы для разных классов, для базового и углубленного уровня. С помощью фильтра легко сравнить курсы по стоимости, срокам, формату занятий и другим параметрам. А также вы можете почитать отзывы учеников и их родителей.
Для вашего удобства мы разделили курсы по классам:
Как быстро выучить геометрию
ТОП-7 советов, которые облегчат изучение геометрии:
С помощью онлайн-курсов можно быстро выучить всю теорию по геометрии, закрепить материал на практике и получить дополнительные знания. На занятиях готовят к контрольным, экзаменам и олимпиадам за небольшие сроки. Они длятся от 1 месяца до года. Но если смотреть уроки в записи, по 1-2 часа за один вечер, можно освоить предмет за более короткое время.
Что поможет легко запомнить правила
Для того чтобы любое правило отложилось в голове, его обязательно нужно понять, так как наизусть заученные строки не смогут помочь на практике. В геометрии большую роль играет именно логика, при решении любой задачи нужно вспомнить и применить подходящее правило, теорему или аксиому.
Чтобы легко выучить правила по геометрии, нужно в первую очередь разобраться в чертеже, запомнить его и понять, что и за чем следует. Лучше, чтобы материал объяснял преподаватель, который сможет доходчиво ответить на все вопросы.
Подтягиваем оценки по геометрии: советы ученикам с 7 класса
Геометрию начинают изучать с 7 класса, и чтобы не было проблем с оценками, лучше всего сразу вникнуть в предмет и не допускать пробелов в знаниях. Учите все теоремы последовательно, читайте параграфы и делайте домашние задания. Если что-то непонятно, не нужно бояться тут же подойти к учителю с вопросом.
Как родителям помочь ребенку
Если у ребенка есть проблемы с изучением геометрии, можно попробовать самостоятельно разобрать с ним непонятый материал. Но только в том случае, если вы сами хорошо знаете эти правила и готовы уделить много времени на занятия.
Помогите ребенку ощутить практическую сторону геометрии, приводите в примеры окружающие предметы и явления, рассуждайте о том, какие формулы и теоремы могли бы подойти для них. Это поможет развить логические способности ребенка при решении задач.
Помогайте ребенку учить аксиомы, теоремы и доказательства. В геометрии нужно многое знать на память.
Еще одним правильным вариантом будет получение помощи от специалистов. Чтобы подтянуть ребенка по геометрии, можно записать его на онлайн-курсы, преподаватели помогут пройти весь материал и привьют интерес к предмету. Тогда вам не придется контролировать его и заставлять учиться.
Источник
Основы геометрии
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
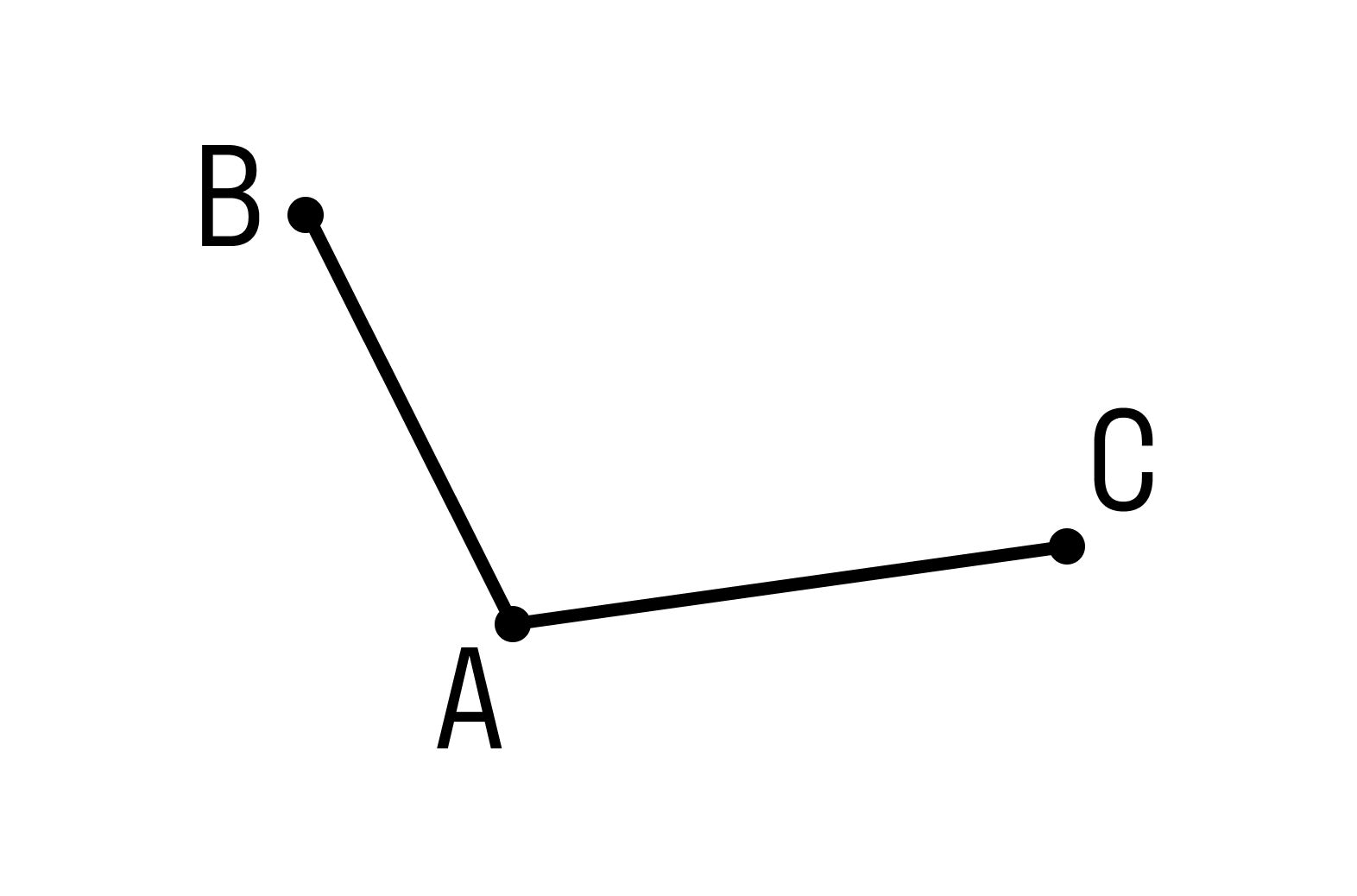
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
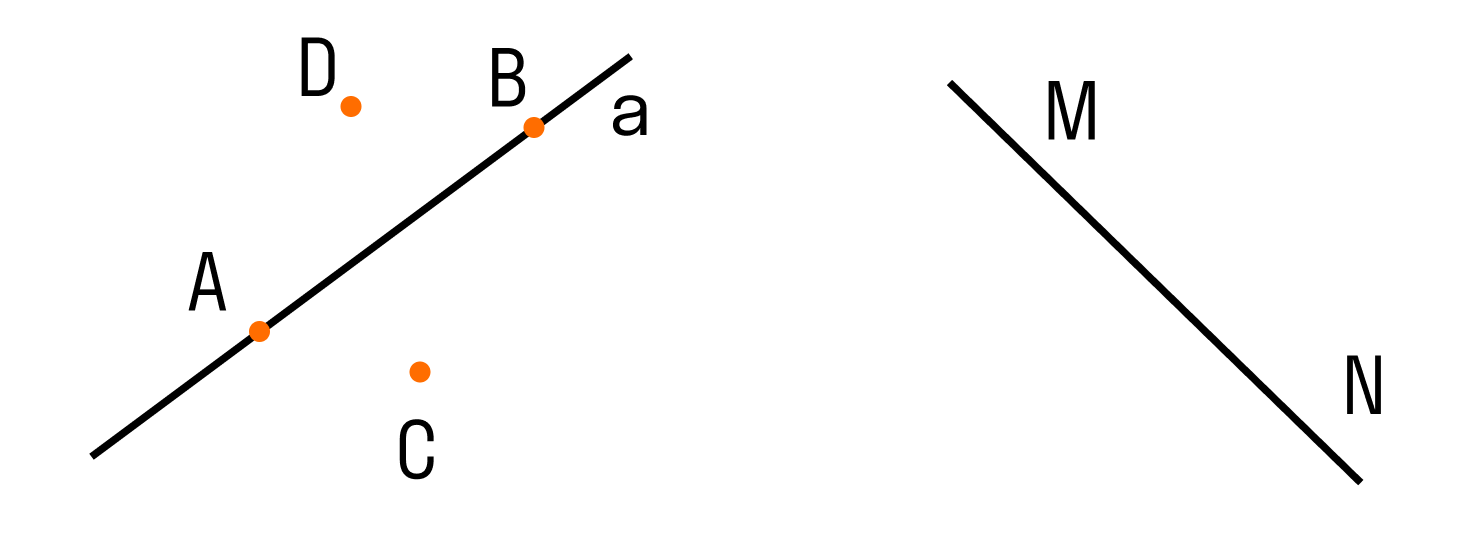
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
Если рассмотреть две прямые, то возможны два варианта их расположения:
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
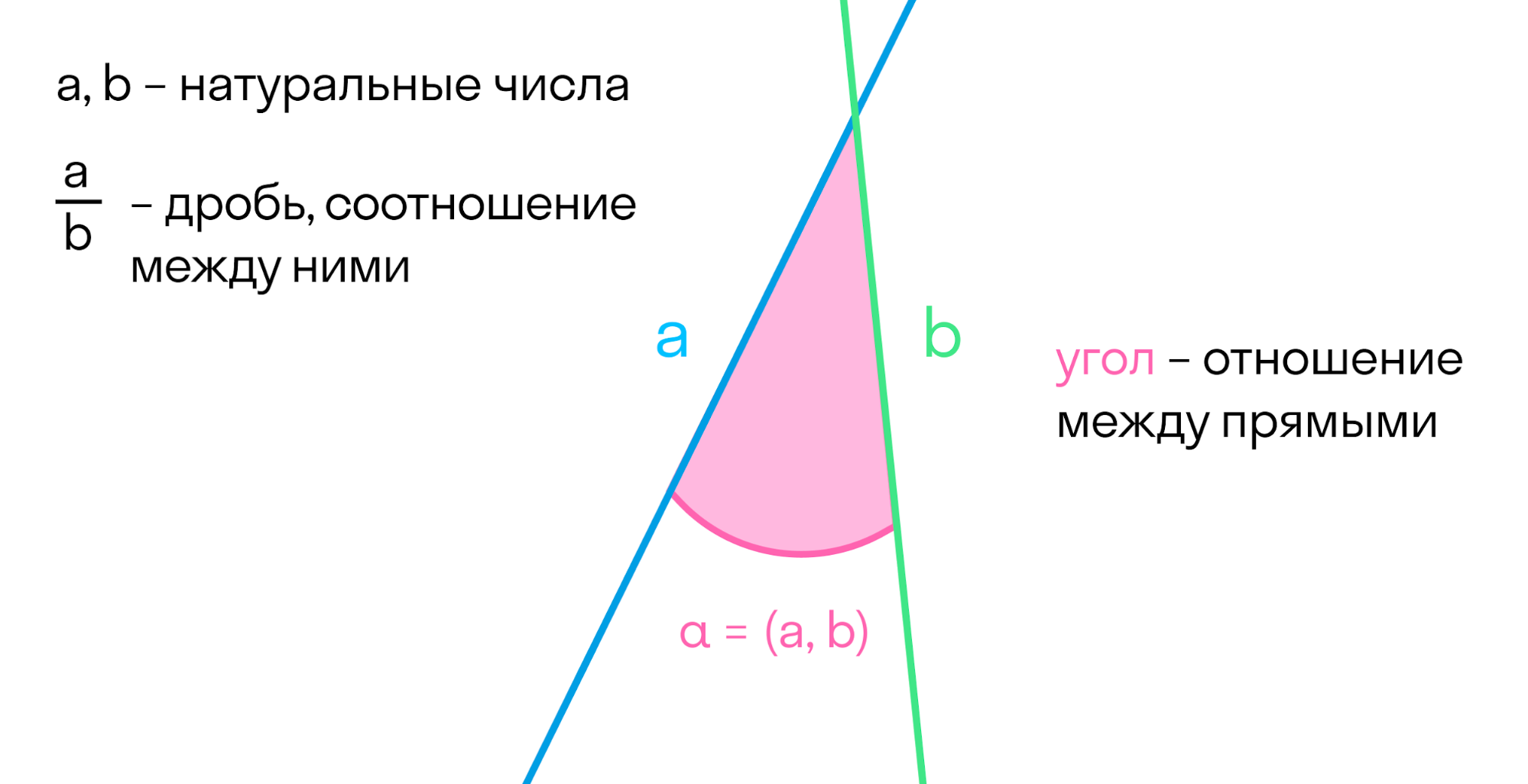
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
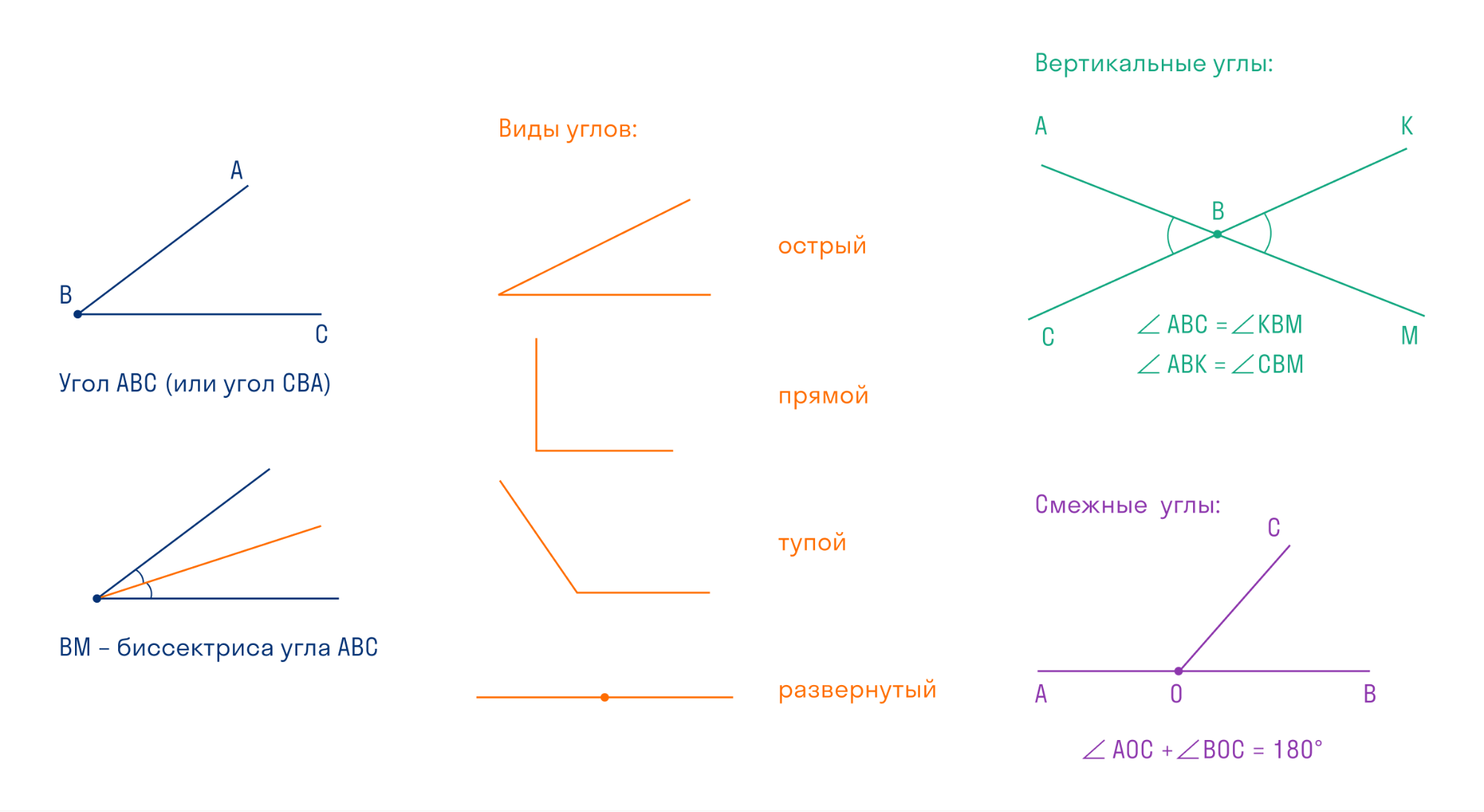
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
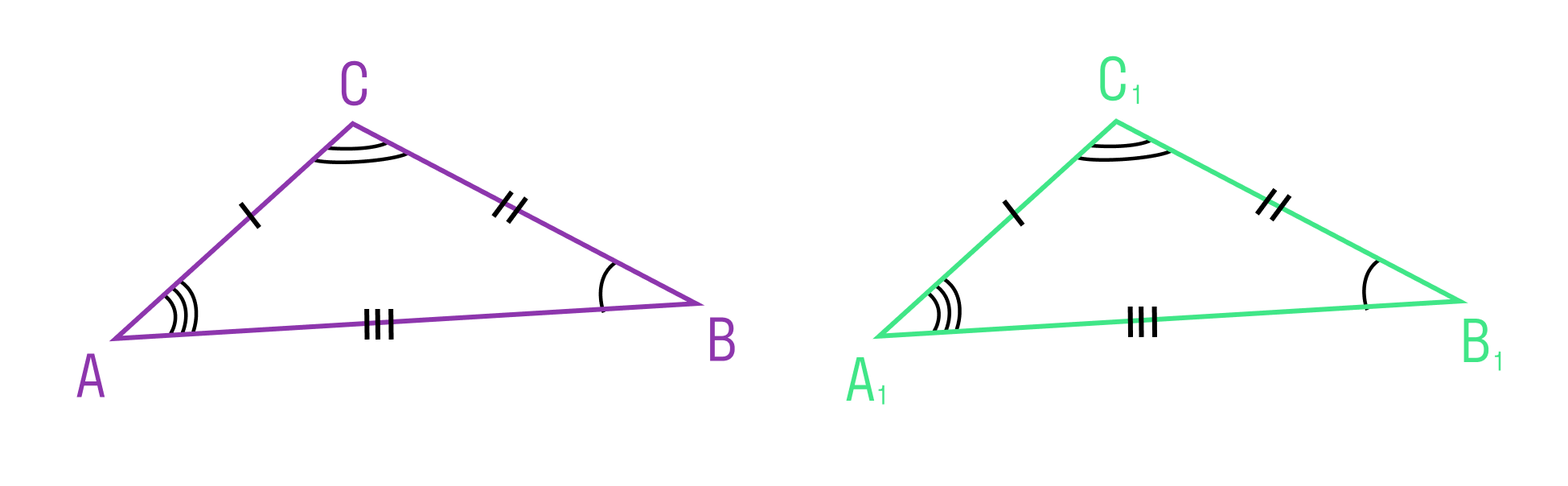
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
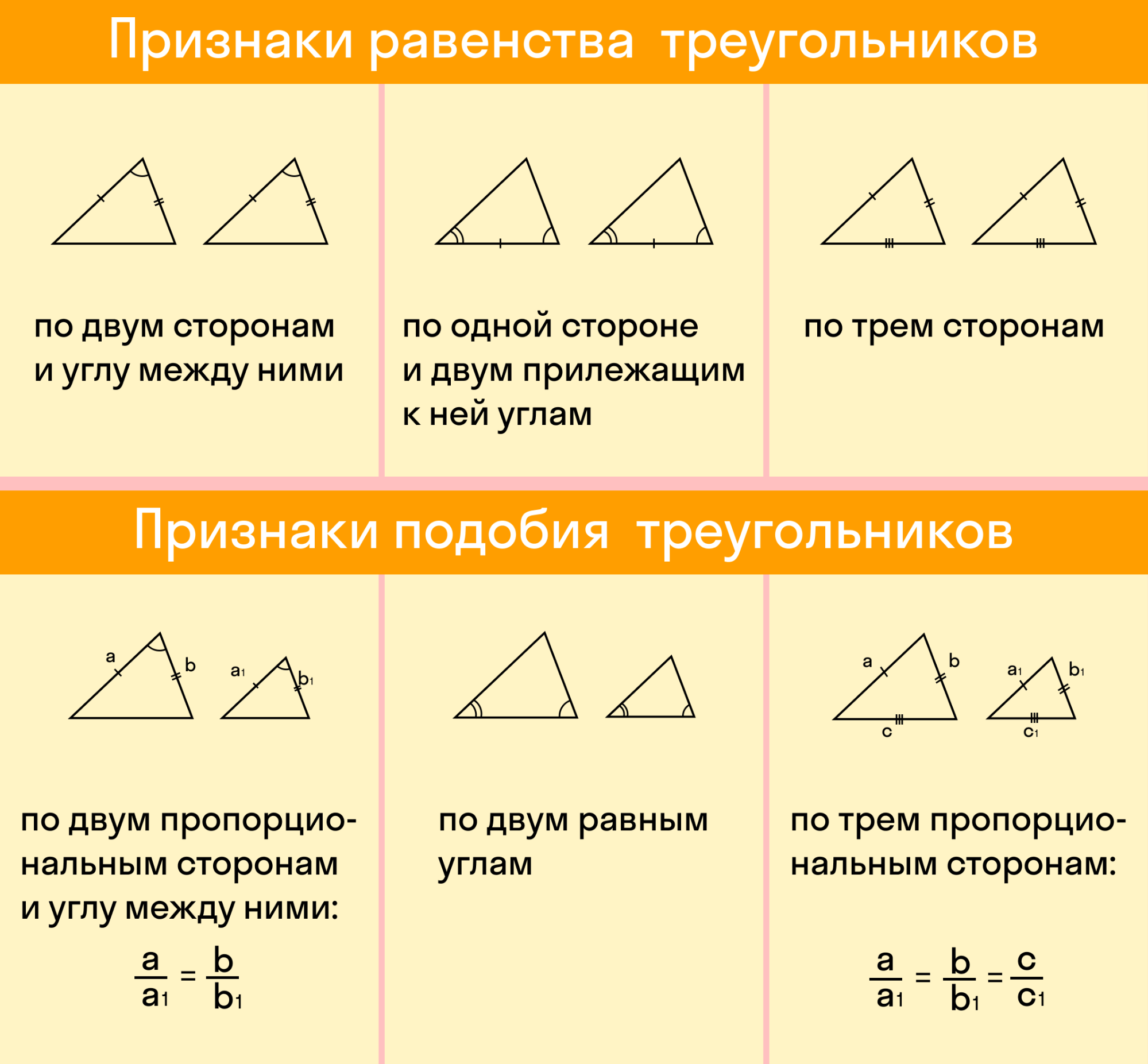
Первый признак равенства треугольников звучит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников
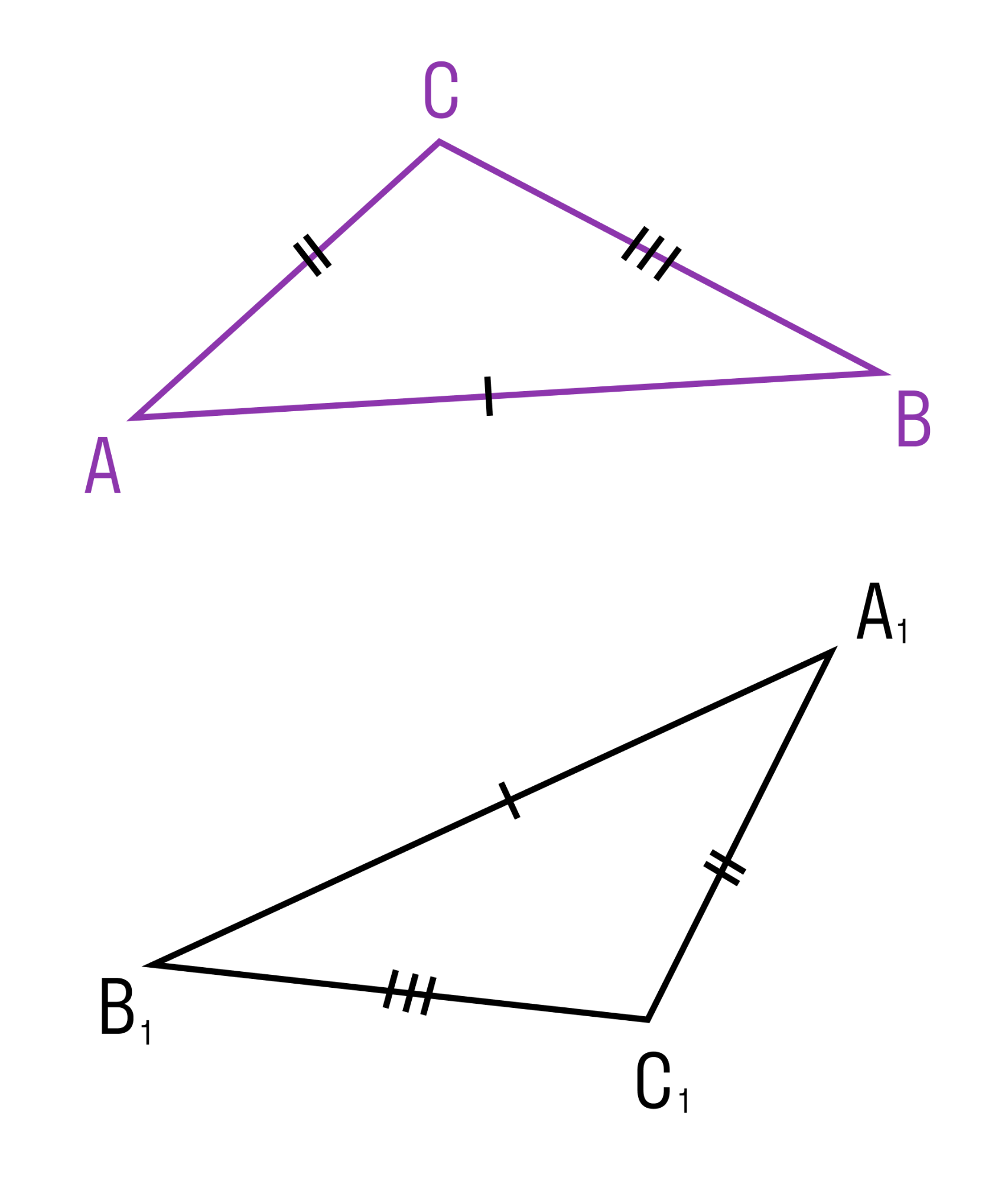
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
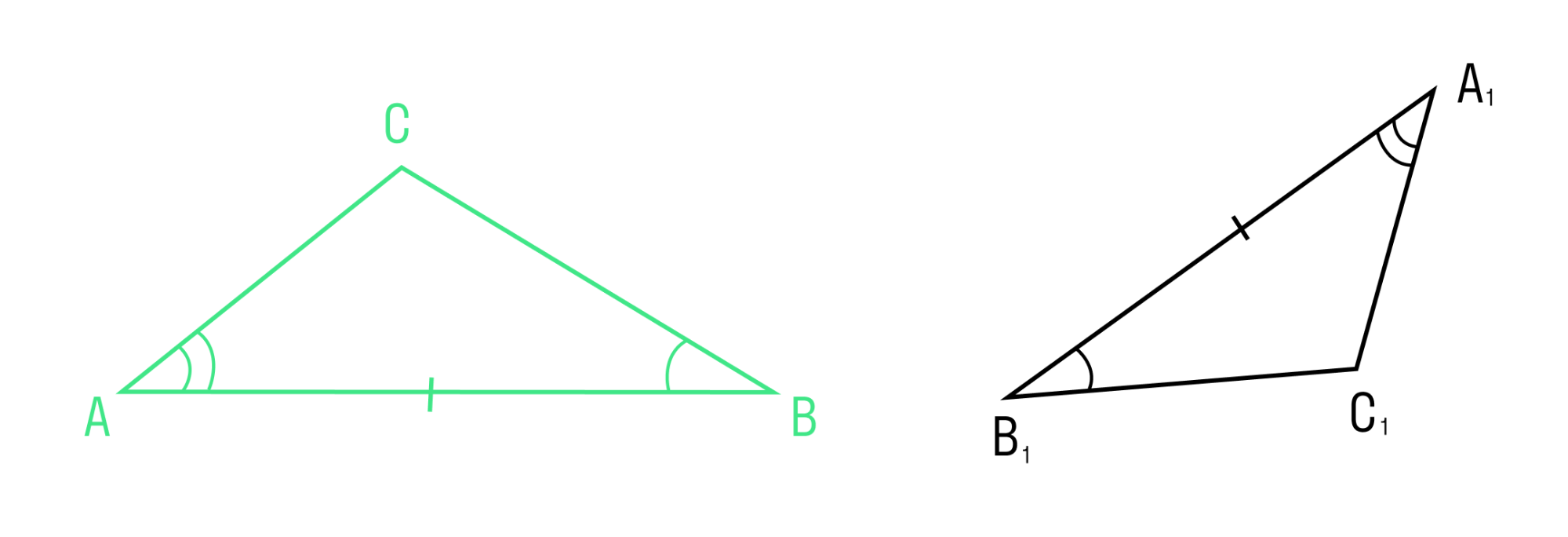
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
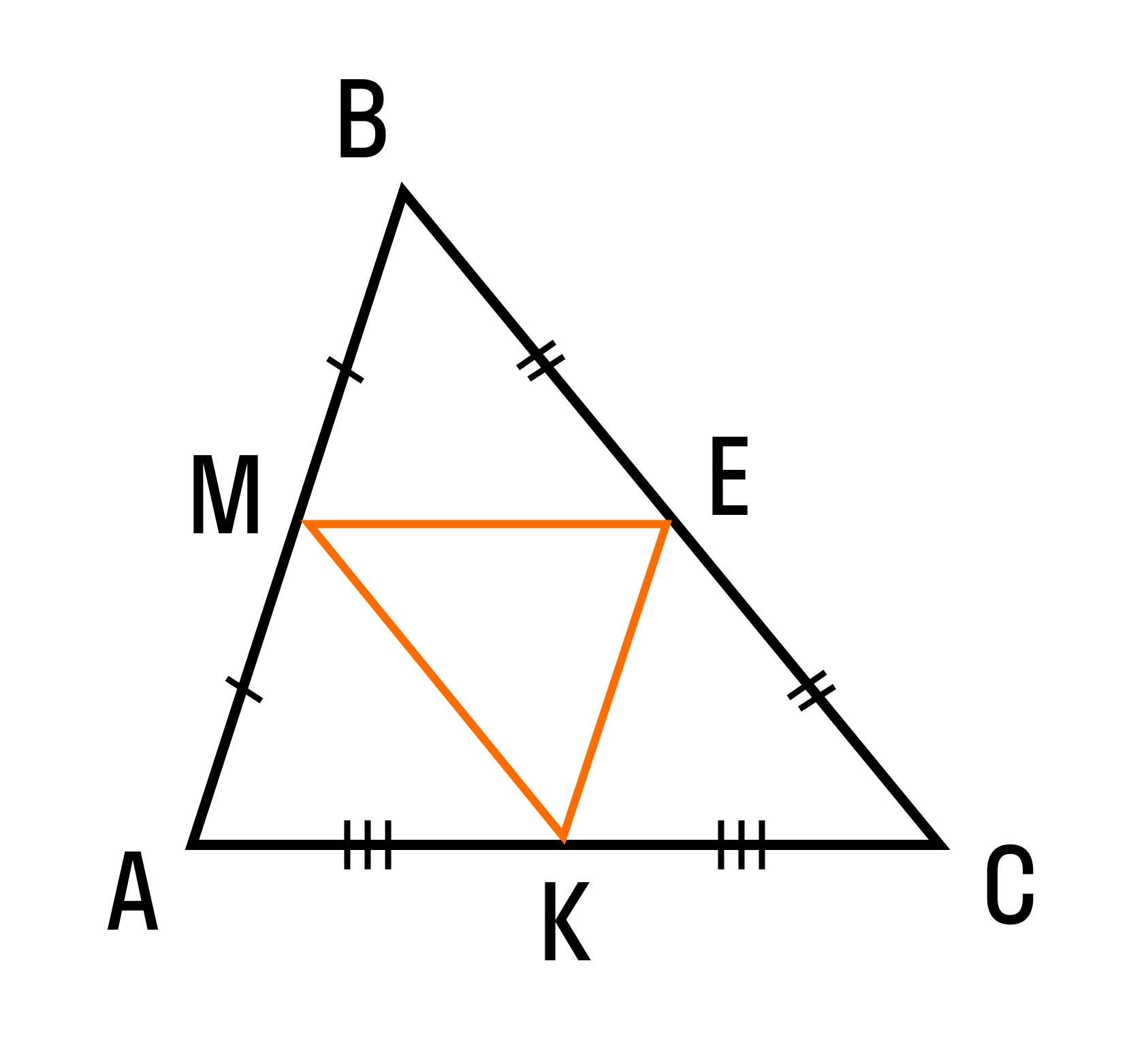
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
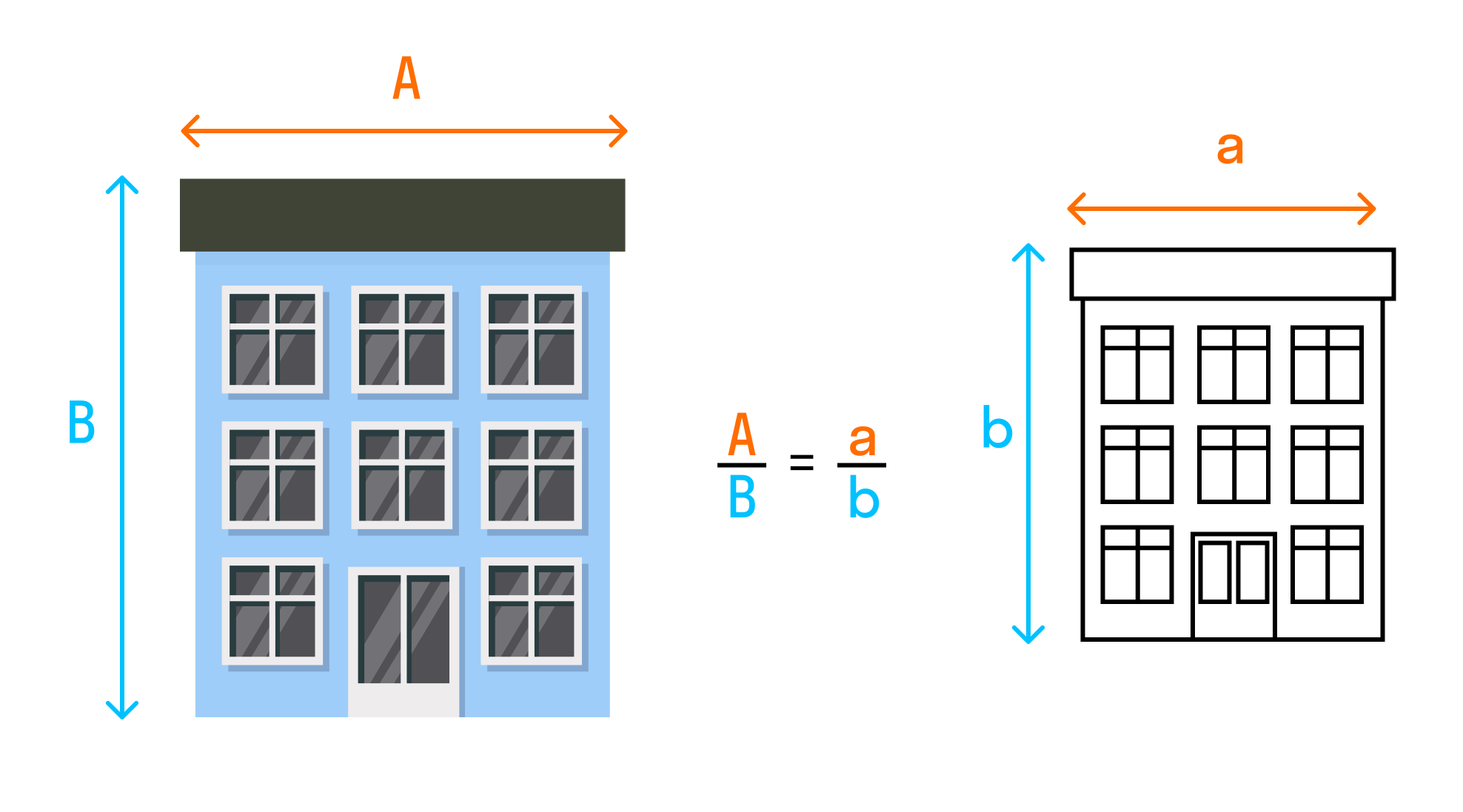
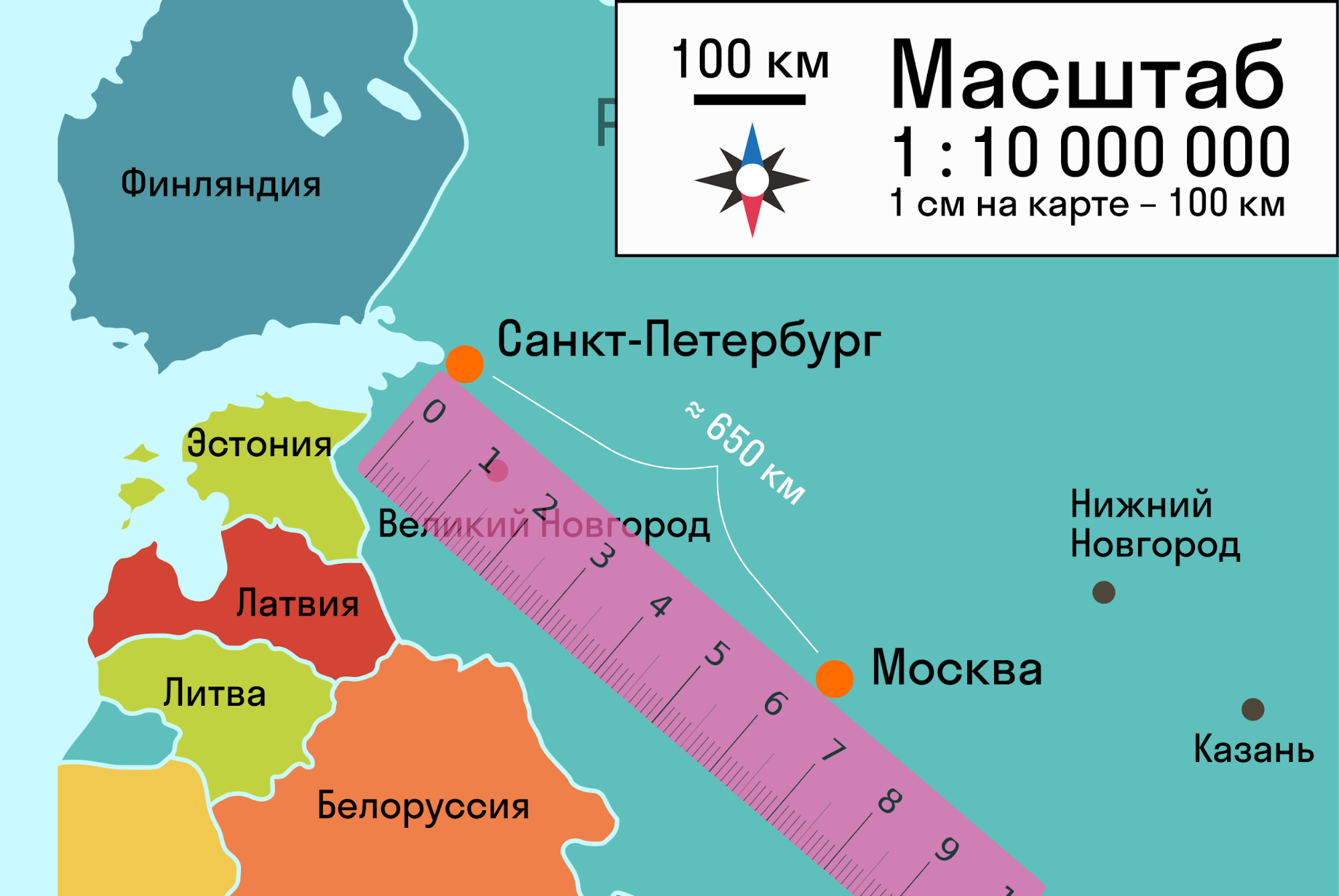
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
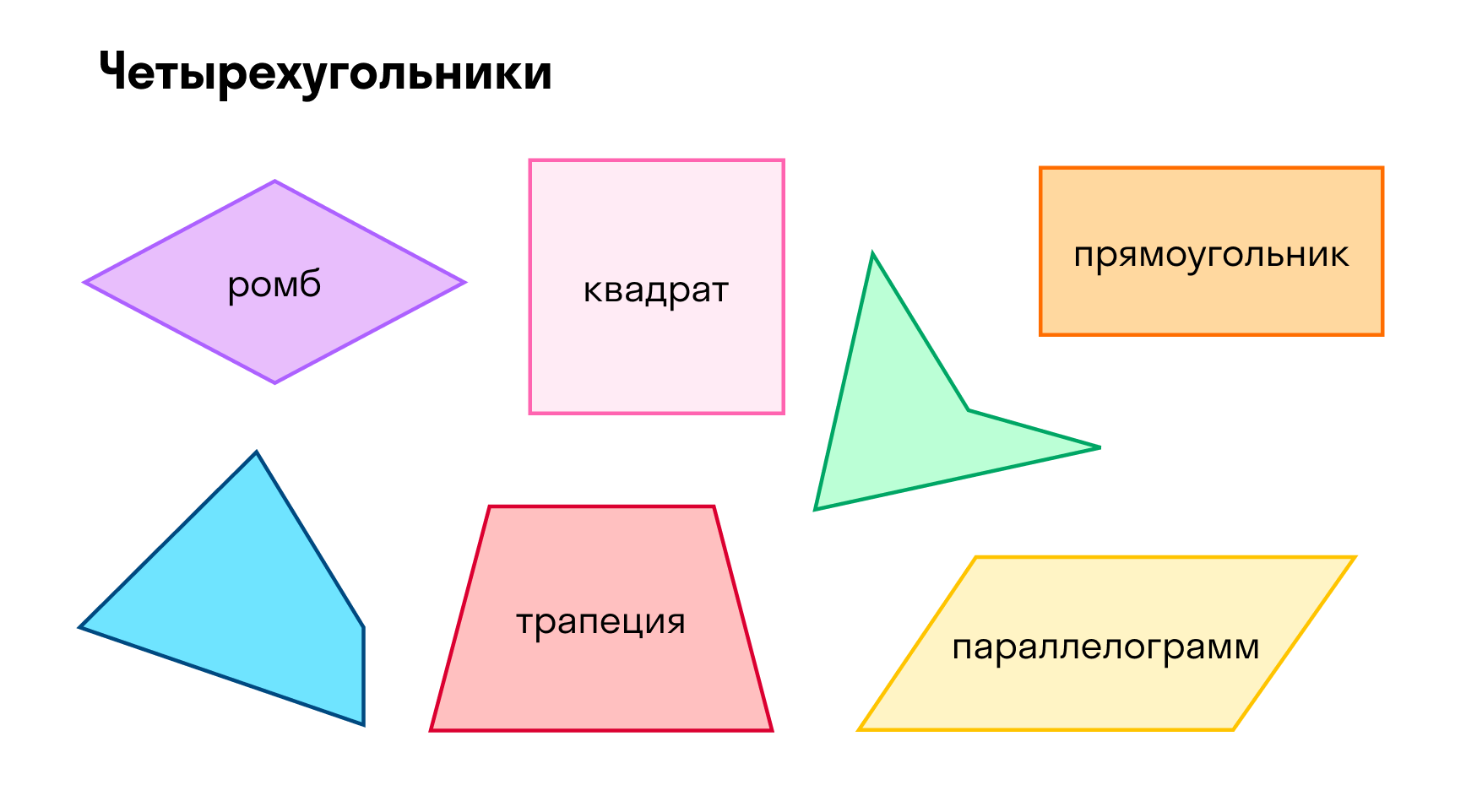
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
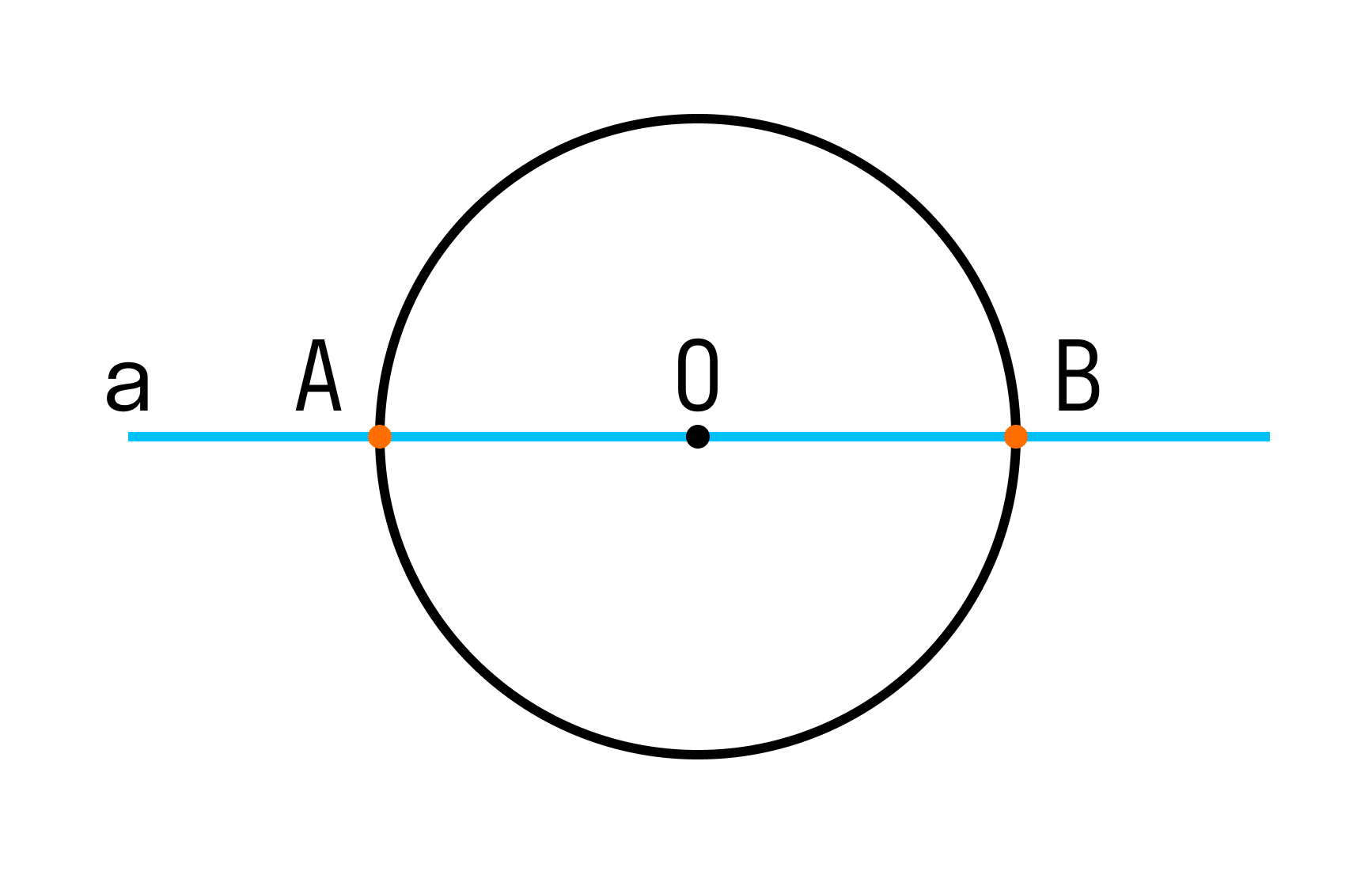
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
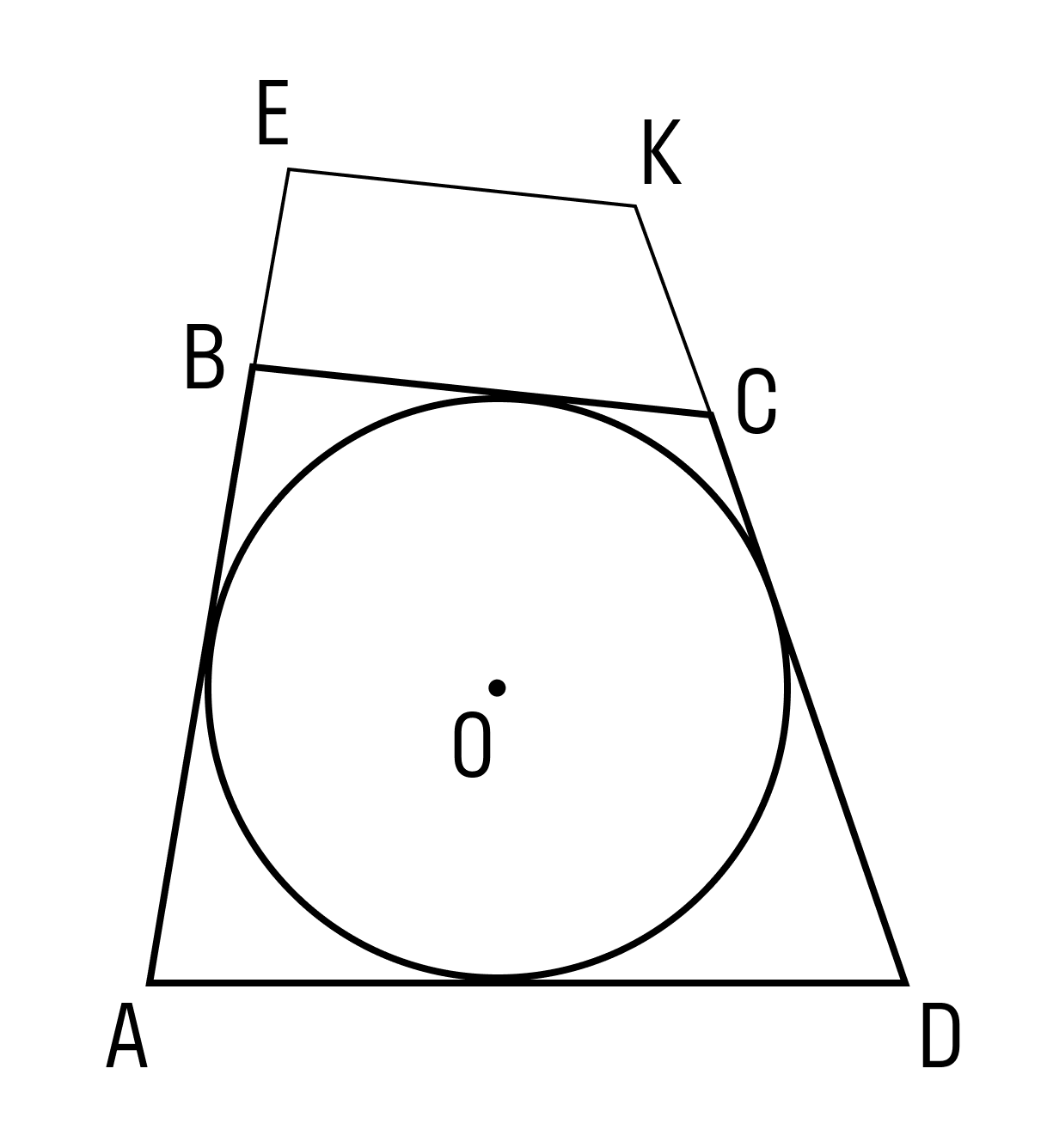
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Источник
Из года в год самым страшным кошмаром на ЕГЭ по математике и для учеников, и для репетиторов считаются не параметры и не финансовая задача, а милая геометрия, которой впору пугать ленивых учеников. В стиле «если домашку по логарифмам не сдашь, на следующей неделе планиметрию начнём». Я вам открою секрет. Далеко не каждый репетитор по математике сам умеет решать С2 и С4. И далеко не каждый вообще за это берётся.
Почему с геометрией такая дикая проблема?
На мой взгляд, проблема не с геометрией как таковой. А с пространственным и творческим мышлением в целом.
Ваш ребёнок умеет составить схему к задаче на движение, на работу, на части и внести туда все необходимые данные? Я чаще всего сталкиваюсь с тем, что нет. А ведь это основа геометрии по сути. Суметь представить текстовые данные в форме схемы, внести информацию так, чтобы текст больше не понадобился и решить задачу, просто глядя на схему. В геометрии грамотный чертёж = 80% задачи. Остальное уже дело техники.
И геометрия должна начинаться не в 7-м классе, а ещё в дошкольном и младшем школьном возрасте. Разрезалки, развёртки, чёткие схемы, игры с площадями и периметрами, проведение отрезков по точкам, задачи на замощение поверхности, задачи со вспомогательной раскраской, пентамино, тетрамино и иже с ними, танграм и другие головоломки на плоскости, сборка конструкций по трём видам, работа с единицами измерения…
Почему-то очень многие математику ограничивают числами, текстовыми задачами и счётом. Но ведь это только вершина айсберга математики, лишь одна небольшая его часть. А потом и получается, что ребёнок в задаче по геометрии видит пару чисел и начинает эксперименты с ними. Сложить, умножить. И неважно, что одно из них расстояние, а другое – угол. У ученика напрочь не сформировано понимание того, что они значат.
Как быть? Добавлять в свою математику геометрию в разных формах. Для этого есть чудесные игры, например: ковры короля Квадратуса, геометрика, оригами, конструктор из зубочисток и пластилина, лабиринты, эксперименты с лентой Мебиуса и разными флексагонами (я фанат объемных флексагонов), поиск предметов по координатам, морской бой.
Из пособий, призванных поставить геометрию с нуля, очень рекомендую посмотреть:
- Наглядная геометрия Шарыгина и Ерганжиевой. Книга адресована ученикам 5–6-го классов, однако отлично может использоваться с детьми более младшего возраста (с адаптацией задач) и для учеников старшей школы, которые испытывают трудности в освоении геометрии. Когда есть проблемы с предметом, не стоит брать другой учебник 7-го класса. Попробуйте сделать шаг назад, к основам.
- Наглядная геометрия (лабораторный метод изложения) Астряба. Старая, проверенная временем книга, у меня вот издание 1923 года. Как понятно из названия, тоже вся работа будет на практике: изучить призму и конус (поверьте, после пары таких уроков стереометрия пойдёт в разы лучше. Современные ученики, даже сильные олимпиадники, порою слабо себе представляют, что будет в таком-то сечении), виды углов, объемы и площади, масштабы и системы координат. Книга закладывает прекрасную базу пространственного мышления. Я вообще не представляю, как можно изучать теоремы, не доказывая их вот прям вырезая и измеряя. А в школах они зачастую даются в параграфе для домашнего изучения, да таким сухим и формальным языком, что ничего не понятно и, если честно, даже не хочется пытаться понять.
- Моя любовь: задачи на разрезание Екимовой и Кукина. Здесь и задачи на клеточной бумаге, и разбиение плоскостей, и танграм с пентамино, и разные раскраски, и задачи на площади. Отличная книга для интереса и подготовки к серьёзной олимпиаде.
- Геометрия в картинках Акопяна. Необычная книга, которая представляет собой сборник теорем и геометрических фактов в картинках, доступных для понимания каждым. В книге почти нет текста, только чертежи. Интересна для сильного ученика, который начинает свой путь в геометрии. Но к ней я бы всё же рекомендовала наставника.
- Математика и конструирование Волковой (для 1–4-го классов). Хорошее пособие для развития конструкторских и графических умений, мелкой моторики (работа с циркулем и линейкой – не самое простое задание), чувства числа, воображения и логики. Все задачи именно практические: нарисуй, проведи, придумай, раздели, отмерь, раскрась.
- И для самых маленьких, у кого ещё всё впереди: «Путешествие по стране геометрия» Житомирского и Шеврина. Это сказка, игра и приключения, которые помогают ученику понять базовые понятия на практике: отрезки и их сравнение, углы, плоские и объемные фигуры, симметрию и разные размерности.
А как у ваших детей дела с геометрией? Как справляетесь?