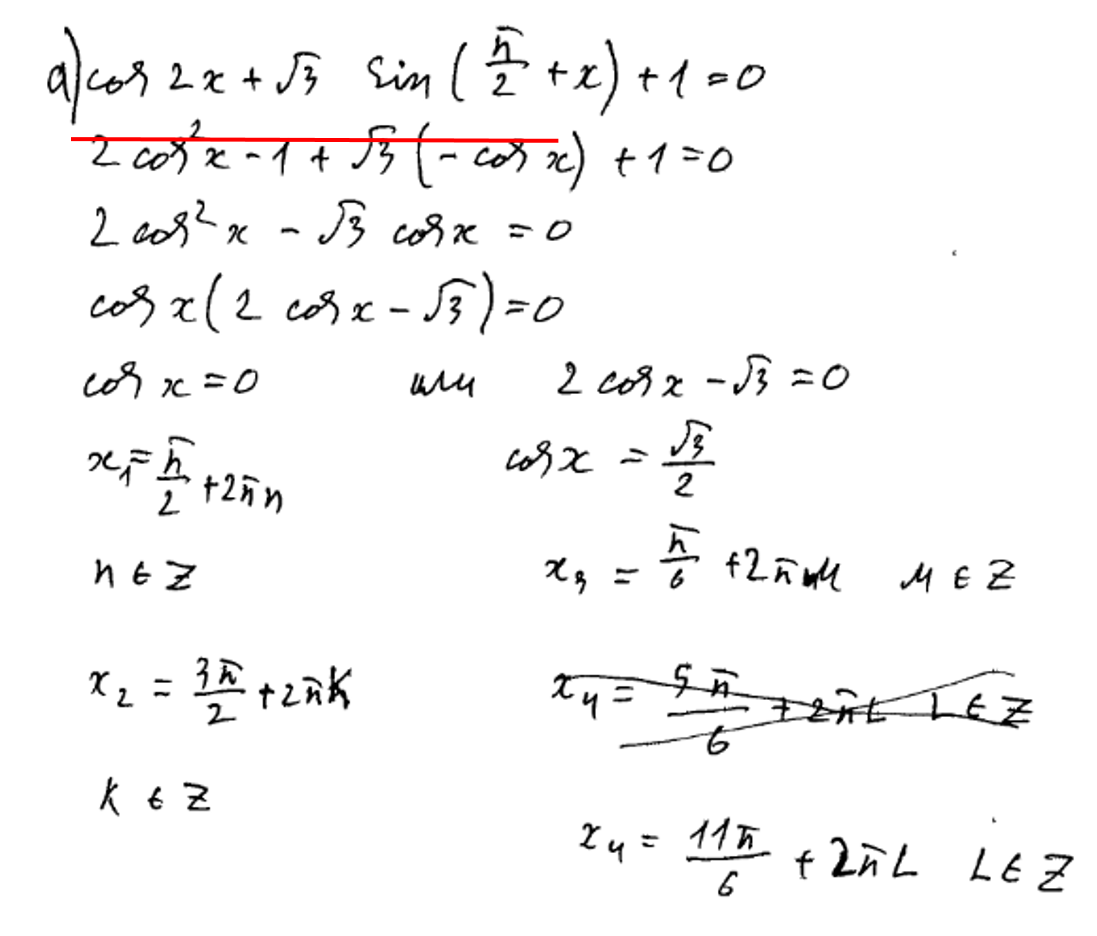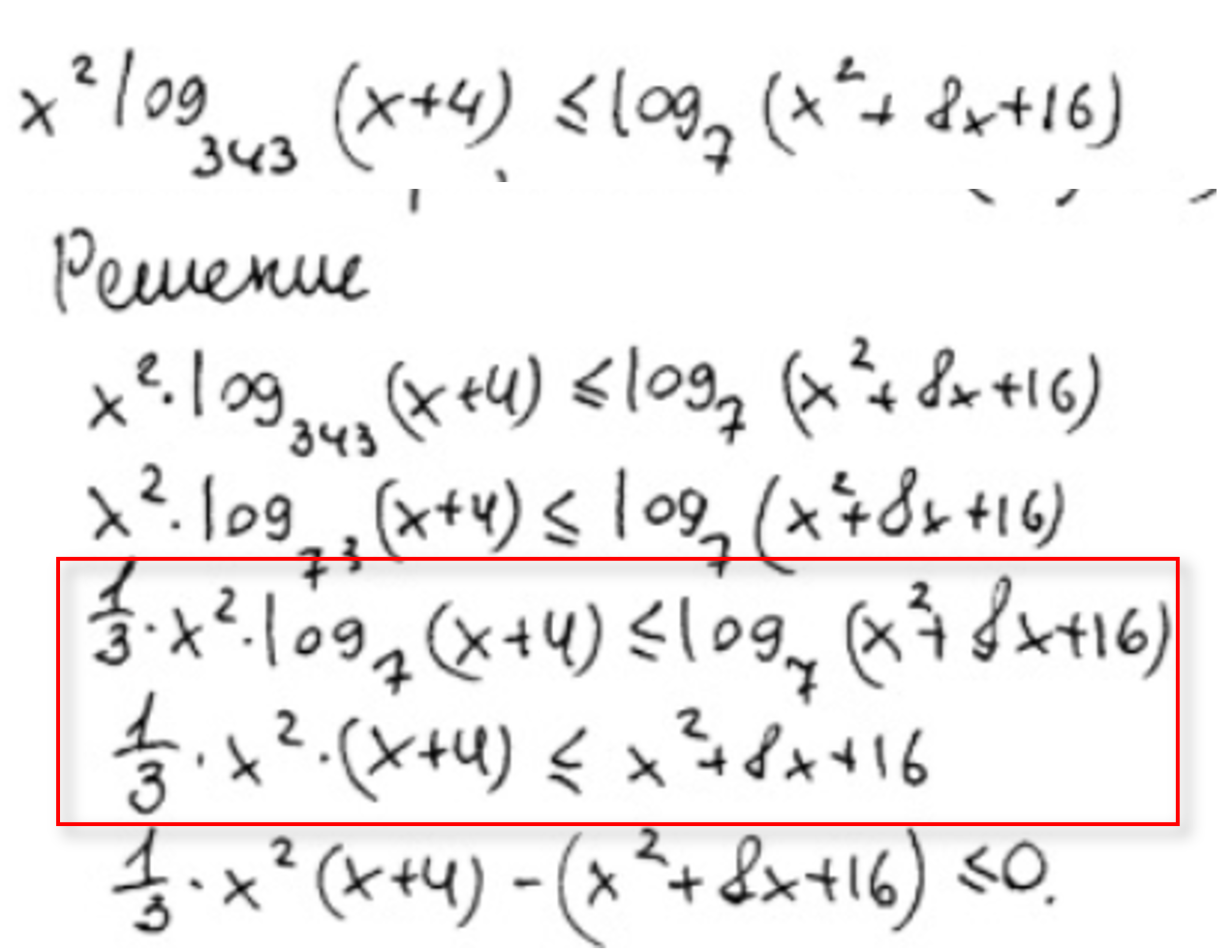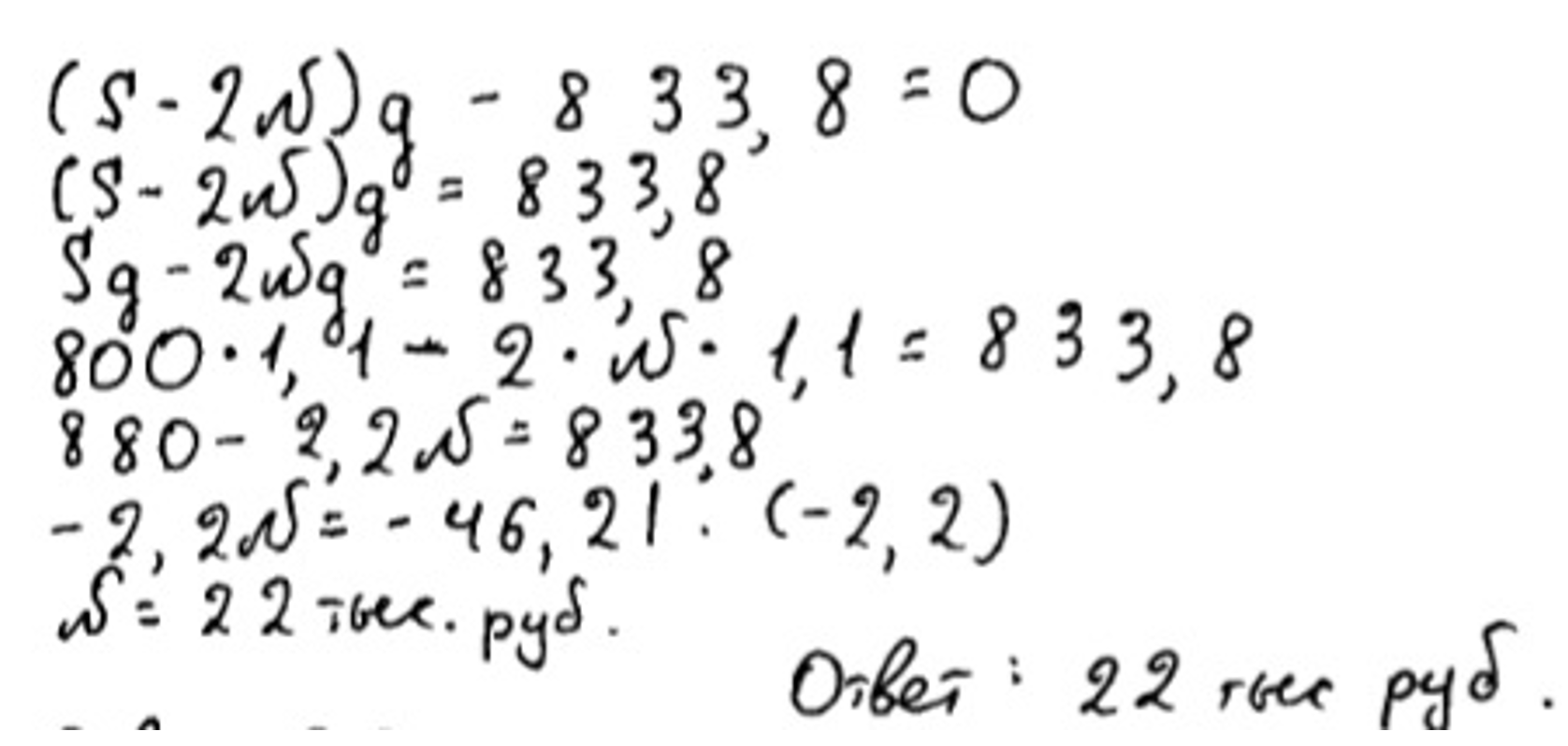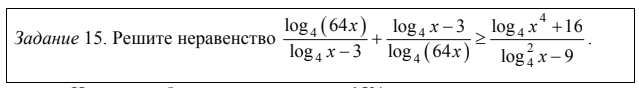Что считается вычислительной ошибкой на егэ по математике
Что считается вычислительной ошибкой на егэ по математике
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 12 № 485973
А) Решите уравнение
Б) Укажите корни уравнения, принадлежащие отрезку
А) Преобразуем уравнение:
Б) С помощью числовой окружности отберем корни на отрезке Получим числа:
Почему в ответе сохранили минус под знаком арккосинуса? в этом случае задание считается решенным не до конца. (см. критерии для экспертов по проверке заданий ЕГЭ)
Честно говоря, я ничего подобного в критериях для экспертах не помню. Собственно, в критериях написано именно то, что написано в критериях выше. Форма записи ответа не является ошибкой.
Симметрию я ещё могу понять, но КАК вы без калькулятора поняли что arccos (1/4) находится именно там??
Я, например, располагал их симметрично в I и IV четвертях.
Косинусы положительны в первой и четвертой четвертях, отрицательны — во второй и третьей.
Задание 12 № 485973
—>
Почему в ответе сохранили минус под знаком арккосинуса.
Ege. sdamgia. ru
04.01.2019 13:42:49
2019-01-04 13:42:49
Источники:
Https://ege. sdamgia. ru/problem? id=485973
МГУ ВМК | Вступительные экзамены на различные специальности » /> » /> .keyword { color: red; } Что считается вычислительной ошибкой на егэ по математике
МГУ ВМК: вступительные испытания
МГУ ВМК: вступительные испытания
Факультет вычислительной математики и кибернетики МГУ является лучшим в области подготовки по прикладной математике, вычислительной математике, теории информации и программированию. Именно поэтому большинство абитуриентов выбирают именно этот факультет. Ещё одно преимущество факультета ВМК — это сотрудничество со многими зарубежными университетами для обучения по обмену, что дает молодым специалистам хороший старт в карьере. Ввиду этого с этим крупные IT-компании постоянно ищут новые таланты именно с факультета Вычислительной математики и кибернетики, предлагая студентам курсы с последующим трудоустройством. Помимо всего на факультете располагаются лаборатории таких известных компаний, как Intel и Microsoft, региональная академия CISCO, а также факультет ВМК принимает участие в программе Microsoft IT-Academy.
Чему учат студентов факультета ВМК?
6-летняя программа подготовки специалистов в области прикладной математики и теории информации позволяет получить квалификацию математика и системного программиста. Математика как наука представляет собой совокупность отраслей. Учебные программы включают следующие математические дисциплины:
Также студенты глубоко изучают курс английского, ведь без него стать хорошим специалистом невозможно. Особое внимание уделяется практической работе, освоению студентами нескольких операционных систем и не менее трех языков программирования на высоком уровне.
Первый и второй семестр факультет дает базовую подготовку по математике и теоретическому и прикладному программированию, потом студенты должны выбрать специализацию. Математика — это наука, которая учит составлять алгоритмы разной сложности. В программировании – математика играет ключевую роль, на ее основе решаются многие задачи.
Также студенты могут заниматься научно-исследовательской работой для этого в их распоряжении лаборатории математики и физики.
Выпускники факультета востребованы различными компаниями и учреждениями в которых применяются IT-технологии, в том числе научно-исследовательскими институтами РАН, высшими учебными заведениями, государственными организациями, банками, страховыми компаниями, финансово-консалтинговыми компаниями, различными и зарубежными предприятиями и др. Около трети выпускников продолжают обучение в аспирантуре на одной из 18-ти кафедр:
Как стать студентом ВМК?
Вот какие требования нужны для поступления в МГУ ВМК: экзамены ЕГЭ по математике, физике и русскому языку и ДВИ по математике. Каждый год большое количество абитуриентов подают заявление на факультет ВМК, поэтому, чтобы поступить, результаты ЕГЭ должны быть внушительными. Для этого тебе надо узнать в МГУ (ВМК) вступительные экзамены и проходные баллы за прошлый год, чтобы примерно знать на какой уровень тебе надо готовиться. Эти данные о факультете ты можешь найти в нашей статье ниже.
Что такое ДВИ?
Для того чтобы поступить на ВМК надо сдать дополнительные вступительные испытания или сокращенно ДВИ по математике. Поступить можно только когда у тебя есть результаты ЕГЭ по трем предметам и ДВИ по математике. То есть на ВМК вступительные испытания по математике являются обязательными. То есть это еще один дополнительный экзамен. Экзамен состоит из 8 заданий повышенной сложности. За все 8 правильно решенных заданий можно получить 100 баллов. Для того чтобы стать студентом факультета ВМК надо набрать 75-100 баллов.
Поступление на бюджет
Как поступить в ВМК на бюджет? Задача это непростая, так как в среднем конкурс на место составляет 5-7 человек. Поэтому тебе нужны превосходные знания, а для этого надо много работать. Даже если у тебя хорошие оценки в школе, это не дает гарантии того, что ты наберешь нужные баллы для поступления в МГУ ВМК на бюджет. Обычная подготовка здесь не подойдет, так как набрать нужно высокий балл. Стоит записаться на курсы при МГУ, а лучше всего найти хорошего репетитора.
План поступления на факультет ВМК
Начинать подготовку в университет нужно заранее за 2 года до поступления, так как проходные баллы на факультет достаточно высокие. Пути подготовки ты можешь выбрать сам:
- олимпиады; школы и курсы от МГУ репетиторы; самостоятельная подготовка;
Олимпиады
Олимпиады – хорошая возможность поступить на факультет ВМК. Принимать участие в олимпиадах могут школьники 9 и 10 классов. Подготовка к олимпиаде сложный процесс, так как обучение нужно начинать за год, за два до участия. Задачи там требуют хороших и нестандартных подходов. Всероссийская олимпиада для школьников – это хороший шанс набрать максимальный балл по выбранному предмету, но для этого тебе надо взять победу на региональных олимпиадах. Призёры олимпиад, кроме всероссийской олимпиады, могут поступать без экзаменов, однако ваш результат по ЕГЭ должен быть не менее 75 баллов по данному предмету. Участие в олимпиаде это шаг в будущее, который требует от тебя терпения, силы воли, времени, упорства на протяжении многих лет обучения. Первое место на региональном уровне не даёт тебе права выставления высшего экзаменационного балла на вступительных испытаниях.
Школы и курсы от МГУ
Школьники 9 и 10 классов имеют право поступать на курсы СУНЦ. СУНЦ — это специализированный учебно-научный центр, точнее школа, дающая аттестат о среднем образовании. Поступить в нее можно, если сдать внутренний экзамен.
Самостоятельная подготовка
Сосредоточенно подойди к своей цели, ведь поступить хочет каждый. Поэтому все свободное время планируй правильно: решай тесты по ЕГЭ, заполни пробелы в знаниях, повторяй пройденные темы. Результаты ЕГЭ по математике нужны для поступления в МГУ ВМК по специальностям:
- прикладная математика и информатика. фундаментальная информатика и информационные технологии.
Курсы по математике от Альфа-школы хороший вариант подготовки к ЕГЭ по математике. У тебя будет личный репетитор, который будет постоянно направлять тебя. Подготовка и поступление в университет — очень важный шаг, поэтому к обучению следует подойти серьезно. Правильно планируй время занимайся каждую неделю и не отходи от плана, так как будет весьма обидно, если тебе не хватит пару баллов, чтобы поступить на мехмат. Наиболее действенный и проверенный способ — онлайн-репетитор по математике. У тебя будут большие преимущества: репетитор уделяет время только тебе и ты не тратишь время на дорогу, которого у тебя и так мало. Профессионалы своего дела — репетиторы Альфа-школы знают как лучше подготовить тебя к такому сложному экзамену как математика. Система тестирования Альфа-школы помогает определить твои слабые стороны, поэтому результаты наших учеников высокие при регулярных и действенный занятиях. Также в Альфа-школе есть специальная программа подготовки к ЕГЭ и ДВИ по математике — решаются задания за прошлый и предыдущие года, подробно объясняется решение.
Приём документов
Подавать документы можно одновременно в 5 вузов, на 3 направления в каждом университете. Также можно приносить результаты ЕГЭ за 2013, 2014, 2015, 2016 и 2017 год. Начало приема документов в МГУ факультета ВМК идет после вступительных экзаменов по ЕГЭ и проходит в две волны, подача документов начинается с 20 июня по 26. 26 июля последний день подачи документов по результатам ЕГЭ. Узнать результаты ты уже можешь 3-8 августа. Зачисление происходит по результатам набранных баллов по ЕГЭ абитуриенты, набравшие наибольшее количество баллов поступают первые. Проходной балл за прошлый год ты узнаешь ниже. Каждый год количество баллов разное, в зависимости от количества поданных заявлений абитуриентов.
Документы, которые нужны для поступления:
Льготы
- Льгота первой степени – олимпиады. Всероссийская олимпиада и олимпиада «Ломоносов». Победителям всероссийской олимпиады выставляется максимальный балл по предмету. Победители олимпиады «Ломоносов» получают возможность максимального балла по экзамену, при условии, что они наберут не менее 75 баллов по тому же предмету на ЕГЭ. Льготы имеют категория граждан:
Для получения льгот необходимо предоставить документы, доказывающие данное положение.
Выпускники школы СУНЦ не имеют право льготы при поступлении.
- Абитуриентам, окончившим школу с золотой или серебряной медалью, дается льгота: плюс 5 баллов. Также льгота за спортивные достижения – 2 балла. Школьное сочинение -3 балла;
Если же льгот у тебя нет, то не стоит расстраиваться, с репетиторами Альфа школы ты сможешь хорошо подготовиться как к экзамену ЕГЭ так и к ДВИ по математике и набрать высокий балл для поступления в МГУ ВМК. Также ты сможешь бесплатно пройти первое занятие и протестировать свои знания. Удачи тебе!
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
МГУ ВМК: вступительные испытания
Факультет вычислительной математики и кибернетики МГУ является лучшим в области подготовки по прикладной математике, вычислительной математике, теории информации и программированию. Именно поэтому большинство абитуриентов выбирают именно этот факультет. Ещё одно преимущество факультета ВМК — это сотрудничество со многими зарубежными университетами для обучения по обмену, что дает молодым специалистам хороший старт в карьере. Ввиду этого с этим крупные IT-компании постоянно ищут новые таланты именно с факультета Вычислительной математики и кибернетики, предлагая студентам курсы с последующим трудоустройством. Помимо всего на факультете располагаются лаборатории таких известных компаний, как Intel и Microsoft, региональная академия CISCO, а также факультет ВМК принимает участие в программе Microsoft IT-Academy.
6-летняя программа подготовки специалистов в области прикладной математики и теории информации позволяет получить квалификацию математика и системного программиста. Математика как наука представляет собой совокупность отраслей. Учебные программы включают следующие математические дисциплины:
Также студенты глубоко изучают курс английского, ведь без него стать хорошим специалистом невозможно. Особое внимание уделяется практической работе, освоению студентами нескольких операционных систем и не менее трех языков программирования на высоком уровне.
Первый и второй семестр факультет дает базовую подготовку по математике и теоретическому и прикладному программированию, потом студенты должны выбрать специализацию. Математика — это наука, которая учит составлять алгоритмы разной сложности. В программировании – математика играет ключевую роль, на ее основе решаются многие задачи.
Также студенты могут заниматься научно-исследовательской работой для этого в их распоряжении лаборатории математики и физики.
Выпускники факультета востребованы различными компаниями и учреждениями в которых применяются IT-технологии, в том числе научно-исследовательскими институтами РАН, высшими учебными заведениями, государственными организациями, банками, страховыми компаниями, финансово-консалтинговыми компаниями, различными и зарубежными предприятиями и др. Около трети выпускников продолжают обучение в аспирантуре на одной из 18-ти кафедр:
Также в Альфа-школе есть специальная программа подготовки к ЕГЭ и ДВИ по математике — решаются задания за прошлый и предыдущие года, подробно объясняется решение.
Myalfaschool. ru
19.02.2019 2:05:46
2020-07-20 11:37:14
Источники:
Https://myalfaschool. ru/articles/mgu-vmk-vstupitelnye-ispytaniya
Вторая часть ЕГЭ по профильной математике: лайфхаки решения заданий » /> » /> .keyword { color: red; } Что считается вычислительной ошибкой на егэ по математике
Вторая часть ЕГЭ по профильной математике: лайфхаки решения заданий
Вторая часть ЕГЭ по профильной математике: лайфхаки решения заданий
Профильная математика — один из самых сложных экзаменов для большинства выпускников, от которого зависит аттестат. Именно стоит узнать, как решается вторая часть профильной математики ЕГЭ, так как именно за нее даются баллы, необходимые для результата 85+.
Что из себя представляет вторая часть в 2021
В 2021 году вторая часть профильной математики ЕГЭ состоит из одиннадцати номеров (четыре с кратким ответом, семь — с развернутым). Для их решения необходимо приобрести определенные знания и навыки:
- умение решать задачи (текстовые, прикладные, экономические, олимпиадные), умение анализировать функции, умение составлять и решать выражения, умение решать уравнения, умение решать неравенства, умение работать с параметром, знание стереометрии, знание планиметрии.
Критерии оценивания
Вторая часть профильной математики ЕГЭ весит 24 первичных балла из 32 возможных:
- № 9-12 — 1б, № 13-15 — 2б, № 16-17 — 3б, № 18-19 — 4б.
Для получения балла за № 9-12 необходимо записать правильный ответ в бланк, решение номера не рассматривается, однако по сложности это все же вторая часть профильной математики ЕГЭ.
В №13 балл могут дать за написание верного ответа или верного хода решения при неверном ответе.
В №14 балл дадут за решение одного из двух пунктов.
В №15 балл дадут за вычислительную ошибку или неверное исключение точки.
В №16 можно получить баллы за решение одного из пунктов: более сложного (2 балла) или более простого (1 балл).
В №17 баллы дают за верную математическую модель: два — за доведенное до конца решение с вычислительной ошибкой или недостаточным обоснованием, один — за не доведенное до конца решение.
В №18 три балла можно получить, если назвать два верных решения (и два неверных или недостаточно их обосновать), два балла за одно верное решение и один балл за верный ход мысли.
В №19 три балла дадут за три верных ответа, два — за два, один — за один (с обоснованием, если решение легкое).
Как решать вторую часть ЕГЭ по профильной математике
Вторая часть профильной математики ЕГЭ требует углубленных знаний в области дисциплины. При этом, каждый номер направлен на отработку каких-то конкретных знаний и навыков. Поэтому готовиться стоит к каждому номеру отдельно.
Задание 9
Задание №9 — это проверка простейших вычислений, для которых необходимо знать свойства логарифмов, тригонометрических функций, корней и степеней. Чтобы решить этот номер, можно воспользоваться приложенным к КИМ списком формул. Заранее стоит научиться выводить из них другие полезные формулы, это избавит от лишнего заучивания и поможет подготовиться к решению более сложных задач.
Задание 10
Вторая часть профильной математики ЕГЭ включает также задачу прикладного характера с формулой для ее решения. Нужно проследить, чтобы все значения измерялись однотипно (все время в секундах, например), а переменные представлялись в общем виде. Также лучше попробовать сократить выражение, если это возможно: так можно исключить вычислительную ошибку при подставлении.
Обязательно следует перепроверять свое решение.
Задание 11
В №11 может встретиться задача на один из шести типов. Решение любой из этих типов задач начинается с составления уравнения: искомая величина — Х. Оно чаще всего выходит линейным или квадратным. Для составления уравнения стоит пользоваться основными формулами: пути, работы и концентрации.
Задание 12
Для подготовки к заданию на точки экстремумов необходимо изучить таблицу основных производных и их графики, а также их свойства. Помимо этого, стоит попрактиковаться в нахождении нулей производных. Они помогут определить все точки экстремумов, из которых можно будет найти наибольшее и наименьшее значения функций.
Задание 13
Задание № 13, с которого начинается настоящая (с проверкой решения) вторая часть профильной математики ЕГЭ, проверяет умение выпускников ориентироваться в тригонометрии. Чтобы выполнить этот номер на максимум, необходимо, во-первых, найти ОДЗ, а во-вторых, с ее учетом решить полученное уравнение. Для этого может пригодится огромное количество формул и свойств, запомнить которые поможет мнемотехника. Так, одним из полезный упражнений на запоминание будет правило лошади: если она качает головой по вертикали, получается кивок — «да», поэтому вдоль оси ординат функция меняется; а вот качание головой по горизонтали, это «нет», функция не меняется.
Задание 14
№14 содержит два задания: на доказательство и вычисление. С первым могут помочь теорема Фалеса и подобие треугольников, а в последнем очень выручают теоремы синусов и косинусов, Пифагора, о трех перпендикулярах и тригонометрические функции в частности.
Задание 15
Неравенства задания №15 решаются благодаря постоянности логарифмической функции. От изменчивого основания можно избавиться, если перейти к новому постоянному основанию. Отдельное внимание стоит уделить ОДЗ, которое может меняться.
При решении важно помнить про методы интервалов и рационализации, правила замены тригонометрических функций.
Задание 16
Лучше запомнить все теоремы, свойства и аксиомы, связанные с треугольниками, так как они содержатся в любой фигуре и, соответственно, будут полезны при решении любого номера, который содержит вторая часть профильной математики ЕГЭ. Также особое внимание в №16 следует уделить рисунку: он должен быть наглядным, содержать необходимые пометки. Это поможет в решении любой задачи по планиметрии.
Задание 17
Вторая часть профильной математики ЕГЭ под видом №17 может предложить три типа задач:
Для их решения следует постепенно преобразовывать каждое условие задачи в уравнение или его часть. При подготовке следует заранее ознакомиться со схемами кредитования (дифференцированные и аннуитетные платежи), к задаче на оптимизацию нужно будет попрактиковаться в работе с целевыми функциями с точками экстремумов.
Задание 18
Этот номер проверяет умение мыслить логически и составлять схему рассуждений. Каждая из задач под этим номером нестандартна, поэтому помочь в их решении может только регулярная практика по вариантам прошлых лет. Однако стоит отметить, что в задании допустимо и графическое решение: так, в уравнениях с двумя переменными часто прячутся фигуры, которые могут оказаться ответом на задание.
Задание 19
№19 — последний, который включает вторая часть профильной математики ЕГЭ. Это задание олимпиадного уровня, поэтому оно требует нестандартного мышления. Для подготовки к нему можно изучить признаки делимости чисел (четное окончание как признак деления на «2» — это недостаточно для экзамена), а также формулы арифметической и геометрической прогрессий. Отлично помогут также решение заданий из вариантов прошлых лет, разборы олимпиадных заданий похожего типа.
Таким образом, видно, что вторая часть профильной математики ЕГЭ — это действительно сложные задачи, решить которые под силу не каждому выпускнику. Поэтому для того, чтобы сдать экзамен на 85+ баллов, необходимо усердно готовиться.
Таким образом, видно, что вторая часть профильной математики ЕГЭ это действительно сложные задачи, решить которые под силу не каждому выпускнику.
Umschool. net
24.07.2019 19:03:07
2020-12-23 04:34:34
Источники:
Https://umschool. net/journal/ege/vtoraya-chast-ege-po-profilnoj-matematike-lajfhaki-resheniya-zadanij/
Вернуться на основную страницу «Школы экспертов»
Ниже представлены ученические решения экзаменационных заданий. Оцените каждое из них в соответствии с критериями проверки заданий ЕГЭ. После нажатия кнопки «Проверить» вы узнаете правильный балл за каждое из решений. В конце будут подведены итоги.
Задание 485932
Задание 500131
Задание 500366
Задание 505470
Задание 511337
Задание 513071
Задание 513091
Задание 513092
Задание 513093
Задание 515919
Задание 559475
Задание 559477
Задание 559478
Задание 559481
Задание № 485932
Дано уравнение
а) Решите уравнение;
б) Укажите корни уравнения, принадлежащие отрезку
Решение
Используем формулу приведения и синуса двойного угла:
б) С помощью единичной окружности отберём корни на отрезке Находим:
Ответ: а) б)
Примечание.
Уравнение может быть так же решено при помощи следующей теоремы:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Пример 1.
Оцените это решение в баллах:
Задание № 500131
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение
а) Запишем уравнение в виде
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Задание № 500366
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение
а) Запишем уравнение в виде
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Пример 2.
Оцените это решение в баллах:
Пример 3.
Оцените это решение в баллах:
Задание № 505470
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение
а) Преобразуем исходное уравнение:
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Задание № 511337
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение
а) Имеем:
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Задание № 513071
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение
Имеем:
б) На указанном промежутке лежат точки
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Задание № 513091
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решение
а) Имеем:
б) С помощью числовой окружности (см. рис.) отберём корни, принадлежащие отрезку Получим точку
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Задание № 513092
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решение
а) Имеем:
б) На указанном промежутке лежат точки
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Задание № 513093
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решение
Имеем:
Либо
либо
что невозможно.
б) На указанном промежутке лежат точки
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Задание № 515919
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение
a) Воспользуемся формулой косинуса двойного угла:
и введем обозначение
Имеем:
Вернемся к исходной переменной:
б) С помощью числовой окружности (см. рис.) отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Пример 1.
Оцените это решение в баллах:
Пример 2.
Оцените это решение в баллах:
Пример 3.
Оцените это решение в баллах:
Задание № 559475
Решение
Пример 1.
Оцените это решение в баллах:
Пример 2.
Оцените это решение в баллах:
Пример 3.
Оцените это решение в баллах:
Задание № 559477
Решение
Пример 1.
Оцените это решение в баллах:
Пример 2.
Оцените это решение в баллах:
Пример 3.
Оцените это решение в баллах:
Задание № 559478
Решение
Пример 1
Оцените это решение в баллах:
Пример 2
Оцените это решение в баллах:
Пример 3
Оцените это решение в баллах:
Пример 4
Оцените это решение в баллах:
Задание № 559481
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение
а) Запишем уравнение в виде
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Пример 1
Оцените это решение в баллах:
Пример 2
Оцените это решение в баллах:
Наверх
Вернуться на основную страницу «Школы экспертов»
Математику базового уровня часто недооценивают, пренебрегая подготовкой к ней. Однако от нее зависит судьба аттестата: без «отлично» за математику отличник не получит красный аттестат, а без порогового балла выпускники в принципе рискуют уйти из школы со справкой! Типичные ошибки на ЕГЭ по математике помогут избежать этой участи.
Типичные ошибки ЕГЭ по математике в задачах на проценты
Проблемы возникают из-за неумения рассчитывать процент от суммы. Так, стоит обратить внимание, что процент повышения или понижения стоимости вычисляется от старой, а не новой цены, поэтому принимать новую цену за 100% и исходить из нее станет причиной ошибки на ЕГЭ по математике. Новая цена — это 100% ± процент повышения (+) или понижения (-).
Частые ошибки в вычислениях
Вычислительные ошибки на ЕГЭ по математике не редкость, но от этого они не перестают быть опасными и обидными. Стоит следить за наличием минуса (и его сокращением), а также помнить правила преобразования выражений, действий с дробями. Не стоит полагаться исключительно на умение считать в уме: лучше выполнять свои вычисления на бумаге и обязательно производить проверку (подставляя значение на место неизвестной в уравнениях и производя смежные действия (сложение-вычитание, деление-умножение) в простых примерах).
Основные ошибки теоретического характера
Ошибки на ЕГЭ по математике часто возникают из-за неумение работать с чертежами и терминологией. Большинство выпускников пытается найти заданную в номере величину с помощью инструментов или на глаз, часть из них не знает терминологии и находит не ту величину. Чтобы не допустить этого, стоит научиться работать с объемными фигурами: находить площадь их поверхности (всей или боковой), объемы и их части.
Также стоит обратить внимание на важные аспекты теории: основные теоремы, аксиомы, свойства.
Распространенные ошибки в алгоритмах и методах решения
Последовательность выполнения действий проходится еще во втором классе, однако даже такие ошибки на ЕГЭ по математике встречаются. Стоит помнить как простейшие алгоритмы решения примеров: сначала действия в скобках, а потом остальные; первыми идут умножение и деление, потом сложение и вычитание, — так и более сложные. Так, в дробях ни в коем случае нельзя забывать про знаменатель, а сокращаться из числителя и знаменателя могут только множители (простые числа и выражения в скобках).
Ошибки при чтении и построении чертежа
Ошибки на ЕГЭ по математике, касающиеся чертежа, возникают при работе как с объемными фигурами, так и с расположенными в одной плоскости. Они связаны с отсутствием пространственного представления и невнимательностью, вызванной неправильным прочтением буквенной записи (угол АВС — это не то же самое, что углы АСВ и САВ). Также сложности могут возникнуть при неумении ориентироваться в основных обозначениях на чертеже (равные стороны, равные углы, прямые углы).
Типовые ошибки в заданиях по тригонометрии
Раздел тригонометрии построен на знании тригонометрических тождеств и свойств тригонометрических функций, поэтому ошибки на ЕГЭ по математике могут быть допущены из-за недостаточного владения теорией. В КИМ-е базовой математике даны основные формулы, которые могут быть полезны выпускникам, однако стоит также научиться выводить из них остальные.
Ошибки математического моделирования
Трудности, связанные с математическими моделями, вызваны неумением решать практические текстовые задачи. Для их решения необходимо понимать принцип работы действия (чаще всего, один из видов движения). Сложности возникают с подстановкой в формулу неверных данных, из-за чего искажается ответ.
Таким образом, базовая математика не так проста, как может показаться на первый взгляд. Она не займет так много времени, как профильная, но все равно требует подготовки.
И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.
В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.
Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.
Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.
Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.
Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…
Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:
Уравнения
Основные ошибки:
1) неправильное использование формул приведения.
При преобразовании допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.
2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.
Классическая ошибка! – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.
3) неправильное или некорректное использование тригонометрических формул.
Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида .
Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.
4) Самое банальное. Неверное решение простейших тригонометрических уравнений.
При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.
Неравенства
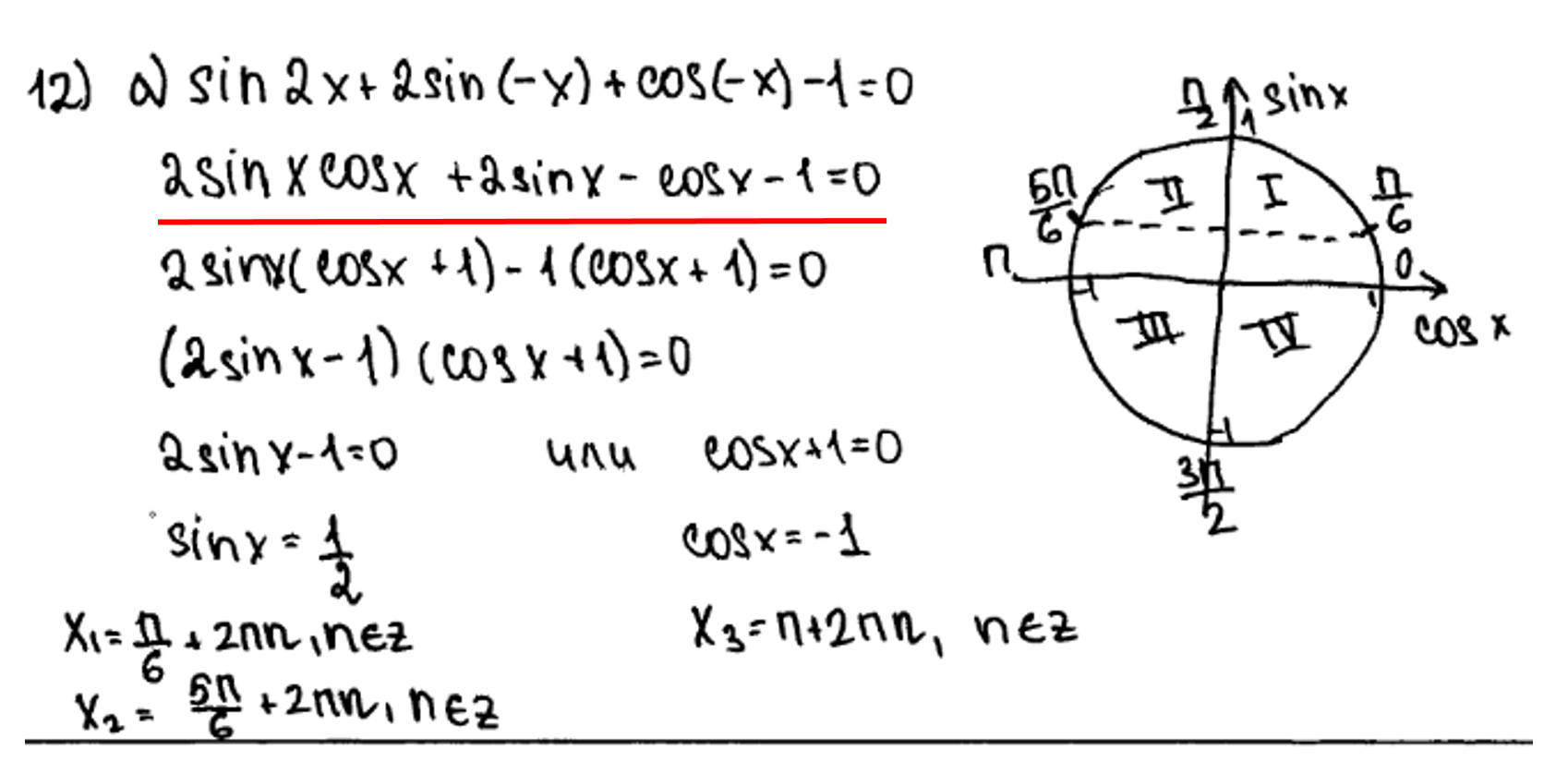
С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.
1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.
Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.
2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.
Это привело к тому, что на координатной прямой не хватает нулей двух скобок: .
Такая грубая ошибка на экзамене не прощается.
Оценка эксперта – 0 баллов.
3) Неравносильный переход от неравенства к системе неравенств.
Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.
4) Ошибки при использовании свойств логарифмов.
Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.
Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.
Экономические задачи
В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования – с дифференцированными платежами, аннуитентными или иная форма кредитования.
Могу выделить несколько основных ошибок.
1)Неверное построение математической модели, связанное с неверным определением формы кредитования.
Для лучшего понимания начну с условия задачи.
В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:
– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года
– размер платежей в 2027 и 2028 годах одинаковый
– к июлю 2029 года долг выплачивается полностью.
Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?
Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: .
Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.
Идем дальше. Наверняка Вы встречали задачи вида:
15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:
– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.
– со 2 по 14 число необходимо выплатить часть долга;
– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;
– 15 июля 2027 года долг составит 300 тыс рублей.
– 15 августа 2027 года долг должен быть выплачен полностью.
Найдите общую сумму выплат после полного погашения кредита.
В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так:
. Как Вы понимаете, и выплаты будет принимать совсем другой вид, так как они получаются путем вычитания из долга после начисления процентов самого остатка. Для примера запишем первую выплату:
.
С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.
2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.
Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:
25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.
— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;
— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;
– с февраля по июль необходимо выплатить часть долга;
– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;
– к августу 2032 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.
Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.
В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.
PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.
В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.
На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!
Все, что не убивает, делает нас сильнее!
P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!
10 основных ошибок, допускаемых в ЕГЭ по математике
Совет учиться на ошибках других бесполезен; научиться чему-либо можно только на собственных ошибках.
Б. Шоу
-
Обзор основных ошибок
Обзор составлен на основе материалов ФИПИ за 2016, 2017 гг.
https://drive.google.com/file/d/0B8MkXVdvfYcrZUdvcmk0TEpia1k/view
http://www.fipi.ru/sites/default/files/document/1476454097/matematika.pdf
Профильный уровень
|
Задание |
Процент выполнения |
Типичные ошибки |
|
1 |
90% |
Неумение читать условие и непонимание процентов |
|
2 |
95% |
Невнимательное чтение условия и непонимание единиц измерения |
|
3 |
88% |
Невнимательное чтение условия |
|
4 |
89% |
Невнимательное чтение условия |
|
5 |
91% |
Ошибки в свойствах степеней |
|
6 |
65% |
Непонимание математической записи угла и неверное чтение чертежа |
|
7 |
54% |
Невнимательное чтение условия |
|
8 |
57% |
Отсутствие базовых пространственных представлений и знаний соотношений |
|
9 |
47% |
Ошибки в определении знака тригонометрической функции |
|
10 |
65% |
Невнимательное чтение условия или непонимание текста |
|
11 |
36% |
Невнимательное чтение условия |
|
12 |
38% |
Непонимание алгоритма исследования функции с помощью производной |
|
13 |
36% |
Неумение и небрежность отбора корней тригонометрического уравнения с помощью единичной окружности |
|
14 |
6% |
Неумение доказывать, непонимание взаимосвязи элементов геометрической конструкции, ошибки в теоретических фактах |
|
15 |
15% |
Невнимательное чтение математической записи неравенства, непонимание алгоритма решения совокупностей и систем логарифмических неравенств, забыт знаменатель при решении дробно-рационального неравенства, небрежность при изображении множества решений на координатной прямой |
|
16 |
3% |
Неверное понимание логики построения доказательства, ошибки в построении чертежа |
|
17 |
11% |
Неверное составление модели задачи (непонимание взаимосвязи величин) и вычислительные ошибки |
|
18 |
3,5% |
Недостаточная сформированность графического метода решения – отсутствие объяснений и обоснований, отсутствие ответа на поставленный вопрос |
|
19 |
3,5% |
Непонимание того, что на вопрос «Может ли…?» нужно давать аргументированное решение, а не ответ «да» или «нет» |
Базовый уровень
Основные факторы, вызывающие ошибки:
-
недостаточный уровень понимания условия при чтении задания,
-
вычислительные ошибки,
-
недостаточная развитость наглядных геометрических представлений.
-
Анализ 10 типичных ошибок на примерах заданий ЕГЭ
Задачи на проценты – непонимание механизма начисления процентов.
В большинстве случаев причина ошибок – непонимание сущности процента. Например, если в условии сказано, что цена товара сначала была повышена на 25%, а затем понижена на 25%, то эти проценты не будут одной и той же суммой денег, т.к. база начисления этих процентов разная.
Пример:
При решении этого задания 6% участников экзамена посчитали, что если цена была повышена на 25%, то для нахождения старой цены нужно новую цену понизить на 25%. В действительности же новая цена составляет 125% от старой цены, а узнать нужно, сколько рублей соответствуют 100%.
В более сложной экономической задаче требуется понимание механизма начисления простых и сложных процентов, обоснованное применение формул, выбор правильного способа решения. Типичные ошибки здесь связаны с неверным составлением модели задачи, непониманием взаимосвязи величин, непониманием того, что важен не только ответ, но и способ решения задачи.
Невнимательное чтение условия.
К сожалению, это самая распространенная ошибка согласно анализу типичных ошибок ЕГЭ, проведенному ФИПИ.
Конечно, многое здесь можно списать на волнение и психологическое напряжение. Даже самые подготовленные ученики на экзамене могут растеряться, переволноваться или поспешить в решении более простых заданий. Однако факт остается фактом, и при подготовке к экзаменам на него нужно обратить внимание.
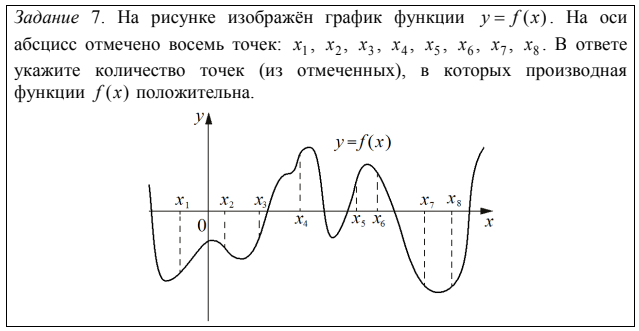
Примеры:
Почти 24% участников экзамена указали количество точек, в которых значение функции (а не ее производной) положительно, а еще около 2% участников пытались перечислить номера точек, в которых производная принимает положительное значение.
Около 2,5% участников экзамена нашли вероятность выбора подтекающего насоса, не обратив внимания на частицу «не» в условии.
Практико-ориентированные задания базового и повышенного уровня – непонимание текста задачи.
Кроме ошибок, связанных с невнимательным чтением условия, на первое место здесь выходит непонимание текста задачи, незнание единиц измерения величин, неумение работать с формулами. Многие выпускники даже не приступают к технически не сложным практико-ориентированным задачам повышенного уровня.
Пример:
Выполнение задания – около 57%. Отмечается, что 8% участников не дали никакого ответа; 6% решили, что чем ближе, тем лучше; 4% решили, что лампочку нужно поместить в середину разрешенного интервала, а еще 4,5% решили, что самый главный параметр – это фокус.
Вычислительные ошибки.
Привычка вычислять все с помощью калькулятора, вплоть до таблицы умножения и действий с круглыми числами доставляет учащимся немало проблем на экзамене. Отсутствие навыков быстрого счета в уме или на бумаге часто приводит к тому, что участники экзамена допускают грубые ошибки в элементарных примерах. «Слабые» места многих старшеклассников – это дроби, отрицательные числа, элементарные преобразования выражений, т.е. проблемы, накопившиеся с 5 класса.
Ошибки в теоретических фактах.
Незнание необходимых для решения задач теоретических фактов, как по алгебре, так и по геометрии, существенно снижает процент выполнения большинства заданий как базового, так и повышенного уровня сложности.
Примеры:
Около 8% выпускников не дали никакого ответа; 38% ошиблись в формуле боковой поверхности конуса, а еще 12% в формуле его объема. Отмечается, что процент выполнения этого задания существенно ниже, чем, например, формально гораздо более сложного задания с полным решением на решение уравнения и осуществление отбора корней. Это означает, что низкий процент выполнения заданий по стереометрии вызван именно существенными проблемами в ее преподавании.
В задании 5 проверялось умение решать показательные и логарифмические уравнения. Из семи процентов выпускников, не справившихся с заданием, 2% ошиблись в свойствах степеней.
Незнание алгоритмов и методов решения.
Знание алгоритмов и методов решения проверялось во многих заданиях экзаменационной работы. Например, в задании 12 требовалось продемонстрировать понимание алгоритма исследования функции с помощью производной, а в заданиях 5,13,15 знание общих и частных методов решения уравнений и неравенств.
Пример:
Ненулевые баллы получило около 15% участников экзамена. Типичные ошибки связаны с невнимательным чтением математической записи неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств. Очень много ошибок при решении дробно-рационального неравенства (забыт знаменатель).
Неверное чтение чертежей, непонимание взаимосвязи элементов геометрической конструкции, отсутствие базовых пространственных представлений, ошибки в построении чертежа.
В преподавании геометрии очень важным является не только умение решать вычислительные задачи с геометрическим содержанием (по формулам), но и формировать геометрические представления о фигурах (телах). При отсутствии базовых пространственных представлений сложно ожидать высокого процента выполнения стереометрического задания с полным решением.
Пример:
Отмечается, что около 10% участников экзамена при решении этой задачи неверно определили углы по их записи (перепутали буквы или не понимают, какая из букв в записи угла соответствует его вершине). Около 5% участников «увидели» прямоугольный треугольник ACD, а еще 3% — равносторонний треугольник ABD.
Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. В целом при решении геометрических задач более половины выпускников продемонстрировали отсутствие знания взаимосвязей элементов геометрической конструкции и соотношений между величинами пространственных фигур.
Неумение доказывать, обосновывать.
К заданиям повышенного уровня относились задания второй части 14 (стереометрия) и 16 (планиметрия) с развернутым ответом. Оба задания содержали два пункта. В первом пункте задание доказать, а во втором пункте вычислить. Основной проблемой оказалось выполнение первого пункта. Участники экзамена продемонстрировали неумение доказывать. При этом много встречается различного рода логических ошибок. Наибольшие затруднения участники испытывали при оформлении доказательства.
Пример:
Типичные ошибки связаны с непониманием логики построения доказательства. Например, доказательство начинается так: «Пусть точка О является серединой отрезка СК…». Т.е. в начале доказательства уже допускается факт, который и требуется доказать.
Задания 18 и 19 высокого уровня сложности предназначены для конкурсного отбора в ВУЗы с повышенными требованиями к математической подготовке абитуриентов. Это задания на комбинацию различных методов. Для успешного их выполнения, кроме прочих математических знаний, необходим высокий уровень математической культуры, который предполагает, в частности, умение обосновывать выбранные методы и способы решения.
Примеры:
Ненулевые баллы при решении этого задания получило около 17% участников экзамена. Многие выпускники попробовали исследовать несколько примеров, а потом обобщить полученный результат. Типичным заблуждением для многих оказалось, что на вопрос «Может ли?» нужно давать аргументированное решение, а не качественный ответ «да» или «нет».
Ненулевые баллы при решении этого задания получило около 3% участников экзамена. Основной проблемой оказалось применение графического метода, который, как показали работы участников экзамена, не достаточно сформирован. Без объяснений и обоснований на координатной плоскости отмечаются графики, и считывается множество значений параметра. Во многих случаях на координатной плоскости обозначено много верных объектов, а ответа на поставленный вопрос так и не последовало.
Задания по тригонометрии требуют тщательности решения.
Представленные в экзаменационной работе задания по тригонометрии не относятся к числу самых сложных, однако их выполнение требует тщательности решения, аккуратности, внимания, знания большого количества теоретических фактов и умения их применять на практике.
Примеры:
Выполнение задания – около 34%. Типичные ошибки связаны в первую очередь с определением знака тригонометрической функции – почти 12% участников экзамена потеряли знак «минус». Еще 22% решили, что ответ ожидается «хорошим» — 1 или 2.
Задание 13 проверяло умение решать тригонометрические уравнения и производить отбор корней. Основной проблемой первого пункта оказалось неумение вводить новую переменную (ошибки в свойствах степеней), незнание формул решения простейшего тригонометрического уравнения. При выполнении второго пункта участники продемонстрировали неумение или небрежность отбора корней.
Отсутствие навыков математического моделирования.
Способность к построению и исследованию простейших математических моделей проверяется в заданиях 11 (текстовая задача) и 17 (текстовая задача с экономическим содержанием). Текстовые задачи, как правило, являются стандартными задачами на составление уравнений курса алгебры 8 класса. В экономической задаче требуется верно построить математическую модель и исследовать ее. Важную роль при этом играет сюжетная, практико-ориентированная часть условия. При составлении математических моделей основные ошибки являются следствием непонимания взаимосвязи величин. Так, например, в задачах на движение около 10% участников экзамена продемонстрировали непонимание движения по реке – собственную скорость умножили на время движения.
-
Задачи с ошибками как форма работы на уроке.
Одной из форм работы на уроках является поиск и исправление ошибок. «Задачи с ошибками» являются заданиями творческого типа, они приучают обращать внимание на особо тонкие места в логических рассуждениях, помогают различать во многом сходные понятия, приучают к точности суждений и математической строгости и т. д.
Мой опыт преподавания показывает, что такие задания нравятся учащимся и являются достаточно эффективным способом совершенствования навыков решения задач.
Методика работы с задачами с ошибками может быть следующей:
1 этап: Индивидуальная, парная или групповая работа, в зависимости от уровня подготовленности учащихся, по поиску и исправлению ошибок. Задачи с ошибками могут быть представлены в раздаточном материале (карточки) или на слайдах презентации.
2 этап: Совместное обсуждение ошибок.
3 этап: Снова индивидуальная или парная работа – составление памятки «Советы ученику, решающему задачу».
4 этап: Проверка результатов и подведение итогов учителем.
Примеры заданий с ошибками по многим темам можно составить самим или найти в литературных и интернет-источниках.
Мои рекомендации:
-
Черкасов О.Ю., Якушев А.Г. Математика для поступающих в ВУЗы.
У меня старое издание 1996 года, но есть и более поздние издания этой книги.
Раздел 7 этого пособия так и называется: «Учимся на чужих ошибках».
-
http://math4school.ru/rabota_nad_oshibkami.html
Раздел сайта «Мath4school» называется «Работа над ошибками», содержит большое количество примеров с решениями и подробным анализом ошибок.