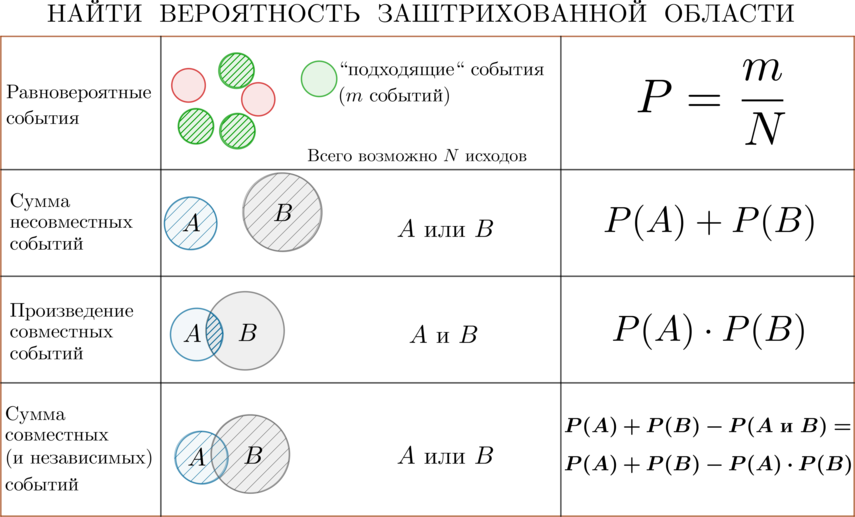
4. Введение в теорию вероятностей
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Общая памятка по всем разделам теории вероятностей:
Задание
8
#3093
Уровень задания: Сложнее ЕГЭ
Миша и Маша играют в игру: Миша пишет на доске натуральное число (a), а Маша – натуральное число (b). Затем Миша стирает свое число и вместо него записывает модуль суммы (a) и (b), а Маша – стирает свое и пишет модуль разности (a) и (b). Затем с новыми числами они проделывают то же самое. Найдите вероятность того, что через 100 таких действий произведение чисел, записанных на доске, будет кратно 4.
Рассмотрим все возможные варианты:
1) Миша написал четное число, Маша – нечетное. Тогда на втором шаге на доске будут написаны нечетное и нечетное числа. На третьем шаге: четное и четное числа. На четвертом, пятом и т.д.: четное и четное. Тогда на 100 шаге произведение этих чисел будет всегда делиться на 4.
2) Миша написал четное, Маша – тоже четное. Тогда аналогично первому случаю на всех последующих шагах на доске тоже будут написаны два четных числа, следовательно, на 100 шаге их произведение всегда будет делиться на 4.
3) Миша и Маша написали нечетные числа. Тогда на втором шаге на доске будут написаны четные числа, как и на всех следующих шагах (аналогично второму случаю). Следовательно, на 100 шаге их произведение будет всегда делиться на 4.
Таким образом, в любом случае произведение чисел будет делиться на 4. Значит, вероятность этого события равна 1.
Ответ: 1
Задание
9
#2670
Уровень задания: Сложнее ЕГЭ
Артур считает вероятность наступления некоторого события (A) в случае, если он подбросит правильную игральную кость дважды. У него получилось, что вероятность наступления события (A) равна (0,01). Известно, что Артур ошибся, но его ошибка наименьшая из возможных при данных условиях. Насколько ошибся Артур? Ответ округлите до сотых.
При подбрасывании правильной игральной кости дважды можно получить (6cdot 6 = 36) различных исходов. Так как вероятность – это отношение числа подходящих исходов к числу всевозможных исходов, то результат Артура мог быть либо (0), либо его можно было представить в виде дроби [dfrac{N}{36},,] где (Ninmathbb{N}) – число подходящих исходов.
Таким образом, в случае, если (P(A)neq 0), то минимальное значение, которое могла принять (P(A)), составляет [dfrac{1}{36} > dfrac{1}{50} = 0,02,.]
Таким образом, ответ Артура ближе к (0), чем к любому числу вида (dfrac{N}{36},,) где (Ninmathbb{N}), следовательно, чтобы ошибка Артура была минимальной, необходимо, чтобы было выполнено (P(A) = 0). Тогда ошибка Артура составит (0,01).
При этом такое действительно возможно, если, например, (A =) “В сумме за два подбрасывания выпадет (13)”. В итоге, ответ: (0,01).
Ответ: 0,01
Задание
10
#2683
Уровень задания: Сложнее ЕГЭ
Тимур считает вероятность наступления некоторого события (A) в случае, если он подбросит правильную игральную кость сто раз. У него получилось, что вероятность наступления события (A) равна (0,045). Известно, что Тимур ошибся, но его ошибка наименьшая из возможных при данных условиях. Учитель задумался, насколько ошибся Тимур (учителя интересует ответ, округлённый до десятых). Какой результат должен получить учитель?
Рассмотрим ситуацию, когда (P(A) = 0) (она возможна при данных условиях), тогда ошибка Тимура составит (0,045). Так как ошибка Тимура наименьшая из возможных, то она не превосходит (0,045), но все числа, не превосходящие (0,045), при округлении до десятых дают (0). Таким образом, ответ: (0).
Ответ: 0
Задание
11
#192
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 1001 раз. Какова вероятность того, что выпало более 500 орлов? Ответ округлите до десятых.
Вероятность выпадения более 500 орлов равна вероятности выпадения более 500 решек (орёл и решка “равноправны”). Но “выпало более 500 решек”( =) “выпало менее 501 орла”. Таким образом, вероятность выпадения более 500 орлов равна вероятности выпадения менее 501 орла.
Но события “выпало более 500 орлов”( ) и “выпало менее 501 орла”( ) в объединении содержат все возможные исходы серии из 1001 подбрасывания.
При этом эти события не могут наступить одновременно, следовательно, вероятность того, что наступит какое-нибудь из них равна сумме их вероятностей и равна 1.
Таким образом, вероятность события “выпало более 500 орлов”( ) равна (0,5).
Ответ: 0,5
Задание
12
#193
Уровень задания: Сложнее ЕГЭ
За круглый стол в случайном порядке рассаживаются Белоснежка, злая ведьма и 5 гномов (двое охраняют мероприятие). Найдите вероятность того, что Белоснежка и злая ведьма не будут сидеть вместе. Ответ округлите до сотых.
Проще сначала найти вероятность того, что Белоснежка и злая ведьма окажутся сидящими вместе. Для этого можно мысленно объединить Белоснежку и злую ведьму, как занимающих одно место на двоих из 6 мест за столом. Тогда на первое место можно посадить одного из 6 кандидатов, на второе одного из 5 и т.д., значит количество различных рассадок за таким столом будет равно (6cdot 5cdot 4cdot 3cdot 2cdot 1 = 6!).
При этом каждая рассадка за таким столом дает две различных рассадки за обычным 7-местным столом (Белоснежку и злую ведьму “на одно место из 6”( )можно посадить вместе двумя способами). Тогда общее количество рассадок за начальным столом, в которых Белоснежка и злая ведьма сидят вместе равно (2cdot 6!).
Общее количество всевозможных рассадок за столом равно (7cdot 6cdot 5cdot 4cdot 3cdot 2cdot 1 = 7!). В итоге вероятность того, что они окажутся сидящими вместе равна [dfrac{2cdot 6!}{7!} = dfrac{2}{7} = 0,2857dots,] следовательно, вероятность того, что они не сядут вместе равна (1 — 0,2857… = 0,7142…). После округления окончательно получаем (0,71).
Ответ: 0,71
Задание
13
#194
Уровень задания: Сложнее ЕГЭ
Компания “Light”( )изготавливает лампочки. Вероятность того, что готовая лампочка неисправна, равна (0,04). Каждую лампочку дополнительно проверяет упаковщик. Вероятность того, что упаковщик обнаружит (и изымет) неисправную лампочку, равна (0,96). Вероятность того, что упаковщик по ошибке изымет исправную лампочку, равна (0,01). Найдите вероятность того, что случайно выбранная изготовленная лампочка будет изъята упаковщиком.
Лампочка может быть изъята в двух случаях: лампочка исправна, но упаковщик ошибся или лампочка неисправна и упаковщик не ошибся. Вероятность первого из этих исходов составляет [(1 — 0,04)cdot 0,01 = 0,0096.]
Вероятность второго из этих исходов равна [0,04cdot 0,96 = 0,0384.] Так как эти исходы несовместны (нельзя изъять одну лампочку одновременно в обоих случаях), то вероятность того, что наступит хотя бы один из них есть просто сумма их вероятностей.
Тогда (0,0096 + 0,0384 = 0,048) – искомая вероятность.
Ответ: 0,048
Задание
14
#195
Уровень задания: Сложнее ЕГЭ
Чтобы поступить в университет на механико-математический факультет, абитуриент должен набрать на ЕГЭ не менее 75 баллов по каждому из трёх предметов – математика, русский язык и физика, и не менее 75 баллов за внутренний экзамен по математике. Чтобы поступить на факультет вычислительной математики и кибернетики, нужно набрать не менее 75 баллов за ЕГЭ по каждому из четырех предметов – математика, русский язык, физика и информатика, и не менее 60 баллов за тот же внутренний экзамен по математике, что и на механико-математический факультет. Вероятность того, что абитуриент Cubert получит не менее 75 баллов за ЕГЭ по математике, равна 0,8, по русскому языку – 0,9, по физике – 0,85, по информатике – 0,7. Вероятность того, что Cubert сдаст внутренний экзамен не менее, чем на 60 баллов равна (0,9). Вероятность того, что Cubert сдаст внутренний экзамен не менее, чем на 75 баллов равна (0,7). Найдите вероятность того, что Cubert’у хватит баллов хотя бы на один из двух упомянутых факультетов. Ответ округлите до сотых.
Вероятность того, что Cubert’у хватит баллов на механико-математический факультет равна [0,8cdot 0,9cdot 0,85cdot 0,7 = 0,4284.] Вероятность того, что Cubert’у хватит баллов на факультет вычислительной математики и кибернетики равна [0,8cdot 0,9cdot 0,85cdot 0,7cdot 0,9 = 0,38556.] Вероятность того, что Cubert’у хватит баллов на оба факультета равна [0,8cdot 0,9cdot 0,85cdot 0,7cdot 0,7 = 0,29988,] тогда вероятность того, что ему хватит хотя бы на один факультет равна [0,4284 + 0,38556 — 0,29988 = 0,51408.] После округления окончательно получаем (0,51).
Ответ: 0,51

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Тема 4.
Задачи на теорию вероятностей
4
.
04
Задачи повышенного уровня сложности
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи на теорию вероятностей
4.01Умножение вероятностей вдоль цепочки событий
4.02Условная вероятность
4.03Комбинаторика
4.04Задачи повышенного уровня сложности
Решаем задачу:
Чтобы поступить в университет на механико-математический факультет, абитуриент должен набрать на
ЕГЭ не менее 75 баллов по каждому из трёх предметов – математика, русский язык и физика, и не
менее 75 баллов за внутренний экзамен по математике. Чтобы поступить на факультет вычислительной
математики и кибернетики, нужно набрать не менее 75 баллов за ЕГЭ по каждому из четырех
предметов – математика, русский язык, физика и информатика, и не менее 60 баллов за тот же
внутренний экзамен по математике, что и на механико-математический факультет. Вероятность того,
что абитуриент Cubert получит не менее 75 баллов за ЕГЭ по математике, равна 0,8, по русскому языку
– 0,9, по физике – 0,85, по информатике – 0,7. Вероятность того, что Cubert сдаст внутренний
экзамен не менее, чем на 60 баллов равна . Вероятность того, что Cubert сдаст внутренний
экзамен не менее, чем на 75 баллов равна . Найдите вероятность того, что Cubert’у
хватит баллов хотя бы на один из двух упомянутых факультетов. Ответ округлите до сотых.
Показать ответ и решение
Вероятность того, что Cubert’у хватит баллов на механико-математический факультет равна
Вероятность того, что Cubert’у хватит баллов на факультет вычислительной математики и кибернетики
равна
Вероятность того, что Cubert’у хватит баллов на оба факультета равна
тогда
вероятность того, что ему хватит хотя бы на один факультет равна
После округления окончательно получаем .
Решение.
Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов. Пусть A, B, C и D — это события, в которых З. сдает соответственно математику, русский, иностранный и обществознание не менее, чем на 70 баллов. Тогда поскольку
для вероятности поступления имеем:
Ответ: 0,408.
Приведем другую запись этого решения.
В силу независимости событий, вероятность успешно сдать экзамены на лингвистику: 0,6 · 0,8 · 0,7 = 0,336, вероятность успешно сдать экзамены на коммерцию: 0,6 · 0,8 · 0,5 = 0,24, вероятность успешно сдать экзамены и на «Лингвистику», и на «Коммерцию»: 0,6 · 0,8 · 0,7 · 0,5 = 0,168. Успешная сдача экзаменов на «Лингвистику» и на «Коммерцию» — события совместные, поэтому вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Тем самым, поступить хотя бы на одну из этих специальностей абитуриент может с вероятностью 0,336 + 0,24 − 0,168 = 0,408.
Приведём решение Алексея Столбова из Магнитогорска.
Есть три варианта поступления абитуриента хотя бы на одну специальность:
а) поступить на лингвистику при этом не поступив на коммерцию: вероятность 0,6 · 0,8 · 0,7 · 0,5;
б) поступить и на лингвистику, и на коммерцию: вероятность 0,6 · 0,8 · 0,7 · 0,5;
в) не поступить на лингвистику, при этом поступив на коммерцию: вероятность 0,6 · 0,8 · 0,3 · 0,5.
Эти события несовместные, искомая вероятность суммы этих событий равна сумме их вероятностей:
0,6 · 0,8 · (0,35 + 0,35 + 0,15) = 0,48 · 0,85 = 0,408.
Приведём решение Ирины Шраго из Санкт-Петербурга.
Для поступления З. необходимо сдать математику и русский язык хотя бы на 70 баллов, а также сдать иностранный язык или обществознание не менее, чем на 70 баллов. Это события независимые, причём событие «сдать хотя бы один экзамен не менее, чем на 70 баллов» противоположно событию «сдать оба предмета менее, чем на 70 баллов». Получаем, что вероятность искомого события: 0,6 · 0,8 · (1 − 0,3 · 0,5) = 0,408.
Приведём решение с помощью двоичного дерева.
Для того, чтобы поступить на специальность «автоматизация» абитуриент должен сдать И математику, И русский язык, И физику (союз И — логическое умножение):
0,4 · 0,5 · 0,3 = 0,06.
Для того, чтобы поступить на специальность «мехатроника» абитуриент должен сдать И математику, И русский язык, И информатику (союз И — логическое умножение):
0,4 · 0,5 · 0,2 = 0,04.
Вероятность того, что абитуриент поступит на автоматизацию ИЛИ на мехатронику (союз ИЛИ — логическое сложение) равна:
0,06 + 0,04 = 0,1.
Но не стоит исключать тот факт, что абитуриент может сдать все экзамены и поступить сразу на две специальности, а это нам не подходит, поэтому
0,1 — 0,4 · 0,5 · 0,3 · 0,2 = 0,1 — 0,012 = 0,088
(0,4 · 0,5 · 0,3 · 0,2 = 0,012 — это успешная сдача всех экзаменов, которая позволяет поступить на обе специальности).
Ответ: 0,088.
Решение одним выражением:
Р = 0,4 · 0,5 · 0,3 + 0,4 · 0,5 · 0,2 — 0,4 · 0,5 · 0,3 · 0,2 = 0,088.
Формула для сложения совместных событий:
P(A + B) = P(A) + P(B) — P(A·B).
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
Артикул: 1135418
Раздел:Технические дисциплины (82933 шт.) >
Математика (31384 шт.) >
Теория вероятности (3866 шт.) >
Теория вероятности и математическая статистика (ТВиМС) (2450 шт.)
Название или условие:
Чтобы поступить в университет на механико-математический факультет, абитуриент должен набрать на ЕГЭ не менее 75 баллов по каждому из трёх предметов – математика, русский язык и физика, и не менее 75 баллов за внутренний экзамен по математике. Чтобы поступить на факультет вычислительной математики и кибернетики, нужно набрать не менее 75 баллов за ЕГЭ по каждому из четырех предметов – математика, русский язык, физика и информатика, и не менее 60 баллов за тот же внутренний экзамен по математике, что и на механико-математический факультет. Вероятность того, что абитуриент Cubert получит не менее 75 баллов за ЕГЭ по математике, равна 0,8, по русскому языку – 0,9, по физике – 0,85, по информатике – 0,7. Вероятность того, что Cubert сдаст внутренний экзамен не менее, чем на 60 баллов равна 0,9. Вероятность того, что Cubert сдаст внутренний экзамен не менее, чем на 75 баллов равна 0,7. Найдите вероятность того, что Cubert’у хватит баллов хотя бы на один из двух упомянутых факультетов. Ответ округлите до сотых.
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Чтобы поступить в институт на специальность «Переводчик», абитуриент должен набрать на ЕГЭ не менее 67 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент», нужно набрать не менее 67 баллов по каждому из трёх предметов – математика, русский язык и обществознание.
Вероятность того, что абитуриент Р. получит не менее 67 баллов по математике, равна 0,5, по русскому языку – 0,6, по иностранному языку – 0,9 и по обществознанию – 0,7.
Найдите вероятность того, что Р. сможет поступить на одну из двух упомянутых специальностей.
Источник: statgrad
Решение:
Вероятности не менее 67 баллов:
математика = 0,5
русский язык = 0,6
иностранный язык = 0,9
обществознание = 0,7
Абитуриент будет сдавать все 4 экзамена.
Найдём вероятность того, что абитуриент поступит на «Переводчик», но не поступит на «Менеджмент»:
0,5·0,6·0,9·(1 – 0,7) = 0,081
Найдём вероятность того, что абитуриент поступит на «Менеджмент», но не поступит на «Переводчик»:
0,5·0,6·(1 – 0,9)·0,7 = 0,021
Вероятность того, что он поступит только на одну из двух специальностей, равна сумме вероятностей:
0,081 + 0,021 = 0,102
Ответ: 0,102.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.4 / 5. Количество оценок: 18
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Чтобы поступить в институт на специальность «Переводчик», абитуриент должен набрать на ЕГЭ не менее 67 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент», нужно набрать не менее 67 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Р. получит не менее 67 баллов по математике, равна 0,5, по русскому языку — 0,6, по иностранному языку — 0,9 и по обществознанию — 0,7.
Найдите вероятность того, что Р. сможет поступить на одну из двух упомянутых специальностей.
Решение:
Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский язык, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов. Пусть А — сдает математику не менее, чем на 70 баллов В — сдает русский не менее, чем на 70 баллов С — сдает иностранный не менее, чем на 70 баллов D — сдает обществознание не менее, чем на 70 баллов Вероятность того, что он сможет поступить хотя бы на одну из двух упомянутых специальностей будет состоять из суммы вероятностей независимых событий: абитуриент сдаст Математика > 70 Русский > 70 Иностранный > 70 Обществознание > 70 Математика > 70 Русский > 70 Иностранный < 70 Обществознание > 70 Математика > 70 Русский > 70 Иностранный > 70 Обществознание < 70 Вероятности этих событий соответственно равны:
0,6∙0,8∙0,7∙0,5
0,6∙0,8∙0,3∙0,5
0,6∙0,8∙0,7∙0,5
Таким образом, вероятность поступить хотя бы на одну из специальностей равна: 0,6∙0,8∙0,7∙0,5 + 0,6∙0,8∙0,3∙0,5 + 0,6∙0,8∙0,7∙0,5 = = 0,48∙0,35 + 0,48∙0,15 + 0,48∙0,35 = = 0,48∙(0,35 + 0,15 + 0,35) = 0,48∙0,85 = 0,408
Ответ: 0,408