

Подборка по базе: Дополнительные тестовые вопросы — копия.docx, ПО_Экзамен. ответы на вопросы.docx, ПУШКИН К ПУЩИНУ ВОПРОСЫ 6.doc, Тестовые вопросы к разделу 6_ просмотр попытки.pdf, Тестовые вопросы к разделу 2_ просмотр попытки (1).pdf, Тестовые вопросы к разделу 4 Морфемика и словообразование. Морфо, Тестовые вопросы к разделу 5 Синтаксис_ просмотр попытки.pdf, Тестовые вопросы к разделу 6_ просмотр попытки.pdf, Общие вопросы.docx, Ответы на контрольные вопросы.docx
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
по дисциплине «Цифровая обработка сигналов»
- Какие преобразования сигналов выполняются в системе цифровой обработки аналоговых сигналов?
Дискретизация, квантование, кодирование. Смотреть ниже.
Из аналогово в цифровой из цифрового в аналоговый.
Преобразование аналогового сигнала в цифровой выполняется в три этапа: дискретизация, квантование, кодирование.
Преобразование цифрового сигнала в аналоговый:
- Что такое дискретный сигнал и дискретная последовательность? Из каких условий выбирается частота дискретизации аналоговых сигналов? Каким образом могут быть уменьшены искажения, связанные дискретизацией сигнала?
Аналоговый сигнал можно дискредитировать с помощью аналогово элемента – АЦП аналогово цифровой преобразователь. АЦП дискредитирует аналоговый сигнал. На его вход подаются аналоговые сигналы на его выходе имеется последовательность точек – цифровой сигнал. Дискретизация сигнала сводится к тому, чтобы из аналогово напряжения, поданного на вход АЦП брать точки и брать эти точки через равные промежутки времени.
| Рис. Аналоговый сигнал
|
Рис. Дискретный сигнал
|
Сигнал, который представляет собой точки, взятые через определённый промежуток времени, называется дискретным. Сигнал дискретный по оси времени по напряжению сигнал остаётся непрерывным. АЦП срабатывает одни раз за промежуток времени называемым периодом дискретизации. Период дискретизации — это величина постоянная.
Период дискретизации – это временной интервал, через который срабатывает АЦП.
Дискретный сигнал – это последовательность дискретных значений, каждое значение имеет свой порядковый номер.
Чем больший временной интервал дискретизации, тем больше будет дискретных значений при условии, что частота дискретизации остаётся неизменной. Последовательность отчётов представляет собой конечную последовательность – она имеет конечную длину. Аналоговый сигнал считается бесконечным.
Чтобы восстановление сигнала произошло полностью должны быть выполнены условия. Эти условия определяются теоремой Котельникова, которая говорит о том, как связать период дискретизации с параметрами сигнала.
Теорема Котельникова: если сигнал 






Главное условие частота дискретизации должна быть как минимум в два раза больше, чем максимальная частота в спектре.

Чтобы дискредитировать аналоговый сигнал нужно иметь сведения о его амплитудном спектре.
Так, к примеру для аудиозаписей берут частоту дискретизации чуть больше 40 кГц и теорема Котельникова выполняется немного с запасом.
Если спектр сигнала не когда не равен нулю, то в таком случае максимальную частоту исходного сигнала берут условно.
Рис. Амплитудный спектр сигнала асимптотически приближается к оси абсцисс
В задачах, где важна форма сигнала частоту дискретизации нужно брать с запасом значительно больше, чем x2 от максимальной частоты в спектре.
Теорема Котельникова предполагает, что сигнал, который необходимо будет восстановить является гармоническим (два отчёта на период синусоиды). Если сигнал имеет сложную форму, то нужно брать частоту дискретизации значительно больше, чем это указано в теореме Котельникова. Приборы для снятия кардиограммы берут частоту дискретизации в сотни раз больше максимальной частоты спектра (250 ГЦ — 1кГц).
Часто недостаточно брать частоту дискретизации строго по теореме Котельникова так как данная теорема включает в себя ряд допущений. Согласно теореме Котельникова на период сигнала приходится два отчёта, при этом эти два отчёта должны попадать именно на период сигнала. Во-вторых, речь идёт о восстановление по двум отчётам синусоиды. Согласно теореме Котельникова время наблюдения сигнала является бесконечным, и имеется брать два отчёта сигнала именно на его период. Частоту дискретизации выбирают так чтобы можно было восстановить необходимую характеристику сигнала. Обычно необходимо восстанавливать либо корреляционную функцию сигнала, либо плотность корреляции. Это касается случайных процессов.
Можно измерить СКО при определении каждой характеристики в зависимости от частоты дискретизации.
Повышенная частота дискретизации требует повышенной быстродействия процессора, что не всегда реально осуществить, такие микропроцессоры стоят дорого. Если нужно восстановить не определённые характеристики сигнала, а именно его форму, то частоту дискретизации нужно брать в значительно число раз больше, чем этого требует теорема Котельникова.
Когда сигнал дискредитируется, то спектр такого сигнала становится периодическим.
Рис 1. Спектр сигнала.
На рисунки частота дискретизации была взята в соответствии с теоремой Котельникова. Если взять частоту меньше, чем это требует теорема Котельникова то спектры начнут накладываться друг на друга.
Рис. Явление наложения спектров
Для уменьшения искажений необходимо либо увеличивать частоту дискретизации, либо использовать перед АЦП дополнительный фильтр нижних частот, ограничивающий спектр исходного сигнала перед его аналого-цифровым преобразованием.
- Какова математическая модель квантования сигнала по уровню, т. е. какой алгоритм используется для преобразования дискретного сигнала в дискретный квантованный? Как определяется погрешность квантования дискретного квантованного сигнала?
Чтобы сигнал сохранить в цифровой форме его нужно представить в виде дискретных кодов. Если сигнал откодирован, то такой сигнал уже называется цифровым.
Цифровой сигнал – это последовательность кодов.
Чтобы присвоить дискретным значениям цифровые коды нужно квантовать сигнал по времени и по уровню. Дискретный сгинул квантован только по времени. При квантовании по уровню берутся наибольшее к первоначальному значению по уровню.
Операция дискретизации и квантования являются независимыми и в большинстве случаев делаются одним и тем же устройством – АЦП.
Полученные дискретные значения в дальнейшем должны быть квантованы по уровню. Определяется шаг квантования 
Рис 1. Связь аналогово и дискретного сигнала
Округление происходи в сторону ближайшего уровня квантования. Уровни квантования сформированы внутри АЦП. У АЦП имеется напряжение питания из этого напряжения питания обычно путём деления формируются уровни квантования. Число уровней квантования определяется разрядностью АЦП.
Число уровней квантования: 

Число разрядов кода:
N – число уровней квантования, n – разрядность кода, int – определение наименьшего целого числа, не менее заданного.
Каждому из уровней квантования присваивается определённый код (порядковый номер). Обычно уровни квантования кодируются целыми беззнаковыми числами. АЦП с повышенной разрядностью стоят дороже и работают медленнее.
При использовании системы с фиксированной запятой и представлении в прямом коде шаг квантования сигнала равен:



При срабатывании АЦП значение, которое было в момент его срабатывания должно быть зафиксировано. Поэтому пока выполняются операции аналогово цифрового преобразования считается, что напряжение на входе не меняется.
Обычно АЦП делаются с разрядность 8 и выше.
Разность между квантованным и точным значениями дискретного сигнала: 

Относительная максимальная погрешность:
Относительная среднеквадратическая погрешность:
Максимальная ошибка квантования: 

Среднеквадратическая ошибка квантования:
Для получения минимальной относительной погрешности квантования динамический диапазон сигналов на входе системы ЦОС 



Дисперсия шума квантования цифрового сигнала определяется как 

Спектральная плотность мощности цифрового шума
n – разрядность, 
- Что такое аналого-цифровой преобразователь? Из каких условий выбирается необходимая разрядность аналого-цифрового преобразователя?
Аналоговый сигнал можно дискредитировать с помощью аналогово элемента – АЦП аналогово цифровой преобразователь. АЦП дискредитирует аналоговый сигнал. На его вход подаются аналоговые сигналы на его выходе имеется последовательность точек – цифровой сигнал.
Условия и способы выбора разрядности АЦП основываются на допустимых соотношениях погрешности квантования и значения уровней дискретного или цифрового сигналов. Для дискретных сигналов при этом учитывается характеризующие АЦП максимальный диапазон преобразуемых в код напряжений и шаг квантования по уровню.
Шаг квантования 
Первый способ. Выбор разрядности осуществляется по допустимой относительной погрешности квантования сигнала, приведённой ко входу АЦП (смотреть вопрос 3 конец). Сначала нужно определить необходимые значения шага квантования:

Требуемая разрядность АЦП:
int – определение наименьшего целого числа, не менее заданного.

Выбор разрядности АЦП по допустимой относительной погрешности квантования дискретного сигнала используется в измерительных системах ЦОС.
Второй способ. Разрядность АЦП находят из допустимого отношения 


Мощность шума квантования определяется по формуле:
Добавление одного разряда АЦП увеличивает отношение сигнал/шум квантования на 6 дБ.
Третий способ. Разрядность АЦП выбирается в соответствии условия соизмеримости дисперсии шума квантования с дисперсией, действующего совместно с входным сигналом внешнего дискретизированного шума.
- В соответствии с каким алгоритмом осуществляется обработка сигнала рекурсивным цифровым фильтром? Какой объём вычислительных операций выполняется в рекурсивном фильтре при обработке одного отсчёта сигнала? Какие способы описания цифровых фильтров вы знаете?
Характеристики цифрового фильтра: АЧХ, ФЧХ, ИХ, ПФ, групповая задержка, фазовая задержка.
| Рис 3. Структурная схема рекурсивного цифрового фильтрат
|
Рекурсия — это приём, который предполагает, что для текущих расчётов используются результаты, полученные на предыдущих этапах. Рекурсивный фильтра позволяет получить более качественный результат чем нерекурсивный фильтр того же порядка. Но рекурсивный фильтр менее устойчивый. Рекурсия означает наличие в фильтре обратной связи, т.е. зависимости выходного сигнала y(n) от его предыдущих отсчетов y(n − k).
Причиной неустойчивости может быть представление коэффициентов с недостаточным количеством разрядов. И получается, что при отсутствии колебания в реальности оно появится в результате расчётов. В таком случае фильтр превращается в генератор. |
Вопросы к экзамену по ЦОС (Вопросы к зачету/экзамену по дисциплине «Цифровая обработка сигналов»)
PDF-файл Вопросы к экзамену по ЦОС (Вопросы к зачету/экзамену по дисциплине «Цифровая обработка сигналов») Цифровая обработка сигналов (ЦОС) (22342): Вопросы/задания — 8 семестрВопросы к экзамену по ЦОС (Вопросы к зачету/экзамену по дисциплине «Цифровая обработка сигналов») — PDF (22342) — СтудИзба2019-01-292019-01-29СтудИзба
Описание файла
PDF-файл из архива «Вопросы к зачету/экзамену по дисциплине «Цифровая обработка сигналов»»,
который расположен в категории «».
Всё это находится в предмете «цифровая обработка сигналов (цос)» из 8 семестр, которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана.
Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. Архив можно найти в разделе «к экзамену/зачёту», в предмете «цифровая обработка сигналов» в общих файлах.
Просмотр PDF-файла онлайн
Текст из PDF
Вопросы к зачету (экзамену) ЦОСПорядок сдачиВ зависимости от группы, контрольным мероприятием может быть либо зачет, либоэкзамен.Для допуска к экзамену либо зачету нужно выполнить и защитить домашнее задание илабораторную работу.Для получения зачета необходимо ответить на все вопросы (см. ниже). Для сдачи экзаменанеобходимо также решить одну задачу (см. ниже).Количество преподаваемого материала за семестр тоже зависит от группы. Это количествоменьше для тех групп, у которых контрольным мероприятием является зачет.
Количествовопросов, соответственно, тоже меньше; не используются вопросы, выделенные в отдельныйблок.Вопросы1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.Что такое цифровой сигнал. Как его получить из непрерывного.Частота дискретизации: понятие и критерии выбора.Неоднозначность частоты цифрового сигнала.Спектр цифрового сигналаШумы квантованияАпертурные погрешностиOversampling: что это такое, для чего нужно, как работаетОшибки переполненияДПФa. Применения ДПФb. Растекание спектра при ДПФc. Дополнения нулямиd. БПФe. БабочкаОкна: описание, применениеВ чем преимущества КИХ фильтров перед БИХ фильтрами?Четыре крестаИХ ЦФОпределение и критерий устойчивости БИХПЛИС: устройство и преимуществаDSP: виды ускорителей обработкиШина USBa.
Общие сведения, устройство, применениеb. Питание: виды устройств по питанию, максимальный ток, напряжениеc. Архитектураd. Скорости передачи данныхОтдельный блок1.2.3.4.5.Полифазное БПФ. Принцип работы, плюсы и минусы.Всепропускающие фильтры. Применение, принцип работы, характеристики.Режекторный фильтр на основе всепропускающих.Параметрический эквалайзер на основе всепропускающих фильтров.Особенности аппроксимации АЧХ фильтра: по Баттерворту, по Чебышеву (первогои второго рода), по Кауэру.6. Сигналы DTMF: что это, где применяется, как обеспечивается защита от совпаденияс голосом.7. Модифицированный алгоритм Герцеля.Задачи1. Рассчитайте режекторный фильтр с частотой подавленияB, при частоте дискретизации д ., ГцB, Гц№д , Гц150210000255205000344020015000410002010000, с полосой подавленияидля2.
Рассчитайте параметры модифицированного алгоритма Герцеля N,различения частотипри минимизации растекания спектра. Частотадискретизации д ., Гц, Гц№д , Гц5104711751000061319139750007148015681500083729400010000.
Свежие статьи
Популярно сейчас
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
650
Средний доход
с одного платного файла
Обучение Подробнее
Вопросы к
экзамену по курсу «Цифровая обработка сигналов»
МП-38, МП-39, ИМЭ-36
1.
Понятие сигнала.
Классификация сигналов по способу обработки, по физическим свойствам.
2.
Спектральное
представление сигналов, преобразование Фурье, АЧХ и ФЧХ сигналов.
3.
Свойства АЧХ и ФЧХ
действительных сигналов.
4.
Примеры спектров
некоторых сигналов. Прямоугольный импульс. Эффективная ширина спектра.
5.
Прямоугольный
импульс, задержанный во времени — АЧХ и ФЧХ.
6.
Дуальность
преобразования Фурье. Несимметричный треугольный импульс — АЧХ и ФЧХ.
7.
Односторонний
экспоненциальный импульс, Гауссов импульс — АЧХ и ФЧХ.
8.
Основные понятия
функционального анализа. Линейное пространство. Линейное нормированное
пространство.
9.
Неравенство
Минковского. Метрика. Метрическое пространство.
10.
Понятие шара, сферы
e — окрестности. Предел
последовательности.
11.
Расстояние от
точки до подпространства. Элемент наилучшего приближения (ЭНП).
12.
Банахово
пространство. Фундаментальная последовательность. Критерий сходимости.
13.
Пространство со
скалярным произведением. Неравенство Коши-Буняковского. Ортогональный базис.
14.
Гильбертово
пространство. Аппроксимация в гильбертовом пространстве. Неравенство Бесселя.
15.
Ряд Фурье по
ортогональной системе элементов. Коэффициенты ряда Фурье. Равенство Парсеваля-Стеклова.
16.
Примеры
ортогональных систем в пространстве L2.
17.
Система функций
Радемахера и её свойства.
18.
Система функций
Уолша и её свойства.
19.
Система функций
Хаара и её свойства.
20.
Тригонометрические
ряды Фурье. Свойства рядов Фурье. Эффект Гиббса.
21.
Комплексная форма
рядов Фурье. Интегральное преобразование Фурье.
22.
Спектральный
анализ и преобразование Фурье.
23.
Свойства
преобразования Фурье. Линейность. Изменение масштаба.
24.
Свойства
преобразования Фурье. Задержка сигнала. Свертка сигналов.
25.
Свойства
преобразования Фурье. Произведение сигналов. Равенство Парсеваля.
26.
Свойства
преобразования Фурье. Дифференцирование по временной области. Дифференцирование
в частотной области.
27.
Обобщенное
преобразование Фурье.
28.
Принцип
неопределенности для сигналов в плоскости время-частота.
29.
Спектр дискретного
сигнала. Шаг дискретизации. Частота Найквиста. Свойства спектра дискретного
сигнала.
30.
Спектральные
свойства сигналов трех основных типов.
31.
Соотношение между
спектрами непрерывного и дискретного сигналов.
32.
Теорема
Котельникова.
33.
Дискретное
преобразование Фурье (ДПФ). Графическая иллюстрация.
34.
Свойства ДПФ.
Симметрия. Линейность. Графическая иллюстрация.
35.
Свойства ДПФ.
Циклический сдвиг влево. Циклический сдвиг влево на m позиций. Графическая иллюстрация.
36.
Свойства ДПФ.
Циклический сдвиг вправо на m
позиций. Графическая иллюстрация.
37.
Свойства ДПФ. Свертка
векторов. Графическая иллюстрация.
38.
Вычисление
спектров дискретного и непрерывного сигналов с помощью ДПФ.
39.
Быстрое
преобразование Фурье (БПФ). Алгоритм прореживания по времени.
40.
БПФ на примере 8 —
ми точечного преобразования.
41.
Аналоговая
обработка сигналов. Линейность системы. Принцип суперпозиции.
42.
Характеристики
линейных систем. Импульсная характеристика системы.
43.
Условие физической
реализуемости системы.
44.
Комплексный
коэффициент передачи. Фазовая и групповая задержка системы.
45.
Основное уравнение
линейной системы с постоянными параметрами (ЛПП). Функция передачи системы.
46.
Нули и полюсы
функции передачи системы.
47.
Линейные
дискретные фильтры (ЛДФ). Свойства линейности и стационарности ЛДФ.
48.
Импульсная
характеристика ЛДФ.
49.
Условие физической
реализуемости ЛДФ. Устойчивость ЛДФ.
50.
Основное уравнение
ЛДФ. Рекурсивные и не рекурсивные фильтры.
51.
Z – преобразование.
52.
Свойства Z – преобразования. Линейность.
Задержка последовательности.
53.
Свойства Z – преобразования. Опережающий сдвиг
последовательности. Умножение последовательности на степенную
функцию.
54.
Свойства Z – преобразования. Умножение
последовательности на номер элементов. Z – преобразование свертки.
55.
Обращение Z – преобразования. Теорема о вычетах.
56.
Решение разностных
уравнений с помощью Z – преобразования.
57.
Линейный
дискретный фильтр и Z – преобразование.
58.
Передаточная
функция ЛДФ. Связь передаточной функции с основным уравнением ЛДФ.
59.
Способы соединения
фильтров.
60.
Структурные схемы
ЛДФ. Прямая форма ЛДФ.
61.
Структурные схемы
ЛДФ. Прямая каноническая форма ЛДФ.
62.
Свойства линейных
дискретных фильтров. Условия устойчивости ЛДФ.
63.
Частотная
характеристика ЛДФ.
64.
КИХ и БИХ фильтры.
65.
Рекурсивные и не рекурсивные
фильтры, и их связь с КИХ и БИХ фильтрами.
66.
Аналоговые
фильтры. Классификация фильтров по АЧХ.
67.
Фильтр
Баттерворта.
68.
Фильтр Чебышева
первого рода, полюсы и нули.
69.
Три основных
условия синтеза фильтров.
70.
Фильтр Чебышева
второго рода, полюсы и нули.
71.
Эллиптический
фильтр, полюсы и нули.
72.
Преобразование
фильтров. Изменение частоты среза фильтра низких частот (ФНЧ).
73.
Преобразование ФНЧ
в фильтр высоких частот (ФВЧ).
74.
Преобразование ФНЧ
в полосовой фильтр.
75.
Преобразование ФНЧ
в режекторный фильтр.
76.
Синтез
рекурсивного фильтра по аналоговому прототипу.
77.
Метод билинейного —
преобразования.
78.
Геометрические
свойства билинейного преобразования.
79.
Метод инвариантной
импульсной характеристики.
80.
Синтез
нерекурсивных фильтров с использованием окон.
81.
Весовые функции,
окна.
82.
Прямоугольное
окно. Треугольное окно.
83.
Окно Бартлетта.
Окно Ханна.
84.
Окно Хэмминга.
Окно Блэкмена.
85.
Окно Кайзера. Окно
Чебышева.
86.
Синтез не рекурсивных
фильтров методом Ремеза.
87.
Синтез
нерекурсивных фильтров методом среднеквадратичного отклонения.
88.
Дискретизация и
квантование сигналов.
Вопросы теоретического теста № 2 по курсу «Цифровая обработка сигналов»
Осенний семестр 2014/2015 уч. г.
1.Запишите формулы прямого и обратного ДПФ.
2.Как связаны друг с другом результаты ДПФ и спектр дискретного сигнала (преобразование Фурье в дискретном времени)? Приведите соответствующую формулу.
3.Чему равен шаг частотной сетки ДПФ?
4.(В тестовом задании будут фигурировать конкретные числовые значения) Частота дис-
кретизации сигнала равна … Гц, размерность ДПФ N = … . Какой частоте соответствует результат вычисления ДПФ, имеющий индекс n = … (нумерация начинается с нуля)? Привести соответствующие расчеты.
5.(В тестовом задании будут фигурировать конкретные числовые значения) Частота дис-
кретизации сигнала равна … Гц, размерность ДПФ N = … . Какой (с каким номером n) элемент ДПФ соответствует частоте … Гц? (Нумерация элементов ДПФ начинается с нуля.) Привести соответствующие расчеты.
6.В чем заключается основная идея алгоритма быстрого преобразования Фурье с прореживанием по времени?
7.Что такое «бабочка» в алгоритмах БПФ? Изобразите ее структурную схему.
8.Что такое бит-реверсная адресация? Где и с какой целью она применяется?
9.Как зависит число математических операций, требуемое для вычисления ДПФ по прямой формуле, от длины преобразуемого сигнала? Привести соответствующую формулу.
10.Как зависит число математических операций, требуемое для вычисления быстрого преобразования Фурье, от длины преобразуемого сигнала? Привести соответствующую формулу, считая, что длина сигнала равна степени двойки.
11.Охарактеризуйте изменения в результатах ДПФ, происходящие при дополнении преобразуемого сигнала нулями.
12.Изобразите схему системы, реализующей алгоритм Герцеля. Для чего он применяется? В каких случаях его целесообразно использовать?
13.Каким образом можно вычислить линейную свертку с помощью круговой свертки? Для чего используется такой способ ее вычисления?
14.Опишите процедуру фильтрации в частотной области методом перекрытия с суммирова-
нием (overlap-add).
15.Опишите процедуру фильтрации в частотной области методом перекрытия с накоплени-
ем (overlap-save).
16.Что такое растекание спектра? Каковы причины этого явления?
17.Для чего используются весовые функции (окна) при спектральном анализе? Охарактеризуйте изменения результатов вычисления спектра в результате применения окон.
18.Каков типичный набор исходных данных при проектировании фильтра нижних частот?
19.Опишите процедуру синтеза дискретного фильтра по аналоговому прототипу методом билинейного z-преобразования.
20.Приведите формулу, описывающую трансформацию частотной оси при билинейном z-преобразовании.
21.У какого фильтра нижних частот крутизна спада АЧХ больше — у аналогового прототипа или у дискретного фильтра, синтезированного по этому прототипу методом билинейного z-преобразования? Ответ обосновать.
22.На каких частотах дискретный фильтр, синтезированный методом билинейного z-преобразования, имеет такой же комплексный коэффициент передачи, как аналоговый прототип при частоте, стремящейся к бесконечности?
1
23.На каких частотах дискретный фильтр, синтезированный методом билинейного z-преобразования, имеет такой же комплексный коэффициент передачи, как аналоговый прототип при частоте, равной нулю?
24.Накладывает ли метод инвариантной импульсной характеристики какие-либо ограничения на тип АЧХ синтезируемых фильтров? Если да, то какие именно?
25.Как связаны между собой импульсные характеристики аналогового прототипа и полученного на его основе дискретного фильтра при использовании метода инвариантной импульсной характеристики? Приведите соответствующую формулу.
26.Как связаны между собой частотные характеристики аналогового прототипа и полученного на его основе дискретного фильтра при использовании метода инвариантной импульсной характеристики? Приведите соответствующую формулу.
27.Можно ли при синтезе фильтра методом инвариантной импульсной характеристики заранее гарантировать выполнение конкретных требований к АЧХ фильтра (допустимые отклонения в заданных полосах и т. п.)? Почему?
28.В каких целях используются весовые функции при прямом оптимальном синтезе дискретных фильтров?
29.Запишите формулу для целевой функции, используемой при прямом синтезе дискретных фильтров по заданной АЧХ в случае p = 2. Какой характерной чертой обладают частотные характеристики нерекурсивных фильтров, синтезированных данным методом?
30.Запишите формулу для целевой функции, используемой при прямом синтезе дискретных фильтров по заданной АЧХ в случае p = . Какой характерной чертой обладают частотные характеристики нерекурсивных фильтров, синтезированных данным методом?
31.Опишите процедуру прямого синтеза нерекурсивного дискретного фильтра оконным методом.
32.Опишите искажения идеализированной АЧХ, происходящие при синтезе нерекурсивных дискретных фильтров оконным методом.
33.Как рассчитать импульсную характеристику идеализированного фильтра по его частотной характеристике? Приведите соответствующую формулу.
34.Как рассчитать импульсную характеристику идеализированного фильтра во временной области? Опишите соответствующую последовательность действий.
35.Приведите формулу для импульсной характеристики идеального фильтра нижних частот, изобразите АЧХ и ФЧХ данного фильтра.
36.Приведите формулу для импульсной характеристики идеального дифференцирующего фильтра, изобразите АЧХ и ФЧХ данного фильтра.
37.Перечислите основные эффекты, связанные с конечной разрядностью представления чисел в цифровых системах обработки сигналов.
38.Каковы достоинства и недостатки форматов представления чисел с фиксированной запятой?
39.Каковы достоинства и недостатки форматов представления чисел с плавающей запятой?
40.(В тестовом задании будут фигурировать конкретные числовые значения) Формат с фиксированной запятой a.b использует a двоичных разрядов для представления целой части (включая знак; для представления отрицательных чисел используется дополнительный код) и b двоичных разрядов для представления дробной части. Какое максимальное по модулю положительное число может быть представлено в этом формате? Как выглядит его двоичное представление в этом формате?
41.(В тестовом задании будут фигурировать конкретные числовые значения) Формат с фиксированной запятой a.b использует a двоичных разрядов для представления целой части (включая знак; для представления отрицательных чисел используется дополнительный код) и b двоичных разрядов для представления дробной части. Какое минимальное по модулю ненулевое отрицательное число может быть представлено в этом формате? Как выглядит его двоичное представление в этом формате?
2
42.При использовании каких форматов (с фиксированной или плавающей запятой) эффекты конечной точности представления чисел сказываются сильнее? Почему?
43.Какие предположения о статистических свойствах шума квантования обычно используются для его аналитического описания? При каких условиях они хорошо выполняются на практике?
44.Для каких фильтров — рекурсивных или нерекурсивных — ошибки квантования коэффициентов сказываются сильнее? Почему?
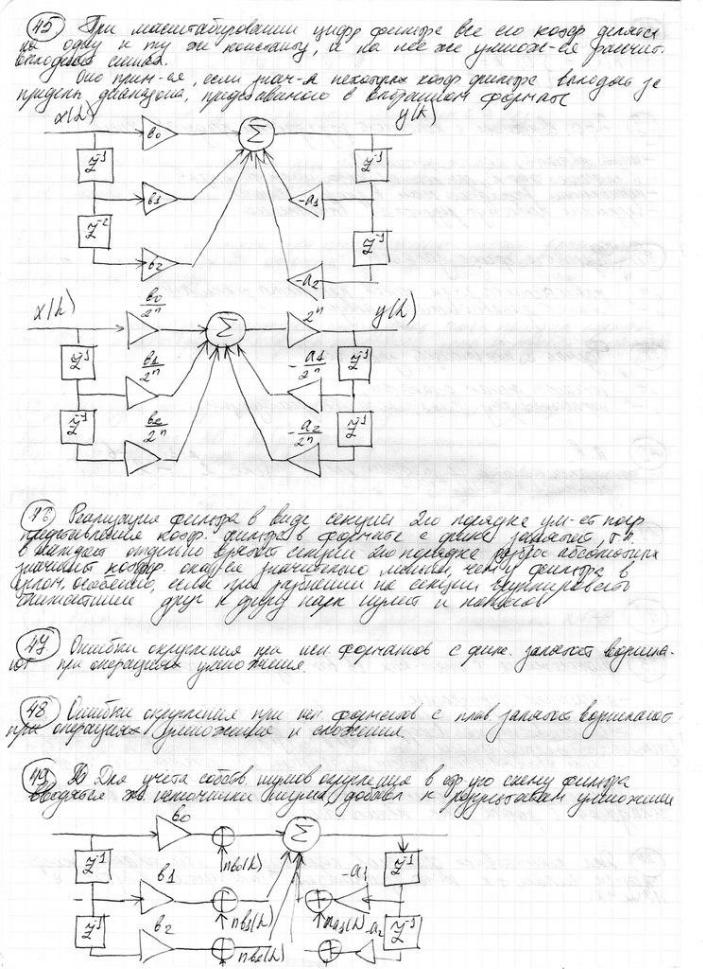
45.Что такое масштабирование коэффициентов цифровых фильтров? С какой целью оно применяется? Покажите на примере фильтра второго порядка, как при масштабировании коэффициентов модифицируется структурная схема фильтра.
46.Почему реализация фильтра в виде каскада секций второго порядка уменьшает погрешности представления коэффициентов фильтра в формате с фиксированной запятой?
47.При каких арифметических операциях возникают ошибки округления результата при использовании форматов с фиксированной запятой?
48.При каких арифметических операциях возникают ошибки округления результата при использовании форматов с плавающей запятой?
49.Как выглядит модель цифрового фильтра с учетом собственных шумов округления при использовании форматов с фиксированной запятой? Приведите пример в виде структурной схемы произвольного фильтра и поясните, в какие точки схемы вводятся шумовые сигналы.
50.Что такое предельные циклы? Опишите их типы и причины их возникновения.
51.Как осуществляется интерполяция дискретного сигнала (повышение частоты дискретизации в целое число раз)? Приведите соответствующую структурную схему.
52.Как осуществляется прореживание дискретного сигнала (понижение частоты дискретизации в целое число раз)? Приведите соответствующую структурную схему.
53.Чему должны быть равны частота среза и коэффициент передачи в полосе пропускания для фильтра нижних частот, используемого в схеме прореживания?
54.Чему должны быть равны частота среза и коэффициент передачи в полосе пропускания для фильтра нижних частот, используемого в схеме интерполяции?
55.К каким последствиям может привести удаление ФНЧ из схемы прореживания?
56.Почему при реализации интерполяции и прореживания обычно используются нерекурсивные фильтры?
57.Как осуществляется передискретизация сигнала (изменение частоты дискретизации с рациональным коэффициентом)? Приведите соответствующую структурную схему.
58.За счет чего можно уменьшить число необходимых вычислительных операций при выполнении интерполяции?
59.За счет чего можно уменьшить число необходимых вычислительных операций при выполнении прореживания?
60.Для чего при реализации интерполяции и прореживания применяют многокаскадные структуры?
3

4

5

6

7

8
9

10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цифровая обработка сигналов. Вопросы к экзамену.
-
Временные ряды и дискретные системы. Линейные дискретные системы инвариантные к сдвигу.
-
Коммутативность ЛДИС. Импульсная характеристика.
-
Дискретизация непрерывного сигнала. Алиасинг. Дискретизация низкочастотных сигналов.
-
Дискретизация сигналов в полосе частот.
-
Дискретное преобразование Фурье. Свойства ДПФ. Утечка между отсчетами ДПФ. Окна. Потея амплитуды для некратных частот.
-
Разрешение ДПФ, дополнение нулями и связь с дискретизацией спектра сигнала. Усиление сигнала в результате ДПФ.
-
ДПФ прямоугольного окна.
-
Быстрое преобразование Фурье. Вывод БПФ-2, перестановка битов в индексах.
-
Фильтры с конечной импульсной характеристикой (КИХ). Связь со сверткой, теорема о свертке. Расчет НЧ фильтров.
-
Расчет полосовых КИХ фильтров.
-
Фазовая характеристика КИХ фильтров.
-
Анализ КИХ фильтров. Групповая задержка, АЧХ, оценка количества коэффициентов.
-
Фильтры с бесконечной импульсной характеристикой (БИХ). Преобразование Лапласа. Устойчивость непрерывного фильтра.
-
z-преобразование. Устойчивость дискретного фильтра.
-
Использование полюсов и нолей для анализа фильтров. Сравнение КИХ и БИХ фильтров.
-
Вычислительно-эффективные реализации БИХ фильтров.
-
Расчет дискретных БИХ фильтров по непрерывному прототипу.
-
Расчет дискретных БИХ фильтров с использованием билинейного преобразования.
-
Специальные фильтры. Дифференциатор. Интегратор. Согласованный фильтр. Гребенчатый фильтр.
-
Интерполированный НЧ фильтр.
-
Банки узкополосных фильтров.
-
Квадратурная составляющая сигнала.
-
Квадратурная демодуляция.
-
Дискретное преобразование Гильберта.
-
Передискретизация сигналов. Прореживание, интерполяция.
-
Полифазные фильтры.
-
Фильтры половинной частоты. Передискретизация с использованием интерполированных КИХ фильтров.
-
Каскад интеграторов и гребенчатых фильтров.
-
Усреднение сигналов.
-
Форматы данных и точность вычислений. Вычисления с фиксированной точкой.
-
Вычисления с плавающей точкой.























