Цилиндр, конус, шар
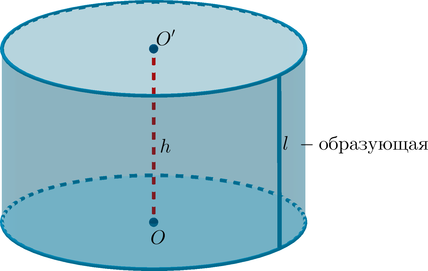
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.
$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V=πR^2·h$
Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Пример:
Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.
Решение:
Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.
$R_{цилиндр}=R_{шар}; h_{цилиндр}=2R_{шар}$
Распишем формулы объема цилиндра и шара.
$V_{цилиндра}=πR_{цилиндр}^2·h_{цилиндр}=πR_{шар}^2·2R_{шар}=2πR_{шар}^3$
$V_{шара}={4π·R_{шар}^3}/{3}$
Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.
${V_{цилиндра}}/{V_{шара}}={2πR_{шар}^3·3}/{4π·R_{шар}^3}={3}/{2}=1.5$
Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
$V_{шара}=30:1.5=20$
Ответ: $20$
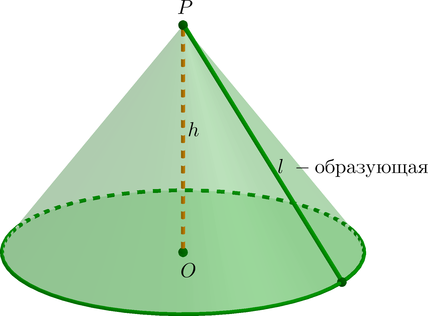
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ — высота и ось конуса.
Свойства конуса:
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
- Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
- Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
$S_{бок.пов.}=πR·l$
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$
Объем конуса равен трети произведения площади основания на высоту.
$V={πR^2·h}/{3}$
Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
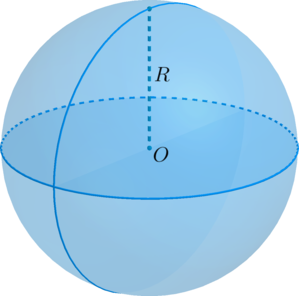
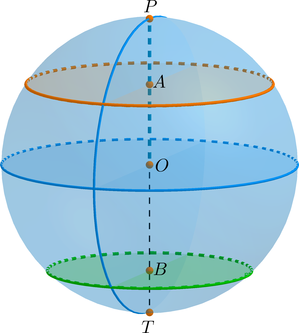
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы
Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Цилиндр — это геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны.
Основаниями цилиндра являются два равных круга, высота цилиндра — расстояние между плоскостями оснований.
Рис. (1). Цилиндр, его высота и радиус основания
Площадь боковой поверхности цилиндра находится по формуле
S=2πRh
, где (R) — радиус основания, (h) — высота цилиндра.
Объём цилиндра равен
V=πR2h
, где (R) — радиус основания, (h) — высота цилиндра.
Подробнее о цилиндре:
- элементы цилиндра;
- объём и площадь поверхности цилиндра.
Конус — геометрическое тело, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Рис. (2). Конус, его высота, образующая и радиус основания
Площадь боковой поверхности конуса находится по формуле
S=πRl
, где (R) — радиус основания, (l) — образующая конуса.
Объём конуса равен
V=13πR2h
, где (R) — радиус основания, (h) — высота конуса.
Подробнее о конусе:
- элементы конуса;
- пощадь поверхности и объём конуса.
Шаром называется геометрическое тело, которое состоит из всех точек пространства, находящихся на расстоянии не больше данного от данной точки.
Поверхность шара называется сферой.
Рис. (3). Шар, его радиус
Площадь поверхности шара (сферы) находится по формуле
S=4πR2
, где (R) — радиус.
Объём шара (сферы) равен
V=43πR3
, где (R) — радиус.
Подробнее о шаре и сфере можно узнать здесь. Все формулы площадей поверхностей и объёмов нужно выучить наизусть.
В задании (8) может встретиться комбинация геометрических тел. Для успешного решения таких задач важно определить их общие точки и соотношение элементов этих тел.
Вписанные и описанные геометрические тела:
- комбинации цилиндра и призмы;
- конус с цилиндром и пирамидой;
- шар и куб, цилиндр, конус.
Источники:
Рис. 1. Цилиндр, его высота и радиус основания. © ЯКласс.
Рис. 2. Конус, его высота, образующая и радиус основания. © ЯКласс.
Рис. 3. Шар, его радиус. © ЯКласс.
ЕГЭ Профиль №13. Фигуры вращения: цилиндр, конус, шар
Скачать файл в формате pdf.
ЕГЭ Профиль №13. Фигуры вращения: цилиндр, конус, шар
Цилиндр
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны – образующие цилиндра, а две другие – параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это – сечение цилиндра плоскостью, проходящей через его ось.
Площадь боковой поверхности цилиндра находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = 2,pi ,R,H); площадь полной поверхности цилиндра находится по формуле: (S = 2,pi ,R,H + 2pi ,{R^2}); объем цилиндра находится по формуле: (V = pi ,{R^2},H), где R – радиус основания; H – длина высоты цилиндра.
Конус
Прямым круговым конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет. Другой катет треугольника, вращаясь вокруг этой же оси, дает круг, который называется основанием. При вращении вокруг этой оси гипотенузы получается фигура, называемая боковой поверхностью конуса. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Осью конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса.
Площадь боковой поверхности конуса находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = pi ,R,L,); площадь полной поверхности конуса находится по формуле: (S = pi ,R,L, + pi ,{R^2}); объем конуса находится по формуле: (V = frac{1}{3}pi ,{R^2},H), где R – радиус основания; L – длина образующей; H – длина высоты конуса.
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.
Площадь боковой поверхности усеченного конуса находится по формуле:({S_{{text{б}}{text{.п}}}} = pi ,left( {,{R_1} + {R_2},} right),L); объем усеченного конуса находится по формуле:(V = frac{1}{3}pi ,H,left( {,R_1^2 + {R_1} cdot {R_2} + R_2^2,} right)), где ({R_1}) и ({R_2}) – радиусы оснований; L – длина образующей; H – длина высоты конуса.
Шар
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии от данной точки, не большем данного положительного числа. Эта точка называется центром шара, а данное расстояние радиусом шара. Шаровой поверхностью или сферой шара называется множество всех точек пространства, находящихся на равном положительном расстоянии от некоторой точки. Эта точка называется центром сферы, а данное расстояние радиусом сферы. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.
Площадь поверхности шара находится по формуле: (S = 4,pi ,{R^2}); объем шара находится по формуле: (V = frac{4}{3}pi ,{R^3}), где R – радиус шара.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость. Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью. Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Шаровой сегмент можно получить, вращая круговой сегмент вокруг диаметра, перпендикулярного его хорде.
Площадь сегментной поверхности находится по формуле: (S = 2,pi ,R,H); объем шарового сегмента находится по формуле: (V = pi ,{H^2},left( {,R — frac{H}{3},} right)), где H – высота сегмента; R – радиус шара.
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полушара, то он дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.
Объем шарового сектора находится по формуле: (V = frac{2}{3}pi ,{R^2}H); площадь полной поверхности шарового сектора складывается из площади сегментной поверхности и площади боковой поверхности конуса и находится по формуле:({S_{{text{шар}}{text{.}};{text{сект}}}} = {S_{{text{шар}}{text{.}};{text{сегм}}}} + {S_{{text{б}}{text{.}};{text{п}}{text{.}};{text{кон}}}} = 2,pi ,R,H + pi ,R,sqrt {,2,R,H — {H^2}} ), где H – высота соответствующего шарового сегмента; R – радиус шара.
1В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1, причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что (angle ,ACB = 30^circ ,;;AB = sqrt 2 ,) (C{C_1} = 2.)
а) Докажите, что угол между прямыми AC1 и BC равен (45^circ ).
б) Найдите объём цилиндра.
2В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите угол между прямыми ВВ1 и АС1, если АВ = 6, ВВ1 = 15, В1С1 = 8.
ОТВЕТ: ({rm{arctg}}frac{2}{3}).
3В. В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.
а) Изобразите осевое сечение комбинации этих тел.
б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.
4В. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно (sqrt {730} ).
а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
ОТВЕТ: ({rm{arctg}}frac{{21}}{{17}}).
5В. Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60°.
а) Докажите, что ABCD — квадрат.
б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен (sqrt 2 ).
6В. В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
ОТВЕТ: (64 + 32sqrt 3 ).
7В. Отрезок AB — диаметр верхнего основания цилиндра, CD — диаметр нижнего, причём отрезки AB и CD не лежат на параллельных прямых.
а) Докажите, что у тетраэдра ABCD скрещивающиеся рёбра попарно равны.
б) Найдите объём этого тетраэдра, если AC = 6, AD = 8, а радиус цилиндра равен 3.
ОТВЕТ: (frac{{64}}{3}).
8В. Высота конуса равна 6, а радиус основания равен 8.
а) Докажите, что наибольшая площадь сечения конуса плоскостью, проходящей через его вершину, равна 50.
б) Найдите расстояние от центра основания конуса до этой плоскости.
ОТВЕТ: (frac{{6sqrt 7 }}{5}.)
9В. Проведены две параллельные плоскости по одну сторону от центра сферы на расстоянии 3 друг от друга. Эти плоскости дают в сечении две окружности, длины которых равны 18π и 24π.
а) Точка H — ортогональная проекция произвольной точки меньшей окружности на плоскость большей. Докажите, что точка H делит проходящий через неё диаметр большей окружности в отношении 1 : 7.
б) Найдите объём шара, ограниченного данной сферой.
ОТВЕТ: (4500{rm{pi }}).
10В. Плоскость α проходит через диаметр AB сферы. Через произвольную точку M, лежащую на сфере, но не лежащую в плоскости α, проведена плоскость β, перпендикулярная прямой AB. Отрезок CD — общая хорда окружностей сечений сферы плоскостями α и β.
а) Докажите, что (angle ,CMD = 90^circ ).
б) Вершина конуса совпадает с точкой A, а окружность основания — с окружностью сечения сферы плоскостью β. Найдите объём конуса, если диаметр сферы равен 15, а (MB = 3sqrt 5 ).
ОТВЕТ: (144{rm{pi }}).
11В. На окружности основания конуса с вершиной P выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 2.
а) Пусть MN — диаметр окружности основания, перпендикулярный хорде AB. Докажите, что объём одной из пирамид PABN и PABM втрое больше объёма другой.
б) Найдите площадь сечения конуса плоскостью ABP, если радиус основания конуса равен 6, а длина его образующей равна 7.
12В. Угол при вершине осевого сечения конуса равен (arccos frac{7}{8}).
а) Докажите, что площадь полной поверхности конуса в пять раз больше площади его основания.
б) Найдите угол в развёртке боковой поверхности.
13В. Радиус основания конуса с вершиной S и центром основания О равен 13, а его высота равна (3sqrt {41} ). Точки А и В – концы образующих, М – середина SA, N – точка в плоскости основания такая, что прямая MN параллельна прямой SB.
а) Докажите, что угол ANO – прямой.
б) Найдите угол между прямой ВМ и плоскостью основания конуса, если АВ = 10.
14В. Два конуса имеют общее основание, причем один из них находится внутри другого. Образующие этих конусов составляют с плоскостью основания углы ({60^ circ }) и ({30^ circ }).
а) Докажите, что вершина меньшего конуса делит высоту большего конуса в отношении (2:1), считая от вершины большего конуса.
б) Найдите объем тела, заключенного между боковыми поверхностями этих конусов, если известно, что сумма высот обоих конусов равна 4.
15В. В конус вписан шар.
а) Докажите, что отношение площади полной поверхности конуса к площади поверхности шара равно отношению их объемов.
б) Найдите угол между образующей конуса и плоскостью основания конуса, если отношение объема конуса к объему вписанного шара равно (frac{9}{4}), а отношение радиуса шара к радиусу основания конуса меньше (frac{3}{5}).
16В. Точки А, В и С лежат на окружности основания конуса с вершиной S, причем А и С диаметрально противоположны. Точка М – середина ВС.
а) Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если АВ = 6, ВС = 8 и (SC = 5sqrt 2 .)
ОТВЕТ: (arcsin frac{{3sqrt {17} }}{{17}}.)
17В. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания – точка С1, причем СС1 – образующая цилиндра, а АС – диаметр основания. Известно, что (angle ACB = {45^ circ },,,,AB = 3sqrt 2 ,,,,C{C_1} = 6.)
а) Докажите, что угол между прямыми АС1 и ВС равен (60^circ ).
б) Найдите расстояние от точки В до прямой АС1.
ОТВЕТ: (frac{{3sqrt 6 }}{2}.)
18В. Полушар и вписанный в него конус имеют общее основание и общую высоту.
а) Докажите, что объем части полушара, лежащей вне конуса равен объему конуса.
б) Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите площадь сечения, заключенного между боковой поверхностью конуса и поверхностью полушара, если радиус полушара равен 4.
19В. На окружности основания конуса с вершиной S отмечены точки A, B и С так, что AB = BC. Медиана АМ треугольника ACS пересекает высоту конуса.
а) Точка N – середина отрезка АС. Докажите, что угол MNB прямой.
б) Найдите угол между прямыми АМ и SB, если (AS = 2,,,,AC = sqrt 6 .)
ОТВЕТ: (arccos frac{5}{{16}}.)
20В. Трапеция ABCD и цилиндр расположены таким образом, что AD — диаметр нижнего основания цилиндра, а точки C и B лежат на окружности верхнего основания и хорда CB равна радиусу основания. Прямая AB образует с плоскостью основания цилиндра угол равный (arccos frac{2}{3}.)
а) Докажите, что в трапецию ABCD можно вписать окружность.
б) Найдите угол между плоскостью основания цилиндра и плоскостью ABCD.
ОТВЕТ: (arccos frac{{sqrt 6 }}{4}.)
21В. Прямоугольник ABCD является осевым сечением цилиндра (AB и CD — образующие). Диаметры AD и KM пересекаются в точке О под прямым углом и (DO = CD.)
а) Докажите, что площадь поверхности цилиндра относится к площади описанной около этого цилиндра сферы как 4 : 5.
б) Найдите площадь сечения цилиндра, проходящего через точки K, M и B, если (AB = 
ОТВЕТ: (32sqrt 2 {rm{pi }}.)
[{Large{text{Цилиндр}}}]
Рассмотрим окружность (C) с центром (O) радиуса (R) на плоскости (alpha). Через каждую точку окружности (C) проведем прямую перпендикулярно плоскости (alpha). Поверхность, образованная этими прямыми, называется цилиндрической поверхностью.
Сами прямые называются образующими данной поверхности.
Проведем теперь через некоторую точку некоторой образующей плоскость (betaparallel alpha). Множество точек, по которым образующие пересекут плоскость (beta), образует окружность (C’), равную окружности (C).
Часть пространства, ограниченная двумя кругами (K) и (K’) с границами (C) и (C’) соответственно, а также частью цилиндрической поверхности, заключенной между плоскостями (alpha) и (beta), называется цилиндром.
Круги (K) и (K’) называются основаниями цилиндра; отрезки образующих, заключенных между плоскостями, – образующими цилиндра; часть цилиндрической поверхности, образованная ими, — боковой поверхностью цилиндра. Отрезок, соединяющий центры оснований цилиндра равен образующей цилиндра и равен высоте цилиндра ((l=h)).
Теорема
Площадь боковой поверхности цилиндра равна [S_{text{бок.пов-ти цилиндра}}=2pi Rcdot h]
где (R) – радиус основания цилиндра, (h) – высота (образующая).
Теорема
Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей обоих оснований [S_{text{полн.пов-ти
цилиндра}}=2pi Rcdot h+2pi R^2=2pi R(R+h)]
Теорема
Объем цилиндра вычисляется по формуле [V_{text{цилиндра}}=pi R^2cdot h]
[{Large{text{Конус}}}]
Рассмотрим плоскость (alpha) и на ней окружность (C) с центром (O) и радиусом (R). Через точку (O) проведем прямую, перпендикулярную плоскости (alpha). Отметим на этой прямой некоторую точку (P). Поверхность, образованная всеми прямыми, проходящими через точку (P) и каждую точку окружности (C), называется конической поверхностью, а эти прямые – образующими конической поверхности. Часть пространства, ограниченная кругом с границей (C) и отрезками образующих, заключенными между точкой (P) и точкой на окружности, называется конусом. Отрезки (PA), где (Ain text{окр. }
C), называются образующими конуса; точка (P) – вершина конуса; круг с границей (C) – основание конуса; отрезок (PO) – высота конуса.
Замечание
Заметим, что у конуса высота и образующая не равны друг другу, как было в случае с цилиндром.
Теорема
Площадь боковой поверхности конуса равна [S_{text{бок.пов-ти конуса}}=pi Rcdot l]
где (R) – радиус основания конуса, (l) – образующая.
Теорема
Площадь полной поверхности конуса равна сумме площади боковой поверхности и площадей основания [S_{text{полн.пов-ти
конуса}}=pi Rcdot l+pi R^2=pi R(R+l)]
Теорема
Объем конуса вычисляется по формуле [V_{text{конуса}}=dfrac13pi R^2cdot h]
Замечание
Заметим, что цилиндр в каком-то смысле является призмой, только в основании находится не многоугольник (как у призмы), а круг.
Формула объема цилиндра такая же, как и формула объема призмы: произведение площади основания на высоту.
Аналогично конус в каком-то смысле является пирамидой. Поэтому формула объема конуса такая же, как и у пирамиды: треть площади основания на высоту.
[{Large{text{Сфера и шар}}}]
Рассмотрим множество точек пространства, равноудаленных от некоторой точки (O) на расстояние (R). Это множество называется сферой с центром в точке (O) радиуса (R).
Отрезок, соединяющий две точки сферы и проходящий через ее центр называется диаметром сферы.
Сфера вместе со своей внутренностью называется шаром.
Теорема
Площадь сферы вычисляется по формуле [S_{text{сферы}}=4pi R^2]
Теорема
Объем шара вычисляется по формуле [V_{text{шара}}=dfrac43 pi R^3]
Определение
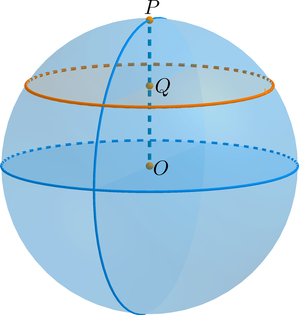
Шаровой сегмент – это часть шара, отсекаемая от него некоторой плоскостью.
Пусть плоскость пересекла шар по кругу (K) с центром в точке (Q). Соединим точки (O) (центр шара) и (Q) и продлим этот отрезок до пересечения со сферой – получим радиус (OP). Тогда отрезок (QP) называется высотой сегмента.
Теорема
Пусть (R) – радиус шара, (h) – высота сегмента, то объем шарового сегмента равен [V_{text{}}=pi h^2 (R-dfrac13h)]
Определение
Шаровой слой – это часть шара, заключенная между двумя параллельными плоскостями, пересекающими этот шар. Круги, по которым плоскости пересекают шар, называются основаниями шарового слоя, отрезок, соединяющий центры оснований – высотой шарового слоя.
Две оставшиеся части шара являются в этом случае шаровыми сегментами.
Объем шарового слоя равен разности объема шара и объемов шаровых сегментов с высотами (AP) и (BT).
Формулы объема и площади поверхности. Цилиндр, конус и шар
Если
в задаче В9 на ЕГЭ по математике
вам надо просто посчитать объем конуса
или площадь сферы — считайте, что
повезло. Применяйте формулы объема
и площади поверхности цилиндра,
конуса и шара. Все они есть в нашей
таблице.
В некоторых
задачах В9, кроме формул, нужна еще
и элементарная логика. Например, если
линейные размеры тела вращения уменьшились
в два раза — его площадь поверхности
уменьшится в 4, а объем — в 8 раз
(ведь 2?=4, 2?=8). Как, например, в этой
задаче. Как и остальные, она взята
из банка заданий ФИПИ.
1.
Объем конуса равен 16. Через середину
высоты параллельно основанию конуса
проведено сечение, которое является
основанием меньшего конуса с той же
вершиной. Найдите объем меньшего конуса.
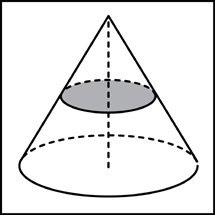
Очевидно,
что объем меньшего конуса в 8 раз
меньше объема большого и равен двум.
Для
решения некоторых задач полезны хотя бы
начальные знания стереометрии. Например —
что такое правильная пирамида или прямая
призма. Полезно помнить, что у цилиндра,
конуса и шара есть еще общее название —
тела вращения. Что сферой называется
поверхность шара. А, например, фраза
«образующая конуса наклонена к плоскости
основания под углом 30?» предполагает,
что вы знаете, что такое угол между
прямой и плоскостью. Вам также может
пригодиться теорема Пифагора и простые
формулы
площадей фигур.
Иногда
неплохо нарисовать вид сверху. Или, как
в этой задаче, — снизу.
2.
Во сколько раз объем конуса, описанного
около правильной четырехугольной
пирамиды, больше объема конуса, вписанного
в эту пирамиду?
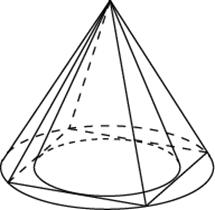
Всё
просто — рисуем вид снизу. Видим, что
радиус большего круга в
раз
больше, чем радиус меньшего. Высоты
у обоих конусов одинаковы. Следовательно,
объем большего конуса будет в 2 раза
больше.
Еще
один важный момент. Помним, что в задачах
части В вариантов ЕГЭ по математике
ответ записывается в виде целого
числа или конечной десятичной дроби.
Поэтому никаких
или
? у вас в ответе в части В
быть не должно. Подставлять приближенное
значение ? тоже не нужно! Помните,
что оно обязательно должно сократиться.
Именно для этого в некоторых задачах
задание формулируется, например, так:
«Найдите площадь боковой поверхности
цилиндра, деленную на ?».
А где же
еще применяются формулы объема и площади
поверхности тел вращения? Конечно же,
в задаче С2. Мы тоже расскажем
о ней, потому что это наиболее доступная
задача из части С.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2 июля 2022
В закладки
Обсудить
Жалоба
Цилиндр. Конус. Шар
Формулы для расчёта площади поверхности и объёма.
formuly.pdf
Тела и поверхности вращения. Шар. Цилиндр. Конус
Тела и поверхности вращения.
Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.
Подробная теория с наглядными иллюстрациями и основные формулы.
Читай эту статью, здесь все это есть.
Всего за 15 минут ты полностью во всём разберешься!
Тело вращения – это тело в пространстве, которое возникает при вращении какой-нибудь плоской фигуры вокруг какой-нибудь оси.
Вот самый простой пример: цилиндр.
Берем прямоугольник и начинаем вращать его вокруг одной из сторон.
Смотри.
Было–вращаем–стало:
А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.
Например, так:
Вращаем:
Что получится? Бублик. А по-научному – ТОР.
Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.
Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.
Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.
Шар
Шар – тело вращения, полученное вращением полуокружности вокруг диаметра.
Было–вращаем–стало:
Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)
Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.
Скажу тебе по секрету, что, хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде:
“ну …там есть центр и радиус…”, подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.
Ну, в общем, шар он и есть шар.
Названия, которые ты должен знать:
Незнакомое тебе, наверное, только одно.
Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.
А вообще:
- Любое сечение шара – круг.
- Граница шара называется сфера. (Так же, как граница круга – окружность.)
Площадь поверхности сферы
( {{S}_{поверхности }}=4pi {{R}^{2}})
( R) – радиус
Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.
Объем шара
( {{V}_{шара}}=frac{4}{3}pi {{R}^{3}})
( R) – радиус
Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.
Если ты знаком с производной, то можешь заметить это:
( {{V’}_{шара}}={{S}_{поверхности}})
И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!
Цилиндр
Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.
Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:
Основания у цилиндра – это круги
Еще у цилиндра есть так называемая развертка.
Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.
Что получится? Представь себе, прямоугольник.
Развертка цилиндра – прямоугольник.
Площадь боковой поверхности цилиндра
( {{S}_{бок.}}=2pi RH)
( R) – радиус
( H) – высота, она же образующая.
Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник ( 2pi Rcdot H).
Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра.
Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому
( {{S}_{бок.}}=2pi RH)
Площадь полной поверхности цилиндра
Прибавляем теперь площадь двух кругов – оснований и получаем:
( {{S}_{полн .}}=2pi RH+2pi {{R}^{2}})
Можно вынести (хотя и не обязательно) ( 2pi R):
( {{S}_{полн .}}=2pi Rleft( H+R right))
Но эту формулу неудобно запоминать!
Гораздо проще запомнить, что полная поверхность – сумма боковой поверхности и еще двух кругов – оснований, а боковая поверхность – прямоугольник. И тогда ( {{S}_{полн .}}) можно вообще не запоминать, ты всегда сам напишешь, что
( {{S}_{полн .}}=underbrace{2pi RH}_{прямоугольник}+underbrace{2pi {{R}^{2}}}_{два круга})
Объем цилиндра
( V=pi {{R}^{2}}H)
( R) – радиус основания ( H) – высота
Это точно как у призмы и параллелепипеда!
( V={{S}_{основания}}cdot H), только у призмы и параллелепипеда ( {{S}_{основания}}) – это площадь многоугольника, а у цилиндра ( {{S}_{основания}}) – это площадь круга.
Конус
Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.
Было–вращаем–стало:
И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».
Названия, относящиеся к конусу:
Что тут нужно твердо помнить?
- Основание корпуса – круг
- Все образующие конуса – равны.
Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.
У конуса тоже есть развертка.
Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?
Представь себе сектор круга. Пусть длина образующей равна ( l).
Развертка конуса – сектор круга радиуса ( l)
Площадь поверхности конуса
Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.
По формуле площади сектора ( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}) Где ( alpha ) – угол при вершине в радианах.
И это уже формула. В некоторых задачах бывает дан именно угол при вершине в развертке конуса.
Но если все же даны только образующая и радиус основания, как быть?
Нужно осознать, что же такое дуга в развертке? Это бывшая окружность основания! Поэтому длина этой дуги равна ( 2pi R).
С другой стороны, длина этой же дуги равна ( alpha cdot l), так как это дуга окружности радиуса ( l). Поэтому
( alpha cdot l=2pi R)
Подставляем
( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}=frac{l}{2}cdot alpha cdot l=frac{l}{2}cdot 2pi R)
Итак,
( {{S}_{бок.}}=pi Rl), где
( R) – радиус окружности основания,
( l) – длина образующей
Ну, и осталось площадь полной поверхности конуса. Прибавим к боковой поверхности площадь круга основания, и получаем:
( {{S}_{полн. }}=pi Rl+pi {{R}^{2}})
Можно вынести ( pi R):
( {{S}_{полн. }}=pi Rleft( l+R right))
Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.
Объём конуса
( V=frac{1}{3}pi {{R}^{2}}H)
( R) – радиус основания (
H) – высота
Это так же, как у пирамиды
( V=frac{1}{3}{{S}_{осн.}}cdot H), только
( {{S}_{осн. }}) – это не площадь многоугольника, а площадь круга.
А вот откуда взялась ( frac{1}{3})?, по-прежнему остается загадкой, потому что эта ( frac{1}{3}) получена в результате довольно хитрых рассуждений умных математиков.
А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта ( frac{1}{3}) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!
Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой
В этом видео мы научимся “видеть” 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам – находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.
Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020
В этом видео:
- Как нарисовать шестиугольную пирамиду.
- Как подписать вершины пирамиды чтобы потом легче было решать задачу.
- Как исправить рисунок, если грани пирамиды сливаются.
- Доказательство пунктов А и Б, а также их правильная запись, которую примет любой проверяющий на ЕГЭ.
- Нахождение площади основания и объема пирамиды.
- Самое главное, на что нужно обратить внимание.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.