Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.)
а) Докажите, что площадь боковой поверхности пирамиды относится к площади основания как
б)Найдите площадь этой сферы.
Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 601.
2
В правильную шестиугольную пирамиду, боковое ребро которой равно а высота равна
вписана сфера. (Сфера касается всех граней пирамиды.)
а) Докажите, что двугранный угол при основании пирамиды равен
б) Найдите площадь этой сферы.
Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 602., Задания 14 (С2) ЕГЭ 2013
3
Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4.
а) Докажите, что сечение является равнобедренным остроугольным треугольником.
б) Найдите расстояние от центра основания конуса до плоскости сечения.
Раздел: Математический анализ
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервная волна. Центр. Вариант 501, Задания 14 (С2) ЕГЭ 2013
4
Радиус основания конуса равен 5, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 6.
а) Докажите, что сечение — равнобедренный остроугольный треугольник.
б) Найдите расстояние от центра основания конуса до плоскости сечения.
Раздел: Математический анализ
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервная волна. Центр. Вариант 502, Задания 14 (С2) ЕГЭ 2013
5
В правильную четырёхугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.)
а) Докажите, что двугранный угол при основании пирамиды больше
б) Найдите площадь вписанной.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 701., Задания 14 (С2) ЕГЭ 2013
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 114.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 138.
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Цилиндр описан около шара. Объем шара равен 38. Найдите объем цилиндра.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 116. Найдите объем конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 42. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 156. Найдите объём конуса.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 36. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 63. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: Основная волна ЕГЭ по математике 29.05.2019. Центр
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 2. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
Источник: ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 3
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.
а) Изобразите осевое сечение комбинации этих тел.
б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
2
Основанием пирамиды является трапеция с основаниями 25 и 7 и острым углом Каждое боковое ребро пирамиды наклонено к основанию под углом 60°.
а) Докажите, что существует точка M, одинаково удаленная от всех вершин пирамиды (центр описанной сферы).
б) Найдите объем данной пирамиды.
Источник: А. Ларин: Тренировочный вариант № 104.
3
Шар касается основания АВС правильной треугольной пирамиды SABC в точке В и ее бокового ребра SA. Найдите радиус шара, если сторона основания пирамиды равна 3, а боковое ребро равно 4.
Источник: А. Ларин: Тренировочный вариант № 111.
4
Основанием пирамиды является равнобедренная трапеция с основаниями 18 и 8. Каждая боковая грань пирамиды наклонена к основанию под углом 60°.
а) Докажите, что существует точка О (центр вписанной сферы), одинаково удаленная ото всех граней пирамиды.
б) Найдите площадь полной поверхности данной пирамиды.
Источник: А. Ларин: Тренировочный вариант № 103.
5
В одном основании прямого кругового цилиндра с высотой 12 и радиусом основания 6 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
Пройти тестирование по этим заданиям
ЕГЭ Профиль №8. Цилиндр, конус, шар
По теме: методические разработки, презентации и конспекты
Проверочная работа при подготовке к ЕГЭ, 11 класс
Проверочная работа составлена в двух вариантах. Рекомендуется проводить после повторения тем «Показательная функция» и «Логарифмическая функция». 11 класс…
Анализ результатов проверочной работы по подготовке к ЕГЭ по обществознанию (11класс)
Назначение работы.Единый государственный экзамен (ЕГЭ) представляет собой форму объективной оценки качества подготовки лиц, освоивших образовательныепрограммы среднего общего образования, с испол…
Методическая разработка проверочной работы по подготовке к Всероссийской проверочной работе, 11 класс
Веселова Татьяна Андреевна, учитель географии ГБОУ лицея №150 Калининского района Санкт-Петербурга.Данная методическая разработка позволит учителю подготвоить учащихся 11-х классов к итоговой ат…
9 класс. Подготовка к ОГЭ. Задание № 20. Задания для подготовки и проверочная работа.
В данной методической разработке представлены 12 заданий из сборника подготовки к ОГЭ, 9 класс «Анализ геометрических высказываний» (задание № 20). Эти задания можно разобрать в классе…
Организация и подготовка к Всероссийским проверочным работам. (из опыта работы)
МБОУ «Ивановская ООШ»…
Практика работы по подготовке к Всероссийской проверочной работе по русскому языку
Здесь можно узнать о формах организации учебной деятельности при подготовке учащихся 5-8-х классов к ВПР, познакомиться с электронными ресурсами, которые помогут успешно подготовиться к ВПР…
Проверочные работы для подготовки к ЕГЭ «ПЛАНИМЕТРИЯ»
1. Проверочная рработа по теме «Треугольник».2. Проверочная работа по теме :»Четырехугольник»3. Проверочная работа по теме : «Окружность».Материалы взяты с сайта «Ре…
Тема 13.
Задачи по стереометрии
13
.
04
Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи по стереометрии
13.01Задачи из ЕГЭ прошлых лет
13.02Задачи из сборника И.В. Ященко ЕГЭ 2023
13.03Задачи формата ЕГЭ на многогранники. Пирамида, призма
13.04Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус
13.05Аксиомы. Доказательство базовых фактов
13.06Параллельность. Доказательство базовых фактов
13.07Перпендикулярность. Доказательство базовых фактов
13.08Тела вращения. Доказательство базовых фактов
13.09Задачи на построение
13.10Упрощенные задачи
13.11Построение сечений
13.12Нахождение площади сечения
13.13Расстояние от точки до прямой
13.14Расстояние от точки до плоскости
13.15Угол между прямой и плоскостью
13.16Угол между плоскостями
13.17Нахождение объема или площади поверхности
13.18Угол между скрещивающимися прямыми
13.19Расстояние между скрещивающимися прямыми
13.20Метод объемов
Решаем задачи
Показать ответ и решение
а) Пусть — центр основания конуса. Так как точки
и
делят окружность
основания на две дуги, которые относятся как 1:5, то можно меньшую дугу
принять за а большую за
Тогда вся окружность равна
следовательно,
меньшая дуга составляет от всей окружности, то есть в градусах равна
Таким образом, как центральный угол. Так как
—
радиусы, то равнобедренный. Поскольку один из его углов равен
, то
равносторонний и
Проведем
также является и медианой. Тогда для
прямоугольного треугольника и треугольника
имеем:
б) Из формулы площади треугольника находим радиус основания
конуса:
Тогда по теореме Пифагора в треугольнике
Тогда объем конуса равен
Ответ:
б)
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |
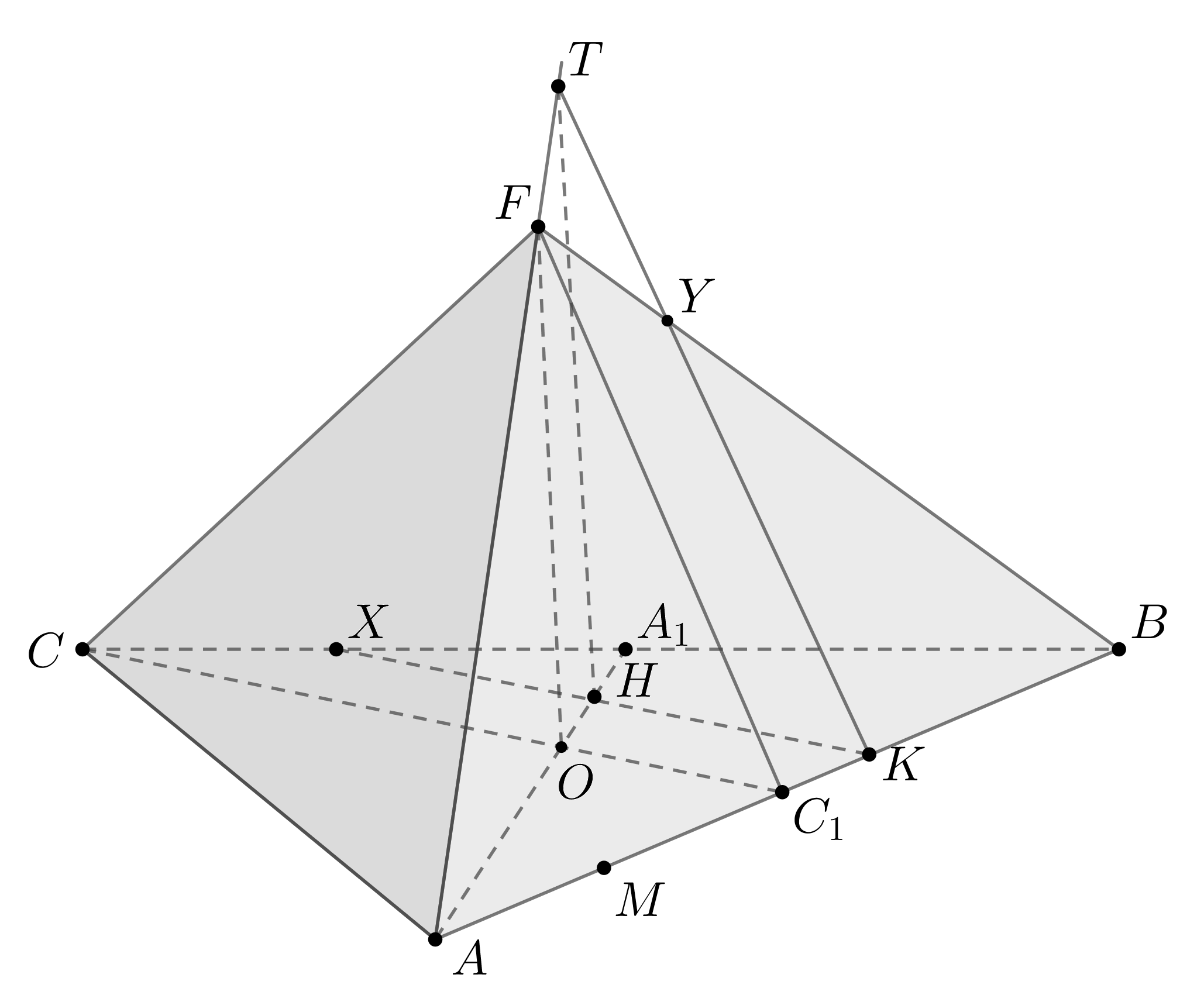
Конус вписан в правильную четырехугольную пирамиду. Общая высота
пирамиды и конуса равна , а радиус вписанной в конус сферы равен
1.
а) Докажите, что данная сфера касается боковых граней пирамиды, причем
точки касания лежат на апофемах.
б) Найдите разность объемов пирамиды и конуса.
Показать ответ и решение
а) Пусть дана пирамида ,
— точка пересечения диагоналей
основания . По свойству правильной пирамиды
— ее высота,
следовательно, и высота конуса. Пусть — центр сферы, вписанной
в конус, следовательно, лежащий на . Тогда
— радиус этой
сферы.
Окружность основания конуса касается стороны в ее середине. Назовем
эту точку касания . Тогда
,
— радиус основания конуса.
Рассмотрим . Проведем
. Так как
— проекция
на
плоскость и
, то по ТТП и
. Следовательно,
перпендикулярна двум прямым и
из плоскости
, следовательно,
. Значит,
— точка касания сферы с гранью
, лежащая на
. А так как
— середина
, то по определению
— апофема грани
. Для других граней пирамиды доказательство аналогично, так как
пирамида правильная.
Чтд.
Заметим, что — образующая конуса и
— одна из точек касания
сферы с боковой поверхностью конуса.
б) Пусть сторона основания равна
.
(так как
— средняя линия в ).
Прямоугольные по острому углу (
— общий),
следовательно,
Следовательно,
Ответ:
б)
Показать ответ и решение
а) По формуле площади произвольного четырехугольника имеем:
Следовательно, если
— диаметры сферы и
то есть
Следовательно,
— квадрат.
Расстояние от точки до плоскости
наибольшее, если
и — радиус сферы. Тогда объем пирамиды равен
Что и требовалось доказать.
б) Проведем где
Тогда
и
Так как то
следовательно, по теореме о трех
перпендикулярах где
Далее имеем:
Тогда по теореме Пифагора в треугольнике
Так как , то площадь треугольника
равна
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |
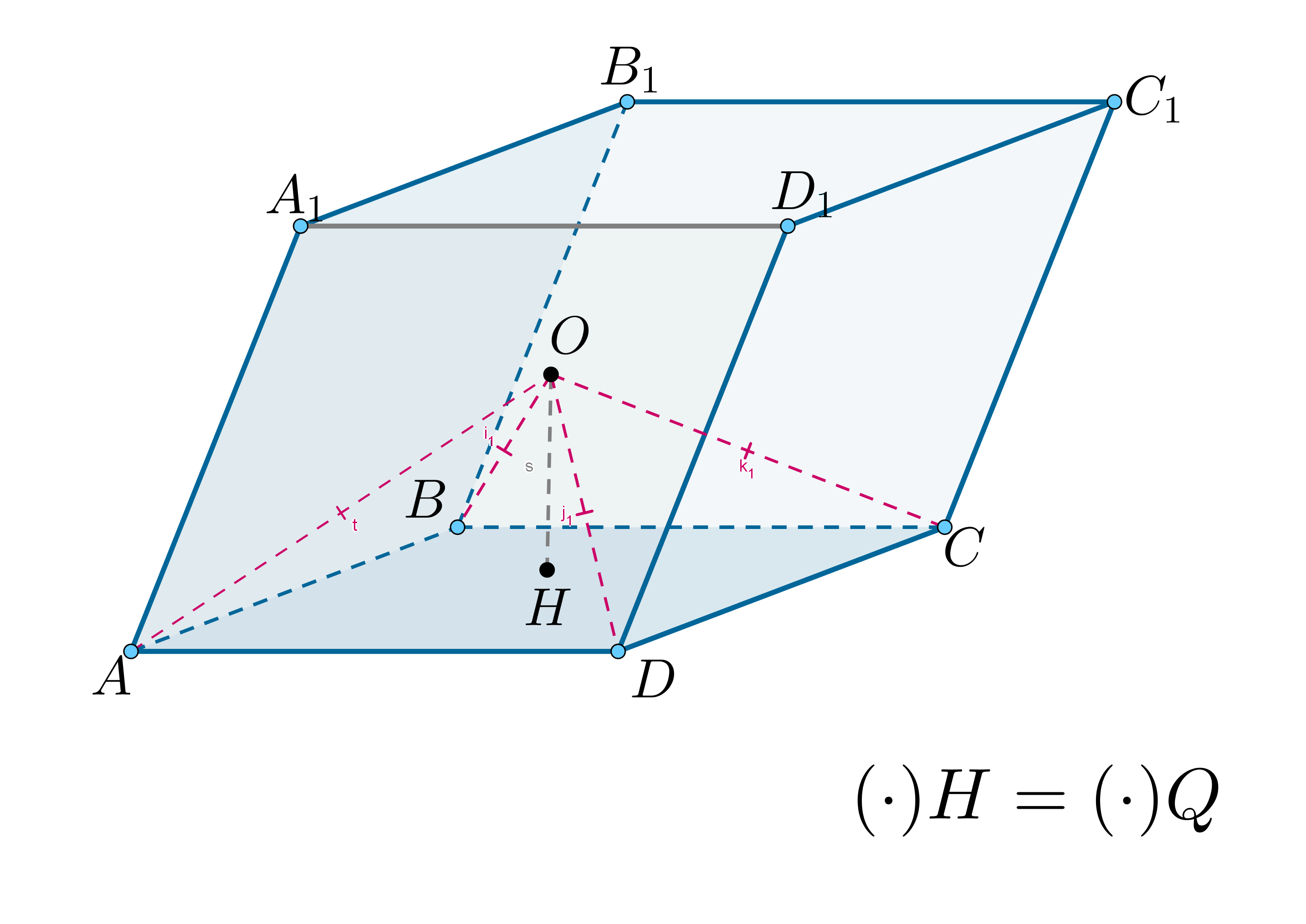
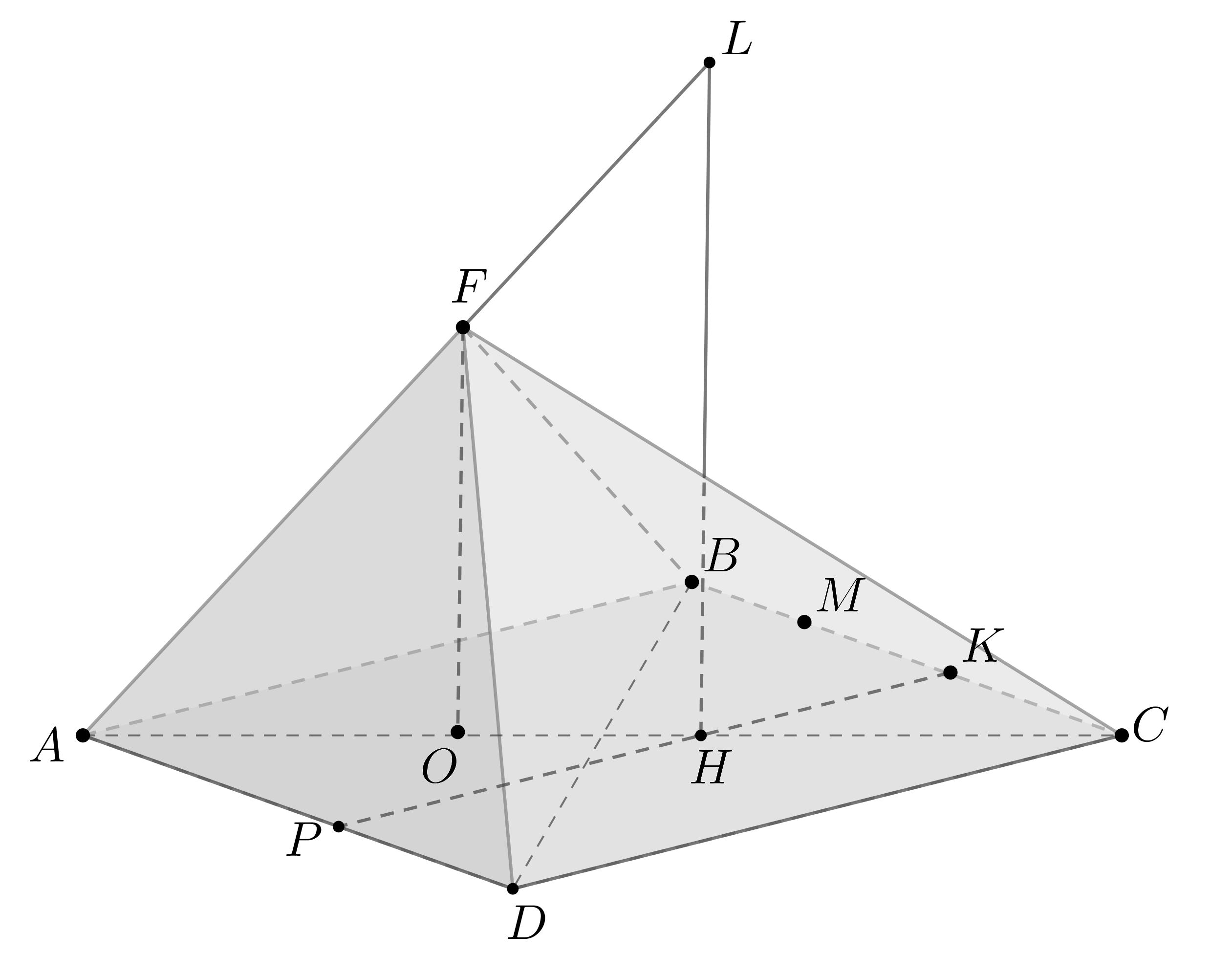
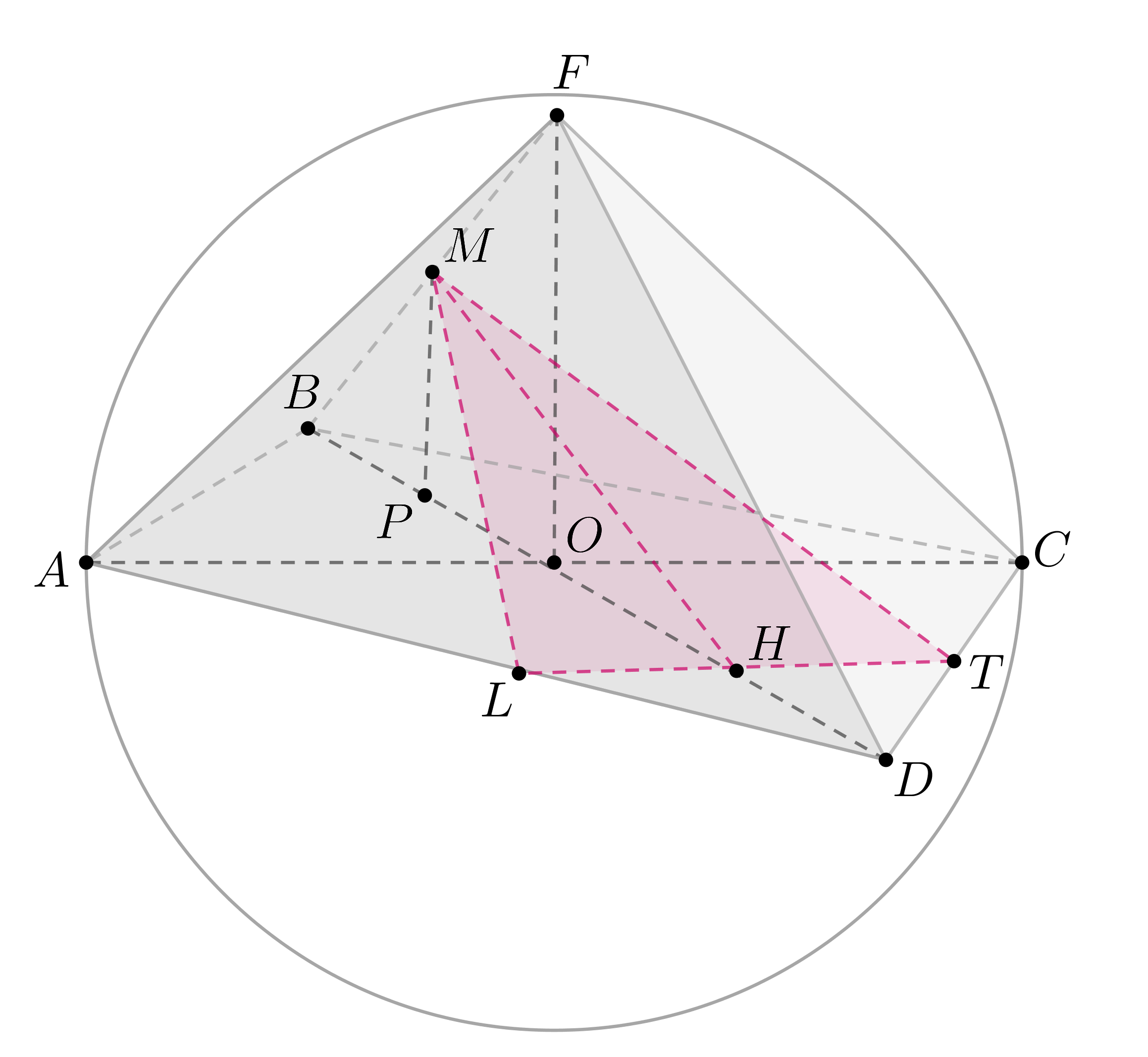
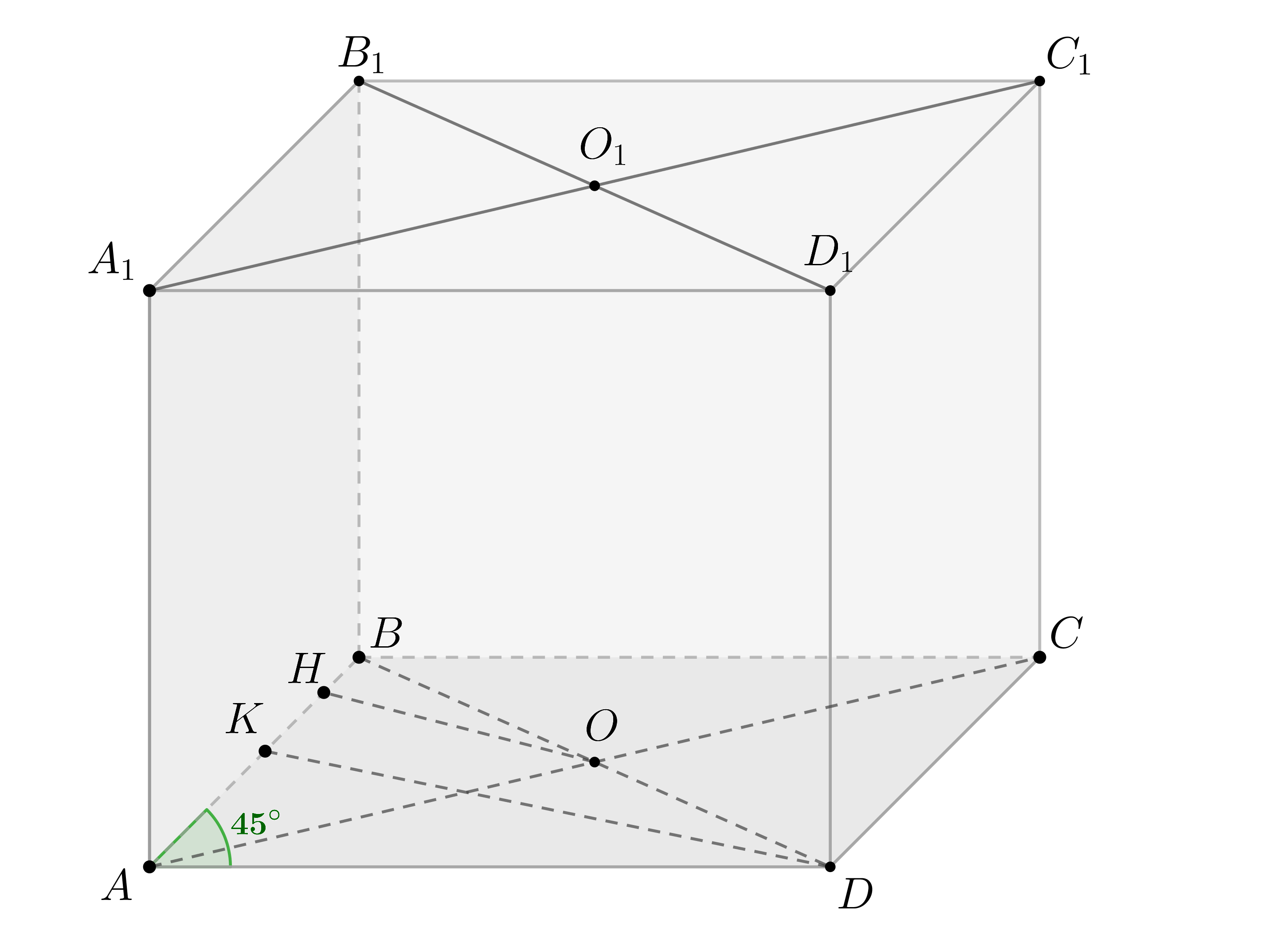
Дан параллелепипед .
а) Докажите, что около параллелепипеда можно описать сферу тогда и только
тогда, когда он прямоугольный.
б) Найдите площадь поверхности данного параллелепипеда, если его
объем равен 8, а радиус сферы, описанной около параллелепипеда, равен
.
Показать ответ и решение
а) Если сфера описана около параллелепипеда, то ее центр находится на
одинаковом расстоянии от всех вершин параллелепипеда.
Будем сокращенно записывать как
.
— вписанный
— прямоугольный
Пусть — центр сферы. Расстояния от точки
до вершин
одинаковы и равны .
Проведем . Рассмотрим
,
,
,
. Они равны как прямоугольные по общему катету
и гипотенузе.
Следовательно, равноудалена от вершин
, то есть
— центр
описанной около окружности. Если около параллелограмма можно
описать окружность, то он — прямоугольник.
Аналогично поступаем с каждой гранью и получаем, что все
его грани — прямоугольники. Это по определению и есть прямоугольный
параллелепипед.
— прямоугольный
— вписанный
Все грани — прямоугольники. Рассмотрим прямую
, где
и
— центры нижнего и верхнего оснований соответственно (точки пересечения
диагоналей). параллельна боковым ребрам
и перпендикулярна
основаниям. Пусть — середина
. Так как расстояния от точки
до вершин равны, расстояния от
до вершин
равны, а также все эти расстояния равны между собой, имеем: треугольники
как прямоугольные по двум катетам. Следовательно, гипотенузы равны, то есть
расстояния от точки до всех вершин
одинаковы. Значит, около него
можно описать окружность.
Зааметим, что диагонали параллелепипеда пересекают в точке
,
следовательно, центр сферы, описанной около параллелепипеда есть точка
пересечения его диагоналей, причем диагонали являются диаметрами
сферы.
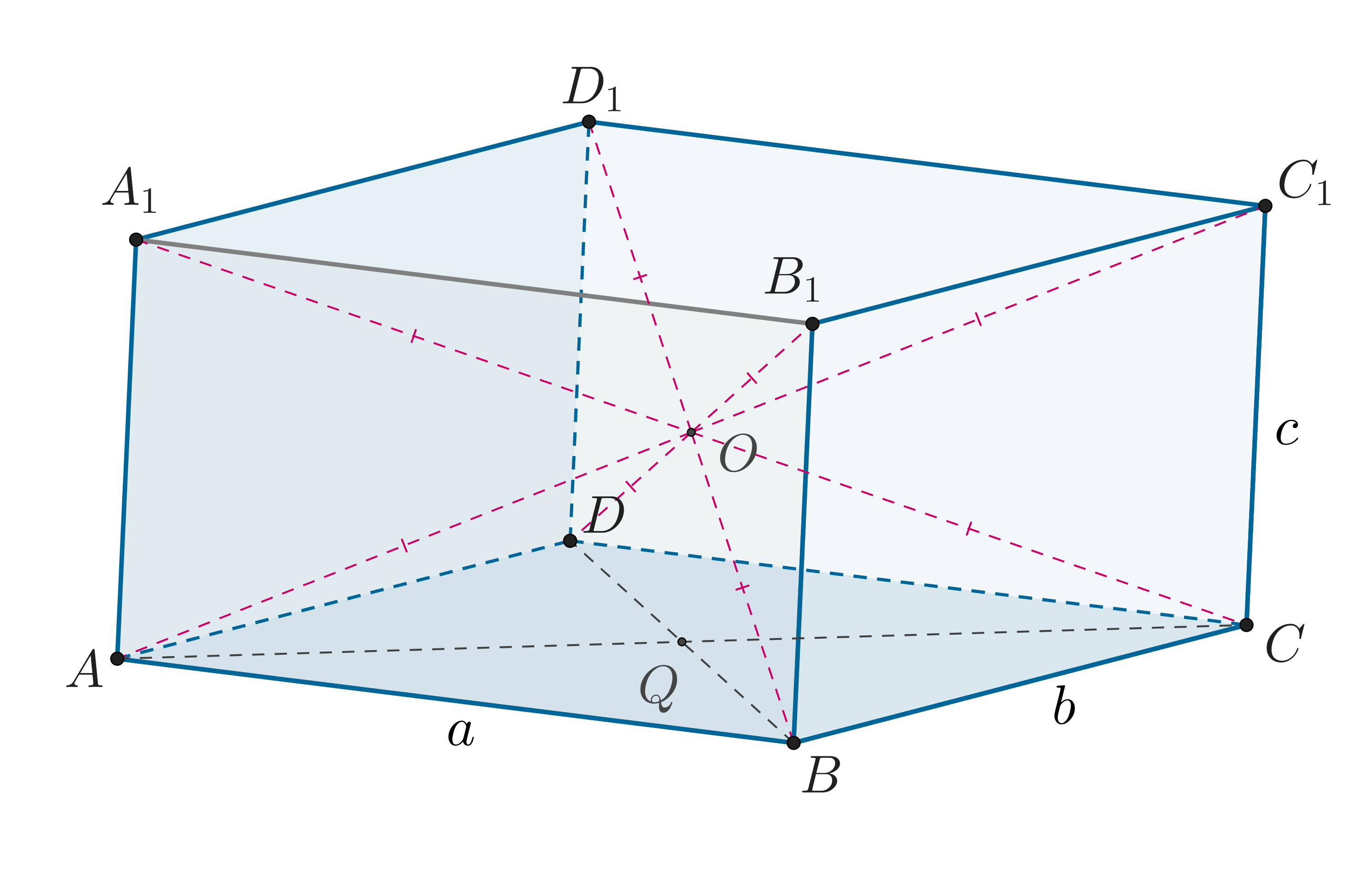
б) Обозначим ребра как
,
,
, как показано на рисунке.
В пункте а) мы доказали, что точка пересечения диагоналей есть
центр описанной сферы. Следовательно, половина диагонали параллелепипеда есть
радиус этой сферы. То есть .
Нам требуется найти площадь полной поверхности , то есть выражение
.
Известно, что ,
.
По неравенству о среднем
Равенство достигается тогда и только тогда, когда .
Следовательно,
Ответ:
б)
Показать ответ и решение
Сечение шара многоугольником — окружность с центром в точке
,
и все вершины этого многоугольника лежат на этой окружности, следовательно,
он вписанный. Аналогично вписан в окружность с центром
.
Пусть — центр шара. Проведем
и
Следовательно, лежат на одной прямой, перпендикулярной основаниям
(так как основания параллельны). Рассмотрим — прямоугольник,
так как ,
,
. Следовательно,
, то есть
перпеникулярна основаниям призмы. Значит, призма
прямая.
б) ,
— центры оснований. Проведем
. Тогда
следовательно,
— проекция
на плоскость
. Значит,
. Получили прямоугольный равнобедренный
, значит,
. Пусть
,
Тогда
— середина
, следовательно, из
Объем призмы равен
Следовательно, площадь поверхности шара равна
Ответ:
б)
Показать ответ и решение
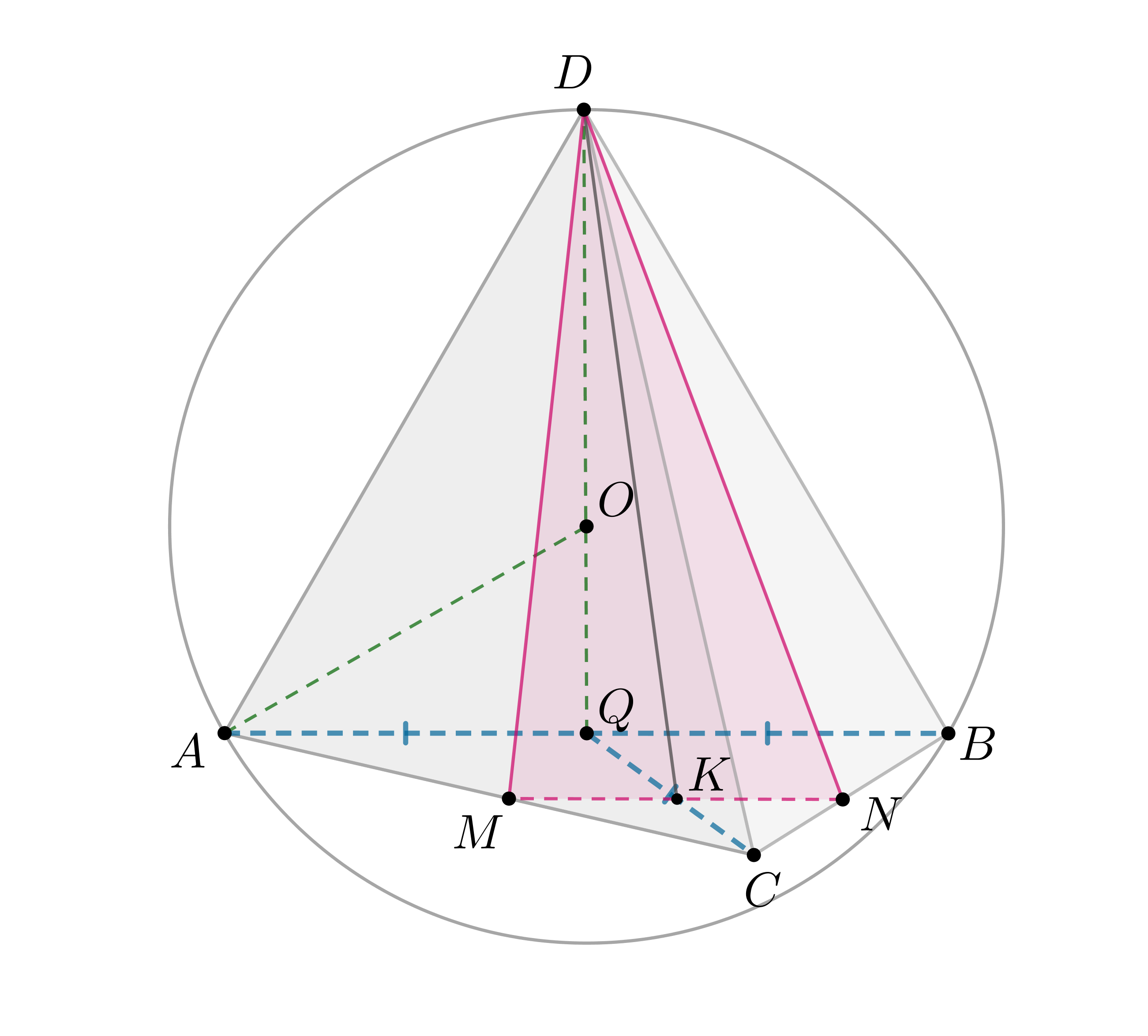
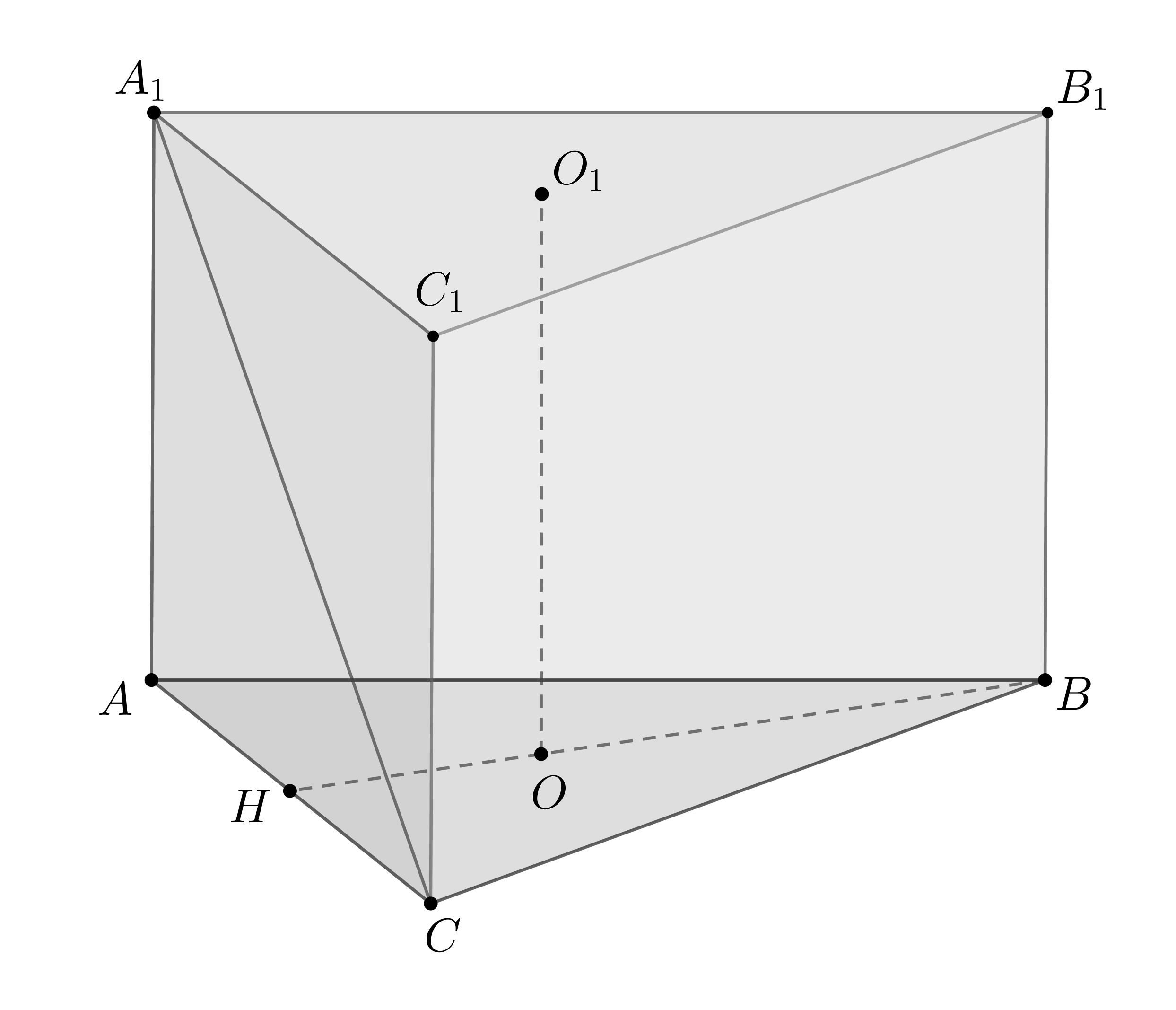
а) Боковые ребра пирамиды равны, так как это образующие конуса.
Так как плоские углы при вершине равны, то пирамида правильная,
следовательно, равносторонний. Рассмотрим основание. Наибольший
объем пирамида имеет тогда, когда наибольшую площадь имеет
. Так как основание этого треугольника фиксировано, то наибольшую
площадь он имеет, когда высота к наибольшая. Следовательно, точка
—
середина дуги . Тогда
, следовательно,
следовательно, — диаметр.
Если — радиус окружности, описанной около правильного треугольникав, то
сторона треугольника равна . Следовательно,
Найдем — высоту. Пусть
. Тогда
.
, следовательно, из
:
Следовательно, объем
Чтд.
б) — перпендикуляр на
. Пусть
. Тогда если
, то по подобию
.
следовательно,
, следовательно,
то есть
Таким образом,
Пусть . Тогда для
:
Следовательно,
Тогда
Так как , то
следовательно,
Ответ:
б)
Показать ответ и решение
а) Боковые ребра пирамиды равны, так как это образующие конуса.
Так как плоские углы при вершине равны, то пирамида правильная,
следовательно, равносторонний. Рассмотрим основание. Наибольший
объем пирамида имеет тогда, когда наибольшую площадь имеет
. Так как основание этого треугольника фиксировано, то наибольшую
площадь он имеет, когда высота к наибольшая. Следовательно, точка
—
середина дуги . Тогда
, следовательно,
следовательно, — диаметр. Чтд.
б) — перпендикуляр на
. Пусть
. Тогда ессли
, то по подобию
.
следовательно,
, следовательно,
то есть
Таким образом,
У правильного треугольника со стороной радиус описанной окружности
равен от высоты треугольника, то есть
Следовательно,
. Из
прямоугольного равнобедренного треугольника
Тогда
Ответ:
б)
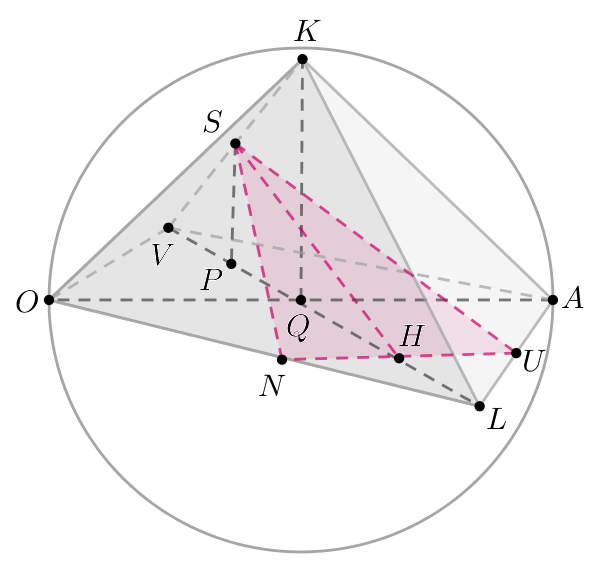
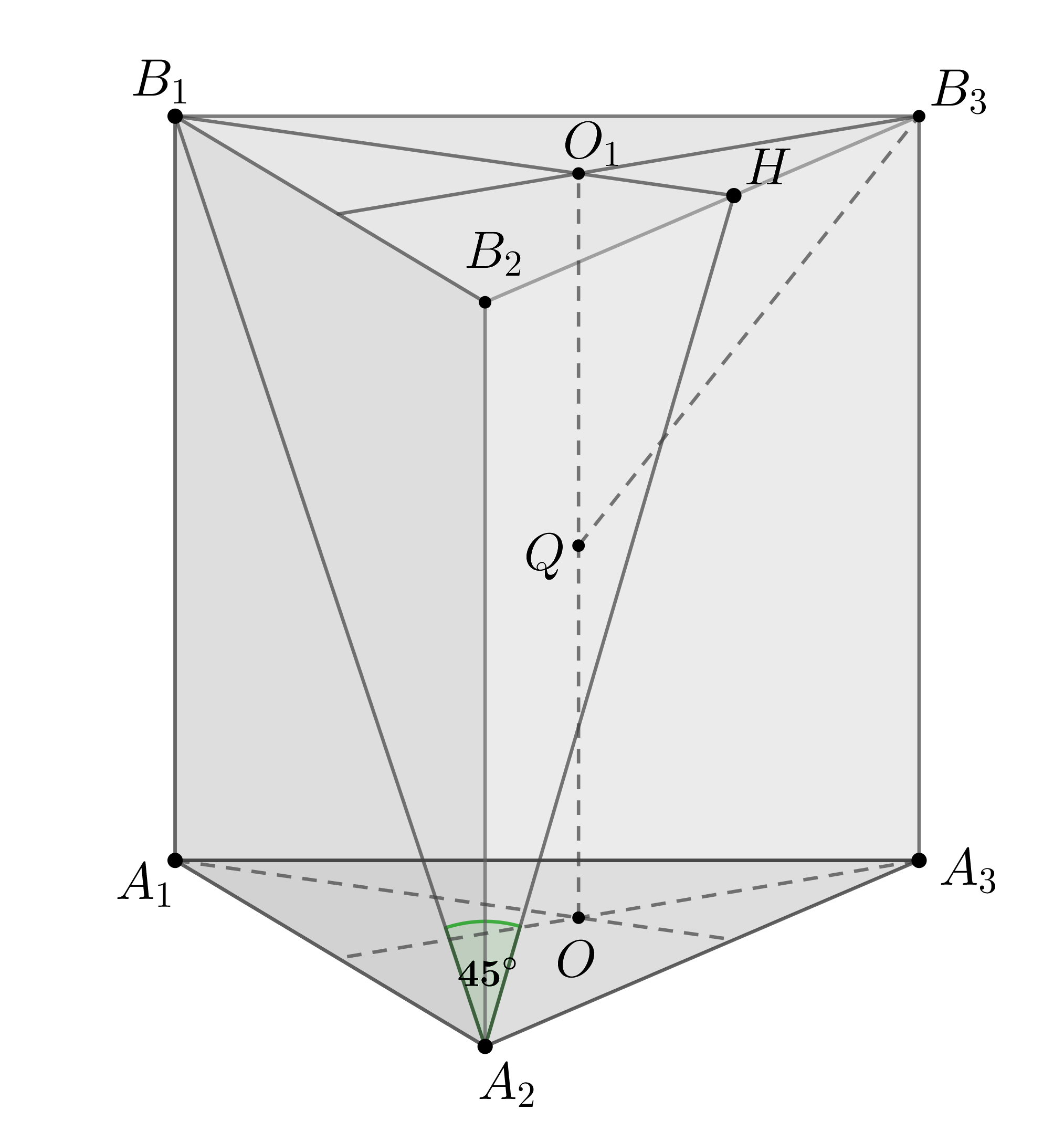
Дана правильная треугольная пирамида со стороной основания, равной
. Центр
основания пирамиды является вершиной конуса, окружность
основания которого вписана в боковую грань пирамиды.
а) Пусть — высота основания. Докажите, что
б) Найдите радиус основания конуса.
Показать ответ и решение
а) Пусть ,
— центр вписанной в
окружности. Тогда
, следовательно,
,
Рассмотрим :
Тогда
Чтд.
б) Так как то
, тогда из
Решая это уравнение, получаем
Тогда следовательно,
Ответ:
б)
Показать ответ и решение
а) По условию центр описанной сферы лежит на . Следовательно, так как он
равноудален от точек и
, то центр
— середина
. Также имеем
. Если медиана треугольника равна половине стороны, к
которой она проведена, то она проведена из прямого угла треугольника,
следовательно, Чтд.
б) Отметим — середину
. Тогда
.
Если провести перпендикуляр из точки на плоскость
, то его основание
будет лежать на (так как плоскости
и
перпендикулярны).
Следовательно, — проекция
на
. Тогда из
следует, что
Проведем и восстановим из точки
перпендикуляр к
,
который пересечет в точке
. Тогда точка
лежит в плоскости,
перпендикулярной и проходящей через его середину, следовательно,
любая точка этой плоскости равноудалена от и
, следовательно,
По теореме Пифагора ;
Тогда
, следовательно,
Следовательно,
Площадь сферы равна , следовательно,
Тогда
, откуда
Подставляя это значение
в выражение
объема получаем
Ответ:
б)
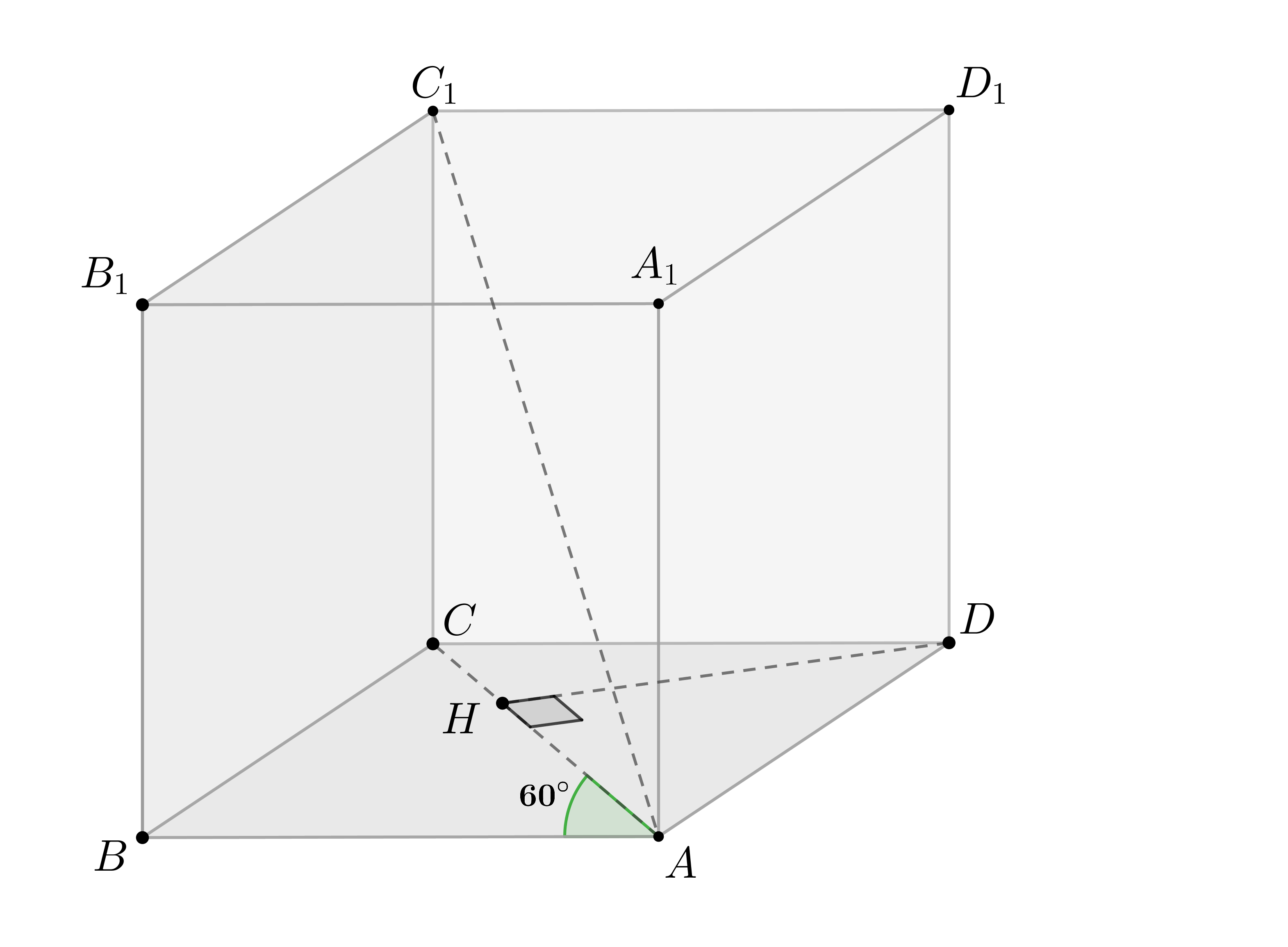
Показать ответ и решение
а) Так как , то
,
. Проведем через
точку — середину отрезка
, прямую
,
.
Проведем , тогда
. Следовательно,
,
следовательно, — плоскость, проведенная через середину отрезка
перпендикулярно ему. Значит, любая точка этой плоскости равноудалена от
концов этого отрезка. Следовательно, равноудалена от точек
и
.
Если , то
, следовательно,
— угол между
прямой и плоскостью
. Тогда
, тогда
,
. Тогда
,
.
, следовательно,
. Чтд.
б) , следовательно, если
, то
Из по теореме Пифагора получаем
. Следовательно,
Так как центр описанной сферы лежит в основании , то центр сферы —
точка пересечения диагоналей и
. Следовательно,
Ответ:
б)
Показать ответ и решение
а) Так как пирамида правильная, то центр сферы, описанной около пирамиды,
лежит на перпендикуляре, проведенном через центр основания. В нашем случае
центр основания и есть центр этой сферы. Следовательно, и
. Следовательно,
прямоугольный и равнобедренный„ то есть
. Это и есть угол между ребром
и плоскостью основания.
Аналогично доказывается для других боковых ребер пирамиды.
б) Пусть — середина
. Проведем
,
.
Следовательно, так как , то
. Таким образом, в
плоскости любая точка равноудалена от точек
и
, так как лежит
на серединном перпендикуляре к этому отрезку. Продлим до пересечения с
получим точку
.
и
.
Рассомтрим основание . Пусть
,
,
,
. Следовательно, по теореме Фалеса
.
Следовательно, по теореме Фалеса , откуда
(
— радиус сферы).
.
Следовательно, получаем
Ответ:
б)
Показать ответ и решение
а) Имеем
Следовательно, , если
— диаметры сферы,
, то есть
. Следовательно,
— квадрат.
Расстояние от до
наибольшее, если
,
— радиус
сферы. Тогда
Чтд.
б) Проведем
,
. Тогда
. Так как
, то
, следовательно, по ТТП
(
).
, следовательно,
,
, следовательно, по теореме Пифагора
Так как , то
Ответ:
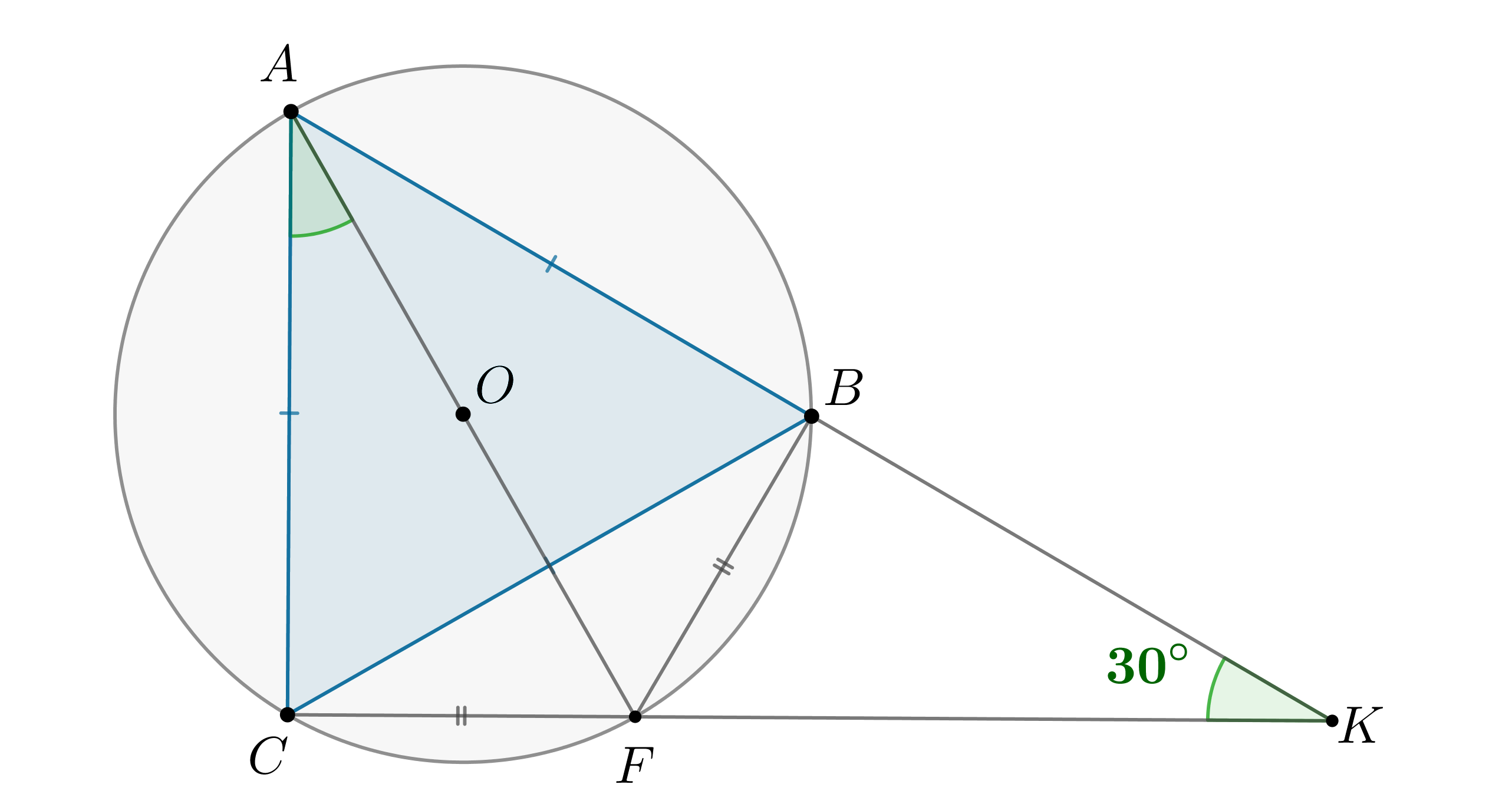
б)
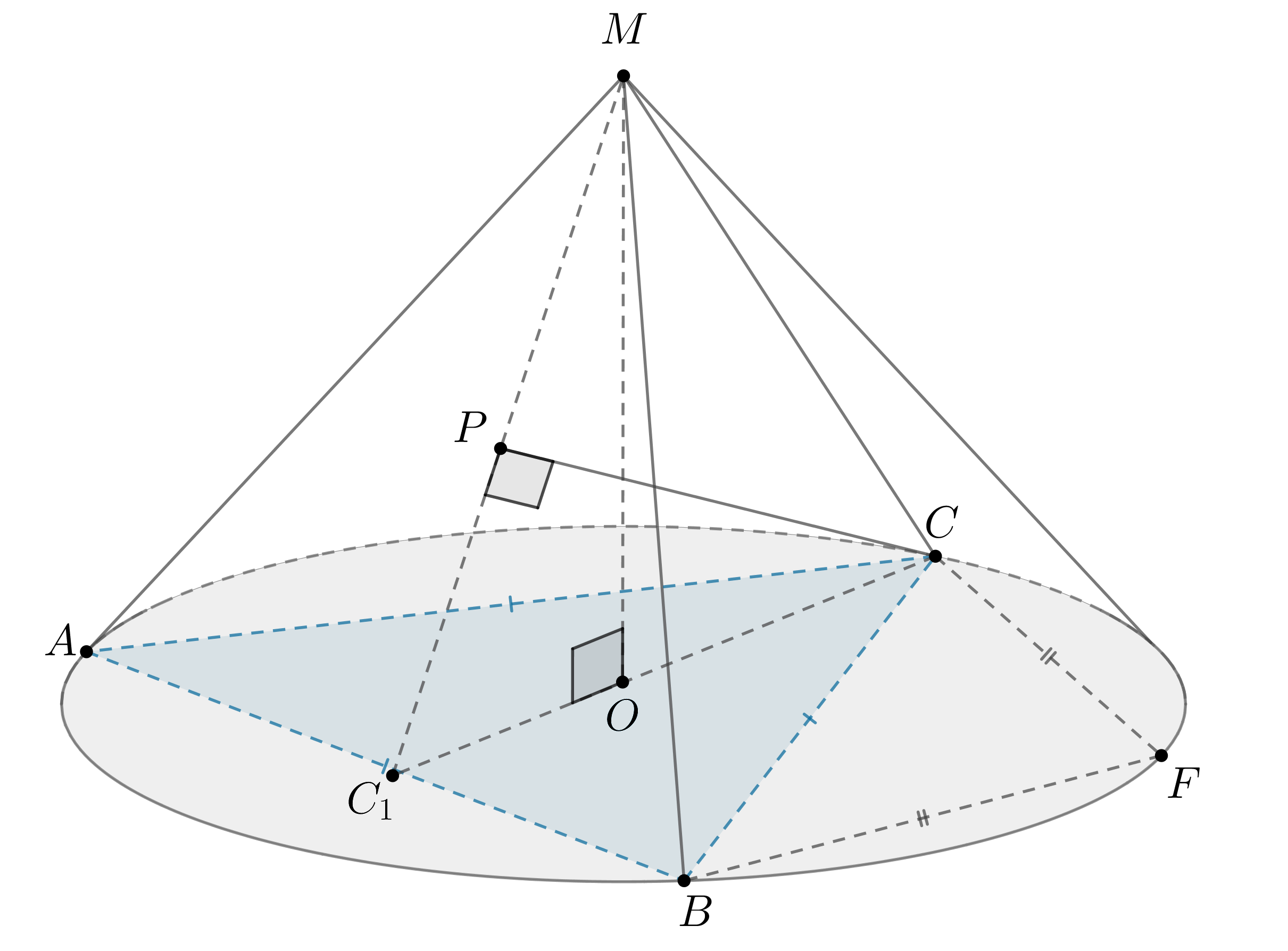
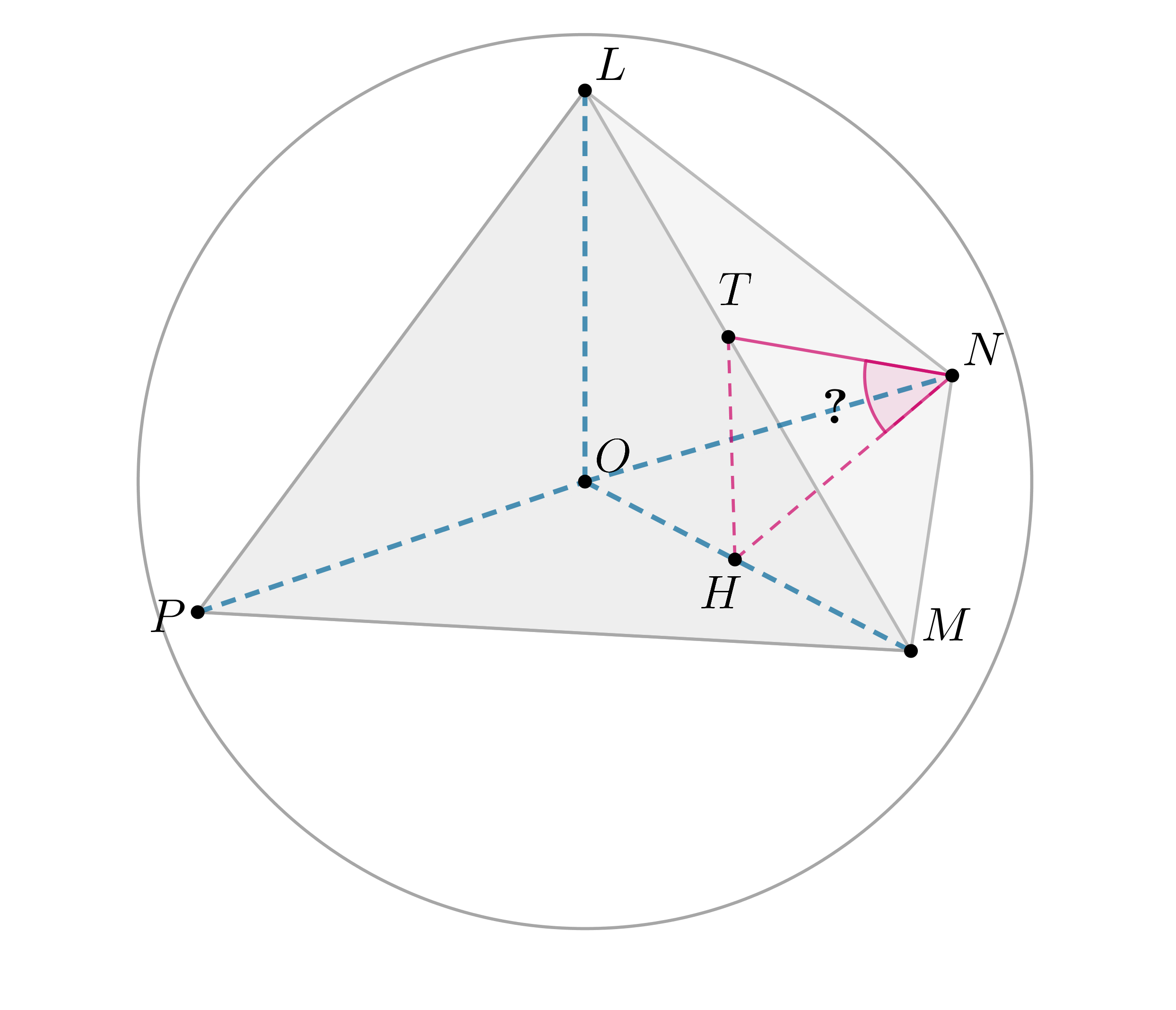
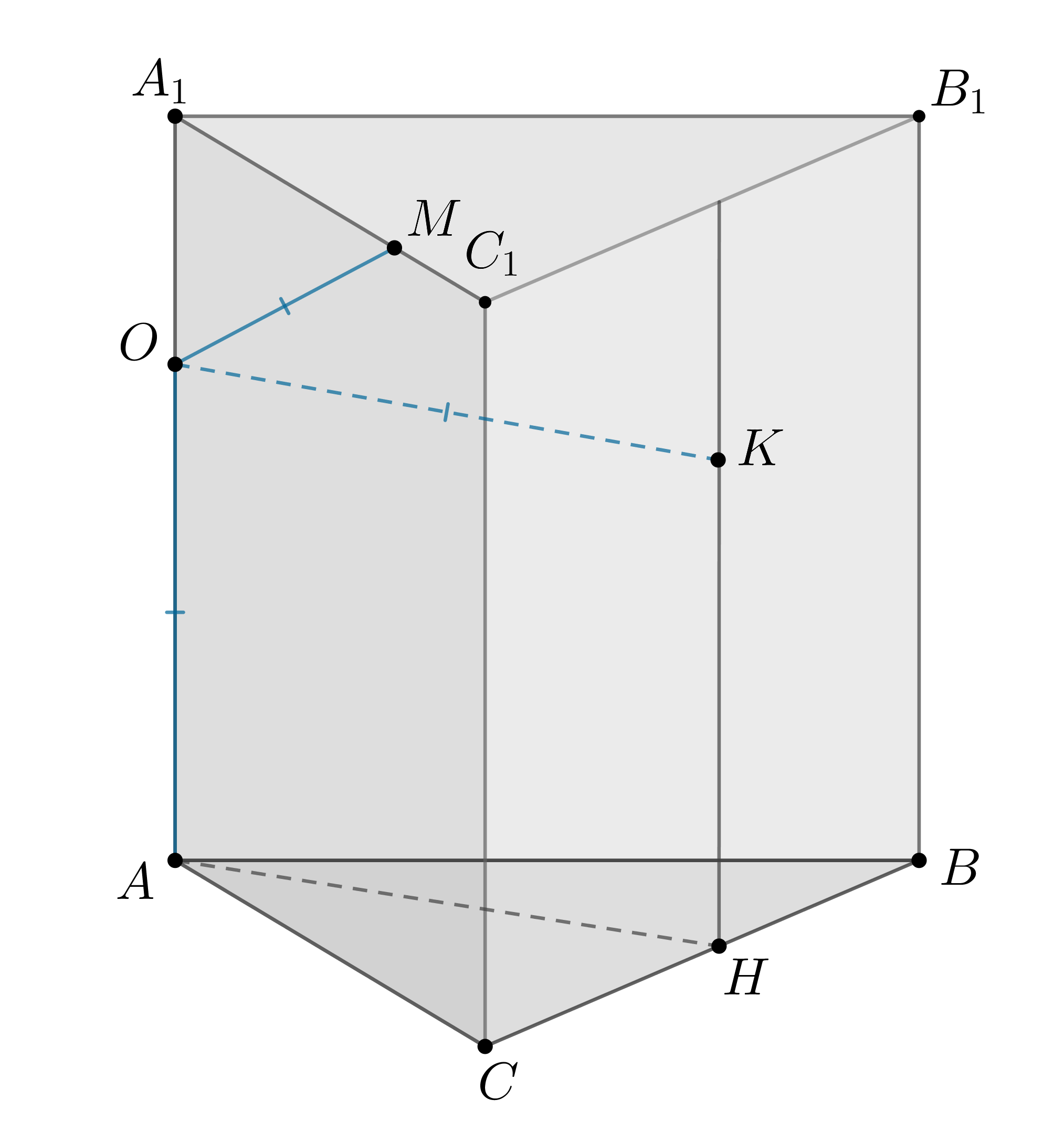
Показать ответ и решение
а) Пусть — перпендикуляр к плоскости
, следовательно,
— центр
окружности, описанной около . Наибольшее расстоние от точки
, лежащей на сфере, до
достигается, если
один из концом
диаметра сферы, проходящего через
, причем
.
наибольшая, если — равнобедренный прямоугольный, то есть
. Тогда имеем:
, следовательно,
,
чтд.
б) Пусть . По ТТП (так как
) имеем
.
По теореме Пифагора из
Следовательно, по теореме Пифагора из :
Так как , то
Ответ:
б)
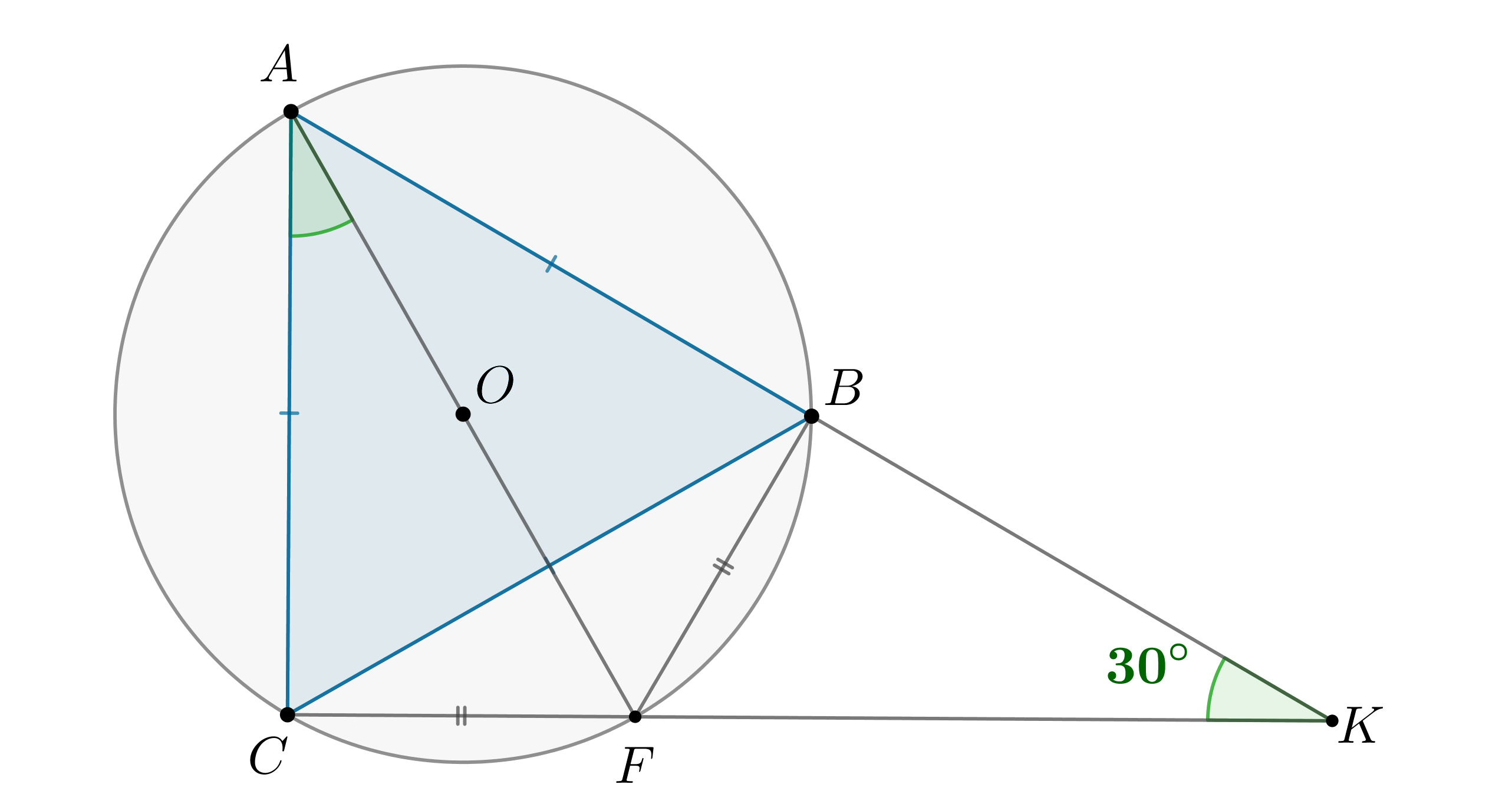
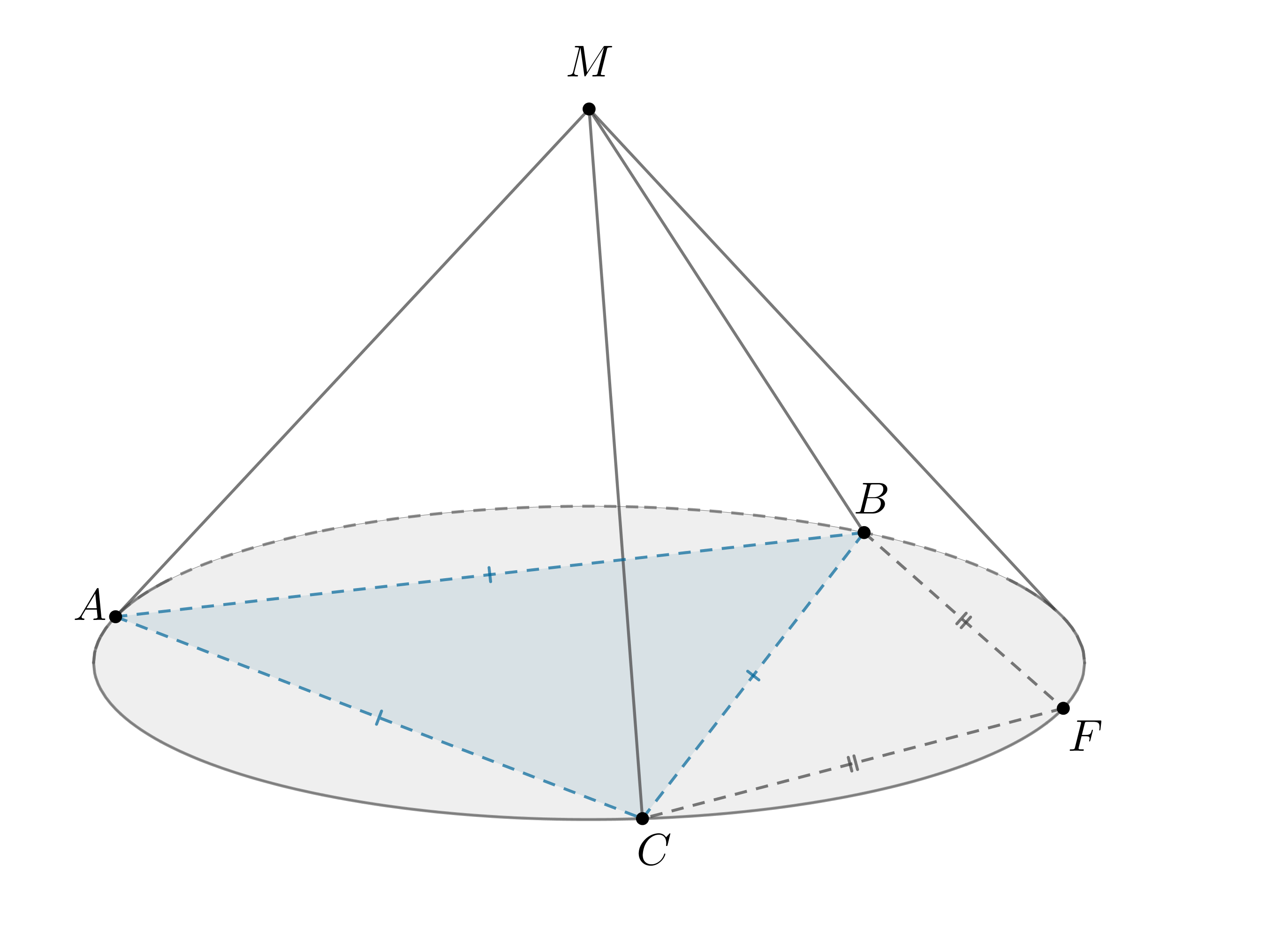
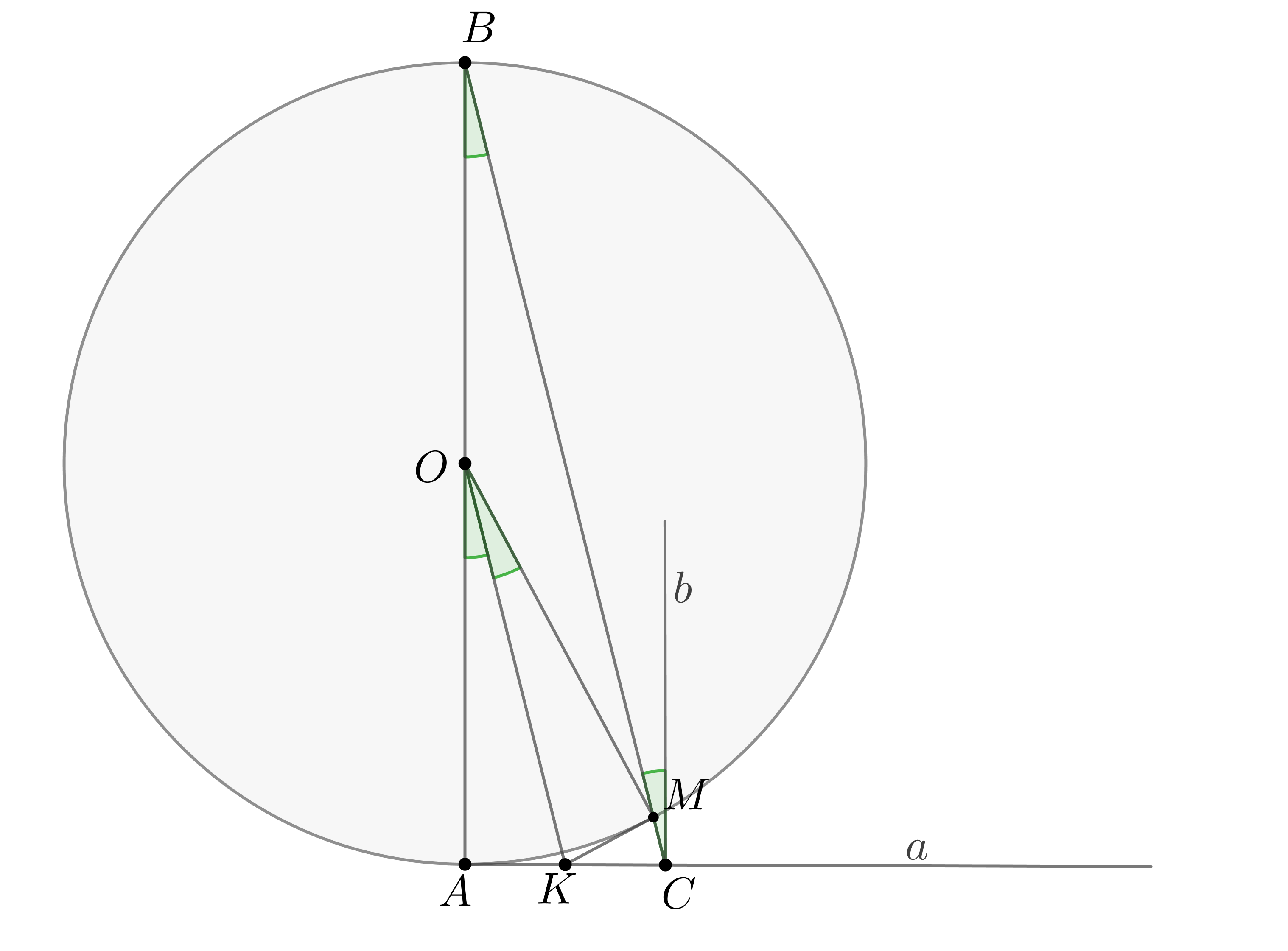
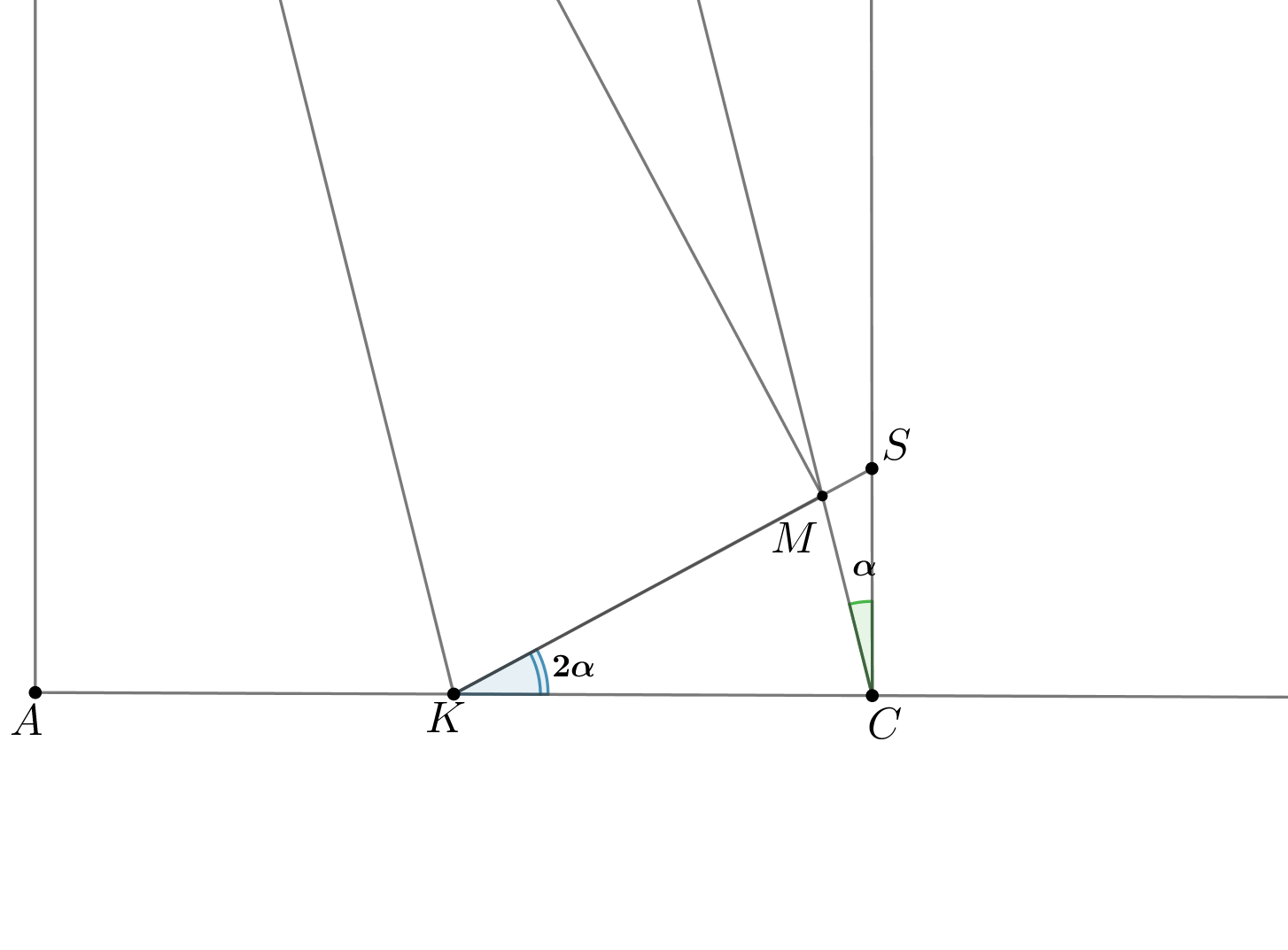
Показать ответ и решение
а) Рассмотрим плоскость . Треугольник
прямоугольный,
, так как опирается на диаметр. Его площадь наибольшая в том случае,
если он равнобедренный, то есть . Расстояние от точки
до
наибольшее, если
, то есть
— прямоугольный
равнобедренный. Тогда ,
, следовательно, по ТТП
. Чтд.
б) Проведем ,
,
. Тогда если
— радиус
сферы, то ,
Тогда
Следовательно,
Ответ:
б)
Показать ответ и решение
а) Так как , то
— точка касания сферы с
. Проведем
. Следовательно,
,
,
— точка касания сферы и
. Заметим, что
— квадрат, так как
это прямоугольник с равными смежными сторонами, и его стороны равны радиусу
сферы. Следовательно, если , то
.
Рассмотрим .
, следовательно,
Следовательно, , чтд.
б) Так как , то
. Следовательно,
Ответ:
б)
Показать ответ и решение
а) Рассмотрим диаметральное сечение сферы плоскостью, проходящей через
диаметр . Прямая
касается этой окружности в точке
.
пересекает окружность в точке .
— касательная к окружности,
. По свойству касательной, проведенной из одной точки к окружности,
.
Пусть ,
.
Тогда .
Заметим, что , то
. Следовательно,
. Следовательно, радиус основания конуса
.
б) Проведем ,
. Рассмотрим
:
.
, следовательно,
Следовательно, , следовательно,
Ответ:
б)
В прямую призму, в основании которой лежит ромб с углом , вписан цилиндр.
Расстояние между осью цилиндра и диагональю боковой грани призмы равно
.
а) Докажите, что отношение объема призмы к объему цилиндра равно
.
б) Найдите площадь полной поверхности цилиндра, если объем призмы равен
120.
Показать ответ и решение
а) Пусть дана призма ,
,
— центры нижнего и
верхнего оснований соответственно (точки пересечения диагоналей, центры
вписанных окружностей). Следовательно, — ось цилиндра.
Пусть . Тогда
, следовательно,
перпендикулярна
диагонали боковой грани, следовательно, и
— радиус
основания цилиндра.
Проведем . Получаем прямоугольный равнобедренный треугольник
, откуда
.
Если — боковое ребро призмы, то
Чтд.
б)
Следовательно,
Ответ:
б)
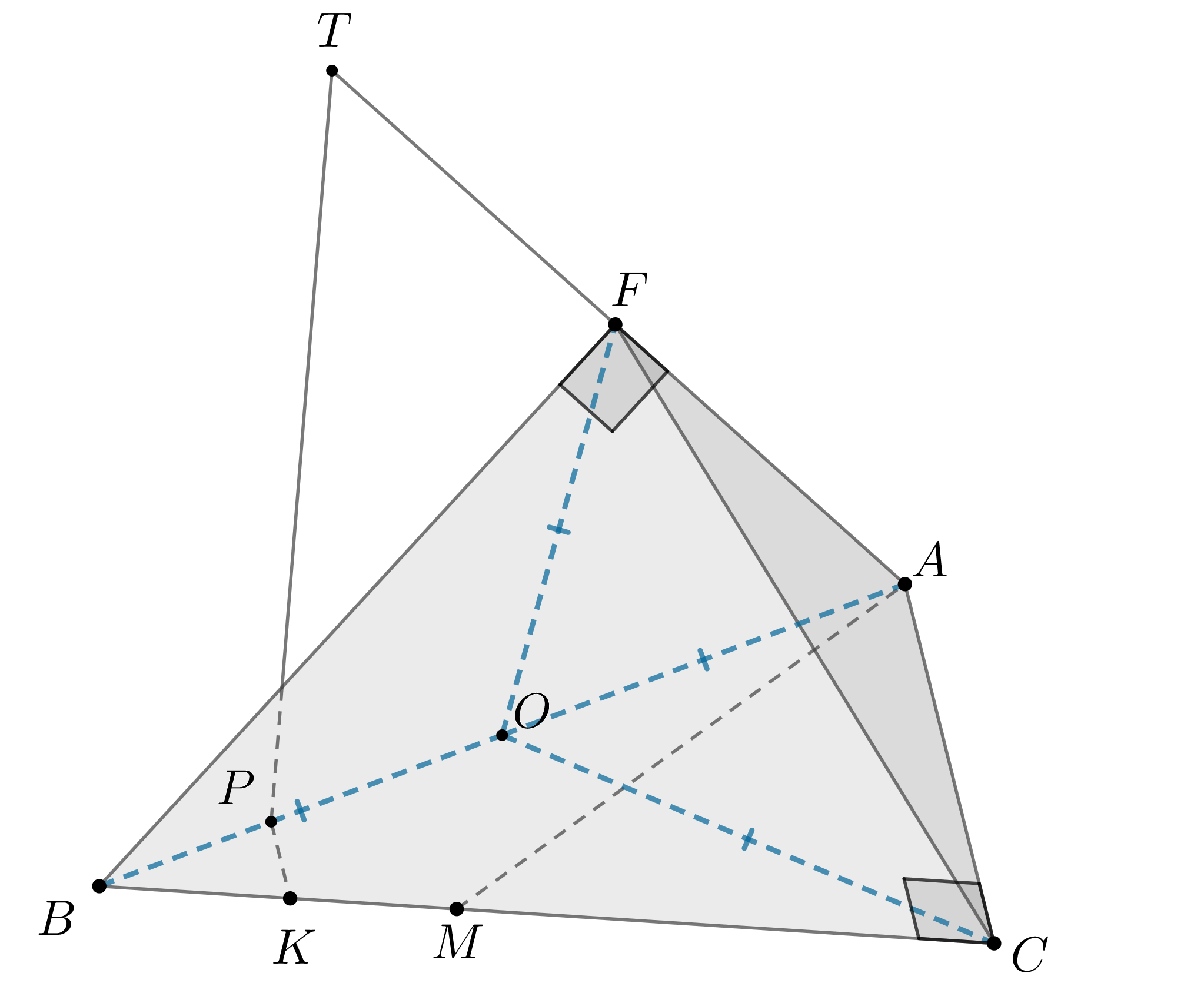
Около треугольной призмы, объем которой равен 288, описан цилиндр.
Расстояние между осью цилиндра и диагональю боковой грани призмы равно
.
а) Докажите, что отрезок, соединяющий центры окружностей, описанных около
оснований данной треугольной призмы, параллелен и равен боковому ребру
призмы, а также перпендикулярен основаниям призмы.
б) Пусть призма правильная. Найдите площадь полной поверхности
цилиндра.
Показать ответ и решение
а) Пусть дана призма . Если около нее описан цилиндр, то
основания цилиндра описаны около оснований призмы. Пусть — центры
описанных около оснований призмы окружностей. Тогда — ось цилиндра.
Следовательно, . Тогда боковые ребра призмы —
образующие цилиндра, следовательно, они параллельны и равны
.
б) — точка пересечения высот основания
,
,
.
, следовательно,
, следовательно,
, то
есть .
,
, следовательно,
Так как , то
Ответ:
б)
Около четырехугольной призмы описан цилиндр.
а) Докажите, что призма является прямоугольным параллелепипедом.
б) Диагональ и меньшая сторона основания призмы образуют угол .
Площадь боковой поверхности призмы равна , а расстояние между боковым
ребром и скрещивающейся с ним диагональю основания равно . Найдите
объем цилиндра.
Показать ответ и решение
а) Призма прямая, так как ее боковые ребра параллельны оси цилиндра.
Основание призмы вписано в окружность (условие цилиндра), следовательно,
является прямоугольном. Таким образом, призма — прямоугольный
параллелепипед.
б) Пусть . Расстояние между
и скрещивающейс с ней
диагональю основания — это
. Пусть
, тогда
,
,
Пусть . Площадь боковой поверхности призмы равна
Тогда
Ответ:
б)
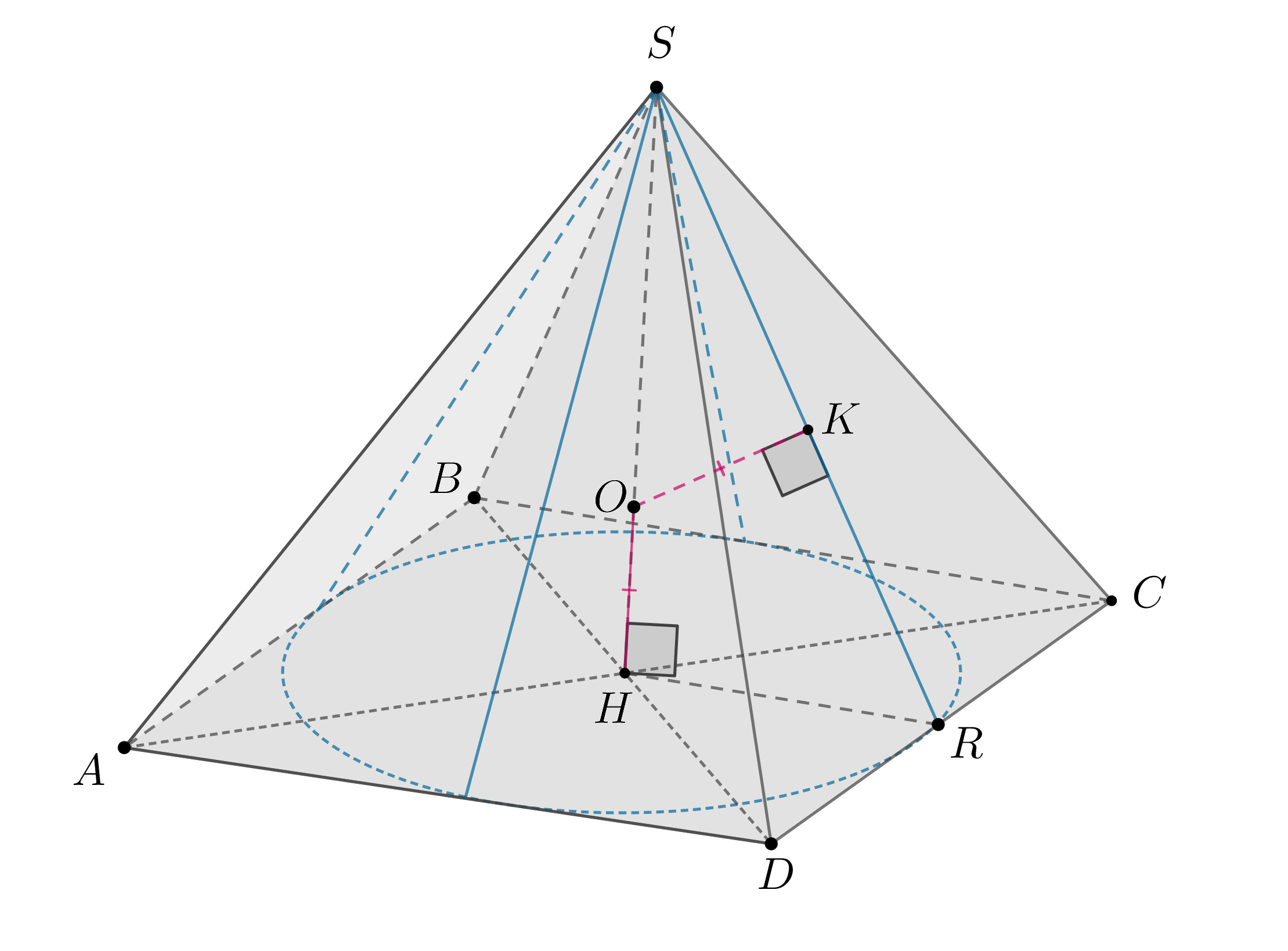
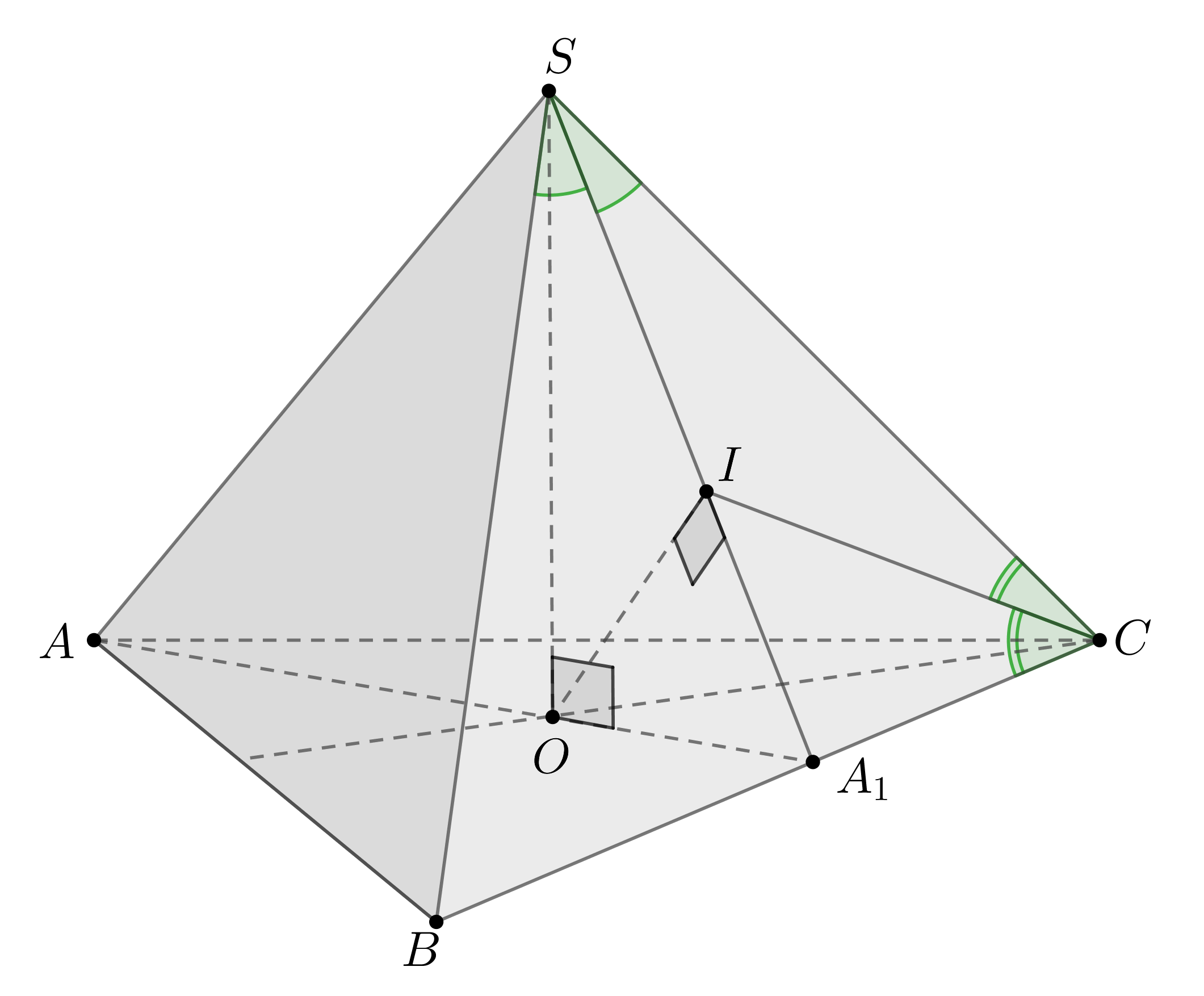
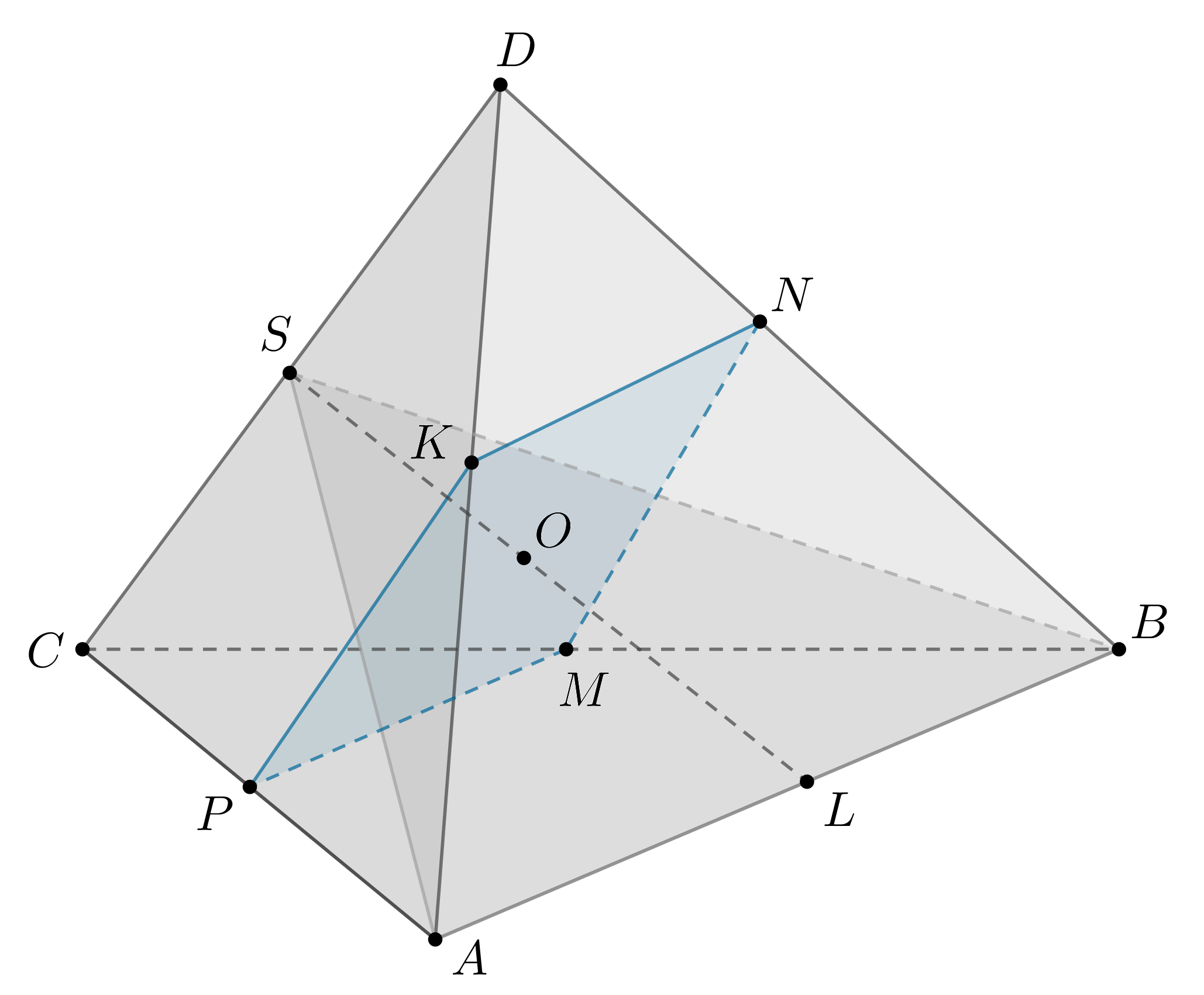
Внутри правильного тетраэдра расположен конус, вершина которого
является серединой ребра . Основание конуса вписано в сечение тетраэдра,
проходящее через середину ребра параллельно прямым
и
.
а) Докажите, что сечением является квадрат.
б) Найдите объем конуса, если ребро тетраэдра равно 12.
Показать ответ и решение
а) Пусть — середина
. Тогда
равнобедренный, так как
и
— медианы (высоты) в равных правильных треугольниках. Следовательно,
Назовем сечением .
,
. Так как
,
то ,
. Следовательно,
— параллелограмм.
Так как , то
, то есть
— ромб. Так как
,
,
, то
— квадрат со стороной
.
б) Проведем ,
. Тогда
, следовательно,
, следовательно,
— высота конуса.
.
. Следовательно,
Ответ:
б)
Цилиндр, конус, шар
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.
$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V=πR^2·h$
Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Пример:
Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.
Решение:
Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.
$R_{цилиндр}=R_{шар}; h_{цилиндр}=2R_{шар}$
Распишем формулы объема цилиндра и шара.
$V_{цилиндра}=πR_{цилиндр}^2·h_{цилиндр}=πR_{шар}^2·2R_{шар}=2πR_{шар}^3$
$V_{шара}={4π·R_{шар}^3}/{3}$
Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.
${V_{цилиндра}}/{V_{шара}}={2πR_{шар}^3·3}/{4π·R_{шар}^3}={3}/{2}=1.5$
Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
$V_{шара}=30:1.5=20$
Ответ: $20$
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ — высота и ось конуса.
Свойства конуса:
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
- Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
- Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
$S_{бок.пов.}=πR·l$
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$
Объем конуса равен трети произведения площади основания на высоту.
$V={πR^2·h}/{3}$
Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы
Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.