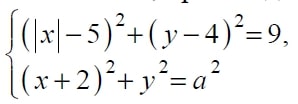1 августа 2021
В закладки
Обсудить
Жалоба
Демоверсии 2023
Утверждённые демоверсии ЕГЭ 2022 по математике от ФИПИ.
Обновлено 10 ноября.
→ Демоверсия профильного уровня: math-demo2022-pro-v2.pdf
→ Демоверсия базового уровня: math-demo2022-b-v2.pdf
→ Спецификация профильного уровня: math-s2022-pro-v2.pdf
→ Спецификация базового уровня: math-s2022-b-v2.pdf
→ Кодификатор: math-k2022-v2.pdf
→ Скачать одним архивом: math-demo2022-v2.zip
Изменения в КИМ ЕГЭ 2022 года профильного уровня в сравнении с КИМ 2021 года
1. Исключены задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни, задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.
2. Добавлены задание 9, проверяющее умение выполнять действия с функциями, и задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
3. Внесено изменение в систему оценивания: максимальный балл за выполнение задания повышенного уровня 13, проверяющего умение выполнять действия с геометрическими фигурами, координатами и векторами, стал равен 3; максимальный балл за выполнение задания повышенного уровня 15, проверяющего умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни, стал равен 2.
4. Количество заданий уменьшилось с 19 до 18, максимальный балл за выполнение всей работы стал равным 31.
Изменения в КИМ ЕГЭ 2022 года базового уровня в сравнении с КИМ 2021 года
1. Исключено задание 2, проверяющее умение выполнять вычисления и преобразования (данное требование внесено в позицию задачи 7 в новой нумерации).
2. Добавлены задание 5, проверяющее умение выполнять действия с геометрическими фигурами, и задание 20, проверяющее умение строить и исследовать простейшие математические модели.
3. Количество заданий увеличилось с 20 до 21, максимальный балл за выполнение всей работы стал равным 21.
Демо вариант профильного ЕГЭ по математике 2022 года. Критерии оценивания, ответы.
- 25.08.2021
Обновление 15.11.2021
Официальная демоверсия ЕГЭ для 2022 года по математике + спецификация + кодификатор для этого варианта. Автор-составитель: ФИПИ.
В декабре 2020 года публиковалась первая демоверсия 2022, которая называлась перспективная, она была выложена для ОБСУЖДЕНИЯ. Т.е. это не окончательный и даже не предварительный вариант демоверсии ЕГЭ 2022. Это всего лишь вариант от ФИПИ для обсуждения.
- Посмотреть перспективную модель 2022
Документы по актуальной демоверсии ЕГЭ 2022 по математике
- Кодификатор по математике 2022
- Спецификация по математике 2022
Изменения ЕГЭ 2022 по профильной математике
- Удалены задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни, задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.
- Добавлены задание 9, проверяющее умение выполнять действия с функциями, и задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
- Внесено изменение в систему оценивания: максимальный балл за выполнение задания повышенного уровня 13, проверяющего умение выполнять действия с геометрическими фигурами, координатами и векторами, стал равен 3; максимальный балл за выполнение задания повышенного уровня 15, проверяющего умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни, стал равен 2.
- Количество заданий уменьшилось с 19 до 18, максимальный балл за выполнение всей работы стал равным 31.
Другие предметы:
- Демоверсии ЕГЭ 2022 по всем предметам
Текущая версия уже идёт как «предварительные варианты», которые (как правило) не меняются.
- Тренировочные варианты ЕГЭ по математике профиль
Оставляйте свои комментарии ниже. Задавайте вопросы!
Видеоразбор демоверсии ЕГЭ 2022
Задания из демоверсии ЕГЭ 2022 по математике
ЗАДАНИЕ 2
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
ЗАДАНИЕ 3
В ромбе ABCD угол DBA равен 13° . Найдите угол BCD. Ответ дайте в градусах.
ЗАДАНИЕ 8
Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси?
ЗАДАНИЕ 10
Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
ЗАДАНИЕ 13
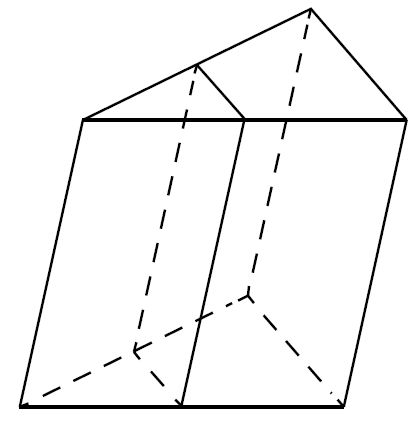
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N – середины рёбер AA1 и A1C1 соответственно.
- Докажите, что прямые BM и MN перпендикулярны.
- Найдите угол между плоскостями BMN и ABB1.
ЗАДАНИЕ 16
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B. Прямая BK пересекает
первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
- Докажите, что прямые AD и BC параллельны.
- Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
КИМ демоверсии ЕГЭ 2022 по профильной математике в PDF
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Решение и ответы заданий №1–11, 12, 13, 14, 15, 16, 17, 18 демонстрационного варианта ЕГЭ 2022 по математике (профильный уровень). Полное решение. ДЕМОВЕРСИЯ от ФИПИ для 11 класса профиль.
Задание 1.
Найдите корень уравнения 3x–5 = 81
ИЛИ
Найдите корень уравнения
ИЛИ
Найдите корень уравнения log8 (5x + 47) = 3
ИЛИ
Решите уравнение . Если корней окажется несколько, то в ответ запишите наименьший из них.
Задание 2.
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
ИЛИ
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Задание 3.
Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.
ИЛИ
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне АВ. Найдите площадь треугольника CDE.
ИЛИ
В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.
ИЛИ
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.
Задание 4.
Найдите sin2α, ecли cosα = 0,6 и π < a < 2π.
ИЛИ
Найдите значение выражения 16·log74√7
ИЛИ
Найдите значение выражения
Задание 5.
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.
ИЛИ
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
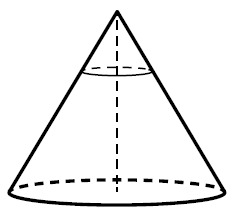
Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
Задание 6.
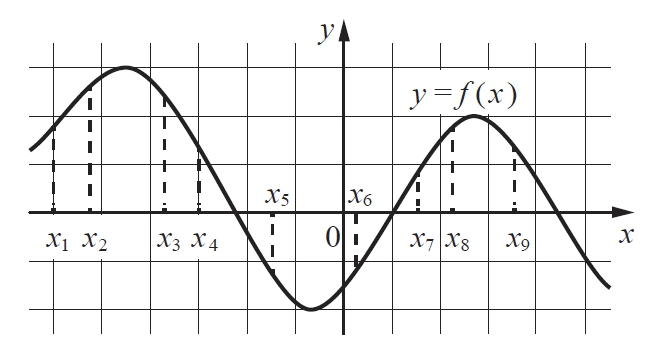
На рисунке изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены девять точек: x1, x2, … x9.
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
ИЛИ
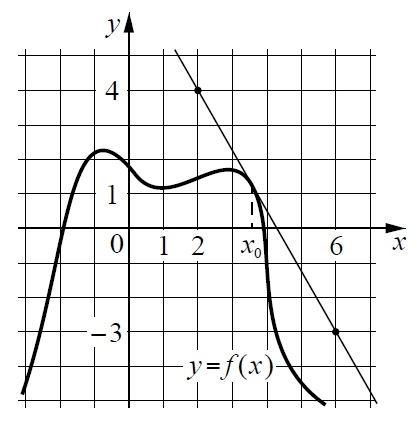
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Задание 7.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
где с = 1500 м/с — скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Задание 8.
Весной катер идёт против течения реки в 1 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
ИЛИ
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
ИЛИ
Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Задание 9.
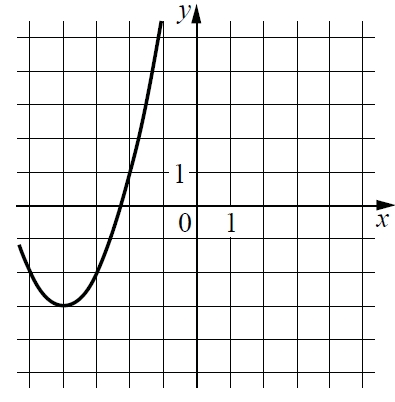
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−12).
Задание 10.
Симметричную игральную кость бросили три раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?
ИЛИ
В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Задание 11.
Найдите наименьшее значение функции
y = 9x – 9ln(x + 11) + 7
на отрезке [–10,5 ; 0].
ИЛИ
Найдите точку максимума функции y = (x + 
ИЛИ
Найдите точку минимума функции
Задание 12.
а) Решите уравнение 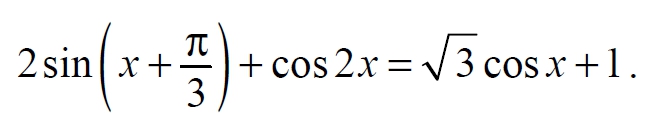
Задание 13.
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N – середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Задание 14.
а) Решите неравенство
Задание 15.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
Задание 16.
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Задание 17.
Найдите все положительные значения a, при каждом из которых система
имеет единственное решение.
Задание 18.
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
ЕГЭ по математике базового уровня относится к списку обязательных, а профильная математика считается одним из наиболее сложных госэкзаменов. Поэтому важно правильно организовать подготовку к этим испытаниям и учесть при этом все актуальные изменения.
Ознакомиться с самыми последними данными можно в этом разделе. Здесь представлены официальные документы ФИПИ — проект демоверсии КИМ-2022, в котором вы найдете примеры всех заданий и проект спецификации, в котором определены требования к сдаче экзаменов.
С 2022 года планируются некоторые изменения в структуре госэкзаменов по математике: несмотря на то, что количество заданий останется прежним, их сложность и содержание могут поменяться.
Пока не понятно, вступят ли все изменения в силу. Но, изучив документы, представленные в данном разделе, вы сможете эффективно подготовиться к любым вопросам ЕГЭ.

![[−3pi;-3pi/2] Укажите корни этого уравнения, принадлежащие отрезку.](https://ege314.ru/wp-content/uploads/2020/06/2-2.jpg)