Демонстрационная версия ЕГЭ—2019 по математике. Профильный уровень.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
Ответ:
2
На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией. Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия.
Ответ:
3
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ:
4
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
Ответ:
5
Найдите корень уравнения 3x − 5 = 81.
Ответ:
6
Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32°.
Ответ:
7
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.
Ответ:
8
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.
Ответ:
9
10
11
Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Ответ:
12
Найдите точку максимума функции
Ответ:
13
а) Решите уравнение
б) Определите, какие из его корней принадлежат отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N— середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) |
1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Найдите все положительные значения a , при каждом из которых система
имеет единственное решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали, по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Демо вариант профильного ЕГЭ по математике 2019 года. Критерии оценивания, ответы.
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике Профильного уровня. ЕГЭ по математике – это один из обязательных экзаменов для выпускников 11-го класса. Есть два варианта сдачи ЕГЭ по математике: базовый и профильный. Этот демо вариант поможет ученикам сдающим ЕГЭ по математике в 2019 году, получить представление о сложности профильного уровня. Демо вариант содержит 12 заданий с кратким вариантом ответов и 7 заданий с развернутым ответом. На последние 7 заданий представлены подробные решения и объяснения. Демо вариант можно скачать бесплатно по ссылке выше.
Комментарии для сайта Cackle
Единый государственный экзамен по математике. Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике (профильный уровень) подготовлен Федеральным государственным бюджетным научным учреждением «Федеральный институт педагогических измерений» (ФИПИ)
13. а) Решите уравнение $2sin left(x + dfrac{pi}{3}right) + cos 2x = sqrt{3} cos x + 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $left[ -3pi; -dfrac{3pi}{2} right]$.
14. Все рёбра правильной треугольной призмы $ABCA_1B_1C_1$ имеют длину 6. Точки $M$ и $N$ — середины рёбер $AA_1$ и $A_1C_1$ соответственно.
а) Докажите, что прямые $BM$ и $MN$ перпендикулярны.
б) Найдите угол между плоскостями $BMN$ и $ABB_1$.
15. Решите неравенство $$log_{11} left( 8x^2 + 7 right) — log_{11} left( x^2 + x + 1 right) geqslant log_{11} left( dfrac{x}{x + 5} + 7right).$$
16. Две окружности касаются внешним образом в точке $K$. Прямая $AB$ касается первой окружности в точке $A$, а второй — $в$ точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что прямые $AD$ и $BC$ параллельны.
б) Найдите площадь треугольника $AKB$, если известно, что радиусы окружностей равны 4 и 1.
17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число $r$ процентов по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение $r$, при котором общая сумма выплат будет меньше 1,2 млн рублей.
18. Найдите все положительные значения $a$, при каждом из которых система $$begin{cases} (|x| — 5)^2 + (y − 4)^2 = 9, \ (x + 2)^2 + y^2 = a^2end{cases}$$ имеет единственное решение.
19. В школах #1 и #2 учащиеся писали тест. Из каждой школы тест писали, по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы #1 в школу #2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе #1 уменьшиться в 10 раз?
б) Средний балл в школе #1 уменьшился на 10%, средний балл в школе #2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе #2 равняться 7?
в) Средний балл в школе #1 уменьшился на 10%, средний балл в школе #2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе #2.
- 24.08.2018
Официальная демоверсия по профильной математике ЕГЭ 2019 от 24 ноября 2018 года с кодификатором и спецификацией от ФИПИ.
Изменения по профильной математике в 2019 году:
ИЗМЕНЕНИЙ НЕТ
- Подробный разбор и решение всех задач демоверсии 2019 (Видеоформат и текстовый)
- Тренировочные варианты 2019 по профилю
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить

измерительных материалов (КИМ) единого государственного экзамена (ЕГЭ)
2019 г. следует иметь в виду, что задания, включённые в него, не отражают
всех вопросов содержания, которые будут проверяться с помощью вариантов
КИМ в 2019 г. Полный перечень вопросов, которые могут контролироваться на
едином государственном экзамене 2019 г., приведён в кодификаторе элементов
содержания и требований к уровню подготовки выпускников образовательных
организаций для проведения единого государственного экзамена 2019 г. по
математике.
Назначение демонстрационного варианта заключается в том, чтобы дать
возможность любому участнику ЕГЭ и широкой общественности составить
представление о структуре будущих КИМ, количестве заданий,
об их форме и уровне сложности. Приведённые критерии оценки выполнения
заданий с развёрнутым ответом, включённые в этот вариант, дают
представление о требованиях к полноте и правильности записи развёрнутого
ответа.
Эти сведения позволят выпускникам выработать стратегию подготовки
к ЕГЭ в 2019 году.
Экзаменационная работа состоит из двух частей, включающих в себя
19 заданий. Часть 1 содержит 8 заданий с кратким ответом базового уровня
сложности. Часть 2 содержит 4 задания с кратким ответом повышенного уровня
сложности и 7 заданий с развёрнутым ответом повышенного и высокого
уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа
55 минут (235 минут).
Ответы к заданиям 1–12 записываются по приведённому ниже образцу
в виде целого числа или конечной десятичной дроби. Числа запишите в поля
ответов в тексте работы, а затем перенесите их в бланк ответов № 1.
При выполнении заданий 13–19 требуется записать полное решение
и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается
использование гелевой или капиллярной ручки.
При выполнении заданий можно пользоваться черновиком. Записи
в черновике, а также в тексте контрольных измерительных материалов
не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее
количество баллов.
После завершения работы проверьте, чтобы ответ на каждое задание в
бланках ответов № 1 и № 2 был записан под правильным номером.
Желаем успеха!
Условия задач и ответы
Решение задач смотрите здесь
Часть 1
- Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
- На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 г. По горизонтали указаны номера месяцев; по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией. Сколько месяцев средняя температура была больше 18 градусов Цельсия?
- На клетчатой бумаге с размером клетки 1 см х 1 см изображён треугольник. Найдите его площадь. Ответ дайте в см2.
- В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
- Найдите корень уравнения
- Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32o. Найдите угол BOC . Ответ дайте в градусах.
- На рисунке изображён график дифференцируемой функции
. На оси абсцисс отмечены девять точек:
. Найдите все отмеченные точки, в которых производная функции
отрицательна. В ответе укажите количество этих точек.
- В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ выразите в см.
Часть 2 - Найдите
, если
и
.
- Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
, где
м/c — скорость звука в воде;
— частота испускаемого сигнала (в МГц);
— частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
- Весной катер идёт против течения реки в
раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
- Найдите точку максимума функции
- а) Решите уравнение
.
б) Укажите корни этого уравнения, принадлежащие отрезку.
- Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1C 1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1. - Решите неравенство
- Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1. - 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицейНайдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
- Найдите все положительные значения
, при каждом из которых система
имеет единственное решение.
- В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали,
по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Решение задач здесь
смотрите также Демо ЕГЭ 2017 Базовый уровень
Ответы
- 8
- 4
- 6
- 0,08
- 9
- 64
- 4
- 4
- -0,96
- 751
- 5
- -5
- а)
б)
- б)
- 3,2
- 7
- а) да; б) нет; в) 5.
Решение задач смотрите здесь
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике, Профильный уровень.
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания с кратким ответом повышенного уровня сложности и 7 заданий с развернутым ответом повышенного и высокого уровней сложности. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут). Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1.
Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское)и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике, Профильный уровень — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 11.06.2019 10:00 UTC
Теги:
тренировочный вариант ЕГЭ :: ЕГЭ по математике :: 11 класс :: математика :: профильный уровень :: 2019
Следующие учебники и книги:
- Рекомендации по подготовке к выполнению задания №13 ЕГЭ профильного уровня, Прокофьев А.А., 2017
- Сборник заданий с досрочного ЕГЭ 2019 по профильной математике
- Досрочный вариант 29.03.2019 единого государственного экзамена профильный уровень
- ЕГЭ 2019, Математика, Досрочный вариант
Предыдущие статьи:
- ЕГЭ 2019, Математика, Профильный уровень
- ЕГЭ 2019, Математика, Базовый уровень, Досрочный вариант
- Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике, Базовый уровень, Решения
- Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике, Базовый уровень
Статьи
Среднее общее образование
Алгебра
Геометрия
Предлагаем вашему вниманию разбор демоверсии ЕГЭ-2019 года по математике (профильный уровень).
Этот материал содержит пояснения и подробный алгоритм решения, а также рекомендации по использованию справочников и пособий, которые могут понадобиться при подготовке к ЕГЭ.
26 августа 2018
Официальная демоверсия ЕГЭ 2019 по математике, а также кодификатор и спецификация доступны по ссылке:
Математика (скачать архив с файлами PDF 1.4 Mb)
Что нового?
В этот раз никаких изменений в структуре и содержании нет. Рекомендуем посмотреть демоверсии базового и профильного уровней 2018 года, а новый вариант мы разберем уже скоро на вебинарах и в эфире YouTube.
Источник: сайт
ФИПИ

ЕГЭ-2020. Математика. Сборник заданий: 500 заданий с ответами
Книга содержит задания разных типов и уровней сложности по темам, знание которых проверяется на ЕГЭ, а также комментарии к ним. Ко всем заданиям приводятся ответы. Поможет потренироваться в выполнении заданий, повторить пройденный материал и эффективно подготовиться к сдаче ЕГЭ.
Купить



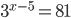
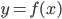
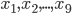

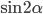
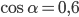
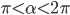
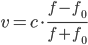
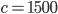
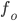
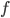
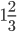
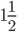
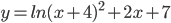
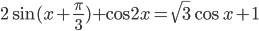
![[-3pi;-3pi/2]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_fb4342b92385ff8dda5d1bc21b9cb50e.gif)
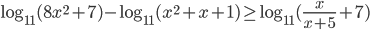
 Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
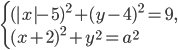
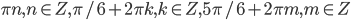
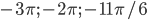
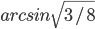
![(-infty;-12]; (-35/8;0]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_987d091bf920c062aeabde6b0a8e3ea0.gif)