Поступление в лицей НИУ ВШЭ
в 10 класс. Математика.
— проходные баллы прошлых лет
— официальные демоверсии по математике.
— видео-разборы демоверсий
— советы по подготовке и сдаче вступительных.
До экзамена осталось:
*Пройди тестирование на основе реального варианта и определи свой уровень подготовки.
Подготовка к поступлению В Лицей ВШЭ
- Подготовка с репетитором к поступлению В Лицей ВШЭ
- Подготовка к поступлению в Лицей ВШЭ
- Проходные баллы прошлых лет
- Разборы вариантов сборника ХВЛ
- Математика 9 класс
- Контакты
Важно! Мы не являемся сотрудниками Лицея ВШЭ (подробнее в разделе «о нас»). Никаких реальных вариантов мы не продаем и не распространяем! Подборка заданий и все задания в сборниках составлена нами, реальные задания составлены со слов учеников и публикуются в ознакомительных целях ПОСЛЕ экзамена!
Проходные баллы прошлых лет
Максимальный балл по каждому направлению — 50
Разборы вариантов сборника ХВЛ
Сам сборник вы можете приобрести в Буквышке
Разбор демоварианта 2023 г (Часть 1)
Тренировочные варианты 2023
*Варианты взяты из официального сборника для подготовки к вступительным в лицей ВШЭ. Сборник можно скачать по
ссылке.
Разбор демоварианта 2022 г (Часть 1)
Тренировочные варианты 2022
*Задания составлены аналогично демовариантам
Разбор демоварианта 2021г (Часть 1)
Разбор демоварианта 2021г (Часть 2)
Реальные вариант 2021
*Задания составлены со слов учеников
Тренировочные варианты 2021
*Задания составлены аналогично демовариантам
Разбор демоварианта 2020г (Часть 1)
Разбор демоварианта 2020г (Часть 2)
Реальный вариант 2020
*Задания составлены со слов учеников
Тренировочные варианты 2020
*Задания составлены аналогично демовариантам
Разбор демоварианта 2019г(Базовый уровень)
Разбор демоварианта 2019г (Профильный уровень)
Тренировочные варианты
*Задания составлены аналогично демовариантам
Разбор демоварианта 2018г (Базовый уровень) Матэк
Разбор демоварианта 2018г (Базовый уровень) Соцэк
Разбор демоварианта 2018г (Профильный уровень)
Разбор демоварианта 2017г (Базовый уровень)
Разбор демоварианта 2017г (Профильный уровень)
Лицей НИУ ВШЭ
1
Место в рейтинге школ Москвы
Общая информация по набору
| Адрес | Большой Харитоньевский переулок, д. 4 м. Сретенский бульвар |
| Сайт | https://school.hse.ru// |
| Рейтинг | 2 место (2016 год), 1 место (2017 год), 1 место (2019 год) среди школ Москвы 40 место среди школ России— конкурентоспособность выпускников (2019 год) |
| Обучение | С 9 по 11 классы |
| Прием | 9, 10 классы (11 возможен добор) |
| Вступительные экзамены | Математика,русский язык, иностранный язык |
Последние новости по набору
Подготовка к поступлению в лицей НИУ ВШЭ с Лицей-гуру
Основное направление – подготовка к поступлению в лицей НИУ «Высшая школа экономики» (ВШЭ).
В рамка курса прорабатываются темы в соответствие со структурой экзамена в ВШЭ:
- Уравнения, вычисления — 0,5 балла
- Задача на проценты — 0,5 балла
- Иррациональные числа и выражения — 0,5 балла
- Графики функций — 0,5 балла
- Логическая задача — 1 балл
- Преобразования — 1 балл
- Геометрическая задача — 1 балл
- Текстовая задача — 1 балл
- Параметры — 2 балла
- Нестандартная задача 2 балла
При обучении используются внутренние методички ВШЭ и методички для подготовки к поступлению в ВШЭ, программа углубляется и обогащается за счет материалов из методичек других ведущих математических лицеев, а так же включен разбор большого количества вариантов прошлых лет.
Мы делаем основной упор на понимание тем, а не на натаскивание на определенный тип задач. Ежегодно задачи меняются и предугадать, что будет в этот раз – невозможно. Поэтому мы даем углубленную программу текущего класса с запасом по сложности.
Перед сдачей экзамена в лицей ВШЭ мы очень рекомендуем посещать пробные контрольные раз в месяц или чаще, это один из важнейших аспектов поступления, т.к. тренирует концентрацию, стрессоустойчивость ученика, выявляет проблемные темы и развивает способность рассчитывать время вступительного экзамена.
Т.к в лицей ВШЭ конкурс очень высок, в среднем около 5 – 8 человек на место, желательно выбрать несколько вариантов для поступления – например, школа «Покровский квартал», школа 109, Лицей 1535, Лицей Плеханова, Предуниверситарий МИФИ (1511) и др. Программа поможет подготовиться к поступлению и в эти учебные заведения, а посещение экзаменов так же будет полезно для тренировки.
Очень часто ученики 8-9 классов при написании экзамена в ВШЭ и другие лицеи теряют значительную часть баллов из-за невнимательности и вычислительных ошибок. На наших курсах мы стараемся решить данную проблему за счет домашних заданий с автоматической проверкой на нашей специальной платформе. Когда ученик отправляет домашнюю работу на проверку, ему сразу приходит результат, и он может самостоятельно найти ошибку в задании. Таким образом, развивается навык самопроверки, важный при подготовке к экзамену в Лицей ВШЭ. Каждое домашнее задание по структуре напоминает вступительный вариант экзамена, т.к. включает в себя сразу много тем – на повтор уже пройденных ранее, закрепление текущей темы + логические и текстовые задачи.
История Лицея
Лицей при НИУ ВШЭ открылся совсем недавно, в сентябре 2013 года. Изначально набирали только учеников в 10 класс, затем открылся набор и в 9 класс, а в 2017 году проводился дополнительный набор и в 11 класс. Не смотря на столь юный «возраст» лицей занимает 1 или 2 место в рейтинге школ Москвы последние 4 года.
Учебный процесс
Учебный процесс совсем не похож на стандартный в общеобразовательных школах.
В 9 классе всего две специализации: универсальная и математическая. В универсальной все предметы изучаются на примерно одном уровне углубленности. В математических классах уделяется особое внимание всем естественно-научным предметам: математике, физике, химии, информатике, биологии. Часть предметов ученики могут выбрать для изучения по своему желанию.
В 10 «классах» уже 10 специализаций:
- «Экономика и математика»,
- «Экономика и социальные науки»,
- «Гуманитарные науки»,
- «Дизайн»,
- «Востоковедение»,
- «Информатика, инженерия и математика»,
- «Юриспруденция»,
- «Психология»,
- «Математика»,
- «Естественные науки»
«Классах» в кавычках, потому что как таковых классов нет, есть группы по 6-20 человек, которые на каждом предмете разные. Каждый ученик составляет себе индивидуальный план, какие предметы и углубленно или на базовом уровне он хочет изучать. Конечно, есть и обязательные предметы для изучения: математика, русский язык и хотя бы один иностранный язык.
Есть большое количество разнообразных кружков и факультативов: начиная от современных молодежных культур до изучения китайских иероглифов. Но обучение на этих факультативах идет очень серьезное — с учетом посещаемости, сдачей зачетов и экзаменов.
Прием в Лицей НИУ ВШЭ
Прием осуществляется в 9 и 10 классы.
При подаче заявления для поступления его необходимо сопроводить эссе на 400 слов, в котором должен быть ответ на вопрос: «Почему я хочу учиться в лицее НИУ ВШЭ».
Сами вступительные испытания представляют собой комплексный тест из двух этапов. На первом этапе проверяются школьные знания по русскому языку, математике и иностранному языку. На втором этапе проводятся испытания по профильным предметам выбранного направления ( при подаче заявления на поступление можно указать два желаемых профиля).
Еще варианты вступительных экзаменов в лицей НИУ ВШЭ
Лицей-гуру
Курсы по подготовке к экзаменам
Данная статья посвящена разбору комплексного теста по математике для абитуриентов лицея НИУ ВШЭ, поступавших в 10 класс в 2018 году. Разбор теста в лицей ВШЭ выполнен профессиональным репетитором, который на протяжении нескольких лет занимается подготовкой школьников к поступлению в это учебное заведение. Представленные задания не являются точной копией тех, что были на вступительном экзамене, но они составлены по мотивам теста, который предлагался для решения абитуриентам лицея ВШЭ в 2018 году. Данный материал может оказаться полезным для тех, кто готовится к вступительным экзаменам в лицей ВШЭ в этом году.
Также предлагаем вам воспользоваться сайтом онлайн-школы CleverFox.info, где выложены варианты комплексных тестов, составленные по мотивам экзаменов прошлых лет, а также ответы и подробные решения к каждому заданию. Идеальный вариант для самостоятельной подготовки к комплексному тесту в лицей ВШЭ.
Первая часть теста в лицей ВШЭ (направления Ю, Д, В, Г, МИ, Экмат)
В этом разделе представлен разбор типовых заданий первой части комплексного теста по математике в лицей ВШЭ за 2018 год (направления «Юриспруденция», «Дизайн», «Востоковедение», «Гуманитарные науки», «Математика, информатика и инженерия», «Экономика и математика»).
Вычисляем по частям:
.
Правильный ответ: .
- 14
- 12
- 11
- 13
Количество кусков, которые получаются при распиливании стержня, всегда на 1 больше, чем число распилов. То есть на стержне 4 фиолетовых линии, 2 чёрных и 6 зелёных. Значит, если распилить стержень по линиям всех трёх цветов, то получится кусков.
Правильный ответ: 13.
Если вы пишите тест в лицей ВШЭ, то скорее всего вам обязательно попадётся подобное задание. Давайте разберём его решение.
Поскольку стоимость мяча до распродажи составляла 850 рублей, что соответствует 100%, то 1% соответствует 850 : 100 = 8.5 рубля. Алёша сэкономил на покупке футбольного мяча 850 — 510 = 340 рублей. Значит, в процентах это составляет 340 : 8.5 = 40%.
Правильный ответ: 40.
- 28
- 36
- 21
- 35
Раскроем обе скобки в левой части неравенства, используя формулы «квадрат суммы» и «квадрат разности»:
После приведения подобных слагаемых получаем следующее неравенство:
Теперь прибавим к обеим частям неравенства 84 и поделим обе части на 28. Знак неравенства при этом не изменится, так как мы делим на положительное число. В результате приходим к следующему неравенству: .
Сумма целых положительных решений неравенства равна .
Правильный ответ: 36.
- 4
- 5
- 9
- 7
Здесь мы имеем дело с арифметической прогрессией, у которой первый член равен , а разность равна
. Требуется количество
первых членов этой прогрессии, если известна их сумма
, так как 2 часа 25 минут = 145 минут. Можно использовать для этого готовую формулу:
Подставляем все величины в эту формулу:
Коэффициенты последнего квадратного уравнения равны ,
и
. Тогда дискриминант равен:
Значит, один из корней равен:
Второй корень не подходит, так как он отрицателен.
Правильный ответ: 5.
- Лжец
- Рыцарь
- Если человек, которого спрашивал проводник, лжец, то проводник — рыцарь
- Может быть как рыцарем, там и лжецом
Любой человек на острове не мог бы сказать про себя, что он лжец. Действительно, если этот житель лжец, то он сказал бы правду, а если рыцарь — солгал бы. То есть проводник сказал неправду, что человек, которого он спрашивал, сказал о себе, что он лжец. Значит, проводник — лжец.
Правильный ответ: лжец.
- 30
- 60
- 24
- 48
Поскольку гипотенуза этого треугольника равна , а один из катетов равен
, то по теореме Пифагора можно найти длину другого катета:
. Для наглядности изобразим данный треугольник на рисунке:
Площадь такого треугольника равна половине произведения длин его катетов. То есть .
Правильный ответ: 24.
a) Если Иммануил Альбертович не надел шарф, значит, он не ведёт занятие
b) Если Иммануил Альбертович надел шарф, значит, он ведёт занятие
c) Если Иммануил Альбертович проводит на занятии контрольную работу по риторике, значит, он надел шарф
d) Если Иммануил Альбертович не ведёт занятие, значит, он не надел шарф
- a, c и d
- a и c
- b и d
- a и d
a) Верно, так как Иммануил Альбертович обязательно надевает шарф, когда ведёт занятие.
b) Неверно, так как Иммануил Альбертович мог надеть шарф не из-за того, что он ведёт занятие, а по какой-то иной причине.
c) Верно, так как контрольная работа проводится на занятии, а Иммануил Альбертович обязательно надевает шарф, когда ведёт занятие.
d) Неверно, так как Иммануил Альбертович мог надеть шарф по какой-то иной причине, нежели проведение занятия.
Правильный ответ: a и c.
- 60 км/ч
- 70 км/ч
- 65 км/ч
- 72 км/ч
Пусть скорость второго мотоциклиста равна км/ч. Тогда скорость первого мотоциклиста равна
км/ч. Значит, время движения второго мотоциклиста равно
ч, а время движения первого мотоциклиста равно
ч. Поскольку известно, что первый мотоциклист прибывает к финишу на 1 час раньше второго, то имеет место уравнение:
Для и
, что соответствует смыслу задачи, последнее уравнение эквивалентно следующему:
или
. Корни последнего уравнения находятся по теореме Виета:
и
. По смыслу задачи подходит только положительный. Итак, скорость второго мотоциклиста равна 60 км/ч.
Правильный ответ: 60 км/ч.
Если уравнение имеет более одного корня, в ответ запишите сумму корней уравнения.
- 8,2
- 3,8
- -8,2
- 7,2
Перепишем уравнение в виде:
Для последнее уравнение эквивалентно уравнению
. Дискриминант данного квадратного уравнения положителен. Значит, оно имеет два различных корня. При этом прямой подстановкой легко убедиться, что ни число
, ни число
не являются корнями этого уравнения. Разделим обе части полученного уравнения на
, после чего уравнение примет вид:
. По теореме Виета сумма корней этого уравнения равна коэффициенту при переменной
, взятому с противоположным знаком. То есть
.
Правильный ответ: 3,8.
Первая часть теста в лицей ВШЭ (направления П, Соцэк)
- 3125
- -310,5
- 25
- 0,008
Вычисляем по частям:
1)
2)
3)
Правильный ответ: 3125.
- 10%
- 11.8%
- 12%
- 13%
100% стоимости телефона до повышения цены составляли 16000 руб. То есть 1% составляли 16000 : 100 = 160 руб. После подорожания цена телефона составила 17920 руб., что составляет 17920 : 160 = 112%. Значит, телефон стал дороже после повышения цены на 112-100 = 12%.
Правильный ответ: 12%.
- 0
- 2
- 3
- 4
Упростим неравенство:
Наименьшим целым решением последнего неравенства является число 3.
Правильный ответ: 3.
- 50
- 58
- 63
- 84
Поскольку количество задач, которые решал Алёша, увеличивалось каждую ночь на одно и то же число, то во вторую ночь он решил столько, сколько он решал в среднем за все три ночи, то есть 189 : 3 = 63 задачи. Значит, в первую и третью ночь Алёш решил вместе 189-63 = 126 задач. Пусть в первую ночь он решил задач. Известно, что в третью ночь он решил в 2 раза больше задач, чем в первую. То есть в третью ночь он решил
задач. Тогда имеет место уравнение
, откуда получаем
. Значит, в первую ночь Борис решил 42 задачи, а в третью в 2 раза больше, то есть 84 задачи.
Правильный ответ: 84.
- 1
- 2
- 0
- 3
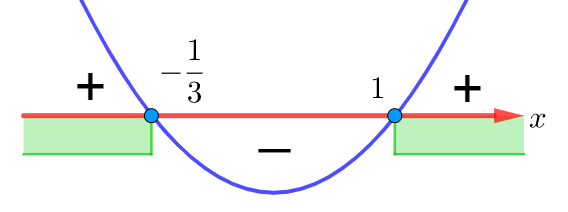
Выражение, стоящее под знаком корня, должно быть большим или равным нулю, а выражение, стоящее в знаменателе, не должно быть равным нулю. Значит, область определения данной функции задаётся следующей системой:
1) Решаем первое неравенство системы. Найдём сперва корни уравнения . Они находятся с помощью дискриминанта или по теореме Виета:
и
. Наносим найденные значения на числовую прямую (соответствующие точки будут закрашены, так как неравенство нестрогое) и определяем знаки на полученных промежутках:
Итак, решение первого неравенства системы имеет вид:
.
2) Из второго неравенства системы получаем, что . То есть число
нужно исключить из полученного выше решения.
Тогда область определения функции имеет вид:
.
В неё не входят только два целых числа: 0 и 1.
Правильный ответ: 2.
- 10
- 14
- 9
- 12
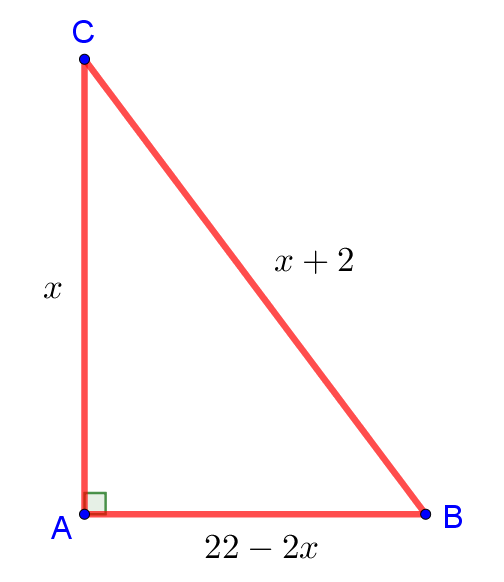
Пусть один из катетов этого прямоугольного треугольника равен см, тогда его гипотенуза равна
. Поскольку периметр этого треугольника равен 24, то второй его катет равен
. Для наглядности изобразим данный прямоугольный треугольник на рисунке:
По теореме Пифагора получаем, что . То есть имеет место уравнение:
Корни последнего уравнения находим через дискриминант или по теореме Виета. Они равны: и
. Но второй вариант не подходит, так как в этом случае гипотенуза должна быть равна
. То есть сумма длин этого катета и гипотенузы равна
, что больше периметра треугольника. То есть один из катетов равен 8 см, а гипотенуза равна
см.
Правильный ответ: 10.
- -8
- 8 и -8
- 8
- 4 и -4
Формула n-го члена геометрической прогрессии имеет вид: , где
— первый член прогрессии,
— знаменатель геометрической прогрессии. Значит, имеет место система уравнений:
Разделим почленно второе уравнение на первое. В результате получаем:
Возможны оба варианта, как с положительным знаменателем, так и с отрицательным.
Теперь находим первый член прогрессии. Для этого подставим найденное значение в первое уравнение исходной системы:
Находим теперь пятый член прогрессии с помощью формулы n-го члена:
Правильный ответ: -8.
- 7
- 8
- 8,5
- 9
Переведём 6 часов 40 минут в часы. Поскольку 40 минут = часа, то 6 часов 40 минут =
часа.
Назовём производительностью бригады то, какую часть поля она пропалывает в одиночку за 1 час. Пусть производительность первой, второй, третей и четвёртой бригад равны, соответственно, ,
,
и
. Тогда, согласно условию, имеет место система уравнений:
Сравнивая первое и третье уравнение системы, находим сразу, что . Тогда первое и второе уравнение в системе можно переписать в следующем виде:
Вычтем теперь почленно из первого уравнения полученной системы второе:
Значит, производительность группы, состоящей из первой и четвёртой бригады, равна . Значит, работая вместе, первая и четвёртая бригады справятся с прополкой поля за
часов.
Правильный ответ: 8.
и
Если точек пересечения несколько, в ответе укажите их сумму.
- -2
- -1
- 1
- 3
Для нахождения абсциссы точки пересечения графиков указанных функций нужно решить уравнение: :
Переносим все дроби в одну сторону равенства и приводим их к общему знаменателю:
В знаменателе не должно быть нуля, поэтому . При остальных значениях
последнее уравнение эквивалентно уравнению
или, после деления на
обеих частей,
. Данное квадратное уравнение решается с помощью дискриминанта или по тереме Виета:
и
. Второй корень не входит в область определения обеих функций. Итак, у графиков исходных функций будет только одна точка пересечения, абсцисса которой равна
.
Правильный ответ: 1.
- 1
- 2
- 3
- 4
Заметим сразу, что при уравнение становится линейным:
. Полученное уравнение имеет единственный корень:
. Значит, этот случай нам подходит.
При уравнение является квадратным, поэтому оно будет иметь единственный корень, если его дискриминант равен нулю:
Последнее квадратное уравнение имеет два различных корня и
,так как его дискриминант положителен:
Причём, во-первых, прямой подстановкой можно убедиться, что ни один из этих корней не равен , а во-вторых, по теореме Виета сумма этих корней равна
.
Итак, сумма всех значений, при которых исходное уравнение имеет единственное решение равна .
Правильный ответ: 4.
Вторая часть теста в лицей ВШЭ
В данном разделе представлен разбор типовых заданий второй части вступительного комплексного теста по математике в лицей ВШЭ за 2018 год. Задания не являются точной копией тех, которые были на самом вступительном экзамене, но они составлены таким образом, чтобы полностью соответствовать заданиям второй части реального комплексного теста, который сдавали абитуриенты лицея в 2018 году. Так что если вы зададитесь целью решить из самостоятельно, то вы как бы окажитесь на самом вступительном экзамене в лицей ВШЭ. Проверьте свои знания!
Выражения, стоящие под каждым корнем в знаменателе, должны быть больше или равны нулю, но не должны обращаться в нуль одновременно (то есть при одном и том же значении ), так как в знаменателе не должно находиться нуля. Поэтому искомое множество значений задаётся следующей системой неравенств:
Умножим обе части второго неравенства системы на . В результате знак неравенства изменится на обратный, так как умножаем на отрицательное число:
Решим сперва каждое неравенство по отдельности:
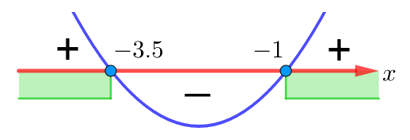
1) Корни уравнения равны
и
. Наносим полученные корни на числовую прямую. Соответствующие точки будут закрашены, так как неравенство нестрогое. Далее определяем знаки на каждом промежутке:
Ответ к первому неравенству: .
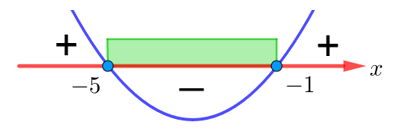
2) Корни уравнения равны
и
. Наносим полученные корни на числовую прямую. Соответствующие точки будут закрашены, так как неравенство нестрогое. Далее определяем знаки на каждом промежутке:
Ответ ко второму неравенству: .
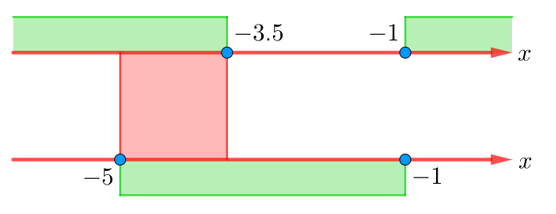
Для наглядности изобразим полученные решения одно под другим:
Видно, что пересечением всех трёх множеств является множество . Однако, оба выражения
и
обращаются в нуль при
, и знаменатель исходной дроби становится равным нулю, то есть выражение теряет смысл. Поэтому данное число нужно исключить из окончательного ответа.
Ответ:
Задание 2. Алёша положил в банк 8000 рублей. Проценты по вкладу начислялись в конце каждого года и прибавлялись к текущей сумме вклада. В конце второго года после выплаты процентов сумма на вкладе составила 9680 рублей. Каков был годовой процент по вкладу, если Алёша не проводили никаких дополнительных операций по вкладу в течение всего срока его действия?
И вновь задание, связанное с процентами. Это обычная практика для теста в лицей ВШЭ. Рассмотрим решение этого задания.
Пусть годовой процент по вкладу составлял процентов. Тогда в конце первого года после выплаты процентов сумма на вкладе составила в рублях:
Аналогично, в конце второго года вклада после выплаты процентов сумма на вкладе составила в рублях:
Поскольку в конце второго года вклада Алёша снял со счёта 9680 руб., то имеет место уравнение:
Поскольку по смыслу задачи , то из последнего равенства получаем, что
и
. Итак, процент по вкладу составлял 10% годовых.
Ответ: 10%
не имеет решений. Для данного значения параметра изобразите на координатной плоскости прямые, задаваемые каждым из уравнений системы, и определите графически расстояние между этими прямыми. В ответе укажите значение параметра и найденное расстояние.
Выразим в обоих уравнениях переменную через переменную
. Для этого обе части первого уравнения системы придётся делить на
, поэтому нужно убедиться, что
. Действительно, при
система принимает вид:
система имеет единственное решение . Этот случай нам не интересен.
Для мы можем поделить обе части первого уравнения системы на
, а обе части второго — на
. В результате после преобразований система примет более удобный вид:
Теперь видно, что система не будет иметь решений при таких значениях параметра , когда коэффициенты перед переменной
в обоих уравнениях окажутся равными, а свободные члены, стоящие справа от знака равенства, напротив, окажутся неравными:
Упростим систему для :
Решаем первое уравнение системы:
Последнее уравнение имеет два корня: и
. Однако, второму условию в системе удовлетворяет только второй корень. Действительно, при подстановке первого корня получаем, что
или
, а при подстановке второго корня получаем, что
или
.
Итак, при система не будет иметь решений. При этом значении параметра система принимает вид:
Изобразим на координатной плоскости прямые, задаваемые каждым из уравнений полученной системы:
Найдём теперь расстояние между этими прямыми. Для этого проведём перпендикуляр от одной прямой к другой и найдём его длину , используя подобие отмеченных на рисунке треугольников:
Гипотенуза большого прямоугольного треугольника равна . Тогда из подобия этих треугольников получаем следующее соотношение:
Ответ: ,
- Докажите, что треугольник BMC равнобедренный.
- Найдите радиус окружности, описанной около треугольника KMC, если AC = 4, BC = 5, AB = 6.
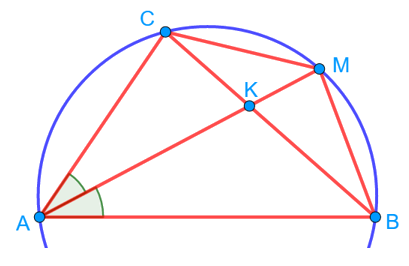
1. Начнём с доказательства. Изобразим ситуацию на рисунке:
Дуги CM и BM равны, так как на них опираются равные вписанные углы. Значит, равны и хорды, стягивающие эти дуги. То есть CM = MB, а значит, треугольник CMB является равнобедренным. Что и требовалось доказать.
2. Найдём теперь радиус окружности, описанной около треугольника KMC:
1) Пусть , тогда
. Используем свойство биссектрисы AK треугольника ABC и получаем следующее равенство:
. Из этого равенства получаем, что
или
.
2) Заметим также, что ∠CMA = ∠CBA = , так оба являются вписанными и опираются на одну дугу AC. Ищем
. Для этого запишем теорему косинусов для треугольника ABC:
3) Поскольку , то угол
— острый. Используя основное тригонометрическое тождество, находим теперь
:
4) Теперь в треугольнике CMK нам известна сторона и синус противолежащего угла
. Значит, мы можем воспользоваться теоремой синусов для нахождения радиуса
описанной около него окружности:
Ответ:
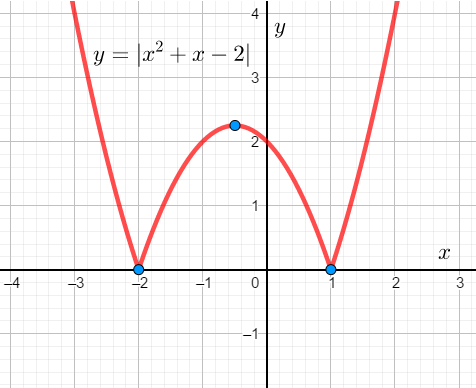
имеет ровно четыре различных решения.
Перепишем уравнение в более удобном виде . Рассмотрим две функции:
и
.
Построим график первой функции. Для этого нужно построить график функции , а затем все точки с отрицательными ординатами, принадлежащие этому графику, отразить относительно оси OX. График получается следующим:
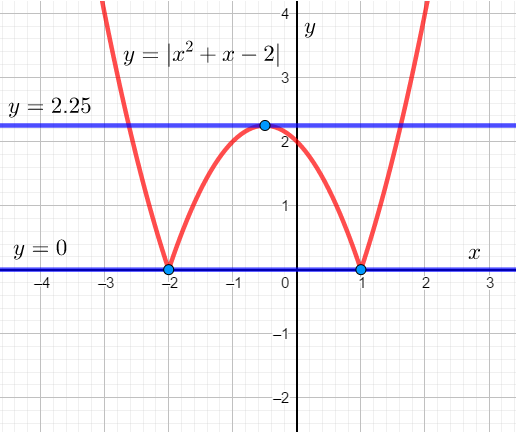
График второй функции представляет собой прямую, параллельную оси OX и перемещающуюся вверх или вниз в зависимости от значения параметра . При этом существует положение этой прямой, при котором она имеет ровно три общие точки с графиком. Уравнение соответствующей прямой имеет вид:
. При перемещении этой прямой «вниз» вплоть до
она будет иметь ровно четыре точки пересечения с построенным графиком:
Значит, искомое множество значений параметра задаётся двойным неравенством:
, то есть
.
Ответ:
Подготовка к тесту в лицей ВШЭ
Если вам требуется подготовка к тесту в лицей ВШЭ по математике, вы можете обратиться за помощью к репетитору в Москве, который занимается такого рода подготовкой на профессиональном уровне и имеет огромный опыт. Контакты репетитора вы найдёте на этой странице. Также вы можете воспользоваться сайтом онлайн-школы CleverFox.info, на котором выложены варианты комплексных тестов, составленные по мотивам экзаменов прошлых лет, а также ответы и подробные решения к каждому заданию теста. Успехов Вам в подготовке к поступлению в лицей НИУ ВШЭ!
Материал подготовил профессиональный репетитор по математике и физике в Москве, Сергей Валерьевич
Примеры вариантов комплексного теста по математике для поступления в 9 и 10 классы лицея НИУ ВШЭ (все направления) с подробным разбором каждого задания от профессионального репетитора.
По структуре примеры тестов полностью соответствуют тестам, доступ к которым открывается по платной подписке. Перед приобретением подписки рекомендуем ознакомиться с данным курсом, чтобы убедиться, что это именно то, что вам нужно.
Доступ к примерам абсолютно бесплатный. Пройдите короткую регистрацию на сайте и получите неограниченный доступ к примерам тестов.
18 типовых вариантов комплексного теста по математике (первая и вторая части) для поступления в 10 класс лицея НИУ ВШЭ (направления «Информатика, инженерия и математика», «Экономика и математика») с подробным разбором каждого задания от профессионального репетитора.
Стоимость доступа к онлайн-тестам| Временной промежуток | Стоимость |
|---|---|
| 30 дней | 1290 руб. |
Для доступа к онлайн-тестам вам нужно зарегистрироваться на сайте и оплатить подписку с помощью сервиса защищённых платежей PayAnyWay. Доступ откроется сразу после подтверждения оплаты.
18 типовых вариантов первой части комплексного теста при поступлении в 10 класс лицея НИУ ВШЭ (задания по математике, все направления) с подробным разбором каждого задания от профессионального репетитора.
Стоимость доступа к онлайн-тестам| Временной промежуток | Стоимость |
|---|---|
| 30 дней | 1290 руб. |
Для доступа к онлайн-тестам вам нужно зарегистрироваться на сайте и оплатить подписку с помощью сервиса защищённых платежей PayAnyWay. Доступ откроется сразу после подтверждения оплаты.
18 типовых вариантов комплексного теста по математике при поступлении в 9 класс лицея НИУ ВШЭ (специализация «Универсальная») с подробным разбором каждого задания от профессионального репетитора.
Стоимость доступа к онлайн-тестам| Временной промежуток | Стоимость |
|---|---|
| 30 дней | 1290 руб. |
Для доступа к онлайн-тестам вам нужно зарегистрироваться на сайте и оплатить подписку с помощью сервиса защищённых платежей PayAnyWay. Доступ откроется сразу после подтверждения оплаты.
|
Вторая часть комплексного теста Задания по МАТЕМАТИКЕ 2019 ДЕМО для направлений «Информатика, инженерия и математика», «Экономика и математика» . Задание 1. Решить уравнение:
Для начала рассмотрим область допустимых значений (ОДЗ)
Задание 2. Две бригады проложили
Задание 3. Найдите все значения
Задание 4. В равнобедренной
Задание 5. Найдите все значения параметра а, при которых система неравенств
Задание 2. Найдите наибольшее натуральное число n,
Ответ. 50. Задание 3. Конькобежцы Иванов, Петров и Сидоров одновременно стартуют из одного и того же
Задание 4. Изобразите множество
Решение первого неравенства — множество точек, попадающих в круг, ограниченный Задание 5. Окружность проходит
Решение: Обозначим расстояние от точки K до прямой CD как KM.
Задание 6. Найдите все значения параметра
Решение: Нетрудно заметить, что при
Из рисунка видно, что для того, чтобы увадратное уравнение имело бы
Александр Анатольевич, репетитор по математике в лицей НИУ ВШЭ.
|

Имею большой опыт работы репетитором. За два десятилетия выработаны собственные методики занятий. Окончил технический ВУЗ – Московский автомобильно-дорожный институт в 1987 г. Ответы на часто задаваемые вопросы |
Общая схема занятия:
1. Входящий контроль
2. Элементы темы
3. Задачи группы А
4. Задачи группы В
5. Задачи группы С
6. Планиметрия
7. Домашняя работа
Календарно-тематический план.
1. Вычисления и числовые закономерности
1. Понятие рационального числа.
2. Обращение бесконечных периодических десятичных дробей в обыкновенные с помощью уравнения.
3. Правило обращения бесконечных периодических дробей в обыкновенные. Понятие рационального числа. Обращение бесконечных периодических десятичных дробей в обыкновенные с помощью уравнения. Правило обращения бесконечных периодических дробей в обыкновенные.
Треугольник Паскаля и его применение (степени двойки, степени числа 11, формулы сокращенного умножения). Последовательность Фибоначчи. Понятие факториала.
2. Проценты
1. Основные типы задач на проценты: процентное отношение двух чисел; процент от числа; число по его проценту.
2. Основные формулы в задачах на проценты: на сколько процентов одно число больше другого; на сколько процентов одно число меньше другого.
3. Понятие «сложных процентов» и формула.
3. Целые выражения. Разложение на множители.
1. Формулы сокращенного умножения (разность квадратов; квадрат суммы и квадрат разности; сумма и разность кубов; куб суммы и куб разности).
2. Способы разложения на множители.
3. Разложение на множители квадратного трехчлена.
4. Квадрат суммы нескольких слагаемых; разность п-х степеней.
4. Дробные выражения.
Самостоятельная работа
5. Арифметический корень и его свойства
1. Определение арифметического квадратного корня и следствия из определения.
2. Свойства арифметического квадратного корня (без доказательства).
5*. Преобразования выражений, содержащих квадратные корни
Свойства арифметического квадратного корня (корень из квадрата; произведение корней).
6. Обобщение материала. Подготовка к контрольной работе
7. Контрольная работа
8. ?
9. Уравнения с модулями
1. Определение модуля выражения с переменной. 2. Равносильные переходы при решении стандартных модульных уравнений.
Геометрия: Элементы прямоугольного треугольника
10. Уравнения, сводящиеся к квадратным уравнениям.
1. Биквадратное уравнение.
2. Однородное алгебраическое уравнение 2-го порядка.
3. Основные методы решения уравнений: замена переменной и разложение на множители.
4. План решения дробно-рационального уравнения.
Геометрия: Пропорциональные отрезки в прямоугольном треугольнике
11. Теоремы Виета
1. Теорема Виета.
2. Теорема, обратная теореме Виета.
3. Основные задачи, связанные с теоремой Виета: нахождение значений симметрических комбинаций; составление квадратного уравнения, корни которого связаны с корнями данного уравнения; анализ знаков корней квадратного уравнения.
Геометрия: Биссектриса треугольника
12. Целые рациональные уравнения.
Самостоятельная работа
Геометрия: Биссектриса треугольника
13. Системы уравнений
1. Основные методы решения систем уравнений.
2. Симметрические системы.
3. Системы, содержащие однородные уравнения.
4. Количество решений системы из двух линейных уравнений с двумя переменными.
Геометрия: Медиана треугольника
14. Обобщение материала. Подготовка к контрольной работе.
15. Контрольная работа
16. Решение текстовых задач
1. Типы задач на движение
2. Позиционная запись числа
3. Делимость
Геометрия: Высота треугольника
17. Функция
Область определения и множество значений.
Четные и нечетные функции. Монотонные функции.
Нули функции.
Обратная функция.
Геометрия: Элементы прямоугольного треугольника
18. Линейная функция
Геометрический смысл коэффициентов.
Условия параллельности и перпендикулярности графиков линейной функции.
Геометрия: теорема косинусов
19. Квадратичная функция
Геометрический смысл коэффициентов.
Основные способы построения эскизов парабол: по точкам, выделение полного квадрата, по нулям функции.
Наименьше и наибольшее значение функции. 6 основных расположений парабол.
Элементарные экономические задачи.
Геометрия: теорема косинусов
20. Графики квадратного корня, степенной и дробно-рациональной функций
Построение графиков вида y = v(x + b), y = v(-x + b). Графики степенных функций с четными и нечетными показателями.
Дробно-рациональная функция.
Алгоритм построения графика.
Геометрия: теорема синусов.
21. Обобщение материала. Подготовка к контрольной работе
22. Контрольная работа
23. Графики функций и уравнений, содержащих модули.
Графики функций вида f(|x|), |f(x)|, |f(|x|)|.
Использование определения модуля при построении графиков.
Кусочно-заданная функция.
Геометрия: окружность и касательные
24. Решение задач с параметрами с использованием графиков функций и графиков уравнений
Геометрия: две касающиеся окружности
25. Линейные и квадратные неравенства
Геометрия: Пропорциональные отрезки и окружность
26. Числовые последовательности; арифметическая и геометрическая прогрессии
Геометрия: Подобие
27. Избранные задачи теории вероятности и статистики
Геометрия: Параллелограмм
28. Задачи на движение и задачи на работу
Геометрия: Трапеция. Трапеции и окружности.
29. Задачи экономического содержания
Геометрия: Площади
Следующие pdf файлы содержат часть этих материалов.
Файл 1.
Методичка 1
Страницы 5 – 46
Занятия 1 — 6, контрольная работа 1, 2 (стр. 45)
Методичка 2
Страницы 4 – 35
Занятия 9 – 14, 16
Методичка 3
Страницы 4 — 46
Занятия 17 – 21, 23, 24, контрольная работа 3 (стр. 43), список литературы (стр. 46)
Файл 2.
Методичка 1 полностью, 2019 год. Есть некоторые отличия от методички из предыдущего файла
Занятия: 1-6, 8
Файл 3.
Методичка 2 без первой страницы
Занятия 9 – 14, 16
C103.
x4 — 2√2 * x3 — x + 2 — √2 = 0
Сначала подбираем корни среди выражений, на которые можно поделить свободный член 2 — √2.
x = √2 — 1 является корнем данного уравнения, поэтому многочлен
p(x) = x4 — 2√2 * x3 — x + 2 — √2
можно нацело поделить на многочлен
q(x) = (x — √2 + 1).
То есть,
x4 — 2√2 * x3 — x + 2 — √2 = (x — √2 + 1) * (x3 + a * x2 + b * x + c).
Раскроем скобки и найдем a, b, c методом неопределенных коэффициентов:
x4 — 2√2 * x3 — x + 2 — √2 = (x — √2 + 1) * (x3 + a * x2 + b * x + c) =
x4 +
(a + 1 — √2) * x3 +
(b + a — a√2) * x2 +
(c + b — b√2) * x +
c * (1 — √2)
a + 1 — √2 = -2√2
b + a — a√2 = 0
c + b — b√2 = -1
c * (1 — √2) = 2 — √2
a = -1 — √2
b = -1
c = -√2
Пособие «Хочу в лицей» периодически продается в магазине БукВышка на Мясницкой:
https://bookshop.hse.ru/
Полезная информация
Задачи из вступительных тестов
Содержание 👉


![Rendered by QuickLaTeX.com [ frac{7}{x+1}+frac{x+4}{2(x-1)}-frac{3x^2-38}{(x-1)(x+1)}=0 ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4986830e00aff72ed2550f46ea5935ef_l3.png)
![Rendered by QuickLaTeX.com [ frac{14(x-1)+(x+4)(x+1)-2(3x^2-38)}{2(x-1)(x+1)}=0 ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7a051f4fca8bb0efa52d47b31180f1f2_l3.png)
![Rendered by QuickLaTeX.com [ frac{5x^2-19x-66}{2(x-1)(x+1)}=0 ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-fd0a98eb2eba321f80de13cd40762271_l3.png)
![Rendered by QuickLaTeX.com [ dfrac{left(dfrac{5}{2}-1,875right):0,125}{(-0,2)^4} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-eff833492c7a6fbd9ada8ea25bfd34c8_l3.png)
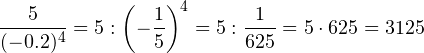
![Rendered by QuickLaTeX.com [ begin{cases} 3x^2-2x-1geqslant 0 \ x-1ne 0 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c26f704691a35d9bf1980f7967ff3641_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} -2=b_1q^{3-1} \ -32=b_1q^{7-1} end{cases}Leftrightarrow begin{cases} -2=b_1q^2 \ -32=b_1q^6 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bb54c2818bbdceecc0039724b12a1a96_l3.png)
![Rendered by QuickLaTeX.com [ dfrac{-32}{-2}=dfrac{b_1q^6}{b_1q^2} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-aa7d5c6c4ccc30bfa963b0e9977d3d3e_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x+y+z=dfrac{1}{8} \ y+z+k=dfrac{3}{20} \ x+y+z+k=dfrac{1}{5} end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b2a25e16b5cbafe867f072a10c94dd63_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x+y+z=dfrac{1}{8} \ y+z+dfrac{3}{40}=dfrac{3}{20} end{cases}Leftrightarrow begin{cases} x+y+z=dfrac{1}{8} \ y+z=dfrac{3}{40} end{cases}]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-d1ce8dc078fa2eebf951c6a3be007f1e_l3.png)
![Rendered by QuickLaTeX.com [ frac{8-x(x-2)-(x+2)^2}{(x-2)(x+2)} = 0 ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e633bc8c59ea9c260cde11e2ea5e5f14_l3.png)
![Rendered by QuickLaTeX.com [ dfrac{-2x^2-2x+4}{(x-2)(x+2)} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-ae003443d25437b621bd27f43522d9e1_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} 2x^2+9x+7geqslant 0 \ -x^2-6x-5geqslant 0 \ sqrt{2x^2+9x+7}+sqrt{-x^2-6x-5}ne 0 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-24ede8e0fafef69bef7f3b69e5162e6a_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} 2x^2+9x+7geqslant 0 \ x^2+6x+5leqslant 0 \ sqrt{2x^2+9x+7}+sqrt{-x^2-6x-5}ne 0 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-29cb48a16d3c427f824a3bf4020a263e_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x-(a-1)y=2 \ (a+2)x+2y=4-a^2 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-cc16b90dafef3fa819271f292dd1375c_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x=2 \ 3x+2y=3 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-943acf6c87cbed2b8c6fc42d36054016_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} y = dfrac{1}{a-1}x-dfrac{2}{a-1} \ y = -dfrac{a+2}{2}x+dfrac{4-a^2}{2} end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3d76693da6018ff6b33e0416a0f114d6_l3.png)
![Rendered by QuickLaTeX.com [begin{cases} dfrac{1}{a-1} = -dfrac{a+2}{2} \ -dfrac{2}{a-1}ne dfrac{4-a^2}{2} end{cases}]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-cd9c90a8ac5335c562d3d27048122c30_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} (a+2)(a-1)=-2\ (a-1)(4-a^2)ne-8 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e474bd4c04b977c3a3515442118046b8_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x+2y=2 \ x+2y=3 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bb96a488f3aa96602d1e83371e02c78d_l3.png)
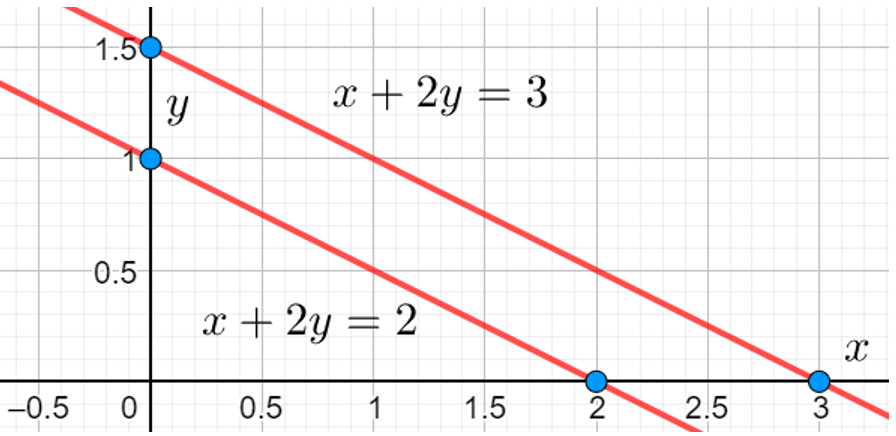
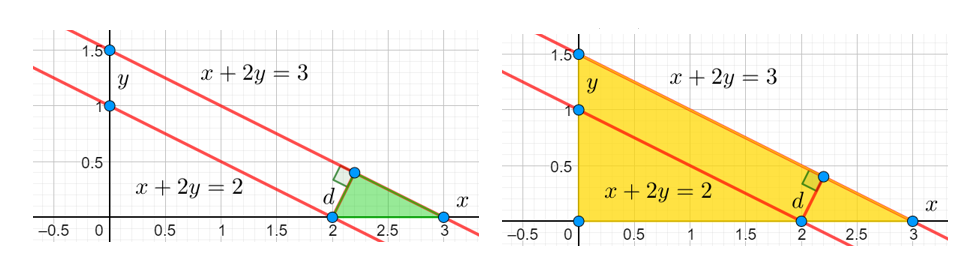
![Rendered by QuickLaTeX.com [ dfrac{d}{1.5}=dfrac{1}{1.5sqrt{5}} Leftrightarrow d = dfrac{sqrt{5}}{5} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b35119561a4ac69be5ccf703f6af2838_l3.png)
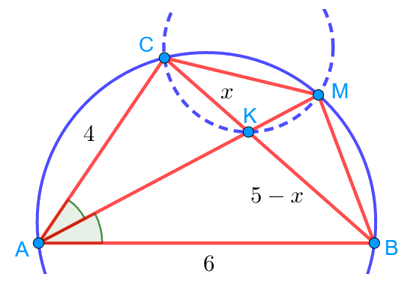
![Rendered by QuickLaTeX.com [ sinbeta = sqrt{1-cos^2beta} = sqrt{1-left(dfrac{3}{4}right)^2} = dfrac{sqrt{7}}{4} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-d693eabc2dfd48257c6927edb72c1e73_l3.png)