Демо вариант Профильного ЕГЭ 2018
2018-02-13
2020-05-24
2018
ЕГЭ 2018
Демоверсия ЕГЭ 2018
Демоверсия базового ЕГЭ по математике 2018
Демоверсия профильного ЕГЭ по математике 2018
Тренировочная работа по математике от 21 сентября 2017
без логарифмов 1, 2; без производной 1, 2; критерии
Тренировочная работа по математике от 21 декабря 2017
база 1, база 2
профиль 1, профиль 2, критерии
Тренировочная работа по математике от 25 января 2018
база 1, база 2
профиль 1, профиль 2
Тренировочная работа по математике от 6 марта 2018
база 1, база 2
профиль 1 (критерии к части С), профиль 2
Тренировочная работа по математике от 18 апреля 2018
база 1, база 2
профиль 1, профиль 2 (ответы 1-19 к вариантам 1, 2)
Досрочный ЕГЭ по математике от 31 марта 2018
Профиль (oтветы, разбор на сайте)
Досрочный ЕГЭ (резервный день) по математике от 11 апреля 2018
задания части С (разбор заданий на сайте)
Реальный ЕГЭ по математике от 1 июня 2018
Вариант I (1-19) –> ответы
Вариант II (часть С) –> ответы
Резервный ЕГЭ по математике от 25 июня 2018
Вариант I (часть С) –> ответы
Вариант II (часть С) –> ответы
Вариант III (часть С) –> ответы

ЕГЭ-2018. Математика (60х84/8) 30 тренировочных вариантов экзаменационных работ для подготовки к единому государственному экзамену. Базовый уровень
Издание содержит 30 тренировочных вариантов экзаменационных работ для подготовки к ЕГЭ. Каждый вариант составлен в полном соответствии с требованиями ЕГЭ, включает задания базового уровня. Структура вариантов едина. В конце пособия даны ответы на все задания.
Купить
Задание 1
Поезд оправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
Решение
Учитывая тот факт, что в сутках 24 часа, и начинается день в 00 часов 00 минут, а заканчивается в 24 часа, то поезд находится в пути 10 минут предыдущего дня и 7 часов 50 минут следующего.
7 ч 50 мин + 10 мин = 8 часов
Ответ: 8.
Задание 2
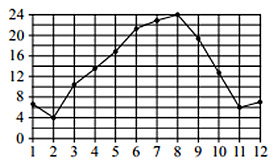
На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 г. По горизонтали указаны номера месяцев; по вертикали – температура в градусах Цельсия. Для наглядности точки соединены линией.
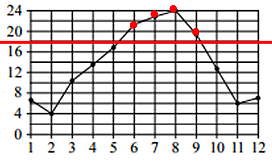
Сколько месяцев средняя температура была выше 18 градусов Цельсия?
Решение
Ответ: 4.
Задание 3
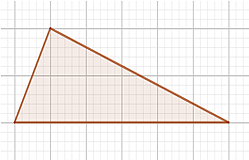
На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник. Найдите его площадь.
Решение
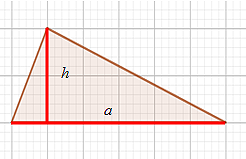
где h – высота, a – сторона, к которой высота проведена.
| S∆ = | 1 | ha = | 1 | · 2 · 6 = 6 |
| 2 | 2 |
Ответ: 6.
Задание 4
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
Решение
Вероятностью события А называется отношение числа благоприятных для А исходов к числу всех равновозможных исходов:
где n – общее число равновозможных исходов, m – число исходов, благоприятствующих событию А.
Всего 25 билетов, значит всего исходов – 25.
Благоприятных исходов – 2.
| Вероятность = | 2 | = 0,08 |
| 25 |
Ответ: 0,08.
Смотрите также: Разбор заданий ЕГЭ-2018 по математике (профильный уровень)

ЕГЭ. Математика. Новый полный справочник школьника для подготовки к ЕГЭ
Справочник включает все темы школьного курса и соответствует современным образовательным стандартам и программам. Книга состоит из двух частей: «Алгебра и начала анализа» и «Геометрия». Основной материал школьного курса математики изложен авторами сжато и системно: математические понятия, аксиомы, теоремы, свойства и т.д. Книга будет незаменимым помощником при изучении и закреплении нового материала, повторении пройденных тем, а также при подготовке к выпускным экзаменам в форме ЕГЭ.
Купить
Задание 5
Найдите корень уравнения 3x – 5 = 81.
Решение
3x – 5 = 81
3x – 5 = 34
x – 5 = 4
x = 9
Ответ: 9.
Задание 6
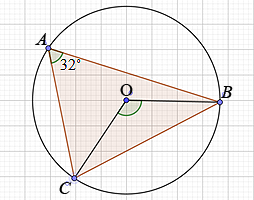
Треугольник ABC вписан в окружность с центром О. Угол BAC равен 32°. Найдите угол BOC. Ответ дайте в градусах.
Решение
∠COB – центральный угол, ∠COB = дуге CB
| ∠CАB – вписанный угол, ∠CАB = | 1 | дугиCB |
| 2 |
∠COB = 64°
Ответ: 64.
Смотрите также: Вебинар «Подготовка к математике. базовый уровень» состоится 2 апреля
Задание 7
На рисунке изображен график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, … , x9.
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
Решение
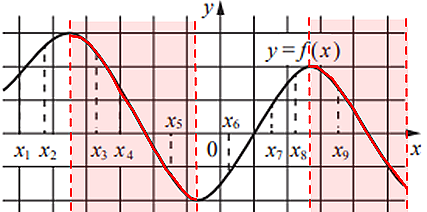
Производная функции отрицательна там, где функция убывает.
В данные промежутки попадают точки x3, x4, x5, x9. Всего 4 точки.
Ответ: 4.

Алгебра в таблицах. 7-11 классы. Справочное пособие
Пособие будет полезно учащимся 7-11 классов, абитуриентам, студентам, учителям и родителям.
Купить
Задание 8
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ выразите в см.
Решение
Формула для вычисления объема цилиндра:
V = πR2H,
где R – радиус цилиндра, H – его высота.
Т.к. уровень жидкости достигает 16 см, значит высота равна 16.
V = πR2H = πR216
Диаметр второго сосуда в два раза больше диаметра первого.
Т.к. d = 2R, тогда радиус второго сосуда также в два раза больше радиуса первого, и равен 2R.
h – высота жидкости во втором сосуде.
Найдем объем жидкости во втором сосуде:
V = π(2R)2h = π4R2h
При переливании жидкости в другой сосуд, ее объем не изменился.
Приравняем объемы жидкости первого и второго сосудов:
πR216 = π4R2h
4h = 16.
h = 4.
Ответ: 4 см.
Задание 9
Найдите sin2α, если cosα = 0,6 и π < α < 2π.
Решение
sin2α = 2sinα · cosα
(sinα)2 + (cosα)2 = 1
(sinα)2 + (0,6)2 = 1
(sinα)2 = 1 – 0,36
(sinα)2 = 0,64
(sinα)2 = ±0,8
Т.к. α ∈ 3 или 4 четверти, значит
sinα = –0,8
sin2α = 2 · (–0,8) · (0,6)
sin2α = –0,96
Ответ: –0,96.
Задание 10
Локатор батискафа, равномерно погружающего вертикально вниз, испускает ультразвуковые сигналы частотой 749 МГц. Приемник регистрирует частоту сигнала, отраженного от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
где c = 1500 м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отраженного сигнала (в МГц). Найдите частоту отраженного сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Решение
Из условия следует, что
v = 2 м/с
с = 1500 м/с
f0 = 749 МГц
Подставим эти данные в формулу
| Подставим эти данные в формулу v = c | f – f0 |
| f + f0 |
| 2 = 1500 · | f – 749 |
| f + 749 |
f + 749 = 750 · (f – 749)
f + 749 = 750f – 750 · 749
f – 750f = –750 · 749 – 749
–749f = –749(750 + 1)
Ответ: 751.

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Учебник
Учебник входит в УМК по математике для 10-11 классов, изучающих предмет на базовом уровне. Теоретический материал разделен на обязательный и дополнительный, система заданий дифференцирована по уровню сложности, каждый пункт главы завершается контрольными вопросами и заданиями, а каждая глава — домашней контрольной работой. В учебник включены темы проектов и сделаны ссылки на интернет-ресурсы.
Купить
Задание 11
Весной катер идет против течения реки в 12/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идет против течения в 1½ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Решение
|
Весна |
Лето |
|
|
Собственная скорость катера |
x (км/ч) |
|
|
Скорость реки |
y (км/ч) |
y – 1 (км/ч) |
|
По течению |
x + y (км/ч) |
x + y – 1 |
|
Против течения |
x – y (км/ч) |
x – y + 1 |
Т.к. весной катер идет против течения медленнее, чем по течению, составим уравнение
Летом катер идет против течения медленнее, чем по течению в 1½, тогда имеем уравнение:
| x + y – 1 | = 1 | 1 |
| x – y + 1 | 2 |
Составим систему:
 |
x + y | = | 5 |
| x – y | 3 | ||
| x + y – 1 | = | 3 | |
| x – y + 1 | 2 |
 |
3(x + y) = 5(x – y) |
| 2(x + y – 1) = 3(x – y + 1) |
 |
2x = 8y |
| x = 5y – 5 |
 |
x = 20 |
| y = 5 |
5 км/ч – скорость течения весной.
Ответ: 5.

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Базовый уровень
Учебник входит в УМК по математике для 10-11 классов, изучающих предмет на базовом уровне. Теоретический материал разделен на обязательный и дополнительный, система заданий дифференцирована по уровню сложности, каждый пункт главы завершается контрольными вопросами и заданиями, а каждая глава — домашней контрольной работой. В учебник включены темы проектов и сделаны ссылки на интернет-ресурсы.
Купить
Задание 12
Найдите точку максимума функции y = ln(x + 4)2 + 2x + 7.
Решение
Учитывая, что ln(x + 4)2 = 2ln │x + 4│ имеем:
| y = |  |
2ln(x + 4) + 2x + 7, | x > –4 |
| 2ln(–x – 4) + 2x + 7, | x < –4 |
| (lnf(x))′ = | 1 | · (f(x))′ |
| f(x) |
| y′ = |  |
2 | + 2, | x > –4 |
| x + 4 | ||||
| 2 | · (–x –4)′ + 2, | x < –4 | ||
| –x – 4 |
| y′ = |  |
2 | + 2, | x > –4 |
| x + 4 | ||||
| 2 | + 2, | x < –4 | ||
| x + 4 |
Найдем критические точки функции (точки, в которых производная либо равна нулю, либо не существует), для этого приравняем y′ к 0.
y′ = 0.
 |
x = –5 |
| x ≠ –4 |
На промежутке (–4; ∞) производная положительна, критических точек нет.
На промежутке (–∞; –4) в точке –5 производная меняет свой знак с «+» на «–», значит точка х = –5 является точкой максимума функции.
Ответ: –5.
Задание 13
| а) Решить уравнение cos2x = 1 – cos( | π | – x) |
| 2 |
б) Найдите все корни этого уравнения, принадлежащие промежутку  – – |
5π | ; – π). |
| 2 |
Решение
Преобразуем левую и правую части уравнения:
cos2x = 1 – 2sin2x (формула двойного угла для косинуса)
| cos( | π | – x) = sinx (формула приведения) |
| 2 |
1 – 2sin2x = 1 – sinx
2sin2x – sinx = 0
sinx(2sinx – 1)= 0
 |
sinx = 0 |
| 2sinx = 1 |
 |
x = πn, | n ∈ Ζ | |
| x = | π | + 2πn, | n ∈ Ζ |
| 6 | |||
| x = | 5π | + 2πn, | n ∈ Ζ |
| 6 |
Б) Найдем корни, принадлежащие данному промежутку  – – |
5π | ; – π) |
| 2 |
с помощью тригонометрического круга.
| Получили корни | –7π | ; | –11π | ; 2π |
| 6 | 6 |
| Ответ: а) | π | + 2πn, n ϵ Ζ; | 5π | + 2πn, n ϵ Ζ; πn, n ϵ Ζ; | ||
| 6 | 6 | |||||
| б) | –7π | ; | –11π | ; 2π. | ||
| 6 | 6 |

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Базовый уровень. Методическое пособие
Методическое пособие «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Базовый уровень» входит в систему «Вертикаль» и соответствует ФГОС.
Купить
Задание 14
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Решение
1) Проведем высоту NB1 в ∆A1B1C1. BN1 = √B1C12 – NC12 = √62 – 32 = 3√3
2) ∆NB1B – прямоугольный с прямым ∠BB1N.
3) Из ∆NB1N по теореме Пифагора: NB2 = NB12 + BB12 = 62 + (3√3)2 = 63.
4) Из прямоугольного ∆MAB по теореме Пифагора: MB2 = MA2 + BA2 = 62 + 32 = 45.
5) Из прямоугольного ∆MA1Nпо теореме Пифагора: NM2 = NA12 + MA12 = 32 + 32 = 18.
6) Рассмотрим ∆MNB:
NB2 = NM2 + MB2
63 = 45 + 18
Тогда по теореме обратной теореме Пифагора получаем, что ∆MNB прямоугольный, с прямым ∠BMN. Значит BM ⊥ MN. Ч.т.д.
Б)
1) Проведем NK ⊥ A1B1.
2) NK ⊥ A1B1, NK ⊥ A1A, значит NK ⊥ (A1B1B)
3) NK перпендикуляр к плоскости, NM – наклонная, KM – проекция наклонной NM на плоскость (A1B1B). По теореме обратной теореме о трех перпендикулярах имеем:
| BM ⊥ MN |  |
BM ⊥ KM |
| BM ⊥ NK |
Тогда ∠KMN линейный угол искомого двугранного угла.
Из прямоугольного ∆NA1K:
MN = 3√2
Т.к. NK ⊥ (A1B1B), а MK ∈ (A1B1B), NK ⊥ MK и ∆MNK прямоугольный.
Задание 15
Решите неравенство:
| 9x – 2 · 3x + 1 + 4 | + | 2 · 3x + 1 – 51 | ≤ 3x + 5 |
| 3x – 5 | 3x – 9 |
Решение
Пусть 3x = y, 9x = y2
| y2 – 6y + 4 | + | 6y – 51 | ≤ y + 5 |
| y – 5 | y – 9 |
| y2 – 6y + 5 – 1 | + | 6y – 54 + 3 | ≤ y + 5 |
| y – 5 | y – 9 |
| y2 – 6y + 5 | – | 1 | + | 6y – 54 | + | 3 | ≤ y + 5 |
| y – 5 | y – 5 | y – 9 | y – 9 |
Разложим трехчлен y2 – 6y + 5 на множители
y2 – 6y + 5 = 0
D = (–6)2 – 4 · 1 · 5 = 16
y2 – 6y + 5 = (y – 5)(y – 1)
| (y – 5)(y – 1) | – | 1 | + | 6(y – 9) | + | 3 | ≤ y + 5 |
| y – 5 | y – 5 | y – 9 | y – 9 |
| y – 1 – | 1 | + 6 + | 3 | ≤ y + 5 |
| y – 5 | y – 9 |
| y – | 1 | + 5 + | 3 | ≤ y + 5 |
| y – 5 | y – 9 |
| – | 1 | + | 3 | ≤ 0 |
| y – 5 | y – 9 |
| –1(y – 9) + 3(y – 5) | ≤ 0 |
| (y – 5)(y – 9) |
| –y + 9 + 3y – 15 | ≤ 0 |
| (y – 5)(y – 9) |
| 2y – 6 | ≤ 0 |
| (y – 5)(y – 9) |
 |
3 ≤ 3x |
| 5 < 3x < 9 |
 |
1 ≤ x |
| log35 < x < 2 |
Ответ: (–∞; 1] ∪ (log35; 2)

ЕГЭ. Математика. Большой сборник тематических заданий для подготовки к единому государственному экзамену. Базовый уровень
В сборник включены задания по всем разделам и темам, проверяемым на едином государственном экзамене базового уровня. Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ЕГЭ. Они помогут учителю организовать подготовку к единому государственному экзамену по математике базового уровня, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
Задание 16
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке С.
а) докажите, что прямые AD и BC параллельны.
б) найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решение
- Проведем общую касательную к окружностям в точке K. Она пересекает AB в точке H.
- AH = HK, HK = HB (по свойству касательных, проведенных из одной точке к окружности)
- В ∆AKB, медиана KH равна половине стороны AB, значит он прямоугольный, с ∠AKB = 90°.
- ∠AKB = ∠AKD = 90° (как смежные), значит ∠AKD опирается на диаметр AD. Тогда AD ⊥ AB.
- ∠AKB = ∠CKB = 90° (как смежные), значит ∠BKCопирается на диаметр BC. Тогда BC ⊥ AB.
- ледовательно AD || BC.
б) Пусть R = 4 радиус первой окружности с центром O1, а r = 1 – радиус второй окружности с центром O2.
1) Рассмотрим ∆СKB и ∆AKD: углы при вершине K прямые, ∠DAK = ∠ACB, как накрест лежащие при AD || BC и секущей AC. Значит ∆СKB ~ ∆AKD по двум углам.
| 2) | AK | = | KD | = | AD | = | 2R | = | 4 | = k |
| KC | BK | BC | 2r | 1 |
3) Отношение площадей подобных треугольников равно k2 (k – коэффициент подобия)
| SAKD | = 16, SAKD = 16SBKC |
| SBKC |
4) ∆AKB и ∆AKD имеют общую высоту AK, значит их площади относятся, как основания, к которым эта высота проведена.
| 5) | SAKD | = | DK | = | AD | = | 4 | , SBKA= | 1 | SAKD = | 1 | · 16SBKC = 4SBKC |
| SBKA | KB | BC | 1 | 4 | 4 |
6) ∆DCK и ∆CKB имеют общую высоту CK, значит их площади относятся, как основания, к которым эта высота проведена.
| SDKC | = | DK | = | 4 | , SDKC = 4SBKC |
| SBKC | KB | 1 |
7) Найдем площадь трапеции ABCD:
SABCD = SDKA + SAKB + SCKB + SDCK
SABCD = 16SBKC + 4SCKB + SCKB + 4SCKB
SABCD = 25SCKB

9) Из прямоугольного ∆O2SO1 по теореме Пифагора найдем O2S:
O2S = √(O2O1)2 – (O1S)2
O2S = √52 – 32 = 4
O2S = AB = 4
SABCD = 25SCKB
20= 25SCKB
SCKB = 0,8
SBKA = 4SBKC = 4 · 0,8 = 3,2.
Ответ: 3,2.

Математика. 5-11 классы. Программа
Представленные программы по курсам «Математика» для 5–6 классов, «Алгебра» и «Геометрия» для 7–9 классов, «Математика: Алгебра и начала математического анализа; Геометрия» для 10-11 классов общеобразовательных учреждений созданы на основе единой концепции преподавания математики в средней школе, разработанной А.Г. Мерзляком, В.Б. Полонским и М.С. Якиром.
Купить
Задание 17
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
- 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
Решение
Долг перед банком (в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля по следующей схеме:
1; 0,6; 0,4; 0,3; 0,2; 0,1; 0.
Тогда долг на 1-е число каждого месяца (вместе с процентами) равен:
| 1 + 1 · | r | ; 0,6 + 0,6 · | r | ; 0,4 + 0,4 · | r | ; 0,3 + 0,3 · | r | ; 0,2 + 0,2 · | r | ; 0,1 + 0,1 · | r | ; |
| 100 | 100 | 100 | 100 | 100 | 100 |
| 1 · | r | ; 0,6(1 + | r | ); 0,4(1 + | r | ); 0,3(1 + | r | ); 0,2(1 + | r | ); 0,1(1 + | r | ) |
| 100 | 100 | 100 | 100 | 100 | 100 |
Выплаты со 2-го по 14-е число каждого месяца составляют:
| 1 · (1 + | r | – 0,6; 0,6 · (1 + | r | – 0,4; 0,4 · (1 + | r | – 0,3; |
| 100 | 100 | 100 |
| 0,3 · (1 + | r | – 0,2; 0,2 · (1 + | r | – 0,1; 0,1 · (1 + | r | ) |
| 100 | 100 | 100 |
Общая сумма выплат составляет:
| 1 · (1 + | r | – 0,6 +0,6 · (1 + | r | – 0,4 + 0,4 · (1 + | r | – 0,3 + |
| 100 | 100 | 100 |
| + 0,3 · (1 + | r | – 0,2 + 0,2 · (1 + | r | – 0,1 + 0,1 · (1 + | r | ) = |
| 100 | 100 | 100 |
| = 1 · (1 + | r | + 0,6 · (1 + | r | + 0,4 · (1 + | r | + 0,3 · (1 + | r | + |
| 100 | 100 | 100 | 100 |
| + 0,2 · (1 + | r | + 0,1 · (1 + | r | ) – 0,6 – 0,4 – 0,3 – 0,2 – 0,1 = |
| 100 | 100 |
| = (1 + | r | ) (1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) – (0,6 + 0,4 + 0,3 + 0,2 + 0,1) = 2,6(1 + | r | ) – 1,6. |
| 100 | 100 |
По условию, общая сумма выплат будет меньше 1,2 млн рублей, тогда
| 2,6(1 + | r | ) – 1,6 < 1,2 |
| 100 |
Наибольшее целое r = 7.
Ответ: 7.
Задание 18
Найдите все положительные значения а, при каждом из которых система
 |
(|x| – 5)2 + (y – 4)2 = 9, |
| (x + 2)2 + y2 = a2. |
Имеет единственное решение.
Решение
Рассмотрим первое уравнение системы:
1) При x ≥ 0, имеем уравнение (x – 5)2 + (y – 4)2 = 9, это уравнение задает окружность d с центром в точке G(5; 4) и радиусом 3.
2)При x ≤ 0, имеем уравнение (–x – 5)2 + (y – 4)2 = 9, (x + 5)2 + (y – 4)2 = 9, это уравнение задает окружность с с центром в точке F(–5; 4) и радиусом 3.
3) Уравнение (x + 2)2 + y2 = a2 задает окружность kс центром в точке H(–2; 0) и радиусом a, где a > 0.
Найдем при каких значениях а окружность k имеет единственную общую точку с окружностями d и c.
4) Проведем из точки H луч HG, он пресекает окружность d в точках O и P, точка О лежит между точками H и G. Расстояние между точками найдем по формуле |HG|= √(xG – xH)2 + (yG – yH)2
|HG|= √(5 + 2)2 + (4 – 0)2 = √65
HG = GO + OH
OH = HG – GO = √65 – 3
HP = √65 + 3
Если а < HO или a > HP окружности d и k не пересекаются.
Если HO < a < HP, то окружности d и k имеют две общие точки.
При a = HOилиa = HPокружности d и k касаются друг друга в одной точке.
5) Проведем луч HF из точки H, он пересекает окружность cв точках M и N, при этом M лежит между H и F. Найдем расстояние между точками HF,
|HF| = √(–5 + 2)2 + 42 = 5
HM = 5 – 3 = 2
HN = 5 + 3 = 8
Если а < HM или a > HN окружности c и k не пересекаются.
Если HM < a < HN, то окружности c и k имеют две общие точки.
При a = HM или a = HN окружности c и k касаются друг друга в одной точке.
Система имеет единственное решение тогда и только тогда, когда окружность kкасается ровно одной из двух окружностей d и cи не пересекается с другой.
Из решения видно, что HM < HO < HN < HP.
Тогда условию задачи удовлетворяют длины отрезков HO = √65 + 3 и HM = 2.
Ответ: √65 + 3; 2.
Задание 19
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно –3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно –8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение
А) Пусть среди написанных чисел
x – положительных
y – отрицательных
z – нулей
| Среднее арифметическое чисел = | сумма чисел |
| количество чисел |
Тогда имеем, что
- сумма положительных чисел равна 4x
- сумма отрицательных чисел равна –8y
- сумма всех чисел ряда 4x + (–8y) + 0z = –3(x + y + z)
4(x – 2y + 0z) = –3(x + y + z)
Т.к. левая часть равенства кратна 4, то и правая часть равенства должна быть кратна 4, значит
x + y + z (количество чисел) кратно 4.
40 < x + y + z < 48,
x + y + z = 44
Значит на доске написано 44 числа.
Б) Рассмотрим равенство 4x + (–8y) + 0z = –3(x + y + z)
4x – 8y = – 3x – 3y – 3z
4x + 3x + 3z = 8y – 3y
7x + 3z = 5y
Отсюда получаем, т.к. z ≥ 0 (количество нулей в ряду)
7x < 5y
x < y
Значит положительных чисел меньше, чем отрицательных.
В) Т.к. x + y + z = 44,подставим это значение в равенство 4x + (–8y) + 0z = –3(x + y + z),
получим
4x – 8y = (–3 · 44)/4
x – 2y = –33
x = 2y – 33
Учитывая, что x + y + z = 44, имеем x + y ≤ 44, подставим x = 2y – 33 в данное неравенство
2y – 33 +y ≤ 44
3y ≤ 77
y ≤ 25, учитывая, что x = 2y – 33 получаем x ≤ 17.
Тогда положительных чисел не больше 17.
Ответ: а) 44; б) отрицательных; в) 17.

ЕГЭ-2018. Математика (60х90/16) 10 тренировочных вариантов экзаменационных работ для подготовки к единому государственному экзамену. Профильный уровень
Издание содержит 10 тренировочных вариантов экзаменационных работ для подготовки к ЕГЭ. Каждый вариант составлен в полном соответствии с требованиями ЕГЭ, включает задания профильного уровня. Структура вариантов едина. В конце пособия даны ответы на все задания.
Купить

В демонстрационном варианте представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию будет предложено только одно задание.
Задания демонстрационного варианта не отражают всех вопросов содержания, которые могут быть включены в контрольные измерительные материалы в 2018 г.
Экзаменационная работа включает в себя 20 заданий.
На выполнение работы отводится 3 часа (180 минут).
Ответы к заданиям записываются по приведённым ниже образцам в виде числа или последовательности цифр. Сначала запишите ответы
к заданиям в поле ответа в тексте работы, а затем перенесите их в бланк ответов № 1 справа от номера соответствующего задания.
Если ответом является последовательность цифр, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов. Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, или капиллярной, или перьевой ручек. При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Условия задач
Часть 1
- Найдите значение выражения
или
Найдите значение выражения - Найдите значение выражения
или
Найдите значение выражения - Ивану Кузьмичу начислена заработная плата 20 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13%. Сколько рублей он получит после уплаты подоходного налога?
или
ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике? - Найдите
из равенства
, если
и
.
или
Найдитеиз равенства
, если
,
и
.
или
Найдитеиз равенства
, если
и
.
- Найдите
, если
и
или
Найдите значение выражения
или
Найдите значение выражения - Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?
или
Килограмм моркови стоит 40 рублей. Олег купил 1 кг 600 г моркови. Сколько рублей сдачи он должен получить со 100 рублей?
или
Для ремонта требуется 63 рулона обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 6 рулонов? - Найдите корень уравнения
.
или
Найдите корень уравнения.
или
Найдите отрицательный корень уравненияКак решать квадратные уравнения?
- Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
или
Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
или
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах. - Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Величины:
А) рост ребенка
Б) толщина листа бумаги
В) протяженность автобусного маршрута
Г) высота жилого дома
Значения:
1) 32 км
2) 30 м
3) 0,2 мм
4) 110 см
или
Величины:
А) масса взрослого человека
Б) масса грузового автомобиля
В) масса книги
Г) масса пуговицы
Значения:
1) 8 т
2) 5 г
3) 65 кг
4) 300 г - В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.
или
Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной? - На диаграмме приведены данные о длине восьми крупнейших рек России (в тысячах километров). Первое место по длине занимает река Лена. На каком месте по длине находится река Амур?
или
В таблице показано распределение медалей на XXII Зимних Олимпийских играх в Сочи среди команд, занявших первые 10 мест по количеству золотых медалей. Определите с помощью таблицы, сколько серебряных медалей у команды, занявшей второе место по числу золотых медалей.или
На графике показано изменение температуры воздуха на протяжении трёх суток. На горизонтальной оси отмечается число, месяц, время суток в часах; на вертикальной оси — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия. - Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице. Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день.
В ответе укажите какой-нибудь один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.
или
Турист подбирает экскурсии. Сведения об экскурсиях представлены в таблице. Пользуясь таблицей, подберите набор экскурсий так, чтобы турист посетил четыре объекта: крепость, загородный дворец, парк и музей живописи, а суммарная стоимость экскурсий не превышала 650 рублей.
В ответе укажите какой-нибудь один набор номеров экскурсий без пробелов, запятых и других дополнительных символов.
или
Строительная фирма планирует купить 70 м3 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой? - Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в четыре раза больше, чем у данного? Ответ дайте в сантиметрах.
или
От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)? - На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси — температура двигателя в градусах Цельсия. Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
или
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
Точки Значения производной A 1) -4 B 2) 3 C 3) 3/2 D 4) — 1/2 - В треугольнике ABC угол ACB равен 90o, cos A = 0,8, AC = 4. Отрезок CH — высота треугольника ABC (см. рисунок). Найдите длину отрезка.
- Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
или
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно.
- На координатной прямой отмечены точки A, B, C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
или
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями. - В классе учится 20 человек, из них 13 человек посещают кружок по истории,
а 10 — кружок по математике. Выберите утверждения, которые верны
при указанных условиях.
1) Каждый ученик этого класса посещает оба кружка.
2) Найдутся хотя бы двое из этого класса, кто посещает оба кружка.
3) Если ученик из этого класса ходит на кружок по истории, то он
обязательно ходит на кружок по математике.
4) Не найдётся 11 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
или
Витя выше Коли, но ниже Маши. Аня не выше Вити. Выберите утверждения,
которые верны при указанных условиях.
1) Маша самая высокая из указанных четырёх человек.
2) Аня и Маша одного роста.
3) Витя и Коля одного роста.
4) Коля ниже Маши.
В ответе запишите номера выбранных утверждений без пробелов, запятых
и других дополнительных символов. - Найдите трёхзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
- В обменном пункте можно совершить одну из двух операций:
— за 2 золотых монеты получить 3 серебряных и одну медную;
— за 5 серебряных монет получить 3 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
или
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами.
Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.Система оценивания экзаменационной работы по математике (базовый уровень)Правильное решение каждого из заданий 1–20 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби, или последовательности цифр
смотрите также Досрочный ЕГЭ по математике 2015
Ответы
| Задание | Пример 1 | Пример 2 | Пример 3 |
| 1 | 8,4 | 3,2 | |
| 2 | 40 | 54 | |
| 3 | 17400 | 50 | |
| 4 | 7 | 6 | 8 |
| 5 | -0,6 | 51 | 30 |
| 6 | 6 | 36 | 11 |
| 7 | 7 | 67 | -2 |
| 8 | 135 | 120 | 12 |
| 9 | 4312 | 3142 | |
| 10 | 0,2 | 0,97 | |
| 11 | 7 | 5 | -3 |
| 12 | 135; 153; 315; 351; 513; 531; 256; 265; 526; 562; 625; 652 | 14; 41 | 192000 |
| 13 | 5 | 14 | |
| 14 | 4132 | 2143 | |
| 15 | 3,2 | ||
| 16 | 180 | 16 | |
| 17 | 4213 | 4321 | |
| 18 | 24; 42 | 14; 41 | |
| 19 | 578; 587; 758; 785; 857; 875 | ||
| 20 | 10 | 12 |
В этом разделе сайта расположены демонстрационные версии ЕГЭ 2018 по всем предметам: русскому языку, математике, биологии, химии, географии, истории, информатике, литературе, физике, обществознанию, иностранным языкам – английскому, французскому, немецкому, испанскому.
Эти варианты ЕГЭ были специально разработаны для подготовки к выпускным экзаменам в 11-м классе и одобрены Федеральным институтом педагогических измерений (ФИПИ).
Вы можете посмотреть онлайн или скачать файлы с заданиями (см. ниже), а также пройти демонстрационные тесты ЕГЭ онлайн.
Ответы к задачам для каждого предмета находятся на последних страницах документов в формате PDF. Не подглядывайте раньше времени.
Демонстрационные варианты ЕГЭ
Демоверсии КИМ ЕГЭ 2018 г., утвержденные Федеральным институтом педагогических измерений (ФИПИ).
|
Русский язык |
Математика базовый |
|
Математика профильный |
Обществознание |
|
История |
Биология |
|
Химия |
География |
|
Информатика |
Физика |
|
Литература |
Иностранные языки
Важная информация: каждый год задания на ЕГЭ меняются, вот актуальная информация о нововведениях.
К списку вопросов о ЕГЭ>>
Другие записи
02.09.2016.
Демонстрационные варианты ЕГЭ 2016
Официальные демонстрационные варианты ЕГЭ за 2016 год. Это лучшая возможность потренироваться в решении заданий и проверить свои знания на практике.
Вы можете как скачать файлы в формате PDF, так и пройти…
10.06.2016.
Тренировочные варианты ЕГЭ (Досрочный этап 2015 года)
Хотите порешать реальные задания ЕГЭ? Мы собрали для вас несколько экзаменационных вариантов ЕГЭ, которые были на досрочной сдаче госэкзаменов в 2015 году.
Проверьте свои знания: просто скачайте тест…
10.06.2016.
Демонстрационные варианты ЕГЭ 2011
Официальные демонстрационные варианты ЕГЭ за 2011 год. Это лучшая возможность потренироваться в решении заданий и проверить свои знания на практике.
Вы можете как скачать файлы в формате PDF, так и пройти…
10.06.2016.
Демонстрационные варианты ЕГЭ 2010
Официальные демонстрационные варианты ЕГЭ за 2010 год. Это лучшая возможность потренироваться в решении заданий и проверить свои знания на практике.
Вы можете как скачать файлы в формате PDF, так и пройти…
10.06.2016.
Демонстрационные варианты ЕГЭ 2008
Официальные демонстрационные варианты ЕГЭ за 2008 год. Это лучшая возможность потренироваться в решении заданий и проверить свои знания на практике.
Вы можете как скачать файлы в формате PDF, так и пройти…
Единый государственный экзамен по математике. Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2018 года по математике (профильный уровень) подготовлен Федеральным государственным бюджетным научным учреждением «Федеральный институт педагогических измерений» (ФИПИ)
13. а) Решите уравнение $cos 2x = 1 — cosleft(dfrac{pi}{2} — xright)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $left[ -dfrac{5pi}{2}; -pi right)$.
14. Все рёбра правильной треугольной призмы $ABCA_1B_1C_1$ имеют длину 6. Точки $M$ и $N$ — середины рёбер $AA_1$ и $A_1C_1$ соответственно.
а) Докажите, что прямые $BM$ и $MN$ перпендикулярны.
б) Найдите угол между плоскостями $BMN$ и $ABB_1$.
15. Решите неравенство $dfrac{9^x — 2cdot3^{x+1}+4}{3^x−5} + dfrac{2cdot3^{x+1}−51}{3^x−9} leqslant 3^x+5$.
16. Две окружности касаются внешним образом в точке $K$. Прямая $AB$ касается первой окружности в точке $A$, а второй — $в$ точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что прямые $AD$ и $BC$ параллельны.
б) Найдите площадь треугольника $AKB$, если известно, что радиусы окружностей равны 4 и 1.
17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число $r$ процентов по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение $r$, при котором общая сумма выплат будет меньше 1,2 млн рублей.
18. Найдите все положительные значения $a$, при каждом из которых система $$begin{cases} (|x| — 5)^2 + (y − 4)^2 = 9, \ (x + 2)^2 + y^2 = a^2end{cases}$$ имеет единственное решение.
19. На доске написано более $40$, но менее $48$ целых чисел. Среднее арифметическое этих чисел равно $−3$, среднее арифметическое всех положительных из них равно $4$, а среднее арифметическое всех отрицательных из них равно $−8$.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
- 21.08.2017
Демоверсия по базовой математике ЕГЭ 2018 от 21 августа 2017 года с кодификатором и спецификацией от ФИПИ.
Изменения по базовой математике в 2018 году:
ИЗМЕНЕНИЙ НЕТ
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить

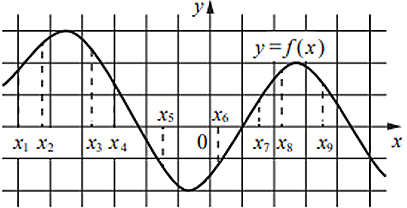














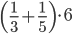
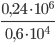
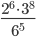

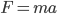
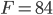

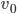
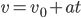
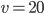
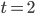
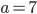
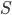
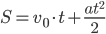
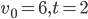
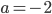

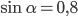
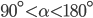
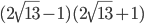
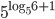
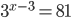
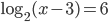
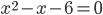


 или
или или
или






 или
или В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.


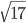

 Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

 Система оценивания экзаменационной работы по математике (базовый уровень)Правильное решение каждого из заданий 1–20 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби, или последовательности цифр
Система оценивания экзаменационной работы по математике (базовый уровень)Правильное решение каждого из заданий 1–20 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби, или последовательности цифр