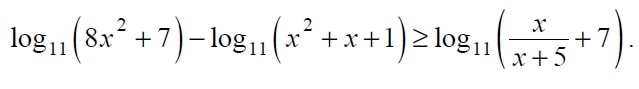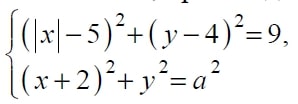Демоверсии ЕГЭ 2022
Официальные демоверсии от ФИПИ на 2021 год.
Изменения структуры и содержания КИМ отсутствуют.
Обновлено 14 ноября. Демоверсии утверждены.
→ Демоверсия (профильный уровень): demo-pro-math-2021.pdf
→ Демоверсия (базовый уровень): demo-baze-math-2021.pdf
→ Спецификация (профильный уровень): spec-pro-math-2021.pdf
→ Спецификация (базовый уровень): spec-baze-math-2021.pdf
→ Кодификатор требований к уровню подготовки выпускников: kd1.pdf
→ Кодификатор элементов содержания по математике: kd2.pdf
→ Скачать одним архивом: math-demo-ege-2021.zip
→ Решение заданий.
Обобщенные планы вариантов КИМ ЕГЭ 2021 года по математике
Профильный уровень:
Базовый уровень:
Шкала перевода баллов по математике и другим предметам →
Демо вариант профильного ЕГЭ по математике 2021 года. Критерии оценивания, ответы.
- ЕГЭ по математике
Официальная демоверсия ЕГЭ 2021 по математике от ФИПИ.
Базовый уровень
→ Демоверсия база — скачать
→ Спецификация база — скачать
Профильный уровень
→ Демоверсия профиль — скачать
→ Спецификация профиль — скачать
Общее
→ Кодификатор содержания — скачать
→ Кодификатор требований — скачать
При ознакомлении с демонстрационным вариантом контрольных измерительных материалов (КИМ) единого государственного экзамена (ЕГЭ) 2021 г. следует иметь в виду, что задания, включённые в него, не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2021 г.
Полный перечень элементов содержания, которые могут контролироваться на едином государственном экзамене 2021 г., приведён в кодификаторе элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена 2021 г. по математике.
В демонстрационном варианте представлены конкретные примеры заданий, не исчерпывающие всего многообразия возможных формулировок заданий на каждой позиции варианта экзаменационной работы.
Связанные страницы:
Демонстрационная версия ЕГЭ—2021 по математике. Профильный уровень.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
ИЛИ
В среднем за день во время конференции расходуется 80 пакетиков чая. Конференция длится 3 дня. В пачке чая 50 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
ИЛИ
Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 140 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
ИЛИ
Весь первый этаж 16-этажного дома занимают магазины, а на каждом из остальных этажей любого его подъезда расположено по 4 квартиры. На каком этаже этого дома находится квартира 165?
Ответ:
2
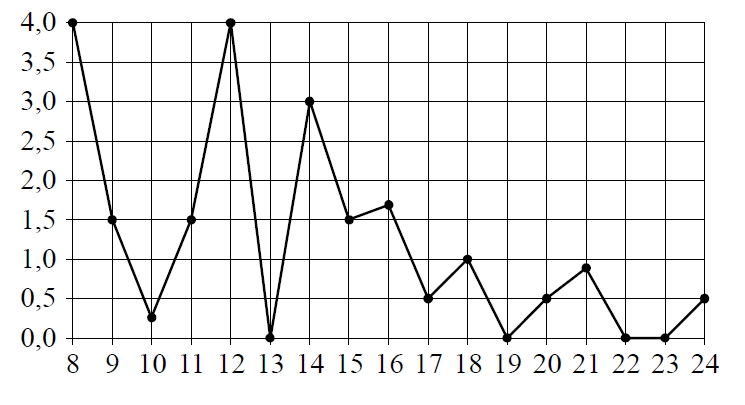
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпало ровно 1,5 миллиметра осадков.
ИЛИ
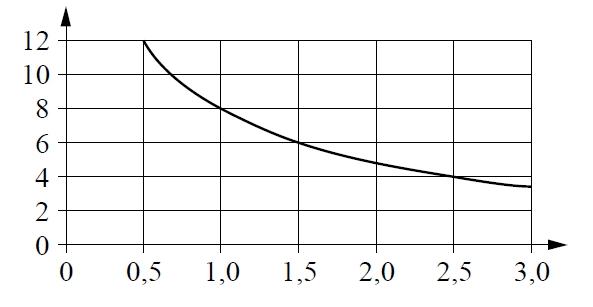
Мощность отопителя в автомобиле регулируется дополнительным сопротивлением. При этом меняется сила тока в электрической цепи электродвигателя: чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На графике показана зависимость силы тока от величины сопротивления. На горизонтальной оси отмечено сопротивление в омах, на вертикальной оси — сила тока в амперах. Определите по графику, на сколько омов увеличилось сопротивление в цепи при уменьшении силы тока с 12 ампер до 4 ампер.
ИЛИ
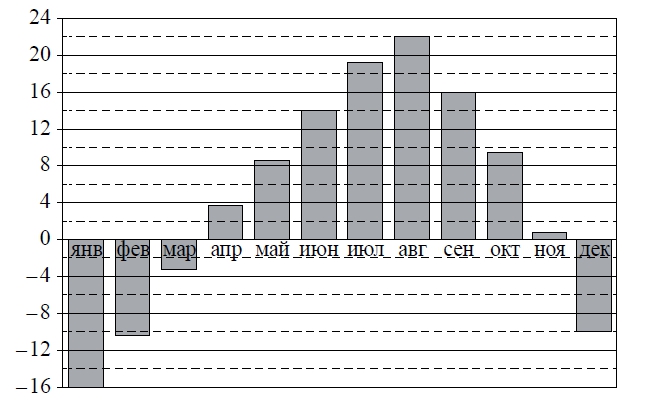
На диаграмме показана среднемесячная температура воздуха во Владивостоке за каждый месяц 2013 г. По горизонтали указываются месяцы; по вертикали — температура в градусах Цельсия.
Определите по приведённой диаграмме, сколько было месяцев с отрицательной среднемесячной температурой.
Ответ:
3
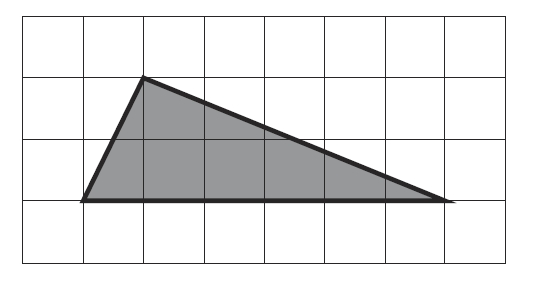
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
ИЛИ
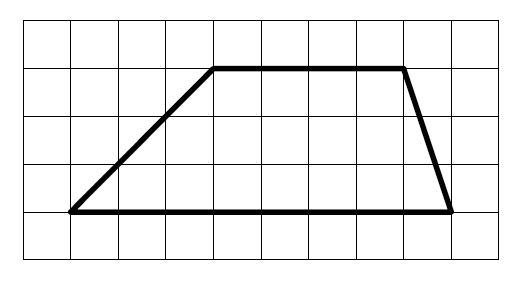
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
Ответ:
4
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
ИЛИ
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
ИЛИ
Стрелок при каждом выстреле поражает мишень с вероятностью 0,3, независимо от результатов предыдущих выстрелов. Какова вероятность того, что он поразит мишень, сделав не более 3 выстрелов?
Ответ:
5
Найдите корень уравнения:
ИЛИ
Найдите корень уравнения
ИЛИ
Найдите корень уравнения
ИЛИ
Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Ответ:
6
Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32°.
ИЛИ
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
ИЛИ
В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.
ИЛИ
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.
Ответ:
7
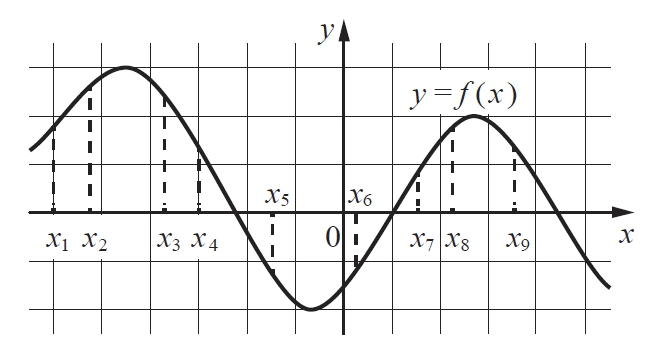
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.
ИЛИ
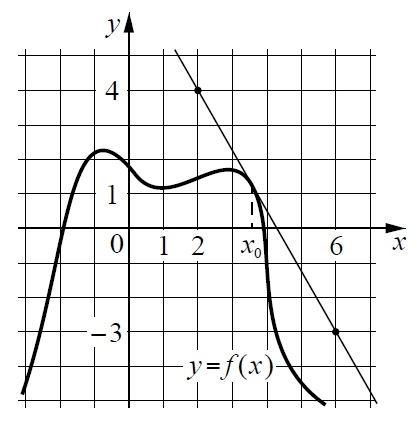
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f(x) в точке x0.
Ответ:
8
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.
ИЛИ
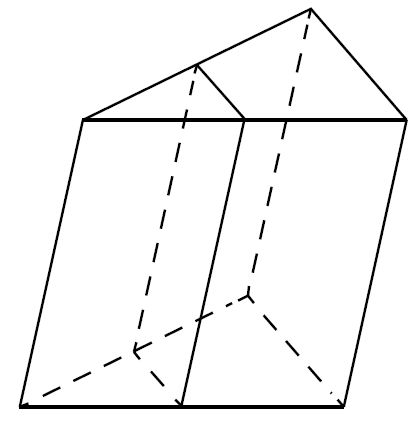
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1 : 2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
Ответ:
9
Найдите если
и
ИЛИ
Найдите значение выражения:
ИЛИ
Найдите значение выражения:
Ответ:
10
11
Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
ИЛИ
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
ИЛИ
Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими
автомобилями через 15 минут после обгона?
ИЛИ
Первая труба наполняет резервуар на 48 минут дольше, чем вторая. Обе трубы, работая одновременно, наполняют этот же резервуар за 45 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Ответ:
12
Найдите наименьшее значение функции на отрезке
ИЛИ
Найдите точку максимума функции
ИЛИ
Найдите точку минимума функции
ИЛИ
Найдите точку максимума функции принадлежащую промежутку
Ответ:
13
а) Решите уравнение:
б) Определите, какие из его корней принадлежат отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N— середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
ИЛИ
В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 16, а высота пирамиды равна 4. На рёбрах AB, CD и AS отмечены точки M, N и K соответственно, причём AM = DN = 4 и AK = 3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) |
1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
ИЛИ
Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Найдите все положительные значения a , при каждом из которых система
имеет единственное решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого, один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
ИЛИ
На доске написано 10 различных натуральных чисел. Среднее арифметическое шести наименьших из них равно 5, а среднее арифметическое шести наибольших равно 15.
а) Может ли наименьшее из этих чисел равняться 3?
б) Может ли среднее арифметическое всех чисел равняться 11?
в) Найдите наибольшее значение среднего арифметического всех чисел.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Перейти к содержимому

Демонстрационный вариант для базового уровня: Скачать
Спецификация для базового уровня: Скачать
Кодификатор требований: Скачать
Кодификатор элементов: Скачать
Демонстрационный вариант для профильного уровня: Скачать
Спецификация для профильного уровня: Скачать
Смотреть демонстрационный вариант по математике ЕГЭ 2021 БАЗА онлайн:
Смотреть демонстрационный вариант по математике ЕГЭ 2021 ПРОФИЛЬ онлайн:
Обобщенные планы вариантов КИМ ЕГЭ 2021 года по математике
🔻 Профильный уровень:
| № |
Требования к уровню подготовки выпускников, проверяемому на ЕГЭ |
Уровень сложности задания |
Макс. балл за выполнение задания |
Время выполнения (мин.) |
Время выполнения выпускником, изучавшим математику на профильном уровне (мин.) |
|
1 |
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б |
1 |
5 |
2 |
|
2 |
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б |
1 |
5 |
2 |
|
3 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
5 |
2 |
|
4 |
Уметь строить и исследовать простейшие математические модели |
Б |
1 |
5 |
3 |
|
5 |
Уметь решать уравнения и неравенства |
Б |
1 |
5 |
3 |
|
6 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
10 |
3 |
|
7 |
Уметь выполнять действия с функциями |
Б |
1 |
10 |
5 |
|
8 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
10 |
5 |
|
9 |
У меть выполнять вычисления и преобразования |
П |
1 |
10 |
5 |
|
10 |
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
П |
1 |
15 |
5 |
|
11 |
Уметь строить и исследовать простейшие математические модели |
П |
1 |
20 |
10 |
|
12 |
Уметь выполнять действия с функциями |
П |
1 |
20 |
10 |
|
13 |
Уметь решать уравнения и неравенства |
П |
2 |
20 |
10 |
|
14 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П |
2 |
40 |
20 |
|
15 |
Уметь решать уравнения и неравенства |
П |
2 |
30 |
15 |
|
16 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П |
3 |
25 |
|
|
17 |
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
П |
3 |
35 |
|
|
18 |
Уметь решать уравнения и неравенства |
В |
4 |
— |
35 |
|
19 |
Уметь строить и исследовать простейшие математические модели |
В |
4 |
40 |
|
| Всего заданий – 19; из них по типу заданий: с кратким ответом – 12; с развернутым ответом – 7; по уровню сложности: Б – 8; П – 9; В – 2. Максимальный первичный балл за работу – 32. Общее время выполнения работы – 235 минут. |
🔻 Базовый уровень:
| № |
Требования к уровню подготовки выпускников, проверяемому на ЕГЭ |
Уровень сложности задания |
Макс. балл за выполнение задания |
Время выполнения (мин.) |
|
1 |
Уметь выполнять вычисления и преобразования |
Б |
1 |
5 |
|
2 |
Уметь выполнять вычисления и преобразования |
Б |
1 |
5 |
|
3 |
У меть использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б |
1 |
7 |
|
4 |
Уметь выполнять вычисления и преобразования |
Б |
1 |
7 |
|
5 |
Уметь выполнять вычисления и преобразования |
Б |
1 |
8 |
|
6 |
У меть использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б |
1 |
8 |
|
7 |
Уметь решать уравнения и неравенства |
Б |
1 |
8 |
|
8 |
У меть строить и исследовать простейшие математические модели |
Б |
1 |
11 |
|
9 |
У меть использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б |
1 |
5 |
|
10 |
У меть строить и исследовать простейшие математические модели |
Б |
1 |
11 |
|
11 |
У меть использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б |
1 |
5 |
|
12 |
У меть строить и исследовать простейшие математические модели |
Б |
1 |
12 |
|
13 |
Уметь выполнять действия с геометрическими фигурами |
Б |
1 |
12 |
|
14 |
У меть выполнять действия с функциями |
Б |
1 |
8 |
|
15 |
Уметь выполнять действия с геометрическими фигурами |
Б |
1 |
9 |
|
16 |
Уметь выполнять действия с геометрическими фигурами |
Б |
1 |
9 |
|
17 |
Уметь решать уравнения и неравенства |
Б |
1 |
9 |
|
18 |
У меть строить и исследовать простейшие математические модели |
Б |
1 |
9 |
|
19 |
Уметь выполнять вычисления и преобразования |
Б |
1 |
16 |
|
20 |
У меть строить и исследовать простейшие математические модели |
Б |
1 |
16 |
| Всего заданий – 20; из них по типу заданий: с кратким ответом – 20; по уровню сложности: Б – 20. Максимальный первичный балл за работу – 20. Общее время выполнения работы – 180 минут. |
Вам будет интересно:
Официальные работы от СтатГрад (задания, ответы и критерии)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
- 25.08.2020
Официальный демонстрационный вариант от ФИПИ для ЕГЭ по математике в 2021 году — профильного уровня.
- Посмотреть другие демоверсии ЕГЭ 2021
ОБНОВЛЕНО 5 декабря 2020: вариант утверждён как официальная демоверсия на 2021 год (ранее в августе этот вариант был представлен как проект).
В документ включены и спецификация, и кодификатор для 2021 года.
- Изменения в 2021 году
- Всё про ЕГЭ 2021
Обсудить задания и их решения вы можете в комментариях ниже.
Видеоразбор демоверсии 2021 по математике профильного уровня
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Решение демонстрационного варианта ЕГЭ 2021 по математике (профильный уровень). Демоверсия ФИПИ для 11 класса.
Задание 1.
Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
ИЛИ
В среднем за день во время конференции расходуется 80 пакетиков чая. Конференция длится 3 дня. В пачке чая 50 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
ИЛИ
Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 140 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
ИЛИ
В 16-этажном доме на каждом этаже любого из его 5 подъездов расположено по 4 квартиры. На каком этаже этого дома находится квартира 165?
Задание 2.
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа в Томске впервые выпало ровно 1,5 миллиметра осадков.
ИЛИ
Мощность отопителя в автомобиле регулируется дополнительным сопротивлением. При этом меняется сила тока в электрической цепи электродвигателя: чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На графике показана зависимость силы тока от величины сопротивления. На горизонтальной оси отмечено сопротивление в омах, на вертикальной оси — сила тока в амперах. Определите по графику, на сколько омов увеличилось сопротивление в цепи при уменьшении силы тока с 12 ампер до 4 ампер.
ИЛИ
На диаграмме показана среднемесячная температура воздуха во Владивостоке за каждый месяц 2013 г. По горизонтали указываются месяцы; по вертикали – температура в градусах Цельсия. Определите по приведённой диаграмме, сколько было месяцев с отрицательной среднемесячной температурой.
Задание 3.
На клетчатой бумаге с размером 1х1 изображён треугольник. Найдите его площадь.
ИЛИ
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Задание 4.
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
ИЛИ
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
ИЛИ
Стрелок при каждом выстреле поражает мишень с вероятностью 0,3, независимо от результатов предыдущих выстрелов. Какова вероятность того, что он поразит мишень, сделав не более 3 выстрелов?
Задание 5.
Найдите корень уравнения 3x–5 = 81
ИЛИ
Найдите корень уравнения
ИЛИ
Найдите корень уравнения log8 (5x + 47) = 3
ИЛИ
Решите уравнение . Если корней окажется несколько, то в ответ запишите наименьший из них.
Задание 6.
Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.
ИЛИ
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне АВ. Найдите площадь треугольника CDE.
ИЛИ
В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.
ИЛИ
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.
Задание 7.
На рисунке изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены девять точек: x1, x2, … x9.
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
ИЛИ
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Задание 8.
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.
ИЛИ
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
Задание 9.
Найдите sin2α, ecли cosα = 0,6 и π < a < 2π.
ИЛИ
Найдите значение выражения 16·log74√7
ИЛИ
Найдите значение выражения 41/5·169/10
Задание 10.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
где с = 1500 м/с — скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Задание 11.
Весной катер идёт против течения реки в 1 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
ИЛИ
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
ИЛИ
Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Задание 12.
Найдите наименьшее значение функции
y = 9x – 9ln(x + 11) + 7
на отрезке [–10,5; 0].
ИЛИ
Найдите точку максимума функции y = (x + 
ИЛИ
Найдите точку минимума функции
ИЛИ
Найдите точку максимума функции
y = (2x − 3)·cos x − 2sin x + 2
на промежутке (0; 2π).
Задание 13.
а) Решите уравнение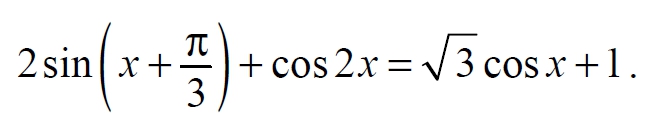
Задание 15.
Решите неравенство
Задание 17.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
Задание 18.
Найдите все положительные значения a, при каждом из которых система
имеет единственное решение.
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.


![[−3pi;-3pi/2] Укажите корни этого уравнения, принадлежащие отрезку.](https://ege314.ru/wp-content/uploads/2020/06/2-2.jpg)