Дерево вероятностей егэ

Дерево вероятностей

В этой статье я покажу вам очень простой способ решения некоторых задач по теории вероятностей.
Рассмотрим задачу. Трое друзей Вася, Петя и Слава купили торт, и решили его съесть. Они разделили торт на три равных части. Внезапно появился четвертый друг Коля, и друзья решили отрезать ему по кусочку от своей доли. Вася отрезал 1/3 от своего куска, Петя 1/4, а Слава – половину. Какую часть всего торта получил в итоге Коля?

Изобразим ситуацию, описанную в задаче в виде такой схемы:

Сначала торт разрезали на три равные части, и каждому из трех друзей досталось по 1/3 торта.

Затем пришел Коля и каждый мальчик отрезал ему соответствующую часть своего куска:

Чтобы найти дробь от числа, нужно число умножить на эту дробь. То есть Вася отдает Коле часть торта, Петя —   часть торта, а Слава  часть торта.

В итоге Коля получит   часть тортa.

Когда мы ищем вероятность события,  мы ищем,  какую часть благоприятные исходы составляют от общего числа исходов. Если в задаче описывается последовательность случайных опытов, и следующий опыт зависит от исхода предыдущего, для разделения возможных сценариев  развития событий часто используют схему «дерева вероятностей», аналогичную приведенной выше.

Решим еще одну задачу.

Две фабрики выпускают одинаковые стекла для автомобильных  фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных  стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Изобразим ситуацию в виде дерева вероятностей:

Все стекла делятся на те, которые выпускает первая фабрика и на те, которые выпускает вторая:

Стекла, которые выпускает каждая фабрика делятся на бракованные и  пригодные. Из стекол, которые выпускает первая фабрика 4% бракованных, и из тех, которые выпускает вторая – 1% бракованных:

Нас интересуют бракованные стекла, которые выпускаются первой или второй фабрикой. Найдем, какую часть эти стекла составляют от всех стекол:

Ответ: 0,019

И.В. Фельдман, репетитор по математике.

1. Теория вероятностей в заданиях ЕГЭ. Дерево вероятностей

2. Задания домашней контрольной работы, вызвавшие затруднения

1. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе
лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон
видит на стене муху, наудачу хватает первый попавшийся револьвер и
стреляет в муху. Найдите вероятность того, что Джон промахнётся.
2. Две фабрики выпускают одинаковые стекла для автомобильных
фар. Первая фабрика выпускает 35 этих стекол, вторая – 65 . Первая
фабрика выпускает 3 бракованных стекол, а вторая – 5 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
3. В волшебной стране бывает два типа погоды: хорошая и отличная,
причем погода, установившись утром, держится потом весь день.
Известно, что с вероятностью 0,9 погода завтра будет такой же, как и
сегодня. 9 мая погода в Волшебной стране отличная. Найдите
вероятность того, что 12 мая в Волшебной стране будет отличная
погода.

3. Задания домашней контрольной работы, вызвавшие затруднения

4. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 85%
яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 65% яиц высшей категории. Всего высшую категорию получает
80% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
5. Семья с детьми совершает прогулку по дорожкам парка. На каждой
развилке они наудачу выбирают следующую дорожку, не возвращаясь
обратно. Схема дорожек показана на рисунке. Часть маршрутов
приводит к киоску с мороженым А, другие к киоску с игрушками В,
третьи к пруду с лебедями С. Найдите вероятность того, что семья
выйдет к пруду с лебедями.
6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность
того, что вынутые наугад 2 шара окажутся красными.
7. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля.
Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите
вероятность того, что обе двухрублёвые монеты лежат в одном кармане.

4.

Дерево вероятностей
Если в задаче описывается последовательность
случайных опытов, и следующий опыт зависит от
исхода предыдущего, для разделения возможных
сценариев развития событий часто используют
схему «дерево вероятностей»

5.  

6. 2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%.

Первая фабрика выпускает 4%
бракованных стекол, а вторая – 1%. Найдите
вероятность того, что случайно купленное в магазине
стекло окажется бракованным.
Ответ: 0,019

7. 3. В волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится потом весь день.

Известно, что с
вероятностью 0,9 погода завтра будет такой же, как и
сегодня. 9 мая погода в Волшебной стране отличная.
Найдите вероятность того, что 12 мая в Волшебной
стране будет отличная погода.
Ответ: 0,756

8. 4. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 65 % яиц из первого хозяйства – яйца высшей категории, а из

второго хозяйства – 85% яиц высшей
категории. Всего высшую категорию получает 80 % яиц.
Найдите вероятность того, что яйцо, купленное у этой
агрофирмы, окажется из первого хозяйства.
Ответ: 0,25

9. 5. Семья с детьми совершает прогулку по дорожкам парка. На каждой развилке они наудачу выбирают следующую дорожку, не

возвращаясь обратно. Схема
дорожек показана на рисунке. Часть маршрутов
приводит к киоску с мороженым А, другие к киоску с
игрушками В, третьи к пруду с лебедями С. Найдите
вероятность того, что семья выйдет к пруду с лебедями.
Ответ: 0,35

10. 6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность того, что вынутые наугад 2 шара окажутся красными.

Вероятность вынуть два определенных шара
одновременно равна вероятности вынуть эти два шара
последовательно без возвращения их в коробку.

11. 7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой

карман. Найдите вероятность того, что
обе двухрублевые монеты лежат в одном кармане.
Обе двухрублевые монеты окажутся в одном кармане, если Петя
переложил в другой карман три монеты по рублю, или две монеты
по 2 рубля и одну монету по 1 рублю.

12. 7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой

карман. Найдите вероятность того, что
обе двухрублевые монеты лежат в одном кармане.

13. РЕФЛЕКСИЯ

• Я знаю…
• Я умею…
• У меня вызывает трудность…

14. Домашняя работа

Выполнить контрольную работу
№6073717 на сайте
http://reshuege.ru/

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Теория вероятностей в заданиях ЕГЭ.
  Дерево вероятностей

• 

  2 слайд

  Задания домашней контрольной работы, вызвавшие затруднения
  1. Ков­бой Джон по­па­да­ет в муху на стене с ве­ро­ят­но­стью 0,9, если стре­ля­ет из при­стре­лян­но­го ре­воль­ве­ра. Если Джон стре­ля­ет из не­при­стре­лян­но­го ре­воль­ве­ра, то он по­па­да­ет в муху с ве­ро­ят­но­стью 0,4. На столе лежит 10 ре­воль­ве­ров, из них толь­ко 2 при­стре­лян­ные. Ков­бой Джон видит на стене муху, на­уда­чу хва­та­ет пер­вый по­пав­ший­ся ре­воль­вер и стре­ля­ет в муху. Най­ди­те ве­ро­ят­ность того, что Джон про­махнётся.
  2. Две фаб­ри­ки вы­пус­ка­ют оди­на­ко­вые стек­ла для ав­то­мо­биль­ных фар. Пер­вая фаб­ри­ка вы­пус­ка­ет 35  этих сте­кол, вто­рая – 65 . Пер­вая фаб­ри­ка вы­пус­ка­ет 3  бра­ко­ван­ных сте­кол, а вто­рая – 5 . Най­ди­те ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным.
  3. В волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится потом весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 9 мая погода в Волшебной стране отличная. Найдите вероятность того, что 12 мая в Волшебной стране будет отличная погода.

• 

  3 слайд

  Задания домашней контрольной работы, вызвавшие затруднения
  4. Аг­ро­фир­ма за­ку­па­ет ку­ри­ные яйца в двух до­маш­них хо­зяй­ствах. 85% яиц из пер­во­го хо­зяй­ства — яйца выс­шей ка­те­го­рии, а из вто­ро­го хо­зяй­ства — 65% яиц выс­шей ка­те­го­рии. Всего выс­шую ка­те­го­рию по­лу­ча­ет 80% яиц. Най­ди­те ве­ро­ят­ность того, что яйцо, куп­лен­ное у этой аг­ро­фир­мы, ока­жет­ся из пер­во­го хо­зяй­ства.
  5. Семья с детьми совершает прогулку по дорожкам парка. На каждой развилке они наудачу выбирают следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к киоску с мороженым А, другие к киоску с игрушками В, третьи к пруду с лебедями С. Найдите вероятность того, что семья выйдет к пруду с лебедями.
  6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность того, что вынутые наугад 2 шара окажутся красными.
  7. В кар­ма­не у Пети было 4 мо­не­ты по рублю и 2 мо­не­ты по два рубля. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что обе двух­рублёвые мо­не­ты лежат в одном кар­ма­не.

• 

  4 слайд

  Дерево вероятностей
  Если в задаче описывается последовательность случайных опытов, и следующий опыт зависит от исхода предыдущего, для разделения возможных сценариев развития событий часто используют схему «дерево вероятностей»

• 

• 

  6 слайд

  2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

    Ответ: 0,019

• 

  7 слайд

  3. В волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится потом весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 9 мая погода в Волшебной стране отличная. Найдите вероятность того, что 12 мая в Волшебной стране будет отличная погода.

       Ответ: 0,756

• 

  8 слайд

  4. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 65 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 85% яиц высшей категории. Всего высшую категорию получает 80 % яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

      Ответ: 0,25

• 

  9 слайд

  5. Семья с детьми совершает прогулку по дорожкам парка. На каждой развилке они наудачу выбирают следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к киоску с мороженым А, другие к киоску с игрушками В, третьи к пруду с лебедями С. Найдите вероятность того, что семья выйдет к пруду с лебедями.

       Ответ: 0,35

• 

  10 слайд

  6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность того, что вынутые наугад 2 шара окажутся красными.
  Вероятность вынуть два определенных шара одновременно равна вероятности вынуть эти два шара последовательно без возвращения их в коробку.

• 

  11 слайд

  7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
  Обе двухрублевые монеты окажутся в одном кармане, если Петя переложил в другой карман три монеты по рублю, или две монеты по 2 рубля и одну монету по 1 рублю.

• 

  12 слайд

  7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.

• 

  13 слайд

  РЕФЛЕКСИЯ
  Я знаю…

  Я умею…

  У меня вызывает трудность…

• 

  14 слайд

  Домашняя работа
  Выполнить контрольную работу №6073717 на сайте http://reshuege.ru/

Краткое описание документа:

Одним из важных разделов  ЕГЭ по математике  является решение  комбинаторных задач  путем организованного перебора возможных вариантов,  с использованием правила умножения, нахождение  вероятности случайных событий. 

Урок «Теория вероятностей в заданиях ЕГЭ. Дерево вероятностей» является вторым в разделе «Теория вероятностей», организованном при повторении и обобщении знаний при подготовке к ЕГЭ в 11классе. Урок построен с использованием приёмов информационно-коммуникационных технологий, а также беседы. 

Презентация составлена с использованием компьютерной программы Microsoft PowerPoint, что позволяет ярко представить материал с необходимой информацией. Использование презентации сокращает время обучения, и облегчает усвоение материала. 

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 558 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Решение задач с помощью дерева вероятностей.
RAR / 5.92 Мб
Муниципальное общеобразовательное учреждение

Верхнедонская гимназия

Ст. Казанская

Ростовская область

Мастер-класс

«Решение задач с помощью дерева вероятностей»

 

Подготовила

учитель математики

Полиёва Е.И.

Ст. Казанская

Цели:

познакомить с понятием графа, вероятностного дерева;

рассмотреть методы решения задач с помощью графа, дерева вероятностей;

рассмотреть формы и методы закрепления знаний, умений и навыков

Оборудование:

интерактивная доска SmartBoard;

мультимедийный проектор;

персональный компьютер (ПК) учителя

презентация «Решение задач с помощью дерева вероятностей»

раздаточный материал (распечатать каждому ученику)

тренажер

самостоятельная работа

Слайд 1.

Слайд 2.

Слайд 4.

Решение задач. Тренажер. (приложение распечатать и выполнять на этих же листочках).

Данный материал предназначен для отработки умений и навыков по теме «Решение задач с помощью дерева вероятностей». Тренажер можно использовать и на уроке, и на дополнительных заданиях по подготовке к ЕГЭ.

Задачи №1- №5 решаются совместно с учителем, №6 — №10 – самостоятельно с последующей проверкой.
 

Контроль усвоения материала. Самостоятельная работа.

Я обещала разобрать задачи по теории вероятностей из итоговой диагностики 8 класса.
https://klarissa45.livejournal.com/406026.html
Диагностика проходила за компьютерами, учитывались только ответы

В одном из вариантов задача была такой
В группе туристов 51 человек. Среди них Алексей и Иван.
Туристы в случайном порядке рассаживаются в красный, синий и зелёный автобусы.
а) Какова вероятность, что Алексей и Иван окажутся в одном автобусе?
б) Какова вероятность, что в красном автобусе не окажутся ни Алексей, ни Иван?

А в другом варианте были два профессора со своими докладами

На конференции запланировано 16 докладов, в том числе доклад профессора А и доклад профессора Б
Конференция проходит с понедельника по четверг, оргкомитете распределяет докладчиков случайным образом
по 4 доклада в день.
а) Какова вероятность, что доклад профессора А и доклад профессора Б будут назначены на один день?
б) Какова вероятность, что доклад профессора А и доклад профессора Б не будут запланированы на понедельник?

Скажем прямо-это задачи ЕГЭ.
Хотя там тоже можно загнуть ещё более сложную задачу
[Spoiler (click to open)] Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна) выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур, который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет победителя турнира. Всего в турнире участвует 20 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом?
Но одновременно это и задачи курса теории вероятностей Математической вертикали.
Чтобы решить эти задачи, надо уметь строить деревья.
Хотя на первый вопрос задачи можно ответить и без дерева.

«Пусть Алексей занял место в каком-то автобусе. Тогда в этом месте осталось 17-1=16 мест, на которые претендуют 51-1=50 человек. Вероятность равна 16/50 или 0,32»

« Пусть профессор А уже выступает в определенный день, тогда у профессора Б есть возможность стать одним из 3 выступающих в этот день. Но таких претендентов 15. А значит вероятность равна 3/15 или 0,2»

Или с помощью дерева

Задание а)
Первый уровень — уровень Алексея ( мы его первым сажаем в автобус), а второй уровень — уровень Ильи, потом мы его сажаем.

Задания а) и б)

Крестиками зачеркнуты ветки дерева, которые нам не нужны.
То есть первый мальчик в красном автобусе или второй мальчик в красном

А теперь теория, это статья И.Р. Высоцкого из журнала «Математика»

https://ptlab.mccme.ru/sites/ptlab.mccme.ru/files/ob_uslovnoy_veroyatnosti.pdf

В другой статье И.Р.Высоцкий пишет: «Дерево позволяет рассматривать составной эксперимент как бы по частям. Иногда удобно мысленно расположить случайные события во времени, хотя нужно помнить, что эта очередность условная. Событие А можно рассматривать при условии, что событие В произошло. Точно так же можно считать, что случилось событие А, и тогда ставить вопрос о вероятности события В. Эти условные вероятности удобно надписывать около соответствующих ребер дерева. Это наглядно, и этому легко научиться. Даже при небольшом навыке деревья становятся излюбленным способом решения многих задач.»

• Готовимся к ЕГЭ по математике 2014

  /

• Решение задач по теории вероятностей

  /

• Задачи, решаемые с помощью построения дерева вероятностей

РЕШЕНИЕ ЗАДАЧ НА ВЕРОЯТНОСТЬ С ПОМОЩЬЮ ДЕРЕВА ВАРИАНТОВ

Учитель математики высшей квалификационной категории Шутова О.Н.

город Ульяновск

Задачи на вероятность

1) Решение с помощью дерева возможных вариантов

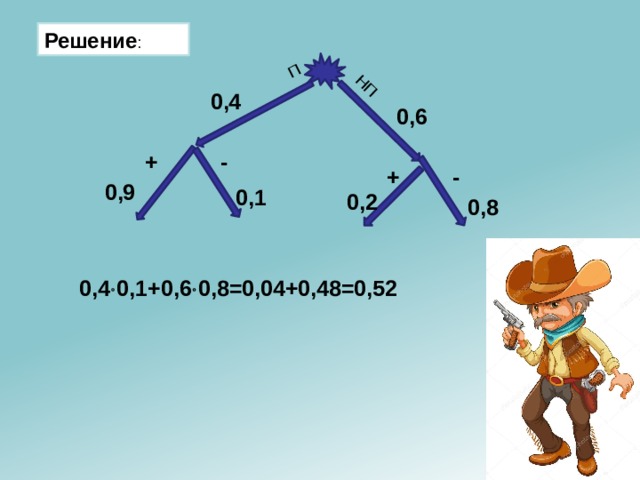
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Макрос создан программистом Хансом Хофманом (Германия)

П

НП

Решение :

0,4

0,6

—

+

+

—

0,9

0,1

0,2

0,8

0,4  0,1+0,6  0,8=0,04+0,48=0,52

1) Решение с помощью дерева возможных вариантов

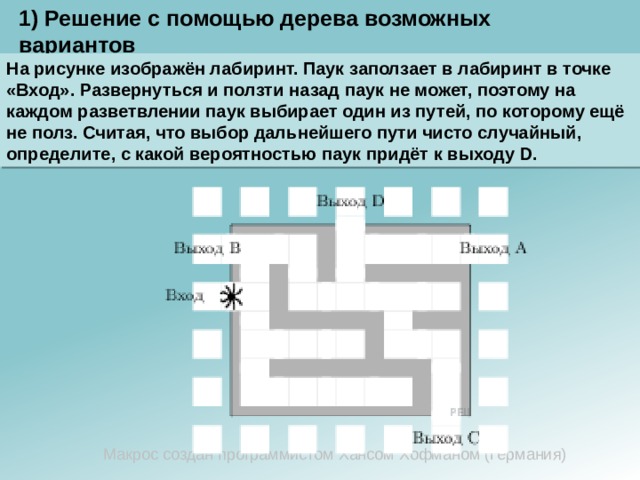
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.

Макрос создан программистом Хансом Хофманом (Германия)

1) Решение с помощью дерева возможных вариантов

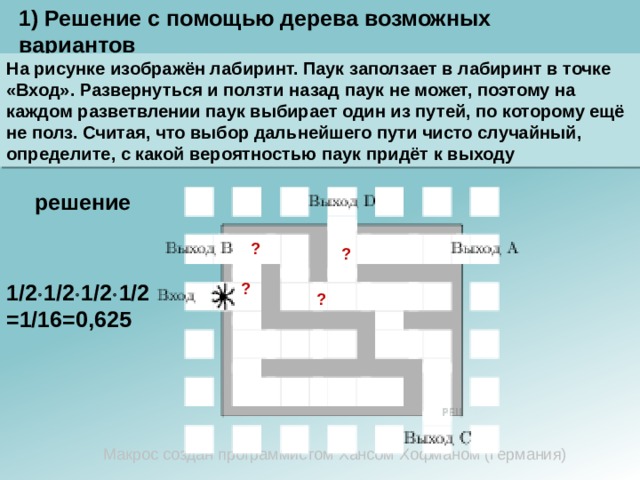
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу 

решение

?

?

1/2  1/2  1/2  1/2=1/16=0,625

?

?

Макрос создан программистом Хансом Хофманом (Германия)

Задачи на вероятность

1) Решение с помощью дерева возможных вариантов

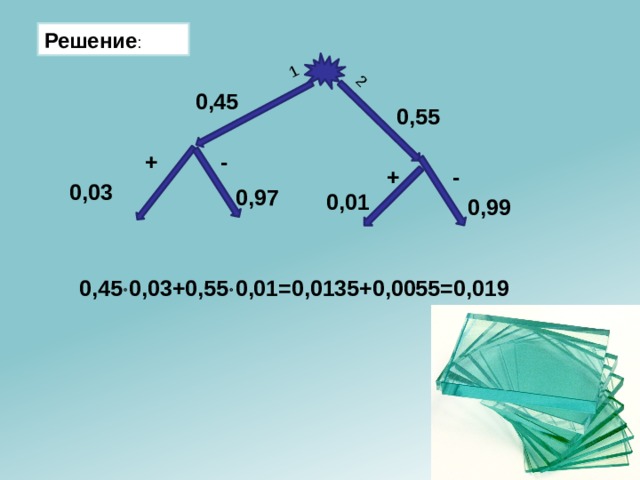
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Макрос создан программистом Хансом Хофманом (Германия)

1

2

Решение :

0,45

0,55

—

+

—

+

0,03

0,97

0,01

0,99

0,45  0,03+0,55  0,01=0,0135+0,0055=0,019

Задачи на вероятность

1) Решение с помощью дерева возможных вариантов

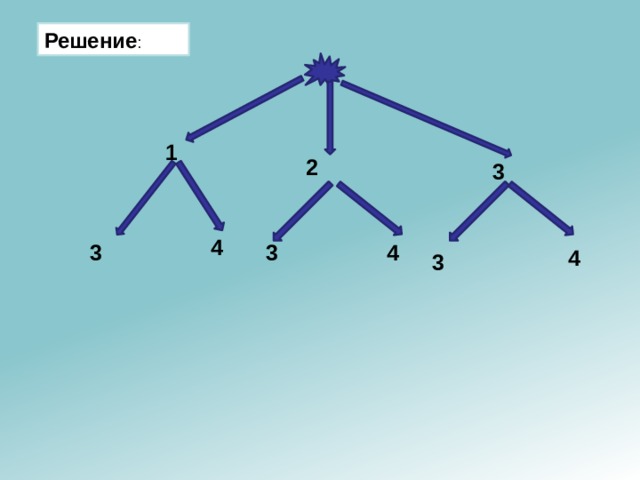
Нарисовать дерево возможных вариантов для вычисления значения дроби

(2х-у)/(х+у), если при х=1;2;3 переменная у=3;4

Макрос создан программистом Хансом Хофманом (Германия)

Решение :

1

2

3

4

4

3

3

4

3

Самостоятельная работа

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25 этих стекол, вторая – 75 Первая фабрика выпускает 4 бракованных стекол, а вторая – 2 Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 35 этих стекол, вторая – 65 Первая фабрика выпускает 3 бракованных стекол, а вторая – 5 Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

2. Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он по­па­да­ет в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

2. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Макрос создан программистом Хансом Хофманом (Германия)