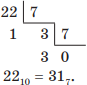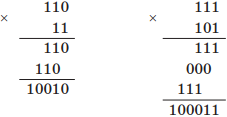Десятичная запись числа егэ

Краткая теоретическая справка

Всякое натуральное число NЕдинственным образом представимо в виде

N = αn• 10″ + απ.1 ∙ 10π^1 + an_2∙10″^2 +… + a2∙IO2 + a1∙IO1+ a0,

Где П — натуральное число или 0, aπ, aπ.1, an_2, ∙∙∙, <⅛ aι, ao — цифры от 0 до 9, причем цифра aπ ≠ 0.

Это представление натурального числа в десятичной системе счис­ления называют десятичной записью числа. Для краткости мы будем записывать это (и + 1)-значное число в виде:

N= Aπaπ—Laπ-2∙∙∙A2ALa0

(черта, как правило, ставится, чтобы отличить десятичную запись числа от произведения цифр aπ, an.1, An-2> ∙∙∙, a2, aι, ⅝)∙

Натуральное число MЯвляется n-значным в том и только в том случае, когда оно удовлетворяет неравенству 10π^1 ≤ M< 10π.

Всякая правильная дробь представима в виде конечной десятич­ной дроби или бесконечной периодической десятичной дроби. Дробь называется чисто периодической, если ее период начинается сразу после запятой, отделяющей целую и дробную часть числа.

Несократимая правильная дробь — представляется в виде конеч­ной десятичной дроби в том и только в том случае, когда ее знамена­тель П не делится на простые числа, отличные от 2 и 5.

Подготовительные задачи

2.1. Цифры двузначного числа AbПоменяли местами и из получен­ного числа вычли исходное. Докажите, что разность Ab — Ьа всегда делится на 9.

2.2. Двузначное число умножили на произведение его цифр. В от­вете получилось трехзначное число из одинаковых цифр, совпадаю­щих с цифрой в разряде единиц исходного числа: Ab ∙ а ∙ B = Bbb.Какое двузначное число мы умножали?

2.3. Докажите, что десятичная запись числа З20 содержит не более 10 цифр.

2.4. Натуральные числа от 1 до 20 выписали в строчку подряд: 123456789101112… 181920. В полученном натуральном числе нужно вычеркнуть 10 цифр так, чтобы натуральное число, образованное оставшимися цифрами, было как можно больше. Как это сделать?

Основные задачи

Пример 2.1. В трехзначном числе AbcПоменяли местами цифры, стоящие в разряде сотен и в разряде единиц, и из полученного чис­ла вычли исходное. Докажите, что разность Abc — CbaВсегда делится на 99.

Решение. Запишем разность:

Abc — Cba = 100α+ 10b+ c — (100с+ 10b +α) = 99(а —с).

Это число делится на 99, что и требовалось доказать.

Пример 2.2. В примере на умножение двузначных чисел одина­ковые цифры заменили одинаковыми буквами, а разные цифры — разными. Докажите, что при вычислении была допущена ошибка: Ab∙Cd = Eeff.

Решение. Равенство невозможно, потому что для различных цифр А, Ь, с и DЛевая часть Ab ∙ CdНе делится на 11, а правая часть Eeff = 11 • (100е +/) —делится.

Пример 2.3. Докажите, что квадрат натурального числа, оканчи­вающегося цифрой 5, оканчивается на 25.

Решение. Всякое натуральное число, оканчивающееся цифрой 5, можно представить в виде 10а + 5, где а — количество его десятков (не обязательно цифра!). Например, 1945 = 10 • 194 + 5. Квадрат чис­ла будет равен (10α + 5)2 = 100α2 + 100а + 25. Это число оканчивается на 25, так как первые два слагаемых оканчиваются двумя нулями и не влияют на последние две цифры суммы.

Пример 2.4. Найдите все двузначные числа, которые равны сум­ме цифры десятков и квадрата цифры, стоящей в разряде единиц.

Ответ: 89.

Решение. Из уравнения Ab = а+ b2следует, что 9a = b(b — 1), от­куда А= 8, b = 9.

Пример 2.5. Сложили шесть трехзначных чисел, полученных пе­рестановками трех различных цифр в разном порядке. Докажите, что полученная сумма делится на 37.

Решение. Запишем сумму всех данных трехзначных чисел:

αbc + αcb + bαc + bcα + cαb + cbα = 222(α + b + c) = 37 ∙6(α + b + c).

Это число делится на 37.

Пример 2.6. При каком наименьшем натуральном П в десятичной записи правильной дроби после запятой могут подряд встретиться цифры 0,…501…?

Ответ: При П= 251.

Решение. Домножая дробь на подходящую степень десятки, мы можем получить дробь, у которой цифры 501 встречаются сразу после десятичной запятой (при этом знаменатель полученной дроби будет меньше или равен п). Таким образом, можно считать, что — = 0,501…. Тогда — — | < 0,502 — 0,5 = π⅛:. C другой стороны, П Fl Δ O∖z∖z

Т1 2т-п. . 1 1^,1 o. r. o

И — 2 = ~2п~ >2^’ 0ТКУДа 2п <500’ Т0 еСТЬ n >25°’3наЧИТ’ ЗНа’ менатели, меньшие 251, не подходят. Нетрудно проверить, что дробь 126 λ cλi 251 =0,501… подходит.

Пример 2.7. Может ли произведение всех цифр десятичной запи­си натурального числа равняться 2010?

Ответ: Не может.

Решение. 2010 = 2 • 3 • 5 • 67, а простое число 67 нельзя предста­вить в виде произведения цифр.

Пример 2.8. Докажите, что десятичная запись числа 2300 содер­жит более 90, но не более 100 цифр.

Решение. 230° = 810° < IO100, поэтому 2300 имеет не более 100 цифр. C другой стороны, 230° = 1O2430> IOOO30 = IO90, откуда следует, что 2300 имеет более 90 цифр.

Задачи для самостоятельного решения

2.5. Натуральные числа от 1 до 20 выписали подряд после запя­той и получили десятичную дробь: 0,123456789101112…181920. Как вычеркнуть 10 цифр, чтобы десятичная дробь, образованная оставши­мися цифрами, была как можно меньше?

2.6. Число AbcdeДелится на 41. Докажите, что число EabcdТакже делится на 41.

2.7. Найдите все трехзначные числа, для которых любое число, по­лученное из них произвольной перестановкой цифр, делится на 7.

2.8. Найдите все двузначные числа, квадрат которых оканчивается теми же двумя цифрами, что и само число.

2.9. Найдите все трехзначные числа, квадрат которых оканчивает­ся теми же тремя цифрами, что и само число.

2.10. Сколько существует двузначных чисел, которые ровно в 9 раз больше суммы своих цифр? А сколько существует таких трехзначных чисел?

2.11. В натуральном числе поменяли местами две соседние цифры и из полученного числа вычли исходное. Докажите, что полученная разность всегда делится на 9.

2.12. В натуральном числе поменяли местами две цифры, стоящих через одну, и из полученного числа вычли исходное. Докажите, что разность всегда делится на 99.

2.13. В примере на умножение двузначных чисел одинаковые циф­ры заменили одинаковыми буквами, а разные — разными. Докажите, что при вычислении была допущена ошибка: Ab ∙ Cd = Efef.

2.14. ПустьA,B,C,D — различные цифры. Докажите, что Cdcdcdcd Не делится на Aabb.

2.15. На чем основан следующий способ возведения в квадрат чи­сел, оканчивающихся цифрой пять: отбросьте цифру 5 и умножьте полученное число на следующее за ним натуральное число, а к ре­зультату справа припишите число 25 (например, для получения квад­рата числа 115 нужно 11 умножить на 11 + 1 = 12 ик произведению 11 × 12 = 132 приписать 25, получив в ответе 13225)?

2.16. Какое наибольшее значение может принимать частное от де­ления трехзначного числа на сумму всех его цифр?

2.17. Найдите все четырехзначные числа AbedТакие, что Abed + + Abc + Ab + а= 2011.

2.18. Из трех различных цифр составили всевозможные двузнач­ные числа без повторений цифр в одном числе. Сумма шести полу­ченных чисел оказалась равной 528. Найдите эти цифры.

2.19. Друг за другом подряд выписали десятичную запись чисел 2100 и 5100. Сколько всего цифр выписали?

2.20. При некотором натуральном П десятичная запись чисел 2π и 5πначинается с одной и той же цифры. Какая это может быть циф­ра?

2.21. Существует ли натуральное число, которое при зачеркивании первой слева цифры уменьшается ровно в 2011 раз?

2.22. Девятизначное число, в записи которого есть все цифры, кро­ме нуля, после некоторой перестановки цифр уменьшилось в 8 раз. Найдите все такие числа.

2.23. При каком наименьшем натуральном П в десятичной записи дроби — после запятой могут подряд встретиться цифры 0,…142…?

А в десятичной записи правильной дроби?

2.24. а) Сколько существует натуральных чисел и, меньших 100, та-

11 .

Ких, что каждое из чисел — и выражается конечной десятичной дробью?

Б) Найдите все такие натуральные П.

Представление числовой информации. Сложение и умножение в разных системах счисления

Представление числовой информации с помощью систем счисления

Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.

Система счисления — это система записи чисел с помощью определенного набора цифр.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.

Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.

Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.

Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.

Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.

Например: 8527 = 8 ⋅ 10³ + 5 ⋅ 10² + 2 ⋅ 10¹ + 7 ⋅ 10⁰.

Развернутая форма записи чисел произвольной системы счисления имеет вид

$∑↙{i=n-1}↖{-m}a_iq^i$,

где $X$ — число;

$a$ — цифры численной записи, соответствующие разрядам;

$i$ — индекс;

$m$ — количество разрядов числа дробной части;

$n$ — количество разрядов числа целой части;

$q$ — основание системы счисления.

Например, запишем развернутую форму десятичного числа $327.46$:

$n=3, m=2, q=10.$

$X=∑↙{i=2}↖{-2}a_iq^i=a_2·10^2+a_1·10^1+a_0·10^0+a_{-1}·10^{-1}+a_{-2}·10^{-2}=3·10^2+2·10^1+7·10^0+4·10^{-1}+6·10^{-2}$

Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.

Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В₁₂ можно расписать так:

7А,5В₁₂ = В ⋅ 12^-2 + 5 ⋅ 2^-1 + А ⋅ 12⁰ + 7 ⋅ 12¹.

В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.

Перевод чисел в позиционных системах счисления

Перевод чисел из произвольной системы счисления в десятичную

Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂ = 1 ⋅ 2³ + 1 ⋅ 2² + 0 ⋅ 2¹ + 1 ⋅ 2⁰ = 13₁₀;

17D,ECH = 12 ⋅ 16^–2 + 14 ⋅ 16^–1 + 13 ⋅ 160 + 7 ⋅ 16¹ + 1 ⋅ 16² = 381,921875.

Перевод чисел из десятичной системы счисления в заданную

Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

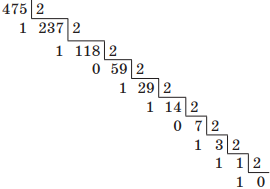
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:

Читая остатки от деления снизу вверх, получим 111011011.

Проверка:

1 ⋅ 2⁸ + 1 ⋅ 2⁷ + 1 ⋅ 2⁶ + 0 ⋅ 2⁵ + 1 ⋅ 2⁴ + 1 ⋅ 2³ + 0 ⋅ 2² + 1 ⋅ 2¹ + 1 ⋅ 2⁰ = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 475₁₀.

Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например, переведем десятичную дробь 0,375₁₀ в двоичную систему счисления:

Полученный результат — 0,011₂.

Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно

Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2^І; І = 3).

Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

Например:

1234,777₈ = 001 010 011 100,111 111 111₂ = 1 010 011 100,111 111 111₂;

1234567₈ = 001 010 011 100 101 110 111₂ = 1 010 011 100 101 110 111₂.

При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Например:

1100111₂ = 001 100 111₂ = 147₈;

11,1001₂ = 011,100 100₂ = 3,44₈;

110,0111₂ = 110,011 100₂ = 6,34₈.

Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2^І; І = 4).

Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.

Например:

1100111₂ = 0110 0111₂ = 67₁₆;

11,1001₂ = 0011,1001₂ = 3,9₁₆;

110,0111001₂ = 0110,0111 0010₂ = 65,72₁₆.

Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.

Например:

1234,AB77₁₆ = 0001 0010 0011 0100,1010 1011 0111 0111₂ = 1 0010 0011 0100,1010 1011 0111 0111₂;

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂.

При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.

Например, переведем троичное число 211₃ в семеричную систему счисления. Для этого сначала преобразуем число 211₃ в десятичное, записав его развернутую форму:

211₃ = 2 ⋅ 3² + 1 ⋅ 3¹ + 1 ⋅ 3⁰ = 18 + 3 + 1 = 22₁₀.

Затем переведем десятичное число 22₁₀ в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:

Итак, 211₃ = 31₇.

Примеры решения задач

Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.

Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 12₁₀ = 110_n = 0 ·n⁰ + 1 · n¹ + 1 · n². Составим уравнение: n² + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 110₃ = 0· 3⁰ + 1 · 3¹ + 1 · 3² = 0 + 3 + 9 = 12 .

Ответ: 3.

Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.

Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 22₁₀ = 34₆ = 24₉ = 14₁₈.

Ответ: 6, 9, 18.

Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.

Решение. Для удобства воспользуемся восьмеричной системой счисления. 101₂ = 5₈. Тогда число х можно представить как x = 5 · 8⁰ + a₁ · 8¹ + a₂ · 8² + a₃ · 8³ + … , где a₁, a₂, a₃, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 8² > 25), т. е. такие числа должны иметь представление x = 5 + a₁ · 8. Поскольку x ≤ 25 , допустимыми значениями a₁ будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:

a₁ = 0; x = 5 + 0 · 8 = 5;.

a₁=1; x = 5 + 1 · 8 = 13;.

a₁ = 2; x = 5 + 2 · 8 = 21;.

Выполним проверку:

5₁₀ = 101₂;

13₁₀ = 1101₂;

21₁₀ = 10101₂.

Ответ: 5, 13, 21.

Арифметические операции в позиционных системах счисления

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.

Сложение	Вычитание	Умножение
0 + 0 = 0	0 – 0 = 0	0 ⋅ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ⋅ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ⋅ 0 = 0
1 + 1 = 10	10 – 1 = 1	1 ⋅ 1 = 1

Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.

Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:

Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:

Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:

Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.

Например, выполним сложение восьмеричных чисел 36₈ и 15₈, а также вычитание шестнадцатеричных чисел 9С₁₆ и 67₁₆:

При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.

Представление чисел в компьютере

Формат с фиксированной запятой

В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно

1 ⋅ 2⁷ + 1 ⋅ 2⁶ + 1 ⋅ 2⁵ + 1 ⋅ 2⁴ + 1 ⋅ 2³ + 1 ⋅ 2² + 1 ⋅ 2¹ + 1 ⋅ 2⁰ = 255₁₀.

Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.

Для п-разрядного представления диапазон будет составлять от 0 до 2ⁿ – 1.

Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.

Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2ⁿ − |А|.

Алгоритм получения дополнительного кода отрицательного числа:

1. Записать прямой код числа в п двоичных разрядах.

2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)

3. Прибавить единицу к полученному обратному коду.

Например, получим дополнительный код числа –2014₁₀ для шестнадцатиразрядного представления:

Прямой код	Двоичный код числа 201410 со знаковым разрядом	1000011111011110
Обратный код	Инвертирование (исключая знаковый разряд)	1111100000100001
	Прибавление единицы	1111100000100001 + 0000000000000001
Дополнительный код		1111100000100010

При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.

Например:

1) Найдем разность 13₁₀ – 12₁₀ для восьмибитного представления. Представим заданные числа в двоичной системе счисления:

13₁₀ = 1101₂ и 12₁₀ = 1100₂.

Запишем прямой, обратный и дополнительный коды для числа –12₁₀ и прямой код для числа 13₁₀ в восьми битах:

	1310	–1210
Прямой код	00001101	10001100
Обратный код	—	11110011
Дополнительный код	—	11110100

Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):

Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.

2) Найдем разность 8₁₀ – 13₁₀ для восьмибитного представления.

Запишем прямой, обратный и дополнительный коды для числа –13₁₀ и прямой код для числа 8₁₀ в восьми битах:

	810	–1310
Прямой код	00001000	10001101
Обратный код	—	11110010
Дополнительный код	—	11110011

Вычитание заменим сложением:

В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:

11111011 – 00000001 = 11111010.

Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –5₁₀.

Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2^n–1, а максимальное: |А| = 2^n–1 или А = –2^n–1 – 1.

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно

А = –2³¹ = –2147483648₁₀.

Максимальное положительное число равно

А = 2³¹ – 1 = 2147483647₁₀.

Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.

1512. Если к десятичной записи натурального числа а приписать справа запятую, а потом некоторый бесконечный набор цифр, то получится десятичная запись такого иррационального числа с, что (2с — 3)² = 3а² — 12с + 46. Найдите все возможные значения числа с.

1513. Если к десятичной записи натурального числа а приписать справа запятую, а потом некоторый бесконечный набор цифр, то получится десятичная запись такого иррационального числа с, что 2с² + с = 20a + 10. Найдите все возможные значения числа с.

1514. Найдите все такие пары взаимно простых натуральных чисел а и b, а < b, что если к десятичной записи числа b—а приписать справа через запятую десятичную запись числа 6, то получится десятичная запись числа, равного

1515. Найдите сумму всех трёхзначных натуральных чисел n, таких, что первая и последняя цифры числа n² равны 1.

1516. Пусть х — 5-значное натуральное число, состоящее из цифр от 1 до 9, взаимно простое с числом В = 10⁵ — 1. Найдите количество различных чисел (включая число х), взаимно простых с числом Б, получаемых из х циклической перестановкой цифр.

1517. Трёхзначные числа тип являются полными квадратами. Причём m получено из п уменьшением на число вида 111а, где а — натуральное число. Найдите все такие числа а.

1518. Найдите все такие пары однозначного числа а и двузначного числа 5, что если к десятичной записи числа а приписать справа через запятую десятичную запись числа Ъ и учетверить это число, то получится квадратный корень из трёхзначного числа, записанного, не меняя порядка, цифрами чисел а и 6.

1519. Обозначим через S(n) сумму цифр натурального числа n. Найдите все такие натуральные п, при которых n + S(n) = 2012.

1520. Если к двузначному числу а приписать справа двузначное число b, то полученное число будет в 3 раза больше произведения чисел а и b. Найдите эти числа.

1521. Можно ли составить из цифр 2, 3, 4, 9 (каждую цифру можно использовать неограниченное количество раз) два числа, одно из которых в 1234567789 раз больше другого?

1522. Найдите натуральное двузначное число, сумма цифр которого равна 14 и при увеличении которого на 46 получается число, произведение цифр которого равно 6.

1523. Найдите трёхзначное натуральное число, если сумма его цифр равна 12 и оно равно 107/41 числа, записанного теми же цифрами, но в обратном порядке.

1524. Какую наименьшую сумму цифр может иметь число вида 6n² — n + 1 при натуральном числе n?

1525. Какую наименьшую сумму цифр может иметь число вида 8n² — 3n + 1 при натуральном числе n?

1526. Найдите все трёхзначные натуральные числа, квадрат которых оканчивается этим же числом.

1527. Найдите количество двузначных натуральных чисел, куб которых заканчивается этим же числом.

1528. Существует ли такое натуральное число n, при котором число 2ⁿ будет начинаться на 3842561?

1529. Существует ли такое натуральное число n, при котором число 7ⁿ будет начинаться на 100032452?

1530. Найдите все натуральные значения n, при которых число является квадратом натурального числа.

1531. Найдите трёхзначное число, зная, что число его единиц есть среднее геометрическое числа сотен и десятков. Если в его записи поменять местами цифры сотен и десятков и вычесть полученное число из искомого, то разность будет равна 270.

1532. Найдите все натуральные трёхзначные числа, каждое из которых обладает следующими двумя свойствами:

1) первая цифра числа в 4 раза меньше суммы двух других его цифр;

2) разность между самим числом и числом, получающимся из него перестановкой двух последних его цифр, неотрицательна и делится на 72 без остатка.

1533. Найдите наибольшее натуральное число, не оканчивающееся нулём, которое при вычёркивании одной (не первой) цифры уменьшается в целое число раз.

1534. Факториалом натурального числа n (пишут n!) называется произведение всех натуральных чисел от 1 до n включительно. Также по определению считается, что 0! = 1. Найдите все трёхзначные числа, равные сумме факториалов своих цифр.

1535. Четырёхзначное число А оканчивается цифрой 1. Двузначное число, образованное цифрами тысяч и сотен, цифра десятков и цифра единиц числа А — три последовательных члена арифметической прогрессии. Среди всех таких чисел А найдите то, у которого разность цифры десятков и цифры сотен наименьшая.

ЕГЭ №18 (19). Теория чисел. Рекуррентная задача – самая сложная задача мартовского статграда 2021

ЕГЭ 18 (19) – это задачи на теорию чисел, на свойства чисел, на последовательности. Что такое рекуррентная последовательность?

Сейчас узнаете…

Последовательности чисел нам хорошо известны ещё с 8 – 9 класса. Например, прогрессии – арифметическая и геометрическая.

На ЕГЭ довольно часто попадаются задачи на последовательности – как на стандартные прогрессии, так и на необычные – у каждой из которых какая-то своя формула. И формулы у таких последовательностей обычно рекуррентные – то есть такие, когда каждое следующее число вычисляется через значения каких-то предыдущих.

Например, самая известная не-прогрессия – это последовательность Фибоначчи: каждое число равно сумме двух предыдущих.

Такие последовательности – это не просто очередные бессмысленные упражнения математиков (которым, как известно, делать нечего, вот и грузят всех своими задачками). Последовательности очень часто встречаются нам в жизни, и с их помощью очень удобно описывать некоторые процессы.

Например, говорят, что Фибоначчи свою последовательность придумал, наблюдая за размножением кроликов: первые 2 месяца жизни кролик просто растёт, а потом начинает каждый месяц рожать нового кролика (в среднем).

Сколько будет кроликов через полгода? Через год? В задаче 18 (19 из последнего статграда нам попалась как раз такая последовательность.

Смотрите видео, и вы научитесь исследовать такие последовательности, а также узнаете, как правильно решается эта задача.

Тема:   Решение задания (цифровая запись числа) из базовой части ЕГЭ

Почему то дети  хорошо запоминают признаки делимости на 2 и на 5, а остальные признаки забывают.

В связи с эти тем, рекомендую на уроках в 10-11 классах уделить время на повторение признаков делимости чисел. Напомним признаки делимости, которые изучаются в школе:

 1.Натуральное число делится на 2 тогда и только тогда, когда последняя цифра числа оканчивается на четную цифру т.е 0, 2, 4, 6 или 8.

 2. Натуральное число делится на  3 тогда и только тогда когда  сумма его цифр делится соответственно на 3 .

 3. Натуральное число делится на 5 тогда и только тогда, когда последняя цифра числа оканчивается на  0 или на 5.

 4. Натуральное число делится на  4 или 25 тогда и только тогда когда число, образованное последними его двумя цифрами нули или делится   соответственно

на 4 или 25.

 5. Натуральное число делится на 9 тогда и только тогда когда  сумма его цифр делится соответственно на 9.

 5.1. Все натуральные числа, которые делятся на 9, всегда делятся и на 3.

Теперь рассмотрим признаки делимости некоторые простые числа:

 6. Натуральное число делится на  7 тогда и только тогда когда разность между числом десятков и удвоенной цифрой единиц делится на 7.

 7. Натуральное число делится на  11 тогда и только тогда когда разность между суммой цифр, стоящих на четных местах и суммой цифр, стоящих на нечетных местах делится на 11

 8.Натуральное число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13

 9. Натуральное число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17

 10. Натуральное число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19.

11. Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков, кратно 23.

12.Натуральноечисло делится на 29 тогда и только тогда, когда число десятков, сложенное с утроенным числом единиц, делится на 29.

Немного об общих свойствах.

Если m, k не имеют общих делителей, кроме 1, и число n делится на m и делится на k, то n делится на mk.. Если же наибольший общий делитель m и k выше 1, такой признак использовать нельзя. Например, если число одновременно делится на 4 и 6, то не факт, что оно делится на 24 (пример — 36). 

Только что названный признак можно обобщить так: если число n делится на m и делится на k, то n делится на наименьшее общее кратное m и k. Например, если число делится на 4 и на 6, то оно делится на 12. 

Пусть p = kq, где k > 1 — натуральное число. Если n делится на p, то n делится на q, а если n не делится на q, то n не делится и на p. Яркий пример: нечётное число не делится на 4, поскольку оно не делится на 2, в итоге тут можно даже не использовать правило последней пары цифр, названное выше (в случае чётного числа для проверки делимости на 4 придётся применять то правило).

Теперь, рассмотрим признаки делимости на некоторые составные числа:

на 6, 8. 12,18,20,24.

1.Натуральное число делится на  8 тогда и только тогда когда число, образованное последними его тремя цифрами нули или делится  на 8.

2.Натуральное число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.

3. Натуральное число делится на 18 тогда и только тогда, когда оно делится на 2 и на 9.

4. Натуральное число делится на 20 тогда и только тогда, когда оно делится на 4 и на 5.

5. Натуральное число делится на 24 тогда и только тогда, когда оно делится на 3 и на 8.

 Теперь рассмотрим конкретные примеры из ЕГЭ. Начнем с самых простеньких.

1. Вычеркните в числе 141565041 три цифры так, чтобы получившееся число делилось

на 30. В ответе укажите ровно одно получившееся число.

Решение: Натуральное число делится на 30 тогда и только тогда, когда оно

делится на 3 и на 10 т.к 3 и 8  — взаимно простые числа. Поэтому последней цифрой должен быть обязательно 0, тогда последние две цифры уходят сразу.

Делимость на 10 выполнилось, осталось выполнить делимость на 3 и вычеркнуть одно число.

Сумма оставшихся цифр равна 1+4+1+5+6+5+0=22.Значит, можно вычеркнуть либо1(в любой позиции) либо 4. Тогда получаются три числа:415650, 145650 и 115650.В ответе укажем одно из них.

2. Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9.

Решение: Трехзначное число, сумма цифр которых равно 20 можно можно записать следующими способами ( позиция цифр не имеет значение т.к. речь идет о сумме цифр):

Для удобства начнем с чисел, начинающихся с 9, таких у нас четыре, числа, начинающихся с цифры 8 две и одно число начинается с цифры 7.

992, 983,974,965    884,875,866,  776.

И так таких чисел всего 8. Из них 1,2,4,6 явно видно, что сумма квадратов цифр не делятся на 3( так кА по 2 цифры кратно 3, а одна не кратно 3.

3. Найдите трёхзначное натуральное число, большее 400, которое при делении на 6 и на 5 даёт равные ненулевые остатки и первая слева цифра которого является средним арифметическим двух других цифр. В ответе укажите какое-нибудь одно такое число.

Решение: Число делится на 5 и 6 если оно делится на 30.

Ненулевые одинаковые остатки при делении на 5 и 6  могут быть только 1,2,3 или 4.

Потому искомые числа могут иметь вид: 30k +1, 30k +2, 30k +3, или30k +4.

Так как 400:3= 13,(3), то первое искомое  трехзначное число  вида 30k +1   равно 421.Дальше составим список:

421,451,481,511,541,571,601,631,661,691,721,751,781,811,841,871,901,931,961,991.

422,452,482,512,542,572,602,632,662,692,722,752,782, 812,842,872,902,932,962,992

423,453,483,513,543,573,603,633,663,693,723,753,783, 813,843,873,903,933,963,993

424,454,484,514,544,574,604,634,664,694,724,754,784, 814,844,874,904,934,964,994

Я понимаю, что слишком много чисел получилось, но они легко составляются.

Теперь осталось выполнить последнее условие: первая слева цифра является средним арифметическим двух других цифр. Это легко подобрать устно из этого списка, это числа: 453, 573 и 693. В ответе нужно указать одно из них.

4. Найдите трёхзначное число, кратное 25, все цифры которого различны, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.

Решение: Чтобы число делилось на 25, оно должно заканчиваться на 00, 25, 50 или 75.Выпишем все такие трехзначные числа:

100,125,150,175,200,225, 250,275,300,325,350.475,500,525,550,575,600,625,650,

675,700,725,750,775,800,825,850,875,900,925,950,975.

Учитывая, что все цифры различны, из этого списка остаются: 125,150,175, 250,275, 325,350,475, 525, 575, 625,650,675, 725,750, 825,850,875, 925,950,975.

Легко проверить, что среди этих чисел только у следующих чисел сумма квадратов делится на 3: 125,175, 275, 425,475,725,825 и 875.  

Осталось отсеять из них числа, сумма квадратов которых кратно 9. В итоге остаются числа 125, 175, 275, 725, 825, 875. В ответе укажем одно из них.

5. Найдите четырёхзначное число, кратное 88, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.

Решение: Число делится на 88, если оно делится на 8 и на 11. Признак делимости на 8: число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на 8. Признак делимости на 11: число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо разность этих сумм делится на 11. Используя признак делимости на 8, и учитывая, что все цифры искомого числа должны быть чётны и различны получаем, что последними цифрами числа могут быть: 024, 048, 064, 208, 240, 264, 280, 408, 480, 608, 624, 640, 648, 680, 824, 840, 864. Используя признак делимости на 11 получим, что условию задачи удовлетворяют числа: 6248, 8624, 2640.

Ответ: 2640, 6248 или 8624.

Пример 11. Десятичная запись числа в общем виде. Понятие оценки сверху и снизу