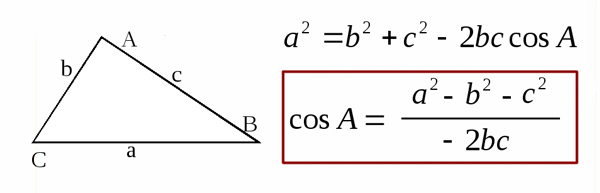Девятое задание егэ информатика

На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 9 задания. Объясняется тема о работе в электронных таблицах и базах данных.

Содержание:

  • ЕГЭ по информатике 9 задания объяснение
    • Анализ диаграмм и графиков в электронных таблицах
    • Типы ссылок в ячейках
    • Построение диаграмм
  • Тренировочные задания 9 ЕГЭ по информатике и их решение
    • Встроенные функции в электронных таблицах
    • Задания с диаграммами (задания прошлых лет для тренировки)

9-е задание: «Электронные таблицы»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— да,

Максимальный балл

— 1,

Примерное время выполнения

— 6 минут.

  
Проверяемые элементы содержания: Умение обрабатывать числовую информацию в электронных таблицах

До ЕГЭ 2021 года — определенные типы этого задания были заданием № 7 ЕГЭ

Ниже рассмотрены наиболее часто встречающиеся функции и их смысл. Наводите курсор на пример для просмотра ответа.

Таблица: Наиболее часто используемые функции

русский англ. действие синтаксис
СУММ SUM Суммирует все числа в интервале ячеек СУММ(число1;число2)
Пример:
=СУММ(3; 2)
=СУММ(A2:A4)
СЧЁТ COUNT Подсчитывает количество всех непустых значений указанных ячеек СЧЁТ(значение1, [значение2],…)
Пример:
=СЧЁТ(A5:A8)
СРЗНАЧ AVERAGE Возвращает среднее значение всех непустых значений указанных ячеек СРЕДНЕЕ(число1, [число2],…)
Пример:
=СРЗНАЧ(A2:A6)
МАКС MAX Возвращает наибольшее значение из набора значений МАКС(число1;число2; …)
Пример:
=МАКС(A2:A6)
МИН MIN Возвращает наименьшее значение из набора значений МИН(число1;число2; …)
Пример:
=МИН(A2:A6)
ЕСЛИ IF Проверка условия. Функция с тремя аргументами: первый аргумент — логическое выражение; если значение первого аргумента — истина, то результатом выполнения функции является второй аргумент. Если ложно — третий аргумент. ЕСЛИ(лог_выражение;
значение_если_истина;
значение_если_ложь)
Пример:
=ЕСЛИ(A2>B2;»Превышение»;»ОК»)
СЧЁТЕСЛИ COUNTIF Количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. СЧЁТЕСЛИ(диапазон, критерий)
Пример:
=СЧЁТЕСЛИ(A2:A5;»яблоки»)
СУММЕСЛИ SUMIF Сумма непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. СУММЕСЛИ
(диапазон, критерий, [диапазон_суммирования])
Пример:
=СУММЕСЛИ(B2:B25;»>5″)
  • следует иметь в виду, что при использовании функции СРЗНАЧ не учитываются пустые ячейки и текстовые ячейки; например, после ввода формулы в C2 появится значение 2 (не учитывается пустая А2):

    • 1

    Анализ диаграмм и графиков в электронных таблицах

    Типы ссылок в ячейках

    Формулы, записанные в ячейках таблицы, бывают относительными, абсолютными и смешанными.

    • Имена ячеек в относительной формуле автоматически меняются при переносе или копировании ячейки с формулой в другое место таблицы:

      • Относительная адресация

      Относительная адресация:
      имя столбца вправо на 1
      номер строки вниз на 1

    • Имена ячеек в абсолютной формуле не меняются при переносе или копировании ячейки с формулой в другое место таблицы.
    • Для указания того, что не меняется столбец, ставится знак $ перед буквой столбца. Для указания того, что не меняется строка, ставится знак $ перед номером строки:

      • объяснение егэ по информатике

      Абсолютная адресация:
      имена столбцов и строк при копировании формулы остаются неизменными

    • В смешанных формулах меняется только относительная часть:

      • информатика егэ теория

      Смешанные формулы

    Построение диаграмм

    • Диаграммы используются для наглядного представления табличных данных.
    • Разные типы диаграмм используются в зависимости от необходимого эффекта визуализации.
    • Так, круговая и кольцевая диаграммы отображают соотношение находящихся в выбранном диапазоне ячеек данных к их общей сумме. Иными словами, эти типы служат для представления доли отдельных составляющих в общей сумме.
    • Соответствие секторов круговой диаграммы (если она намеренно НЕ перевернута) начинается с «севера»: верхний сектор соответствует первой ячейке диапазона.

      • круговая диаграмма, объяснение 9 задания егэ

    • Типы диаграмм Линейчатая и Гистограмма (на левом рис.), а также График и Точечная (на рис. справа) отображают абсолютные значения в выбранном диапазоне ячеек.

      • гистограмма, 9 задание егэ

    Егифка ©:

    решение 9 задания ЕГЭ

    * Некоторые изображения, представленные в изложении теоретического материала, заимствованны с сайта К. Полякова

    Тренировочные задания 9 ЕГЭ по информатике и их решение

    Плейлист видеоразборов задания на YouTube:
    Задание демонстрационного варианта 2022 года ФИПИ

    Встроенные функции в электронных таблицах

    9_00: 9 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
    Найдите разность между максимальным значением температуры и её средним арифметическим значением.
    В ответе запишите только целую часть получившегося числа.

    Типовые задания для тренировки

    9_01: Задание 1:

    Задание выполняется с использованием прилагаемых файлов

      
    Найдите разность между максимальным и минимальным числом в диапазоне C48:Y360. В ответе запишите только целую часть числа.

    ✍ Решение:

      Добавим формулы в пустые ячейки:

    • Ячейка A502 = МАКС(C48:Y360)
    • Ячейка B502 = МИН(C48:Y360)
    • любая пустая ячейка =A502-B502
    • Оставляем только целую часть (отсекаем дробную, не округляя число).

    Ответ: 920

    9_02: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл 9-J1.xls электронной таблицы, содержащей вещественные числа – показатели высот над уровнем моря географических точек.

    Найдите среднее значение всех отрицательных показателей и максимальное положительное значение.

    В качестве ответа укажите целую часть суммы найденных значений.

    ✍ Решение:

    • Перейдите в пустую ячейку (например, АО1).
    • Поскольку для вычисления среднего арифметического используется дополнительное условие (только отрицательные показатели), то проще использовать формулу СРЗНАЧЕСЛИ. Внесите формулу в заготовленную ячейку:
      • =СРЗНАЧЕСЛИ(A1:AN500;"<0")

      Здесь условие обязательно должно быть в кавычках.

    • Таким же образом вычислим максимальное положительное значение, используя функцию МАКСЕСЛИ.
    • Добавьте формулу в пустую ячейку AO2:
      • =МАКСЕСЛИ(A1:AN500;A1:AN500;">0")
    • Вычислим сумму в ячейке АО3:
      • =СУММ(AO1;AO2)

      Получилось 502,531856

    • Отбрасывая дробную часть, получаем 502.

    Ответ: 502

    9_03: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл 9-j2.xl s электронной таблицы, содержащей вещественные числа – успеваемость учеников школ города по учебным дисциплинам за четвертую четверть.

    Найдите школы с максимальным и минимальным средними показателями.
    В качестве ответа укажите два числа – номера найденных школ, сначала с наименьшим показателем, затем с наибольшим.

    ✍ Решение:

    • Поскольку средние значения по дисциплинам расставлены по столбцам, то необходимо выполнить вычисление общего среднего арифметического по каждой школе в каждом столбце.
    • Для этого в пустой ячейке B18 для школы №1 напишите формулу вычисления среднего арифметического:
      • =СРЗНАЧ(B2:B16)
    • Скопируйте формулу на всю строку вправо (во все столбцы школ).
    • Для поиска максимального значения из всех средних значений будем рассуждать следующим образом: если максимальное значение из диапазона всех найденных средних значений совпадает со средним значением конкретной школы, то выводим значение ячейки номера школы, иначе – оставляем значение пустым.
    • Т.е. поставьте курсор на ячейку B20 и введите формулу:
      • =ЕСЛИ(МАКС($B$18:$AI$18)=B18;B1;"")
    • Здесь обязательно для диапазона необходимо использовать абсолютную адресацию (знаки $), иначе при копировании диапазон изменится, а нам этого не надо.
    • Скопируйте формулу на всю строку вправо. В строке появилось значение 8.
    • Для поиска минимального значения будем придерживаться таких-же рассуждений.
    • Т.е. поставьте курсор на ячейку B21 и введите формулу:
      • =ЕСЛИ(МИН($B$18:$AI$18)=B18;B1;"")
    • Скопируйте формулу на всю строку вправо. В строке появилось значение 32.

    Ответ: 32 8

    9_04: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
    Найдите разность между максимальным значением температуры и её средним арифметическим значением в первой половине дня (до 12:00 включительно).
    В ответе запишите только целую часть получившегося числа.

    ✍ Решение:

      Добавим формулы в пустые ячейки:

    • Ячейка A94 = МАКС(B2:N92) = 35,6
    • Ячейка A95 =СРЗНАЧ(B2:N92) = 21,4
    • любая пустая ячейка =A94-A95 = 14,2
    • Оставляем только целую часть (отсекаем дробную, не округляя число).

    Ответ: 14

    9_05: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
    Найдите разность между максимальным значением температуры в апреле и её средним арифметическим значением во второй половине дня (с 12:00) за тот же период.
    В ответе запишите только целую часть получившегося числа.

    ✍ Решение:

      Добавим формулы в пустые ячейки. Возьмем значения ячеек только за апрель (04 месяц). Для поиска среднего арифметического значения учтем также, что время должно быть с 12.00, то есть со столбца N:

    • Ячейка A94 = МАКС(B2:Y31) = 26,0
    • Ячейка A95 = СРЗНАЧ(N2:Y31) = 21,0
    • любая пустая ячейка =A94-A95 = 5,0
    • Оставляем только целую часть (отсекаем дробную, не округляя число).

    Ответ: 5

    9_06: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
    Найдите разность между максимальным и минимальным значением температуры среди измерений, сделанных в 17:00.
    В ответе запишите только целую часть получившегося числа, округлять не нужно.

    ✍ Решение:

      Добавим формулы в пустые ячейки. Возьмем значения ячеек только за 17.00, то есть со столбца S:

    • Ячейка A94 =МАКС(S2:S92) = 37,8
    • Ячейка A95 =МИН(S2:S92) = 22,4
    • любая пустая ячейка =A94-A95 = 15,4
    • Оставляем только целую часть (отсекаем дробную, не округляя число).

    Ответ: 15

    9_07: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
    Посчитайте сумму средних арифметических значений температур в 16:00 и в 23:00.
    Округлите полученное число до целого и запишите его в ответ.

    ✍ Решение:

      Добавим формулы в пустые ячейки. Возьмем значения ячеек только в 16.00, то есть со столбца R и в 23.00, то есть со столбца Y:

    • Ячейка A94 =СРЗНАЧ(R2:R92) = 29,9
    • Ячейка A95 =СРЗНАЧ(Y2:Y92) = 20,8
    • любая пустая ячейка =A94+A95 = 50,7
    • После округления получаем 51.
    • Можно также решить данное задание, записав все в одну строку:
      •  = СРЗНАЧ(R2:R92)+СРЗНАЧ(Y2:Y92)

    Ответ: 51

    9_08: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
    Найдите результат деления суммы всех значений температуры на максимальное значение.
    В ответе запишите только целую часть получившегося числа, округлять не нужно.

    ✍ Решение:

      Добавим формулы в пустые ячейки. Используем в формулах вcю таблицу, то есть диапазон ячеек от B2 до Y92 (B2:Y92):

    • Ячейка A94 =МАКС(B2:Y92) = 38,0
    • Ячейка A95 =СУММ(B2:Y92) = 51807,0
    • любая пустая ячейка (поделим сумму на максимальное значение) =A95/A94 = 1363,3
    • Оставляем только целую часть = 1363.

    Ответ: 1363

    9_09: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
    Посчитайте чему будет равно самое часто встречаемое значение температуры и среднее арифметическое значений температуры за всё время измерений. Найдите разницу между самым встречаемым значением и средним арифметическим значением.
    В ответе запишите только целую часть числа (разницы).

    ✍ Решение:

      Добавим формулы в пустые ячейки. Используем в формулах вcю таблицу, то есть диапазон ячеек от B2 до Y92 (B2:Y92):

    • Для более достоверных расчетов будем использовать числа с тремя знаками после десятичной запятой. Воспользуемся кнопкой
    • Ячейка A94 =СРЗНАЧ(B2:Y92) = 23,721
    • Ячейка A95 =МОДА(B2:Y92) = 25,700

      • Для нахождения наиболее часто встречаемого значения используется функция МОДА ()

    • любая пустая ячейка =A95-A94 = 1,979
    • Оставляем только целую часть = 1.

    Ответ: 1

    9_14: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.

    В каком количестве измерений температура оказалась выше 25 градусов?

    ✍ Решение:

    • Поскольку нам необходимо посчитать количество, то будем использовать функцию СЧЁТ(). Но так как считать надо количество измерений температуры выше 25 градусов, то нужно использовать функцию с критерием, а именно, СЧЁТЕСЛИ().
    • Введите формулу в любую пустую ячейку:
      • =СЧЁТЕСЛИ(B2:Y92;">25")

      Обратите внимание, что так как с условием сравнивается диапазон, а не единственная ячейка, то само условие необходимо разместить в кавычках.

    Ответ: 942

    9_15: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    Откройте файл электронной таблицы 9-j5.xls, содержащей вещественные числа – количество баллов, которое набрали участники тестирования. В первой строке указаны дисциплины, во второй – максимальный балл за тест по дисциплине, в левом столбце – фамилии участников. Считается, что тест пройден, если участник тестирования набрал больше 60% от максимального балла. В качестве ответа укажите, сколько участников тестирования прошли больше трёх тестов.

    ✍ Решение:

    • Для начала будем сравнивать максимальный балл * 0,6 с баллом, набранным участником. Если балл участника больше, будем ставить в ячейку цифру 1, иначе — 0.
    • В ячейку B35 введем формулу:
      • =ЕСЛИ(B4>B$2*0,6;1;0)
    • Скопируем формулу на всю 35-ю строку. И затем вниз до 64 строки (так как нумерация не сначала).
    • Затем выделим полностью столбец с формулой и скопируем его вправо, до столбца О включительно (последний столбец с данными).
    • Теперь необходимо посчитать кол-во единиц в каждой строке: если их больше трех, то считаем такой вариант. Будем использовать функцию ЕСЛИ().
    • В ячейку А35:
      • =ЕСЛИ(СУММ(B35:O35)>3;1;"")
    • Копируем формулу до ячейки B64.
    • Выделяем часть столбца c рассчитанными значениями и в нижней части экрана смотрим сумму – 18.

    Ответ: 18

    9_16: Задание:

    Задание выполняется с использованием прилагаемых файлов

      
    В электронной таблице в файле 9-j10.xls хранятся вещественные числа – результаты ежечасного измерения скорости ветра на протяжении трех месяцев.

    Найдите количество дней, когда максимальная скорость ветра составляла не менее 90% от максимального значения за весь период.

    ✍ Решение:

    • Сначала найдем максимальную скорость ветра за весь период. Введем формулу в ячейку AB2:
      • =МАКС(B2:Y91)
    • Теперь посчитаем количество дней по всему диапазону дней с условием, что скорость ветра составляла бы не менее 90% от максимального значения за весь период, т.е. рассчитанного значения в ячейке AB2. Будем использовать функцию СЧЁТЕСЛИ(), так как считаем при условии.
    • Введем формулу в любую пустую ячейку:
      • =СЧЁТЕСЛИ($Z$2:$Z$91;">="&AB2*0,9)

      Обратите внимание, что в условии используются кавычки, но для добавления к условию рассчитанного значения в ячейке AB2, необходимо «приклеить» это значение с помощью знака &

    Ответ: 80

    Также можно посмотреть некоторые аналогичные задания ОГЭ

    Задания с диаграммами (задания прошлых лет для тренировки)

    9_7:

    Задан фрагмент электронной таблицы:
    1

    Как изменится значение ячейки C3, если после ввода формул переместить содержимое ячейки B2 в B3?
    («+1» означает увеличение на 1, «-1» означает уменьшение на 1):

    Варианты:
    1) -2
    2) -1
    3) 0
    4) +1

    ✍ Решение:

      Проанализируем данные электронной таблицы до перемещения:

    • В ячейке C2 будет находиться число 4, так как функция СЧЁТ подсчитывает количество непустых ячеек указанного диапазона.
    • В ячейке С3 будет находиться число 3:
      • (1 + 2 + 2 + 6 + 4) / 5 = 3

      Теперь посмотрим, что произойдет после перемещения:

    • Перемещение содержимого ячейки означает, что ячейка B2 окажется пустой, а в ячейке B3 появится число 6.
    • Тогда расчёт формулы в ячейке C2 поменяется: количество непустых ячеек диапазона A1:B2 станет равным 3.
    • Соответственно изменится и значение после расчёта формулы ячейки C3: среднее значение содержимого диапазона ячеек A1:C2 станет равным:
      • (1 + 2 + 2 + 3) / 4 = 2

      (нужно не забывать, что функция СРЗНАЧ не учитывает пустые ячейки, поэтому ячейка B2 не учтена).

    • Таким образом, значение после перемещения формулы изменилось, уменьшившись на 1. Верный ответ 2

    Результат: 2

    Подробное решение задания на видео:

    📹 YouTube здесь (теоретическое решение)

    📹 Видеорешение на RuTube здесь (теоретическое решение)

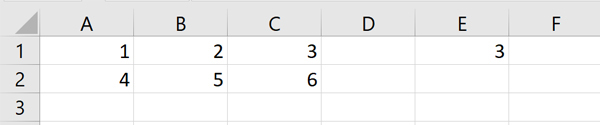
    Задание:

    В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3.

    Чему равно значение формулы =СУММ(С2:С4), если значение ячейки С5 равно 5?

    ✍ Решение:

    • Функция СРЗНАЧ предназначена для вычисления среднего арифметического значения указанного диапазона ячеек. Т.е. в нашем случае среднее значение ячеек C2, C3, C4, C5.
    • Результат функции =СРЗНАЧ(С2:С5) задан по условию, подставим его в формулу:
      • (C2 + C3 + C4 + C5)/4 = 3
    • Примем неизвестную сумму в за x и получим по формуле вычисления среднего значения:
      • x / 4 = 3
    • Найдем x:
      • x = 3 * 4 = 12  ->  C2 + C3 + C4 + C5 = 12
    • По заданию необходимо найти =СУММ(С2:С4). Зная значение в ячейке С5, вычтем его из полученной суммы и найдем ответ:
      • C2 + C3 + C4 = C2 + C3 + C4 + C5 - C5 = 
= 12 - 5 = 7

    Результат: 7

    Подробное решение смотрите на видео:

    📹 YouTube здесь

    Рассмотрим еще один пример решения 9 задания ЕГЭ по информатике:

    9_10:

    Дан фрагмент электронной таблицы:
    разбор 9 задания егэ по информатике

    Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
    Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.

    ✍ Решение:

    • Круговая диаграмма отображает доли отдельных частей в общей сумме. В нашем случае в диаграмме отражаются результаты вычисления формул в ячейках А2:С2
    • По диаграмме можно судить о том, что, скорее всего, полученные значения в формулах во всех ячейках должны быть равны (секторы диаграммы визуально равны).
    • Получим выражения из формул ячеек, подставив вместо С1 -> x:
      • А2: х + 2
В2: 8/2 = 4
С2: х * 2
    • Так как секторы диаграммы равны, то приравняем два из полученных выражений (например, С2 = В2):
      • 2 * х = 4 => x = 2

    Результат: 2

    Детальный разбор можно посмотреть в видеоуроке решения данного 9 задания ЕГЭ по информатике:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь (теоретическое решение)

    9_11:

    Задан фрагмент электронной таблицы:
    1

    Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:C2 соответствовала рисунку:
    2

    ✍ Решение:

    • По диаграмме можно судить только о следующем: если она не перевернута, то значения в ячейках A2 и B2 должны быть равны, а значение ячейки C2 — в два раза больше каждой из них.
    • Поскольку у нас неизвестны значения двух ячеек, то обозначим B1 за x, а C1 за y.
    • Подставим неизвестные в формулы и получим:

      • 1

    • Исходя из первого пункта, получаем:
      • A2 = B2 = C2/2
    • Составим систему уравнений:
      • 4y = x - y
2 * 4y = x - y + 4
    • Первое уравнение нам дает x = 5y. Подставим это значение во второе уравнение:
      • 8y = 5y - y + 4  ->  y = 1
    • Таким образом, x=5. А значения ячеек A2 = B2 = 4, C2 = 8. Т.е. изображение диаграммы действительно сходится с полученными значениями.

    Результат: 5

    Подробное теоретическое решение смотрите на видео:

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь (теоретическое решение)

    9_12:

    Дан фрагмент электронной таблицы в режиме отображения формул:
    задание 9
    После копирования диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 была построена диаграмма (график) по значениям столбцов диапазона ячеек В2:Е6.
    1_11

    Значениям D2:D6 соответствует график:

     
    Варианты:
    1) А   2) Б   3) В   4) Г

    ✍ Решение:

    • Копирование диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 буквально означает выделение диапазона АЗ:ЕЗ и протягивание маркера копирования до конца указанного блока ячеек.
    • Поскольку нас интересует только столбец D, то посмотрим, что там за формула, и что с ней произойдет при копировании:

      • 1

    • в ячейке D3 значение зависит от ячейки A3 и оно равно 2;
    • при копировании формулы столбец остается тот же (D), поэтому и в формуле буквы остаются теми же (D и A), а вот строки копируются вниз, т.е. цифры в формуле увеличиваются на единицу при движении вниз на каждую строку; соответственно, нас интересуют еще ячейки A4, A5, A6;
    • формулы ячеек A4, A5, A6 зависят от ячеек столбца B, поэтому рассмотрим получившиеся при копировании формулы столбцов A и B:

      • 1_11

    • Теперь вычислим значения в этих столбцах:

      • 2

    • Получаем точки по столбцу D: 1, -1, -1, -7, -15, что соответствует графику Г (ответ 4)

    Результат: 4

    Разбор задания смотрите на видео:

    📹 YouTube здесьздесь (теоретическое решение)

    9_13:

    Дан фрагмент электронной таблицы:
    1
    1
    Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, положительные.

    ✍ Решение задания 7:

    • На изображенной диаграмме (если она преднамеренно не перевернута) секторы соответствуют указанному диапазону ячеек при движении по часовой стрелке с «севера на юг»: т.е. А2 — синий сектор, B2 — красный и т.п. Таким образом, делаем следующий вывод:
      • А2 = B2 = 2 * C2 = 2 * D2
    • Поскольку необходимо найти C1, и оно встречается в формулах, то примем его за x.
    • Перепишем формулы согласно введенному обозначению:

      • 1_11

    • Приравняем формулы в ячейках B2 и D2 (см. п.1) и получим: 
      • B2 = 2 * D2
2(x + 5) = x + 21
2x - x = 21 - 10
x = 11
    • Т.е. С1 = 11

    Результат: 11

    Видеоразбор задания:

    📹 YouTube здесьздесь (теоретическое решение)

    Источник

    Девятое задание из ЕГЭ по информатике 2022 проверяет умение обрабатывать числовую информацию с помощью таблиц Excel.

    При подготовке к 9 заданию из ЕГЭ по информатике может быть полезна и прошлогодняя статья.

    В 2022 году пошла тенденция давать задачи, в которых применяются знания по математике и геометрии.

    Задача (Равнобедренный треугольник)

    (№ 4335) (А. Богданов) Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами равнобедренного треугольника. В ответе запишите только число.

    Источник задачи: https://kpolyakov.spb.ru/

    Решение:

    Для каждой тройки проверим:

    • Являются ли числа сторонами треугольника.
    • Есть ли среди трёх чисел два равных числа.

    Чтобы проверить первое условие, нужно вспомнить неравенство треугольника: любая сторона треугольника должна быть меньше суммы двух других сторон.

    Поставим «1» в столбце D напротив тех троек, которые подходят под первое условие.

    Сначала напишем формулу для первой строчки в ячейке D1.

    Кликаем в ячейку D1 и нажимаем кнопку Вставить функцию.

    ЕГЭ по информатике 2022 - задание 9 (Кнопка вставить функцию)

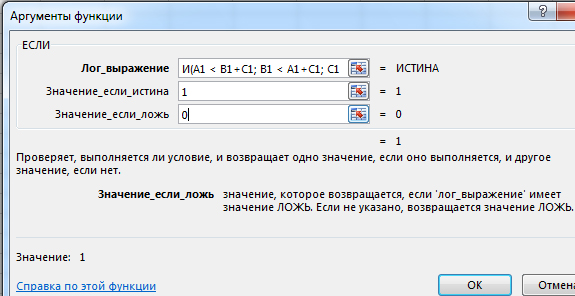
    Выбираем функцию ЕСЛИ. Пишем логическое выражение:

    И(A1 < B1+C1; B1 < A1+C1; C1 < A1+B1)

    Союз И говорит о том, что три условия должны сработать одновременно.

    В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

    ЕГЭ по информатике 2022 - задание 9 (Формула)

    Если одновременно выполняются три условия, то в ячейку идёт 1, иначе 0.

    Распространим формулу на весь столбец. Подведём курсор к правому нижнему углу. Как только загорелся чёрный крестик, кликаем два раза, и формула должна распространится на весь столбец.

    Возле тех строчек, которые удовлетворяют условию, будут нули, возле тех, которые не удовлетворяют, будут единицы.

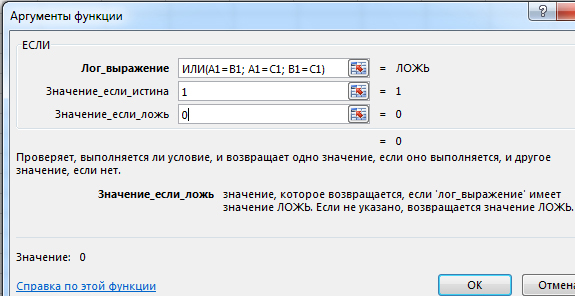
    За второе условие будет отвечать столбец E. Напишем условие в ячейку E1.

    ИЛИ(A1=B1; A1=C1; B1=C1)

    Союз ИЛИ говорит о том, что если одно условие сработает, значит, выражение будет считаться истинным.

    В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

    ЕГЭ по информатике 2022 - задание 9 (Формула)

    Распространяем всю формулу на весь столбец E. Напротив тех строчек, которые удовлетворяют второму условию, будут стоять «1», в противном случае «0».

    В столбце F ставим «1» в тех строчках, где в столбцах D И E одновременно «1», используя функцию ЕСЛИ.

    И(D1=1; E1=1)

    В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

    Выделив столбец F, в правом нижнем углу посмотрим сумму единиц в этом столбце.

    ЕГЭ по информатике 2022 - задание 9 (Формула)

    Получается ответ 229.

    Ответ: 229

    Ещё одна тренировочная задача из ЕГЭ по информатике 2022.

    Задача (Тупоугольный треугольник)

    (А. Богданов) Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами тупоугольного треугольника. В ответе запишите только число.

    Источник задачи: https://kpolyakov.spb.ru/

    Решение:

    Во-первых проверим: удовлетворяют ли числа условию неравенства треугольника (аналогично прошлой задаче). За это будет отвечать столбец D.

    В столбцах E, F, G мы будем вычислять косинусы трёх углов треугольника. Косинусы будем находить по теореме косинусов. Косинусы будем вычислять для всех троек, но учитывать только те, где выполняется неравенство треугольника.

    ЕГЭ по информатике 2022 - задание 9 (Теорема косинусов)

    В ячейке E1 напишем формулу:

    =(A1^2-B1^2-C1^2)/(-2*B1*C1)

    В ячейке F1 напишем формулу:

    =(B1^2-A1^2-C1^2)/(-2*A1*C1)

    В ячейке G1 напишем формулу:

    =(C1^2-A1^2-B1^2)/(-2*A1*B1)

    Распространим вышеуказанные формулы на соответствующие столбцы.

    Получается примерно такая картина:

    ЕГЭ по информатике 2022 - задание 9 (задача тупоугольный треугольник)

    Остался последний шаг: проверить, есть ли у какой-нибудь тройки, которая удовлетворяет неравенству треугольника, отрицательный косинус. Тупой угол имеет отрицательный косинус.

    Кликаем в ячейку H1, нажимаем кнопку «Вставить функцию» и выбираем ЕСЛИ.

    В поле Лог_выражение пишем:

    И(D1=1; ИЛИ(E1 < 0; F1 < 0; G1 < 0))

    В поле Значение_если_истина ставим «1», в поле Значение_если_ложь ставим «0». Распространяем формулу на весь столбец H, и посчитаем количество единиц в этом столбце.

    Количество единиц равно 1720.

    Ответ: 1720

    Снова нужно знать математические формулы в следующей задаче из примерных вариантов ЕГЭ по информатике 2022.

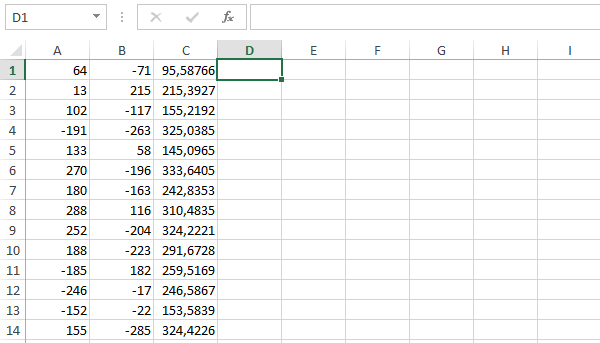
    Задача (Координаты точки)

    (А. Комков) Откройте файл электронной таблицы 9-103.xls, содержащей в каждой строке два целых числа – координаты точки на плоскости. Найдите наибольшее расстояние точки от начала координат. В ответе запишите целую часть найденного расстояния.

    Источник задачи: https://kpolyakov.spb.ru/

    Решение:

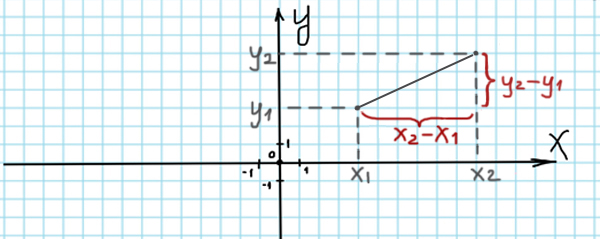
    Посмотрим, как найти расстояние от точки с координатами (x1, y1) до точки с координатами (x2, y2).

    ЕГЭ по информатике 2022 - задание 9 (задача тупоугольный треугольник)

    Здесь работает теорема Пифагора. Здесь s — расстояние между двумя точками.

    s2 = (x2-x1)2 + (y2-y1)2

    В нашей задаче первая точка — это начало координат, следовательно, x1=0 и y1=0.

    В столбце С получим расстояние от конкретной точки до начала координат.

    В ячейке C1 напишем формулу и распространим эту формулу на весь столбец.

    =КОРЕНЬ(A1^2 + B1^2)

    Получается следующее:

    ЕГЭ по информатике 2022 - задание 9 (распространяем формулу)

    Найдём максимальное значение в столбце С. Теперь кликнем в ячейку D1. Нажмём кнопку «Вставить функцию». Выберем функцию МАКС. Укажем мышкой столбец С. Нажмём «ОК».

    Целая часть получившегося числа равна 425.

    Ответ: 425

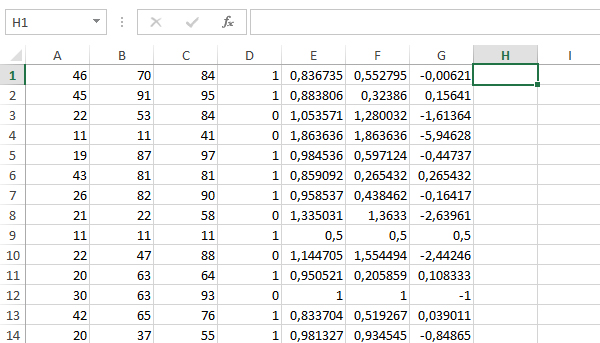
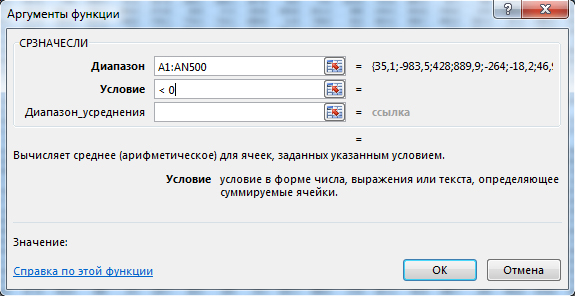
    Задача (Прочие функции)

    (Е. Джобс) Откройте файл электронной таблицы 9-j1.xls, содержащей показатели высот над уровнем моря географических точек. Найдите среднее значение всех отрицательных показателей и максимальное положительное значение. В качестве ответа укажите целую часть суммы найденных значений.

    Источник задачи: https://vk.com/inform_web

    Решение:

    Эта задача уже не связана c математическими аспектами. Здесь просто достаточно воспользоваться встроенными функциями Excel.

    Нужно найти среднее значение только отрицательных значений. Для нахождения среднего значения есть функция СРЗНАЧ. Но нам нужно именно отрицательных значений. Для нахождения среднего значения с условием есть функция СРЗНАЧЕСЛИ. Щёлкним по пустой ячейки и вы

    В поле Диапазон мы должны указать все ячейки. Это можно легко сделать с помощью мышки.

    В поле Условие укажем «< 0» (Нас интересуют числа меньше нуля).

    ЕГЭ по информатике 2022 - задание 9 (Функция значения СРЗНАЧЕСЛИ)

    Среднее значение примерно равно -497,47.

    Для определения максимального значения, можно просто воспользоваться просто функцией МАКС, т.к. всё равно максимальное число будет положительным.

    Максимальное значение получается 1000.

    Сумма равна: 1000 + (-497,47) = 502,53

    Целая часть равна 502.

    Ответ: 502

    Решим ещё одну old school’ную задачу, которая также полезна при изучении 9 задания из ЕГЭ по информатике 2022.

    Задача (old school)

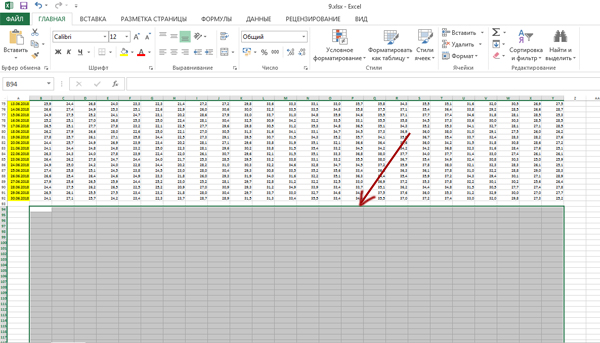
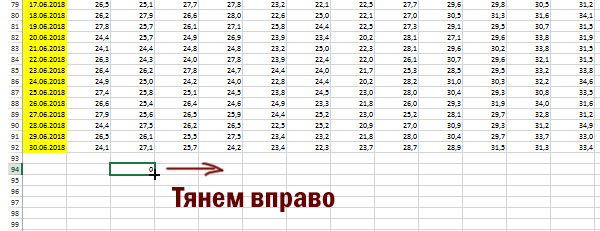
    Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений результат очередного измерения оказывался ниже результата предыдущего на 2 и более градусов.

    Источник задачи: https://inf-ege.sdamgia.ru/

    Решение:

    Внизу под числами представим мысленно область, где будет наше решение.

    ЕГЭ по информатике 2022 - задание 9 (Область решения)

    Таким образом, каждой ячейке соответствует своя ячейка в области решения.

    Если выполняется условие задачи (т.е. предыдущее значение больше, чем данное значение на 2 и более градусов), то в соответствующей ячейке из области решения будет стоять «1», в противном случае «0».

    Первая ячейка в каждой строчке нуждается в особой формуле, т.к. эта ячейка должна сравниваться с последней ячейкой предыдущей строчки.

    Для остальных ячеек формула будет одинаковая, т.к. их значение сравнивается с предыдущем значение, т.е. с левой ячейкой.

    Для первой ячейке не будем писать формулу, т.к. ей не с кем сравниваться.

    Пишем формулу для строчек в ячейке C94:

    =ЕСЛИ(B2-C2>=2;1;0)

    Здесь используем функцию ЕСЛИ, как мы делали в предыдущих задачах.

    Распространяем эту формулу на всю строчку.

    ЕГЭ по информатике 2022 - задание 9 (Распространяем формулу вправо)

    И распространяем на всё пространство (кроме первого столбца)

    ЕГЭ по информатике 2022 - задание 9 (Распространяем формулу вправо)

    Важно: Всего должно быть 91 строчка, как и в оригинале.

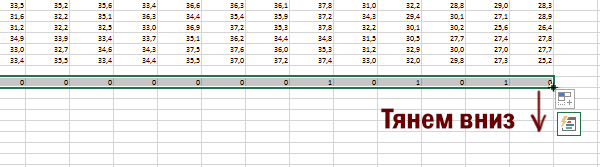
    Теперь составим формулу для первого столбца. Кликаем в ячейку B95. И пропишем формулу:

    =ЕСЛИ(Y2-B3>=2;1;0)

    Распространим данную формулу на весь столбец (на 91 строчку).

    Осталось подсчитать количество единиц во всём рабочем пространстве, например, с помощью стандартной функции СУММ.

    Количество единиц равно 458.

    Ответ: 458

    Задача (Три минимальных, три максимальных)

    Откройте файл электронной таблицы, содержащей вещественные числа — результаты ежечасного измерения концентраций примесей в исследуемой воде на протяжении трёх месяцев. Найдите количество значений концентраций, не совпадающих по значению ни с тремя минимальными, ни с тремя максимальными, полученными за весь период наблюдений.

    Решение:

    В Еxcel есть прекрасная функция СЧЁТЕСЛИ(). Рассмотрим пример.

    ЕГЭ по информатике 2023 - задание 9 (Функция СЧЁТЕСЛИ)

    Здесь в ячейке E1 написана формула:

    =СЧЁТЕСЛИ(A1:C2;»>3″)

    Первый параметр A1:C2 — это диапазон, где мы подсчитываем ячейки. Второй параметр «>3» — это условие, по которому будет считать ячейки функция.

    Эту функцию так же можно найти через кнопку Вставить функцию.

    Рассмотрим ещё одну интересную функцию НАИБОЛЬШИЙ().

    ЕГЭ по информатике 2023 - задание 9 (Функция НАИБОЛЬШИЙ)

    В ячейке E1 находится функция:

    =НАИБОЛЬШИЙ(A1:C2;1)

    В ячейке E2: =НАИБОЛЬШИЙ(A1:C2;2), в ячейке E3: =НАИБОЛЬШИЙ(A1:C2;3).

    Видим, что первый параметр у этой функции — это диапазон, где обрабатываются числа. Второй параметр — это номер наибольшего элемента, начиная с самого большого.

    Но нам эта функция не решит всех проблем, как кто-то мог подумать. Рассмотрим пример.

    ЕГЭ по информатике 2023 - задание 9 (Функция НАИБОЛЬШИЙ) пример

    Видим, что в этом примере два наибольших числа 6. И функции НАИБОЛЬШИЙ(A1:C2;1) и НАИБОЛЬШИЙ(A1:C2;2) дадут одно и то же значение.

    Вернёмся к нашей задаче. Найдём в начале наибольшее первое число. Это можно сделать, как с помощью функции МАКС(), так и с помощью функции НАИБОЛЬШИЙ().

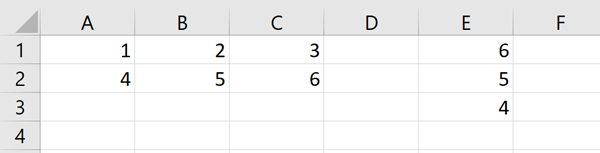
    К примеру, в ячейку Z3 пропишем формулу:

    =МАКС(B2:Y92)

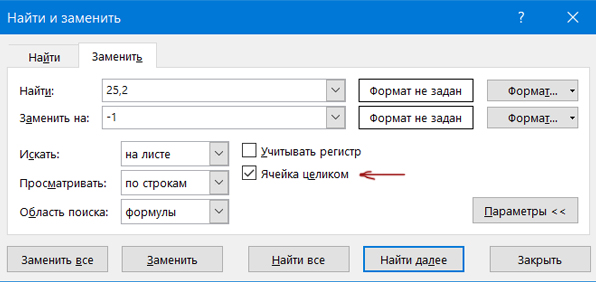
    Получается число 25,2. C помощью сочетания клавиш Ctrl + F, заменим это число очень маленьким значением, которое точно не встречается в таблице.

    Выделяем исследуемые ячейки и нажимаем Ctrl + F. Выбираем «Заменить». Раскрываем параметры замены.

    ЕГЭ по информатике 2023 - задание 9 (Замена, ячейка целиком)

    Очень важно поставить галочку «Ячейка целиком». Нажимаем Заменить всё.

    В ячейке Z3 получается следующее по максимальности число, это 19,9. Его аналогично заменяем на -1. Третье число 19,8 тоже заменяем на -1.

    Получается, что мы убрали из нашего диапазона три самых больших значения.

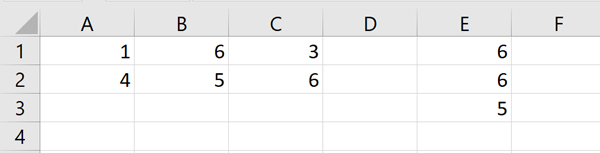
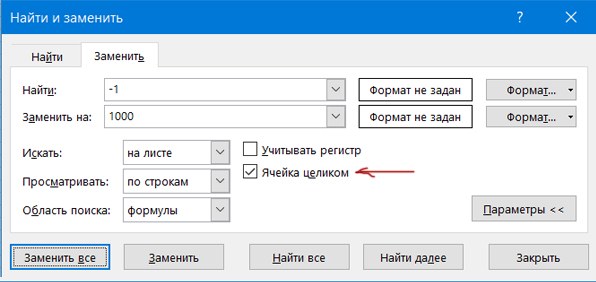
    Аналогично нужно сделать и с минимальными. Пропишем в ячейке Z3:

    =МИН(B2:Y92)

    Чтобы эта функция не находила наше значение -1, заменим число -1 на очень большое значение, которое точно отсутствует в таблице. Выделяем все числа, где хотим произвести замену и нажимаем Ctrl + F. Заменим -1 на 1000.

    ЕГЭ по информатике 2023 - задание 9 (Замена, ячейка целиком) 2

    С тремя минимальными значениями делаем то же самое, но заменяем их теперь на 1000.

    Минимальные значения будут получатся: 0,3 ; 1,3 ; 1,4.

    После того, как в нашей таблице три максимальных значения и три минимальных значения заменились на число 1000, можно применить функцию СЧЁТЕСЛИ().

    В ячейке Z3 пропишем:

    =СЧЁТЕСЛИ(B2:Y92;»<>1000″)

    Обратите внимание, если мы пишем вручную эту формулу, то второй параметр идёт в кавычках. Если мы формируем эту формулу через кнопку Вставить функцию, то кавычки подставятся автоматически. В Excel неравно обозначается <>.

    Получается ответ 2128.

    Ответ: 2128

    Счастливых экзаменов.

    Источник


    Пройти тестирование по этим заданиям
    Вернуться к каталогу заданий

    Версия для печати и копирования в MS Word

    1

    Откройте файл электронной таблицы, содержащей вещественные числа  — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.

    Задание 9

    Найдите разность между максимальным значением температуры и её средним арифметическим значением. В ответе запишите только целую часть получившегося числа.

    Источник: Демонстрационная версия ЕГЭ−2021 по информатике

    2

    Откройте файл электронной таблицы, содержащей вещественные числа  — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.

    Задание 9

    Найдите разность между максимальным значением температуры и её средним арифметическим значением. В ответе запишите только целую часть получившегося числа.

    3

    Откройте файл электронной таблицы, содержащей вещественные числа  — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.

    Задание 9

    Найдите разность между минимальным значением температуры и её средним арифметическим значением. Ответ округлите до целого числа.

    4

    Откройте файл электронной таблицы, содержащей вещественные числа  — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.

    Задание 9

    Сколько раз встречалась температура, равная округленному до десятых среднему арифметическому значению всех измерений в таблице?

    5

    Откройте файл электронной таблицы, содержащей вещественные числа  — результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.

    Задание 9

    Сколько раз встречалась температура, которая равна максимальному значению?

    Пройти тестирование по этим заданиям

    Источник

    За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: базовый.
    Средний процент выполнения: 63%
    Ответом к заданию 9 по информатике может быть цифра (число) или слово.

    Разбор сложных заданий в тг-канале

    Задачи для практики

    Задача 1

    Откройте файл электронной таблицы, содержащей в каждой строке пять натуральных чисел. Определите сколько существует строк, в которых сумма квадратов максимального и минимального значения больше, чем произведение оставшихся.

    Решение

    Для начала нужно расположить числа по возрастанию (или убыванию)

    Для этого запишем формулы, в ячейки соседние с числами:
    =НАИБОЛЬШИЙ(A1:E1;1)
    =НАИБОЛЬШИЙ(A1:E1;2)
    =НАИБОЛЬШИЙ(A1:E1;3)
    =НАИБОЛЬШИЙ(A1:E1;4)
    =НАИБОЛЬШИЙ(A1:E1;5)

    Далее найдём сумму квадратов наибольшего и наименьшего: =F1^2+J1^2
    и произведение оставшихся: =G1*H1*I1:

    Проверим в каких строчках соблюдается условие: =ЕСЛИ(K1>L1;1;0)

    После этого, просто найдём сумму столбца: =СУММ(M:M) Это и будет нашим ответом.

    Ответ: 23

    Задача 2

    Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел, координаты и радиус двух окружностей: x1, y1, r1, x2, y2, r2. Определите количество строк, в которых эти две окружности касаются, пересекаются или одна окружность находится внутри другой. В ответе запишите только число.

    Решение

    В данном случае достаточно проверить, что расстояние между окружностями меньше или равно сумме их радиусов.

    Воспользуемся формулой: =ЕСЛИ(КОРЕНЬ((D1-A1)^2+(E1-B1)^2)<=C1+F1;1;0)

    Посчитать количество окружностей, удовлетворяющих условию: =СУММ(H:H)

    В ответе запишем полученный результат.

    Ответ: 6692

    Задача 3

    Откройте файл электронной таблицы, содержащей в первой строке координаты центра и радиус окружности (x, y, R), в каждой последующей строке два целых числа, координаты точки: x1, y1. Найдите количество точек, которые лежат на окружности с центром в точке x, y и радиуса R. При решении нужно воспользоваться уравнением окружности. В ответе запишите только одно число.

    Решение

    В общем виде уравнение окружности выглядит следующим образом: (x – a)2 + (y – b)2 = R2, где a и b – координаты центра окружности.

    Для начала нужно проверить, лежит точка на окружности или нет, если точка находится на окружности, то поставить 1, иначе 0: =ЕСЛИ((A2-$A$1)^2+(B2-$B$1)^2=$C$1^2;1;0)

    Обратите внимание на то, что некоторые ссылки являются абсолютными, т.к. уравнение окружности применимо только для первой строки из таблицы.

    Посчитать количество точек, которые расположены на окружности можно по формуле: =СУММ(D:D)

    В ответе запишем полученный результат.

    Ответ: 5

    Задача 4

    Откройте файл электронной таблицы, содержащей в первой строке координаты центра и радиус окружности (x, y, R), в каждой последующей строке два целых числа, координаты точки: x1, y1. Найдите сколько точек лежит внутри круга с центром в точке x, y и радиуса R. При решении можно воспользоваться уравнением окружности. В ответе запишите только одно число.

    Решение

    В общем виде уравнение окружности выглядит следующим образом: (x – a)2 + (y – b)2 = R2, где a и b – координаты центра окружности.

    Для начала нужно проверить, лежит точка внутри окружности или нет, если точка находится внутри окружности, то поставить 1, иначе 0: =ЕСЛИ((A2-$A$1)^2+(B2-$B$1)^2<$C$1^2;1;0)

    Обратите внимание на то, что некоторые ссылки являются абсолютными, т.к. уравнение окружности применимо только для первой строки из таблицы.

    Посчитать количество точек, которые расположены внутри окружности можно по формуле: =СУММ(D:D)

    В ответе запишем полученный результат.

    Ответ: 134

    Задача 5

    Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа, координаты двух точек, начала и конца отрезка: x1, y1, x2, y2. Найдите количество отрезков, у которых длина больше 30 и не больше 50. При решении воспользоваться формулой вычисления длины отрезка по двум точкам. В ответе запишите только целую число.

    Решение

    Длина отрезка вычисляется по формуле: =КОРЕНЬ((A1-C1)^2+(B1-D1)^2)

    Найдём количество отрезков, удовлетворяющих условию задачи =СЧЁТЕСЛИМН(E:E;»>30″;E:E;»<=50″)

    В ответе запишем полученное число.

    Ответ: 2136

    Задача 6

    Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа, координаты двух точек, начала и конца отрезка: x1, y1, x2, y2. Найдите максимальную длину среди всех отрезков. При решении воспользоваться формулой вычисления длины отрезка по двум точкам. В ответе запишите только целую часть числа.

    Решение

    Длина отрезка вычисляется по формуле: =КОРЕНЬ((A1-C1)^2+(B1-D1)^2)

    Найдём наибольшее значение, при условии, что длины отрезков записаны в столбце Е: =МАКС(E:E)

    В результате получим 126,732

    В ответе запишем только целую часть.

    Ответ: 126

    Задача 7

    Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Назовём тройку «подходящей», если в ней среднее по величине число равно среднему арифметическому большего и меньшего чисел: b = (a+c)/2. Посчитайте количество «подходящих» троек. В ответе запишите только число.

    Решение

    Чтобы определить наибольшее из чисел, воспользуемся формулой в ячейке E1: =МАКС(A1:C1)

    Чтобы определить наименьшее из чисел, воспользуемся формулой в ячейке F1: =МИН(A1:C1)

    Чтобы определить среднее число, воспользуемся формулой в ячейке G1: =СУММ(A1:C1)-МАКС(A1:C1)-МИН(A1:C1)

    Формулу из условия проверим функцией: =ЕСЛИ(G1*2=E1+F1;1;0)

    Посчитаем количество строк, принимающих единицу в финальном столбце столбцах. Таких 17.

    Ответ: 17.

    Ответ: 17

    Задача 8

    Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Назовём тройку «подходящей», если в ней самое большее число равно сумме удвоенного среднего (по величине) числа и утроенного меньшего числа: a = 2b+3c. Посчитайте количество «подходящих» троек. В ответе запишите только число.

    Решение

    Чтобы определить наибольшее из чисел, воспользуемся формулой в ячейке E1: =МАКС(A1:C1)

    Чтобы определить наименьшее из чисел, воспользуемся формулой в ячейке F1: =МИН(A1:C1)

    Чтобы определить среднее число, воспользуемся формулой в ячейке G1: =СУММ(A1:C1)-МАКС(A1:C1)-МИН(A1:C1)

    Формулу из условия проверим функцией: =ЕСЛИ(E1=2*G1+3*F1;1;0)

    Посчитаем количество строк, принимающих единицу в финальном столбце столбцах. Такая только одна.

    Ответ: 1.

    Ответ: 1

    Задача 9

    Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Определите максимальную площадь треугольника, который можно составить из троек чисел. При решении воспользоваться неравенством треугольника и формулой Герона. В ответе запишите только одно число — значение максимальной площади, округлённое до целого.

    Решение

    Согласно неравенству треугольника, в любом треугольнике сумма длин двух сторон всегда должна быть больше третьей. Чтобы проверить неравенство треугольника, достаточно убедиться, что сумма длин двух наименьших сторон больше длины наибольшей стороны. Площадь треугольника будем находить по формуле Герона.

    Чтобы определить наибольший из отрезков, воспользуемся формулой в ячейке E1: =МАКС(A1:C1)

    Чтобы определить наименьший из отрезков, воспользуемся формулой в ячейке F1: =МИН(A1:C1)

    Чтобы определить средний отрезок, воспользуемся формулой в ячейке G1: =СУММ(A1:C1)-МАКС(A1:C1)-МИН(A1:C1)

    Чтобы определить полупериметр, воспользуемся формулой в ячейке H1: =СУММ(A1:C1)/2

    Неравенство треугольника проверим формулой =ЕСЛИ(E1<F1+G1;1;0)

    Добавим в эту формулу вместо единицы формулу Герона: =ЕСЛИ(E1<F1+G1;КОРЕНЬ(H1*(H1-E1)*(H1-F1)*(H1-G1));0)

    Максимальную площадь найдём поиском максимума в столбце площадей: =МАКС(I:I)

    Наибольшая площадь: 3942,653. Округлив до целого, получим окончательный ответ: 3943.

    Ответ: 3943.

    Ответ: 3943

    Задача 10

    Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Определите количество троек чисел, из которых возможно составить треугольник согласно неравенству треугольника. В ответе запишите только число.

    Решение

    Согласно неравенству треугольника, в любом треугольнике сумма длин двух сторон всегда должна быть больше третьей. Чтобы проверить неравенство треугольника, достаточно убедиться, что сумма длин двух наименьших сторон больше длины наибольшей стороны.

    Чтобы определить наибольший из отрезков, воспользуемся формулой в ячейке E1: =МАКС(A1:C1)

    Чтобы определить наименьший из отрезков, воспользуемся формулой в ячейке F1: =МИН(A1:C1)

    Чтобы определить средний отрезок, воспользуемся формулой в ячейке G1: =СУММ(A1:C1)-МАКС(A1:C1)-МИН(A1:C1)

    Неравенство треугольника проверим формулой =ЕСЛИ(E1<F1+G1;1;0)

    Посчитаем количество единиц в финальном столбце, получим 528 подходящих троек.

    Ответ: 528.

    Ответ: 528

    Задача 11

    Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа — координаты концов отрезка x1, y1, x2, y2 соответственно. Определите количество отрезков, расположенных горизонтально (параллельно оси Ох). В ответе запишите только число.

    Решение

    Отрезок параллелен оси Ох, если y1 = y2.

    В ячейку F1 запишем =ЕСЛИ(B1=D1;1;0)

    Посчитаем количество единиц в финальном столбце F, получим 12 подходящих отрезков.

    Ответ: 12.

    Ответ: 12

    Задача 12

    Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Определите максимальную площадь треугольника, который можно составить из троек чисел. При решении воспользоваться неравенством треугольника и формулой Герона. В ответе запишите только одно число — значение максимальной площади, округлённое до целого.

    Решение

    Согласно неравенству треугольника, в любом треугольнике сумма длин двух сторон всегда должна быть больше третьей. Чтобы проверить неравенство треугольника, достаточно убедиться, что сумма длин двух наименьших сторон больше длины наибольшей стороны. Площадь треугольника будем находить по формуле Герона.

    Чтобы определить наибольший из отрезков, воспользуемся формулой в ячейке E1: =МАКС(A1:C1)

    Чтобы определить наименьший из отрезков, воспользуемся формулой в ячейке F1: =МИН(A1:C1)

    Чтобы определить средний отрезок, воспользуемся формулой в ячейке G1: =СУММ(A1:C1)-МАКС(A1:C1)-МИН(A1:C1)

    Чтобы определить полупериметр, воспользуемся формулой в ячейке H1: =СУММ(A1:C1)/2

    Неравенство треугольника проверим формулой =ЕСЛИ(E1<F1+G1;1;0)

    Добавим в эту формулу вместо единицы формулу Герона: =ЕСЛИ(E1<F1+G1;КОРЕНЬ(H1*(H1-E1)*(H1-F1)*(H1-G1));0)

    Максимальную площадь найдём поиском максимума в столбце площадей: =МАКС(I:I)

    Наибольшая площадь: 3658,396. Округлив до целого, получим окончательный ответ: 3658.

    Ответ: 3658.

    Ответ: 3658

    Задача 13

    Откройте файл электронной таблицы, содержащей натуральные числа — еженедельные замеры стоимости автомобилей в течение года. В какой месяц средняя цена на все автомобили была максимальная? В ответ запишите целую часть максимальной средней цены.

    Решение

    Откроем файл электронной таблицы. В удобной для вас пустой ячейке (например, в ячейке Q2) запишем формулу =СРЗНАЧ(B2:P6), чтобы посчитать среднее арифметическое значение цены на автомобили в январе. Аналогичным образом считаем среднее арифметическое значение цены автомобилей в другие месяцы. Для удобства формулы будем записывать в ячейки Q3-Q13 включительно. Теперь нужно выбрать из получившихся чисел наибольшее. Для этого в любой свободной ячейке запишем формулу =МАКС(Q2:Q13). Получается 566682,5167. В ответ записываем только целую часть (не округляем!), получается ответ 566682.

    Ответ: 566682

    Задача 14

    Откройте файл электронной таблицы, содержащей натуральные числа — результаты ежечасного замера температуры воздуха в течение трёх месяцев. Найдите разность между средним арифметическим значением температуры в апреле и средним арифметическим значением температуры в марте. В ответ запишите только целую часть получившего числа.

    Решение

    Откроем файл электронной таблицы. В удобной для вас пустой ячейке (например, в ячейке Z2) запишем формулу =СРЗНАЧ(B2:Y32), чтобы посчитать среднее арифметическое значение температуры в марте. В другой пустой ячейке запишем формулу =СРЗНАЧ(B33:Y62), чтобы посчитать среднее арифметическое значение температуры в апреле. Теперь нужно вычесть первое число из второго. Получается 10,51890681. В ответ записываем только целую часть (не округляем!), получается ответ 10.

    .

    Ответ: 10

    Задача 15

    Откройте файл электронной таблицы, содержащей натуральные числа — результаты ежедневных продаж крепёжных материалов на протяжении шести месяцев. Найдите разность между материалами, проданными за всё время, и материалами, проданными за лето.

    Решение

    Откроем файл электронной таблицы. В удобной для вас пустой ячейке (например, в ячейке N2) записываем формулу =СУММ(B2:M184), чтобы посчитать количество товаров, проданных за всё время. В соседней пустой ячейке (например, в ячейке N3) записываем формулу =СУММ(B63:M154), чтобы посчитать количество материалов, проданных за лето. Теперь нам осталось найти разность двух чисел. Для удобства можно посчитать разность в таблице. Получается ответ 2751277.

    Ответ: 2751277

    Задача 16

    Откройте файл электронной таблицы, содержащей натуральные числа — результаты ежедневных продаж крепёжных материалов на протяжении шести месяцев. Найдите, каких крепёжных материалов продали за сентябрь больше всего, а каких — меньше всего. Посчитайте разность этих чисел.

    Решение

    Откроем файл электронной таблицы. В удобной для вас пустой ячейке (например, в ячейке B185) записываем формулу =СУММ(B155:B184), чтобы посчитать количество проданных гвоздей 15 мм за сентябрь. Далее нужно посчитать количество остальных проданных товаров за сентябрь. Для удобства тянем за правый нижний угол ячейки с формулой вправо, до ячейки M185 включительно. Теперь необходимо узнать, какого материала было продано больше всего, а какого — меньше всего, и посчитать разность этих чисел. Для удобства в пустой ячейке (например, в ячейке N185) запишем формулу =МАКС(B185:M185)-МИН(B185:M185). Получилось число 16154, которое является ответом.

    Ответ: 16154

    Рекомендуемые курсы подготовки

    Источник

    ЕГЭ информатика 9 задание разбор, теория, как решать.

    Функции в электронных таблицах, (Б) — 1 балл

    Е9.39 в строке только одно число повторяется ровно два раза

    Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: – в строке только одно число повторяется ровно два раза, остальные числа различны; – среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел. В ответе запишите только число. XLSX   Ответ:   …

    Читать далее

    Е9.38 из которых можно выбрать три числа с чётной суммой

    В каждой строке электронной таблицы записаны четыре натуральных числа. Определите, сколько в таблице таких четвёрок, из которых можно выбрать три числа с чётной суммой. XLSX Ответ: СтатГрад Вариант ИН2110402 30.03.2022 – задание №9

    Читать далее

    Е9.37 среднее арифметическое максимального и минимального чисел в тройке не превышает третьего

    Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Определите количество строк таблицы, в которых среднее арифметическое максимального и минимального чисел в тройке не превышает третьего (среднего по значению) числа. В ответе запишите только число — количество троек чисел, удовлетворяющих условию. XLSX Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание №9 …

    Читать далее

    Е9.36 которые не могут быть сторонами никакого треугольника

    В каждой строке электронной таблицы записаны четыре натуральных числа. Определите, сколько в таблице таких четвёрок, из которых можно выбрать три числа, которые не могут быть сторонами никакого треугольника, в том числе вырожденного (вырожденным называется треугольник, у которого сумма длин двух сторон равна длине третьей стороны). XLSX Ответ: СтатГрад Вариант ИН2110301 08.02.2022 – задание №9

    Читать далее

    Е9.35 принятое количество товаров больше среднего показателя количества товаров

    В таблице приведена информация о количестве принятых товаров на склад в каждые 5 минут суток. Определите количество часов, в которые принятое количество товаров больше среднего показателя количества товаров за все часы суток. XLSX   «Некрыловские варианты» от Евгения Джобса — Вариант 6

    Читать далее

    Е9.34 какое количество пар точек может являться концами отрезка

    Откройте файл электронной таблицы, содержащей в каждой строке четыре целых числа: первые два числа — координаты точки (х0; у0), следующие два числа — координаты точки (х1; у1). Выясните, какое количество пар точек может являться концами отрезка, не пересекающего ни ось Х, ни ось Y. XLSX   «Некрыловские варианты» от Евгения Джобса — Вариант 5

    Читать далее

    Е9.33 которые могут быть сторонами остроугольного треугольника

    В каждой строке электронной таблицы записаны три натуральных числа. Определите сколько среди заданных троек чисел таких, которые могут быть сторонами остроугольного треугольника. XLSX   СтатГрад Вариант ИН2110101 27.10.2021– задание №9

    Читать далее

    Е9.32 третье число может являться средней линией трапеции

    Определите количество троек, в которых третье число может являться средней линией трапеции. Откройте файл электронной таблицы, содержащий в каждой строке три натуральных числа. Первые два числа — основания трапеции. XLSX   Открытый пробник 01.11.2021 kompege.ru Л. Шастин – задание №9 

    Читать далее

    Е9.31 какое количество троек чисел может являться сторонами треугольника

    Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел может являться сторонами треугольника, то есть удовлетворяет неравенству треугольника. В ответе запишите только число. Ответ: CSV     ODS     XLS     XLSX Демонстрационный вариант ЕГЭ 2022 г.  – задание №9

    Читать далее

    Е9.30. сколько раз суточные колебания температуры не превышали 15 градусов

    Cколько раз суточные колебания температуры не превышали 15 градусов. В файле содержатся результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений суточные колебания температуры (разность между максимальной и минимальной температурой в течение суток) не превышали 15 градусов. Ответ: XLSX Источник: «Алексей Кабанов»

    Читать далее

    Источник

    Автор материалов — Лада Борисовна Есакова.

    При оцифровке звука в памяти запоминаются только отдельные значения сигнала. Чем чаще записывается сигнал, тем лучше качество записи.

    Частота дискретизации f – это количество раз в секунду, которое происходит преобразование аналогового звукового сигнала в цифровой. Измеряется в Герцах (Гц).

    Глубина кодирования (а также, разрешение) – это количество бит, выделяемое на одно преобразование сигнала. Измеряется в битах (Бит).

    Возможна запись нескольких каналов: одного (моно), двух (стерео), четырех (квадро).

    Обозначим частоту дискретизации – f (Гц), глубину кодирования – B(бит), количество каналов – k, время записи – t(Сек).

    Количество уровней дискретизации d можно рассчитать по формуле: d = 2B.

    Тогда объем записанного файла V(бит)  = f * B * k * t.

    Или, если нам дано количество уровней дискретизации,

    V(бит)  = f * log2d * k * t.

    Единицы измерения объемов информации:

    1 б (байт) = 8 бит

    1 Кб (килобайт) = 210 б

    1 Мб (мегабайт) = 220 б

    1 Гб (гигабайт) = 230 б

    1 Тб (терабайт) = 240 б

    1 Пб (петабайт) = 250 б

    При оцифровке графического изображения качество картинки зависит от количества точек и количества цветов, в которые можно раскрасить точку.

    Если X – количество точек по горизонтали,

    Y – количество точек по вертикали,

    I – глубина цвета (количество бит, отводимых для кодирования одной точки), то количество различных цветов в палитре N = 2I. Соответственно, I = log2N.

    Тогда объем файла, содержащего изображение, V(бит) = X * Y * I

    Или, если нам дано количество цветов в палитре, V(бит) = X * Y * log2N.

    Скорость передачи информации по каналу связи (пропускная способность канала) вычисляется как количество информации в битах, переданное за 1 секунду (бит/с).

    Объем переданной информации вычисляется по формуле V = q * t, где q – пропускная способность канала, а t – время передачи.

    Кодирование звука

    Пример 1.

    Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

    1) 30               2) 45           3)  75         4)  90

    Решение:

    V(бит)  = f(Гц)* B(бит) * k * t(Сек),

    где V – размер файла, f – частота дискретизации, B – глубина кодирования, k – количество каналов, t – время.

    Значит, V(Мб) = (f * B * k * t ) / 223

    Переведем все величины в требуемые единицы измерения:

    V(Мб) = (16*1000 * 32 * 2 * 12 * 60 ) / 223

    Представим все возможные числа, как степени двойки:

    V(Мб) = (24 * 23 * 125 * 25 * 2 * 22 * 3 * 15 * 22) / 223 = (5625 * 217) / 223 = 5625 / 26 =

    5625 / 64 ≈ 90.

    Ответ: 4

    !!! Без представления чисел через степени двойки вычисления становятся намного сложнее.

    !!! Частота – это физическая величина, а потому 16 кГц = 16 * 1000 Гц, а не 16 * 210. Иногда этой разницей можно пренебречь, но на последних диагностических работах она влияла на правильность ответа.

    Пример 2.

    В те­че­ние трех минут про­из­во­ди­лась четырёхка­наль­ная (квад­ро) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 16 КГц и 24-бит­ным раз­ре­ше­ни­ем. Сжа­тие дан­ных не про­из­во­ди­лось. Какая из при­ве­ден­ных ниже ве­ли­чин наи­бо­лее близ­ка к раз­ме­ру по­лу­чен­но­го файла?

    1) 25 Мбайт

    2) 35 Мбайт

    3) 45 Мбайт

    4) 55 Мбайт

    Решение:

    V(бит)  = f(Гц)* B(бит) * k * t(Сек),

    где V – размер файла, f – частота дискретизации, B – глубина кодирования (или разрешение), k – количество каналов, t – время.

    Значит, V(Мб) = (f * B * k * t ) / 223 = (16 * 1000 * 24 * 4 * 3 * 60) / 223 = (24 * 23 * 125 * 3 * 23 * 22 * 3 * 15 * 22) / 223 = (125 * 9 * 15 * 214) / 223 = 16875 / 29 = 32, 96 ≈ 35

    Ответ: 2

    Пример 3.

    Ана­ло­го­вый зву­ко­вой сиг­нал был записан сна­ча­ла с ис­поль­зо­ва­ни­ем 64 уров­ней дис­кре­ти­за­ции сиг­на­ла, а затем с ис­поль­зо­ва­ни­ем 4096 уров­ней дис­кре­ти­за­ции сиг­на­ла. Во сколь­ко раз уве­ли­чил­ся ин­фор­ма­ци­он­ный объем оциф­ро­ван­но­го звука?

                1) 64

    2) 8

    3) 2

    4) 12

    Решение:

    V(бит)  = f * log2d * k * t, где V – размер файла, f – частота дискретизации, d – количество уровней дискретизации, k – количество каналов, t – время.

    V1 = f * log264 * k * t = f * 6 * k * t

    V2 = f * log24096 * k * t = f * 12 * k * t

    V2 / V1 = 2

    Пра­виль­ный ответ ука­зан под но­ме­ром 3.

    Ответ: 3

    Кодирование изображения

    Пример 4.

    Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64×64 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

    Решение:

    V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.

    V (Кб) = (64 * 64 * log2256) / 213 = 212 * 8 / 213 = 4

    Ответ: 4

    Пример 5.

    Для хранения растрового изображения размером 64×32 пикселя отвели
    1 килобайт памяти. Каково максимально возможное число цветов в палитре изображения?

    Решение:

    V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.

    log2N = V /( X*Y) = 213 / (26 * 25) = 4

    N = 16

    Ответ:16

    Сравнение двух способов передачи данных

    Пример 6.

    До­ку­мент объ­е­мом 5 Мбайт можно пе­ре­дать с од­но­го ком­пью­те­ра на дру­гой двумя спо­со­ба­ми:

    А) Сжать ар­хи­ва­то­ром, пе­ре­дать архив по ка­на­лу связи, рас­па­ко­вать.

    Б) Пе­ре­дать по ка­на­лу связи без ис­поль­зо­ва­ния ар­хи­ва­то­ра.

    Какой спо­соб быст­рее и на­сколь­ко, если

    – сред­няя ско­рость пе­ре­да­чи дан­ных по ка­на­лу связи со­став­ля­ет 218 бит в се­кун­ду,

    – объем сжа­то­го ар­хи­ва­то­ром до­ку­мен­та равен 80% от ис­ход­но­го,

    – время, тре­бу­е­мое на сжа­тие до­ку­мен­та – 35 се­кунд, на рас­па­ков­ку – 3 се­кун­ды?

    В от­ве­те на­пи­ши­те букву А, если спо­соб А быст­рее или Б, если быст­рее спо­соб Б. Сразу после буквы на­пи­ши­те ко­ли­че­ство се­кунд, на­сколь­ко один спо­соб быст­рее дру­го­го. Так, на­при­мер, если спо­соб Б быст­рее спо­со­ба А на 23 се­кун­ды, в от­ве­те нужно на­пи­сать Б23. Слов «се­кунд», «сек.», «с.» к от­ве­ту до­бав­лять не нужно.

    Решение:

    Спо­соб А. Общее время скла­ды­ва­ет­ся из вре­ме­ни сжа­тия, рас­па­ков­ки и пе­ре­да­чи. Время пе­ре­да­чи t рас­счи­ты­ва­ет­ся по фор­му­ле t = V / q, где V — объём ин­фор­ма­ции, q — скорость пе­ре­да­чи дан­ных.

    Объем сжатого документа: 5 * 0,8 = 4 Мб =4 * 223 бит.

    Найдём общее время: t = 35 с + 3 с + 4 * 223 бит / 218 бит/с = 38 + 27 с = 166 с.

    Спо­соб Б. Общее время сов­па­да­ет с вре­ме­нем пе­ре­да­чи: t = 5 * 223 бит / 218 бит/с = 5 * 25 с = 160 с.

    Спо­соб Б быст­рее на 166 — 160 = 6 с.

    Ответ: Б6

    Определение времени передачи данных

    Пример 7.

    Ско­рость пе­ре­да­чи дан­ных через ADSL─со­еди­не­ние равна 128000 бит/c. Через дан­ное со­еди­не­ние пе­ре­да­ют файл раз­ме­ром 625 Кбайт. Опре­де­ли­те время пе­ре­да­чи файла в се­кун­дах.

    Решение:

    Время t = V / q, где V — объем файла, q — скорость пе­ре­да­чи дан­ных.

    t = 625 * 210 байт / (2 7 * 1000) бит/c = 625 * 213 бит / (125 * 210) бит/c = 5 * 23 с = 40 с.

    Ответ: 40

    Пример 8.

    У Васи есть до­ступ к Ин­тер­нет по вы­со­ко­ско­рост­но­му од­но­сто­рон­не­му ра­дио­ка­на­лу, обес­пе­чи­ва­ю­ще­му ско­рость по­лу­че­ния им ин­фор­ма­ции 217 бит в се­кун­ду. У Пети нет ско­рост­но­го до­сту­па в Ин­тер­нет, но есть воз­мож­ность по­лу­чать ин­фор­ма­цию от Васи по низ­ко­ско­рост­но­му те­ле­фон­но­му ка­на­лу со сред­ней ско­ро­стью 215 бит в се­кун­ду. Петя до­го­во­рил­ся с Васей, что тот будет ска­чи­вать для него дан­ные объ­е­мом 4 Мбай­та по вы­со­ко­ско­рост­но­му ка­на­лу и ре­транс­ли­ро­вать их Пете по низ­ко­ско­рост­но­му ка­на­лу. Ком­пью­тер Васи может на­чать ре­транс­ля­цию дан­ных не рань­ше, чем им будут по­лу­че­ны пер­вые 512 Кбайт этих дан­ных. Каков ми­ни­маль­но воз­мож­ный про­ме­жу­ток вре­ме­ни (в се­кун­дах), с мо­мен­та на­ча­ла ска­чи­ва­ния Васей дан­ных, до пол­но­го их по­лу­че­ния Петей? В от­ве­те ука­жи­те толь­ко число, слово «се­кунд» или букву «с» до­бав­лять не нужно.

    Решение:

    Нужно опре­де­лить, сколь­ко вре­ме­ни будет пе­ре­да­вать­ся файл объ­е­мом 4 Мбай­та по ка­на­лу со ско­ро­стью пе­ре­да­чи дан­ных 215 бит/с; к этому вре­ме­ни нужно до­ба­вить за­держ­ку файла у Васи (пока он не по­лу­чит 512 Кбайт дан­ных по ка­на­лу со ско­ро­стью 217 бит/с).

    Время скачивания дан­ных Петей: t1= 4*223 бит / 215 бит/с = 210 c.

    Время за­держ­ки: t2 = 512 кб / 217 бит/с = 2(9 + 10 + 3) — 17 c = 25 c.

    Пол­ное время: t1 + t2 = 210 c + 25 c = (1024 + 32) c = 1056 c.

    Ответ: 1056

    Пример 9.

    Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 219 бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 220 бит в секунду. Задержка в пункте Б (время между окончанием приема данных из пункта А и началом передачи в пункт В) составляет 25 секунд. Сколько времени (в секундах) прошло с момента начала передачи данных из пункта А до их полного получения в пункте В? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

    Решение:

    Полное время складывается из времени передачи из пункта А в пункт Б (t1), задержки в пункте Б (t2) и времени передачи из пункта Б в пункт В (t3).

    t1 = (60 * 223) / 219 =60 * 16 = 960 c

    t2 = 25 c

    t3 = (60 * 223) / 220 =60 * 8 = 480 c

    Полное время t1 + t2 +t3 = 960 + 25 + 480 = 1465 c

    Ответ: 1465

    Спасибо за то, что пользуйтесь нашими материалами.
    Информация на странице «Задача №9. Кодирование звуковой и графической информации. Передача информации, Время записи звукового файла, время передачи данных, определение объема информации.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
    Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
    Также вы можете воспользоваться другими статьями из разделов нашего сайта.

    Публикация обновлена:
    08.03.2023

    Источник

    Like this post? Please share to your friends:
  • Девятиклассникам отменили егэ
  • Девятиклассник после успешной сдачи экзамена решил поступить в пожарно спасательный колледж
  • Девятиклассник после успешной сдачи основного государственного экзамена решил поступить в пожарно
  • Девяноста рублями егэ
  • Девушки сдают экзамен порно