Инфоурок
›
Другое
›Другие методич. материалы›Дидактические материалы для подготовки к ЕГЭ: формулы сложения (10-11 класс)
-
Скачать материал
-
30.08.2015
20427
-
ZIP
82.4 кбайт -
113
скачиваний -
Рейтинг:
5 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Склярова Галина Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 6 месяцев
- Подписчики: 1
- Всего просмотров: 239412
-
Всего материалов:
24
- Преподавателю
- Математика
- Дидактические материалы для подготовки к ЕГЭ: формулы сложения (10-11 класс)
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Другие методич. материалы |
| Автор | |
| Дата | 30.07.2015 |
| Формат | zip |
| Изображения | Есть |
Поделитесь с коллегами:
Шрифт — 8 пт, интервал — 150 %
А-10 Ср-04
ВАРИАНТ 1
А-10 Ср-04
ВАРИАНТ 2
А-10 Ср-04
ВАРИАНТ 3
А-10 Ср-04
ВАРИАНТ 4
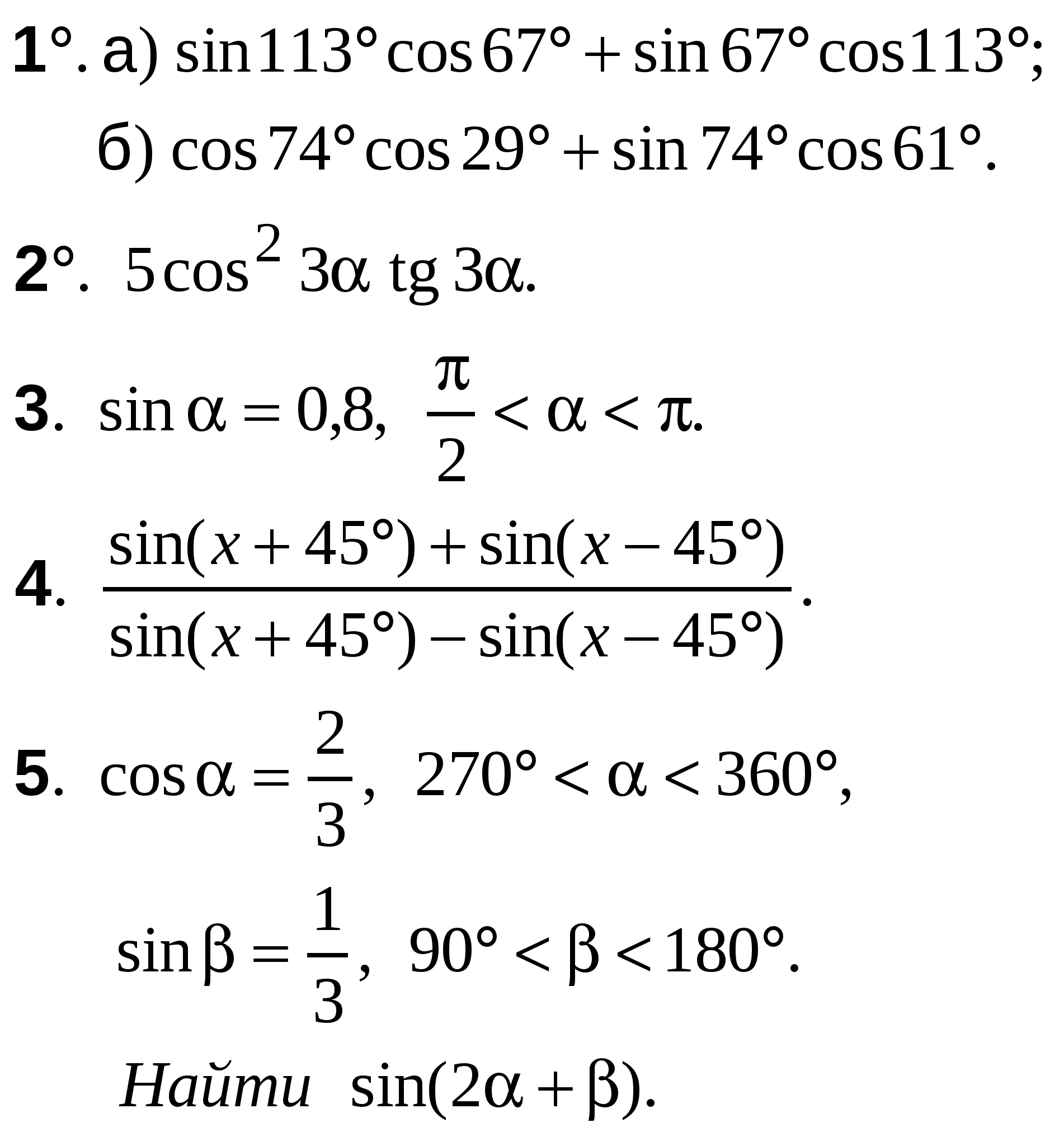
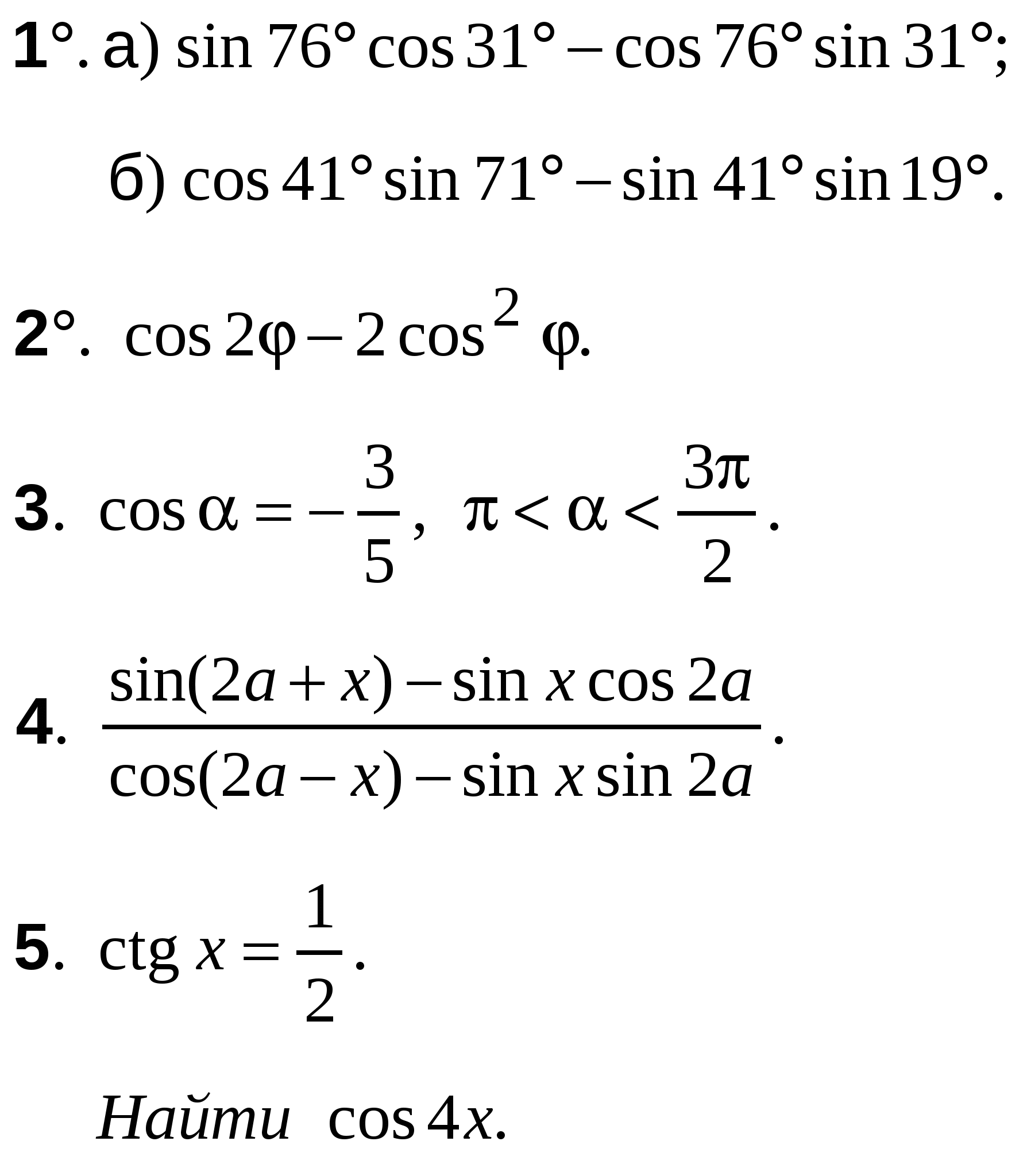
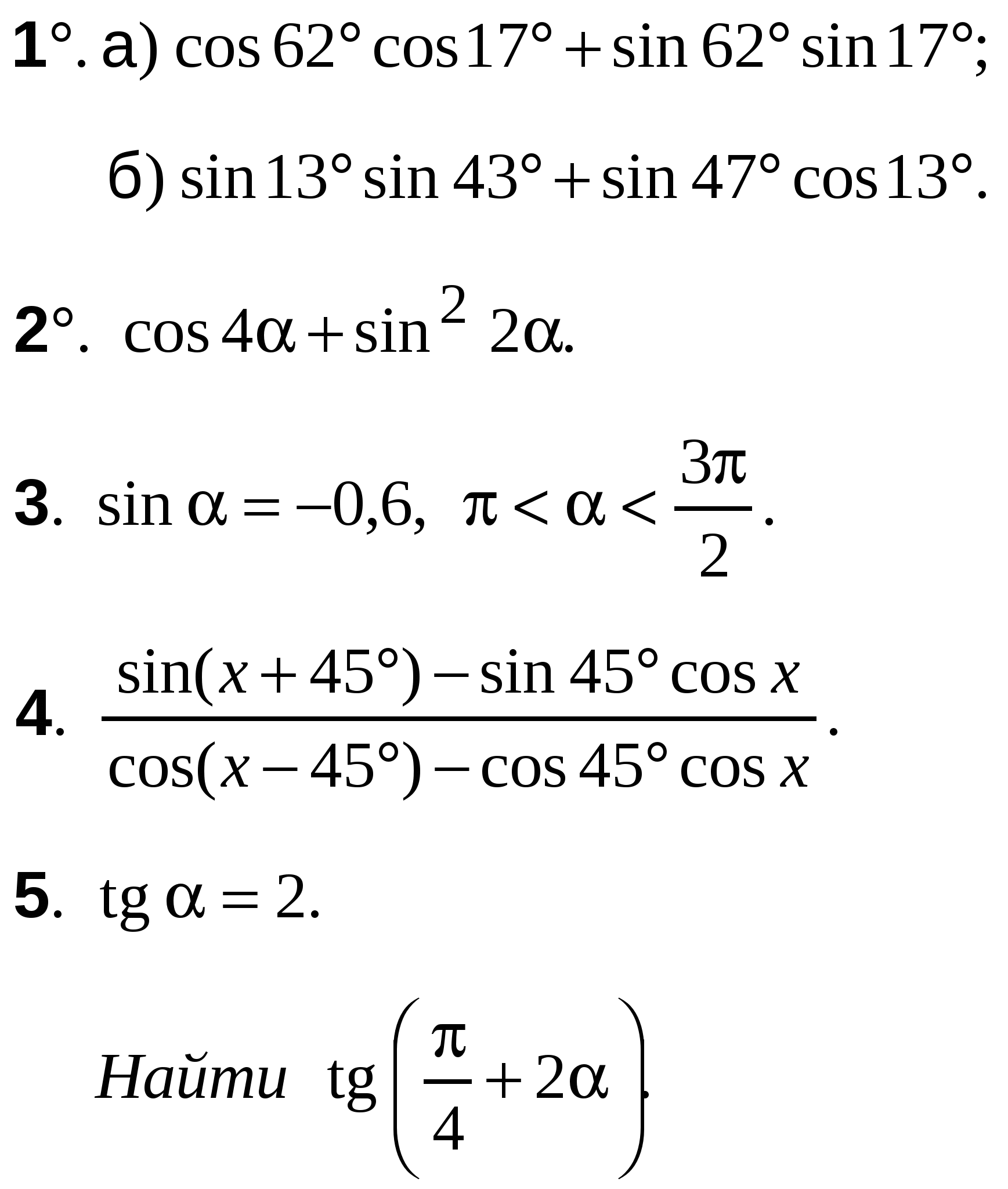

А-10 Ср-04
ВАРИАНТ 5
А-10 Ср-04
ВАРИАНТ 6
А-10 Ср-04
ВАРИАНТ 7
А-10 Ср-04
ВАРИАНТ 8
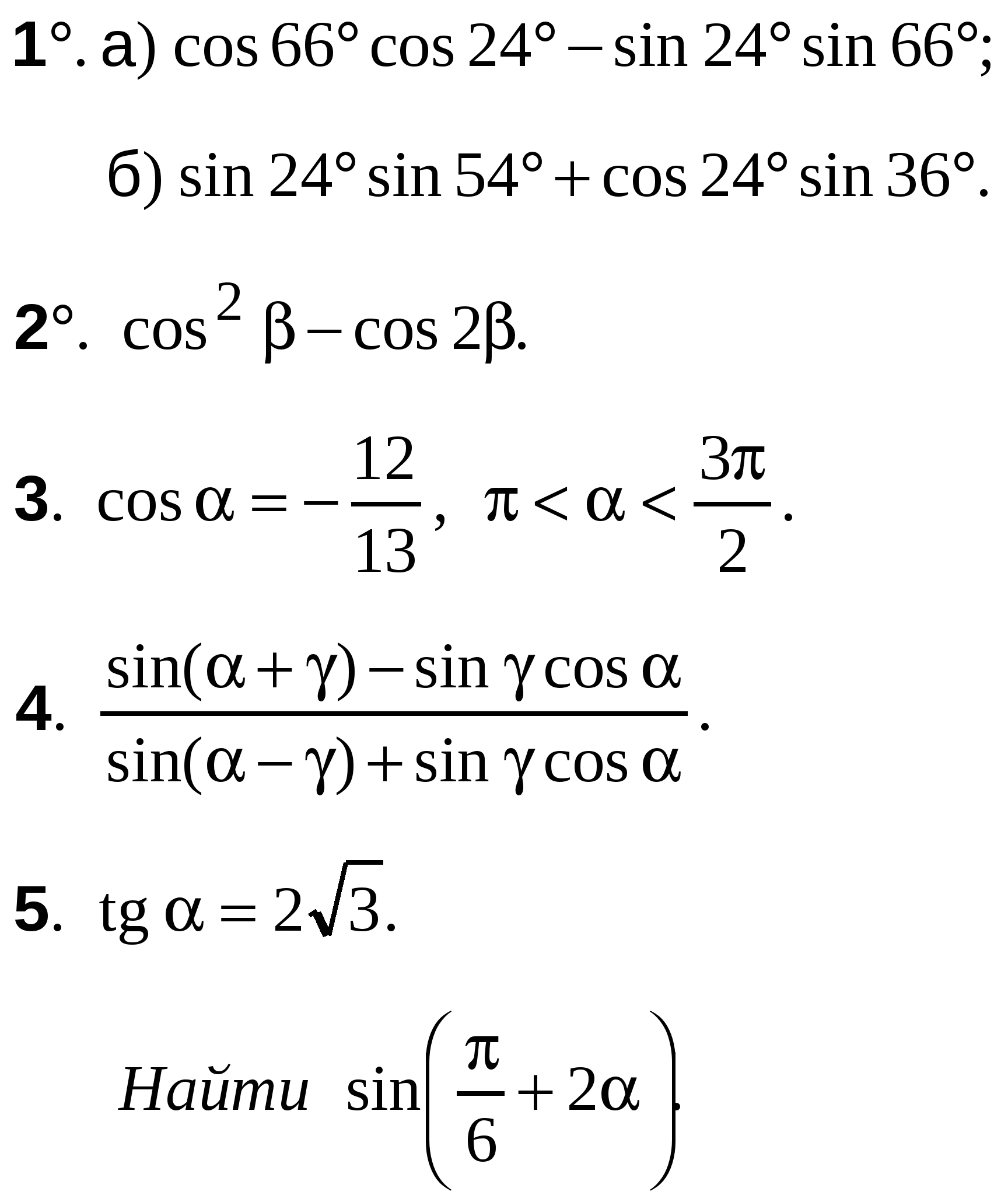
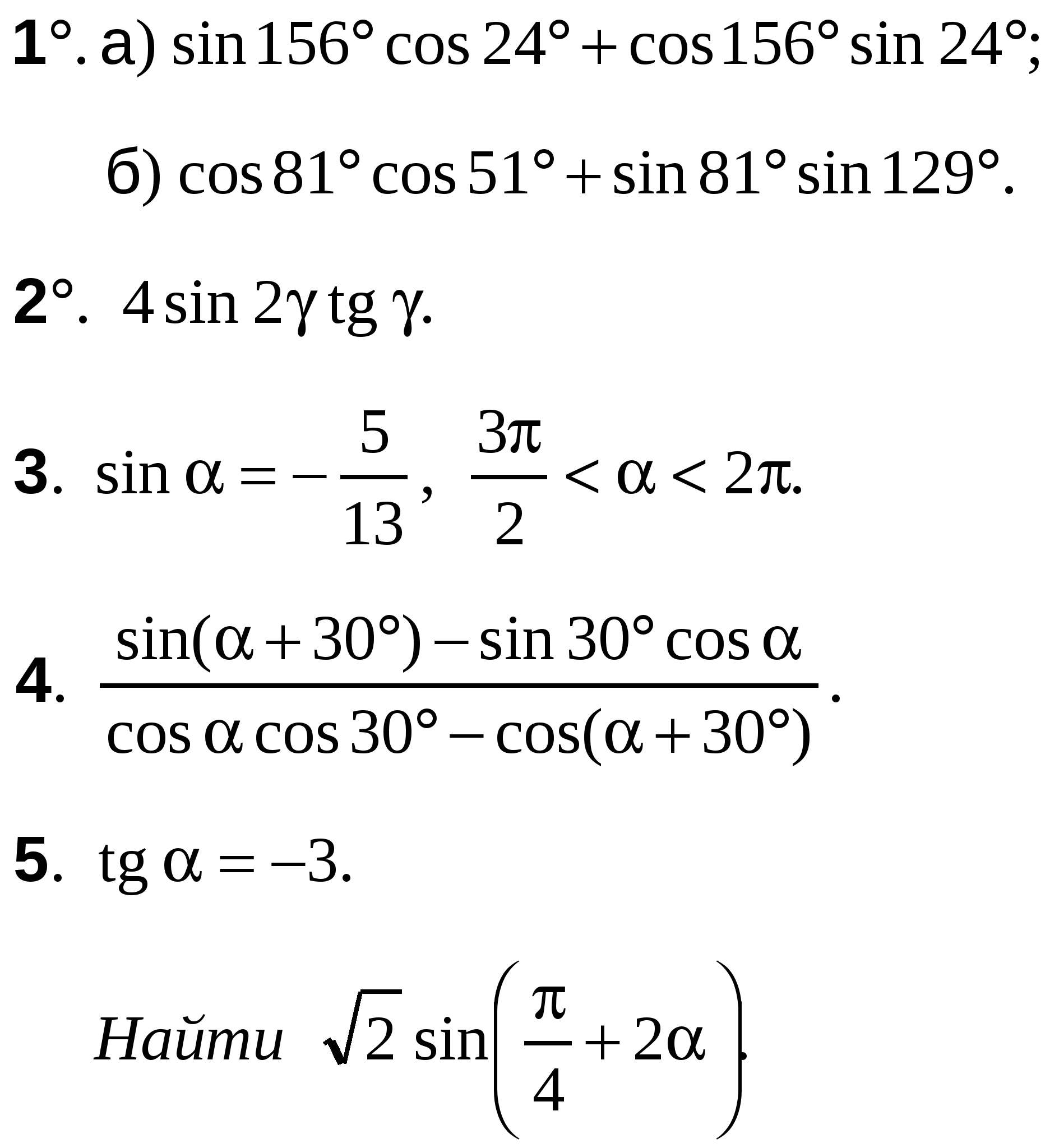
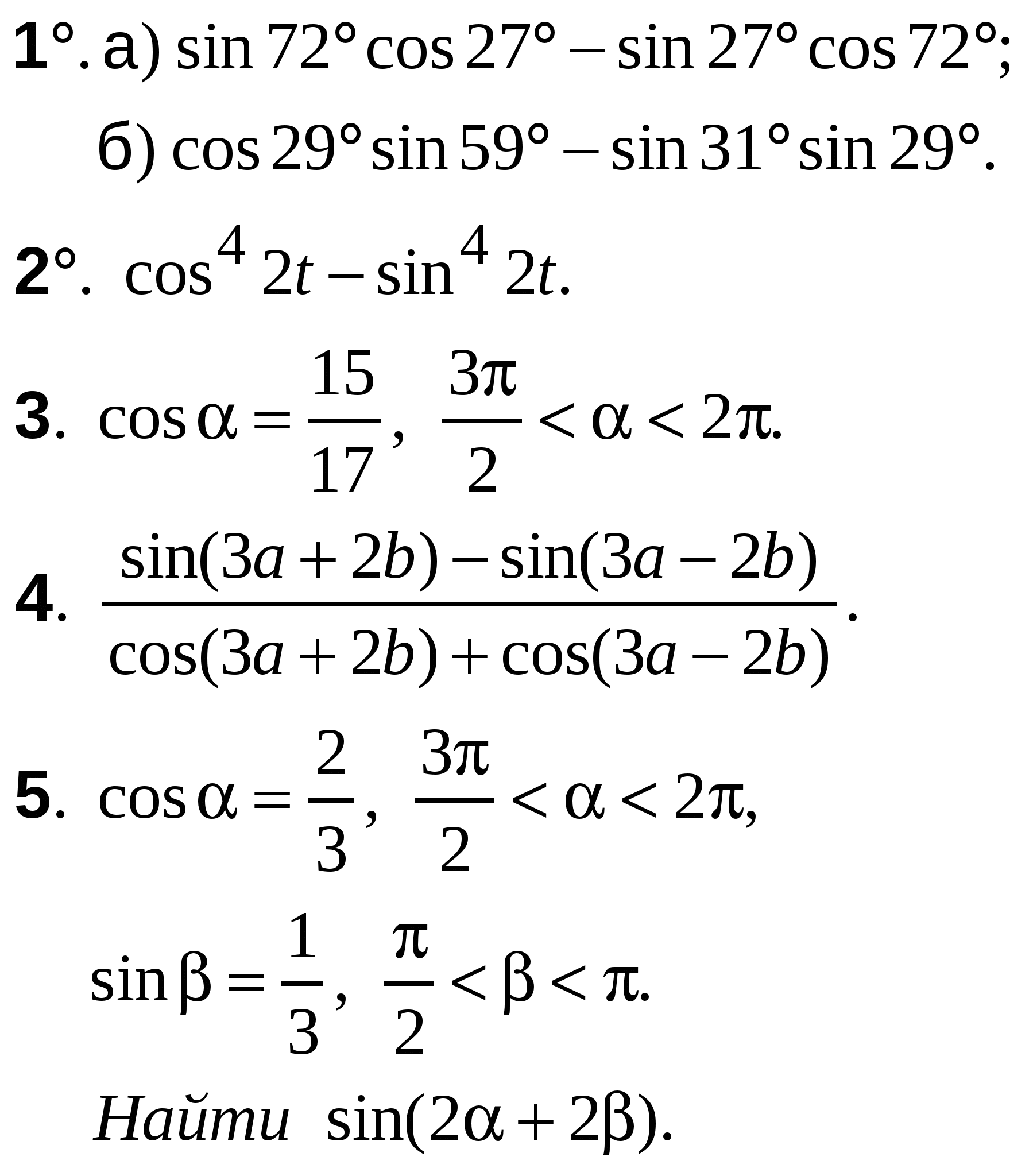

А-10 Ср-04
ВАРИАНТ 9
А-10 Ср-04
ВАРИАНТ 10
А-10 Ср-04
ВАРИАНТ 11
А-10 Ср-04
ВАРИАНТ 12

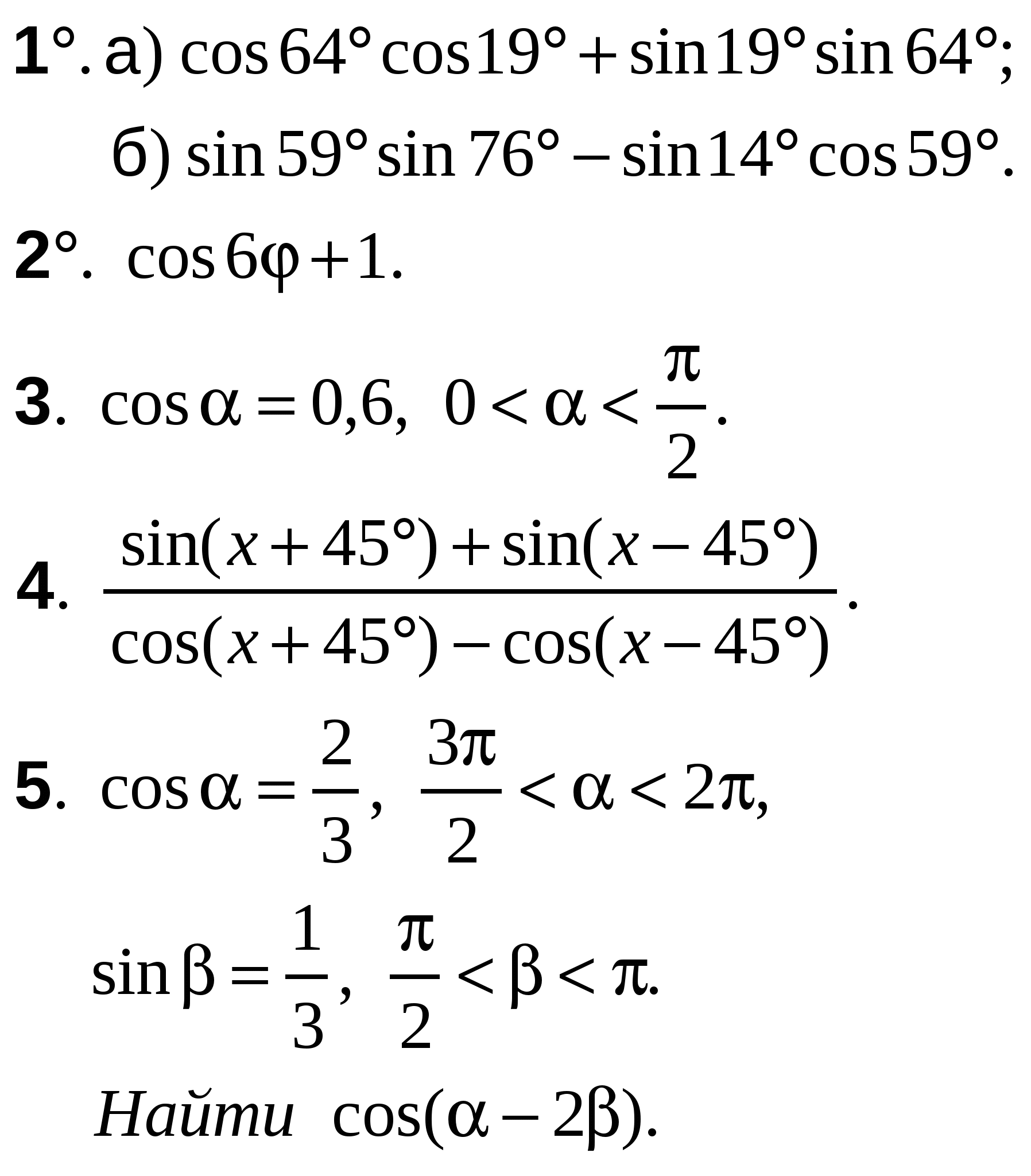
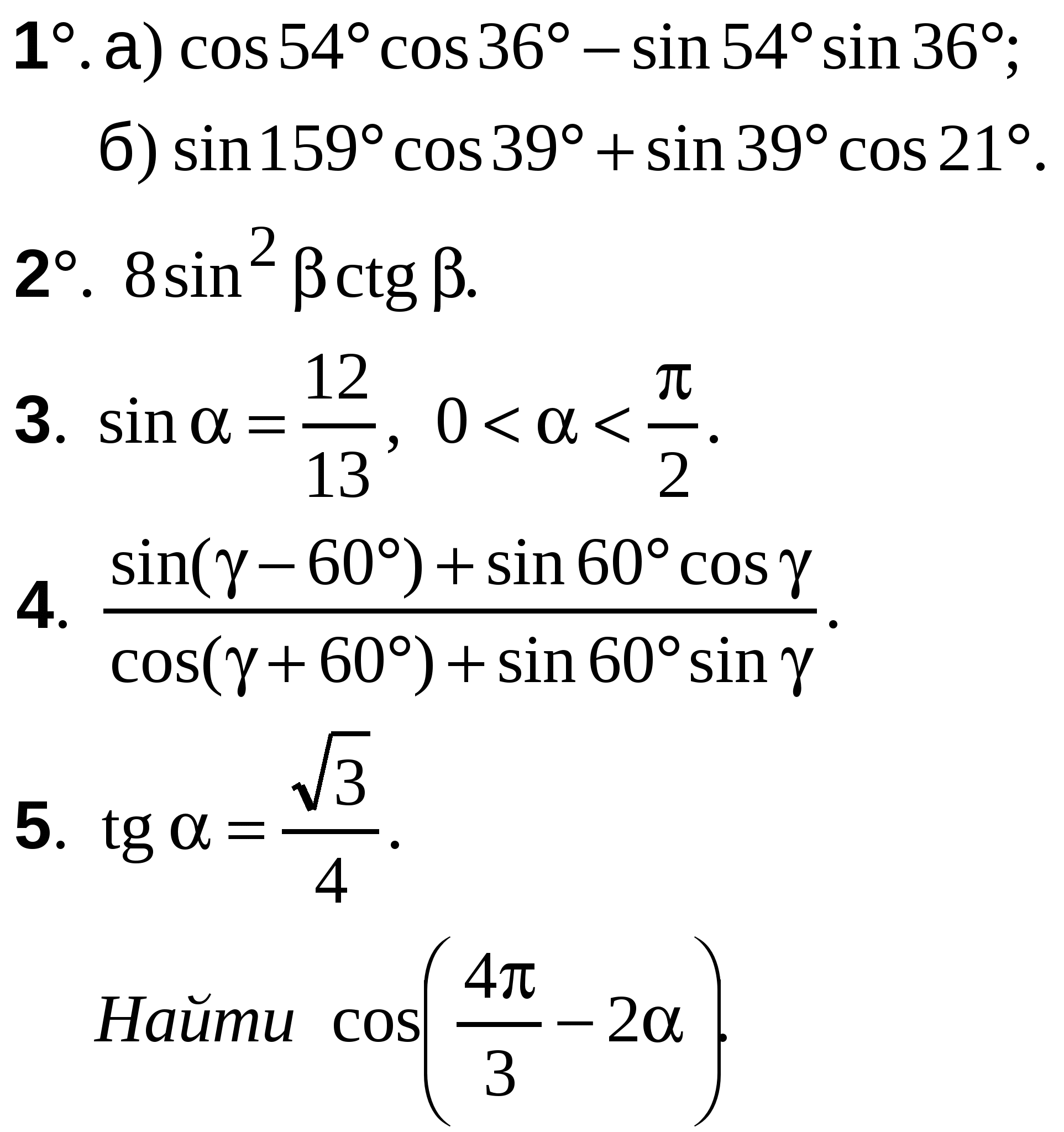
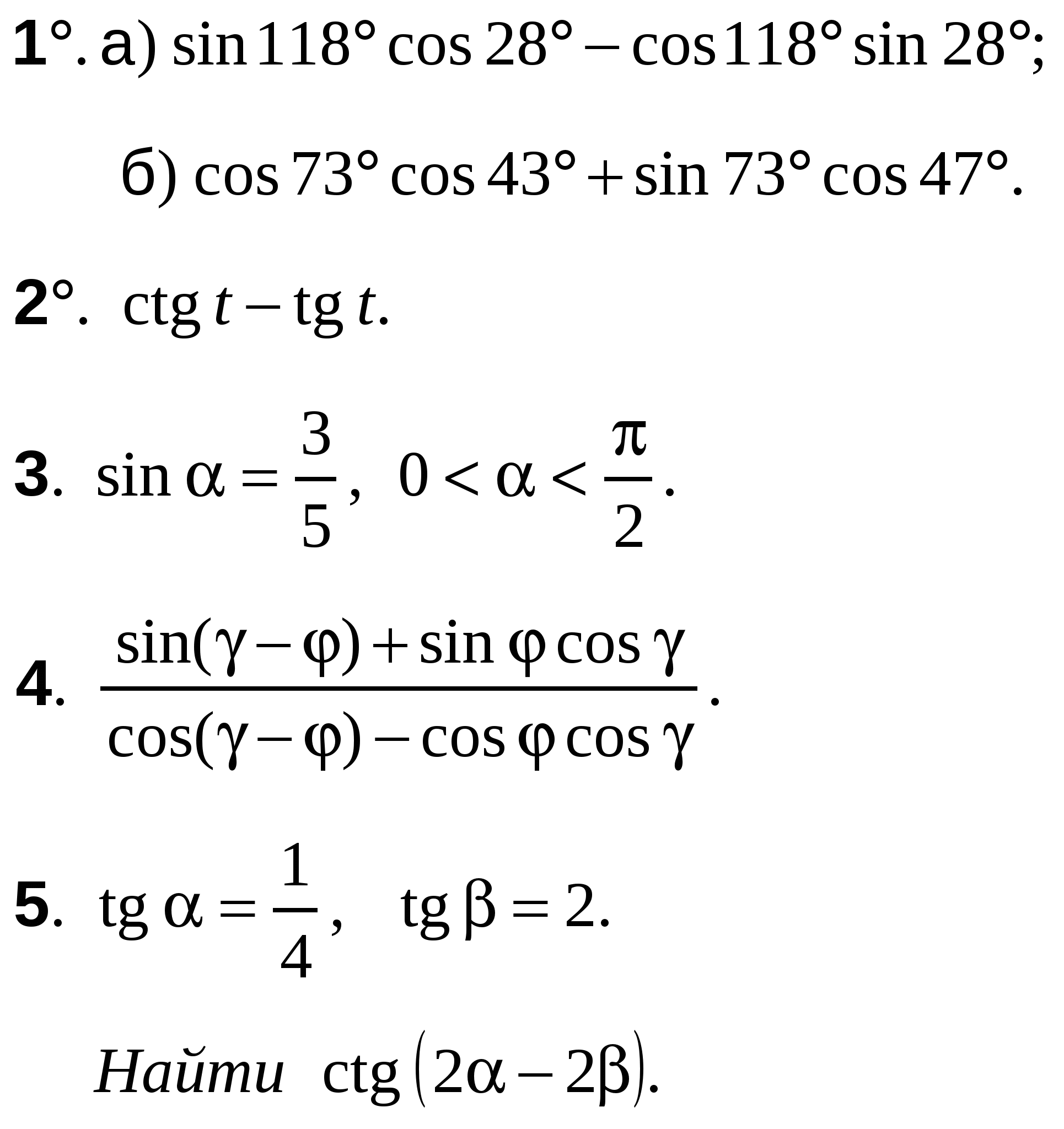
А-10 Ср-04
ВАРИАНТ 13
А-10 Ср-04
ВАРИАНТ 14
А-10 Ср-04
ВАРИАНТ 15
А-10 Ср-04
ВАРИАНТ 16
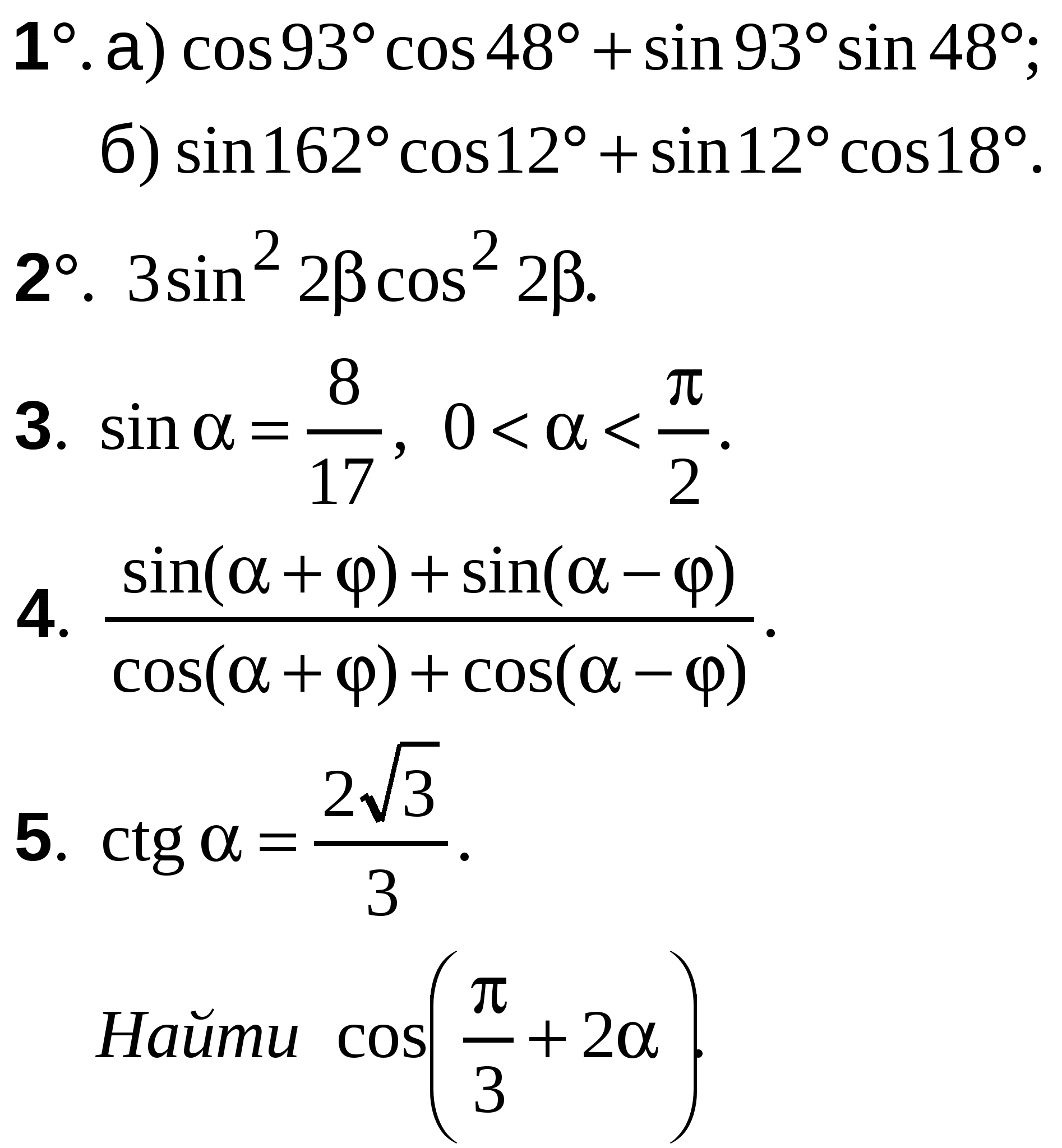
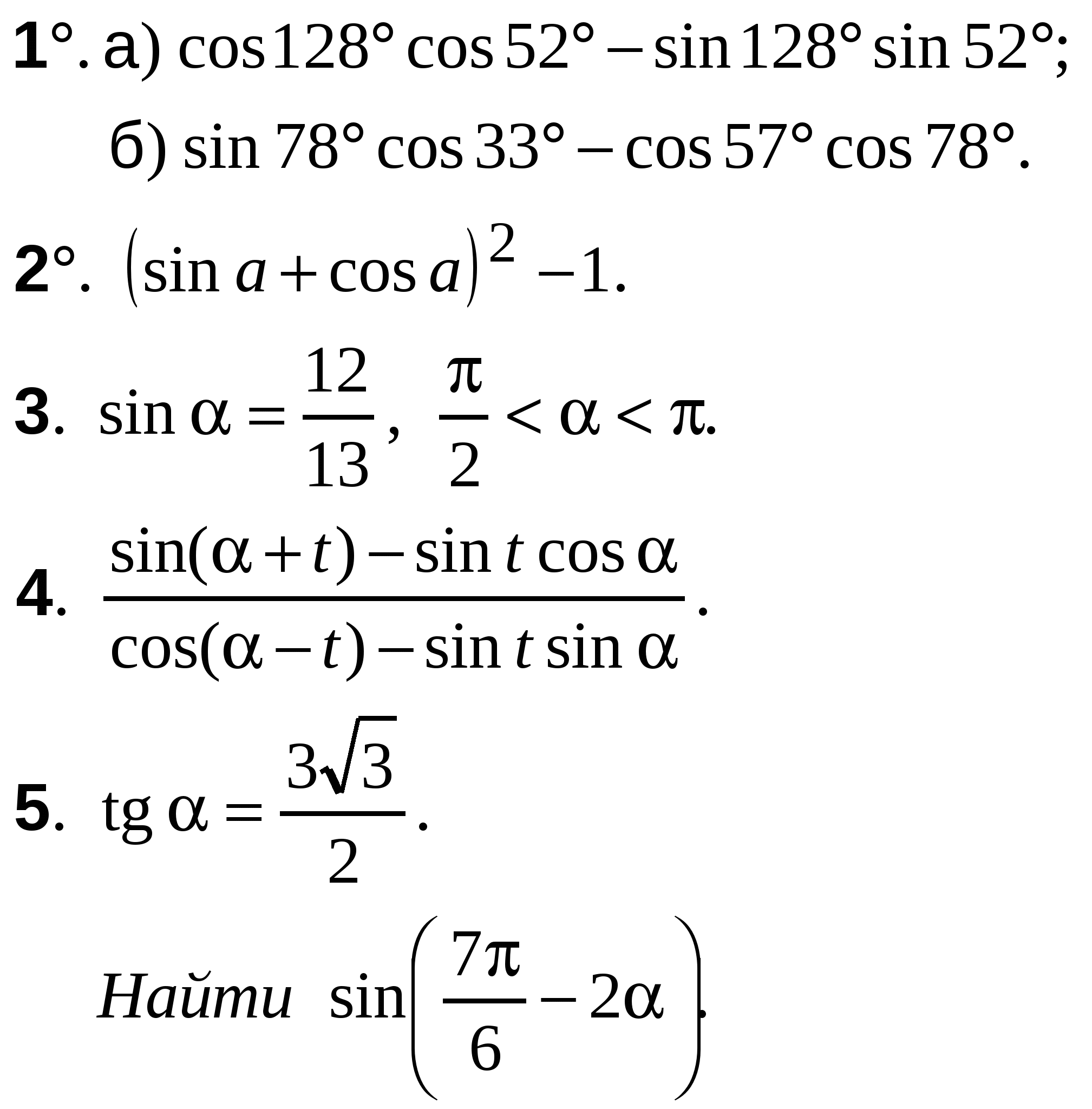
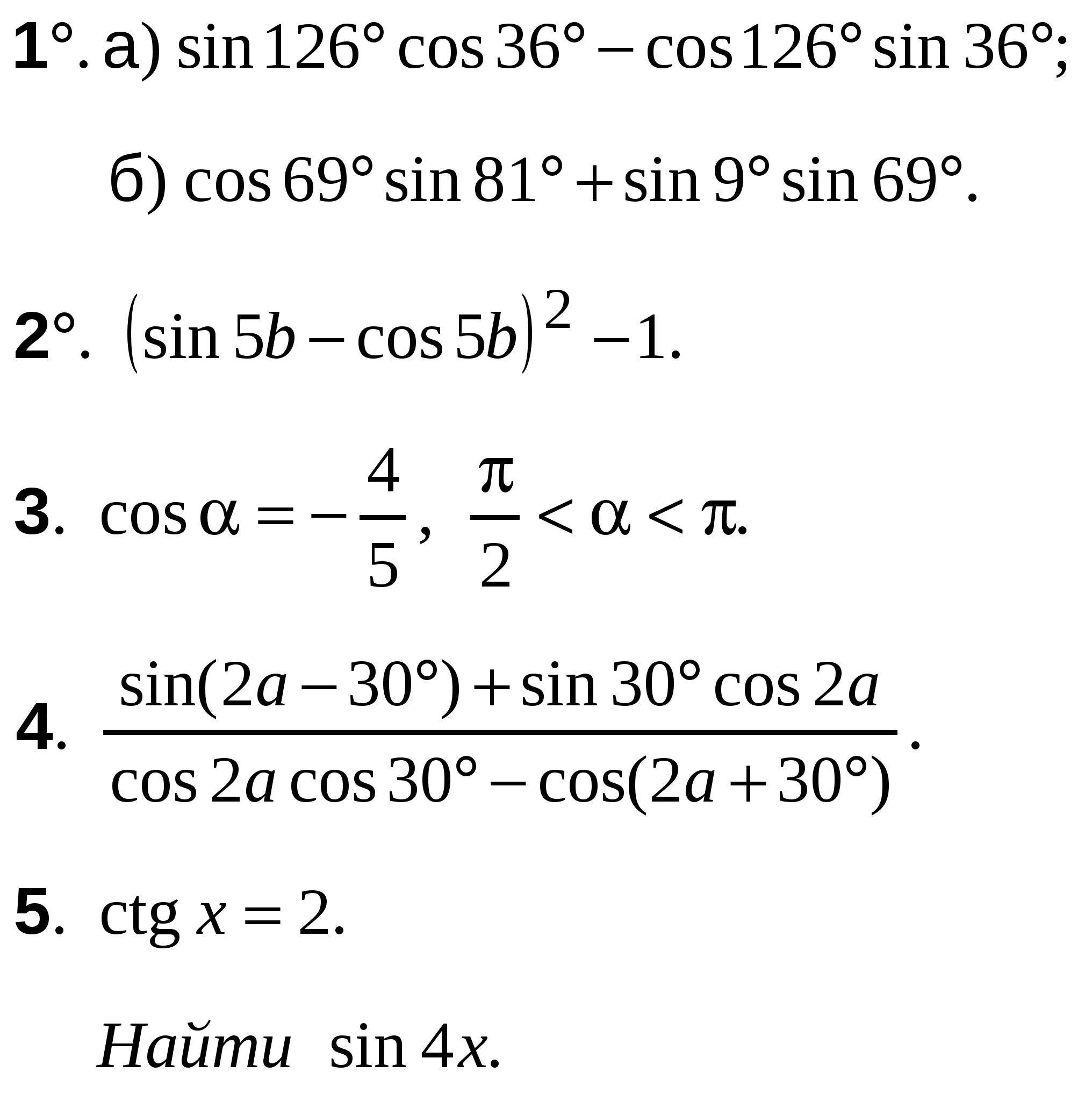
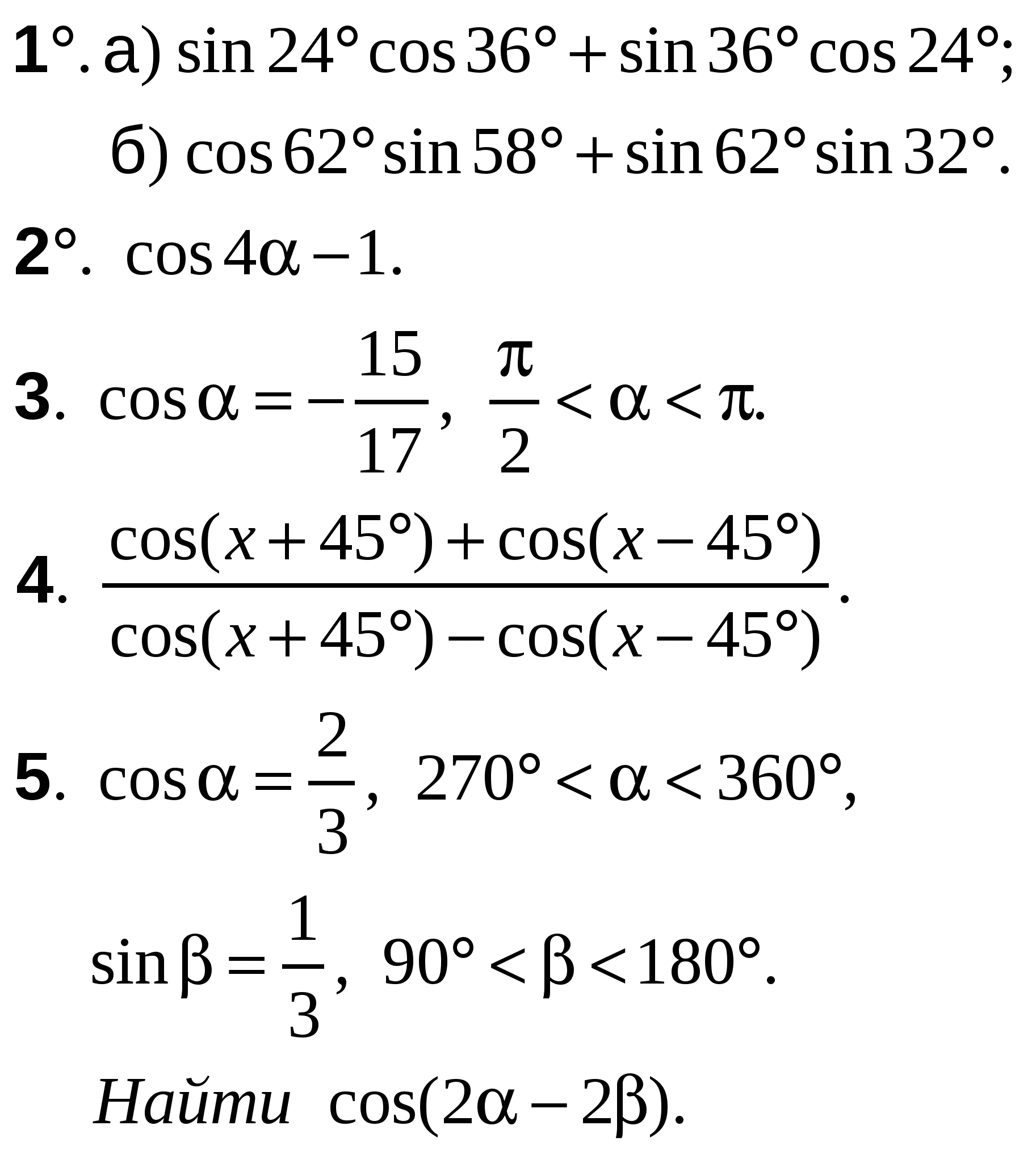
А-10 Ср-04
ВАРИАНТ 17
А-10 Ср-04
ВАРИАНТ 18
А-10 Ср-04
ВАРИАНТ 19
А-10 Ср-04
ВАРИАНТ 20
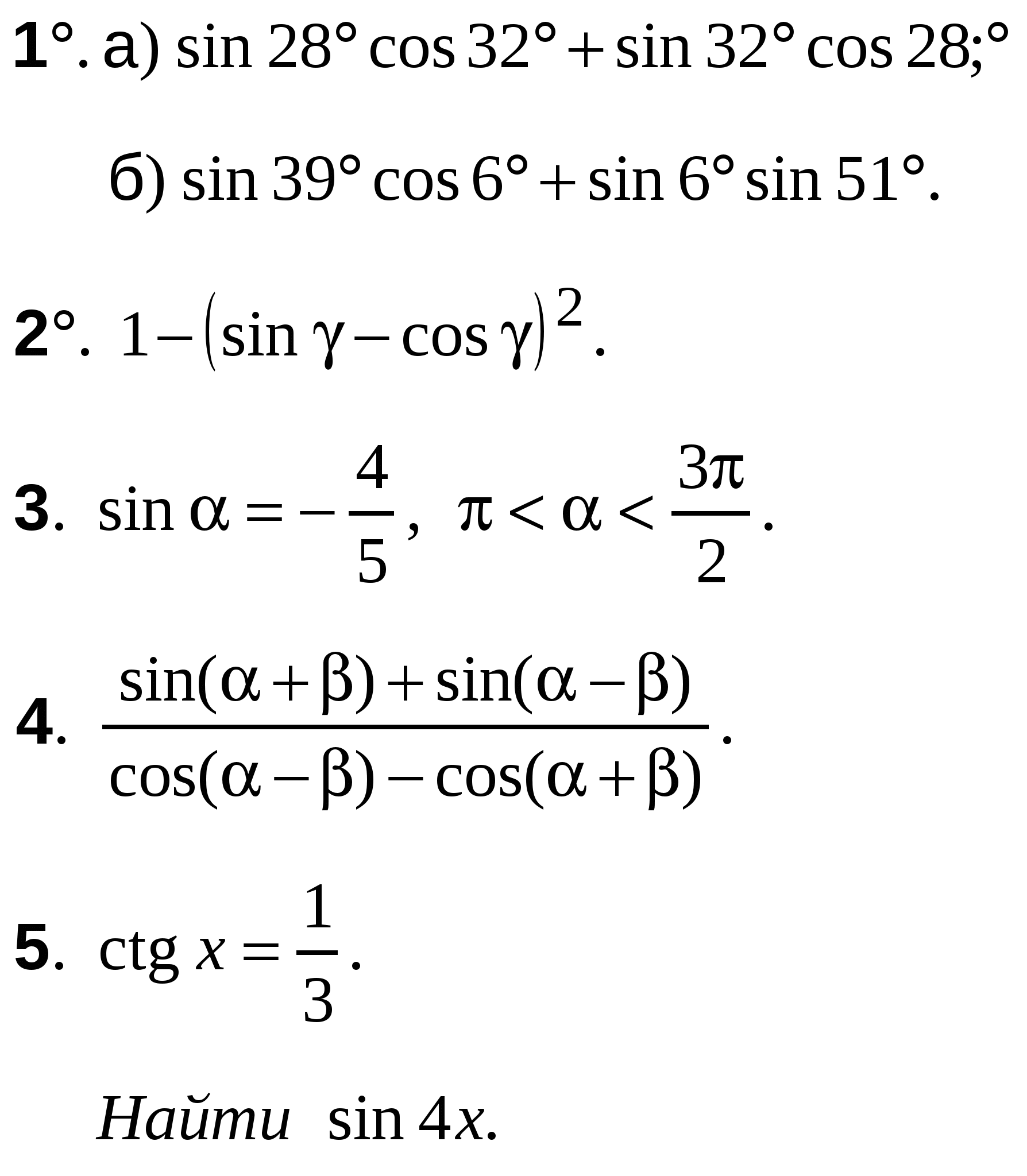
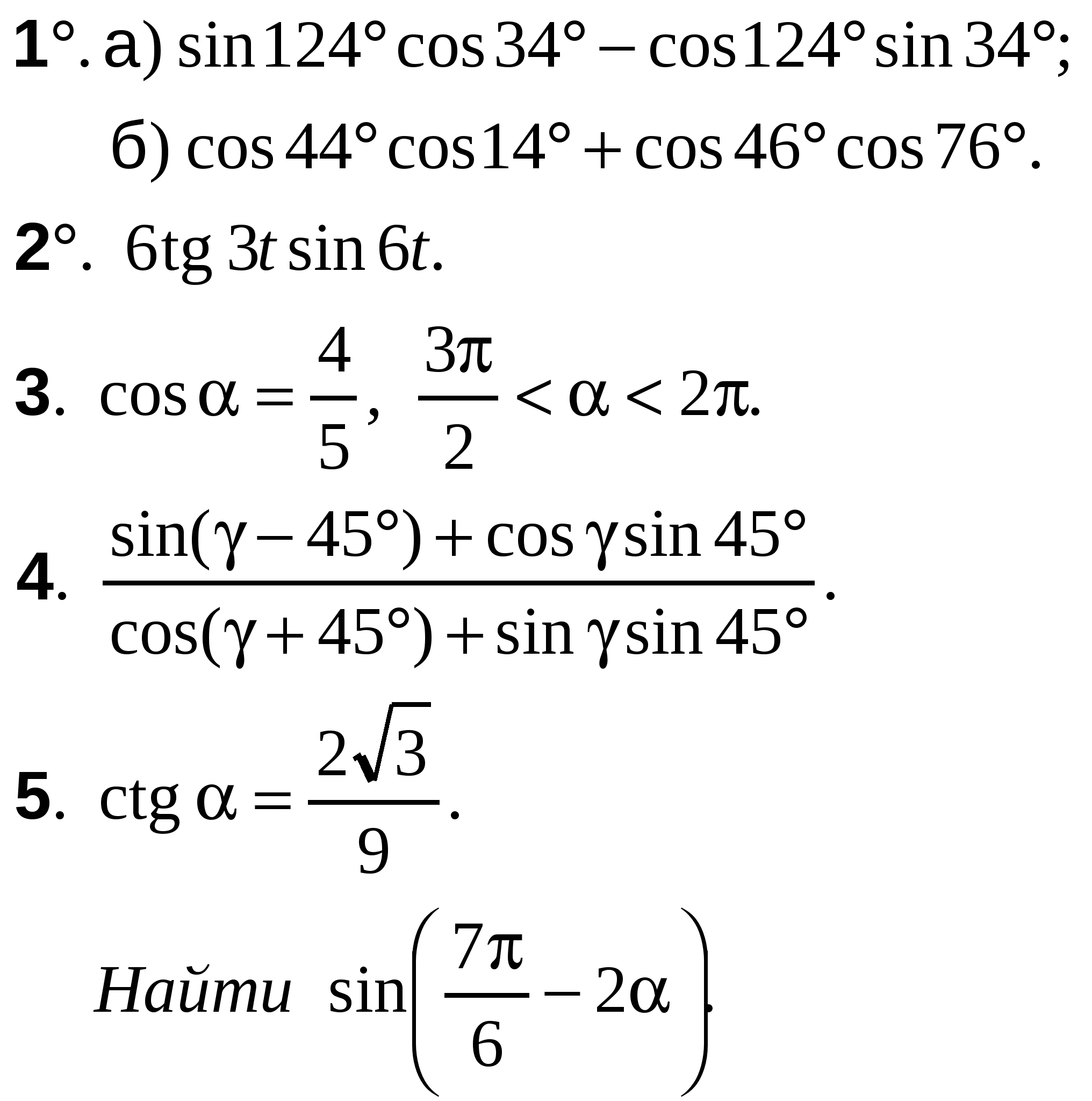
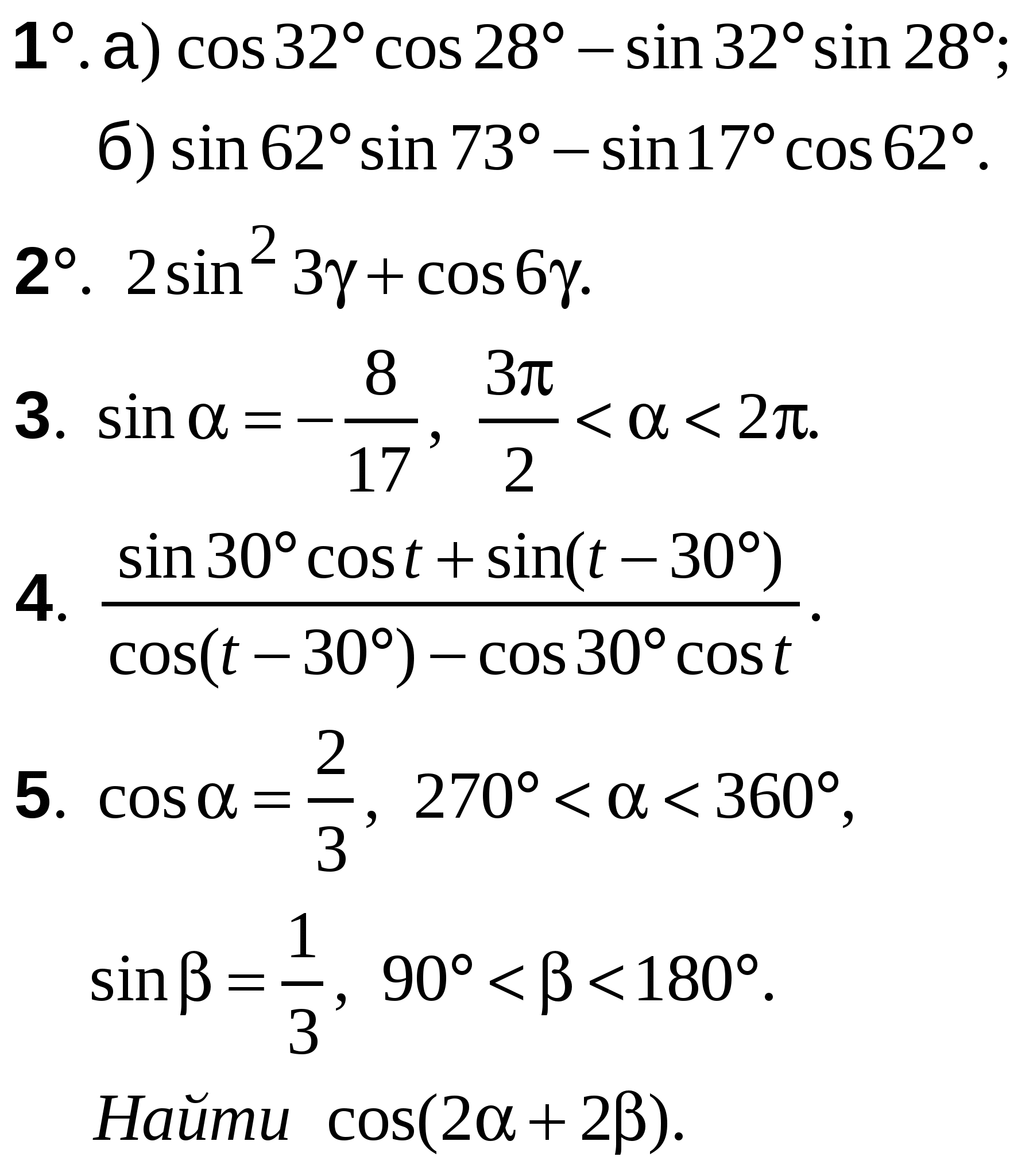
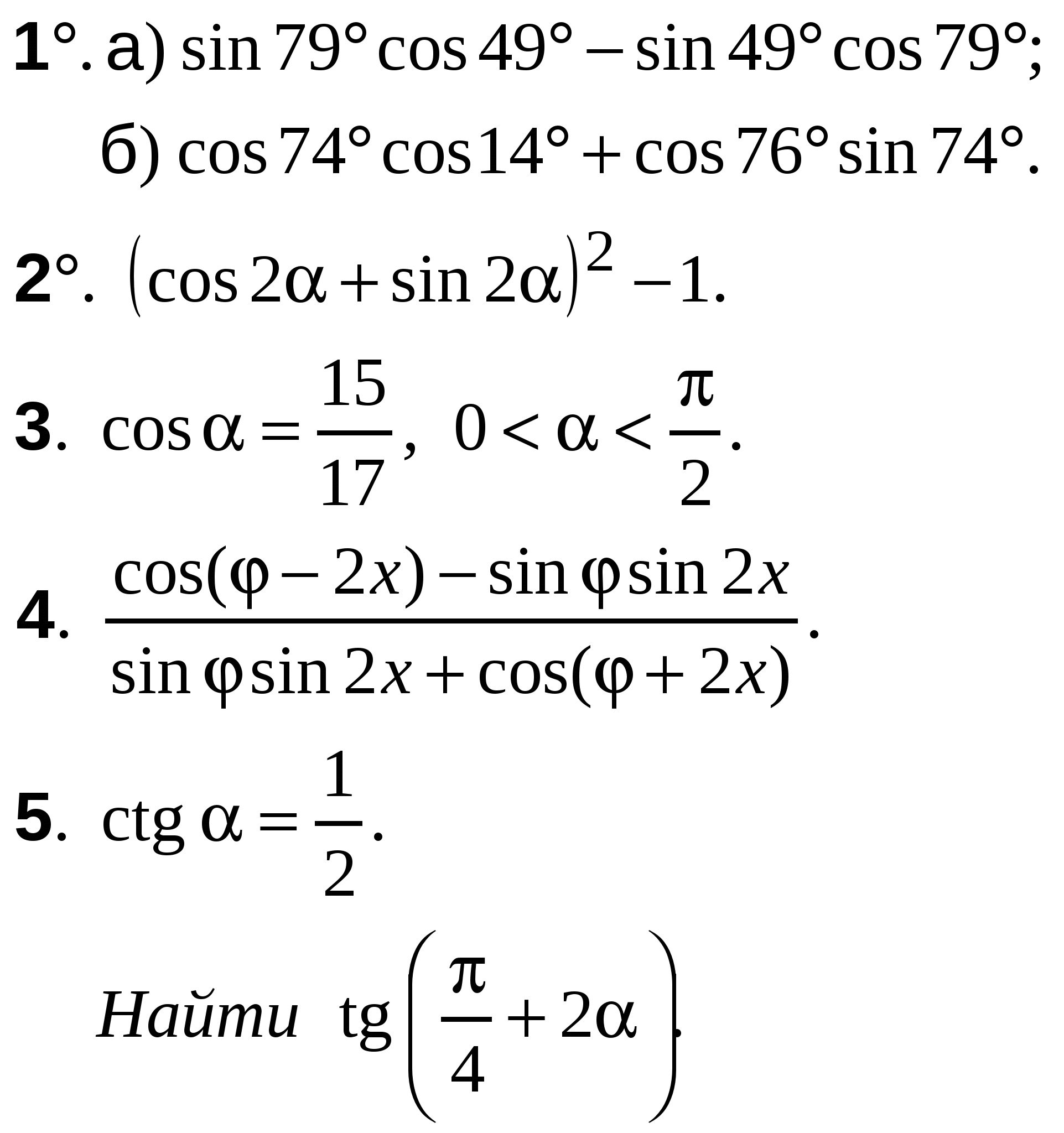
А-10 Ср-04
ВАРИАНТ 21
А-10 Ср-04
ВАРИАНТ 22
А-10 Ср-04
ВАРИАНТ 23
А-10 Ср-04
ВАРИАНТ 24
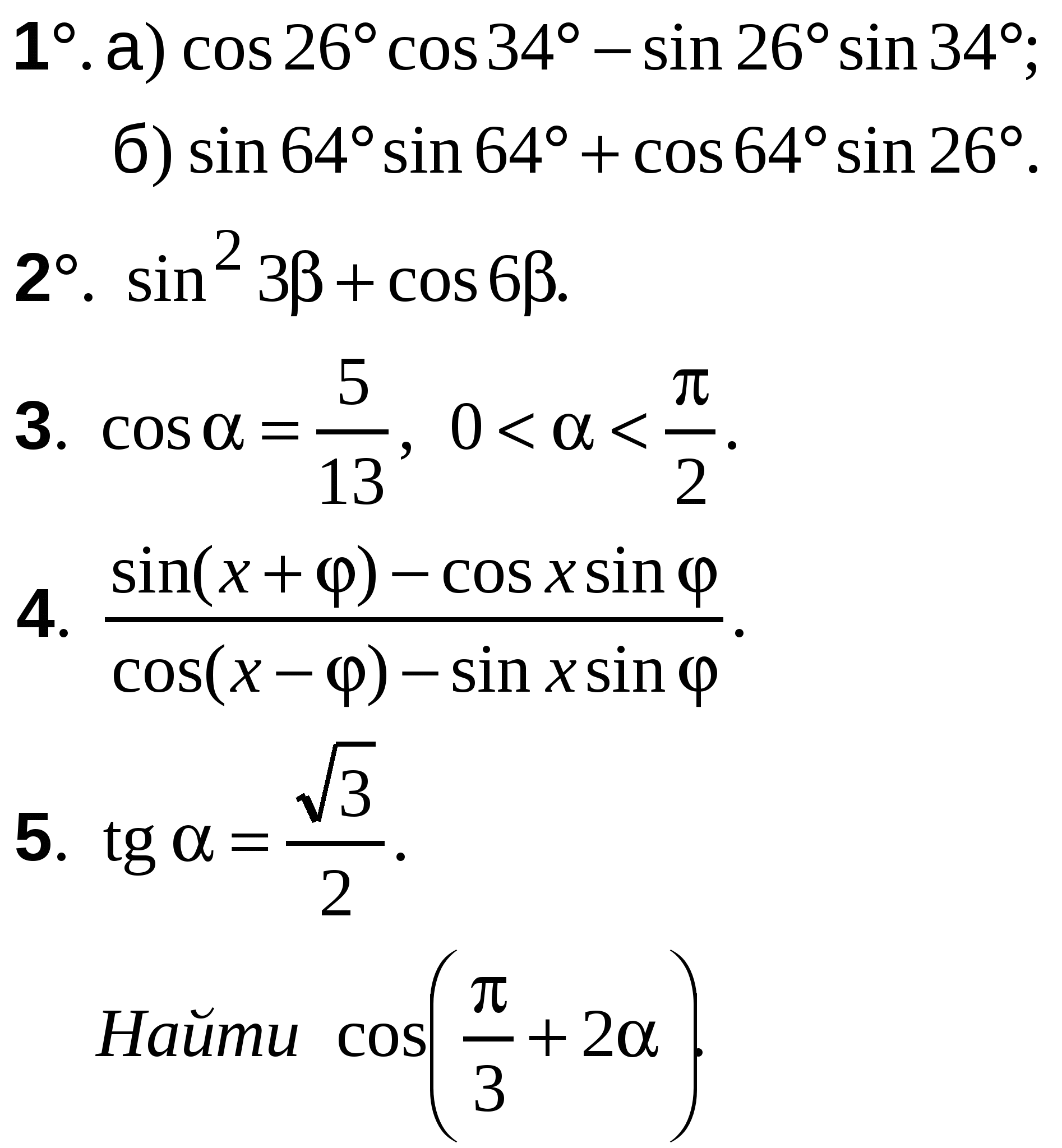
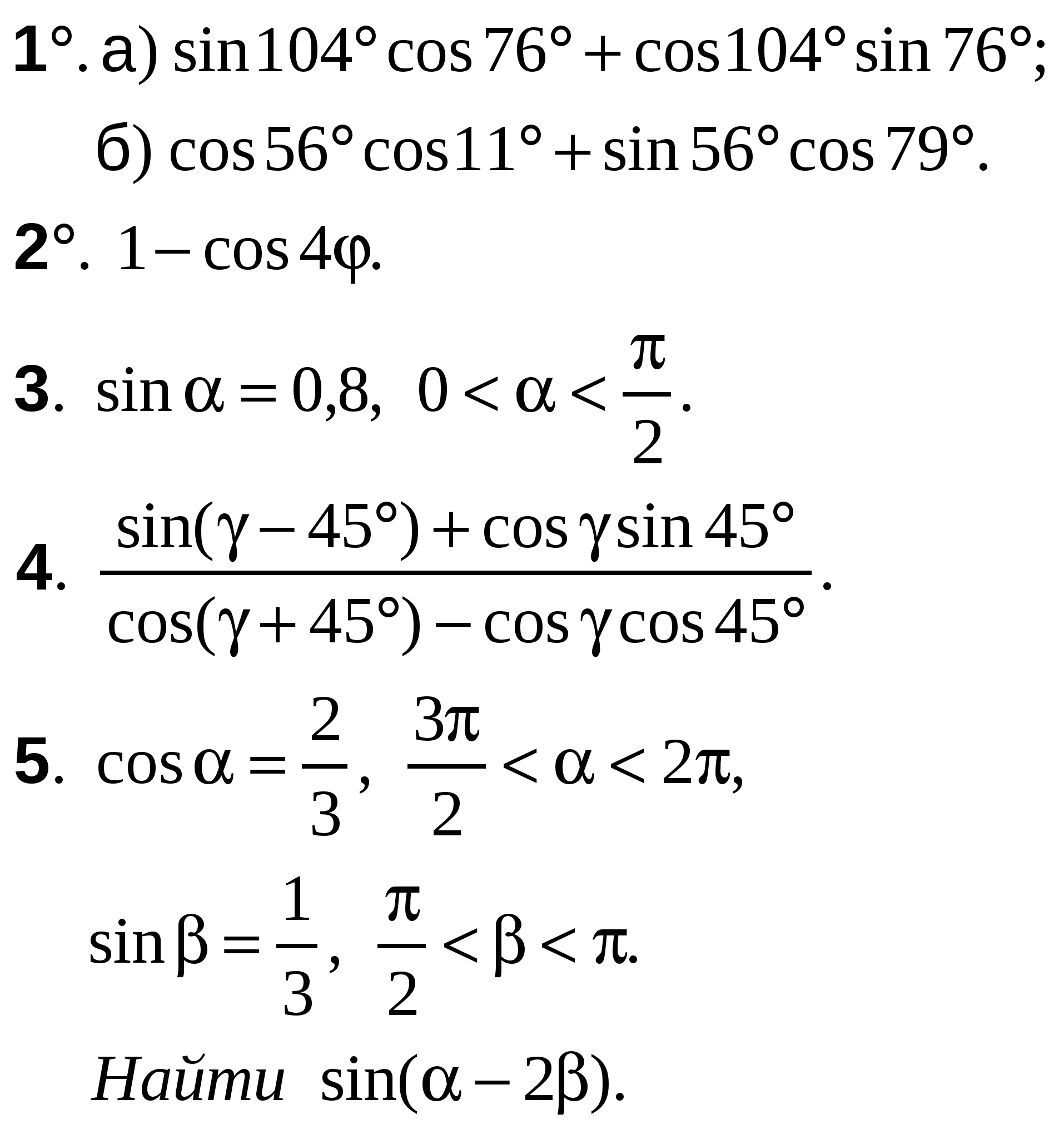
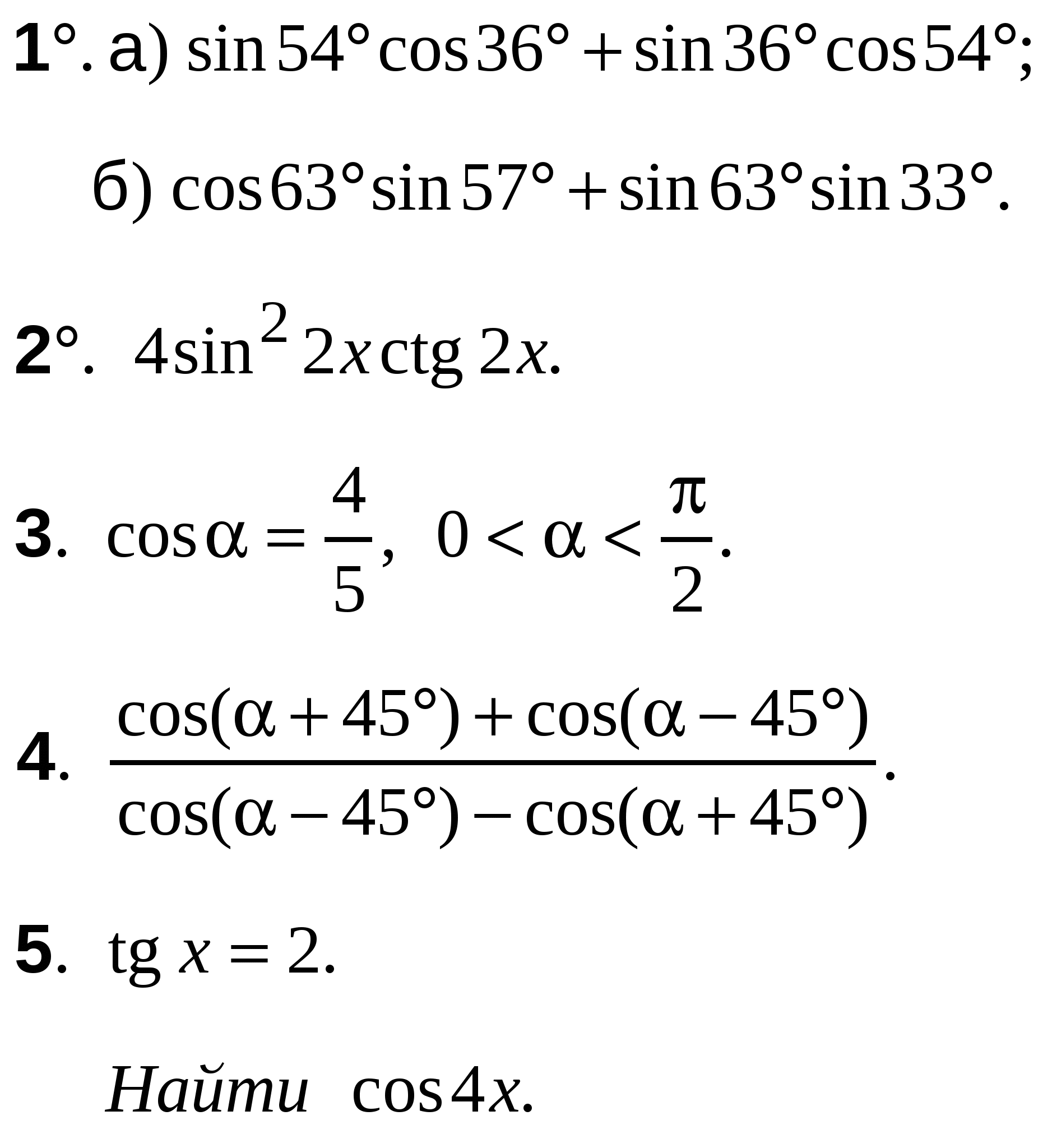
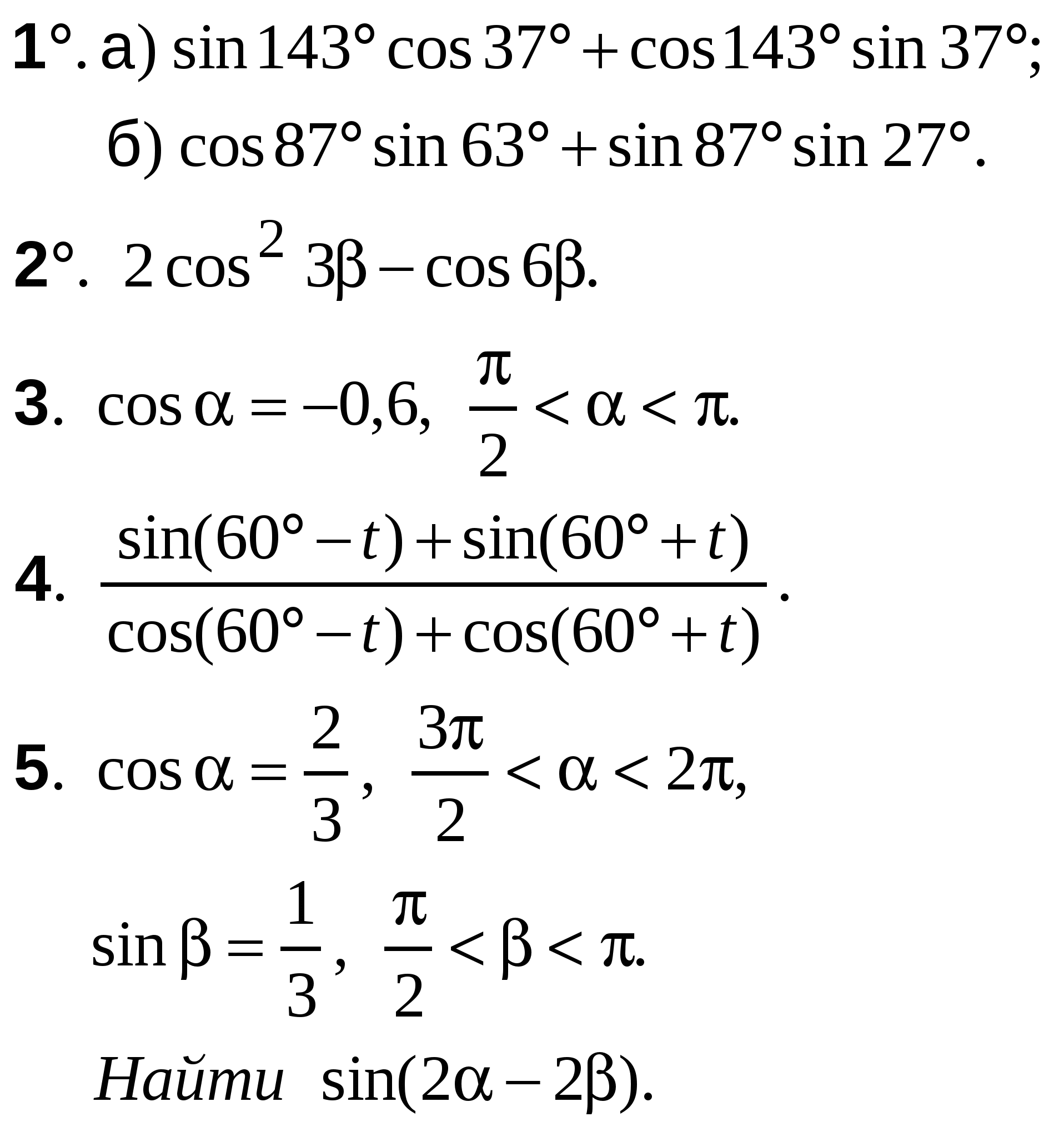
А-10 Ср-04
ВАРИАНТ 25
А-10 Ср-04
ВАРИАНТ 26
А-10 Ср-04
ВАРИАНТ 27
А-10 Ср-04
ВАРИАНТ 28
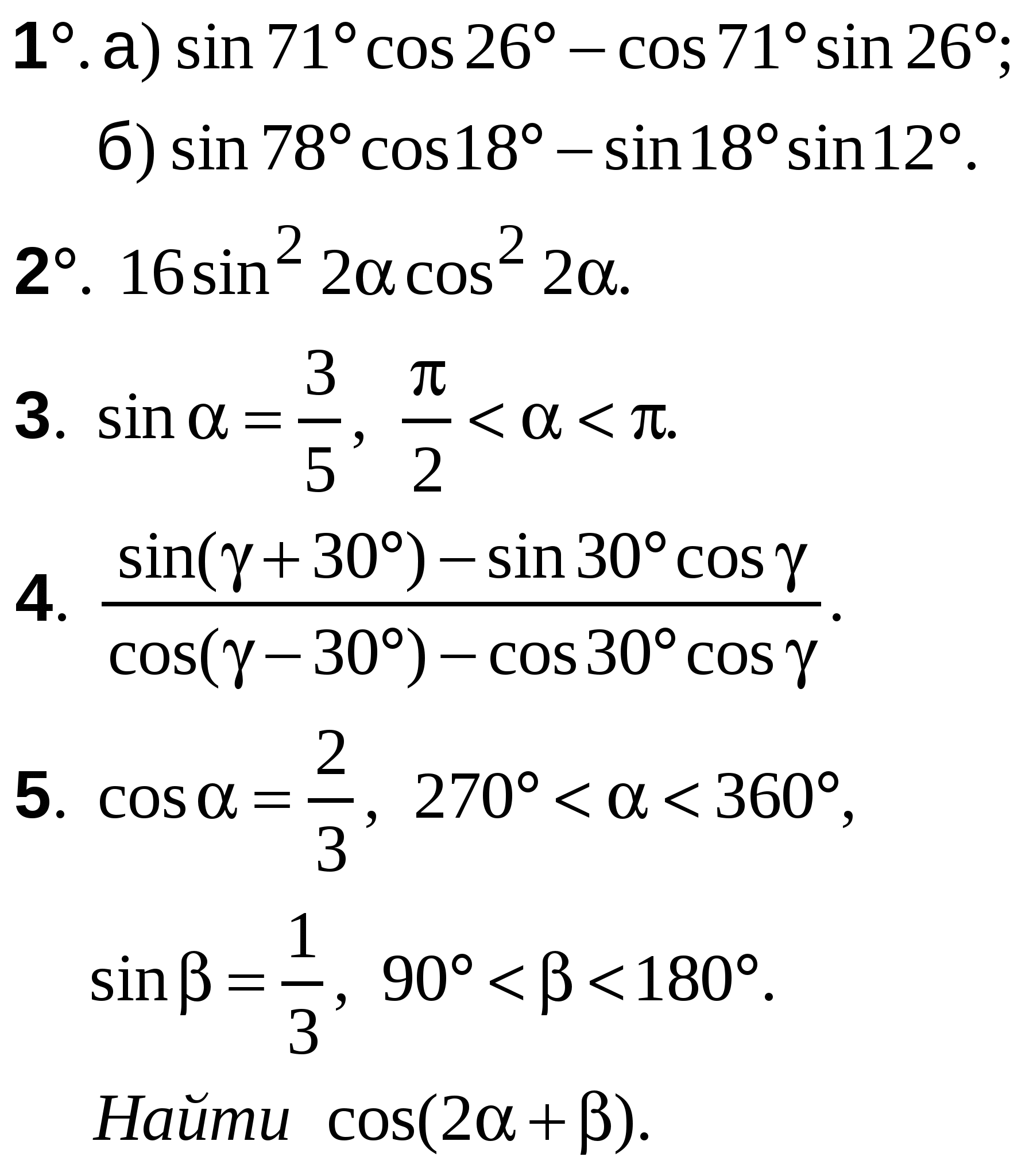

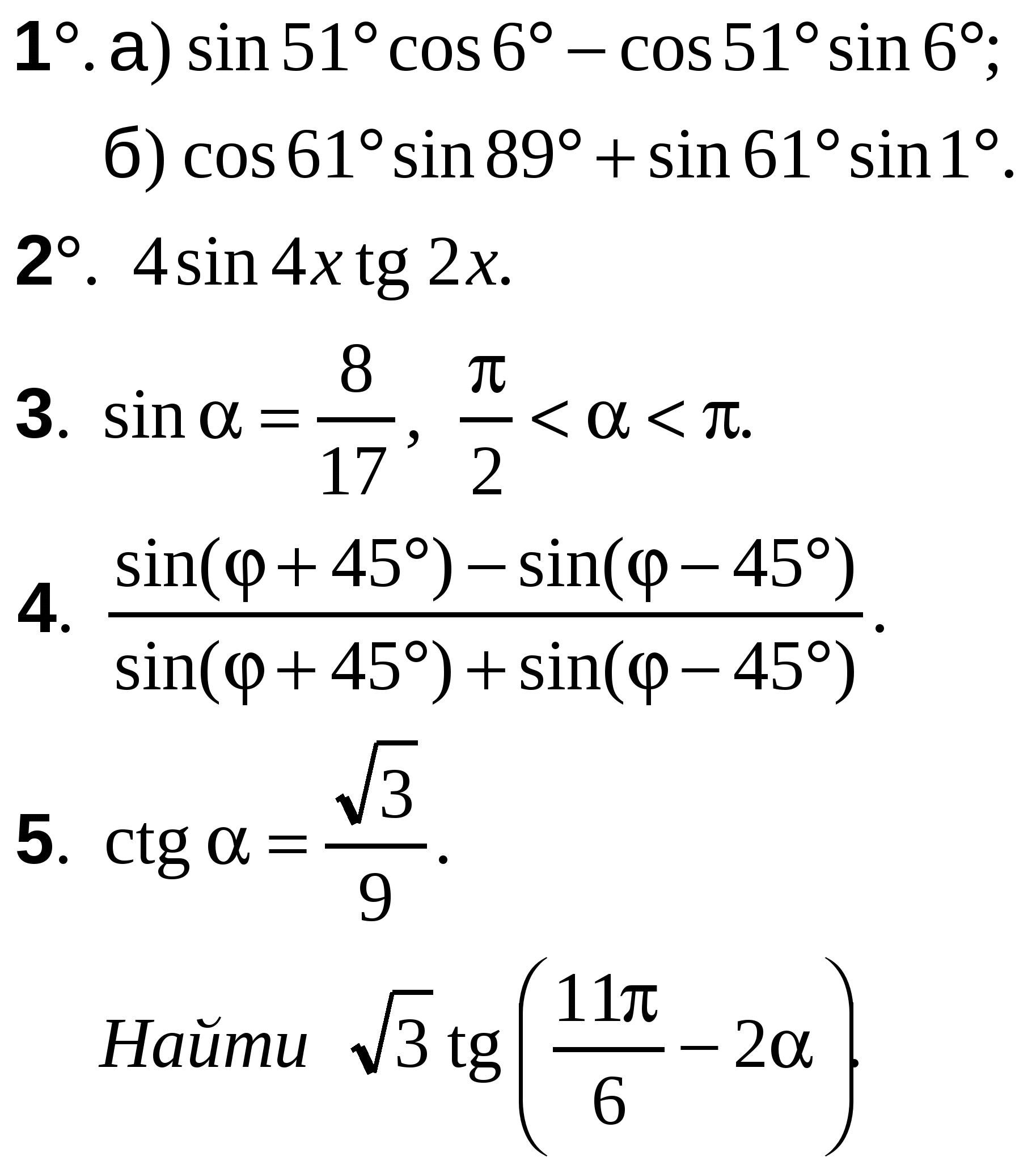
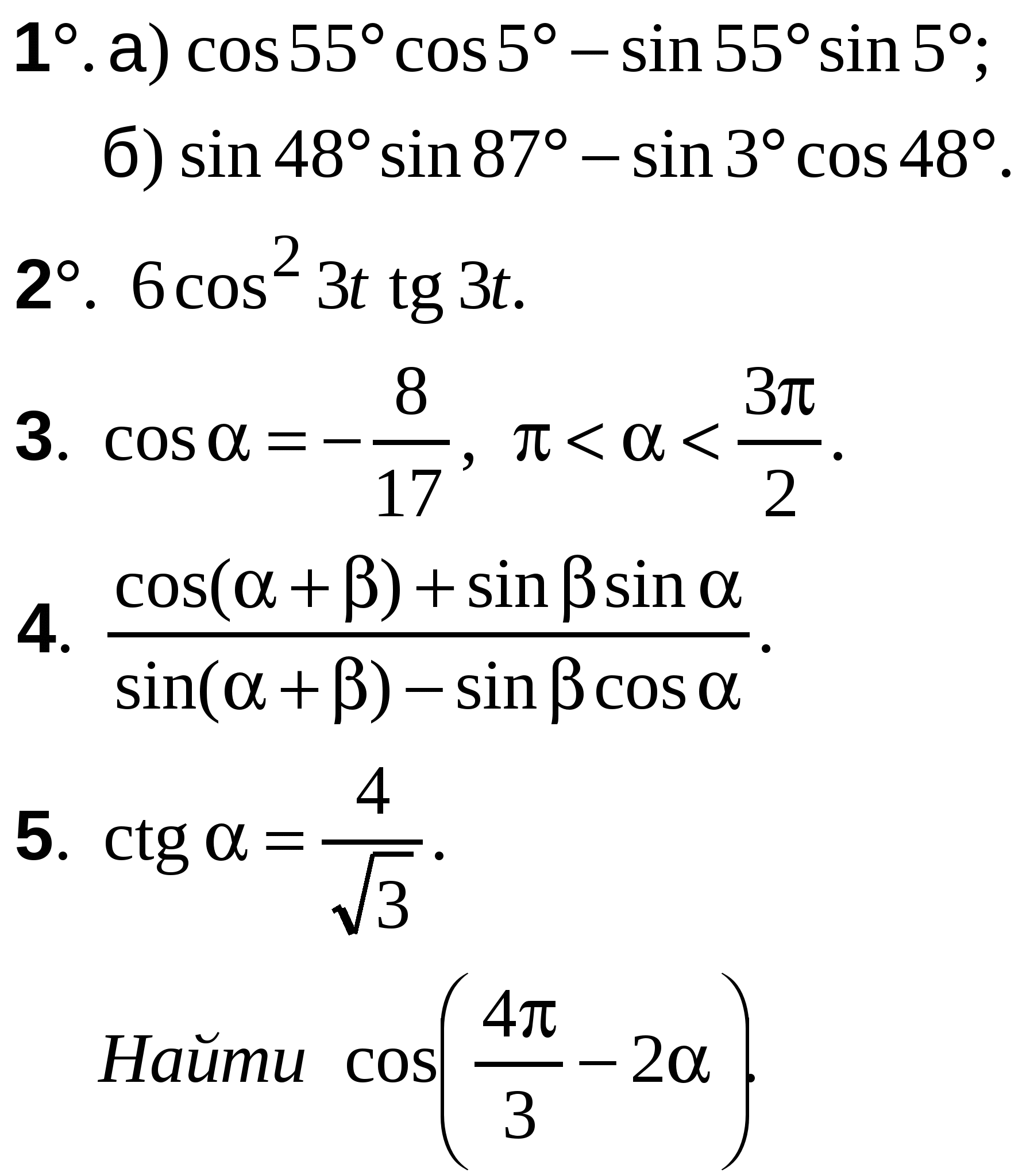
А-10 Ср-04
ВАРИАНТ 29
А-10 Ср-04
ВАРИАНТ 30
А-10 Ср-04
ВАРИАНТ 31
А-10 Ср-04
ВАРИАНТ 32
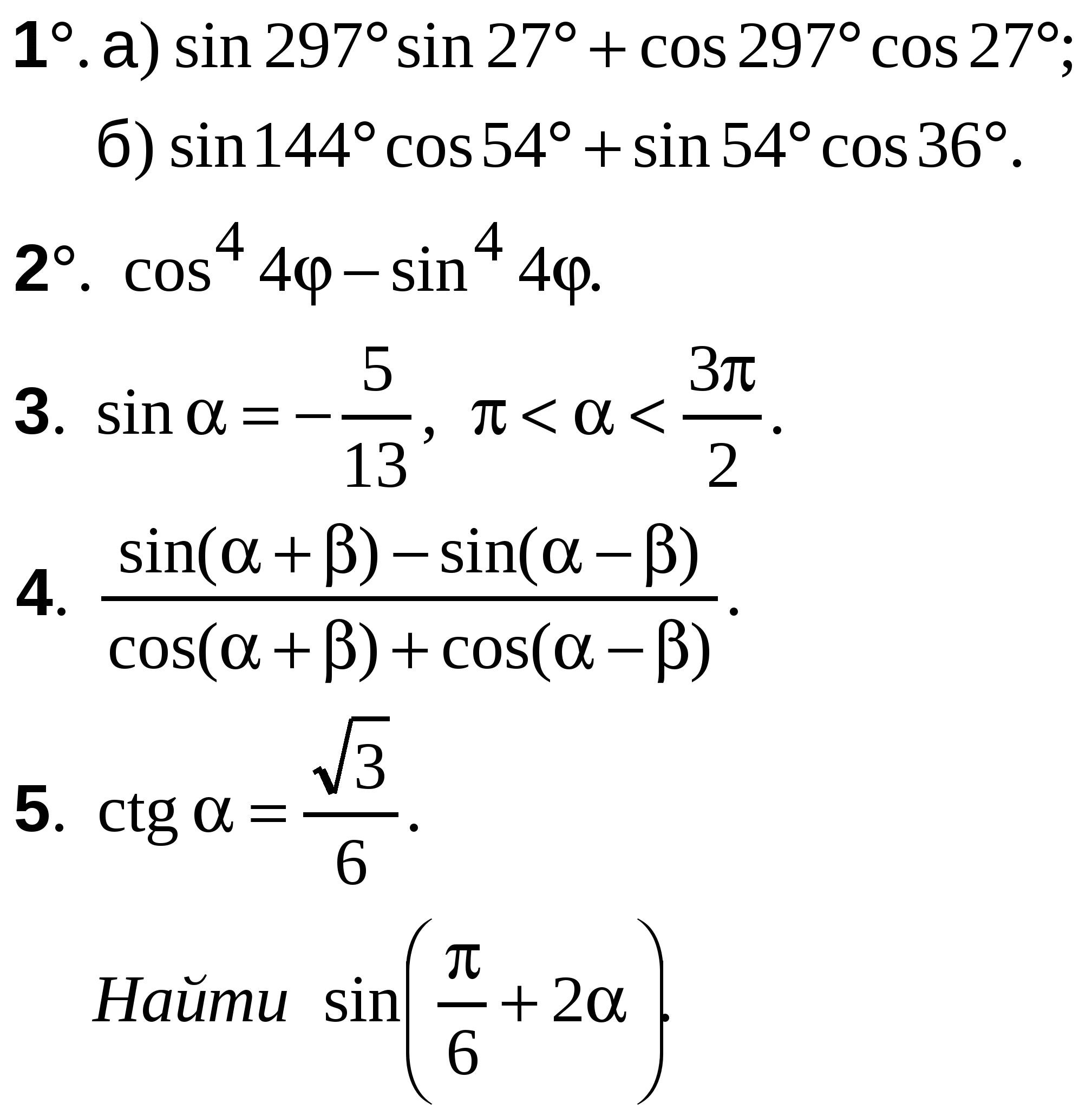
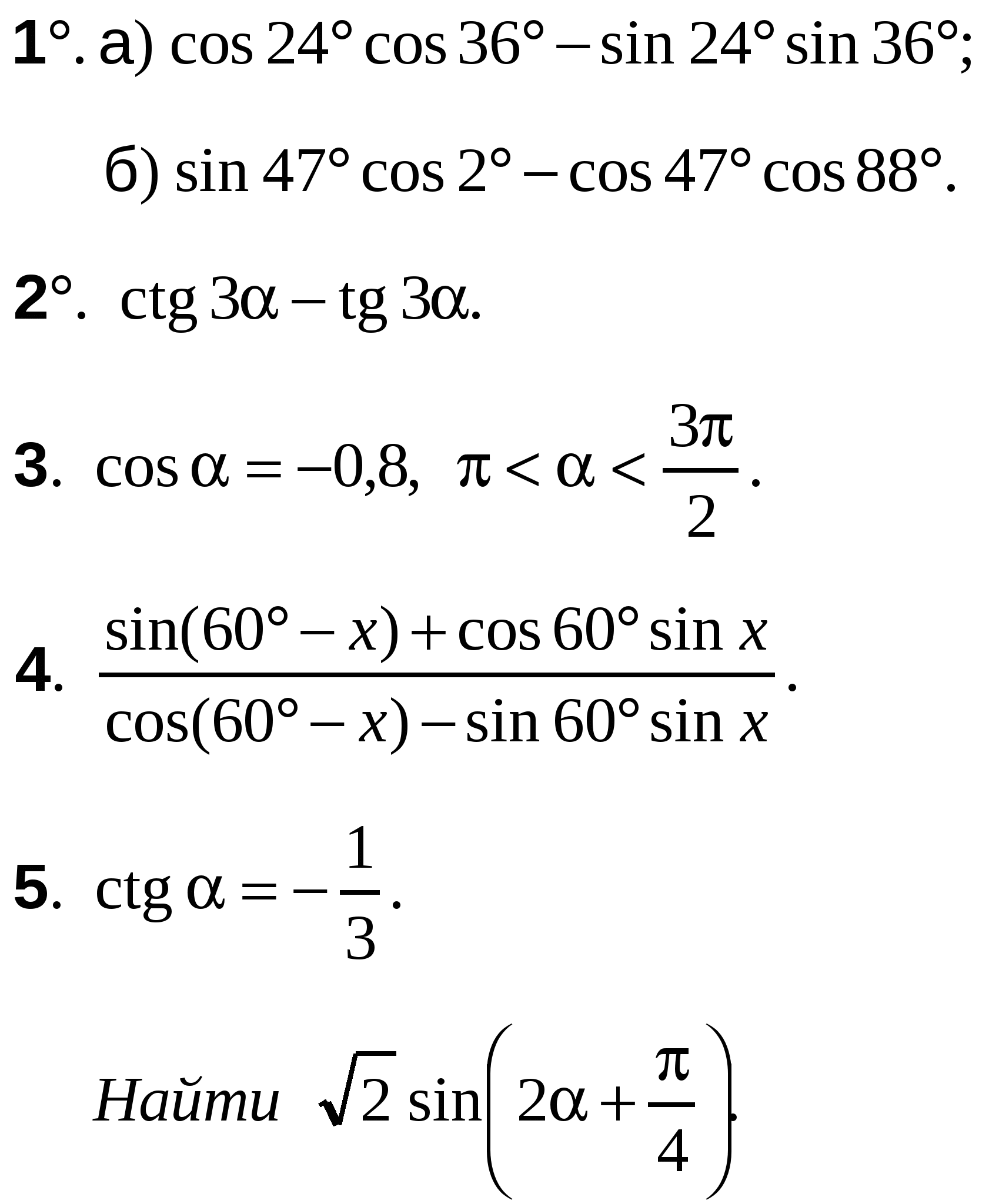
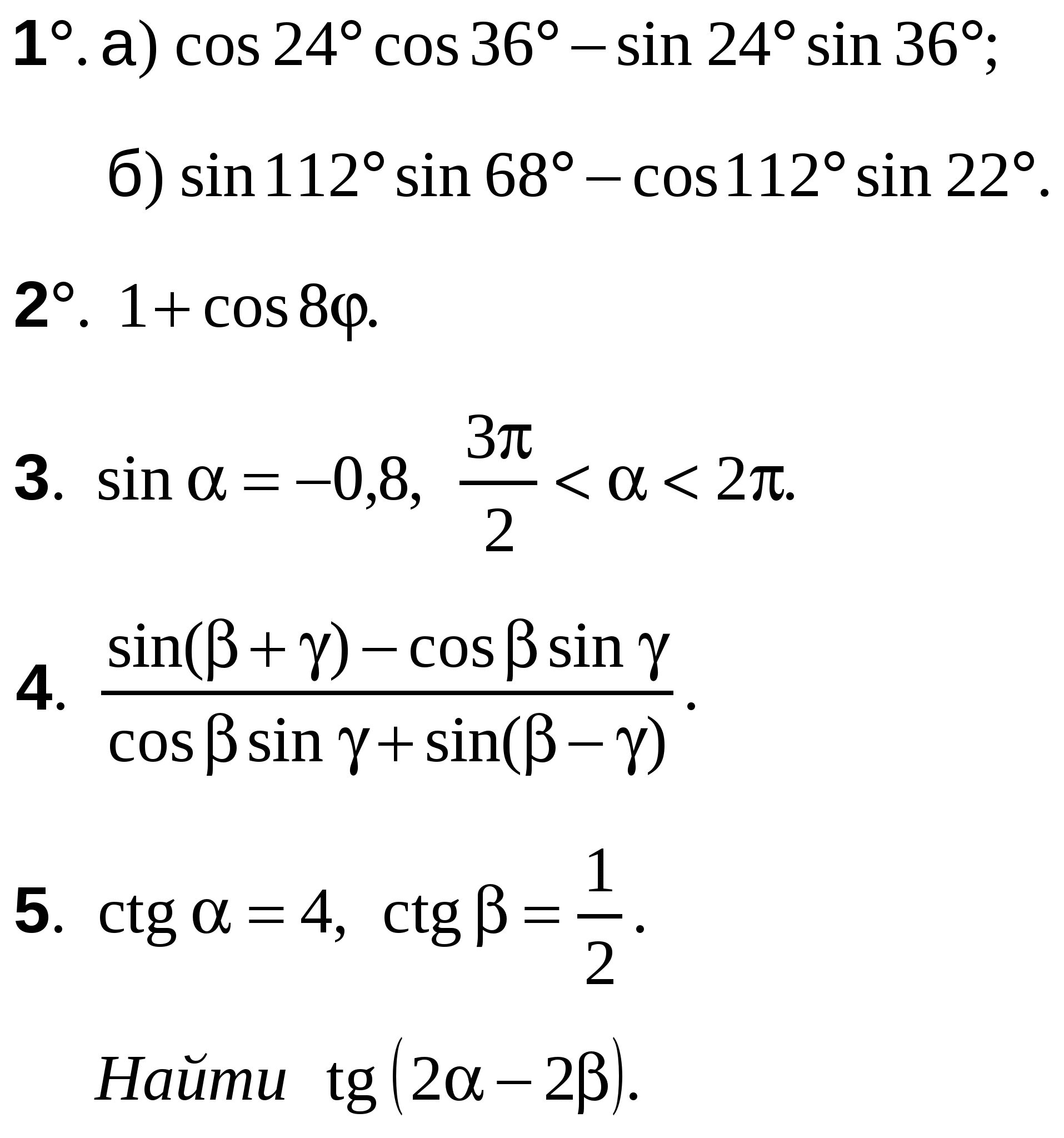
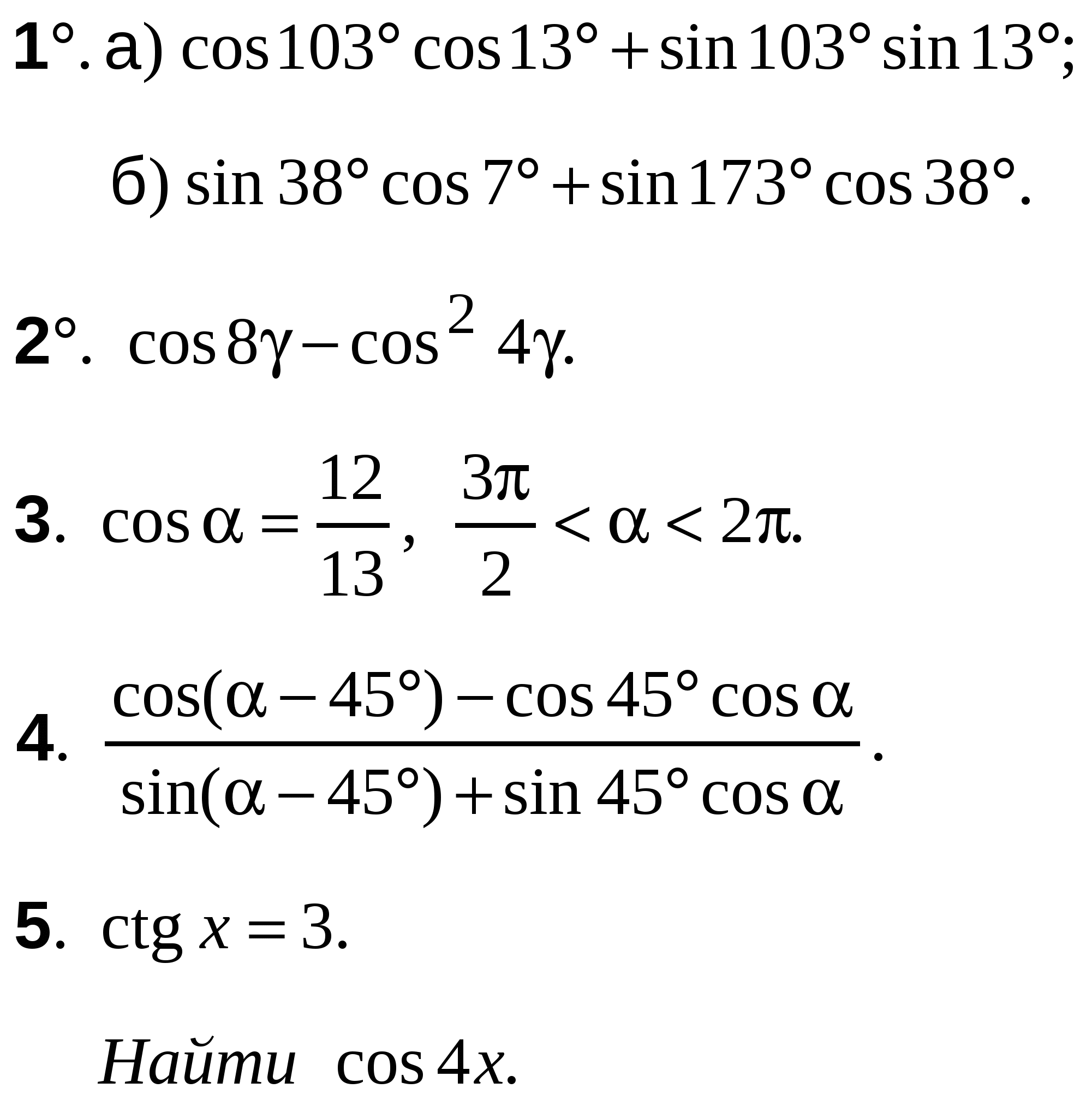
-
Число:
-
Тема урока: Формулы сложения
-
Тип урока: урок ознакомления с новым материалом
-
Цель урока: сформировать умение применять тригонометрические формулы сложения
-
Учебно-воспитательные задачи урока:
Образовательные:
-
вывод формул сложения для тригонометрических функций
-
отработать навыки использования тригонометрических формул сложения при решении уравнений, в вычислениях и тождественных преобразованиях тригонометрических выражений
Развивающие
-
Развитие умений выделять главное, существенное в изученном материале
-
Развивать познавательный интерес, логическое мышление
Воспитательные
-
воспитание интереса к предмету
-
воспитание ответственного отношения к своему образованию.
-
Средства обучения: индивидуальные конспекты, записи на доске, учебник «Алгебра и начала математического анализа» 10-11 Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин. М.: Просвещение, 2014.
-
План урока
|
№ |
Этапы урока |
время |
Методы и методические приемы |
|
1 |
Орг.момент |
1 мин |
Словесный(приветствие) |
|
2 |
Сообщение темы и целей урока |
1 мин |
Словесный, практический |
|
3 |
Изложение нового материала |
15 мин |
Словесный, практический |
|
4 |
Закрепление материала |
20 мин |
Практический |
|
5 |
Подведение итогов. Домашнее задание. Рефлексия |
3 мин |
Словесный (запись на доске), оценивание |
8. Ход урока
I. Организационный момент. Приветствие учителя. Проверка готовности класса к уроку.
II. Сообщение темы и целей урока.
III. Объяснение нового материала.
Определение: Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.
Формулы сложения — это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенса суммы и разности аргументов.
Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)

Рисунок 1. Единичная окружность
Точка получена поворотом точки Мₒ(1;0) на угол
, а точка
на угол
и точка
на угол
.
Углы и
равны, отрезки
. Значит, треугольник
равен треугольнику
, следовательно у них одинаковые стороны
и
.
Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты
;
;
).
Подставим координаты точек и
в формулу для нахождения расстояния между ними. Получим:
.
Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:
Преобразуем правую часть:

Соединим левую и правую части:
Разделим на каждое слагаемое :
Получили формулу косинуса суммы.
Заменим и учтём, что
, получим формулу косинуса разности
Докажем, что
Так как ,
, то по формуле косинуса разности получаем:
Заменим
получим
Так, например, , потому что
.
Докажем, что
Подставим в формулу значение
, получим:
Для тангенса и котангенса тоже справедливы формулы
Выведем формулу синуса суммы и разности:
В этой формуле заменим и получим формулу синуса разности:
Для тангенса тоже есть формула суммы и разности. По определению .
Тогда tg , разделим числитель и знаменатель на
Получаем формулу тангенса суммы .
Заменим в ней и учтём, что tg〖(-α)=〖-tg〗α 〗, получим формулу тангенса разности
.
Пример. Вычислим .
Для котангенса суммы и разности применяют формулы:
Физкультминутка.
IV. Закрепление материала
Пример 1. Найти
Решение: Представим , так как нам известны значения косинуса углов
и
Подставим в формулу косинуса суммы. Получаем:
.
Ответ: .
Пример 2. Найти .
Решение: Представим , так как нам известны значения синуса углов
и
Подставим в формулу синуса суммы. Получаем:
.
Ответ: .
Пример 3. Вычислите .
Решение: Применяем формулу синуса разности: .
Ответ: .
Выполнение заданий из учебника: №№ 481,482 (1,3), 483 (1), 484 (1,3), 485 (1,3)
V. Итоги урока. Рефлексия
Домашнее задание. П.28 . №№ 482 (2,4), 483 (2), 484 (2,4), 485 (2,4).
Аннотация:
Предлагаемые задания не выходят за пределы учебной программы, поэтому доступны для большинства учащихся 10 классов. Данный ресурс поможет учителю организовать фронтальную и самостоятельную работу учащихся и осуществить контроль их знаний. Учитель может выбрать по своему усмотрению задания для конкретного урока по обозначенной теме и предложить решить задания на этапе первичного повторения или на этапе актуализации знаний — в зависимости от сценария урока. Ресурс можно использовать при обучении по любому УМК.
Техническая составляющая в презентации интуитивно понятна. На 2 слайде можно выбрать задачи необходимые для конкретного урока. Есть возможность решать задачи без выбора, т.е. последовательно, используя переход на последующий слайд по управляющей кнопке.

Целевая аудитория: для 10 класса
Автор: Каратанова Марина Николаевна
Место работы: МБОУ СОШ №256 ГО ЗАТО Фокино Приморский край
Добавил: KarMaN
Уважаемые коллеги! Автор ждёт Ваши отзывы! Оставьте своё мнение о разработке!
Всего комментариев: 0

Физкультминутки
Физкультминутки обеспечивают кратковременный отдых детей на уроке, а также способствуют переключению внимания с одного вида деятельности на другой.

В помощь учителю
Уважаемые коллеги! Добавьте свою презентацию на Учительский портал и получите бесплатное свидетельство о публикации методического материала в международном СМИ.
Для добавления презентации на портал необходимо зарегистрироваться.
Конкурсы
Диплом и справка о публикации каждому участнику!
© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
|
Вариант 1 «Формулы сложения» Вычислите: а) б) в) г) д) |
Вариант 2 «Формулы сложения» Вычислите: а) г) д) |
|
Вариант 1 «Формулы сложения» Вычислите: а) б) в) г) д) |
Вариант 2 «Формулы сложения» Вычислите: а) г) д) |
|
Вариант 1 «Формулы сложения» Вычислите: а) б) в) г) д) |
Вариант 2 «Формулы сложения» Вычислите: а) г) д) |
|
Вариант 1 «Формулы сложения» Вычислите: а) б) в) г) д) |
Вариант 2 «Формулы сложения» Вычислите: а) г) д) |
|
Вариант 1 «Формулы сложения» Вычислите: а) б) в) г) д) |
Вариант 2 «Формулы сложения» Вычислите: а) г) д) |
По теме: методические разработки, презентации и конспекты
Самостоятельная работа «Формулы приведения»
Самостоятельная работа по теме «Формулы приведения» для 10 класса в 6 вариантах….
самостоятельная работа по теме АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ, ФОРМУЛА n-НОГО ЧЛЕНА АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ.
данная работа позволяет установить уровень усвоения данной темы….
Самостоятельные работы по математике 5 класс (сложение, законы сложения, зачетные задания по теме «Сложение»)
Самостоятельные работы по математике 5 класс (сложение, законы сложения и вычитания, зачетные задания по теме «Сложение»)…
«Формулы тригонометрии» — самостоятельная работа для 10 класса
Самостоятельная работа по алгебре для учащихся 10 класса по основным тригонометрическим формулам. Работа рассчитана на 4 варианта….
«Тригонометрические формулы сложения и следствия из них. Формулы двойного аргумента».
Урок по теме «Тригонометрические формулы сложения и следствия из них предназначен для учителей, работающих в старшей школе….
формулы приведения. формулы сложения. формулы двойного и половинного угла
формулы приведения. формулы сложения. формулы двойного и половинного угла…
«Формулы сложения, формулы удвоения»
Практическое занятие по теме:«Формулы сложения, формулы удвоения»…
Алгебра и начала математического анализа, 10 класс
Урок №34. Формулы сложения.
Перечень вопросов, рассматриваемых в теме:
- формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов;
- преобразование тригонометрических выражений на основе использования формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов;
- вычисление значения тригонометрических выражений на основе формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов;
- доказательство тригонометрических тождеств на основе формулы синуса, косинуса, тангенса и котангенса суммы и разности аргументов.
Глоссарий по теме
Формулы сложения — это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)
Рисунок 1 – единичная окружность
Точка 





Углы 






Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты



Подставим координаты точек 


Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:
Преобразуем правую часть:
Соединим левую и правую части:
Разделим на
Получили формулу косинуса суммы.
Заменим 

Докажем, что
Так как 




Так, например,

Докажем, что
Подставим в формулу 

Для тангенса и котангенса тоже справедливы формулы
Выведем формулу синуса суммы и разности:

В этой формуле заменим 
Для тангенса тоже есть формула суммы и разности. По определению 
Тогда tg

Получаем формулу тангенса суммы 
Заменим в ней 

Пример. Вычислим 
Для котангенса суммы и разности применяют формулы:
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Найти
Решение: Представим 



Ответ: 
Пример 2. Найти 
Решение: Представим 



Ответ: 
Пример 3. Вычислите 
Решение: Применяем формулу синуса разности: 
Ответ: 










 если
если  и
и 
 б)
б) в)
в)

 если
если  и
и 























