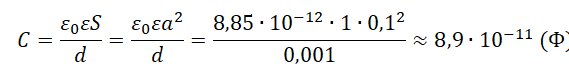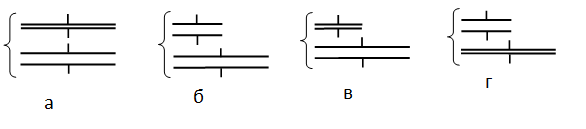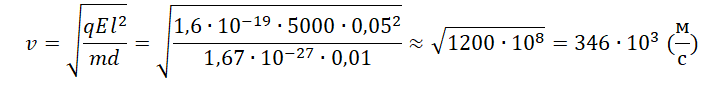Всего: 4 1–4
Добавить в вариант
Между пластинами заряженного плоского конденсатора поместили диэлектрик с диэлектрической проницаемостью так, что он полностью заполнил объем между пластинами. Как изменились емкость конденсатора, заряд на пластинах и напряжение между ними, если конденсатор подключен к источнику?
ФИЗИЧЕСКАЯ ХАРАКТЕРИСТИКА
А) Заряд на пластинах
Б) Напряжение между пластинами
В) Емкость конденсатора
ЕЕ ИЗМЕНЕНИЕ
1) Уменьшится в раз
2) Останется неизменной
3) Увеличится в раз
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Между пластинами заряженного плоского конденсатора поместили диэлектрик с диэлектрической проницаемостью так, что он полностью заполнил объем между пластинами. Как изменились емкость конденсатора, заряд на пластинах и напряжение между ними, если конденсатор отключен от источника?
ФИЗИЧЕСКАЯ ХАРАКТЕРИСТИКА
А) Заряд на пластинах
Б) Напряжение между пластинами
В) Емкость конденсатора
ЕЕ ИЗМЕНЕНИЕ
1) Уменьшится в раз
2) Останется неизменной
3) Увеличится в раз
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Две параллельные металлические пластины больших размеров расположены на расстоянии d друг от друга и подключены к источнику постоянного напряжения (рис. 1). Пластины закрепили на изолирующих подставках и спустя длительное время отключили от источника (рис. 2).
Из приведённого ниже списка выберите все правильные утверждения.
1) Напряжённость электрического поля в точке А больше, чем в точке В.
2) Потенциал электрического поля в точке А больше, чем в точке С.
3) Если увеличить расстояние между пластинами d, то напряжённость электрического поля в точке С не изменится.
4) Если уменьшить расстояние между пластинами d, то заряд правой пластины не изменится.
5) Если пластины полностью погрузить в керосин, то энергия электрического поля конденсатора останется неизменной.
Источник: Демонстрационная версия ЕГЭ−2019 по физике
Стеклянные незаряженные кубики 1 и 2 и алюминиевые незаряженные кубики 3 и 4 сблизили вплотную и поместили в электрическое поле, напряжённость которого направлена горизонтально влево, как показано в левой части рисунка. Затем кубики раздвинули и уже после этого выключили электрическое поле (правая часть рисунка). Выберите все верные утверждения, описывающие данный опыт.
1) В электрическом поле (левая часть рисунка) часть электронов перешла из кубика 4 в кубик 3.
2) Кубик 2, изображённый в правой части рисунка, не заряжен.
3) В электрическом поле (левая часть рисунка) правая грань кубика 2 заряжена положительно.
4) Кубик 3, изображённый в правой части рисунка, имеет положительный заряд.
5) В электрическом поле (левая часть рисунка) разность потенциалов между левой гранью кубика 3 и правой гранью кубика 4 равна нулю.
Всего: 4 1–4
Видеоурок: Диэлектрики в электрическом поле. Диэлектрическая проницаемость
Лекция: Диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества

Диэлектрики — это материалы, не имеющие свободных носителей заряда.
Они слабо проводят ток или совсем его не проводят. В таких элементах все структурные единицы атома крепко связаны друг с другом, поэтому ядерные силы удерживают свои электроны и ионы неподвижными, или позволяют колебаться вблизи ядра или решетки. Если на такие элементы начать действовать электрическим полем, то движения происходить не будет.
Характеристики диэлектриков:
1. Напряженность внутри диэлектриков не обязательно должна быть нулевой.
2. Заряд в некотором объеме диэлектрика может отличаться от нуля.
3. Напряженность поля направлена под любым углом к диэлектрику.
4. Каждая точка диэлектрика имеет различный потенциал.

Это основная характеристика, являющаяся общей для всех диэлектриков. Каждый диэлектрик имеет свою диэлектрическую проницаемость.
Данная величина характеризуется способностью диэлектриков уменьшать напряженность поля. Количество раз, в которое уменьшается напряженность, обозначается буквой Ɛ (эпсилон). Весь принцип диэлектриков заключается в том, что внутри них происходит возбуждение собственного электрического поля, которое направлено против действия внешнего поля. Таким образом, происходит своеобразное гашение поля. Определить проницаемость можно по формуле или же воспользоваться специальной таблицей диэлектриков:
Все формулы взяты в строгом соответствии с Федеральным институтом педагогических измерений (ФИПИ)
3.1 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
3.1.1 Электризация тел и её проявления. Электрический заряд. Два вида заряда. Элементарный электрический заряд. Закон сохранения электрического заряда
1. Существуют заряды двух видов: положительные (+) и отрицательные (-). Положительный заряд возникает при трении стекла о кожу или шелк, а отрицательный — при трении янтаря (или эбонита) о шерсть.
2. Заряды (или заряженные тела) взаимодействуют друг с другом. Одноименные заряды отталкиваются, а разноименные заряды притягиваются.
3. Состояние электризации можно передать от одного тела к другому, что связано с переносом электрического заряда. При этом телу можно передать больший или меньший заряд, т. е. заряд имеет величину. При электризации трением заряд приобретают оба тела, причем одно — положительный, а другое — отрицательный. Следует подчеркнуть, что абсолютные величины зарядов наэлектризованных трением тел равны, что подтверждается многочисленными измерениями зарядов с помощью электрометров.
Объяснить, почему тела электризуются (т. е. заряжаются) при трении, стало возможным после открытия электрона и изучения строения атома. Как известно, все вещества состоят из атомов; атомы, в свою очередь, состоят из элементарных частиц — отрицательно заряженных электронов, положительно заряженных протонов и нейтральных частиц —нейтронов. Электроны и протоны являются носителями элементарных (минимальных) электрических зарядов.
Элементарный электрический заряд (е) — это наименьший электрический заряд, положительный или отрицательный, равный величине заряда электрона:
Закон сохранения электрического заряда — алгебраическая сумма электрических зарядов всех частиц изолированной системы не меняется при происходящих в ней процессах.
3.1.2 Взаимодействие зарядов. Точечные заряды. Закон Кулона:
Электрический заряд (Кл) — это физическая величина, являющаяся источником электрического поля, посредством которого осуществляется взаимодействие частиц, обладающих зарядом.
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Кулон (Кл) — единица СИ количества электричества (электрического заряда).Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.
[1 Кл = 1 А ·Bс]
Точечный заряд — заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
3.1.3 Электрическое поле. Его действие на электрические заряды
Электрическое поле — это особая форма материи, посредством которой осуществляется взаимодействие электрически заряженных частиц.
Главным свойством электрического поля является действие его на электрические заряды с некоторой силой. По этому действию устанавливается факт его существования. Действие поля на единичный заряд — напряженность поля — является одной из его основных характеристик, по которой изучается распределение поля в пространстве.
3.1.4 Напряжённость электрического поля (Н/м) — векторная характеристика поля, сила, действующая на единичный покоящийся в данной системе отсчета электрический заряд:
Поле точечного заряда:
Однородное поле:
Картины линий полей
3.1.5 Потенциальность электростатического поля
Потенциал (потенциальная функция) (от лат. potentia — сила) является энергетической характеристикой векторных полей, к числу которых относятся гравитационное, электромагнитное и электростатическое поля.
Потенциал электростатического поля в данной точке численно равен работе, которую совершают силы поля при перемещении единичного положительного заряда из данной точки в бесконечность.
Разность потенциалов и напряжение
Работа по перемещению заряда (Дж) в однородном электростатическом поле зависит только от начального и конечного положений движущегося заряда и не зависит от формы траектории. При перемещении заряда по замкнутой траектории работа равна нулю.
Потенциальная энергия заряда в электростатическом поле(Дж):
Потенциал электростатического поля(Дж/Кл):
Связь напряжённости поля и разности потенциалов для однородного электростатического поля: U = Ed
3.1.6 Принцип суперпозиции электрических полей:
3.1.7 Проводники в электростатическом поле. Условие равновесия зарядов: внутри проводника
Внутри и на поверхности проводника
3.1.8 Диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества ε.
Диэлектрики (или изоляторы) — вещества, относительно плохо проводящие электрический ток (по сравнению с проводниками).
Полярные диэлектрики состоят из молекул, в которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы можно представить в виде двух одинаковых по модулю разноименных точечных зарядов, находящихся на некотором расстоянии друг от друга, называемых диполем.
Неполярные диэлектрики состоят из атомов и молекул, у которых центры распределения положительных и отрицательных зарядов совпадают.
Относительная диэлектрическая проницаемость среды ε — это физическая величина, показывающая, во сколько раз модуль напряженности электростатического поля Е внутри однородного диэлектрика меньше модуля напряженности поля Е0 в вакууме:
3.1.9 Конденсатор. Электроёмкость конденсатора(Ф):
Электроёмкость плоского конденсатора — величина заряда, которую нужно сообщить конденсатору, чтобы изменить его потенциал на единицу:
3.1.10 Параллельное соединение конденсаторов:
Последовательное соединение конденсаторов:
3.1.11 Энергия заряженного конденсатора (Дж):
Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.
Проводники и диэлектрики в электростатическом поле
Вещества в природе можно разделить на проводники и диэлектрики.
Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.
Типичные проводники — металлы.
Диэлектрическая проницаемость вещества
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
Физическая величина, равная отношению модуля напряженности (vec{E}_0) внешнего электрического поля в вакууме к модулю напряженности (vec{E}) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества (varepsilon).
[varepsilon=dfrac{vec{E}_0}{vec{E}}]
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:
[fbox{$C=dfrac{q}{Delta varphi}$}]
Единицы измерения: (displaystyle [text{Ф}]) (фарад).
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.
Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
Электроемкость плоского конденсатора
Разность потенциалов (Delta varphi) между пластинами в однородном электрическом поле равна (Ed), где (d) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
[C=dfrac{q}{Delta varphi}=dfrac{sigma S}{Ed}=dfrac{varepsilon_0S}{d}]
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в (varepsilon) раз:
[fbox{$C=dfrac{varepsilon_0varepsilon S}{d}$}]
Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
-
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
[fbox{$U=U_1+U_2$}]
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
[dfrac{q}{C}=dfrac{q}{C_1}+dfrac{q}{C_2}]
Сократив выражение на (Q), получим формулу:
[fbox{$dfrac{1}{C}=dfrac{1}{C_1}+dfrac{1}{C_2}$}]
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
[fbox{$C=dfrac{C_1C_2}{C_1+C_2}$}]
-
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
[fbox{$q=q_1+q_2$}]
Так как заряд конденсатора
[q=CU]
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
[CU=C_1U+C_2U]
[fbox{$C=C_1+C_2$}]
-
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.
Вычислим эту энергию: начнём с плоского воздушного конденсатора.
Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора (q), площадь обкладок (S). Возьмём на второй обкладке настолько маленькую площадку, что заряд (q_0) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
[F_0 = q_0E_1,]
где (E_1) — напряжённость поля первой обкладки:
[E_1=dfrac{sigma}{2varepsilon_0}=dfrac{q}{2varepsilon_0S}]
Значит
[F_0=dfrac{qq_0}{2varepsilon_0S}]
Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила (F) притяжения второй обкладки к первой складывается из всех этих сил (F_0), с которыми притягиваются к первой обкладке всевозможные маленькие заряды (q_0) второй обкладки. При этом суммировании постоянный множитель (displaystyledfrac{q}{2varepsilon_0S}) вынесется за скобку, а в скобке просуммируются все (q_0) и дадут (q). В результате получим
[F=dfrac{q^2}{2varepsilon_0S}]
Предположим теперь, что расстояние между обкладками изменилось от начальной величины (d_1) до конечной величины (d_2). Сила притяжения пластин совершает при этом работу [A = F(d_1 -d_2)]
Знак правильный: если пластины сближаются ((d_2 < d_1)), то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины ((d_2 > d_1)), то работа силы притяжения получается отрицательной, как и должно быть.
Получаем
[A=dfrac{q^2}{2varepsilon_0S}(d_1-d_2)=dfrac{q^2d_1}{2varepsilon_0S}-dfrac{q^2d_2}{2varepsilon_0S}=dfrac{q^2}{2C_1}-dfrac{q^2}{2C_2}=W_1-W_2]
Это можно переписать следующим образом: [A =-(W_2-W_1) =-Delta W,]
где [fbox{$W=dfrac{q^2}{2C}$}, (1)]
Работа потенциальной силы (F) притяжения обкладок оказалась равна изменению со знаком минус величины (W). Это как раз и означает, что (W) — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение (q = CU), можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).
[fbox{$W=dfrac{qU}{2}$}, (2)]
[fbox{$W=dfrac{CU^2}{2}$}, (3)]
Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
ЕГЭ
Справочник
ЕГЭ
Физика
Задание 18435
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Аналоги к заданию 18435:
•
18435
•
18908
Раздел кодификатора ФИПИ / Решу ЕГЭ:
•
2.1.2 Уметь описывать и объяснять результаты экспериментов
Задание 18908
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Аналоги к заданию 18908:
•
18435
•
18908
Раздел кодификатора ФИПИ / Решу ЕГЭ:
•
1.3 Знать/понимать смысл физических законов, принципов, постулатов
ЕГЭ
Справочник
© 2023 ЕГЭ.Справочник24. Все права защищены.
Предметы
Русский язык
Математика профильная
Физика
Химия
Информатика и ИКТ
Биология
История
География
Английский язык
Немецкий язык
Французский язык
Обществознание
Испанский язык
Литература
Математика базовая
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
U=Ed
Электроемкость конденсатора
Определение
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
C=ε0εSd
- ε0 — диэлектрическая постоянная, равная 8,85∙10–12 Кл2/(Н∙м2);
- ε — диэлектрическая проницаемость среды;
- S (м2) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
C=QU=qU
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Формула энергии конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
Wэ=q22C=CU22
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
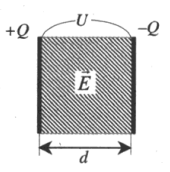
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
10 см = 0,1 м
1 мм = 0,001 м
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
S = a2
Соединения конденсаторов
| Последовательное соединение | Параллельное соединение | |
| Схема | 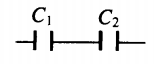 |
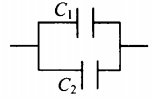 |
| Напряжение |
U=U1+U2 |
U=U1=U2 |
| Заряд |
q=q1=q2 |
q=q1+q2 |
| Электроемкость |
1C=1C1+1C2 |
C=C1+C2 |
Подсказки к задачам
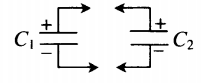
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами:
Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
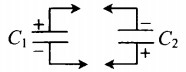
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами. |
Схема соединения конденсаторов разноименными полюсами: Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
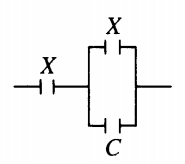
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
Электрическая емкость параллельного соединения равна:
Cпарал=X+C
Электроемкость последовательного соединения:
1Cпослед=1Cпарал+1X=1X+C+1X
Учтем, что суммарная электроемкость равна C:
1C=1X+C+1X
Преобразуем, умножим выражение на CX(X+C):
X(X+C)=CX+C(X+C)
Раскроем скобки:
X2+XC=CX+CX+C2
X2−CX−C2=0
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
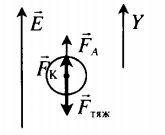
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона:
−Fтяж+−FK+−FA=0 ρш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U |
| Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l? | 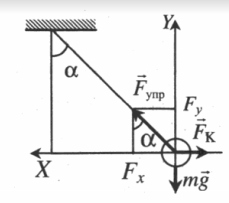
Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2 |
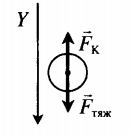
| Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg |
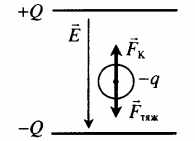
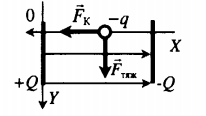
| Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если Fтяж < FK, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая Fтяж > FK: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая Fтяж < FK, получим: t=√2bmqE−mg |
| Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Если сила Кулона направлена вправо, то sx = d. Если сила Кулона направлена вправо, то sx = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE |
Задание EF17979
Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.
2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.
3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.
Решение
Емкость конденсатора определяется формулой:
C=ε0εSd
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
C=qU
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
Ответ: 113
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18574
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Алгоритм решения
1.Проанализировать каждый этап эксперимента.
2.Установить, от чего зависит угол отклонения стрелки электрометра.
3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.
Решение
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
C=ε0εSd
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
C=qU
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
Ответ: Увеличатся
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18695
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18703
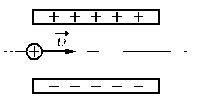
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.
3.Выяснить, при каком условии протон успеет вылететь из конденсатора.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса протона: m = 1,67∙10–27 кг.
• Заряд протона: q = 1,6∙10–19 Кл.
• Расстояние между обкладками конденсатора: d = 1 см.
• Длина пластин конденсатора: l = 5 см.
• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.
1 см = 0,01 м
5 см = 0,05 м
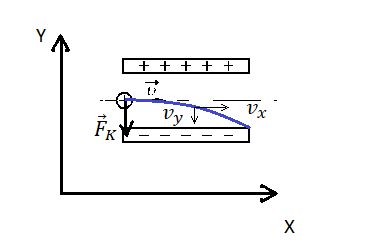
Сделаем рисунок:
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 5.5k