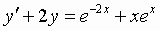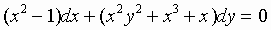Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
Помогите рассортировать файлы. К какому предмету относится данный файл?
Ненужные и мусорные файлы можно перемещать в предмет [НА УДАЛЕНИЕ].
Помогите дать файлам осмысленные названия
Примеры:
lab1 => Лабораторная работа №1. Фотоэффект.
Savelev_molekulyarnaya_fizika => Савельев. Молекулярная физика
| Задание по типовому расчёту | ||
| <описание отсутствует> | ||
| Автор: Ravenbird | Баллы: 3 |  diftip-ok.rar (1,25 Мб) diftip-ok.rar (1,25 Мб) |
| Типовик (задание) по ДифУрам | ||
| <описание отсутствует> | ||
| Автор: Naruto_kun | Баллы: 5 |  ДифУры.rar (2,33 Мб) ДифУры.rar (2,33 Мб) |
| Типовик — непонятный вариант | ||
| Автор, отредактируй комментарий к файлу — укажи вариант. | ||
| Автор: raggazi | Баллы: 15 |  tipovikdiffurivar1.rar (2,74 Мб) tipovikdiffurivar1.rar (2,74 Мб) |
| Типовой расчет 10 вариант | ||
| <описание отсутствует> | ||
| Автор: Nikk | Баллы: 15 |  ДУ_вариант_10.rar (2,4 Мб) ДУ_вариант_10.rar (2,4 Мб) |
| Типовой расчет, вариант №16 | ||
| Губановский типовик. Проверенный и зачтенный. Удачи… | ||
| Автор: Slevin13 | Баллы: 15 |  диф16вар.doc (352,5 Кб) диф16вар.doc (352,5 Кб) |
| Типовой расчёт 2 вариант | ||
| <описание отсутствует> | ||
| Автор: guzich | Баллы: 15 |  tip_2var.rar (708,8 Кб) tip_2var.rar (708,8 Кб) |
| Типовой расчёт, вариант №1 | ||
|
Типовик по диффурам 1 вариант © Akumbl4, ВВ-3-06 |
||
| Автор: Hedger | Баллы: 15 |  tipovikdiffurivar1.pdf (2,89 Мб) tipovikdiffurivar1.pdf (2,89 Мб) |
| Типовой расчёт, вариант №11 | ||
| 11 вариант 2008, решал сам…6 задач полностью, фотки подписаны, если сразу не разберётесь…удачной сдачи=) | ||
| Автор: prey | Баллы: 15 |  difur-var-11.rar (17,09 Мб) difur-var-11.rar (17,09 Мб) |
| Типовой расчёт, вариант №12 | ||
|
Типовик по диффурам 12 вариант © IDALGO-LoVe, ВВ-3-06 |
||
| Автор: IDALGO.LoVe | Баллы: 15 |  tipovikdiffurivar12.pdf (4,67 Мб) tipovikdiffurivar12.pdf (4,67 Мб) |
| Типовой расчёт, вариант №14 | ||
| <описание отсутствует> | ||
| Автор: brainstormer | Баллы: 15 |  Тип_вар_14_difur.rar (1,99 Мб) Тип_вар_14_difur.rar (1,99 Мб) |
| Типовой расчёт, вариант №20 | ||
| <описание отсутствует> | ||
| Автор: groyve | Баллы: 15 |  d20.rar (1,35 Мб) d20.rar (1,35 Мб) |
| Типовой расчёт, вариант №27 | ||
| (с)VV-7-07 | ||
| Автор: woland | Баллы: 15 |  du_3sem_var27.rar (12,06 Мб) du_3sem_var27.rar (12,06 Мб) |
| Типовой расчёт, вариант №3 | ||
| <описание отсутствует> | ||
| Автор: Tdutybz19 | Баллы: 15 |  типовик_3_вариант.rar (7,94 Мб) типовик_3_вариант.rar (7,94 Мб) |
| Типовой расчёт, вариант №4 | ||
|
Типовик по диффурам 4 вариант © KreN.del, ВВ-3-06 |
||
| Автор: krendel | Баллы: 15 |  tipovikdiffurivar4.pdf (2,24 Мб) tipovikdiffurivar4.pdf (2,24 Мб) |
| Типовой расчёт, вариант №5 | ||
| <описание отсутствует> | ||
| Автор: Positive | Баллы: 15 |  d5.rar (1,14 Мб) d5.rar (1,14 Мб) |
| Типовой расчёт, вариант №6 | ||
| <описание отсутствует> | ||
| Автор: Kuroi | Баллы: 15 |  var6.rar (2,72 Мб) var6.rar (2,72 Мб) |
| Типовой расчёт, вариант №7 | ||
| <описание отсутствует> | ||
| Автор: Ravenbird | Баллы: 15 |  diff7.pdf (15,57 Мб) diff7.pdf (15,57 Мб) |
| Типовой расчёт, вариант №9 | ||
| Решённый типовик, 9 вариант. Качество не очень удалось | ||
| Автор: Jack | Баллы: 15 |  9var.rar (2,46 Мб) 9var.rar (2,46 Мб) |
© vv206.ru, дамп файлового архива для itv09.org, 2011
МИРЭА
ТИПОВОЙ РАСЧЕТ
«ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»
Для студентов очной формы обучения институтов ИТ , РТС, ФТИ
Список решенных вариантов данного задания вы можете посмотреть ниже:
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
Решение задач типового расчета позволяет успешно подготовиться к выполнению контрольных работ и к сдаче экзамена (зачета). Наличие выполненного типового расчета является необходимым условием допуска студента к сдаче экзамена по курсу.
Задача 1. Определить тип дифференциального уравнения первого порядка. Найти общее решение (общий интеграл решения) заданного дифференциального уравнения.
Задача 2. Определить тип дифференциального уравнения первого порядка. Найти общее решение (общий интеграл решения) заданного дифференциального уравнения.
Задача 3. Решить задачу Коши. Сделать проверку полученного ответа.
Задача 4. Решить дифференциальное уравнение, используя метод понижение порядка.
Задача 5. Решить линейное неоднородное дифференциальное уравнение с постоянными коэффициентами методом подбора частного решения. Сделать проверку частного решения.
Задача 6. Решить линейное неоднородное дифференциальное уравнение с постоянными коэффициентами методом вариации произвольной постоянной.
Задача 7. Решить задачу Коши для линейного неоднородного дифференциального уравнения с постоянными коэффициентами двумя методами:
– методом подбора частного решения;
– операторным методом (с помощью преобразования Лапласа).
Задача 8. Найти частное решение системы линейных дифференциальных уравнений с заданными начальными условиями двумя методами:
– операторным методом;
– методом исключения.
Пособие по курсу “Дифференциальные уравнения” предназначено для студентов очной формы обучения институтов Информационных технологий, РТС и ФТИ (МИРЭА). Пособие включает следующие разделы: дифференциальные уравнения первого порядка; дифференциальные уравнения, допускающие понижение порядка; методы решения линейных дифференциальных уравнений и систем дифференциальных уравнений. Материал пособия можно использовать при изучении таких курсов, как математический анализ, математическая физика, методы математического моделирования, основы теории электрических цепей, при изучении других специальных и общепрофессиональных дисциплин.
23 января, 2018
Posted In: Дифференциальное исчисление, Дифференциальные уравнения, Матанализ, Математика, МГТУ МИРЭА, Платные работы, Типовой расчет
-
Форум МИРЭА
-
→
Файлы -
→
Технические предметы (общие) -
→
Дифференциальные уравнения
0
Дифференциальные уравнения
- Вы не можете загрузить новый файл
Случайные файлы
-
521
Всего файлов -
166
Всего категорий -
131
Всего авторов -
256 761
Всего загрузок -
Оракул / Oracle
Последний файл -
Just_Like
Последний автор
Типовой расчет дифференциальные уравнения мирэа
Решебник типового расчета по дифференциальным уравнениям для студентов II курса (III семестр) факультета Кибернетики, МГТУ МИРЭА
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
III семестр
ТИПОВОЙ РАСЧЁТ
Список решенных вариантов типового расчета по дифференциальным уравнениям для студентов II курса (III семестр) факультета Кибернетики, МГТУ МИРЭА вы можете посмотреть ниже:
Задание:
Задача 1. Найти общее решение уравнения
используя характеристическое уравнение и метод вариации произвольных постоянных
Задача 2.
1) Проверить, что y1(x) есть частное решение однородного уравнения L(y)=0. Зная это, найти общее решение уравнения L(y)=0.
2) Найти общее решение неоднородного уравнения L(y)=f(x) с заданной правой частью f(x), предположив, что одно из частных решений уравнения L(y)=f(x) является многочленом.
Задача 3. Решить задачу коши
а) с помощью формулы Дюамеля, решив предварительно вспомогательную задачу Коши
б) методом неопределенных коэффициентов (подбором частного решения неоднородного уравнения по правой части).
Задача 4. Найти изображение периодического оригинала с периодом T=2a. На рисунках указан вид его графика на одном периоде.
Задача 5. Операторным методом найти решение задачи коши
Для четных вариантов
для нечетных вариантов
Задача 6. Решить систему уравнений
с начальными условиями x(0)=x0, y(0)=y0 следующими методами:
а) сведением к уравнению второго порядка;
б) операторным методом.
в)* Операторным методом найти матричную экспоненту e At и с помощью нее решить для этой системы задачу Коши.
г) Определить характер фазового портрета точки покоя для линейной системы. Найти собственные значения и собственные векторы, нарисовать эскиз фазового портрета.
Задача 7*. (выполняется по усмотрению преподавателя группы)
Найти все точки покоя системы двух дифференциальных уравнений
Линеаризовать систему в окрестности той точки покоя (x0; y0), в которой максимальна сумма x0+y0. Определить характер фазового портрета для этой точки покоя, исследовать её на устойчивость.
Задача 8*. (выполняется по усмотрению преподавателя группы)
Найти свертку двух оригиналов (сигналов), изобразить геометрически полученную функцию (оригинал). Найти изображение полученного оригинала двумя способами:
1) непосредственно, вычисляя изображение как интеграл;
2) используя теорему об изображении свертки.
Типовой расчет дифференциальные уравнения мирэа
Список текущего и будущего дз
- «Наследие ПМИ» теперь доступно для всех. По-возможности — указывайте на ошибки и дополняйте.
- Задания типовых расчётов в папке Типовики
-
Автоматы и алгоритмы:
Алгебра и геометрия:
- СДО Занятие 1, №2,7,9,12
Математические основы баз данных:
Методы комплексного анализа:
Особенности математического моделирования на различных вычислительных платформах:
Физическая культура и спорт:
About
Архив домашних заданий и прочей информации по направлению «Прикладная математика и информатика» в МИРЭА
Topics
Resources
Stars
Watchers
Forks
Contributors 2
You can’t perform that action at this time.
You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session.
Типовой расчет дифференциальные уравнения мирэа
Типовой расчет по дифференциальным уравнениям для студентов 2-ого курса.
Часть 1. Практические задачи. Вариант №13.1. При помощи изоклин начертить решения дифференциального уравнения :
2. Используя теорему существования и единственности для уравнения
найти на плоскости (t,x) множество точек, через которые проходит только одна интегральная кривая. Изобразить вид интегральных кривых. Найти участки, где решения уравнения возрастают (убывают). Найти точки максимума (минимума) для решений данного уравнения. При каких значениях x0 задача Коши с начальным условием x( — 2) = x0 допускает существования единственного решения в области t > — 2 . Что изменится, если начальное условие имеет вид: x(2) = x0?
3. За какое время вытечет вся вода из цилиндрического бака диаметром 2R = 1,8 м. и высотой H = 2,45 м. через отверстие в дне диаметром 2r = 6 см. Ось цилиндра вертикальна. При решении задачи принять, что жидкость вытекает из сосуда со скоростью
, где g = 9,8 м/сек 2 — ускорение силы тяжести, h — высота уровня воды над отверстием. (А.Ф. Филиппов, Сборник задач по дифференциальным уравнениям. РХД-2000, № 91)
4. Решить дифференциальное уравнение (2-умя способами) .
5. Решить дифференциальное уравнение
(А.Ф. Филиппов, Сборник задач по дифференциальным уравнениям. РХД-2000, № 419) .6. Решить дифференциальное уравнение
(А.Ф. Филиппов, Сборник задач по дифференциальным уравнениям. РХД-2000, № 462).источники:
http://github.com/nektonick/KMBO-01-homework
http://web-tutor.narod.ru/Pages_1024x768/Diffur-2.htm
Автор конспекта: Дмитрий Карих (karikh.d@gmail.com), студент группы ИСБОп-01-14
Часть I
Семинар 1 (2.09.15)
Преподаватель: Миронинко Елена Сергеевна
План семестра
1. Две контрольных работы
(a) Контрольная работа 1
i. Дифференциальные уравнения первого порядка (? задач)
ii. Дифференциальные уравнения, допускающие понижения (2 задачи)
(b) Контрольная работа 2
i. Линейные дифференциальные уравнения (7 задач)
ii. Операционные исчисления (6 задач). Преобразования Лапласа.
2. Типовой расчет
3. Экзамен
Шпаргалки
Шпаргалка 1
1. Свойства и преобразования Лапласа
2. Таблица оригиналов и изображений Оригиналы Изображения
11
p
Шпаргалка 2 — Таблица интегралов и дифференциалов. К следующей паре.
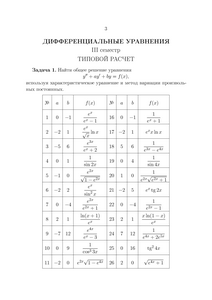
f(x) (f(x))0´f(x) + C
xnn·xn−1xn+1
n+1
ln x1
x
axaxln aax
ln a
exexex
sh xch xch u
ch xsh xsh u
logax1
x·ln a
th x1
ch2x
cth x−1
sh x
f(x) (f(x))0´f(x)
sin xcos x−cos x
cos x−sin xsin x
tg x1
cos2x
ctg x−1
sin2x
arcsin x1
√1−x2
arccos x−1
√1−x2
arctg x1
1+x2
arcctg x−1
1+x2
f(x)´f(x)
1
√x2+aln |x+√x2+a|
1
a2−x2
1
2ln |a+x
a−x|
1
x2−a2
1
2aln |x−a
x+a|
1
√a2−x2arcsin x
a
1
a2+x2
1
aarctg x
a
1
a2+b2x2
1
ab arctg bx
a
1








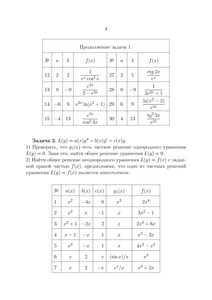

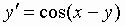
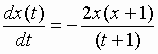
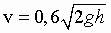 , где g = 9,8 м/сек 2 — ускорение силы тяжести, h — высота уровня воды над отверстием. (А.Ф. Филиппов, Сборник задач по дифференциальным уравнениям. РХД-2000, № 91)
, где g = 9,8 м/сек 2 — ускорение силы тяжести, h — высота уровня воды над отверстием. (А.Ф. Филиппов, Сборник задач по дифференциальным уравнениям. РХД-2000, № 91)