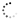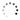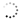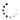
Помогите рассортировать файлы. К какому предмету относится данный файл?
Ненужные и мусорные файлы можно перемещать в предмет [НА УДАЛЕНИЕ].
Помогите дать файлам осмысленные названия
Примеры:
lab1 => Лабораторная работа №1. Фотоэффект.
Savelev_molekulyarnaya_fizika => Савельев. Молекулярная физика
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
| 3 билета по дифурам 2006 г, | ||
| Весьма жесткие, и качество не айс — но хоть чето… | ||
| Автор: Hedger | Баллы: 10 |  df-bil-p.rar (478,14 Кб) df-bil-p.rar (478,14 Кб) |
| 4 варианта кр у Губанова | ||
| <описание отсутствует> | ||
| Автор: Evgeniy | Баллы: 5 |  difkrrar.rar (2,29 Мб) difkrrar.rar (2,29 Мб) |
| Билеты ДифУры 2009 | ||
| 4 билета по диффурам | ||
| Автор: IIapoBo3 | Баллы: 5 |  билеты_2009.rar (1,82 Мб) билеты_2009.rar (1,82 Мб) |
| Билеты по ДиффУрам 2009 | ||
| Билеты по дифференциальным уравнениям за 3й семестр, за авторством Губанова. | ||
| Автор: Dalberg | Баллы: 5 |  difuri_ekzamen_zima_2009.rar (1,72 Мб) difuri_ekzamen_zima_2009.rar (1,72 Мб) |
| Билеты по Диффурам 2010 | ||
| <описание отсутствует> | ||
| Автор: Mcbrain | Баллы: 4 |  9-1516.rar (1,02 Мб) 9-1516.rar (1,02 Мб) |
| Билеты с пересдачи | ||
| 2 билета с пересдачи по дифурам Губанова | ||
| Автор: kensh | Баллы: 7 |  дифуры_пересдача.rar (154,18 Кб) дифуры_пересдача.rar (154,18 Кб) |
| Большая таблица изображений | ||
| Прикольная вещь, но из нее реально надо штук 15 изображений. остальные — на всякий пожарный. | ||
| Автор: Hedger | Баллы: 3 |  orig.rar (374,23 Кб) orig.rar (374,23 Кб) |
| ДУ в примерах и задачах. Боярчук, Головач | ||
|
Дифференциальные уравнения в примерах и задачах. Справочное пособие по высшей математике том 5. |
||
| Автор: Ravenbird | Баллы: 5 |  antidem5.rar (3,38 Мб) antidem5.rar (3,38 Мб) |
| Задачник Филиппова | ||
| По этому задачнику задают домашки. Да и теория решения дифур там неплохо дана -. коротко и ясно | ||
| Автор: $W@T0$@ | Баллы: 7 |  DIFFYRI.rar (5,99 Мб) DIFFYRI.rar (5,99 Мб) |
| Консультация по Диффурам ( Губанов!!!) | ||
| <описание отсутствует> | ||
| Автор: Den strat | Баллы: 2 |  Диффуры_Консультация.rar (10,33 Мб) Диффуры_Консультация.rar (10,33 Мб) |
| Контрольная работа по ДУ | ||
| <описание отсутствует> | ||
| Автор: Nikk | Баллы: 5 |  КР_по_ДУ.rar (451,26 Кб) КР_по_ДУ.rar (451,26 Кб) |
| Лекции по диффурам | ||
| <описание отсутствует> | ||
| Автор: Ravenbird | Баллы: 10 |  difflect.rar (15,36 Мб) difflect.rar (15,36 Мб) |
| Матвеев.»Методы интегрирования обыкновенных дифференциальных уравнений» | ||
| Матвеев.»Методы интегрирования обыкновенных дифференциальных уравнений».Открывать программой WinDjView-0.5 | ||
| Автор: Ваня | Баллы: 4 |  matveev1967ru.rar (14,93 Мб) matveev1967ru.rar (14,93 Мб) |
| Пак в помощь к экзамену | ||
| <описание отсутствует> | ||
| Автор: frio | Баллы: 20 |  difur_help.zip (9,9 Мб) difur_help.zip (9,9 Мб) |
| Пара прошлогодних билетов к экзамену | ||
| <описание отсутствует> | ||
| Автор: Hedger | Баллы: 2 |  dif_ex3sem.rar (110,07 Кб) dif_ex3sem.rar (110,07 Кб) |
| Письменный, часть 2 | ||
| Не без крови добытый на просторах инета Письменый ч.2 всем в помощь =) | ||
| Автор: $W@T0$@ | Баллы: 7 |  Письменный_ч2.rar (2,79 Мб) Письменный_ч2.rar (2,79 Мб) |
| Теоретические вопросы к экзамену | ||
| тупо 30 вопросов по всему курсу | ||
| Автор: Hedger | Баллы: 3 |  ex_difur.rar (3,26 Кб) ex_difur.rar (3,26 Кб) |
| Типовик по диффурам (задания) | ||
| Типовой расчет по дифференциальным уравнением за 2008 год. | ||
| Автор: benchmade | Баллы: 4 |  Методичка_по_Диффурам.rar (2,41 Мб) Методичка_по_Диффурам.rar (2,41 Мб) |
| Типовой расчёт, задания, 2009 | ||
| <описание отсутствует> | ||
| Автор: Мафка | Баллы: 4 |  Дифуры_-_Задания.zip (24,1 Мб) Дифуры_-_Задания.zip (24,1 Мб) |
| Шпоры по диффурам | ||
| Шпора по дифф мне очень помогла) | ||
| Автор: VcR | Баллы: 7 |  дифф.rar (4,26 Мб) дифф.rar (4,26 Мб) |
| Экзаменационные билеты за 2011 ый | ||
| Лектор Н.В. Белецкая | ||
| Автор: zewyti | Баллы: 7 |  Дифуры_2011.rar (2,87 Мб) Дифуры_2011.rar (2,87 Мб) |
© vv206.ru, дамп файлового архива для itv09.org, 2011
|
|
|
||||||||||||||||||||||||||||||
Copyright MyCorp © 2023 |
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
III семестр
ТИПОВОЙ РАСЧЁТ
Список решенных вариантов типового расчета по дифференциальным уравнениям для студентов II курса (III семестр) факультета Кибернетики, МГТУ МИРЭА вы можете посмотреть ниже:
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
Задание:
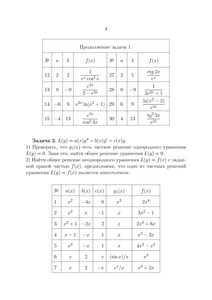
Задача 1. Найти общее решение уравнения
используя характеристическое уравнение и метод вариации произвольных постоянных
Задача 2.
1) Проверить, что y1(x) есть частное решение однородного уравнения L(y)=0. Зная это, найти общее решение уравнения L(y)=0.
2) Найти общее решение неоднородного уравнения L(y)=f(x) с заданной правой частью f(x), предположив, что одно из частных решений уравнения L(y)=f(x) является многочленом.
Задача 3. Решить задачу коши
а) с помощью формулы Дюамеля, решив предварительно вспомогательную задачу Коши
б) методом неопределенных коэффициентов (подбором частного решения неоднородного уравнения по правой части).
Задача 4. Найти изображение периодического оригинала с периодом T=2a. На рисунках указан вид его графика на одном периоде.
Задача 5. Операторным методом найти решение задачи коши
Для четных вариантов
для нечетных вариантов
Задача 6. Решить систему уравнений
с начальными условиями x(0)=x0, y(0)=y0 следующими методами:
а) сведением к уравнению второго порядка;
б) операторным методом.
в)* Операторным методом найти матричную экспоненту eAt и с помощью нее решить для этой системы задачу Коши.
г) Определить характер фазового портрета точки покоя для линейной системы. Найти собственные значения и собственные векторы, нарисовать эскиз фазового портрета.
Задача 7*. (выполняется по усмотрению преподавателя группы)
Найти все точки покоя системы двух дифференциальных уравнений
Линеаризовать систему в окрестности той точки покоя (x0; y0), в которой максимальна сумма x0+y0. Определить характер фазового портрета для этой точки покоя, исследовать её на устойчивость.
Задача 8*. (выполняется по усмотрению преподавателя группы)
Найти свертку двух оригиналов (сигналов), изобразить геометрически полученную функцию (оригинал). Найти изображение полученного оригинала двумя способами:
1) непосредственно, вычисляя изображение как интеграл;
2) используя теорему об изображении свертки.
9 сентября, 2019
Posted In: Дифференциальное исчисление, Дифференциальные уравнения, Матанализ, Математика, МГТУ МИРЭА, Платные работы, Типовой расчет
Дифференциальные уравнения, Тихонов А.Н., Васильева А.Б., Свешников А.Г., 2005
Дифференциальные уравнения, Тихонов А.Н., Васильева А.Б., Свешников А.Г., 2005.
Один из выпусков «Курса высшей математики и математической физики» под редакцией А.Н. Тихонова, В.А. Ильина, А.Г. Свешникова. Учебник создан на базе лекций, читавшихся авторами в течение многих лет на физическом факультете Московского государственного университета им. М.В. Ломоносова. Изложение отвечает современному состоянию теории дифференциальных уравнений в той мере, как это требуется специалистам по физике и математике. Большое внимание уделено численным и асимптотическим методам решения. Воспроизводится с 3-го изд. (1998 г.).
Для студентов высших учебных заведений, обучающихся по специальностям «Физика» и «Прикладная математика».
Понятие дифференциального уравнения.
В настоящей книге рассматриваются дифференциальные уравнения, т. е. соотношения между неизвестной функцией, ее производными и независимыми переменными. Уравнения, содержащие производные по многим независимым переменным, называются уравнениями в частных производных. Уравнения, содержащие производные лишь по одной из независимых переменных, называются обыкновенными дифференциальными уравнениями. Изучение свойств и методов решения обыкновенных дифференциальных уравнений и составляет основное содержание данной книги, лишь последняя глава посвящена некоторым специальным классам уравнений в частных производных.
Независимую переменную, производная по которой входит в обыкновенное дифференциальное уравнение, обычно обозначают буквой х (или буквой t, поскольку во многих случаях роль независимой переменной играет время). Неизвестную функцию обозначают у(х).
ОГЛАВЛЕНИЕ
Предисловие к третьему изданию
Предисловие ко второму изданию
Предисловие к первому изданию
ГЛАВА 1 ВВЕДЕНИЕ
§1. Понятие дифференциального уравнения
§2. Физические задачи, приводящие к дифференциальным уравнениям
ГЛАВА 2 ОБЩАЯ ТЕОРИЯ
§1. Элементарные методы интегрирования
§2. Теоремы существования и единственности решения начальной задачи для одного уравнения первого порядка, разрешенного относительно производной. Алгоритм ломаных Эйлера
§3. Уравнение, неразрешенное относительно производной
§4. Теоремы существования и единственности решения нормальной системы
§5. Зависимость решений от начальных значений и параметров
§6. Метод последовательных приближений (метод Пикара)
§7. Принцип сжимающих отображений. Теорема о неподвижной точке
ГЛАВА 3 ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§1. Уравнение движения маятника как пример линейного уравнения. Основные свойства линейного уравнения с постоянными коэффициентами
§2. Общие свойства линейного уравнения n-го порядка
§3. Однородное линейное уравнение n-го порядка
§4. Неоднородное линейное уравнение n-го порядка
§5. Линейное уравнение n-го порядка с постоянными коэффициентами
§6. Системы линейных уравнений. Общая теория
§7. Системы линейных дифференциальных уравнений с постоянными коэффициентами
§8. Построение решения линейного уравнения в виде степенного ряда
ГЛАВА 4 КРАЕВЫЕ ЗАДАЧИ
§1. Постановка краевых задач и их физическое содержание
§2. Неоднородная краевая задача
§3. Задачи на собственные значения
ГЛАВА 5 ТЕОРИЯ УСТОЙЧИВОСТИ
§1. Постановка задачи
§2. Исследование на устойчивость по первому приближению
§3. Метод функций Ляпунова
§4. Исследование траекторий в окрестности точки покоя
ГЛАВА 6 ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§1. Разностные методы решения начальной задачи
§2. Краевые задачи
ГЛАВА 7 АСИМПТОТИКА РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПО МАЛОМУ ПАРАМЕТРУ
§1. Регулярные возмущения
§2. Сингулярные возмущения
ГЛАВА 8 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
§1. Линейное уравнение
§2. Квазилинейное уравнение
Список литературы
Предметный указатель.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Дифференциальные уравнения, Тихонов А.Н., Васильева А.Б., Свешников А.Г., 2005 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу
Дифференциальные уравнения, Сергеев И.Н., 2013
Дифференциальные уравнения, Сергеев И.Н., 2013.
Учебник создан в соответствии с Федеральным государственным образовательным стандартом по направлениям подготовки «Математика», «Математика и компьютерные науки», «Механика и математическое моделирование», «Прикладная математика и информатика», «Фундаментальная информатика и информационные технологии» (квалификация «бакалавр»)
Материал учебника знакомит с геометрической интерпретацией уравнения первого порядка, с первыми интегралами, особыми точками и предельными циклами автономных систем, с теорией линейных уравнений и систем, в том числе с постоянными и периодическими коэффициентами, с вопросами существования, единственности и продолжаемости решений, их непрерывности и дифференцируемости по параметру, устойчивости по Ляпунову, а также с вопросами существования и единственности решения задачи Коши для уравнения с частными производными первого порядка Даны точные определения, аккуратно сформулированы и доказаны утверждения, строго обоснованы наиболее важные методы решения задач Приведены все необходимые теоретические сведения, сопутствующие понятия и факты из смежных разделов математики Предложены задачи для самостоятельного решения, позволяющие глубже проникнуть в прочитанный материал
Для студентов учреждений высшего профессионального образования.
Теоремы существования, единственности и продолжаемости для уравнения
произвольного порядка выводятся из соответствующих теорем для нормальной системы с помощью леммы 29, которая фактически означает, что указанные две задачи с точки зрения существования, единственности и продолжаемости их решений устроены абсолютно одинаково.
I. Основные теоремы для уравнения. Исходя из перечисленных выше свойств отображения (54) получаем, что указанные в формулировке леммы 29 изоморфизмы (равно как и обратные к ним) сохраняют:
• локальное совпадение решений (как равенство их сужений на некоторую окрестность данной точки);
• глобальное совпадение решений (как равенство их сужений на общую область определения);
• свойство одного решения быть продолжением другого (как равенство сужения первого на область определения второго);
• непродолжаемость решения (как равенство его самого любому его продолжению).
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Дифференциальные уравнения, Сергеев И.Н., 2013 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу
Учебник по дифференциальным уравнениям маи
Чуть больше года назад в сообществе уже был пост, посвященный дифференциальным уравнениям, однако там были ссылки в основном на руководства по решению задач. Последние охватывали, как правило, несколько разделов математического анализа и потому тему ДУ рассматривали достаточно бегло. В настоящее время таким книгам посвящены записи Полные курсы по высшей математике и Руководства по решению задач («Решебники» по высшей математике), советуем обязательно просмотреть их. В данной записи приводятся ссылки на литературу, охватывающую только тему «Дифференциальные уравнения».
Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. 2-е изд., испр. — М.: ФИЗМАТЛИТ, 2005. — 384 с.
Рассматриваются основные направления теории обыкновенных дифференциальных уравнений и практические методы решения таких уравнений. Значительная часть книги содержит стандартный учебный материал по курсу обыкновенных дифференциальных уравнений. Кроме того, рассматриваются матричные дифференциальные уравнения, основы теории устойчивости по Ляпунову, основы теории периодических решений нелинейных уравнений, теория уравнений с разрывной правой частью (дифференциальные включения) и применение теории групп Ли к решению обыкновенных дифференциальных уравнений.
Для студентов университетов и технических вузов, для преподавателей и научных работников, интересующихся обыкновенными дифференциальными уравнениями и их приложениями.
Подробное оглавление и ссылка для скачивания. || rghost.ru || libgen.info
 |
С.А. Агафонов, А.Д. Герман, Т.В. Муратова Дифференциальные уравнения. — МГТУ им. Н.Э. Баумана, 2004. -348 с. — (Математика в техническом университете) Изложены основы теории обыкновенных дифференциальных уравнений (ОДУ) и даны основные понятия об уравнениях с частными производными первого порядка. Приведены многочисленные примеры из механики и физики. Отдельная глава посвящена линейным ОДУ второго порядка, к которым приводят многие прикладные задачи. Содержание учебника соответствует курсу лекций, которые авторы читают в МГТУ Им. Н. Э. Баумана. Для студентов технических университетов и вузов. Может быть полезен интересующимся прикладными задачами теории дифференциальных уравнений. |
 |
Виленкин Н. Я. и др. Дифференциальные уравнения: Учеб. пособие для студентов-заочников IV курса физ.-мат, фак. / Н. Я. Виленкин, М. А. Доброхотова, А. Н. Сафонов.— М.: Просвещение, 1984. — 176 с. — Моск. гос. заоч. пед. ин-т. Предлагаемая вниманию читателя книга является учебным пособием для студентов-заочников физико-математических факультетов пединститутов по разделу «Дифференциальные уравнения» курса «Математический анализ». Она входит в серию пособий по математическому анализу, выходящую под общей редакцией профессора Н. Я. Виленкина («Введение в анализ» (1983 г.), «Дифференциальное исчисление» (1984 г.), «Интегральное исчисление» (1979 г.), «Ряды» (1982 г.) , «Мощность, метрика, интеграл» (1980 г.) «Элементы функционального анализа в задачах» (1978 г.), «Теория аналитических функций» (1985). Основное внимание в пособии уделяется развитию у студентов навыков решать физические и геометрические задачи с помощью дифференциальных уравнений. Структура пособия обеспечивает самостоятельную работу студентов по изучению данного курса. Теоретический материал иллюстрируется многочисленными подробно решенными примерами. Скачать (djvu/rar, 3.74 Мб, 600 dpi+OCR) ifolder.ru || libgen.info |
 |
Демидович Б. П., Моденов В. П. Дифференциальные уравнения: Учебное пособие. 3-е изд., стер. — СПб.: Издательство «Лань», 2008. — 288 с: ил. — (Учебники для вузов. Специальная литература). ISBN 978-5-8114-0677-7 Предлагаемая читателям книга состоит из двух частей: в первой части рассматриваются основы теории обыкновенных дифференциальных уравнений, во второй — дифференциальные уравнения с частными производными. Учебное пособие предназначено для студентов технических вузов. Написанная ясным и простым языком, книга представляется полезной также лицам, занимающимся математикой самостоятельно. Внимание. Скорее всего, это 2-е издание книги (на последней странице указано именно это и количество страниц 277. Исходник (pdf/rar 28.17 Мб, после распаковки 400 мб) ifolder.ru Полученный из исходника djvu, 3,23 мб rghost |
 |
|
 |
Еругин Н.П. Книга для чтения по общему курсу дифференциальных уравнений. — Минск, Наука и техника, 1979. — 744 с. Рассматриваются вопросы качественной теории дифференциальных уравнений, теории устойчивости и вообще анализ и классификация решений дифференциальных уравнений. В третьем издании расширена и использована при исследовании качественных вопросов глава «Теория подвижных особых точек в вещественной области», новая по методам и результатам и имеющая как теоретическое, так и прикладное значение. Шире рассматриваются в новом, издании и вопросы качественной теории и методы обнаружения и построения периодических решений в области центра и изолированных периодических решений. Добавлена и новая XIV глава «Фрагменты из элементарной конструктивной теории периодических решений автономной системы дифференциальных уравнений». Книга рассчитана на математиков, физиков и инженеров-теоретиков. Она будет полезна и студентам старших курсов механико-математических и физических факультетов. Скачать (divu, 10,5 Мб)ifolder || mediafire.com || libgen.info |
 |
Краснов М.Л., Киселев А.И., Макаренко Г.И., Шикин Е.В., и др. Вся высшая математика: Учебник. Т. 3. Теория рядов, обыкновенные дифференциальные уравнения, теория устойчивости — М.: Эдиториал УРСС, 2001. — 240 с. ISBN 5-8360-0153-7 Этот учебник адресован студентам высших учебных заведений (в первую очередь будущим инженерам и экономистам) и охватывает практически все разделы математики, но при этом представляет собой не набор разрозненных глав, а единое целое. В третий том вошел материал по некоторым разделам математического анализа (числовые, степенные, функциональные ряды, ряды Фурье) и обыкновенным дифференциальным уравнениям. Скачать (djvu/rar, ocr, 5,59 Мб) ifolder.ru || libgen.info |
 |
Матвеев Н. М. Дифференциальные уравнения Учеб. пособие для студентов пед. ин-тов по физ.-мат. спец.— М.: Просвещение, 1988.— 256. — ISBN 5-09-000281-9 Книга является единым руководством по изучению вопросов теории дифференциальных уравнений и методов интегрирования, обеспечивающим весь учебный процесс по разделу «Дифференциальные уравнения» программы по математическому анализу педагогических институтов. Скачать (djvu, 5.16 Мб) ifolder.ru || mediafire.com |
 |
Романко В. К. Курс дифференциальных уравнений и вариационного исчисления. — 2-е изд. — М.: Лаборатория Базовых Знаний, 2001 — 344 с: ил. В книге излагаются основные разделы классической теории обыкновенных дифференциальных уравнений и вариационного исчисления. Рассматриваются методы получения точных решений линейных дифференциальных уравнений с постоянными коэффициентами; значительное внимание уделяется вопросам существования, единственности и непрерывной зависимости решения дифференциального уравнения от исходных данных.Приводятся методы решения линейных дифференциальных уравнений с переменными коэффициентами, линейных и нелинейных уравнений первого порядка в частных производных; обсуждаются вопросы качественного исследования этих решений.Основы вариационного исчисления рассматриваются по причине тесной связи данного раздела высшей математики с теорией дифференциальных уравнений. Книга предназначена для студентов высших учебных заведений. По наводке malykh89 Скачать (divu, 5,12 Мб) ifolder || rghost |
 |
Петровский И. Г. Лекции по теории обыкновенных дифференциальных уравнений / Под ред. А. Д. Мышкиса, О. А. Олейиик. — М.: Изд-во МГУ, 1984. — 296 с. Книга представляет собой учебник по курсу обыкновенных дифференциальных уравнений. Тщательно продуманное изложение дало возможность в небольшом объеме вместить обширный материал. Более детально и строго, чем в других руководствах, рассмотрены уравнения простых типов. Подробно изложены общие теоремы о разрешимости уравнений и систем уравнений с непрерывными правыми частими. Теория линейных уравнений сопровождается оригинальным изложением канонической формы систем. Книга включает главу об автономных системах и добавление, содержащее теорию линейных и нелинейных уравнений с частными производными 1-го порядка. Большое количество задач значительно расширяет содержание книги. Обложка от книги другого издания. За книгу спасибо Violent_Violet Скачать (djvu, 3.08 Мб) ifolder.ru или mediafire.com |
 |
Понтрягин Л.С. Обыкновенные дифференциальные уравнения. — 4 изд. — М., Наука, 1974. — 331 с. От автора:Эта книга написана на основе лекций, которые я в течение ряда лет читал на механико-математическом факультете МГУ. При составлении программы лекций я исходил из уверенности, что выбор материала не должен быть случайным и не должен опираться исключительно на сложившиеся традиции.Наиболее важные и интересные применения обыкновенные дифференциальные уравнения находят в теории колебаний и в теории автоматического управления. Эти применения и послужили руководством при выборе материала для моих лекций. Учебник удостоен государственной премии СССР за 1975г. Скачать (divu, 4,75 Мб) ifolder ||eqworld.ipmnet.ru |
 |
Степанов В.В. Курс дифференциальных уравнений. — 6 изд. — 1950. — 473 с. Книга выдающегося российского математика, члена-корреспондента АН СССР В. В. Степанова (1889-1950) выдержала несколько переизданий, став классическим трудом в области дифференциальных уравнений. Автор знакомит читателя с элементарными методами интеграции, теоремами существования, особыми решениями, с общей теорией линейных уравнений — эти главы связаны с теорией групп Ли, с применением методов теории функций действительного и комплексного переменного, с методами линейной алгебры. В курсе дается достаточно развернутая качественная теория распределения интегральных кривых в окрестности особой точки. Рекомендуется студентам университетов, аспирантам и специалистам в области математики и может быть использована в качестве учебника для естественных вузов. Скачать (divu, 7 Мб) ifolder ||eqworld |
 |
Тихонов А. Н., Васильева А. Б., Свешников А. Г. Дифференциальные уравнения: Учеб.: Для вузов. — 4-е изд. — М.: ФИЗМАТЛИТ, 2005. — 256 с. — (Курс высшей математики и математической физики — Вып. 6 ISBN 5-9221-0277-X.). Один из выпусков «Курса высшей математики и математической физики» под редакцией А.Н. Тихонова, В.А. Ильина, А.Г. Свешникова. Учебник создан на базе лекций, читавшихся авторами в течение многих лет на физическом факультете Московского государственного университета им. М.В. Ломоносова. Изложение отвечает современному состоянию теории дифференциальных уравнений в той мере, как это требуется специалистам по физике и математике. Большое внимание уделено численным и асимптотическим методам решения. Воспроизводится с 3-го изд. 1998 г. Для студентов высших учебных заведений, обучающихся по специальностям «Физика» и «Прикладная математика». Скачать (1,7 Мб) mediafire.com || libgen.info |
 |
Ф. Трикоми. Дифференциальные уравнения. 1962 год. 362 стр. Книга посвящена теории дифференциальных уравнений . Книга, предлагаемая вниманию читателя, написана со свойственными автору простотой, ясностью и изяществом. Тщательный отбор материала и продуманность изложения позволяют при сравнительно небольшом объёме осветить многие важные задачи, идеи, методы и результаты со временной теории дифференциальных уравнений, которые обычно опускаются в общих курсах. Книга написана весьма просто. Она может служить пособием для студентов и аспирантов математиков и физиков, а также для инженеров. Немало интересного найдут в ней и специалисты-математики. Скачать (djvu/rar, 1 Мб) ph4s.ru || Подробное оглавление и ссылка для скачивания || libgen.info |
 |
Федорюк М. В. Обыкновенные дифференциальные уравнения. — 2-е изд., перераб. и доц.—-М.: Наука. Главная редакция физико-математической литературы, 1985.— 448 с. Книга содержит наложение основ теории обыкновенных дифференциальных уравнений, включая теорию устойчивости, и вариационное, исчисление. Значительное место уделено уравнениям с частными производными первого порядка, аналитической теории дифференциальных уравнений и асимптотике решений линейных уравнений второго порядка. В этом издании (первое издание выходило в 1980 г.) добавлены методы теории возмущений при исследовании нелинейных дифференциальных уравнений с малым параметром. Для студентов втузов, а также для инженеров-исследователей. Обложка от книги другого издания Скачать (divu, 10,74 Мб) ifolder.ru || libgen.info |
 |
Филиппов Алексей Федорович Введение в теорию дифференциальных уравнений: Учебник. Изд. 2-е, испр. М.: КомКнига, 2007. — 240 с. ISBN 978-5-484-00786-8. Книга содержит весь учебный материал в соответствии с программой Минвуза по курсу дифференциальных уравнений для механико-математических и физико-математических специальностей университетов. Имеется также небольшое количество дополнительного материала, связанного с техническими приложениями. Это позволяет выбирать материал для лекций в зависимости от профиля вуза. Объем книги существенно уменьшен по сравнению с имеющимися учебниками за счет сокращения дополнительного материала и выбора более простых доказательств из имеющихся в учебной литературе. Теория излагается достаточно подробно и доступно не только для сильных, но и для средних студентов. Приводятся с пояснениями примеры решения типовых задач. В конце параграфов указываются номера задач для упражнений из «Сборника задач по дифференциальным уравнениям» А. Ф. Филиппова и указываются некоторые теоретические направления, примыкающие к изложенным вопросам, со ссылками на литературу (книги на русском языке). Скачать (djvu/rar, 4.09 Мб) ifolder.ru || libgen.info |
 |
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. — 424 с. Настоящая книга — классический учебник по дифференциальным уравнениям и вариационному исчислению для студентов физических и физико-математических факультетов университетов. В основу книги положены лекции, которые автор в течение ряда лет читал на физическом факультете МГУ. Цель данного учебника — способствовать глубокому усвоению теории с помощью 300 подробно решенных примеров и 250 задач разного уровня сложности: от простых до самых сложных и нетривиальных. Большинство примеров имеет прямое приложение в физике. Книга состоит из двух независимых частей. В первой части подробно изложены методы интегрирования дифференциальных уравнений и простейшие способы исследования их решений; вторая часть знакомит читателя с методами решения различных вариационных задач. Каждая глава снабжена задачами для самостоятельного решения. Книга будет полезна и интересна и тем, кто только начинает знакомство с предметом, и тем, кто стремится углубить свои знания в этой области. Обложка от книги другого издания Скачать (4,7 мб, djvu,ocr) mediafire.com ||eqworld.ipmnet.ru |
В примерах и задачах
Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах. — М.: Изд-во МАИ, 2000.- 380с: ил.
Изложены аналитические, приближенно-аналитические и численные методы и алгоритмы решения обыкновенных дифференциальных уравнений. Применение каждого метода продемонстрировано на решениях типовых и нетиповых примеров, охватывающих различные приложения к задачам механики, экономики, расчета электрических цепей и биологических систем. Особое внимание уделено специфике решения задач анализа выходных процессов и устойчивости одномерных и многомерных динамических систем, исследуемых в теории управления. Для студентов и аспирантов инженерно-технических и авиационных специальностей вузов. (Обложка от другого издания)
Скачать (3,24 Мб) ifolder.ru
 |
Васильева А. В., Медведев Г. Н., Тихонов Н.А., Уразгильдина Т.А. Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и задачах. — М.: ФИЗМАТЛИТ,2003. — 432 с. — (Курс высшей математики и математической физики. Вып. 10. ISBN 5-9221-0276-1.) Пособие охватывает все разделы курсов «Дифференциальные и интегральные уравнения. Вариационное исчисление». По каждой теме кратко излагаются основные теоретические сведения; приводятся решения стандартных и нестандартных задач; даются задачи с ответами для самостоятельной работы. Для студентов вузов, обучающихся по специальностям «Физика» и «Прикладная математика». Скачать (djvu/rar,2,9 Мб) mediafire.com || libgen.info |
 |
Васильева А. Б., Медведев Г. Н., Тихонов Н. А., Уразгильдина Т. А. Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и задачах. — 2-е изд., испр. — М.: ФИЗМАТЛИТ, 2005. — 432 с. — (Курс высшей математики и математической физики. Вып. 10) — ISBN 5-9221-0628-7. Пособие охватывает все разделы курсов «Дифференциальные и интегральные уравнения. Вариационное исчисление». По каждой теме кратко излагаются основные теоретические сведения; приводятся решения стандартных и нестандартных задач; даются задачи с ответами для самостоятельной работы. Для студентов вузов, обучающихся по специальностям «Физика» и «Прикладная математика». Скачать (djvu/rar, 3,08 Мб) ifolder.ru |
 |
Калинин В.В. Обыкновенные дифференциальные уравнения (пособие для практических занятий). – ФГУП Изд-во «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2005. – 68 с. Пособие предназначено для студентов различных специальностей РГУ нефти и газа им И.М. Губкина. В нем подробно рассматриваются способы и приемы решения обыкновенных дифференциальных уравнений, разобраны реальные практические задачи, сводящихся к решению таких уравнений. В начале каждого раздела сформулированы теоретические вопросы, которые позволяют систематизировать знания по соответствующему разделу учебного курса. Приведены задачи для самостоятельного аудиторного и домашнего решения. В приложениях представлены приемы решения обыкновенных дифференциальных уравнений, несколько расширяющие рамки стандартного курса технического вуза, а также современные компьютерные подходы к решению дифференциальных уравнений (на примере системы «Mathematica»). Пособие будет также полезно магистрантам, аспирантам и специалистам в качестве справочного материала при решении практических задач. Скачать (pdf, 1 Мб) f-bit.ru || ph4s.ru || libgen.info |
 |
Краснов М.Л., Киселев А.И., Макаренко Г.И. Обыкновенные дифференциальные уравнения: Задачи и примеры с подробными решениями: Учебное пособие. Изд. 4-е., испр. — М.: Едиториал УРСС, 2002. — 256 с. (Вся высшая математика в задачах.) ISBN 5-354-00013-0 В предлагаемом сборнике задач (4-е изд., исправл.) особое внимание уделено тем вопросам, которые недостаточно подробно освещены в имеющихся пособиях и которые, как показывает опыт, слабо усваиваются студентами. Детально разобраны метод изоклин для уравнений первого и второго порядков, задачи нахождения ортогональных траекторий, линейная зависимость и независимость систем функций. В задачник включено большое число задач на решение линейных уравнений с постоянными и переменными коэффициентами, задачи на устойчивость по Ляпунову, на применение операционного метода к решению дифференциальных уравнений и систем. Представлены также метод последовательных приближений, особые решения дифференциальных уравнений, уравнения с малым параметром при производной. Фактически пособие можно считать «решебником», излагающим основные методы решения задач и иллюстрирующим их на примерах. Скачать (djvu/rar, 4,06 mb, 600 dpi+OCR) ifolder.ru |
 |
|
 |
NEW Просветов Г. И. Дифференциальные уравнения: задачи и решения: Учебно-практическое пособие. М.: Издательство «Альфа-Пресс», 2011. — 88 с. ISBN 978-5-94280-507-4 В учебно-практическом пособии рассмотрены основные методы и приемы решения дифференциальных уравнений. Приведенные в учебном материале примеры и задачи позволяют успешно овладеть знаниями по изучаемой дисциплине. Пособие содержит программу курса, задачи для самостоятельного решения с ответами и задачи для контрольной работы. Издание рассчитано на преподавателей и студентов высших учебных заведений. За книгу спасибо Гость Источник (pdf, 92 мб) narod.ru Скачать (djvu/rar, ч/б, ocr, 682.6 КБ) f-bit.ru || http://rghost.ru |
 |
Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. — М. Высшая школа, 1989. -383 с. В пособии приводятся краткие теоретические сведения и решения типовых задач по курсу обыкновенных дифференциальных уравнений. Имеются также задачи для самостоятельного решения. Материал пособия позволяет выработать практические навыки в решении и исследовании дифференциальных уравнений, описывающих эволюционные процессы в различных областях естествознания. Скачать (9,29 Мб) ifolder || mediafire.com/ |
 |
Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. — 3е изд.- М., Высшая школа, 1967. — 565 стр. с илл. В книге даются основные понятия и определения теории обыкновенных дифференциальных уравнений, излагаются наиболее важные методы интегрирования, доказываются теоремы существования решений и исследуются свойства последних. Являясь учебником для студентов университетов, она может быть использована в педагогических институтах и в технических вузах, а также студентами-заочниками и лицами, самостоятельно изучающими теорию обыкновенных дифференциальных уравнений. Скачать (15 Мб) mediafire.com || f-bit.ru |


Скачать (pdf, 2.47 Мб) ifolder.ru || libgen.info
Пушкарь Е.А. Дифференциальные уравнения в задачах и примерах: Учебно-методическое пособие. – М.: МГИУ, 2007. – 158 с. ISBN 978-5-2760-1097-7
В учебно-методическом пособии рассматриваются методы и приемы решения обыкновенных дифференциальных уравнений. Пособие включает в себя материал 27 практических занятий и используется при изучении курса “Дифференциальные уравнения” в течение двух семестров. Оно соответствует программе дисциплины «Дифференциальные уравнения» для студентов второго и третьего курсов.
Скачать (pdf, 2.15 Мб) ifolder.ru || libgen.info
Оба пособия предназначены для студентов высших учебных заведений направления «Прикладная математика и информатика» (010500) и специальности «Математическое обеспечение и администрирование информационных систем» (010503). Будут полезны студентам инженерных специальностей, желающих самостоятельно научиться решать дифференциальные уравнения, а также студентам дистанционной формы обучения.
 |
Амелькин В.В. Дифференциальные уравнения в приложениях. — М.: Наука. Главная редакция физико-математической литературы, 1987.—160 с. Книга популярно знакомит с возможностями использования обыкновенных дифференциальных уравнений при изучении реальных явлений и процессов. Приемы составления дифференциальных уравнений, а также некоторые методы их качественного исследования иллюстрируются задачами, возникающими в различных областях знаний. Для школьников старших классов, преподавателей, студентов, для специалистов нематематических профессий, использующих математику в своей работе. Скачать (djvu, 3,3 mb) mediafire.com || libgen.info |
 |
Ибрагимов Н.Х. Практический курс дифференциальных уравнений и математического моделирования. Классические и новые методы. Нелинейные математические модели. Симметрия и принципы инвариантности / Перевод с англ. И. С. Емельяновой. — Нижний Новгород: Издательство Нижегородского госуниверситета, 2007. 421с. ISBN 91-7295-988-6 (Alga Publications, Blekingc Institute of Technology) ISBN 978-5-91326-027-7 Настоящий учебник охватывает обширный материал, включающий составление и анализ математических моделей различных процессов и явлений из области физики, техники, биологии, медицины и экономики. Рассматриваемые модели описываются обыкновенными дифференциальными уравнениями, уравнениями с частными производными и их системами. Излагаются классические и современные методы решения дифференциальных уравнений. В частности, широко представлен инвариантный подход, связанный с привлечением локальных групп Ли, которые позволяет находить решения нелинейных задач а аналитической форме. Учебник предназначен студентам, аспирантам и преподавателям естественно-научных факультетов классических, технических и педагогических университетов, а также специалистам в области чистой и прикладной математики. Скачать (djvu, 4,44 Мб) f-bit.ru || ph4s.ru || libgen.info |
 |
Пономарев К. К. Составление дифференциальных уравнений. — Минск, Вышейшая Школа, 1973. — 560 стр. с илл. Учебное пособие для математических, физических, биологических, химических факультетов университетов, которое является руководством по составлению и решению дифференциальных уравнений. Как известно, в курсе дифференциальных уравнений решению практических задач на составление уделяется все еще недостаточное внимание. Кроме того, в учебниках и учебных пособиях вопросы составления дифференциальных уравнений обычно ограничиваются элементарными задачами геометрического или кинематического типа. Цель автора — создание учебного пособия, которое широко охватило бы различные задачи естествознания и техники и способствовало овладению современной методикой составления дифференциальных уравнений прикладных задач, возникающих в процессе производства или научной деятельности. Характерной особенностью освоения навыков составления дифференциальных уравнений является изучение многочисленных примеров. В связи с этим полнота изложения имеет здесь существенное значение. Книга содержит 325 задач на составление дифференциальных уравнений, из которых 194 задачи анализируются подробно. Скачать (djvu, 4,44 Мб) eqworld.ipmnet.ru || libgen.info |
 |
Матвеев Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям: Для вузов.— 6-е изд., испр. и доп.— Мн.: Выш. шк., 1987.—319 с: ил. Содержится более полутора тысяч зада4 и упражнений по всем разделам университетского курса обыкновенных дифференциальных уравнений. Приводятся краткие сведения из теории, типовые примеры, ответы и указания для решения наиболее трудных задач. Для студентов вузов, обучающихся по специальности «Математика». (Обложка от другого издания) Скачать (3,9 Мб) ifolder || libgen.info |
 |
В.К. Романко, Н.Х. Агаханов, В.В. Власов, Л.И. Коваленко Сборник задач по дифференциальным уравнениям и вариационному исчислению. — М., ЮНИМЕДИАСТАЙЛ, 2002. — 256 с. Задачник обеспечивает практические занятия по курсу «Дифференциальные уравнения и вариационные исчисления». В начале каждого параграфа приводятся решения типовых задач. Ко всем задачам даны ответы. Для студентов физико-математических, инженерно-физических и экономических специальностей. Скачать (2,69 Мб) ifolder.ru || mediafire.com |
 |
Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000, 176 с. Сборник содержит материалы для упражнений по курсу дифференциальных уравнений для университетов и технических вузов с повышенной математической программой. В настоящее издание добавлены задачи, предлагавшиеся на письменных экзаменах на механико-математическом факультете МГУ. Скачать (1,3 Мб) f-bit.ru || mediafire.com |
 |
Дингельдей Ф. Сборник упражнений и практических задач по интегральному исчислению. Пер. с нем. — ГТТИ, 1932. 400 с Предлагаемый вниманию читателя сборник задач по интегральному исчислению чрезвычайно выгодно отличается от существующих у нас задачников. В нем читатель найдет много задач физического и технического содержания, формулировка которых далека как от схематизма, так и от псевдотехницизма. Решая эти задачи, необходимо вдумываться как в конкретное условие, так и в приемы математического их решения; необходимо вдумчиво отнестись к процессу перевода условий задачи на математический язык. Скачать (djvu/rar, 18.63 Мб) ifolder.ru|| f-bit.ru |
Дополнительно
 |
Арнольд В. И. Обыкновенные дифференциальные уравнения. — 4-е изд. — Ижевск: Ижевская республиканская типография. 2000. 308 с. Отличается от имеющихся учебных руководств по обыкновенным дифференциальным уравнениям большей, чем это обычно принято, связью с приложениями, в особенности с механикой, и более геометрическим, бескоординатным изложением. В соответствии с этим п книге мало выкладок, но много понятий, необычных для курса дифференциальных уравнений (фазовые потоки, однопараметрические группы, диффеоморфизмы, касательные пространства и расслоения) и примеров из механики (например, исследование фазовых портретов консервативных систем с одной степенью свободы, теория малых колебаний, параметрический резонанс). Для студентов и аспирантов механико-математических факультетов университетов и вузов с расширенной программой но математике, но будет интересна и специалистам в области математики и ее приложений. За книгу спасибо Violent_Violet и Гостю. Скачать (djvu, 1,9 mb) mediafire.com |
 |
Ф. Хартман Обыкновенные дифференциальные уравнения. — М., Мир, 1970. — 720 с. Книга Ф.Хартмана — одного из крупнейших специалистов по теории дифференциальных уравнений — возникла на основе различных курсов, которые автор неоднократно читал студентам и аспирантам разных специальностей. Только первые ее главы включают традиционный материал. Далее следует изложение качественной теории дифференциальных уравнений, в котором особый интерес представляет круг вопросов, связанных с теоремой о поведении диффеоморфизма в окрестности неподвижной точки. И, наконец, остальная часть книги посвящена более специальным вопросам (асимптотическое интегрирование систем, близких к линейным, уравнения второго порядка, дихотомия и т. д.).Упражнения (содержащие задачи различной трудности, частично с решениями) играют в этой книге особую роль. Они не только позволяют читателю проверить, как он усвоил материал, но и указывают ему возможные направления дальнейшего развития теории. Широта охвата материала, систематичность и четкость изложения делают книгу хорошим учебным пособием для студентов высших учебных заведений. Скачать (djvu,13,8 Мб) fayloobmennik.net || fileswap.com |
Несколько справочников.
Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. Пер. с нем. — 4-е изд., испр. — М.: Наука: Гл. ред. физ-мат. лит., 1971. — 576с.
Справочник Э. Камке не претендует сегодня на всеобъемлющее освещение современного состояния исследований в области обыкновенных дифференциальных уравнений. Он слабо отражает результаты, полученные после (примерно) 1940 года. Тем не менее возможность записать общее решение того или иного дифференциального уравнения или системы в замкнутом виде имеет во многих случаях значительные преимущества. Поэтому обширный справочный материал, который собран в третьей части книги Э. Камке, — около 1650 уравнений с решениями — сохраняет большое значение и сейчас.
Помимо указанного справочного материала, книга Э. Камке содержит изложение (правда, без доказательств) основных понятий и важнейших результатов, относящихся к обыкновенным дифференциальным уравнениям.
Скачать (7,13 Мб) http://eqworld.ipmnet.ru или mediafire.com
Коддингтон Э. А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. М. Иностранная литература, 1958. 475 с.
В книге американских математиков Э. А. Коддингтона и Н. Левинсона «Теория обыкновенных дифференциальных уравнений» дается оригинальное, содержащее ряд новых результатов изложение современной теории обыкновенных дифференциальных уравнений. Представлены следующие разделы: теоремы существования и единственности, линейные уравнения, аналитическая теория дифференциальных уравнений, асимптотика, задачи на собственные значения, теория возмущений, теория Пуанкаре — Бендиксона и теория дифференциальных уравнений на торе.
Книга будет очень полезна всем математикам, физикам и инженерам, так или иначе соприкасающимся с дифференциальными уравнениями.
Скачать (djvu, 7 Мб) rghost.ru || filecloud.io || libgen.info
Айнс Э. Л. Обыкновенные дифференциальные уравнения. Харьков, НТИ Украины, 1939. 719 с.
Выпускаемая в русском переводе книга Айнса представляет ценный вклад в нашу математическую литературу. Книга состоит из 21 главы и разделена на 2 части. В первой части рассматриваются дифференциальные уравнения в вещественной области, во второй — в комплексной области. Можно надеяться, что появление этой содержательной книги будет способствовать повышению уровня математической культуры.
Скачать (djvu, 7,8 Мб) rghost.ru || filecloud.io || libgen.info
Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. М. Наука, 1986. 288 с.
Необходимость решения дифференциальных уравнений явилась одним из первоначальных и основных мотивов для развития как аналоговых, так и цифровых вычислительных машин. Численное решение таких задач и сейчас поглощает значительную часть машинного времени, предоставляемого современными ЭВМ. Цель этой книги — познакомить читателя с численными методами решения как обыкновенных дифференциальных уравнений, так и уравнений в частных производных, хотя в основном мы сосредоточиваем наше внимание на обыкновенных дифференциальных уравнениях и особенно на решении краевых задач для таких уравнений.
Скачать (djvu, 7,8 Мб) rghost.ru || filecloud.io || libgen.info
Уравнения математической физики
 |
Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. — М.: ФИЗМАТЛИТ, 2001. — 576 с. Справочник содержит около 5200 обыкновенных дифференциальных уравнений с решениями (больше, чем любая другая книга). Особое внимание уделяется уравнениям общего вида, которые зависят от произвольных функций. Приведены некоторые точные решения уравнений нелинейной механики и теоретической физики (которые встречаются в задачах теплопроводности, массопереноса, теории упругости, гидродинамики, теории колебаний, теории горения, теории химических реакторов и др.). В ряде разделов указаны также асимптотические решения. Кратко излагаются точные, асимптотические и приближенные методы решения уравнений и задач теории обыкновенных дифференциальных уравнений. Описаны свойства наиболее распространенных специальных функций. Справочник предназначен для широкого круга научных работников, преподавателей вузов, инженеров и студентов, специализирующихся в различных областях математики, физики, механики, теории управления и инженерных наук. Подробное оглавление и ссылка для скачивания ||скачать здесь (4,4 Мб) |
 |
Зайцев В.Ф., Полянин А.Д. Справочник по дифференциальным уравнениям с частными производными первого порядка. М.: ФИЗМАТЛИТ, 2003. — 416 с. Справочник содержит более 3000 дифференциальных уравнений с частными производными первого порядка и их решения. Приведено много новых точных решений линейных и нелинейных уравнений. Особое внимание уделяется уравнениям общего вида, которые зависят от произвольных функций. В целом справочник содержит в несколько раз больше уравнений с частными производными первого порядка и точных решений, чем любые другие книги. В начале каждой главы кратко описаны основные методы решения соответствующих типов дифференциальных уравнений и приведены конкретные примеры их применения. Исследуются как гладкие, так и негладкие и разрывные решения. Рассмотрены уравнения, которые встречаются в дифференциальной геометрии, нелинейной механике, газовой динамике, геометрической оптике, теории волн, теории оптимального управления, дифференциальных играх, химической технологии и других приложениях. В дополнении излагается метод обобщенного разделения переменных. Справочник предназначен для широкого круга научных работников, преподавателей вузов, инженеров и студентов, специализирующихся в различных областях прикладной математики, механики, физики, теории управления и инженерных наук. Скачать (djvu, 3,4 Мб) f-bit.ru || libgen.info Подробное оглавление и ссылка для скачивания alleng.ru |
 |
|
 |
|
 |
|
 |
 |
Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики: Учеб. для вузов. 2-е изд. / Под ред. B.C. Зарубина, А.П. Крищенко. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. — 368 с. (Сер. Математика в техническом университете; Вып. XII). Рассмотрены различные постановки задач математической физики для дифференциальных уравнений в частных производных и основные аналитические методы их решения, проанализированы свойства полученных решений. Изложено большое число линейных и нелинейных задач, к решению которых приводит исследование математических моделей различных процессов в физике, химии, биологии, экологии и др. Содержание учебника соответствует курсу лекций, который авторы читают в МГТУ им. Н.Э. Баумана. Для студентов технических университетов. Может быть полезен преподавателям, аспирантам и инженерам. |
 |
Власова Е.А., Зарубин B.C., Кувыркин Г.Н. Приближенные методы математической физики: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. -700 с. (Сер. Математика в техническом университете; Вып. XIII). Книга является тринадцатым выпуском серии учебников „Математика в техническом университете». Последовательно изложены математические модели физических процессов, элементы прикладного функционального анализа и приближенные аналитические методы решения задач математической физики, а также широко применяемые в научных исследованиях и инженерной практике численные методы конечных разностей, конечных и граничных элементов. Рассмотрены примеры использования этих методов в прикладных задачах. Содержание учебника соответствует курсам лекций, которые авторы читают в МГТУ им. Н.Э. Баумана. Для студентов технических университетов. Может быть полезен преподавателям, аспирантам и инженерам. |
Книги в основном в формате djvu. Для чтения файлов данного формата скачатьWinDjView-1.0 (885Кб) или WinDjView-1.0.1-Setup.exe» (2,71 Мб) или страница с последней версией WinDjView
См. также раздел «Программы; архиваторы; форматы pdf, djvu и др.» на alleng.ru
Он-лайн-ресурсы:
Дифференциальные равения (ОГТУ)
Дифференциальные уравнения и их системы (МГТУ им. Баумана)
http://atomas.ru/mat/difur/
Подборка литературы по дифференциальным уравнениям на eqworld.ipmnet.ru
Подборка литературы по дифференциальным уравнениям на сайте Варгина А.Н.
(ссылки на первые два ресурса помещены в наш эпиграф)
Р.S. Большая просьба к членам сообщества: если у кого-то есть ссылки на понравившиеся учебники в электронном виде, пожалуйста, отметьтесь в комментах. И еще, если вы занимались по каким-то из этих учебников, просьба их кратко охарактеризовать.
Ссылки на посты аналогичной тематики:
источники:
http://nashol.me/2016041489015/differencialnie-uravneniya-sergeev-i-n-2013.html
http://diary.ru/~eek/p48302307_literatura-po-differencialnym-uravneniyam.htm
- Раздел: Математика → Дифференциальные уравнения
Уфимский государственный авиационный технический университет (УГАТУ)
Примеры решения (вычисления) Дифференциальные уравнения.
- №1
- 133,82 КБ
- дата добавления неизвестна
- описание отредактировано 15.06.2011 13:14
- Раздел: Математика → Дифференциальные уравнения
Решение дифференциальных уравнений. Первого порядка: прямого интегрирования; линейные; с разделяющимися переменными; однородные. Второго порядка: 5 типов.
- №2
- 17,29 КБ
- дата добавления неизвестна
- описание отредактировано 16.12.2010 00:41
- Раздел: Математика → Дифференциальные уравнения
Ответы на экзамен. ХГУ, 3 семестр. 8 с. Формулы, пояснение примеры. Содержит исчерпывающую информацию по диф. ура-м: Обыкновенные диф. урав. 1 порядка. Диф. урв. с разделяющими переменными. Однородные диф. ур. Линейные дифференциальные уравнения 1 порядка. урв. Бернулли. Дифференциальные уравнения: полный дифференциал. Дифференциальные уравнения n-го порядка. Уравнения не…
- №3
- 93,89 КБ
- добавлен 03.01.2012 14:20
- описание отредактировано 11.02.2016 15:31
- Раздел: Математика → Дифференциальные уравнения
Задачи, приводящие к понятию диф.уравнения.
Диф.уравнения первого порядка: основные определения, задача Коши, общее и частное решения, общий и частный интеграл.
Диф. уравнения первого порядка: понятие изоклины, особые точки диф. уравнения. Геометрическая интерпретация общего решения диф. уравнения.
Диф. уравнения с разделяющимися переменными. Метод решения. Пример.
Однородные…
- №4
- 146,40 КБ
- добавлен 23.09.2011 15:41
- описание отредактировано 25.09.2011 16:21
- Раздел: Математика → Дифференциальные уравнения
МАИ, 3 семестр, подробные ответы на экзамен по дифференциальным уравнениям и ТФКП. Определение обыкновенного дифференциального уравнения (ОДУ) и его решения. Геометрический смысл уравнения первого порядка. Уравнение с разделяющимися переменными. Уравнение в полных дифференциалах. Линейное дифференциальное уравнение Постановка задачи Коши для уравнения n-го порядка. Теорема…
- №5
- 547,46 КБ
- дата добавления неизвестна
- описание отредактировано 13.01.2011 03:46
- Раздел: Математика → Дифференциальные уравнения
Уфимский государственный авиационный технический университет (УГАТУ)
Примеры решения дифференциальных уравнений. Решить дифференциальное уравнение. Решить задачу Коши.
- №6
- 1,48 МБ
- дата добавления неизвестна
- описание отредактировано 15.08.2011 22:45
- Раздел: Математика → Дифференциальные уравнения
Специальность Прикладная математика. дисциплина Дифференциальные уравнения. Ответы на билеты + шпаргалки. формат DOCX. Список вопросов: Дифференциальные уравнения. Уравнения с разделяющимися переменными. Уравнения, приводящие к уравнениям с разделяющимися переменными. Линейные дифференциальные уравнения 1 порядка. Уравнения 1 порядка, Метод вариации произвольной постоянной….
- №7
- 1,19 МБ
- дата добавления неизвестна
- описание отредактировано 21.01.2016 21:44
- Раздел: Математика → Дифференциальные уравнения
Алгоритм решения квазилинейных задач: Численные методы решения начальной задачи (задачи Коши). Метод Эйлера. Метод Рунге-Кутты. Устойчивость схемы Рунге-Кутты. Порядок точности метода Рунге-Кутты. Оценка погрешности аппроксимации. Устойчивость метода простого прогноза. Устойчивость метода простой коррекции. Численное решение задачи Коши для жестких систем ОДУ. Разностные методы…
- №8
- 525,82 КБ
- дата добавления неизвестна
- описание отредактировано 17.05.2011 09:53
- Раздел: Математика → Дифференциальные уравнения
МАИ ГТУ, 3-семестр
Задачи, приводящие к обыкновенным ДУ, основные определения.
Задача Коши, формулировка теоремы существования и единственности ее решения. Геометрический смысл ДУ 1-го порядка, поле направлений, метод изоклин.
ДУ 1-го порядка с разделяющимися переменными. Однородные ДУ 1-го порядка.
Линейные ДУ 1-го порядка. Уравнение Бернулли.
ДУ в полных дифференциалах….
- №9
- 142,69 КБ
- дата добавления неизвестна
- описание отредактировано 02.02.2010 15:04
- Раздел: Математика → Дифференциальные уравнения
Основные понятия теории ДУ
Агульныя ўраўненні першага парадку і асноўныя азначэнні.
Аднародныя ДУ 1-га парадку і ўраўненні, якія прыводзяцца да іх.
Лінейныя ўраўненні першага парадку. Ураўненні Бернулі.
Ураўненні ў поўных дыферэнцыялах. Інтэгруючы множнік.
Тэарэма аб існаванні і адзінасці рашэння задачы Кашы для ураўненняў першага парадку.
Асаблівыя рашэнні ўраўненняў,…
- №10
- 532,74 КБ
- дата добавления неизвестна
- описание отредактировано 24.02.2011 14:41
- Раздел: Математика → Дифференциальные уравнения
Оформлено как шпоры. По одному примеру на каждую из нижеперечисленных задач.
Задача. Найти общий интеграл дифференциального уравнения.
Задача. Найти общий интеграл дифференциального уравнения.
Задача. Найти общий интеграл дифференциального уравнения.
Задача. Найти решение задачи Коши.
Задача. Найти решение задачи Коши.
Задача. Найти решение задачи Коши.
Задача. Найти общий…
- №11
- 143,99 КБ
- дата добавления неизвестна
- описание отредактировано 10.04.2011 11:42
- Раздел: Математика → Дифференциальные уравнения
Рівняння з відокремлюваними змінними та однорідні рівняння 1-го порядку. Лінійні рівняння першого порядку та рівняння типу Бернуллі. Метод Бернуллі та Лагранжа (варіації довільної сталої). Рівняння Ріккатті. Рівняння у повних диференціалах. Інтегрувальний множник. Неявні ДР 1-го п-ку. Метод введення параметра. Рівняння Лагранжа і Клеро. Теорема Коші-Пікара, теореми про…
- №12
- 293,62 КБ
- дата добавления неизвестна
- описание отредактировано 05.06.2010 03:35
- Раздел: Математика → Дифференциальные уравнения
Уфа,УГАТУ,ФИРТ. Преподаватель:Николаева М.А. Числовые ряды. Сходимость и сумма ряда. Свойства числовых рядов. Ряд геометрической прогрессии. Необходимый признак сходимости числового ряда. Гармонический ряд. Достаточные признаки сходимости. Признаки сравнения. Признак Даламбера. Радикальный и интегральный признак Коши. Обобщенный гармонический ряд. Общий достаточный признак…
- №13
- 814,44 КБ
- добавлен 16.01.2014 20:00
- описание отредактировано 25.01.2014 00:50
- Раздел: Математика → Дифференциальные уравнения
МАИ, Лунева С. Ю. , 2010.
Алгоритм решения ДУ методом решения параметра.
Порядок определения типа ДУ 1-ого порядка:
ДУ с разделяющимися переменными.
Однородное ДУ первого порядка.
Линейное неоднородное ДУ.
Уравнение Бернулли.
Уравнение в полных дифференциалах.
Уравнение неразрешенное относительно производной.
- №14
- 447,27 КБ
- дата добавления неизвестна
- описание отредактировано 25.10.2010 02:19
- Раздел: Математика → Дифференциальные уравнения
МАИ, Лунева С. Ю. , 2010.
Теорема Коши.
Пример задания №1(сформулировать теорему Коши для ДУ 4-го порядка в общем виде).
Пример задания №2(проанализировать поставленные задачи Коши для ДУ 1-го порядка).
- №15
- 399,79 КБ
- дата добавления неизвестна
- описание отредактировано 28.10.2010 14:28
- Раздел: Математика → Дифференциальные уравнения
Метод Эйлера решения СЛОДУ(алгоритм решения).
Составление матрицы системы.
Составление характеристического уравнения.
Анализ корней.
Последовательность действий для каждого простого действительного корня.
Последовательность действий для каждой пары простых комплексно-сопряженных корней.
Последовательность для каждого кратного действительного корня кратности k.
Запись общего…
- №16
- 314,74 КБ
- дата добавления неизвестна
- описание отредактировано 18.11.2010 19:43
В этом разделе нет файлов.
Комментарии
Уважаемые: администратор, модераторы и доверенные пользователи.
Друзья, то что ранее предлагал Денис, я уже предлагаю официально, в разделе Дифференциальные уравнения создать новый подраздел Дифференциальные уравнения в частных производных, который является самостоятельной областью (направлением, ветвью) математики (Дифференциальных уравнений):
Это соответствует требованиям мировых и официальных стандартов, изложенных в Википедии:
1. Википедия (Дифференциальное уравнение):
«Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные».
2. Википедия (Дифференциальное уравнение в частных производных):
«Дифференциальное уравнение в частных производных (частные случаи также известны как уравнения математической физики, УМФ) — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные».
3. Википедия (Категория: Дифференциальные уравнения): Отсюда следует вывод:
«Из Категории «Дифференциальные уравнения» -> Дифференциальное уравнение в частных производных«.
Литература (20 книг) для переноса в новый подраздел Дифференциальные уравнения в частных производных:
…
С уважением, благодарностью и благословением,
- Аккаунт удален
Уважаемый Админ.
Я благодарен Вам за добавление подраздела Дифференциальные уравнения в частных производных.
С уважением,
- Аккаунт удален
Уважаемые: администратор, модераторы и доверенные пользователи.
Друзья, то что ранее предлагал Денис (от 07.03.2015), я уже предлагаю официально, в разделе Дифференциальные уравнения создать новый подраздел Обыкновенные дифференциальные уравнения (ОДУ), который является самостоятельной областью (направлением, ветвью) математики (Дифференциальных уравнений):
Это соответствует требованиям мировых и официальных стандартов, изложенных в Википедии:
1. Википедия (Дифференциальное_уравнение):
«Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, зависящие от одной независимой переменной»
2. Википедия (Обыкновенное дифференциальное уравнение):
«Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальные уравнения для функции от одной переменной».
3. Википедия (Категория: Дифференциальные уравнения): Отсюда следует вывод:
«Из Категории «Дифференциальные уравнения» -> Обыкновенное дифференциальное уравнение«.
Литература (20 книг) для переноса в новый подраздел Обыкновенные дифференциальные уравнения:
…
С уважением, благодарностью и благословением,
- Аккаунт удален
Уважаемый Админ.
Я благодарен Вам за добавление подраздела Обыкновенные дифференциальные уравнения.
С уважением,
- Аккаунт удален
Неплохо бы отделить уравнения в частных производных от обыкновенных дифференциальных уравнений. Книг очень много, сложно ориентироваться.
- Денис
- Dosia
Уважаемые коллеги!
Я столкнулся с тем, что литература о дифференциальном исчислении собирается в разделах «Файлы Математика Высшая математика Дифференциальные уравнения» (/files/mathematics/algebra/diffeq/) и «Файлы Математика Высшая математика Математический анализ» (/files/mathematics/algebra/analysis/).
Было бы желательно как-то объединить или связать эти разделы, или подчинить раздел «Дифференциальные уравнения» разделу «Математический анализ».
- Zarub60
Решения Филиппова можно найти здесь
http://mat-an.ru/filippov.php
- Ramzes000
Где можно найти решения примеров из учебника Филиппова?(по дифурам)
- Ляля
В этом разделе нет комментариев.