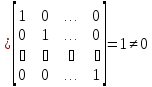
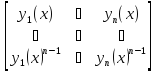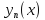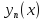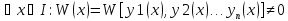шпаргалка по Дифурам (Шпаргалочка)
2017-07-092017-07-09СтудИзба
Описание файла
Файл «шпаргалка по Дифурам» внутри архива находится в папке «Шпаргалочка». Документ из архива «Шпаргалочка»,
который расположен в категории «».
Всё это находится в предмете «математический анализ» из 2 семестр, которые можно найти в файловом архиве РТУ МИРЭА.
Не смотря на прямую связь этого архива с РТУ МИРЭА, его также можно найти и в других разделах. Архив можно найти в разделе «к экзамену/зачёту», в предмете «математический анализ» в общих файлах.
Онлайн просмотр документа «шпаргалка по Дифурам»
Текст из документа «шпаргалка по Дифурам»
|
1.Дифференциальные уравнения. Обыкновенным дифференциальным уравнением 1 порядка называется уравнение вида
Частным решением дифференциального уравнения называется любая функция |
2.Уравнения с разделяющимися переменными. Дифференциальное уравнение 1 порядка Уравнение, записанное в симметричной форме Разделить переменные – значит преобразовать уравнение так, чтобы каждая переменная содержалась только в том слагаемом, которое содержит её дифференциал. Вид уравнения: Решение уравнения: приводим к уравнению с разделенными переменными (
В частности, уравнение вида
Пример. Решение: разделим обе части ур-ния на
Потенцируя, найдем общее решение в виде |
3. Уравнения, приводящие к уравнениям с разделяющимися переменными. Многие дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. К числу таких уравнений относятся, например, уравнения вида
И переменные разделились. Интегрируя, получим Пример. Разделяя переменные получим и интегрируя получим К уравнен. с разделяющимися переменными приводятся и так называемые однородные дифференциальные урав-ния 1 порядка имеющие вид |
|
4. Линейные дифференциальные уравнения 1 порядка. Линейным дифференциальным уравнением порядка называется уравнение, линейное относительно функции и её производной:
Здесь Однородные линейные уравнения (Q=0) могут быть решены разделением переменных. Неоднородные линейные уравнения можно свести к последовательности двух уравнений с разделяющимися переменными подстановкой
В линейном однородном уравнении переменные разделяются: И интегрируя получаем
При делении на у мы потеряли решение у |
5. Уравнения 1 порядка. Метод вариации произвольной постоянной. Для интегрирования неоднородного линейного уравнения
Может быть применен так называемый метод вариации постоянной При применении этого метода сначала интегрируется соответствующее однородное уравнение О При постоянном с, функция Где с(х) – новая неизвестная функция х. Вычисляя производную
И подставляя в исходное неоднородное уравнение получим
Или Откуда интегрируя находим
А следовательно
(*) Итак общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения. и частного решения неоднородного уравнения получающегося из (*) при с1=0. Пример
Интегрируем соответствующее однородное уравнение
Считаем с функцией х, тогда
И подставляя в исходное уравнение после упрощения получаем
Следовательно общее решение
|
6. Уравнение 1 порядка.Метод Бернулли Вид уравнения: Решение уравнения: метод Бернулли. Решение будем искать в виде |
|
7. Уравнение Бернулли Решение осуществляется методом Бернулли или сведением к линейному, путем замены переменных. Например, уравнение Бернулли имеющее вид Или
Заменой переменных
И, подставляя в (*) получим линейное уравнение Пример.
|
8. Уравнения в полных дифференциалах Вид уравнения:
Пример:
|
9. Интегрирующий множитель Рассмотрим уравнение Функция Инт.мн-ль легко находится в след.случаях:
Пример:
Найдем Домножим первоначальное уравнение на
Получили уравнение в полных дифференциалах, где
Интегрируем
Дифференцируем это равенство по y:
|
|
10. Дифференциальные уравнение высших порядков. Общие сведения Диф.уравнения n порядка имеют вид Теорема.Существует единственное решение дифференц. уравнения n порядка
Общим решением дифф.уравнения n порядка называется множество решений, состоящее из всех без исключения частных решений. Если правая часть уравнения в некоторой области изменения аргументов удовлетв.условиям теоремы, то общ.решение зависит от n параметров, в качестве которых могут быть выбраны, например начальные значения искомой функции и ее производных. |
11. Уравнения, допускающие понижение порядка.
Пример.
Пример. |
14. Линейные дифференциальные уравнения высших порядков Лин.Диф.Ур-нием n порядка называется уравнение линейное относительно неизвестной функции и ее производных и, следовательно, имеющее вид:
Если правая часть Т1. Если Т2. Если Замечание: Если 2 решения Т3.Если
Т4. Если на каком либо отрезке Т5. Если 1.это выражение явл-ся решением 2.это решение явл-ся общим решением.( |
|
15. Линейные неоднородные дифференциальные уравнения высших порядков. Метод Подбора
Т.Общее решение лин.неоднородного ур-ния может быть представлено как сумма двух решений.
Пусть
Метод подбора.
Если
Пример.
|
16. Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной
Пример.
…
|
17. Уравнение Эйлера
Линейно входящие в ур-ние Эйл.
Пример.
Если уравнение не однородное то переменную x на Если уравнение более высокого порядка, чем 2 то замена |
|
13. Уравнение Клеро
Интегральная кривая определяемая данными уравнениями является огибающей семейства интегральных прямых.(т.е. огибающая некоторого семейства Особое решение. Необходимо исключить параметр Пример. Общее: Особое решение: Исключая параметр |
18. Общее понятие разностных уравнений В качестве аналогов дифф.уров можно рассм. разностные ур-ния. При использовании обратных разностей линейные неоднородные разностные уравнения имеют вид: Это разностное ур-ние можно рассматривать как рекуррентное отношение позволяющее вычислять значения y[n] для любых n по известному значению функции в правой части уравнения и начальным условиям y[n-1],…y[n-m]. Такие вычисления легко выполняются на счетных машинах, а также не представляют никаких принципиальных трудностей и при ручном счете, даже в тех случаях кошда коэффициенты в левой части уравнения меняются по времени. Это отличает разностные уравнения от непрерывных аналогов – дифф.уров. Общее решение однородного разностного уравнения при некратных корнях характеристичесого уравнения может быть записано след.образом
|
19. Решетчатые функции Решетчатая ф-ция не обязательно должна формироваться из некоторой исходной непрерывной функции. Любая числовая посл-ть некоторой величины, определенной в дискретные равноотстоящие моменты времени, может трактоваться как решетчатая функция. Обратная задача – формирование непрерывной функции из решетчатой – не может быть решена однозначно, т.к. ф-ции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций. Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции. Прямая и обратная разности. Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность
|
|
20. Конечные разности элементарных функций f(n)=bn+a ∆f(n)=b(n+1)+a-b(n)-a=b ∆2f(n)=∆f(n+1)-∆f(n)=0 f(n)=n2+bn+c ∆f(n)=(n+1)2+b(n+1)+c-n2-bn-c=2n+b+1 ∆2f(n)=2(n+1)+b+1-2n-b-1=2 ∆3f(n)=0 f(n)=ean ∆f(n)=ea(n+1)-ean=ean(ea-1) ∆2f(n)=ea(n+1)(ea-1)-ean(ea-1)=ean(ea-1)2 ∆kf(n)=ean(ea-1)k |
21. Разностные уравнения. Линейные разностные уравнения. — уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x1, x2, …, xn.) В экономических исследованиях значения величин часто берутся в определенные дискретные моменты времени. Напр., о выполнении плана судят по показателям на конец планируемого периода. Поэтому вместо скорости изменения какой-либо величины df/dt приходится брать среднюю скорость за определенный конечный интервал времени Δf/Δt. Если выбрать масштаб времени так, что длина рассматриваемого периода равна 1, то скорость изменения величины можно представить как разность y = y(t+1) – y(t), которую часто называют первой разностью. При этом различают правую и левую разности, в частности y = y(t) – y(t–1) — левая, а приведенная выше — правая. Можно определить вторую разность: Δ(Δy) = Δy(t + 1) – Δy(t) = y(t + 2) – – 2y(t + 1) + y(t) и разности высших порядков Δn. Теперь можно определить Р. у. как уравнение, связывающее между собой конечные разности в выбранной точке: f [y(t), Δy(t), …, Δny(t)] = 0. Р. у. всегда можно рассматривать как соотношение, связывающее значения функции в ряде соседних точек y(t), y(t+1), …, y(t+n). При этом разность между последним и первым моментами времени называется порядком уравнения. При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р. у. стремится к решению соответствующего дифференциального уравнения, когда интервал Δt стремится к нулю. При исследовании функций многих переменных по аналогии с частными производными (см. Производная) вводятся также частные разности. Линейные разностные уравнения первого порядка y(x + 1) − ay(x) = 0. Линейное однородное разностное уравнение первого порядка с постоянными коэффициентами. y(x + 1) − ay(x) = f(x). Линейное неоднородное разностное уравнение первого порядка с постоянными коэффициентами. y(x + 1) − xy(x) = 0. y(x + 1) − a(x − b)(x − c)y(x) = 0. y(x + 1) − R(x)y(x) = 0, где R(x) — рациональная функция. y(x + 1) − f(x)y(x) = 0. y(x + a) − by(x) = 0. y(x + a) − by(x) = f(x). y(x + a) − bxy(x) = 0. y(x + a) − f(x)y(x) = 0. Линейные разностные уравнения второго порядка, yn = y(n) yn+2 + ayn+1 + byn = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами. yn+2 + ayn+1 + byn = fn. Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами. y(x + 2) + ay(x + 1) + by(x) = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами. y(x + 2) + ay(x + 1) + by(x) = f(x). Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами. y(x + 2) + a(x + 1)y(x + 1) + bx(x + 1)y(x) = 0. |
23. Линейные стационарные неоднородные разностные уравнения Метод подбора. Методом Лагранжа может быть решено любое неоднородное уравнение с постоянными коэффициентами. Однако если свободный член в уравнении
где Pm1(x) и Qm2(x) — многочлены степеней, соответственно, m1 и m2, можно сразу указать вид частного решения в форме с неопределёнными коэффициентами. Общее правило таково: составим из коэффициентов при x в экспоненте и тригонометрических функциях число Технику работы с этим правилом будем осваивать, начиная с простейших случаев, при этом будем формулировать частные правила, вытекающие из общего. I. Если f(x) = Pm(x) (т.е. f(x) — многочлен степени m), то частное решение ищется в виде yчн(x)= Rm(x), если число 0 не является корнем характеристического уравнения, и в виде yчн(x)= xr Rm(x), если число 0 — корень характеристического уравнения кратности r. Rm(x) — многочлен степени m с неопределёнными коэффициентами. Это правило следует из общего, если записать f(x) = Pm(x) в виде f(x) = e0 x [Pm(x) cos 0x + 0 sin 0x]. В этом случае s0 = 0 + 0i, m1 = m, m2 = 0, max(m1, m2) = m, поэтому yчн(x)= xr e0 x [Rm(x) cos 0x + Sm(x) sin 0x] = xr Rm(x) . Примеры: 1. Найти общее решение уравнения Решение: характеристическое уравнение k2 — 5 k + 6 = 0, его корни k1 = 2, k2 = 3, yoo = C1e 2x + C3e 3x. Степень многочлена m = 3, число 0 не является корнем характеристического уравнения (r = 0), поэтому yчн(x) ищем в виде многочлена третьей степени с неопределёнными коэффициентами: yчн(x)= xr Rm(x) = Ax3 + Bx2 + Dx + E. Тогда x3 6A = 1; A = 1/6; x2 — 15A + 6B =0; B = 15A/6 = 5/12; x 6A – 10B + 6D = -2; D = 5B/3 – A – 1/3 = (25 – 6 – 12)/36 = 7/36; 1 2B – 5D + 6E = 0; E = 5D/6 – B/3 = 35/216 – 5/36 =(35 – 30)/216 = 5/216. Итак,
|
|
24. Линейные стационарные неоднородные разностные уравнения. Метод вариации произвольных постоянных. Общее решение линейного уравнения с правой частью получается из общего решения соответствующего уравнения без правой части с помощью квадратур. Для этого можно применить следующий прием. В общем решении уравнения без правой части заменяем все произвольные постоянные неизвестными функциями. Полученное выражение дифференцируем и попутно подчиняем неизвестные функции добавочным условиям, упрощающим вид последовательных производных. Подставляя выражение производных y’, y’’, y’’’ и т.д. в данное уравнение, получаем еще одно условие, налагаемое на неизвестные функции. Тогда оказывается возможным найти первые производные всех неизвестных функций и остается выполнить квадратуры. Этот метод применим к линейным уравнениям любого порядка как с постоянными, так и с переменными коэффициентами. Рассмотрим уравнение второго порядка: y’’+P(x)y’+Q(x)=R(x) (1) Пусть общее решение соответствующего уравнения без правой части есть y=C1f1(x)+C2f2(x). (2) Ищем общее решения уравнения (1) в виде (2), считая теперь C1 и С2 неизвестными функциями от х. Дифференцируя (2), находим: y’=C1f1’(x)+C2f2’(x)+ C1’f1(x)+C2’f2(x) (3) Вводим добавочное условие C1’f1(x)+C2’f2(x)=0. (4) Тогда вид первой производной упрощается, и мы имеем: y’= C1f1’(x)+C2f2’(x). (5) Дифференцируя еще раз имеем: y’’= C1f1’’(x)+C2f2’’(x)+ C1’f1’(x)+C2’f2’(x) (6) После подстановки выражений (2), (5) и (6) в уравнение (1) все члены, содержащие С1, взаимно уничтожатся (ибо функция y=f1(x) есть решение уравнения y’’+Py’+Qy=0); точно так же взаимно уничтожатся все члены, содержащие С2, и мы получим еще одно условие C1’f1’(x)+C2’f2’(x)=R(x) (7) Условия (4) и (7) позволяют найти выражения производных С1’, C2’ и остается выполнить квадратуры. |
25. Общие сведения о линейных системах. Системой дифференциальных уравнений называется совокупность уравнений, содержащих несколько неизвестных функций и их производные, причем в каждое из уравнений входит хотя бы одна производная. На практике имеют дело с такими системами, где число уравнений равно числу неизвестных. Система называется линейной, если неизвестные функции и их производные входят в каждое из уравнений только в первой степени. Линейная система имеет нормальный вид, когда она решена относительно всех производных. |
26. Метод сведения линейной системы к одному уравнению. Пример 1. Система дифференциальных уравнений
— линейная; она имеет нормальный вид. в этом примере мы имеем линейную систему с постоянными коэффициентами (коэффициенты при неизвестных функциях и их производных постоянны). Из линейной системы (присоединяя к ней уравнения, выведенные дифференцированием) можно исключить все неизвестные (и их производные), кроме одной. Полученное уравнение будет содержать одну неизвестную функцию и ее производную первого и более высоких порядков. Это уравнение тоже будет линейным, а если исходная система была системой с постоянными коэффициентами, то и найденное уравнение высшего порядка будет иметь постоянные коэффициенты. Разыскав неизвестную функцию этого уравнения, подставляем ее выражение в данные уравнения и находим остальные неизвестные функции. Пример 2. Решить линейную систему примера 1. Решение: Чтобы исключить y и
Из уравнения (1) находим выражение y через t, x и
Находим его общее решение x=C1e2t+C2e-3t — Это выражение подставляем в уравнение (1) и находим вторую неизвестную функцию y = — |
|
27. Системы дифференциальных уравнений с постоянными коэффициентами
В векторной форме:
Характеристическое уравнение
Или Нахождение общего решения системы по методу Эйлера Если
2. Если
Коэффициенты многочленов можно определить, подставив выражения для y1, y2, …, yn в исходную систему. Найдя решения, соответствующие каждому корню характеристического уравнения, общее решение системы получим как линейную комбинацию этих решений. Например, если все корни характеристического уравнения простые, а решениями, соответствующими этим корням
то общее решение этой системы имеет вид: О |
28. Решение дифференциальных уравнений с использованием преобразования Лапласса Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. Одной из особенностей преобразования Лапласа, то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так линейные дифференциальные уравнения становятся алгебраическими.
Решение.Находим изображения правых и левых частей уравнения
Решив систему, получим
Разложим каждую дробь на простые дроби вида
Для
Откуда Для
Откуда
Для
Откуда
Ответ:
|
1. Дифференциальные уравнения. 2. Уравнения с разделяющимися переменными. 3. Уравнения, приводящие к уравнениям с разделяющимися переменными. 4. Линейные дифференциальные уравнения 1 порядка. 5. Уравнения 1 порядка. Метод вариации произвольной постоянной. 6. Уравнение 1 порядка.Метод Бернулли 7. Уравнение Бернулли 8. Уравнения в полных дифференциалах 9. Интегрирующий множитель 10. Дифференциальные уравнение высших порядков. Общие сведения 11. Уравнения, допускающие понижение порядка. 13. Уравнение Клеро 14. Линейные дифференциальные уравнения высших порядков 15. Линейные неоднородные дифференциальные уравнения высших порядков. Метод Подбора 16. Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной 17. Уравнение Эйлера 18. Общее понятие разностных уравнений 19. Решетчатые функции 20. Конечные разности элементарных функций 21. Разностные уравнения. Линейные разностные уравнения. 23. Линейные стационарные неоднородные разностные уравнения Метод подбора. 24. Линейные стационарные неоднородные разностные уравнения. Метод вариации произвольных постоянных. 25. Общие сведения о линейных системах. 26. Метод сведения линейной системы к одному уравнению. 27. Системы дифференциальных уравнений с постоянными коэффициентами 28. Решение дифференциальных уравнений с использованием преобразования Лапласса |
Свежие статьи
Популярно сейчас
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
652
Средний доход
с одного платного файла
Обучение Подробнее
Шпаргалка: Дифференциальные уравнения
Основные понятия и определения.
Дифференциальное уравнение называется соотношение вида
связывающее независимую переменную х, ее ф-цию у, а также производные этой функции до н-го порядка включительно. если в уравнении 1 входит одна независимая переменная, то такое диф. ур. называется обыкновенным, если в уравнение 1 входит несколько независимых переменных, то такое диф. ур. называется уравнение в частных производных. Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.
Решением уравнения 1 называется н-раз дифференцированная функция y=f(x), которая при подстановке в уравнение 1 обращает его в тождество. В простейшем случае определение функции y=f(x) сводится к вычислению интеграла, а поэтому процесс нахождения решения диф. уравн. называется его интегрированием, а график ф-ции y=f(x) называется интегральной кривой диф. уравн. Т.к. при интегрировании функции получается множество решений, отличающихся друг от друга постоянным коэффициентом, то любое диф. уравн. также будет иметь множество решений, графически определяемых семейством интегральных кривых. Общим решением (общим интегралом) диф. уравн. н-го порядка называется его решение явно (неявно) выраженное относительно ф-ции у и содержащей н-независимых производных постоянных.
Независимость констант СI означает,что ни одна из них не может быть выражена через остальные, а следовательно число этих констант не может быть уменьшено на единицу.
Частным решением интеграла диф. уравн. н-го понрядка называется такое его решение, в котором произвольным константам Сi присвоены конкретные значения. это конкретные значения находятся из решения системы так называемых начальных условий
В этой системе правые части равенства представляют собой некоторые константы.
Диф. уравн н-го порядка
Диф. уравн. 1-го порядка имеет вид.
Если уравн. 1 разрешить относительно производной y’, то получают дифференциальное уравнение первого порядка разрешенное относительно y’
Диф. уравн. 2 можно представить в так называемой диф. форме
P и Q многочлены зависящие от х и у дифференциальное уравнение описываемое соотношением 1,2,3 в частом случае могут не зависеть от независимой переменной х или ее ф-ции у, но обязательно включают производную y’.
Диф. уравн. с разделяющимися переменными
Диф. ур с раздел переменными называются уравнения вида
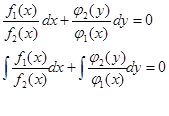
Уравнения (3) и (3¢) называются общими интегралами исходного диф. уравнения.
ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Определение 1. Ф-ция ¦(x,y) наз-ся однородной функцией н-го порядка относительно переменных x и y, если для любого t, отличного от нуля справедливо тождество ¦(tx; ty)=t^n ¦(x;y)
ОДНОРОДНАЯ ФУНКЦИЯ НУЛЕВОГО ПОРЯДКА.
Отношение двух однородных функций одинакового порядка есть однородная функция нулевого порядка.
Определение 2. Диф. уравнение P(x;y)dx + Q(x;y)dy=0 (1) является однородным уравнением , если функции P(x;y) и Q(x;y) являются однородными функциями одного и того же порядка.
Разрешим уравнение (1) относительно производной
Производная является однородной функцией нулевого порядка.
Определение 3. Диф. уравнение у¢=¦(x;y) (2) наз-ся однородным, если его правая часть ¦(x;y) является однородной функцией нулевого порядка относительно своих аргументов.
Однородное диф. уравнение приводится к диф. уравнениям с разделяющимися переменными подстановкой t=y/x ; y=t*x
При такой подстановке правая часть уравнения (2) ¦(tx;ty) = ¦(1/x*x;1/x*y)= ¦(1;y/x) = j(y/x) =j(t)
следовательно однородную функцию ¦(x;y) можно представить как функцию j от аргумента t=y/x
ò dt/(j(t)-t)=ò dx/x + c
общее решение уравнения 2.
ДИФ. УРАВНЕНИЕ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ.
Д.У. P(x;y)dx + Q(x;y)dy=0 (1)
наз-ся уравнением в полных дифференциалах если левая часть этого уравнения представляет собой полный дифференциал некоторой функции U(x;y)/
Необходимым и достаточным условием, того ,что уравнение (1) будет уравнением в полных дифференциалах, выполнение равенства
Действительно, если левая часть равенства (1) есть полный диф. функции U(x;y) ,то dU(x;y)=P(x;y)+Q(x;y)dy
dU(x;y)= dU/dx*dx + dU/dy*dy (3)
Сравнивая рав. 3 и 4
Т.к для диф. ф-ции U(x;y) частная произв. 2-го порядка не зависят от порядка диф., то мы приходим к равенству (2). С учётом равенства(30 равенство (1) может быть зависимо как
Это и есть общее решение нашего д.у.
Для отыскания ф-ции U воспользуемся ф-лой (5)
U= ò(x;y)dx+C=òP(x;y)dx + j(y) (9)
Для отыскания ф-ции j(y) продифференцируем равенство (9) по переменной y
Проинтегрировав левую и правую часть рав. (10) мы получим значение ф-ции j(y):
Подставим равенство (11) в (9)
C=C-C получаем общее решение диф. уравнения.
В ф-ле (12) знаки частной производной и дифференциала можно поменять местами.
Ф-цию U можно было определить из равенства(6)
Mathprofi ru дифференциальные уравнения
- Попробуйте решить приведенные ниже дифференциальные уравнения.
- Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.
Примеры решений дифференциальных уравнений первого порядка
Примеры решений дифференциальных уравнений второго и высших порядков
Примеры решений линейных уравнений в частных производных первого порядка
Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .
Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .
Автор: Олег Одинцов . Опубликовано: 28-01-2016
Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.
Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.
В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям
Как решить дифференциальное уравнение онлайн?
Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?
У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.
Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.
Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.
Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!
Общий интеграл, семейство кривых
Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$
Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$
Решения дифференциальных уравнений 1 порядка
Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$
Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x
e 0).$
Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$
Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$
Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$
Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$
Решение задачи Коши для ДУ
Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.
Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.
Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac , y(1)=1. $$
Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+cos x, quad y(0)=0, y'(0)=0, y»(0)=0. $$
Решения дифференциальных уравнений 2 порядка
Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^ .$
Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=frac > >, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$
Cоставление дифференциальных уравнений
Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?
Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.
Решения нелинейных дифференциальных уравнений
Задача 17. Решить дифференциальное уравнение $y^2
Задача 18. Решить дифференциальное уравнение $
Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.
В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.
Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.
Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.
Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».
Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.
Напомним, что y ‘ = d x d y , если y является функцией аргумента x .
Дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )
Начнем с примеров таких уравнений.
y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3
Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .
Приведем примеры подобных дифференциальных уравнений:
e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1
Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .
Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )
Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».
Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )
Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.
Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x
К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:
y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x
Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.
В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .
К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .
Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .
Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.
Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .
В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.
Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .
Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .
Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0
Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .
Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .
Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».
Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )
Приведем примеры таких уравнений.
К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x
Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».
Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a
Приведем примеры подобных уравнений.
К числу дифференциальных уравнений Бернулли можно отнести:
y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2
Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .
Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.
Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0
Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.
Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0
Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».
Дифференциальные уравнения второго порядка
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R
Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :
- действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
- действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
- комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .
Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:
- y = C 1 e k 1 x + C 2 e k 2 x ;
- y = C 1 e k x + C 2 x e k x ;
- y = e a · x · ( C 1 cos β x + C 2 sin β x ) .
Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:
y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2
Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R
Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y
исходного уравнения. Получаем: y = y 0 + y
Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y
мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.
К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:
y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x
Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».
Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )
Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.
На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .
Частные решения мы можем выбрать из систем независимых функций:
1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x
Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.
Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .
Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y
нам поможет метод вариации произвольных постоянных.
Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .
Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».
Дифференциальные уравнения высших порядков
Дифференциальные уравнения, допускающие понижение порядка
Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.
В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .
Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.
В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:
d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.
Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .
Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )
Решение уравнений данного вида предполагает выполнение следующих простых шагов:
- находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
- записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y
— частное решение неоднородного дифференциального уравнения.
Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y
целесообразно использовать метод вариации произвольных постоянных.
Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .
Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )
Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
— частное решение неоднородного дифференциального уравнения.
y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y
Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».
Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2
Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.
Обыкновенные дифференциальные уравнения
Содержание:
Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение

Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или 
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение 


Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или 
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение 

Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная 
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной 
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение 
которые проходят через начало координат (рис. 1).
Уравнение 
Если задано начальное условие 
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части: 
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение: 
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: 


Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,

Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными:
Интегрируя это уравнение, запишем 
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим 
Интегрируя, получим



Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение:
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:

Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену 

Тогда уравнение (7.10) запишется в виде 
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле

то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение 
то есть 

После интегрирования получим 
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить 
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения
Решение. Заменой y = xu сведем заданное уравнение к уравнению


Отделяя переменные, найдем




Возвращаясь к переменной y, получим общее решение: 
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем 
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16): 
откуда
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:

При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение 
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение: 

Выражение, стоящее в скобках, приравниваем к нулю, имеем

Отделим переменные, домножив обе части уравнения на 

После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18):
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения 
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда 
Подставим v в уравнение и найдем u:
Общее решение дифференциального уравнения будет:
Подставляем начальные условия в найденное решение и находим С:
Из общего решения получаем частное решение 
Дифференциальное уравнение Бернулли
Определение. Уравнения вида


называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»:
Сделаем замену: 
Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим: 
Мы получили линейное дифференциальное уравнение относительно новой переменной
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение. 
Сделаем замену 
Данное уравнение решим, сделав замену z = u (x) ⋅ v (x).
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения
Тогда 
Проинтегрировав правую часть этого уравнения по частям, получим 
Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную 


Обыкновенное дифференциальное уравнение может быть приведено к виду
Здесь 
Число 
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид
В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:
Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение
используя последнее в окрестности тех точек, в которых 
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение
Обе переменные 

Умножая обе части уравнения (3) на некоторую функцию 
где 


Иногда уравнение записывают *з так называемой симметрической форме:
Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2), 




- Существует производная
для всех значений
из интервала
(Отсюда следует, что решение
представляет собою функцию, непрерывную ею всей области определения).
- Функция
обращает уравнение (2) в тождество:
справедливое для всех значений 





Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения 
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.
является решением уравнения
в интервале 
справедливое при всех значениях
Пример 2.
Функция 

Пример 3.
является решением уравнения
в интервале
Иногда функцию 
Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила 
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила

функции определяются из уравнений динамики:
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t):
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:

где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:

Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): 
Заменим производные


Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем 
Продолжая дальше таким образом, получим 
В результате получаем следующую систему уравнений:

Из первых (n-1) уравнений определим y2, y3, . yn:

и подставим их значения в последнее уравнение системы (7.40) для определения y1:
Продифференцируем это выражение (n-1) раз, определим


Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему 
когда заданы начальные условия 
Решение. Дифференцируем по x первое уравнение, имеем: 



Из первого уравнения системы найдем 

Общим решением этого уравнения является

и тогда 
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет:
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:

где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:

Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44):
Сократим на e kt и преобразуем систему, сведя ее к такой системе:

Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы:
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k:
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде:
Пример 2. Найти общее решение системы уравнений:
Решение. Составим характеристическое уравнение:

Решение системы ищем в виде
Составим систему (7.46) для корня k1 и найдем 


Откуда 


Итак, мы получили решение системы:
Далее составляем систему (7.46) для k = 4:
Откуда 
Получим второй решение системы: 
Общее решение системы будет:
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:


Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:

где 

Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы
Решение. Составляем характеристическое уравнение:

Подставляем поочередно k1, k2 в систему (7.46), найдем
Запишем уравнение (7.47) и (7.48) для наших данных
Перепишем эти решения в таком виде:
За частные решения можно взять отдельно действительные и отдельно мнимые части:
Общим решением системы будет
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
источники:
http://web-shpargalka.ru/mathprofi-ru-differencialnye-uravnenija.php
http://natalibrilenova.ru/obyiknovennyie-differentsialnyie-uravneniya/
| Название: Дифференциальные уравнения Раздел: Рефераты по математике Тип: шпаргалка Добавлен 15:01:54 23 июня 2003 Похожие работы Просмотров: 7754 Комментариев: 24 Оценило: 6 человек Средний балл: 4 Оценка: 4 Скачать |
Пусть
Опр 1. Обыкновенным
Опр 2. Функция
Пусть D-область,
Если F(x,y,u1,…,un)= |
2. Пусть Опр Опр Постановка Числа Условная Найти Замечания
|
3. Обобщение Опред. ТСУ1(Локальная)Пусть Замечание Пусть |
|
4.
Уравнения
Теорема
Док-во.
Это равенство |
5.Линейные Ур-е Теор. Док-во(Метод 1) у≡0 у≠0, Потенциируем
{C1,y>0 Введем Решение 2) |
6.Обобщенное D 1) 3) Опред2| Опред3| Ур-е (2) |
|
7.Уравнения Пусть Рассмотрим Постановка Опред| |
8.Общий F(x,y,у(1))=0 γ (1*) |
|
Теор1| Док-во:1) dU=
Нахождение |
Выпишем Св-ва 3) Подставим C(1)=f(x)/ С(x)= Подставим Замечание| Решение Ур-е n≠0,n≠1. |
Замечание.
y’=f(ax+by+c)
Однородные
Уравнения
{ |
|
9.
Ур-ие такое, то Ур-ие |
10. Пусть Опр.: Постановка TCE Физический |
11.Простейшие Примеры. (1) I.F(x, Осуществим z(x) F(x, II. F( t yxx’’ yxxx’’’ F(y, III. Пусть F(x, Пример. y*y’’ Решение: (Х)х’ y*y’ y2 Ответ: |
|
12.Линейное Пусть Уравнение Если Pi(x) (1) Если (2) Ур. Ур. Постановка Пусть Теорема. Пусть y0 Тогда Замечание Пусть y(x0) Эта |
Теор.
Пусть
(7) Док-во.
Укажем
Зафиксируем
y1
По
Рассмотрим
y(k)(x0)=1,
Эта
Получим
Эти
|
|
|
13.ЛДУ Пусть Рассм.
L=d^n/dx^n Теор. 1)
2)Если Реш. |
14
Определитель
1)Пусть
х
2)Функ.
Пусть
Опр-ль
W(x)=W(y1(x),y2(x)… Наз-ся |
15 Т1 Если Следствие: |
|
Пусть
Вычислим
Обозначим
Построим
Z(x)-решение
z(x0)=
и
Итак
Следовательно
z(x)=
y1
Замечание
Если |
||
Соседние файлы в предмете Дифференциальные уравнения
- #
- #
- #
- #
- #
- #
Шпаргалка
на тему: Дифференциальные уравнения
Основные понятия и определения.
Дифференциальное уравнение называется соотношение вида
связывающее независимую переменную х, ее ф-цию у, а также производные этой функции до н-го порядка включительно. если в уравнении 1 входит одна независимая переменная, то такое диф. ур. называется обыкновенным, если в уравнение 1 входит несколько независимых переменных, то такое диф. ур. называется уравнение в частных производных. Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.
Решением уравнения 1 называется н-раз дифференцированная функция y=f(x), которая при подстановке в уравнение 1 обращает его в тождество. В простейшем случае определение функции y=f(x) сводится к вычислению интеграла, а поэтому процесс нахождения решения диф. уравн. называется его интегрированием, а график ф-ции y=f(x) называется интегральной кривой диф. уравн. Т.к. при интегрировании функции получается множество решений, отличающихся друг от друга постоянным коэффициентом, то любое диф. уравн. также будет иметь множество решений, графически определяемых семейством интегральных кривых. Общим решением (общим интегралом) диф. уравн. н-го порядка называется его решение явно (неявно) выраженное относительно ф-ции у и содержащей н-независимых производных постоянных.
Независимость констант СI означает, что ни одна из них не может быть выражена через остальные, а следовательно число этих констант не может быть уменьшено на единицу.
Частным решением интеграла диф. уравн. н-го понрядка называется такое его решение, в котором произвольным константам Сi присвоены конкретные значения. это конкретные значения находятся из решения системы так называемых начальных условий
В этой системе правые части равенства представляют собой некоторые константы.
Диф. уравн н-го порядка
Диф. уравн. 1-го порядка имеет вид.
Если уравн. 1 разрешить относительно производной y’, то получают дифференциальное уравнение первого порядка разрешенное относительно y’
Диф. уравн. 2 можно представить в так называемой диф. форме
P и Q многочлены зависящие от х и у дифференциальное уравнение описываемое соотношением 1,2,3 в частом случае могут не зависеть от независимой переменной х или ее ф-ции у, но обязательно включают производную y’.
Диф. уравн. с разделяющимися переменными
Диф. ур с раздел переменными называются уравнения вида
Где f1 (х) и f2 (х) зависят только от х, и 1 (у) и 2 (у), разделим обе части уравнения (1) на 1 (у) и f1 (х) получим
(3)
Уравнения (3) и (3) называются общими интегралами исходного диф. уравнения.
ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Определение 1. Ф-ция (x,y) наз-ся однородной функцией н-го порядка относительно переменных x и y, если для любого t, отличного от нуля справедливо тождество (tx; ty)=t^n (x;y)
ОДНОРОДНАЯ ФУНКЦИЯ НУЛЕВОГО ПОРЯДКА.
Отношение двух однородных функций одинакового порядка есть однородная функция нулевого порядка.
Определение 2. Диф. уравнение P(x;y)dx + Q(x;y)dy=0 (1) является однородным уравнением , если функции P(x;y) и Q(x;y) являются однородными функциями одного и того же порядка.
Разрешим уравнение (1) относительно производной
dy/dx=-P(x;y)/Q(x;y)
Производная является однородной функцией нулевого порядка.
Определение 3. Диф. уравнение у=(x;y) (2) наз-ся однородным, если его правая часть (x;y) является однородной функцией нулевого порядка относительно своих аргументов.
Однородное диф. уравнение приводится к диф. уравнениям с разделяющимися переменными подстановкой t=y/x ; y=t*x
При такой подстановке правая часть уравнения (2) (tx;ty) = (1/x*x;1/x*y)= (1;y/x) = (y/x) =(t)
t=1/x
y/x=t
следовательно однородную функцию (x;y) можно представить как функцию от аргумента t=y/x
y= t*x+t
t*x+t=(t)
dt/dx*x=(t)-t
dt/((t)-t)=dx/x
dt/((t)-t)= dx/x + c
общее решение уравнения 2.
ДИФ. УРАВНЕНИЕ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ.
Д.У. P(x;y)dx + Q(x;y)dy=0 (1)
наз-ся уравнением в полных дифференциалах если левая часть этого уравнения представляет собой полный дифференциал некоторой функции U(x;y)/
Необходимым и достаточным условием, того ,что уравнение (1) будет уравнением в полных дифференциалах, выполнение равенства
dP/dy=dQ/dx
Действительно, если левая часть равенства (1) есть полный диф. функции U(x;y) ,то dU(x;y)=P(x;y)+Q(x;y)dy
dU(x;y)= dU/dx*dx + dU/dy*dy (3)
dU(x;y)= P(x;y)dx+Q(x;y)dy (4)
Сравнивая рав. 3 и 4
dU/dx=P(x;y) (5)
dU/dy=Q(x;y) (6)
dP/dy=d^2U/dxdy
dQ/dx=d^2U/dydx
Т.к для диф. ф-ции U(x;y) частная произв. 2-го порядка не зависят от порядка диф., то мы приходим к равенству (2). С учётом равенства(30 равенство (1) может быть зависимо как
dU(x;y)=0 (7)
U(x;y)=c (8)
Это и есть общее решение нашего д.у.
Для отыскания ф-ции U воспользуемся ф-лой (5)
dU=P(x;y)dx
U= (x;y)dx+C=P(x;y)dx + (y) (9)
Для отыскания ф-ции (y) продифференцируем равенство (9) по переменной y
dU/dy=d/dyp(x;y)dx+(y)
(y)=Q(x;y)- d/dyp(x;y)dx (10)
Проинтегрировав левую и правую часть рав. (10) мы получим значение ф-ции (y):
(y)=(Q(x;y)-d/dy*P(x;y)dx)dy=C (11)
Подставим равенство (11) в (9)
P(x;y)dx=(Q(x;y)-d/dy*P(x;y)dx)dy +C=C
P(x;y)dx+(Q(x;y)-d/dy*P(x;y)dx)dy=C (12)
C=C—C получаем общее решение диф. уравнения.
Замечание.
В ф-ле (12) знаки частной производной и дифференциала можно поменять местами.
Ф-цию U можно было определить из равенства(6)
Виды дифференциальных уравнений. Интеграл дифференциального уравнения. Общий интеграл. Интегральная кривая.
Виды ду:
— Уравнения с разделяющимися переменными:
— Однородные уравнения:
— Линейные дифференциальные уравнения: 
— Уравнения Бернулли:
— Уравнения Риккати:
— Уравнения Якоби:
— Уравнения в полных дифференциалах :
— Уравнения Клеро:
— Уравнения Лагранжа:
— Уравнения, приводящиеся к уравнению Бернулли: 
Решением (интегралом) ду порядка n называется функция y(x), имеющая на
некотором интервале (a, b) производные до порядка n включительно и удовлетворяющая этому уравнению.
Общий интеграл дифференциального уравнения — это общее решение, которое имеет неявный вид Ф(x, y,C1,C2,C3,…Cn) = 0.
Интегральной кривой называется график решения геометрически неопределённого интеграла (первообразной), представляющего собой семейство «параллельных» кривых 
Задача Коши. Существование и единственность решений уравнений n-го порядка и систем уравнений.
Задача Коши, x0, y0 — начальные данные:
Решением задачи Коши является функция, определённая на интервале <a, b>, включающем x0, являющаяся решением уравнения (1) и удовлетворяющая начальному условию (2).
Определение. Решением интегрального уравнения:


1. (непрерывна)
2. 
3. подстановка 
Лемма. Функция 
Теорема: Существует единственное решения ДУ n-го порядка
yn= f (x, y, y’, y’’ , … y(n-1))удовлетворяющее условию: y (x0) = y0, y’ (x0) = y0`, y«( x0)= y0 ‘’ , … , y(n-1) (x0) = y0(n-1)
Если в окрестности нач. знач. (x0 , y0 , y«0, … , y0(n-1))
Функция f является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица по всем аргументам начиная со второго.
Теорема: Существование и единственности решения системы :

Предположим , что в области D , определённой неравенствами:
x0 – a <= x <= x0 + a i = (1, 2, … ,)
–
правые части уравнения (3.9) удовлетворяют условиям :
1. Все ф-ции (x,

M
2. Все ф-ции fi(x, 
Уравнения вида 

Некоторое уравнение путем подходящей замены переменных, можно привести к уравнению с разделенными переменными.






Ф (x , y)
Правая часть однородного уравнения является однородной функцией х и у нулевой степени однородности, поэтому уравнение вида M (x, y) dx + N (x ,y) dy = 0 будет однородным, если M(x , y) и N (x , y) является однородными функциями x , y одинаковой степени однородности, то есть в этом случае 
Уравнение вида 
Действительно в новых координатах
x = x – x1
y = y – y1
Свободный член в уравнениях этих прямых будет равен 0, коэффициенты при текущих координатах остаются неизменными, а производная
- Раздел: Математика → Дифференциальные уравнения
Уфимский государственный авиационный технический университет (УГАТУ)
Примеры решения (вычисления) Дифференциальные уравнения.
- №1
- 133,82 КБ
- дата добавления неизвестна
- описание отредактировано 15.06.2011 13:14
- Раздел: Математика → Дифференциальные уравнения
Решение дифференциальных уравнений. Первого порядка: прямого интегрирования; линейные; с разделяющимися переменными; однородные. Второго порядка: 5 типов.
- №2
- 17,29 КБ
- дата добавления неизвестна
- описание отредактировано 16.12.2010 00:41
- Раздел: Математика → Дифференциальные уравнения
Ответы на экзамен. ХГУ, 3 семестр. 8 с. Формулы, пояснение примеры. Содержит исчерпывающую информацию по диф. ура-м: Обыкновенные диф. урав. 1 порядка. Диф. урв. с разделяющими переменными. Однородные диф. ур. Линейные дифференциальные уравнения 1 порядка. урв. Бернулли. Дифференциальные уравнения: полный дифференциал. Дифференциальные уравнения n-го порядка. Уравнения не…
- №3
- 93,89 КБ
- добавлен 03.01.2012 14:20
- описание отредактировано 11.02.2016 15:31
- Раздел: Математика → Дифференциальные уравнения
Задачи, приводящие к понятию диф.уравнения.
Диф.уравнения первого порядка: основные определения, задача Коши, общее и частное решения, общий и частный интеграл.
Диф. уравнения первого порядка: понятие изоклины, особые точки диф. уравнения. Геометрическая интерпретация общего решения диф. уравнения.
Диф. уравнения с разделяющимися переменными. Метод решения. Пример.
Однородные…
- №4
- 146,40 КБ
- добавлен 23.09.2011 15:41
- описание отредактировано 25.09.2011 16:21
- Раздел: Математика → Дифференциальные уравнения
МАИ, 3 семестр, подробные ответы на экзамен по дифференциальным уравнениям и ТФКП. Определение обыкновенного дифференциального уравнения (ОДУ) и его решения. Геометрический смысл уравнения первого порядка. Уравнение с разделяющимися переменными. Уравнение в полных дифференциалах. Линейное дифференциальное уравнение Постановка задачи Коши для уравнения n-го порядка. Теорема…
- №5
- 547,46 КБ
- дата добавления неизвестна
- описание отредактировано 13.01.2011 03:46
- Раздел: Математика → Дифференциальные уравнения
Уфимский государственный авиационный технический университет (УГАТУ)
Примеры решения дифференциальных уравнений. Решить дифференциальное уравнение. Решить задачу Коши.
- №6
- 1,48 МБ
- дата добавления неизвестна
- описание отредактировано 15.08.2011 22:45
- Раздел: Математика → Дифференциальные уравнения
Специальность Прикладная математика. дисциплина Дифференциальные уравнения. Ответы на билеты + шпаргалки. формат DOCX. Список вопросов: Дифференциальные уравнения. Уравнения с разделяющимися переменными. Уравнения, приводящие к уравнениям с разделяющимися переменными. Линейные дифференциальные уравнения 1 порядка. Уравнения 1 порядка, Метод вариации произвольной постоянной….
- №7
- 1,19 МБ
- дата добавления неизвестна
- описание отредактировано 21.01.2016 21:44
- Раздел: Математика → Дифференциальные уравнения
Алгоритм решения квазилинейных задач: Численные методы решения начальной задачи (задачи Коши). Метод Эйлера. Метод Рунге-Кутты. Устойчивость схемы Рунге-Кутты. Порядок точности метода Рунге-Кутты. Оценка погрешности аппроксимации. Устойчивость метода простого прогноза. Устойчивость метода простой коррекции. Численное решение задачи Коши для жестких систем ОДУ. Разностные методы…
- №8
- 525,82 КБ
- дата добавления неизвестна
- описание отредактировано 17.05.2011 09:53
- Раздел: Математика → Дифференциальные уравнения
МАИ ГТУ, 3-семестр
Задачи, приводящие к обыкновенным ДУ, основные определения.
Задача Коши, формулировка теоремы существования и единственности ее решения. Геометрический смысл ДУ 1-го порядка, поле направлений, метод изоклин.
ДУ 1-го порядка с разделяющимися переменными. Однородные ДУ 1-го порядка.
Линейные ДУ 1-го порядка. Уравнение Бернулли.
ДУ в полных дифференциалах….
- №9
- 142,69 КБ
- дата добавления неизвестна
- описание отредактировано 02.02.2010 15:04
- Раздел: Математика → Дифференциальные уравнения
Основные понятия теории ДУ
Агульныя ўраўненні першага парадку і асноўныя азначэнні.
Аднародныя ДУ 1-га парадку і ўраўненні, якія прыводзяцца да іх.
Лінейныя ўраўненні першага парадку. Ураўненні Бернулі.
Ураўненні ў поўных дыферэнцыялах. Інтэгруючы множнік.
Тэарэма аб існаванні і адзінасці рашэння задачы Кашы для ураўненняў першага парадку.
Асаблівыя рашэнні ўраўненняў,…
- №10
- 532,74 КБ
- дата добавления неизвестна
- описание отредактировано 24.02.2011 14:41
- Раздел: Математика → Дифференциальные уравнения
Оформлено как шпоры. По одному примеру на каждую из нижеперечисленных задач.
Задача. Найти общий интеграл дифференциального уравнения.
Задача. Найти общий интеграл дифференциального уравнения.
Задача. Найти общий интеграл дифференциального уравнения.
Задача. Найти решение задачи Коши.
Задача. Найти решение задачи Коши.
Задача. Найти решение задачи Коши.
Задача. Найти общий…
- №11
- 143,99 КБ
- дата добавления неизвестна
- описание отредактировано 10.04.2011 11:42
- Раздел: Математика → Дифференциальные уравнения
Рівняння з відокремлюваними змінними та однорідні рівняння 1-го порядку. Лінійні рівняння першого порядку та рівняння типу Бернуллі. Метод Бернуллі та Лагранжа (варіації довільної сталої). Рівняння Ріккатті. Рівняння у повних диференціалах. Інтегрувальний множник. Неявні ДР 1-го п-ку. Метод введення параметра. Рівняння Лагранжа і Клеро. Теорема Коші-Пікара, теореми про…
- №12
- 293,62 КБ
- дата добавления неизвестна
- описание отредактировано 05.06.2010 03:35
- Раздел: Математика → Дифференциальные уравнения
Уфа,УГАТУ,ФИРТ. Преподаватель:Николаева М.А. Числовые ряды. Сходимость и сумма ряда. Свойства числовых рядов. Ряд геометрической прогрессии. Необходимый признак сходимости числового ряда. Гармонический ряд. Достаточные признаки сходимости. Признаки сравнения. Признак Даламбера. Радикальный и интегральный признак Коши. Обобщенный гармонический ряд. Общий достаточный признак…
- №13
- 814,44 КБ
- добавлен 16.01.2014 20:00
- описание отредактировано 25.01.2014 00:50
- Раздел: Математика → Дифференциальные уравнения
МАИ, Лунева С. Ю. , 2010.
Алгоритм решения ДУ методом решения параметра.
Порядок определения типа ДУ 1-ого порядка:
ДУ с разделяющимися переменными.
Однородное ДУ первого порядка.
Линейное неоднородное ДУ.
Уравнение Бернулли.
Уравнение в полных дифференциалах.
Уравнение неразрешенное относительно производной.
- №14
- 447,27 КБ
- дата добавления неизвестна
- описание отредактировано 25.10.2010 02:19
- Раздел: Математика → Дифференциальные уравнения
МАИ, Лунева С. Ю. , 2010.
Теорема Коши.
Пример задания №1(сформулировать теорему Коши для ДУ 4-го порядка в общем виде).
Пример задания №2(проанализировать поставленные задачи Коши для ДУ 1-го порядка).
- №15
- 399,79 КБ
- дата добавления неизвестна
- описание отредактировано 28.10.2010 14:28
- Раздел: Математика → Дифференциальные уравнения
Метод Эйлера решения СЛОДУ(алгоритм решения).
Составление матрицы системы.
Составление характеристического уравнения.
Анализ корней.
Последовательность действий для каждого простого действительного корня.
Последовательность действий для каждой пары простых комплексно-сопряженных корней.
Последовательность для каждого кратного действительного корня кратности k.
Запись общего…
- №16
- 314,74 КБ
- дата добавления неизвестна
- описание отредактировано 18.11.2010 19:43
В этом разделе нет файлов.
Комментарии
Уважаемые: администратор, модераторы и доверенные пользователи.
Друзья, то что ранее предлагал Денис, я уже предлагаю официально, в разделе Дифференциальные уравнения создать новый подраздел Дифференциальные уравнения в частных производных, который является самостоятельной областью (направлением, ветвью) математики (Дифференциальных уравнений):
Это соответствует требованиям мировых и официальных стандартов, изложенных в Википедии:
1. Википедия (Дифференциальное уравнение):
«Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные».
2. Википедия (Дифференциальное уравнение в частных производных):
«Дифференциальное уравнение в частных производных (частные случаи также известны как уравнения математической физики, УМФ) — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные».
3. Википедия (Категория: Дифференциальные уравнения): Отсюда следует вывод:
«Из Категории «Дифференциальные уравнения» -> Дифференциальное уравнение в частных производных«.
Литература (20 книг) для переноса в новый подраздел Дифференциальные уравнения в частных производных:
…
С уважением, благодарностью и благословением,
- Аккаунт удален
Уважаемый Админ.
Я благодарен Вам за добавление подраздела Дифференциальные уравнения в частных производных.
С уважением,
- Аккаунт удален
Уважаемые: администратор, модераторы и доверенные пользователи.
Друзья, то что ранее предлагал Денис (от 07.03.2015), я уже предлагаю официально, в разделе Дифференциальные уравнения создать новый подраздел Обыкновенные дифференциальные уравнения (ОДУ), который является самостоятельной областью (направлением, ветвью) математики (Дифференциальных уравнений):
Это соответствует требованиям мировых и официальных стандартов, изложенных в Википедии:
1. Википедия (Дифференциальное_уравнение):
«Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, зависящие от одной независимой переменной»
2. Википедия (Обыкновенное дифференциальное уравнение):
«Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальные уравнения для функции от одной переменной».
3. Википедия (Категория: Дифференциальные уравнения): Отсюда следует вывод:
«Из Категории «Дифференциальные уравнения» -> Обыкновенное дифференциальное уравнение«.
Литература (20 книг) для переноса в новый подраздел Обыкновенные дифференциальные уравнения:
…
С уважением, благодарностью и благословением,
- Аккаунт удален
Уважаемый Админ.
Я благодарен Вам за добавление подраздела Обыкновенные дифференциальные уравнения.
С уважением,
- Аккаунт удален
Неплохо бы отделить уравнения в частных производных от обыкновенных дифференциальных уравнений. Книг очень много, сложно ориентироваться.
- Денис
- Dosia
Уважаемые коллеги!
Я столкнулся с тем, что литература о дифференциальном исчислении собирается в разделах «Файлы Математика Высшая математика Дифференциальные уравнения» (/files/mathematics/algebra/diffeq/) и «Файлы Математика Высшая математика Математический анализ» (/files/mathematics/algebra/analysis/).
Было бы желательно как-то объединить или связать эти разделы, или подчинить раздел «Дифференциальные уравнения» разделу «Математический анализ».
- Zarub60
Решения Филиппова можно найти здесь
http://mat-an.ru/filippov.php
- Ramzes000
Где можно найти решения примеров из учебника Филиппова?(по дифурам)
- Ляля
В этом разделе нет комментариев.
Дифференциальные уравнения
Основные понятия и определения.
Дифференциальное уравнение называется соотношение вида
связывающее независимую переменную х, ее ф-цию у, а также производные этой функции до н-го порядка включительно. если в уравнении 1 входит одна независимая переменная, то такое диф. ур. называется обыкновенным, если в уравнение 1 входит несколько независимых переменных, то такое диф. ур. называется уравнение в частных производных. Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.
Решением уравнения 1 называется н-раз дифференцированная функция y=f(x), которая при подстановке в уравнение 1 обращает его в тождество. В простейшем случае определение функции y=f(x) сводится к вычислению интеграла, а поэтому процесс нахождения решения диф. уравн. называется его интегрированием, а график ф-ции y=f(x) называется интегральной кривой диф. уравн. Т.к. при интегрировании функции получается множество решений, отличающихся друг от друга постоянным коэффициентом, то любое диф. уравн. также будет иметь множество решений, графически определяемых семейством интегральных кривых. Общим решением (общим интегралом) диф. уравн. н-го порядка называется его решение явно (неявно) выраженное относительно ф-ции у и содержащей н-независимых производных постоянных.
Независимость констант СI означает, что ни одна из них не может быть выражена через остальные, а следовательно число этих констант не может быть уменьшено на единицу.
Частным решением интеграла диф. уравн. н-го понрядка называется такое его решение, в котором произвольным константам Сi присвоены конкретные значения. это конкретные значения находятся из решения системы так называемых начальных условий
В этой системе правые части равенства представляют собой некоторые константы.
Диф. уравн н-го порядка
Диф. уравн. 1-го порядка имеет вид.
Если уравн. 1 разрешить относительно производной y’, то получают дифференциальное уравнение первого порядка разрешенное относительно y’
Диф. уравн. 2 можно представить в так называемой диф. форме
P и Q многочлены зависящие от х и у дифференциальное уравнение описываемое соотношением 1,2,3 в частом случае могут не зависеть от независимой переменной х или ее ф-ции у, но обязательно включают производную y’.
Диф. уравн. с разделяющимися переменными
Диф. ур с раздел переменными называются уравнения вида
Где f1 (х) и f2 (х) зависят только от х, и ϕ1 (у) и ϕ2 (у), разделим обе части уравнения (1) на ϕ1 (у) и f1 (х) получим

Уравнения (3) и (3′) называются общими интегралами исходного диф. уравнения.
ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Определение 1. Ф-ция ƒ(x,y) наз-ся однородной функцией н-го порядка относительно переменных x и y, если для любого t, отличного от нуля справедливо тождество ƒ(tx; ty)=t^n ƒ(x;y)
ОДНОРОДНАЯ ФУНКЦИЯ НУЛЕВОГО ПОРЯДКА.
Отношение двух однородных функций одинакового порядка есть однородная функция нулевого порядка.
Определение 2. Диф. уравнение P(x;y)dx + Q(x;y)dy=0 (1) является однородным уравнением , если функции P(x;y) и Q(x;y) являются однородными функциями одного и того же порядка.
Разрешим уравнение (1) относительно производной
dy/dx=-P(x;y)/Q(x;y)
Производная является однородной функцией нулевого порядка.
Определение 3. Диф. уравнение у′=ƒ(x;y) (2) наз-ся однородным, если его правая часть ƒ(x;y) является однородной функцией нулевого порядка относительно своих аргументов.
Однородное диф. уравнение приводится к диф. уравнениям с разделяющимися переменными подстановкой t=y/x ; y=t*x
При такой подстановке правая часть уравнения (2) ƒ(tx;ty) = ƒ(1/x*x;1/x*y)= ƒ(1;y/x) = φ(y/x) =φ(t)
t=1/x
y/x=t
следовательно однородную функцию ƒ(x;y) можно представить как функцию φ от аргумента t=y/x
y′= t′*x+t
t′*x+t=φ(t)
dt/dx*x=φ(t)-t
dt/(φ(t)-t)=dx/x
∫ dt/(φ(t)-t)=∫ dx/x + c
общее решение уравнения 2.
ДИФ. УРАВНЕНИЕ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ.
Д.У. P(x;y)dx + Q(x;y)dy=0 (1)
наз-ся уравнением в полных дифференциалах если левая часть этого уравнения представляет собой полный дифференциал некоторой функции U(x;y)/
Необходимым и достаточным условием, того ,что уравнение (1) будет уравнением в полных дифференциалах, выполнение равенства
dP/dy=dQ/dx
Действительно, если левая часть равенства (1) есть полный диф. функции U(x;y) ,то dU(x;y)=P(x;y)+Q(x;y)dy
dU(x;y)= dU/dx*dx + dU/dy*dy (3)
dU(x;y)= P(x;y)dx+Q(x;y)dy (4)
Сравнивая рав. 3 и 4
dU/dx=P(x;y) (5)
dU/dy=Q(x;y) (6)
dP/dy=d^2U/dxdy
dQ/dx=d^2U/dydx
Т.к для диф. ф-ции U(x;y) частная произв. 2-го порядка не зависят от порядка диф., то мы приходим к равенству (2). С учётом равенства(30 равенство (1) может быть зависимо как
dU(x;y)=0 (7)
U(x;y)=c (8)
Это и есть общее решение нашего д.у.
Для отыскания ф-ции U воспользуемся ф-лой (5)
dU=P(x;y)dx
U= ∫(x;y)dx+C=∫P(x;y)dx + φ(y) (9)
Для отыскания ф-ции φ(y) продифференцируем равенство (9) по переменной y
dU/dy=d/dy∫p(x;y)dx+φ′(y)
φ′(y)=Q(x;y)- d/dy∫p(x;y)dx (10)
Проинтегрировав левую и правую часть рав. (10) мы получим значение ф-ции φ(y):
φ(y)=∫(Q(x;y)-d/dy*∫P(x;y)dx)dy=C (11)
Подставим равенство (11) в (9)
∫P(x;y)dx=∫(Q(x;y)-d/dy*∫P(x;y)dx)dy +C=C
∫P(x;y)dx+∫(Q(x;y)-d/dy*∫P(x;y)dx)dy=C (12)
C=C-C получаем общее решение диф. уравнения.
Замечание.
В ф-ле (12) знаки частной производной и дифференциала можно поменять местами.
Ф-цию U можно было определить из равенства(6)
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.shpori4all.narod.ru/





 Линейная неоднородная система диф ур с постоянными коэфф.
Линейная неоднородная система диф ур с постоянными коэфф. бщее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Для нахождения общего решения неоднородной системы можно применить метод Лагранжа вариации произвольных постоянных.
бщее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Для нахождения общего решения неоднородной системы можно применить метод Лагранжа вариации произвольных постоянных.



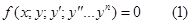
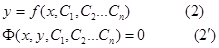
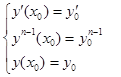
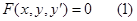
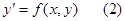
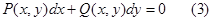
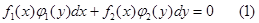
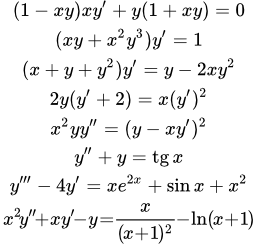
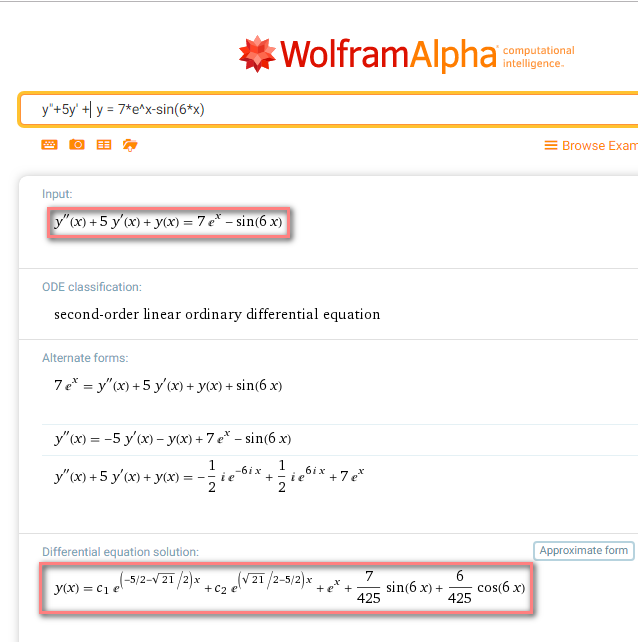


































 для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 



































 |R2
|R2
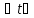 I:
I:
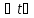 I:
I: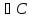 :
:
 U(x,y)
U(x,y)
 |R
|R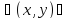
 |R3х,у,р
|R3х,у,р |R2x,y
|R2x,y (x,y)ϵD:
(x,y)ϵD: (x,y)ϵD:
(x,y)ϵD: |R3.
|R3. |R3х,у,р
|R3х,у,р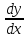 =
=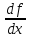 +
+
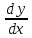 =
=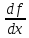 х(1)р+
х(1)р+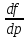 .
.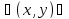
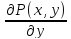 =
=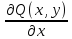 .
.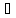 U(x,y)
U(x,y) C1(D)
C1(D)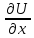 =P(x,y);
=P(x,y);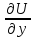 =Q(x,y).
=Q(x,y).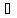 C1(D)
C1(D)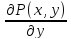 =
=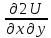 ,
,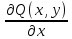 =
=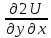 ,
,
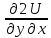
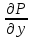 =
= .
.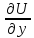 =
=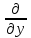 (∫P(x,y)dx+
(∫P(x,y)dx+ (α;β):
(α;β):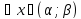
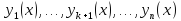 ;
;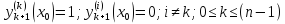

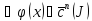
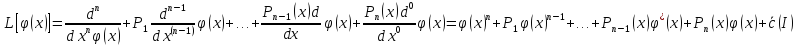
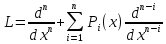
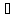 С(I)
С(I)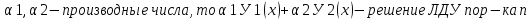

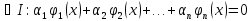
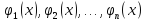
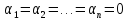
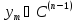 (I)
(I)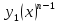
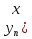 )=
)=