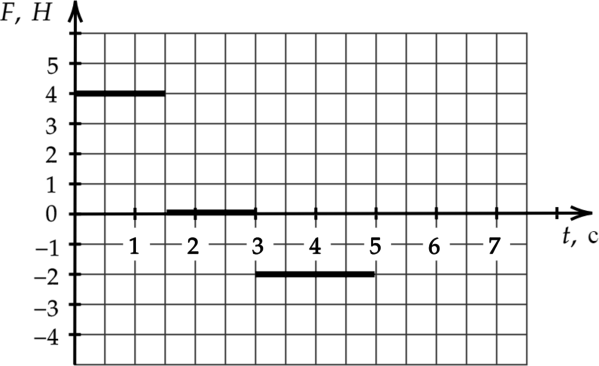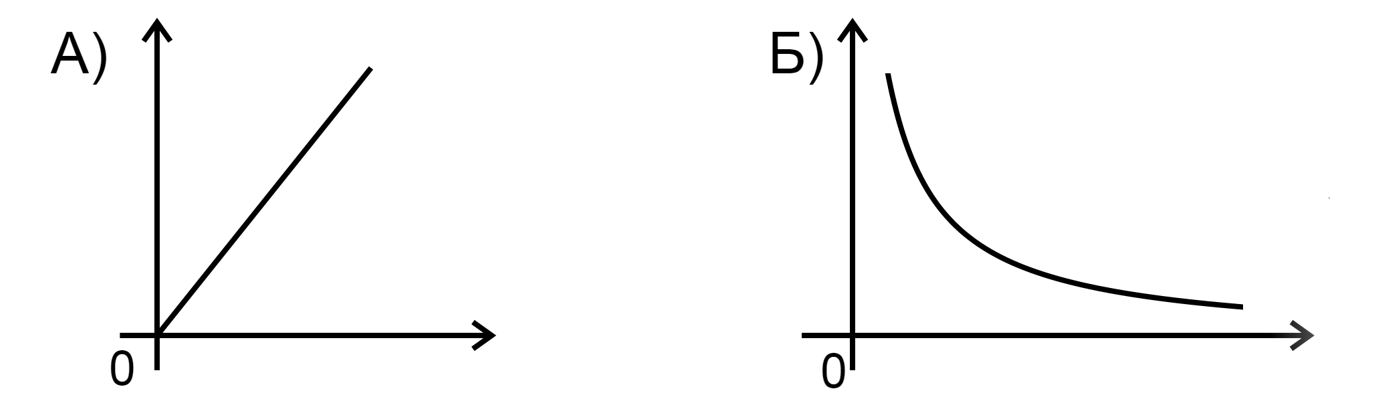1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Мяч массой (m=1{,}5) кг движется вдоль горизонтальной оси (Ox) под действием горизонтальной силы (F). В начальный момент времени тело покоилось. График зависимости силы (F) от времени (t) изображён на рисунке. Чему равен импульс мяча в конце 4 секунды? (Ответ дайте в кг(cdot)м/с)
Воспользуемся законом изменения импульса: [sum F=frac{Delta p}{Delta t}] Тогда же, если сила постоянна, то импульс мы можем найти по следующей формуле: [p=F_1(t_2 — t_1) + F_2(t_3 — t_2) + F_3 (t_4 — t_3) = 4 cdot (1{,}5 — 0) + 0 cdot (3 — 1{,}5) + (-2) cdot (4 — 3) = 4 text{ кг$cdot$м/с}]
Ответ: 4
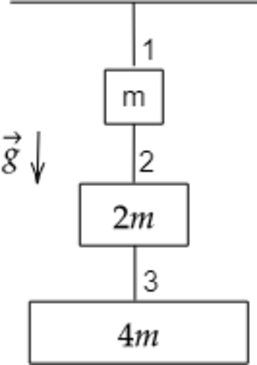
Три бруска массами m, 2m и 4m с помощью невесомых нерастяжимых нитей 1, 2 и 3 соеденены между собой и подвешены к потолку (см. рисунок). Система находится в равновесии. Чему равно отношение модулей сил натяжения нитей 1 и 3?
Масса, которая действует на нерастяжимую нить 1: [m_1=m+2m+4m] [m_1=7m] Масса, которая действует на нерастяжимую нить 3: [m_3=4m] На бруски действуют сила тяжести и сила натяжения нити. По 2 закону Ньютона: [T=mg] Сила натяжения нити для нити 1: [T_1=m_1g] [T_1=7mg] Сила натяжения нити для нити 3: [T_3=m_3g] [T_3=4mg] Тогда отношение модулей сил натяжения нитей 1 и 3: [frac{T_1}{T_3}=dfrac{7mg}{4mg}=1,75]
Ответ: 1,75
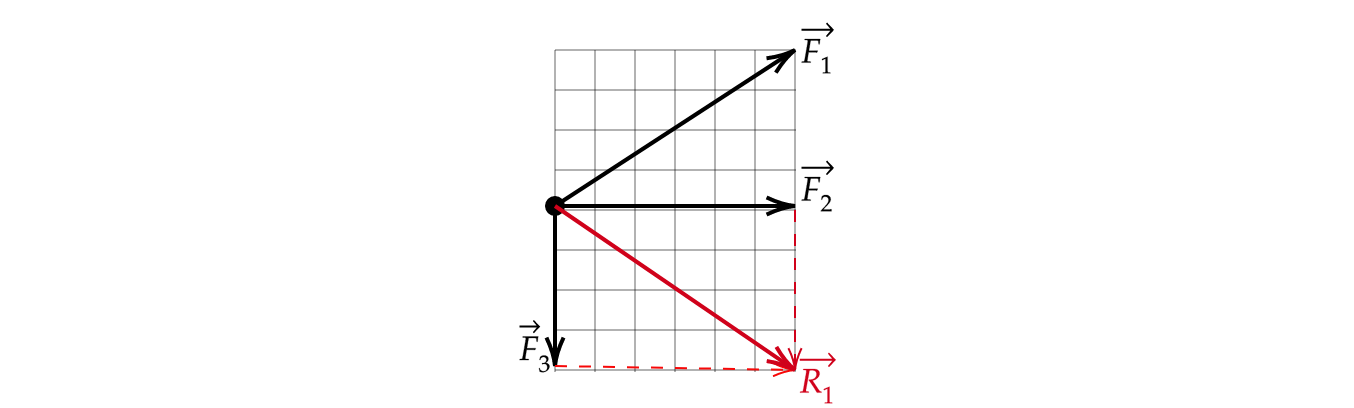
К телу было приложено две силы под углом (90^{circ}) друг к другу. Известно, что равнодействующая этих сил равна (F_text{равн}=10) Н, а одна из приложенных сил равна (F_1=6) Н. Чему равен модуль второй силы (F_2)?
Равнодействующая двух сил – это сумма двух сил: [vec{F}_text{равн}=vec{F}_1+vec{F}_2] Вспомним, что равнодействующая двух сил – это величина результирующего вектора. Изобразим силы на рисунке, воспользовавшись правилом параллелограмма: 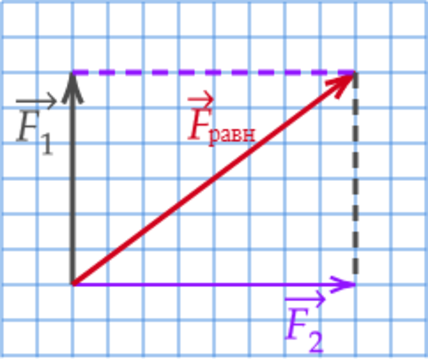
Ответ: 8
К телу было приложено две силы (F_1) и (F_2). Под действием одной силы (F_1) тело двигалось с ускорением (a_1=8) м/с(^2). Под действием другой силы, направленной противоположно силе (F_1), ускорение тела равно (a_2=5) м/с(^2). С каким ускорением тело будет двигаться при одновременном действии сил (F_1) и (F_2)? Ответ дайте в метрах в секундах в квадрате.
Рассмотрим действие силы (F_1) на тело. Спроецируем все силы, действующие на тело на ось (ox). Тогда, по 2-ому закону Ньютона: [F_1=ma_1] Аналогично с (F_2): [F_2=ma_2] Рассмотрим одновременное действие сил (F_1) и (F_2). Спроецируем все силы, действующие на тело на ось (ox). Тогда, по 2-ому закону Ньютона: [F_1-F_2=ma_3] Подставим (F_1) и (F_2) из предыдущих выражений, получаем: [ma_1-ma_2=ma_3] Разделим все выражение на (m), получим: [a_1-a_2=a_3] Подставим исходные значения: [a_3=8text{ м}text{$/c^2$}-5text{ м}text{$/c^2$}=3text{ м}text{$/c^2$}]
Ответ: 3
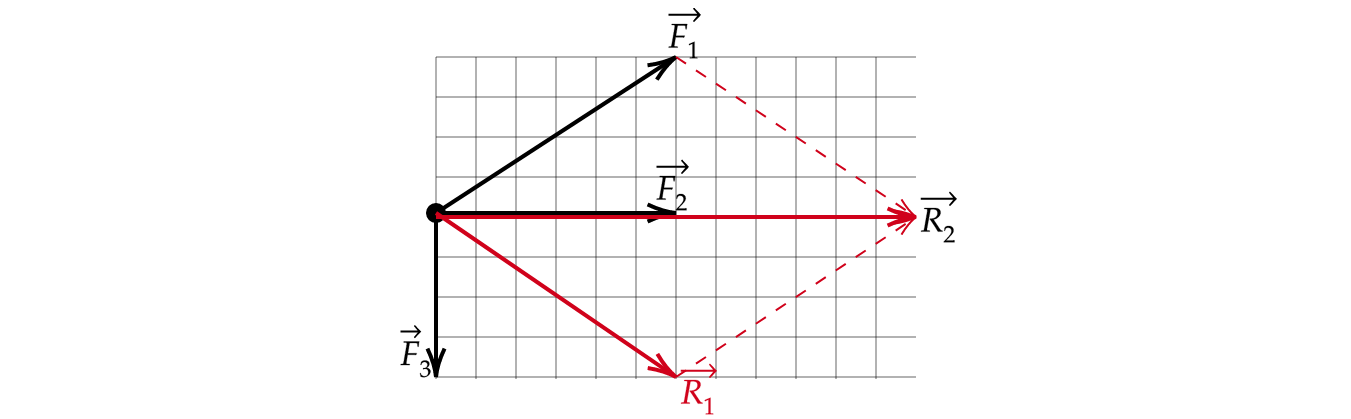
На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Определите модуль равнодействующей этих сил.

Складываем силы по правилу параллелограма (параллельно переносим каждую из сил в конец другой) и находим, что равнодействующая равна 3 Н.
Ответ: 3
На тело массой 2 кг действует сила 60 Н. Найдите ускорение тела “Основная волна 2020”
По второму закону Ньютона: [F=ma Rightarrow a=dfrac{F}{m}=dfrac{60text{ Н}}{2text{ кг}}=30text{ м/с$^2$}]
Ответ: 30
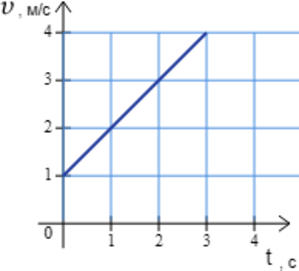
Ящик поднимают с помощью веревки вертикально вверх. На рисунке приведена зависимость проекции скорости (bfupsilon) ящика на ось, направленную вертикально вверх, от времени (t). Определите массу ящика, если известно, что сила натяжения веревки в течение подъёма равна 275 Н. Ответ выразите в кг.
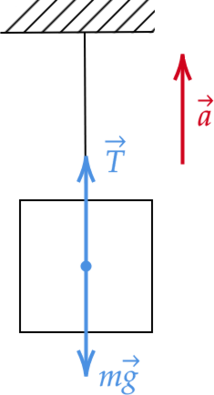
Заметим(из графика), что скорость груза меняется линейно, следовательно тело движется с ускорением равным: [a=dfrac{upsilon-upsilon_{0}}{t}=dfrac{4text{ м/c$^2$}-1text{ м/c$^2$}}{3text{ c}}=1text{ м/c$^2 $}] Изобразим все силы, действующие на тело:
Спроецируем силы на ось (Oy) и воспользуемся 2 законом Ньютона: [T-mg=ma] [m(g+a)=T] [m=frac{T}{(g+a)}] Подставим в полученную формулу исходные значения: [m=dfrac{275text{ H}}{10text{ м/c$^2$}+1text{ м/c$^2$}}=25text{ кг }]
Ответ: 25

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задачи по динамике с решениями
Сила, импульс, законы Ньютона
2.1.1 Тело движется прямолинейно под действием силы 16 Н. Зависимость пути от времени
2.1.2 Тело массой 3 кг движется горизонтально с ускорением 4 м/с2. Определить
2.1.3 На тело массой 5 кг подействовали горизонтальной силой 4 Н. Какую скорость
2.1.4 Под действием какой силы прямолинейное движение частицы массой 100 г
2.1.5 Под действием горизонтальной силы, равной 12 Н, тело движется по горизонтальной
2.1.6 Определить плотность тела массой 100 г и объемом
2.1.7 Определить вес человека массой 70 кг в лифте, опускающемся равнозамедленно
2.1.8 С какой силой давит человек массой 70 кг на вертикальную спинку сиденья
2.1.9 К нити подвешен груз массой 1 кг. Определить силу натяжения нити, если нить
2.1.10 К нити подвешен груз массой 1 кг, который опускается с ускорением 5 м/с2
2.1.11 Поезд, подъезжая к станции со скоростью 72 км/ч, начинает тормозить. Каково
2.1.12 Поезд, подъезжая к станции со скоростью 60 км/ч, тормозит. За какое минимальное
2.1.13 При каком ускорении разорвется трос, прочность которого на разрыв равна
2.1.14 Груз массой 2 кг подвешен на динамометре. Снизу груз тянут с силой 10 Н
2.1.15 Автомобиль массой 1,2 т движется с места с ускорением 0,8 м/с2. Какую силу тяги
2.1.16 Под действием силы 30 Н тело поднимается вверх с ускорением 10 м/с2. Определить
2.1.17 Тело массой 3 кг падает в воздухе вертикально вниз с ускорением 8 м/с2
2.1.18 С какой силой давит тело массой 2 кг на пол лифта, поднимающегося с ускорением
2.1.19 Шар массой 0,1 кг движется со скоростью 5 м/с. После удара о стенку шар стал
2.1.20 Автомобиль массой 2 т, двигаясь равноускоренно, через 4 с достиг скорости 2 м/с
2.1.21 На тело массой 15 кг, лежащее на земле, действует направленная вверх сила 45 Н
2.1.22 Автомобиль массой 2 т, трогаясь с места, прошел путь 100 м за 10 с. Найти
2.1.23 Тело массой 50 г, падающее со скоростью 2 м/с, упруго соударяется с горизонтальной
2.1.24 Из орудия вылетает снаряд массой 10 кг со скоростью 500 м/с. Найти силу давления
2.1.25 Скорость автомобиля изменяется по закону v=10+0,5t. Найдите результирующую
2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми
2.1.27 Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см
2.1.28 Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену
2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы
2.1.30 На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч
2.1.31 Найти модуль изменения импульса шарика массой 20 г за 3 с свободного падения
2.1.32 Определить натяжение каната, к которому подвешена клеть подъемной машины
2.1.33 Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют
2.1.34 Канат может выдержать нагрузку 2,5 кН. С каким максимальным ускорением можно
2.1.35 Летящая пуля попадает в мешок с песком и углубляется на 15 см. На какую глубину
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.37 Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30 градусов к ней
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.39 Два автомобиля с одинаковыми массами m движутся со скоростями v и 2v
2.1.40 Две стальные проволоки одинаковой длины, диаметр первой в 3 раза больше
2.1.41 Ракета на старте с поверхности Земли движется вертикально вверх с ускорением
2.1.42 С каким ускорением будет опускаться груз на нити, если сила натяжения нити в 1,25
2.1.43 С какой минимальной силой, направленной горизонтально, нужно прижать плоский
2.1.44 С какой силой давит человек массой 70 кг на пол лифта, движущегося вниз с ускорением
2.1.45 С какой силой следует придавить тело массой 4,5 кг к вертикальной стене, чтобы
2.1.46 Автомобиль идет по горизонтальной дороге со скоростью 72 км/ч. Найти тормозной
2.1.47 Тело массой 5 кг покоится на горизонтальной поверхности. К телу приложена сила
2.1.48 Тело, брошенное вертикально вверх с начальной скоростью 30 м/с, достигло высшей
2.1.49 Три бруска, массы которых 0,5, 0,3 и 0,1 кг, связаны нитями и лежат на столе
2.1.50 Тело массой 1,5 кг движется вверх по вертикальной стенке под действием силы 20 Н
2.1.51 Тело массой 100 кг движется по горизонтальной поверхности под действием силы
2.1.52 Тело массой 200 кг упало на грунт со скоростью 100 м/с и погрузилось в него
2.1.53 Брусок массой 50 кг прижимается к вертикальной стенке с силой 100 Н. Какая сила
2.1.54 Троллейбус, масса которого 12 т, трогаясь с места, за 5 с проходит по горизонтальному
2.1.55 Через сколько секунд тело, брошенное вертикально вверх со скоростью 44,8 м/с
2.1.56 Чтобы на неподвижном блоке поднимать равномерно груз, требуется усилие 270 Н
2.1.57 На гладкой доске лежат два тела массами 2 и 3 кг, соединенные легкой нерастяжимой
2.1.58 Человек везет двое связанных между собой саней, прикладывая к веревке силу 120 Н
2.1.59 Тело массой 100 г движется вверх по вертикальной стенке под действием силы 2 Н
2.1.60 Груз массой 1 кг падает с высоты 240 м и углубляется в землю на 0,2 м. Определить
2.1.61 Дождевая капля массой 0,02 г под влиянием горизонтально дующего ветра падает
2.1.62 Материальная точка массой 1 кг движется со скоростью, которая изменяется по закону
2.1.63 Канат лежит на плоской горизонтальной крыше так, что часть его свешивается
2.1.64 Мяч массой 0,2 кг движется к стене под углом 30 градусов к ней со скоростью 6 м/с
2.1.65 Пуля массой 0,3 г, выпущенная из пневматической винтовки вертикально вверх, упала
2.1.66 Стержень длиной 0,9 м движется с ускорением под действием приложенной к его
2.1.67 Тело массой 2 кг начинает движение под действием постоянной по направлению
2.1.68 Что покажут пружинные весы в лифте при измерении веса груза массой 1 кг
2.1.69 Хоккейная шайба, имея начальную скорость 5 м/с, скользит до удара о борт площадки
2.1.70 Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут
2.1.71 Есть два способа закинуть льдинку: бросить её под углом 45 градусов к горизонту или
2.1.72 К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок
2.1.73 На гладкой поверхности лежит доска массой 5 кг, на ней находится тело массой 3 кг
2.1.74 Струя сечением 6 см2 ударяет из брандспойта в стенку под углом 60 градусов к нормали
2.1.75 На скользкой дороге коэффициент трения между дорогой и колесами мотоцикла
2.1.76 Груз массой 10 кг привязан к свободно свисающему концу веревки, намотанной
2.1.77 Координаты тела массы m=1 кг, движущегося прямолинейно вдоль оси x, меняются
2.1.78 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.1.79 Молекула массы m, летящая со скоростью v, ударяется о стенку сосуда под углом a
2.1.80 К невесомой нити подвешен груз массы 1 кг. Точка подвеса нити движется
2.1.81 Четыре одинаковых кубика, связанные невесомыми нитями, движутся по гладкому
2.1.82 Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной
2.1.83 Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая
2.1.84 Тело массы 10 кг движется по горизонтальной плоскости под действием силы
2.1.85 В кузове автомобиля лежит груз. При каком минимальном ускорении автомобиля груз
2.1.86 На шероховатой горизонтальной поверхности лежит тело массы 1 кг. Коэффициент
2.1.87 Тело массы m движется под действием силы F. Как изменится модуль ускорения тела
2.1.88 Тело массы m движется под действием двух равных по модулю взаимно
2.1.89 Тело массы 2 кг движется с результирующим ускорением 5 м/с2 под воздействием
2.1.90 На материальную точку массы 1 кг действует две постоянные взаимно перпендикулярные
Неподвижный блок
2.2.1 Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением
2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
2.2.3 Через неподвижный блок перекинута нить, к концам которой подвешены грузы
2.2.4 Два грузика массами m1=0,3 кг и m2=0,2 кг соединены нитью, перекинутой через блок
2.2.5 Два одинаковых груза массами 0,1 кг связаны между собой нитью, перекинутой
2.2.6 Две гири неравной массы висят на концах нити, перекинутой через невесомый блок
2.2.7 Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой
2.2.8 К концам нерастянутой нити, перекинутой через застопоренный блок, подвешенный
2.2.9 К одному концу невесомой и нерастяжимой нити, перекинутой через невесомый блок
Наклонная плоскость
2.3.1 Тело скользит с постоянной скоростью вниз по наклонной плоскости с углом наклона
2.3.2 Льдинка скользит по инерции вверх по наклонной плоскости с углом наклона
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
2.3.4 По наклонной плоскости с углом наклона 30 градусов к горизонту скользит вниз тело
2.3.5 Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине)
2.3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с
2.3.7 Тело скользит равномерно по наклонной плоскости, угол наклона которой 30 градусов
2.3.8 Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона
2.3.9 Автомобиль при полностью включенных тормозах (колеса не вращаются) может
2.3.10 С ледяной горки высотой 3 м и длиной основания 5 м съезжают санки, которые
2.3.11 Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45 градусов
2.3.12 Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной
2.3.13 Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают
2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.15 С каким ускорением движутся грузы m1=0,5 кг и m2=0,6 кг, если высота наклонной
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами
2.3.18 Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом
2.3.19 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень
2.3.20 По наклонной плоскости с углом наклона 60 градусов соскальзывает без трения клин
2.3.21 Груз поднимают с помощью ленточного транспортера, расположенного под углом
2.3.22 На горизонтальной доске лежит брусок. Коэффициент трения скольжения между бруском
Центростремительное ускорение
2.4.1 Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит
2.4.2 Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой
2.4.3 Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с
2.4.4 Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной
2.4.5 Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости
2.4.6 Горизонтально расположенный диск равномерно вращается вокруг вертикальной оси
2.4.7 Диск вращается с частотой 70 об/мин. На каком расстоянии от оси вращения можно
2.4.8 На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной
2.4.9 Определить силу, действующую на летчика, выводящего самолет из пикирования
2.4.10 Поезд движется по закруглению радиуса 765 м со скоростью 72 км/ч. Определить
2.4.11 Трактор массой 8 т проходит по мосту со скоростью 36 км/ч. Какова сила давления
2.4.12 Конькобежец движется по закруглению ледяной дорожки радиусом 2,5 м со скоростью
2.4.13 Шоссе имеет вираж с уклоном 10 градусов при радиусе закругления дороги в 100 м
2.4.14 Камень, подвешенный к потолку на веревке, движется в горизонтальной плоскости
2.4.15 В желобе, наклоненном под углом 30 градусов к горизонту и вращающемся с частотой
2.4.16 Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность
2.4.17 Груз массой 1 кг, привязанный к нити, отклоняют на 90 градусов от положения
2.4.18 Груз, подвешенный на нити длиной 5 м, равномерно движется по окружности
2.4.19 Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности
2.4.20 Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление
2.4.21 Люстра массой 10 кг висит на цепи, прочность которой 196 Н. На какой максимальный угол
2.4.22 На легкой нерастяжимой нити подвешен тяжелый шарик. На какой угол нужно отвести
2.4.23 Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг
2.4.24 По гладкому столу вращается груз, прикрепленный к центру вращения пружиной
2.4.25 Поезд движется по закруглению со скоростью 50 км/ч. Шарик, подвешенный в вагоне
2.4.26 Подвешенный на нити шарик массой 0,3 кг совершает колебания в вертикальной
2.4.27 Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости
2.4.28 Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура
2.4.29 К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается
2.4.30 Какова должна быть максимальная длина выпуклого симметричного относительно
2.4.31 Маленький шарик, подвешенный на нити, движется по окружности так, что нить
2.4.32 Мотоциклист движется по цилиндрической стенке диаметра 12 м. При каком коэффициенте
2.4.33 Спортивный молот – ядро на тросике длиной L, бросают, раскрутив вокруг себя
2.4.34 Тележка, скатившаяся по наклонному желобу с высоты 10 м, описывает в вертикальной
2.4.35 Чаша в форме полусферы радиусом 0,8 м вращается с постоянной угловой скоростью
2.4.36 Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное
2.4.37 Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось
2.4.38 На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают
2.4.39 На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение
2.4.40 Бусинка может скользить вдоль гладкого кольца радиуса R, расположенного
2.4.41 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси
2.4.42 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси с постоянной
2.4.43 В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна
Закон всемирного тяготения
2.5.1 Во сколько раз уменьшится сила тяготения тела к Земле при удалении его
2.5.2 Определить силу взаимодействия тела массой 2 кг и Земли, если тело удалено от
2.5.3 Во сколько раз ускорение свободного падения около поверхности Земли больше
2.5.4 Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения
2.5.5 Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца
2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.7 Определить первую космическую скорость для планеты, масса и радиус которой в два
2.5.8 На некоторой планете сила тяжести, действующая на тело массой 4 кг, равна 8 Н. Найти
2.5.9 На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе
2.5.10 Сколько метров пройдет тело, свободно падая без начальной скорости в течение трех
2.5.11 Чему равно ускорение свободного падения на высоте, равной половине радиуса
2.5.12 Определить, с каким ускорением падают тела на поверхность Луны, зная, что радиус
2.5.13 Человек на Земле прыгает на высоту 1 м. На какую высоту, совершив ту же работу, он
2.5.14 Во сколько раз период обращения искусственного спутника, совершающего движение
2.5.15 Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше
2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период
2.5.18 Тело поднялось на высоту 1600 км над поверхностью Земли. На сколько процентов
2.5.19 Определить минимальный период обращения спутника нейтронной звезды. Её плотность
2.5.20 Радиус Земли равен 6400 км. Какую скорость имеют точки земной поверхности на широте
2.5.21 На каком расстоянии от центра Земли (в долях радиуса Земли R) ускорение свободного
2.5.22 Радиус Земли равен 6400 км. На каком расстоянии от поверхности Земли сила притяжения
Упругая сила
2.6.1 Для сжатия пружины на 2 см надо приложить силу 10 Н. Определить энергию упругой
2.6.2 Какую работу надо совершить, чтобы удлинить на 0,1 м резиновый шнур с коэффициентом
2.6.3 Под действием силы 4 Н пружина удлинилась на 2 см. Чему равна при этом
2.6.4 Какова начальная скорость шарика массой 1 г, которым выстрелили из пружинного
2.6.5 При вращении шарика, прикрепленного к пружине длиной 20 см, с частотой вращения
2.6.6 Груз массой 1 кг, прикрепленный к пружине, равномерно тянут по горизонтальной
2.6.7 Каков коэффициент жесткости буксировочного троса, если при буксировке автомобиля
2.6.8 Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля
2.6.9 Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины
2.6.10 Тело массой 2 кг тянут по горизонтальной поверхности с помощью пружины, которая
2.6.11 Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести, чтобы
2.6.12 К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки
2.6.13 Груз массой 4 кг подвешен на пружине жесткостью 1 кН/м. Определите дополнительную
2.6.14 Какую минимальную работу необходимо совершить, чтобы передвинуть по
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью
Работа, мощность, энергия
2.7.1 Какую работу надо совершить, чтобы растянуть пружину с жесткостью 40 кН/м
2.7.2 Какую работу совершает постоянная сила по перемещению на 5 м тела массой 3 кг
2.7.3 Определить работу, необходимую для поднятия груза массой 3 кг на высоту 10 м
2.7.4 Автомобиль поднимается в гору со скоростью 36 км/ч. Определить силу тяги мотора
2.7.5 Пуля массой 10 г вылетает из винтовки со скоростью 600 м/с. Определить работу
2.7.6 Автомобиль массой 1800 кг, двигаясь с ускорением 2 м/с2, прошел 100 м пути
2.7.7 Найти кинетическую энергию стрелы массой 0,5 кг, пущенную вертикально вверх
2.7.8 Мальчик везет санки, прилагая к веревке силу 10 Н, которая образует угол 30 градусов
2.7.9 При подъеме тела массой 10 кг на высоту 2 м совершена работа 230 Дж
2.7.10 Санки тянут на пути 100 м с силой 80 Н за веревку, составляющую угол 30 градусов
2.7.11 Во сколько раз изменится запас потенциальной энергии упруго деформированного тела
2.7.12 При торможении автомобиля массой 1 т скорость уменьшилась от 72 км/ч до 36 км/ч
2.7.13 Автомобиль массой 1500 кг, двигаясь равноускоренно, проходит путь 20 м за 2 с
2.7.14 На какой высоте над поверхностью Луны тело будет обладать такой же потенциальной
2.7.15 Определить работу, которую нужно произвести для того, чтобы сжать пружину на 10 см
2.7.16 Определить массу тела, имеющего кинетическую энергию 16 Дж, а импульс
2.7.17 Тело массой 1 кг начинает свободно падать. Определить мощность силы тяжести
2.7.18 Автомобиль массой 1,5 т едет со стоянки с постоянным ускорением 2 м/с2. Коэффициент
2.7.19 Автомобиль движется со скоростью 72 км/ч. Мощность двигателя 60 кВт, его КПД 30%
2.7.20 Вертолет весит 3 т. На его подъем тратится 30% мощности мотора. Определить
2.7.21 Двигатели электровоза при движении со скоростью 72 км/ч потребляют мощность
2.7.22 Какая работа совершается внешней силой при поднятии тела массой 5 кг на высоту
2.7.23 Какую работу должен совершить двигатель, чтобы разогнать по горизонтальной
2.7.24 Какую работу надо совершить, чтобы поднять груз массой 30 кг на высоту 10 м
2.7.25 Какую работу надо совершить, чтобы поднять груз массой 3000 кг на высоту 10 м
2.7.26 Какую среднюю мощность и силу тяги должен развивать электровоз, чтобы состав массой
2.7.27 Камень брошен под углом 30 градусов к горизонту. Кинетическая энергия камня в верхней
2.7.28 Камень массой 100 г бросили под углом 60 градусов к горизонту со скоростью 15 м/с
2.7.29 На тело массой 10 кг действует постоянная сила 5 Н. Определить кинетическую энергию
2.7.30 Подъемный кран поднимает груз массой 5 т на высоту 15 м. За какое время поднимется
2.7.31 Поезд массой 1000 т начинает двигаться с места равноускоренно и достигает скорости
2.7.32 Резец токарного станка мощностью 3 кВт снимает в минуту стружку длиной 500 мм
2.7.33 Самолет для взлета должен иметь скорость 25 м/с. Длина пробега перед взлетом 100 м
2.7.34 Тело массой 1 кг, брошенное с вышки в горизонтальном направлении со скоростью
2.7.35 Тепловоз за 5 мин набирает скорость 72 км/ч. Определить среднюю мощность
2.7.36 Укажите график зависимости потенциальной энергии свободно падающего тела
2.7.37 Уравнение движения материальной точки имеет вид: x=t^2-2t^3 (м). Определите
2.7.38 Футбольный мяч весом 8 Н летит со скоростью 15 м/с. Вратарь ловит мяч и за 0,1 с
2.7.39 Пуля летит со скоростью v0. Она пробивает доску толщиной 3,6 см и продолжает полет
2.7.40 Максимальная высота подъема тела массой 2 кг, брошенного с поверхности Земли
2.7.41 На рисунке приведена зависимость потенциальной энергии от времени движения
2.7.42 Начальная скорость пули 600 м/с, её масса 10 г. Под каким углом к горизонту она
2.7.43 Самолет массой 2 т летит со скоростью 50 м/с. На высоте 420 м он переходит на снижение
2.7.44 Тело массой 3 кг падает вертикально вниз с начальной скоростью 2 м/с. Найти работу
2.7.45 Трактор имеет тяговую мощность на крюке, равную 72 кВт. С какой скоростью может
2.7.46 Трактор массой 10 т и мощностью 150 кВт поднимается в гору со скоростью 5 м/с
2.7.47 Ядро массой 8 кг, выпущенное метателем под углом 45 градусов к горизонту с высоты
2.7.48 Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна
2.7.49 Конькобежец движется по горизонтальному пути равномерно, а затем с разгона проезжает
2.7.50 Для растяжения недеформированной пружины на 1 см требуется сила, равная 30 Н
2.7.51 Шайба массы 0,1 кг, пущенная по льду с начальной скоростью 0,5 м/с, остановилась
2.7.52 На тело массы 5 кг действует постоянная сила 10 Н. Чему будет равна кинетическая
2.7.53 Какой кинетической энергией обладает свободно падающее тело массой 0,1 кг
2.7.54 Чему равна кинетическая энергия тела массы 0,2 кг, брошенного вертикально вверх
2.7.55 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.7.56 Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную
2.7.57 Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения
Законы сохранения энергии и импульса
2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с
2.8.2 Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули
2.8.3 Снаряд массой 20 кг, летевший горизонтально, попадает в платформу с песком массой
2.8.4 Тело находится на краю горизонтальной плоскости. Затем этот край плоскости
2.8.5 Какую скорость приобретает ракета массой 2 кг, если продукты горения массой
2.8.6 Тело массой 2 кг падает с высоты 10 м и углубляется в песок на глубину 0,5 м
2.8.7 Брусок массой 1 кг первоначально покоился на вершине наклонной плоскости
2.8.8 Велосипедист движется со скоростью 8 м/с. Определить расстояние, пройденное
2.8.9 Мальчик, стреляя из рогатки, натянул резиновый шнур так, что шнур растянулся
2.8.10 Винтовка массой 2,8 кг подвешена горизонтально на двух параллельных нитях
2.8.11 Во сколько раз изменится потенциальная энергия пружины при увеличении
2.8.12 Два шарика движутся навстречу друг другу со скоростями 1 и 0,5 м/с. После удара
2.8.13 Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия
2.8.14 Маленький шарик массой m, закрепленный на нерастяжимой нити в поле силы
2.8.15 Мальчик раскачивается на качелях. При максимальном отклонении от положения
2.8.16 Оконная штора массой 1 кг и длиной 2 м навертывается на валик, расположенный
2.8.17 Под каким углом к горизонту нужно бросить камень, чтобы в верхней точке траектории
2.8.18 При выстреле из орудия снаряд получил начальную скорость 300 м/с и летит
2.8.19 Телеграфный столб длиной 7 м и массой 140 кг при установке перемещается
2.8.20 Укажите график зависимости кинетической энергии свободно падающего тела
2.8.21 Чему равна работа по подъему лежащей цепи массой 50 кг и длиной 2 м, если
2.8.22 Подъемный кран поднимает груз массой 8 т на высоту 15 м. Определить время
2.8.23 Мяч бросили под углом к горизонту со скоростью 20 м/с. Найти скорость мяча
2.8.24 Какую минимальную работу необходимо совершить, чтобы лежащий на столе груз
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной
2.8.26 Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий
2.8.27 Для откачки воды из шахты глубиной 20 м поставлен насос с двигателем мощностью
2.8.28 Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг
2.8.29 Камень бросили под углом 60 градусов к горизонту со скоростью 15 м/с. Найдите
2.8.30 На нити длиной 1 м подвешено тело массой 1 кг. На какой максимальный угол
2.8.31 Пуля, летящая горизонтально со скоростью 400 м/с, попадает в ящик, лежащий
2.8.32 С какой начальной скоростью v0 нужно бросить вниз мяч с высоты h, чтобы он
2.8.33 Шарик массой m, подвешенный на нити, отклонен от положения равновесия на угол
2.8.34 Шарик подбросили вверх, сообщив ему кинетическую энергию 20 Дж. Через
2.8.35 Мяч падает с высоты 7,5 м на гладкий пол. Какую скорость нужно сообщить мячу
2.8.36 Тело, брошенное с вышки высотой 10 м, упало на землю со скоростью 15 м/с
2.8.37 Мяч скатился с горы высотой 20 м и после короткого горизонтального участка упал
2.8.38 Пуля массой 9 г, летевшая вертикально вверх со скоростью 200 м/с, пробила
2.8.39 Горизонтально летящая пуля массой 10 г насквозь пробивает первоначально
2.8.40 На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка
2.8.41 Определите время подъема камня массой 1 кг, брошенного под углом к горизонту
2.8.42 Пуля массой 10 г подлетает к доске массой 1 кг со скоростью 600 м/с и, пробив ее
2.8.43 Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную
2.8.44 В школьном опыте с “мертвой петлей” шарик массой 0,1 кг отпущен с высоты h=3R
2.8.45 Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси
2.8.46 Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой
2.8.47 Небольшое тело скользит с вершины полусферы вниз. На какой высоте h от вершины
2.8.48 Небольшое тело соскальзывает вниз по наклонному скату, переходящему в мертвую
2.8.49 Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую
2.8.50 Плавательный бассейн площадью 100 м2 заполнен водой до глубины 2 м. Требуется
2.8.51 Подвешенному на нити длиной 1 м шарику сообщили начальную скорость такую
2.8.52 При ударе шарика об идеально гладкую горизонтальную поверхность теряется третья
2.8.53 Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной
Абсолютно упругий удар
2.9.1 Тело массой 1 кг упруго ударяется о покоящееся тело массой 3 кг и летит обратно
2.9.2 Шарик массой 100 г упал с высоты 2,5 м на горизонтальную плиту, масса которой
2.9.3 Во сколько раз уменьшится энергия нейтрона n при столкновении с ядром углерода C
2.9.4 Гранату бросают от поверхности земли под углом 30 градусов к горизонту
2.9.5 Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом
2.9.6 Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с
2.9.7 На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой
Абсолютно неупругий удар
2.10.1 По абсолютно гладкой поверхности движется со скоростью 6 м/с ящик с песком
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.3 Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
2.10.6 Два шара массами 0,3 и 0,2 кг движутся навстречу друг другу. Скорость первого шара
2.10.7 Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость
2.10.8 Груз массой 0,5 кг падает с некоторой высоты на плиту массой 1 кг, укрепленную
2.10.9 Масса пушки 800 кг. Пушка выстреливает ядро массой 10 кг с начальной скоростью
2.10.10 На вагонетку массой 800 кг, катящуюся по горизонтальным рельсам со скоростью
2.10.11 На тележку с песком массой 49 кг, движущуюся по прямой со скоростью 1 м/с, падает
2.10.12 Пушка, стоящая на горизонтальной поверхности, стреляет под углом 30 градусов
2.10.13 Свинцовый шар массой 500 г, движущийся со скоростью 10 м/с, соударяется
2.10.14 Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит
2.10.15 Тележка движется по горизонтальной поверхности со скоростью 0,5 м/с. Её догоняет
2.10.16 Конькобежец, стоя на льду, бросил вперед гирю массой 5 кг и вследствие отдачи
2.10.17 Два мальчика играют в мяч, стоя на льду на расстоянии 10 м друг от друга
2.10.18 Вагон массой 50 т движется со скоростью 12 км/ч и встречает стоящую на пути
2.10.19 Конькобежец, стоя на льду, бросает горизонтально с высоты 1,5 м груз массой 10 кг
2.10.20 Кусок пластилина массой m=32 г попадает в брусок массой 6m, двигавшийся
2.10.21 На горизонтальном столе лежит деревянный брусок массой 5 кг. В брусок попадает
2.10.22 По горизонтальной поверхности стола скользит брусок массой m и сталкивается
2.10.23 Пуля массой 10 г застревает в первоначально покоящемся бруске, масса которого 0,1 кг
2.10.24 Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с
2.10.25 В покоящийся шар массой 1 кг, подвешенный на стержне, попадает пуля массой
2.10.26 Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового
2.10.27 Два груза массами 0,04 и 0,01 кг соединены невесомой нитью, переброшенной
2.10.28 В шар массой 1,5 кг, подвешенный на нерастяжимой нити длиной 55 см, попадает
2.10.29 Какая доля кинетической энергии перейдет в теплоту при неупругом столкновении
2.10.30 Тележка стоит на гладких рельсах. Человек переходит с одного её конца на другой
2.10.31 Человек массой 80 кг захотел спуститься по веревочной лестнице из свободно
2.10.32 Два шарика массами 2 и 3 г движутся в горизонтальной плоскости со скоростями
2.10.33 Космический корабль на скорости 10 км/с попадает в неподвижное облако
2.10.34 На горизонтальной плоскости сделан выстрел из винтовки, ствол которой направлен
2.10.35 С незакрепленной горки (клина) массой 1 кг соскальзывает тело массой 500 г. Угол
2.10.36 Снаряд, выпущенный из пушки под углом 45 градусов к горизонту, разрывается
2.10.37 Человек, сидящий в лодке, бросает камень под углом 60 градусов к горизонту. Масса
Тема 6.
Механика (установление соответствия)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
механика (установление соответствия)
6.01Кинематика
6.02Динамика
6.03Законы сохранения в механике
6.04Статика
6.05Гидростатика
6.06Механические колебания и волны
Решаем задачи
Показать ответ и решение
А) Линейная скорость равна:
Б)
На шайбу действует сила трения и сила упругости пружины. Сила трения равна:
где
– сила реакции опоры.
Длина нерастянутой пружины равна , тогда сила упругости пружины равна:
При
этом и сила упругости и сила трения направлены в центр траектории, так как сила упругости пытается
вернуть пружины в нерастянутое положение, а сила трения препятствует вылету шайбы с поверхности
диска, следовательно, равнодействующая сила равна:
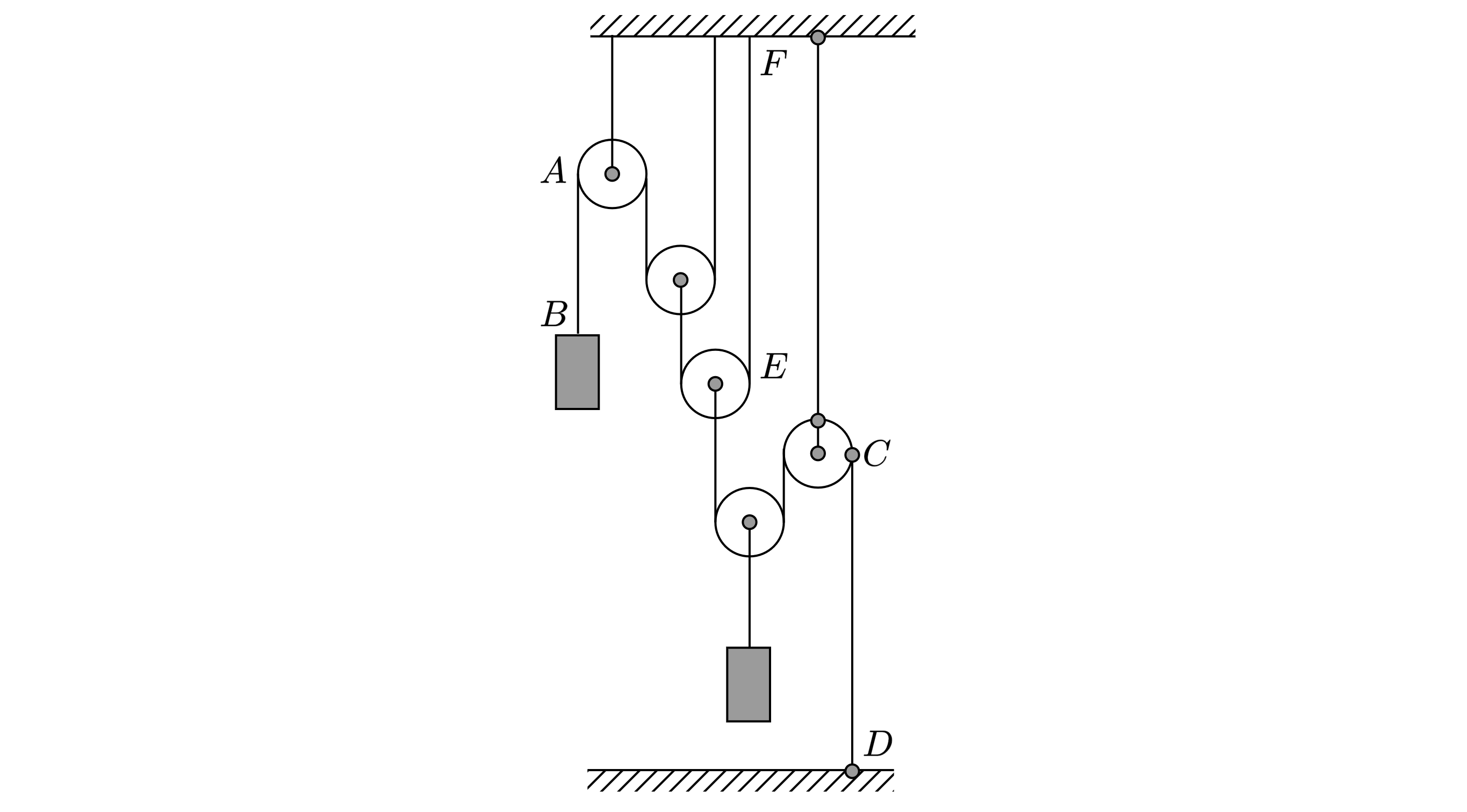
С помощью системы невесомых блоков на невесомых и нерастяжимых нитях уравновешены два груза
(см. рисунок). Модуль силы натяжения участка нити AB равен T. Установите соответствие между
модулями сил натяжения и участками нитей.
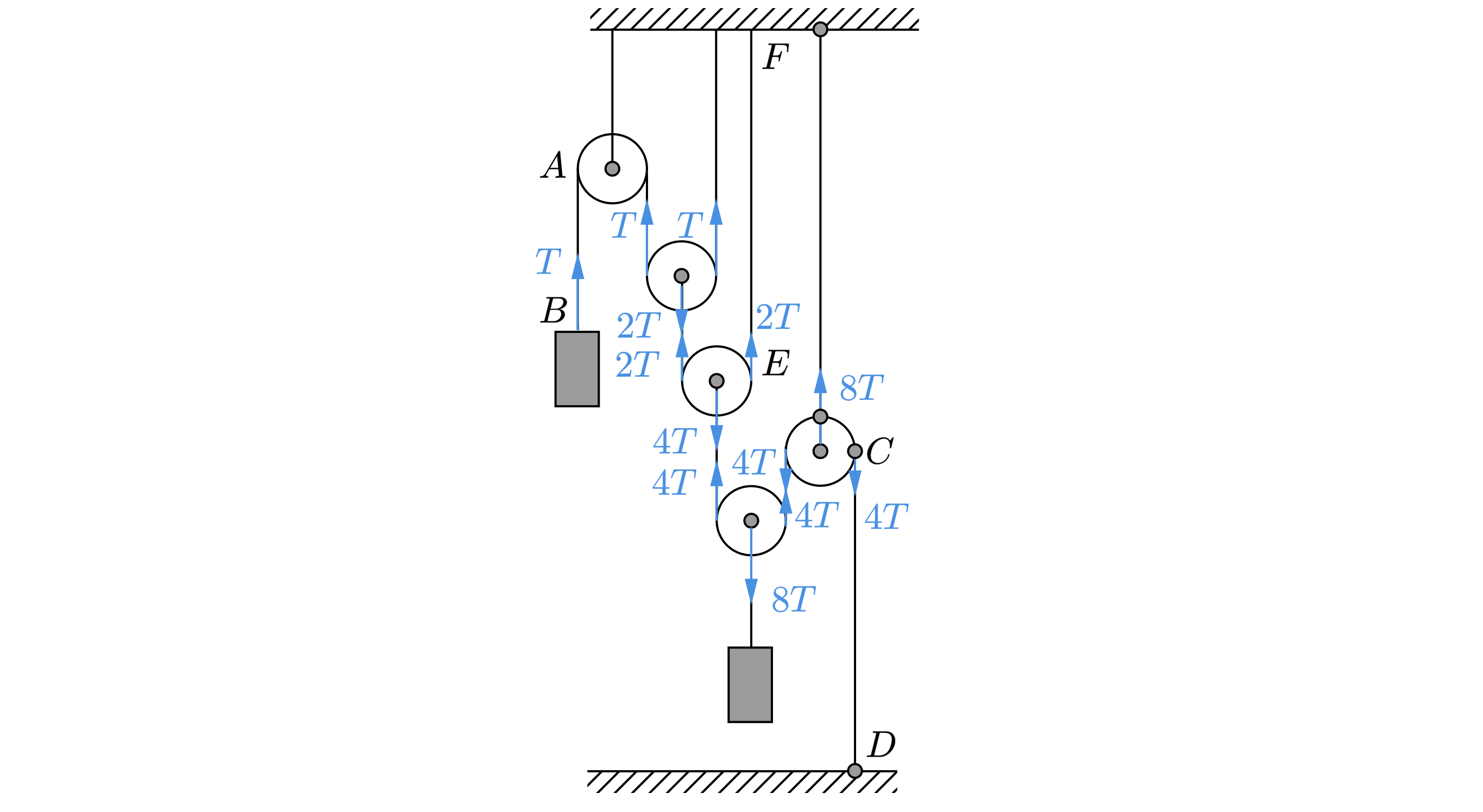
Показать ответ и решение
Так как блоки невесомы, то сумма сил действующих на каждый блок должна быть равна нулю,
тогда
Для участка –
, а для участка
–
.
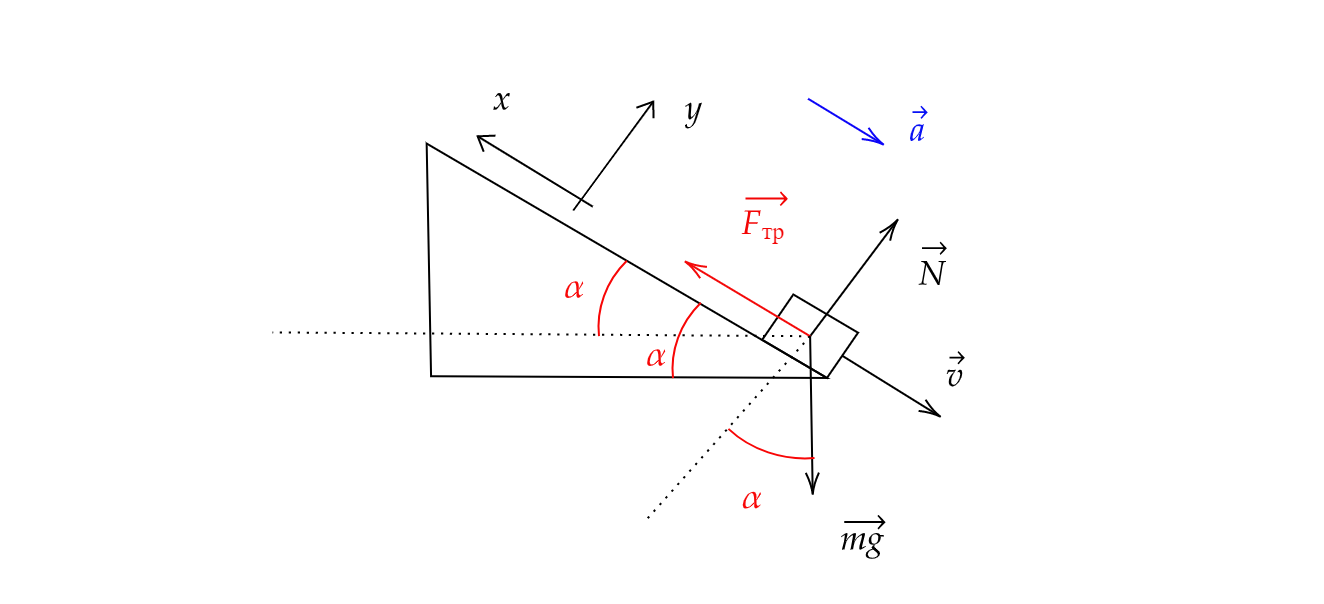
Брусок массой соскальзывает с закреплённой шероховатой поверхности наклонной плоскости с
углом при основании. Коэффициент трения между бруском и наклонной плоскостью равен
,
модуль скорости бруска возрастает. Сопротивлением воздуха пренебречь.
Установите соответствие между физическими величинами и формулами, при помощи
которых их можно вычислить. К каждой позиции первого столбца подберите соответствующую
позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими
буквами.
Показать ответ и решение
Запишем второй закон Ньютона
Спроецируем его на оси и
:
Так
как тело движется, то сила трения равна максимально возможной и равняется
А —
4
Из уравнения на ось найдем ускорение:
Б —
2
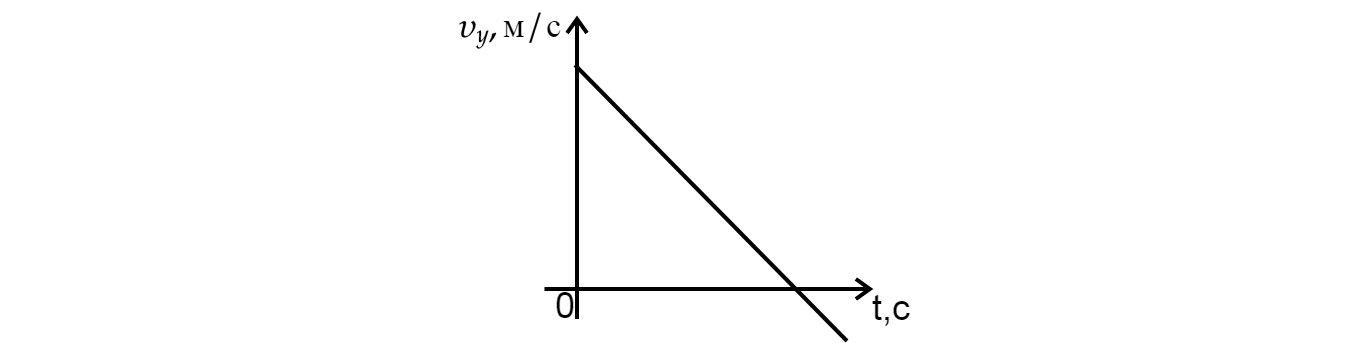
Мальчик кинул мячик так, что координата мячика по оси с течением времени
менялась по
закону: (все величины выражены в СИ).
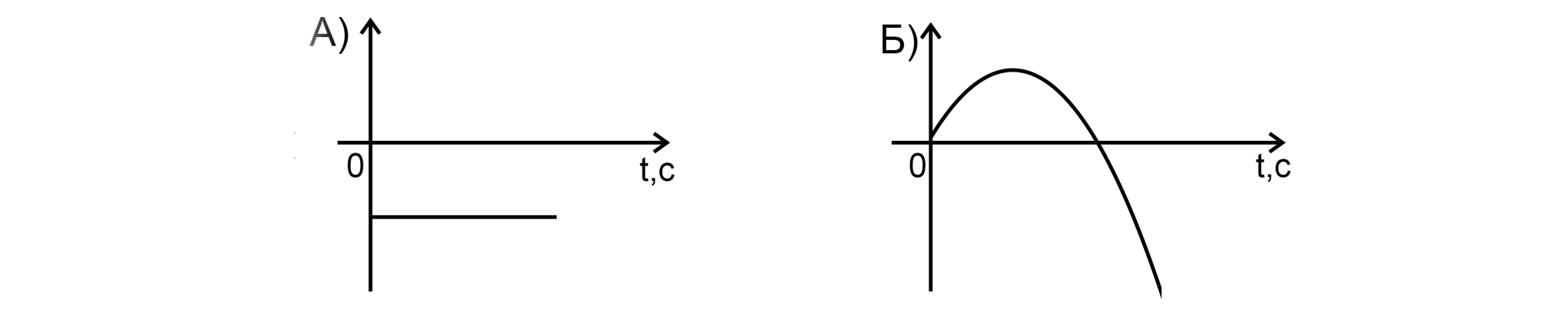
Установите соответствие между графиками зависимости и величинами, зависимости которых от
времени они могут изображать. К каждой позиции первого столбца подберите соответствующую
позицию из второго. В ответ укажите последовательность цифр.
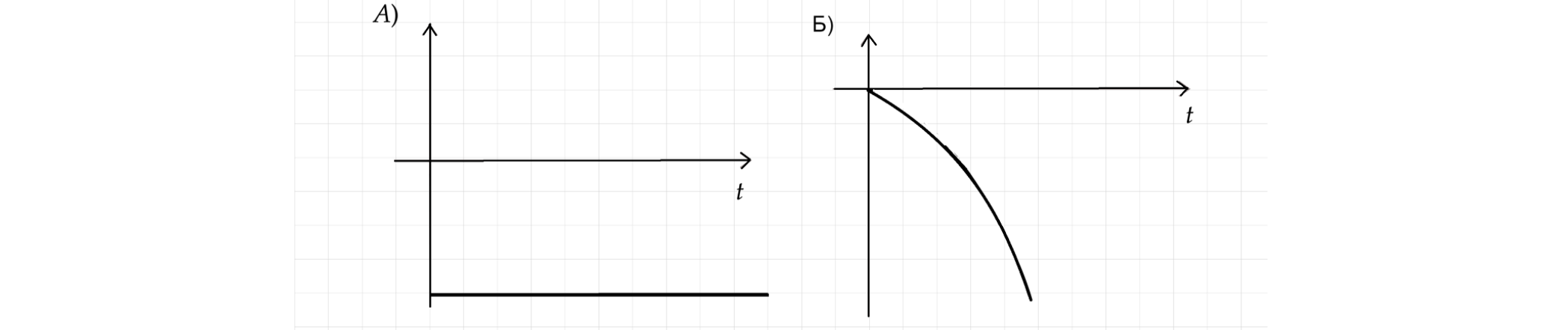
ГРАФИКИ:
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ:
1) Проекция перемещения тела,
2) Модуль равнодействующей всех сил,
3) Проекция ускорения,
4) Проекция скорости тела,
Показать ответ и решение
1) Основное уравнение кинематики
где
— начальная координата,
— проекция скорости на
,
— проекция ускорения на
.
2) Перемещение тела можно найти как разность начальной и конечной координат мячика:
Так
как это квадратное уравнение относительно переменной t, то его график — парабола, у которой ветви
вниз, ведь перед стоит минус. При чём в момент времени
координата по оси
равна нулю.
Это соответствует графику Б Б — 1.
3) Из уравнения видно, что проекция ускорения
график её зависимости от
времени — прямая, проходящая ниже нуля и параллельная
. Этому соответствует график А
А — 3.
4) Модуль равнодействующих всех сил равен:
Значит, график зависимости равнодействующей от времени
будет выглядеть так:
5) Так как скорость — это производная координаты по времени, то:
Значит, график зависимости проекции скорости на от времени будет выглядеть так:
Автомобиль движется вдоль оси , при этом его координата изменяется с течением времени в
соответствии с формулой (все величины выражены в СИ).
Установите соответствие между графиками и физическими величинами, зависимости которых от
времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите
в таблицу выбранные цифры под соответствующими буквами.
1)
проекция скорости автомобиля
2) проекция перемещения автомобиля
3) проекция ускорения автомобиля
4) модуль равнодействующей сил, действующих на автомобиль.
Тело массой 200 г движется вдоль оси , при этом его координата изменяется во времени в
соответствии с формулой (все величины выражены в СИ). Установите соответствие
между физическими величинами и формулами, выражающими их изменения во времени. К каждой
позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу
выбранные цифры под соответствующими буквами.
Демоверсия 2021
Показать ответ и решение
А) Скорость – это первая производная от координаты:
Б)
Ускорение это производная от скорости
Сила
по определению равна
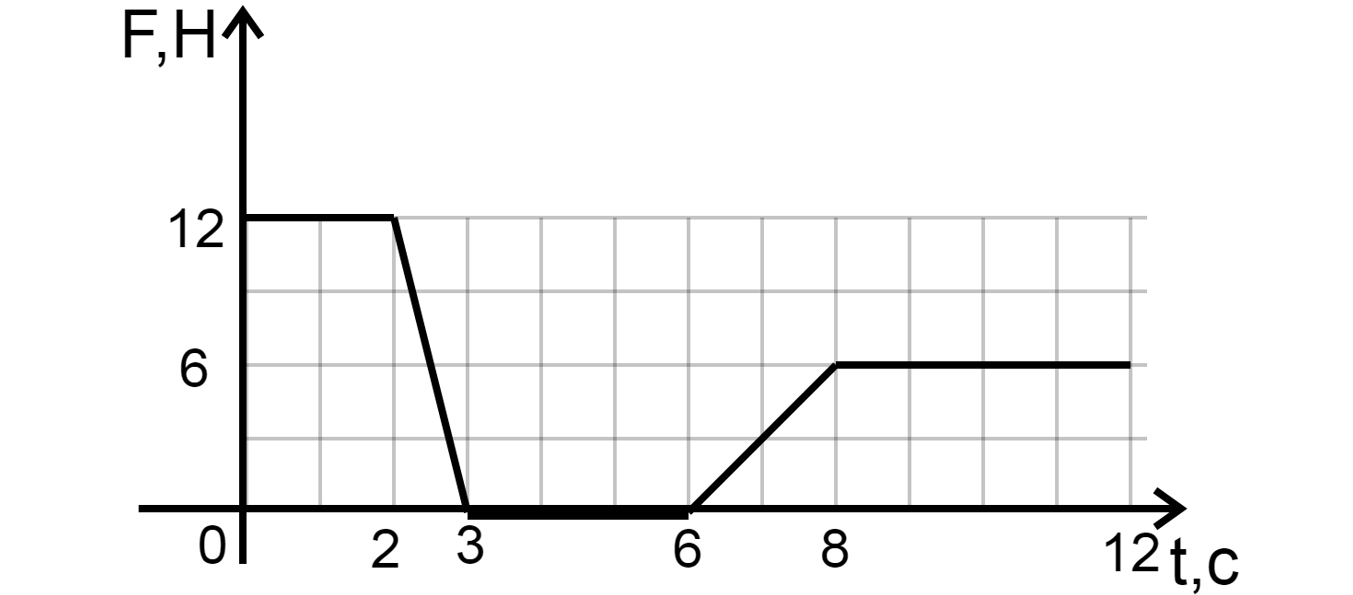
Тело массой кг движется под действием некоторых сил На рисунке приведён график
зависимости результирующей всех сил от времени
. Определите по графику ускорение тела в
период времени от 0 с до 2 с и от 3 с до 6 с.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца. В ответ
укажите последовательность цифр.
Показать ответ и решение
По второму закону Ньютона результирующая всех сил F равна:
Запишем это уравнение для первого и второго случаев соответственно:
Посчитаем нужные нам ускорения:
Спутник вращается вокруг Земли на расстояние . Масса спутника –
, а масса Земли –
,
–
гравитационная постоянная. Чему равны потенциальная энегия спутника и его скорость
?
К каждой позиции первого столбца подберите соответствующую позицию из второго. В ответ
укажите последовательность цифр.
Показать ответ и решение
1) Потенциальная энергия спутника массой , летающего на расстояние
от планеты определяется
формулой:
А — 1
2) На спутник действует сила гравитации. По второму закону Ньютона:
где — ускорение спутника, при чём так как он движется по окружности, то:
Б — 2
Грузик подвесили к лёгкой пружинке, прикреплённой к потолку. Система находится в равновесии. На
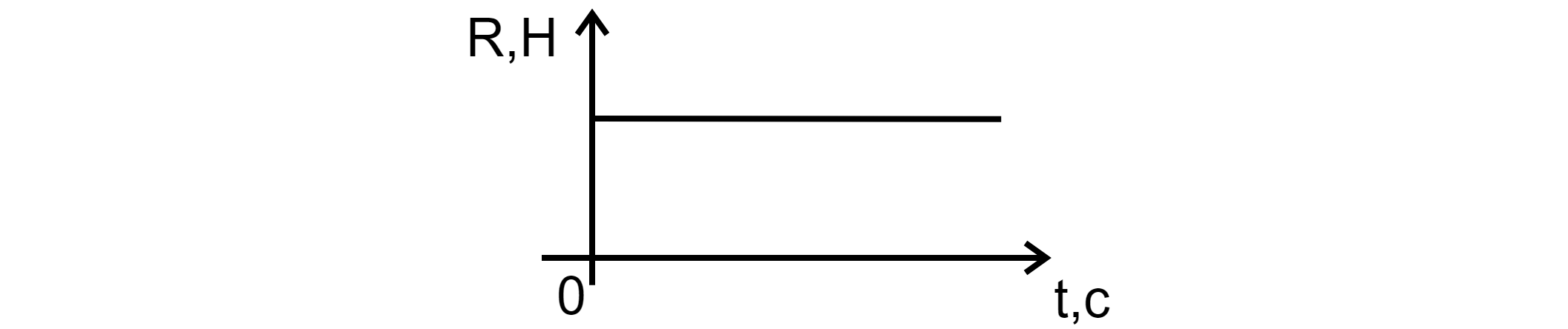
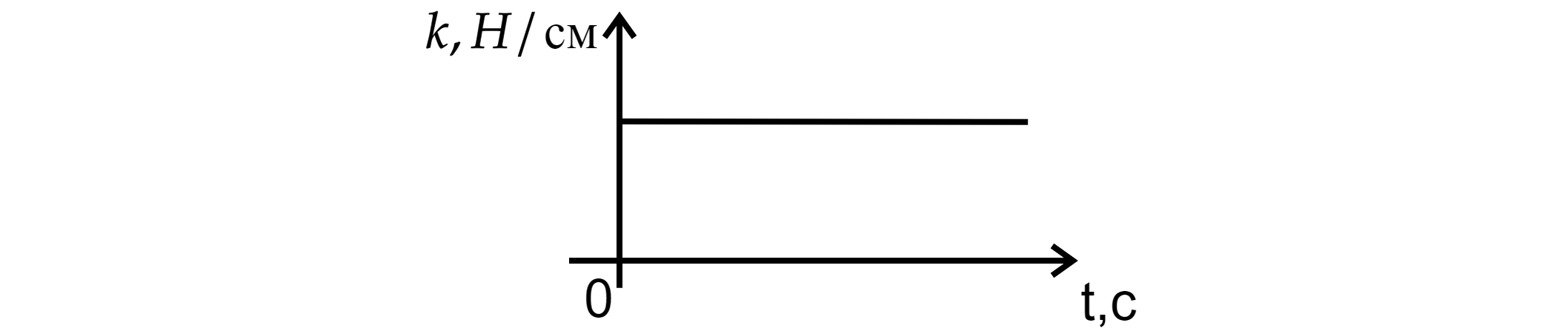
рисунках изображены графики зависимости некоторых физических величин от других величин.
Определите, какие зависимости могут изображать эти графики?
К каждой позиции из первого столбца подберите соответствующую позицию из второго. В ответ
укажите последовательность цифр
ГРАФИКИ:
ЗАВИСИМОСТИ:
1) Растяжение пружинки от жёсткости,
2) Жёсткость пружинки от времени,
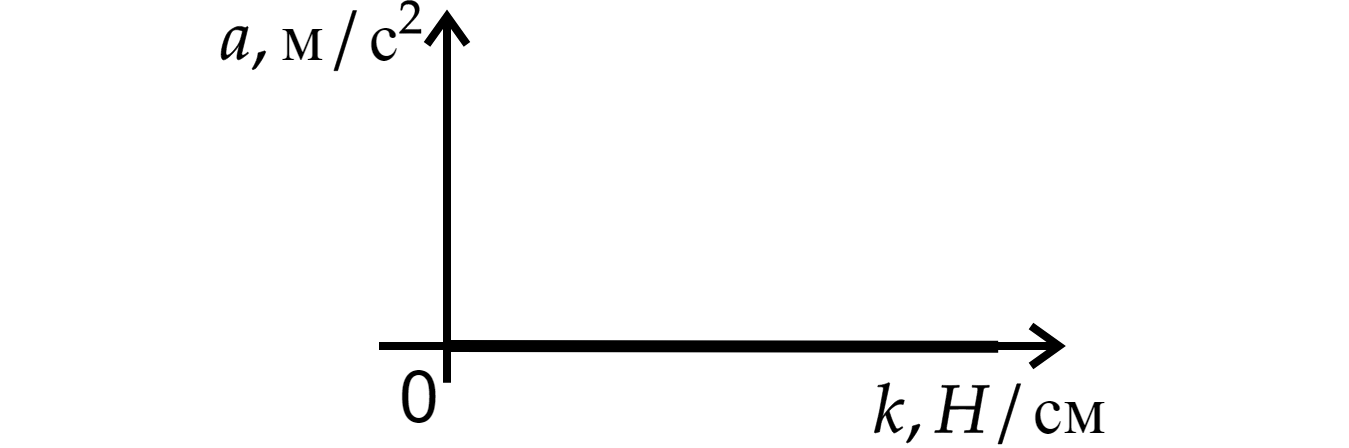
3) Ускорение тела от жёсткости пружинки,
4) Сила упругости от растяжения пружинки,
Показать ответ и решение
1) По закону Гука сила уругости равна:
Значит, график зависимоти – гипербола, что соответсвует графику Б
Б –
1
2) Время никак не влияет на жёсткость пружины (это видно из закона Гука, п.1), следовательно,
график зависимости – прямая, параллельная оси Ох.
3) Так как система в равновесии, то ускорения у грузика нет, при любых значениях жёсткости
ускорение .
4) По закону Гука сила упругости равна:
Значит, сила F зависит от растяжения линейно, что соответствует графику А
А —
4.
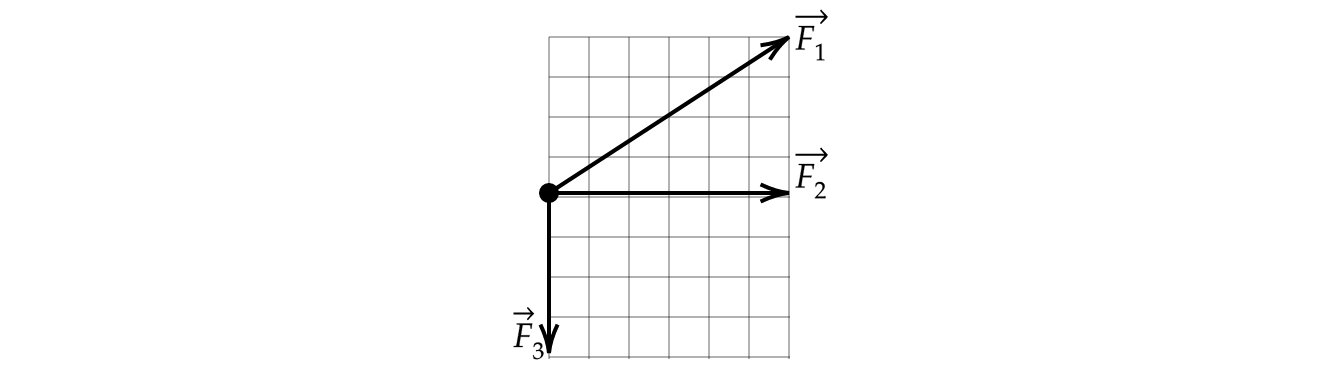
На рисунке изображены векторы, которые приложены к одному точечному телу. Сторона клетки равна
1 Н. Найдите равнодействующую всех сил и ускорение тела
, если его масса
кг. (все силы
находятся в одной плоскости)
Каждой позиции первого столбца подберите соответствующую позицию из второго столбцa, в ответ
укажите последовательность цифр.
Показать ответ и решение
А – 1
Равнодействующая всех сил равна векторной сумме всех сил. Найдём равнодействующую сил
и
:
Теперь найдём равнодействующую сил
и
:
По рисунку видно, что H.
Б – 3
По второму закону Ньютона:
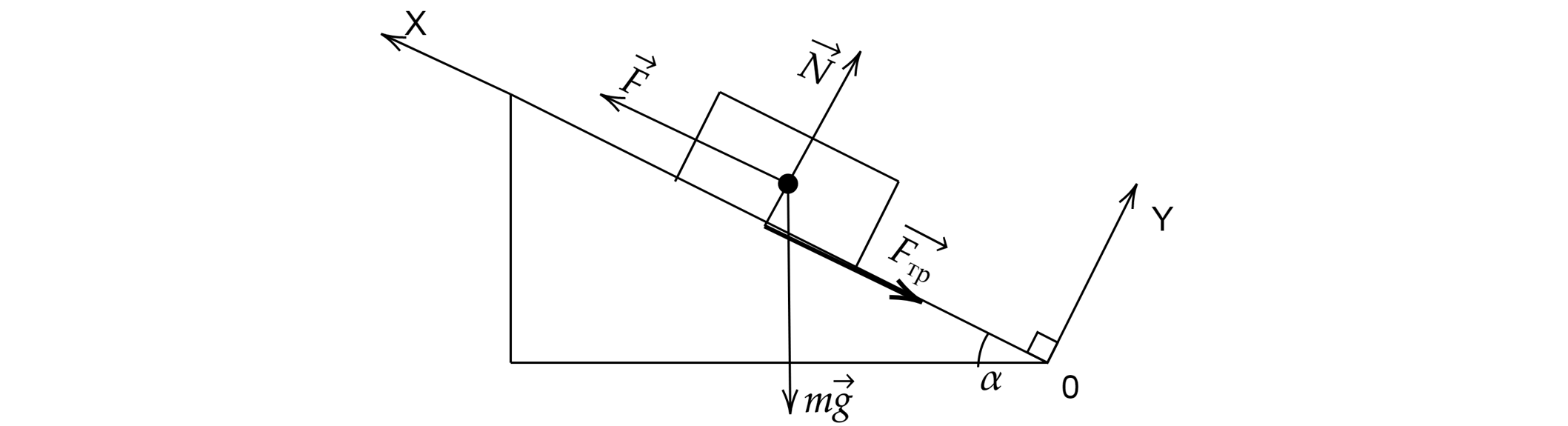
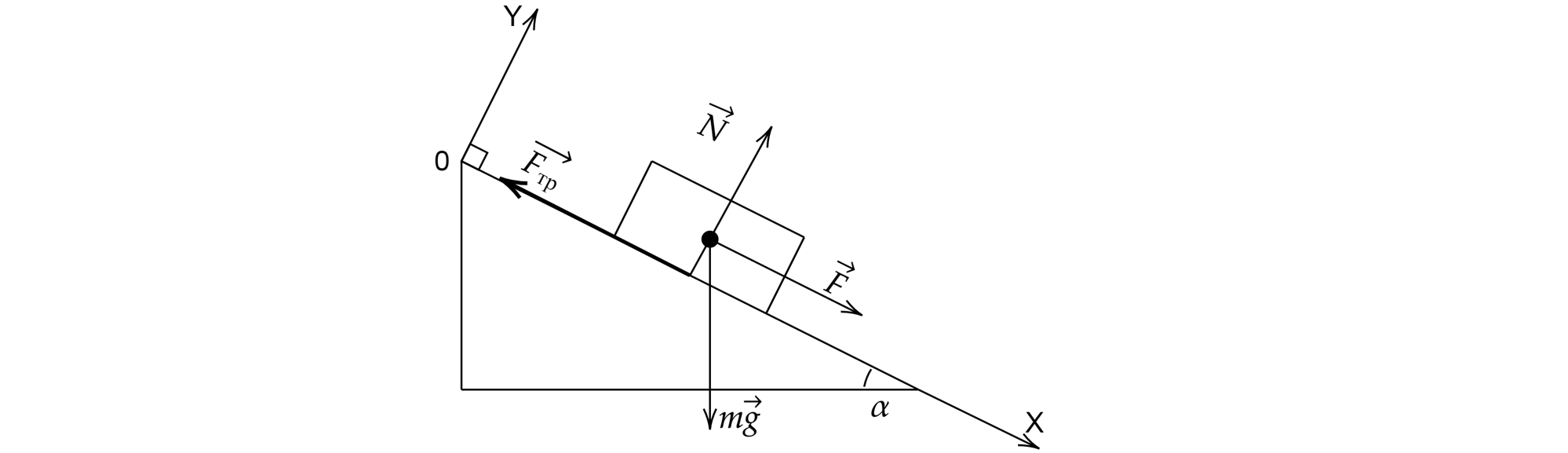
Мальчик тянет равномерно санки массой сначала вниз по горке, а потом – вверх с постоянной силой.
Угол наклона плоскости к горизонту . Коэффициент трения горки о санки равен
.
Определите, по каким формулам можно найти силу , с которой тянет мальчик вверх и
вниз?
Каждой позиции первого столбца подберите соответствующую позицию из второго столбца, в ответ
укажите последовательность цифр.
Показать ответ и решение
А – 1
Рассмотрим силы, действующие на санки:
По второму закону Ньютона:
Спроецируем на оси и
:
По определению сила трения равна:
Отсюда:
Б – 3
Рассмотрим силы, действующие на санки:
По второму закону Ньютона:
Спроецируем на оси и
:
По определению сила трения равна:
Отсюда:
1. После спуска с сортировочной горки железнодорожная платформа массой 9000 кг имела скорость 2 м/с и двигалась до полной остановки в течение 10с. Какова равнодействующая всех сил, действовавших на платформу?
Решение:
2. Лыжник массой 80 кг в конце спуска с горы приобрёл скорость 12 м /с и продолжал двигаться по горизонтальной поверхности. Через сколько времени он остановится, если сила трения, действующая на него, равна 16 Н ?
Решение:
3. Брусок массой m тянут по полу с постоянной скоростью, действуя на него силой F, направленной под углом α к направлению движения. Ускорение свободного падения g. Чему равна вертикальная составляющая силы Fy с которой пол действует на брусок?
Решение:
Ответ:
4. Тело поднимают вверх по наклонной плоскости, прикладывая к нему горизонтальную силу, величина которой вдвое больше действующей на тело силы тяжести. Высота наклонной плоскости 3 м, её длина 5 м. Найдите ускорение тела, если коэффициент трения равен 0,2
Запишем второй закон Ньютона в проекции на направление плоскости в направлении действия силы F.
ma = Fcosα − mgsinα − Fmp,
где
Fmp = μN = μmgcosα + Fsinα.
Тогда
ma = Fcosα − mgsinα − μ(mgcosα + Fsinα). (1)
Учтем, что по условию задачи F = 2mg, а sinα = h/l, а cosα = √(l2 − h2)/l, подставляя в уравнение (1) и сокращая на массу, получим
a = 2g√(l2 − h2)/l − gh/l − μ(g√(l2 − h2)/l + 2gh/l).
Рассчитаем ускорение
a = 2•10•√(52 − 32)/5 − 10•3/5 − 0,2•(10•√(52 − 32)/5 + 2•10•3/5) = 6 м/с2.
Ответ: a = 6 м/с2.
Замечания: при решении задач такого типа, возможно проще будет, если мы рассчитаем отдельно sinα = 3/5 = 0,6 и cosα = √(52 − 32)/5 = 0,8. Тогда уравнение второго закона будет проще
ma = 0,8F − 0,6mg − μ(0,8mg + 0,6F)
или
a = 16 − 6 − 0,2(8 + 12) = 6 м/с2.
5. Вверх по наклонной плоскости высотой 9 м и длиной 15 м пущена шайба. Коэффициент трения равен 0,5. Найдите ускорение шайбы. В ответе укажите абсолютную величину ускорения.
На рисунке шайба движется вверх по наклонной плоскости. Ускорение шайбе сообщают приложенные к ней силы: сила тяжести и сила взаимодействия шайбы с плоскостью, которую для удобства разложим на две составляющие: силу трения и реакцию опоры. Запишем уравнение второго закона Ньютона в проекции на оси x и y:
ma = mgsinα + Fmp и 0 = N – mgcosα
С учетом того, что сила трения скольжения равна
Fmp = μN = μmgcosα,
получим
a = gsinα + μgcosα.
Где sinα = h/l = 0,6, а cosα = √(1 – (h/l) 2) = 0,8.
Вычислим
a = 10•0,6 + 0,5•10•0,8 = 10 м/с2.
Ответ: a = 10 м/с2.
6.По наклонной плоскости скользит с ускорением a = 1 м/с2 брусок массой m = 200 г. С какой силой F нужно прижимать брусок перпендикулярно наклонной плоскости, чтобы он начал двигаться равномерно? Коэффициент трения бруска о наклонную плоскость μ = 0,1.
Запишем уравнение второго закона Ньютона в проекции на направление осей x и y при движении с ускорением a:
ma = mgsinα − Fmp и 0 = N − mgcosα.
С учетом того, что сила трения скольжения равна
Fmp = μN = μmgcosα,
получим
ma = mgsinα − μmgcosα. (1)
При равномерном движении, силы вдоль направления движения по наклонной плоскости, компенсируют друг друга
mgsinα = Fmp = μ(mgcosα + F);. (2)
Сделаем замену (2) в (1)
ma = μ(mgcosα + F) − μmgcosα.
Откуда ma = μF и F = maμ.
Вычислим F = 0,2•1•0,1 = 2 Н.
Ответ: F = 2 Н.
7.На столе лежит деревянный брусок массой М = 2 кг, к которому привязана нить, перекинутая через блок, укрепленный на краю стола. К свободному концу нити подвешен груз массой m = 1 кг, вследствие чего брусок движется с ускорением а = 0,6 м/с2. Каковы будут ускорения груза и бруска, а также натяжение нити, если вся система будет: а) подниматься с ускорением а = 2,2 м/с2; б) опускаться с тем же по модулю ускорением?
Решение.
Запишем уравнение второго закона Ньютона
mg − μMg = (m + M)a. (1)
а) Если переносное ускорение системы a1, относительное ao, то уравнение второго закона Ньютона для груза имеет вид:
T − mg = m(a1 − ao), (2)
для бруска:
T − μN = Mao, (3)
и
N − Mg = Ma1. (4)
Модуль полного ускорения груза
aг = a1 − ao, (5)
бруска
aб = √{ao2 + a12}. (6)
Из уравнений (1) − (6) находим:
aг ≈ 1,46 м/с2; aб ≈ 2,3 м/с2; Т = 11,2 H.
б) aг ≈ 2,66 м/с2; aб ≈ 2,24 м/с2; Т ≈ 7 H.
8. С помощью прочного троса груз равноускоренно поднимают с поверхности земли вертикально вверх. Через Δt = 5,0 с после начала подъема груз уже находился на высоте h = 15 м, продолжая движение. Сила тяги подъемного механизма к этому моменту времени, когда тело достигло высоты h = 15 м, совершила работу А = 8,4 кДж. Определите массу поднимаемого груза.
Решение.
На груз действует сила тяги и сила тяжести.
По второму закону Ньютона
ma = Fтяг + mg. (векторно)
В проекции на вертикальную ось
ma = Fтяг − mg.
Откуда сила тяги
Fтяг = ma + mg.
Работа силы тяги
A = Fтягh = m(a + g)h. (1)
Из кинематики определим ускорение
h = aΔt2/2, a = 2h/Δt2. (2)
Из (1) выражаем искомую массу груза и подставляем ускорение из (2)
m = A/((2h/Δt2 + g)h).
Подставим численные значения
m = 8400/((2•15/52 + 10) × 15) = 50 (кг).
Ответ: масса поднимаемого груза 50 кг.
9. Брусок массой m = 2,0 кг движется без начальной скорости по горизонтальной поверхности под действием силы, модуль которой F = 10 Н, направленной параллельно этой поверхности. Коэффициент трения между бруском и поверхностью μ = 0,20. Через какой промежуток времени Δt, модуль скорости у тела станет равным v = 30 м/с.
Решение:
По второму закону Ньютона, ускорение получаемое телом есть результат приложенных к нему сил (равнодействующей силы).
Результирующая сила равна разности приложенной силы F и силы трения. Сила тяжести и реакция опоры направлены перпендикулярно к направлению движения тела.
a = (F − Fmp)/m = (F − μmg)/m. (1)
Воспользуемся уравнением скорости v = vo + at, при vo = 0, v = at. Искомое время t = v/a. После подстановки (1) получим
t = mv/( F – μmg).
После подстановки численных значений, имеем
t = 2•30/(10 − 0,2•2,0•10) = 10 (c).
Ответ: t = 10 c.
10. С какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать сани массой m = 10 кг по горизонтальному асфальту, если коэффициент трения скольжения μ = 0,7?
Решение.
Запишем уравнения движения санок в проекциях на горизонтальное и вертикальное направления:
где α − угол между веревкой и горизонтом, а сила трения Fmp = μN.
Из написанной выше системы уравнений найдем силу натяжения веревки
Теперь проанализируем зависимость силы F от угла α. Санки будут двигаться равномерно, если горизонтальная составляющая силы реакции веревки Fcosα равна силе трения Fmp. Для обеспечения минимальности силы F веревку, казалось бы, надо тянуть горизонтально, так как в этом случае sinα = sin0° = 0. C другой стороны, желательно, чтобы угол α был побольше, так как в этом случае за счет увеличения вертикальной составляющей Fsinα, стремящейся приподнять санки, уменьшается их давление на опору и, соответственно, уменьшается сила трения. Таким образом, на результат влияют два конкурирующих фактора.
Представим зависимость F(α) в виде графика.
Из графика видно, что исследуемая функция имеет минимум. Для нахождения значений αmin и Fmin воспользуемся аналитическим методом. Функция F(α) минимальна, если знаменатель максимален. Обозначим его буквой y, найдем производную y по α и приравняем ее к нулю:
y/ = −sinα + μcosα = 0.
Отсюда, обозначив соответствующий угол αo, получим
tgαo = μ; αo = 35°.
Тогда
Используя соотношения
найдем искомую величину
11.На рисунке изображены три силы, которые подействовали на тело массой 1 кг, покоящееся в инерциальной системе отсчета. Если одна клеточка соответствует силе 10 Н, то тело тело будет двигаться … с модулем ускорением …
1) по направлению силы F2, 10 м/с2; 2) по направлению силы F3, 5 м/с2;
3) по направлению силы F1, 10 м/с2; 4) против направления силы F2, 10 м/с2;
5) тело будет покоится, 0 м/с2.
Решение.
Разложим вектора сил на направления осей x и y. Обратим внимание на то, что вдоль оси х, результирующая сил равна
Вдоль оси y результирующая сил равна
В результате действия трех сил тело будет двигаться по направлению оси x, т.е. по направлению силы F2, с ускорением равным
Выбираем правильным ответ 1) по направлению силы F2, 10 м/с2.
Обучающие задания ЕГЭ по физике на тему «Динамика», с ответами — теория и практика
- 30.09.2013
Специально подобранные задания с учётом специфики КИМов ЕГЭ. К каждому заданию прилагается поясняющий комментарий, который помогает понять и разобрать задание. С этим материалом вы сможете безупречно изучить раздел физики «Динамика» и хорошо сдать егэ.
Все задания в конце файла содержат ответы.
Дополнительный материал по теме «Динамика»:
- Теория
- Обучающие задания
- Практические задания
- Контрольная работа
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.