Исследовательская работа по математике по теме: “Диофантовы уравнения, типы и способы решения»
Международная научно-практическая конференция
«Первые шаги в науку»
Исследовательская работа по математике по теме:
“Диофантовы уравнения, типы и способы решения»
Предметная область: математика
Работу выполнила:Хомякова Ольга, ученица 10 класса
Учитель:, учитель математики
МБОУ средняя школа №4 с углубленным изучением отдельных предметов
2.Виды диофантовых уравнений и их классификация
3. Диофантовые уравнения в части С ЕГЭ-13
4. Практическое применение теории диофантовых ур-ний -16
В школьном курсе математики диофантовы уравнения практически не изучаются, но, например, в заданиях группы С6 в ЕГЭ встречаются уравнения 2-ой степени. Также с этими заданиями я сталкивалась в математических олимпиадах. Я заинтересовалась этой темой для того, чтобы успешно сдать Единый Государственный Экзамен и принимать участие в олимпиадах и конкурсах. Помимо этого, меня заинтересовала практическая направленность области этой темы.
Предметная областью моего исследования является математика.
Объект работы — диофантовы уравнения, типы и способы их решения.
1. Повысить уровень математической культуры ;
2. Развить в себе навыки исследовательской деятельности в области математики;
3. Научиться самой и научить других решать диофантовы уравнения эффективными методами;
4. Применять эти методы решения к задачам из повседневной жизни человека, а также к задачам, предлагаемым на вступительных экзаменах в ВУЗы и в олимпиадных заданиях;
5. Классифицировать методы решений дифференциальных уравнений;
6. Составить сборник задач с решениями в помощь ученикам нашей школы.
1. изучить исторические корни ;
2. научиться пользоваться научной литературой, строить графики в современных компьютерных программах, быстро и грамотно находить информацию в интернете;
3. исследовать методы решения задач, приводимых к уравнениям первой степени с двумя переменными, выбрав самые удобные и простые;
4. научиться решать задачи из повседневной жизни, вступительных экзаменов в ВУЗы экономического направления и олимпиадных заданий, применив изученные ранее методы;
5. разработать методическое пособие для всех интересующихся (подобрать или самим составить задачи с экономическим содержанием, приводящие к решению уравнений с двумя переменными).
Методы исследования : анализ, синтез, сравнение, противопоставление, ранжирование, прогнозирование, наблюдение.
Гипотеза: изучив типы, классифицировав диофантовы уравнения по способам решения можно успешно справиться с решением текстовых задач, задач с практическим содержанием и с частью заданий С6 ЕГЭ.
1. Изучение истории появления диофантовых уравнений, основной литературы по этой теме;
2. Изучение способов и методов решения диофантовых уравнений;
3. Попытка их классификации ;
4. Поиск практической значимости данной темы.
Основая часть.
1.Историческая справка.
Диофант( вероятно 3 в. н. э. – древнегреческий математик из Александрии)
Диофантовы уравнения – алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, у которых отыскиваются целые или рациональные решения.
Эти уравнения названы по имени Диофанта ( вероятно 3 в. н. э. – древнегреческий математик из Александрии), изучавшего такие уравнения.
Диофант представляет одну из наиболее трудных загадок в истории науки. Нам неизвестно ни время, когда он жил, ни предшественники, которые работали бы в той же области. Достаточно решить уравнение первой степени с одним неизвестным – и мы узнаем, что Диофант прожил 84 года.
Наиболее загадочным представляется творчество Диофанта. До нас дошло шесть из тринадцати книг, которые были объединены в “Арифметику”, стиль и содержание этих книг резко отличается от классических античных сочинений по теории чисел и алгебры, образцы которых мы знаем по “Началам” Евклида, его “Данным”, леммам из сочинений Архимеда и Аполлония. “Арифметика”, несомненно, явилась результатом многочисленных исследований, которые остались совершенно неизвестными. Число неизвестных диофантовых уравнениях превосходит число уравнений, и поэтому иногда их называют неопределенными.
Диофантовы уравнения впервые обстоятельно исследовались в книге Диофанта “Арифметика”. Такие уравнения имеют некоторые особенности:
1. Они сводятся к уравнениям или системам уравнений с целочисленными коэффициентами.
2. Требуется найти только целые, часто натуральные решения.
2. Определение, виды диофантовых уравнений и способы их решений.
Итак, диофантовым уравнением для целочисленных переменных х 1 , х 2 , …, х n называется уравнение, которое может быть приведено к виду
Где Р — некоторый многочлен от указанных переменных с целыми коэффициентами.
Простейшим диофантовым уравнением является уравнение вида ax + by = c , где a и b – целые взаимно простые числа. Такое диофантово уравнение имеет бесконечное число решений: если x 0 и y 0 – одно решение, то числа x = x 0 + bn и y = y 0 — an ( где n — любое целое число ) также будут решениями, которыми исчерпывается вся совокупность решений.
Виды диофантовых уравнений:
Итак, я предлагаю рассмотреть решение следующего уравнения:
Так как 8 и 9 взаимно простые числа, т. е. наибольший общий делитель 8 и 9 равен 1 то решение существует. Одно из решений найдем подбором:
x 0 =2, y 0 =3. Остальные решения вычисляются по формулам:

Если наибольший общий делитель d коэффициентов а и b больше 1, а свободный член с не делится на d , то уравнение ах + by = c не имеет решений в целых числах.
А теперь рассмотрим линейное диофантово уравнение, которое не имеет целых решений:
Для доказательства того, что это уравнение не имеет целых решений, необходимо вынести за скобки общий множитель 5, получим 5( x +7 y )=17 . Тогда левая часть уравнения делится на 5, а правая часть на 5 не делится. Значит, уравнение не имеет решений в целых числах.
Любое уравнение ах + by = с , где НОД(а, b ) = 1, имеет хотя бы одно решение в целых числах.
К диофантовому уравнению приводит и такая задача:
На покупку нескольких открыток по 11 рублей и конвертов по 13 рублей потратили всего 61 рубль. Сколько купили открыток?
Давайте обозначим число открыток через х, а число конвертов через y , то задача сводится к уравнению 11 x +13 y =61 . Очевидно, что по условию задачи здесь пригодны лишь целые положительные числа. Методом подбора найдем такие числа. Данное уравнение имеет только одно такое решение: x =2, y =3 .
Еще в Древнем Вавилоне родилась задача о построении прямоугольного треугольника с попарно соизмеримыми сторонами. Соизмеримость сторон означает, что найдется такой масштаб, в котором катеты и гипотенуза будут выражаться натуральными числами x и y , но тогда:
Таким образом, вавилонская задача сводится к задаче построения всех троек натуральных чисел x , y , z удовлетворяющих предыдущему уравнению. Пифагорейцы нашли способ построения всех его решений. Но, возможно, этот способ был найден еще раньше в Вавилоне и Индии. Так или иначе, решения ( x , y , z ) уравнения x ^2+ y ^2= z ^2 принято называть пифагоровыми тройками: x =2 n +1; y =2 n ( n +1) ; z =2 n ^2+2 n +1 , n принадлежит Z . Примеры пифагорейских троек: 3, 4, 5; 6, 8, 10; 5, 12, 13.
Однако эти формулы не дают возможности найти все пифагорейские тройки чисел, имеющие выбранное исходное число. Формулы Пифагора и Платона и их различные модификации дают только частные решения. Приведем еще примеры пифагорейских троек чисел, которые нельзя получить по указанным формулам: 72, 65, 97; 72, 320, 328.
Эти и другие пифагорейские тройки чисел дает вавилонская клинописная табличка, относимая к эпохе гг. до н. э. Метод вавилонян дает возможность найти все пифагорейские тройки, содержащие выбранные исходные числа.
Известный в теории диофантовых уравнений является проблема Ферма ( Пьер Ферма ( ) – французский математик). Эта проблема носит название великой теоремы Ферма.
Она была сформулирована Ферма примерно в 1630 году на полях книги Диофанта “Арифметика”. Общее доказательство получил английский математик Уайлс в 1995 году.
2уравнения второй степени:
Я предлагаю вам решить 4 уравнения:
Итак, попробуем найти решение для первого уравнения:
Так как число 11 имеет делители только 1 и 11, то возможны следующие сочетания сомножителей:
1. 



Тогда x= -11, y= 10
Ответ запишем в следующем виде: (1;10), (11;-10), (-1;-10), (-11;10).
Задачу №2 я предлагаю решить аналогичным способом, при помощи 4 систем.

Тогда х=2, у=1/3 (т. е. система не имеет решения в целых числах).



Тогда х=-2, у=-1/3 (т. е. система не имеет решения в целых числах).
Из этих пар чисел видно, что уравнение не имеет решений в целых числах.
Задачу № 3 тоже можно решить при помощи 4 систем. Решив системы, получим следующие пары чисел: ( 0;-1), (0;1), ( y =4/5), ( y = -4/5)
Последние две системы не имеют целых решений, следовательно, ответ: (0;-1),(0;1).
Последнее уравнение не похоже на 3 предыдущих.
Преобразуем заданное уравнение (вынесем за скобки y и вычтем и прибавим число 3):
В результате преобразований получаем уравнение:
Так как число 2 может быть представлено 4 способами в виде произведения целых чисел 2= (-2) * (-1); 2=( -1) * ( -2); 2=1 * 2; 2= 2*1, то возможны четыре системы. Из них получаем четыре пары чисел (1; -2), (2; -3), ( 4;1), (5;0). Ответом этого уравнения будут являться все 4 пары.
Запишем данное уравнение в виде (3 x – y ) * (3 x + y )=14 . Так как число 14 с учетом порядка следования множителей может быть представлено в виде произведения целых чисел следующим образом: 14=( -2) * (-7); 14=( -7) *(-2); 14=( -1) * ; 14= (-14) * (-1); 14= 2 * 7; 14= 7 * 2; 14= 1* 14; 14= 14* 1, то будет 8 случаев.
Решив все 8 систем, мы получаем дробные значения, а значит, что это уравнение не имеет решений в целых числах.
Разложим левую часть заданного уравнения на линейные множители: Уравнение примет вид: (3 x + 2 y )( x + y )=7
Так как 7 число простое, то оно равно произведению двух целых чисел в четырех случаях. Решив все 4 системы, получим пары чисел (-5;4), (5; -4), ( -13;20), ( 13;-20). Эти числа и будут ответом.
x^2 + y^2 – 2x + 4y=-5
В левой части уравнения выделим полный квадрат:
x^2 – 2x + 1 + y^2 + 4y + 4=0
Сумма квадратов равна 0 лишь в одном случае

Решив систему, получим, что x = 1, y = -2
x^2 – 6x + y^2 + 6y + 18=0
Докажем, что это уравнение имеет единственное целочисленное решение.
В левой части уравнения выделим полные квадраты :
( x – 3 )^2 + ( y + 3 )^2=0
Данное уравнение имеет решение, когда

Теперь я предлагаю рассмотреть графический метод решения диофантовых уравнений.
Алгоритм построения графика уравнения ах + by + с = 0:
1. Придать переменной х конкретное значение х= х1; найти из уравнения ах1 + by + c = 0 соответствующее значение y = y 1.
2. Придать переменной х другое значение х=х2; найти из уравнения ах2 + by + c = 0 соответствующее значение y = y 2.
3. Построить на координатной плоскости х Oy две точки (х1;у1) и (х2;у2).
4. Провести через эти две точки прямую – она и будет графиком уравнения ах + by + с = 0.
Так, например, уравнение 5 x + 7 y =17 можно решить графическим методом, изобразив прямую 5 x + 7 y = 17, и определив на этой прямой точки, обе координаты которых будут в данном случае натуральными числами.
Целые решения: (2 ;1),( 9;-4), ( 16;-9),(-5;6),(-12;11)
3. Диофантовы уравнения в заданиях С5 ЕГЭ.
Необходимо найти все пары (х, у) целых чисел, удовлетворяющих системе неравенств:

Рассмотрим на координатной плоскости области, которые описываются заданными неравенствами. А затем выберем в них лишь точки с целочисленными координатам х, у.
Получаем два случая:
1) Неравенство (1) путем выделения полных квадратов сводится к условию
Т. е. описывает внутренность круга с центром А(9; -10) и радиусом R 1=√15 .
2) Неравенство (2) сводится к виду
Т. е. описывает внутренность круга с центром В(16; -6) и радиусом R 2=√21 .
Единственной точкой, принадлежащей одновременно двум кругам, будет точка М( 12; -8). Это выясняется подстановкой в систему числовых значений координат всех узлов квадратной сетки, соседних с точкой М.
Найти наименьшее значение суммы тогда 

Пусть искомое значение 
Угловой коэффициент равен -1, 
Треугольник ABC прямоугольный. Чтобы найти c , достаточно найти ординату точки B . Для этого найдем координаты точек A и B . Зная, что точки лежат на прямой с точкой O (1;-2), т. е. на прямой 

A ( 


Согласно рисунку 
B ( 

Ответ:
4.Практическое применение теории диофантовых уравнений.
Неожиданно, лет 20-30 назад, было осознано, что эту чисто абстрактную теорию можно использовать для построения алгоритмов, которые нужны для криптографии, чтобы зашифровывать и безопасно передавать секретные сообщения, а также снимать и класть деньги в банкоматах и т. п. Теория эта оказалась востребована на практике. Яркий пример: в девяностые годы, когда математикам есть было нечего, многие уехали за границу, но многие и остались здесь, и некоторые математики из провинциальных институтов успешно сотрудничали с банками. Банкиры обратились к ним с просьбой помочь в переводе денег из дальних регионов в Москву. В России есть целая Академия криптографии и научно-исследовательские организации, которые используют такие разработки.
Знаменитый мост Золотые Ворота был построен с применением диофантовых уравнений.
Мост Золотые Ворота
Заключение.
В процессе исследования типов диофантовых уравнений мне удалось их классифицировать по способам решения, выработать алгоритм решения некоторых распространенных видов этих уравнений, научиться решать текстовые задачи, успешно справляться с заданиями части С ЕГЭ, о чем свидетельствует диплом 2 степени на всероссийской дистанционной олимпиаде по математике на сайте «Инфоурок. Ру.»
Данная исследовательская работа дала мне возможность совершенствовать навыки работы с научно-популярной литературой и освоить программы графопостроители.
Говоря о практическом использовании полученных результатов нельзя не вспомнить слова Алексея Николаевича Крылова: «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».
Решение диофантовых уравнений для С7(19)
1 Постановка задачи, или что такое диофантово уравнение
В задаче на свойства чисел С7(19) довольно часто возникает необходимость решить диофантово уравнение:
Здесь целые коэффициенты $A$ и $B$ должны быть взаимно простыми числами, то есть, иметь наибольший общий делитель, равный 1. Решение мы ищем в целых числах.
2 Рассмотрим частный пример
Например, требуется решить уравнение
Приведем один из способов решения. Их несколько, но мы приводим самый простой.
1 Найдем частное решение, то есть, подберем любые целые $x_0$ и $y_0$ , удовлетворяющие этому уравнению. Находим, например:
2 Общее решение теперь дается формулами
3 Решение в общем виде
запишем общее решение
Потренируйтесь в решении диофантовых уравнений. Уравнения для тренировки вы можете написать сами, не забывая, что коэффициенты должны быть взаимно простыми.
Линейное диофантово уравнение и 4 способа его решения
Разделы: Математика
Првило 1. Если с не делится на d, то уравнение ах + ву = с не имеет решений в целых числах. Н.О.Д.(а,в) = d.
Правило 2. Чтобы найти решение уравнения ах + ву = с при взаимно-простых а и в, нужно сначала найти решение (Хо ; уо) уравнения ах + ву = 1; числа СХо , Суо составляют решение уравнения ах + ву = с.
Решить в целых числах (х,у) уравнение
Первый способ. Нахождение частного решения методом подбора и запись общего решения.
Знаем, что если Н.О.Д.(а;в) =1, т.е. а и в взаимно-простые числа, то уравнение (1)
имеет решение в целых числах х и у. Н.О.Д.(5;8) =1. Методом подбора находим частное решение: Хо = 7; уо =2.
Итак, пара чисел (7;2) — частное решение уравнения (1).
Значит, выполняется равенство: 5 x 7 – 8 x 2 = 19 … (2)
Вопрос: Как имея одно решение записать все остальные решения?
Вычтем из уравнения (1) равенство (2) и получим: 5(х -7) – 8(у — 2) =0.
Отсюда х – 7 = 

Тем самым все целые решения исходного уравнения можно записать в таком виде:


Второй способ. Решение уравнения относительно одного неизвестного.
Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х — 8у = 19 


Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.
Если у = 0, то х = 

Если у =1, то х = 

Если у = 2, то х = 


Если у =3, то х = 

Если у = 4 то х = 

Итак, частным решением является пара (7;2).
Тогда общее решение: 

Третий способ. Универсальный способ поиска частного решения.
Для решения применим алгоритм Евклида. Мы знаем, что для любых двух натуральных чисел а, в, таких, что Н.О.Д.(а,в) = 1 существуют целые числа х,у такие, что ах + ву = 1.
1. Сначала решим уравнение 5m – 8n = 1 используя алгоритм Евклида.
2. Затем найдем частное решение уравнения (1)по правилу 2.
3. Запишем общее решение данного уравнения (1).
1. Найдем представление: 1 = 5m – 8n. Для этого используем алгоритм Евклида.
8 = 5 
5 = 3
3 = 2 
Из этого равенства выразим 1. 1 = 3 — 2 


= 3 — 5 




= 5
2. Частное решение уравнения (1): Хо = 19m; уо =19n.
Отсюда получим: Хо =19

Пара (-57; -38)- частное решение (1).
3. Общее решение уравнения (1): 

Четвертый способ. Геометрический.
1. Решим уравнение 5х – 8у = 1 геометрически.
2. Запишем частное решение уравнения (1).
3. Запишем общее решение данного уравнения (1).
Отложим на окружности последовательно друг за другом равные дуги, составляющие

На 5 – ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли 



Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1.
2. Частное решение уравнения (1): Хо = 19 
3. Общее решение уравнения (1): 

источники:
http://matematika-ege-otradnoe.ru/content/reshenie-diofantovyh-uravneniy-dlya-s719
http://urok.1sept.ru/articles/501260
19 марта 2020
В закладки
Обсудить
Жалоба
Диофантовы уравнения
Диофантовы уравнения – алгебраические уравнения с двумя или большим числом неизвестных с целыми коэффициентами, для которых находятся целые или рациональные решения.
Первая часть: du1.doc
Вторая часть: du2.docx
Инфоурок
›
Алгебра
›Презентации›Диофантовы уравнения: подготовка к ЕГЭ
Диофантовы уравнения: подготовка к ЕГЭ
Скачать материал

Скачать материал


- Сейчас обучается 31 человек из 21 региона


- Сейчас обучается 20 человек из 12 регионов


- Сейчас обучается 82 человека из 34 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Диофантовы уравнения:
подготовка к ЕГЭ.
Яковлева Татьяна Петровна,
доцент кафедры математики и физики
Камчатского государственного университета имени Витуса Беринга,
кандидат педагогических наук, доцент,
г. Петропавловск — Камчатский -
2 слайд
Теоретические сведения
-
3 слайд
Диофантовы уравнения
первого порядка с двумя неизвестными -
-
5 слайд
Примеры решения задач
-
-
-
-
-
-
11 слайд
Примеры решения задач
-
-
-
-
-
-
-
18 слайд
Теоретические сведения
-
19 слайд
Диофантовы уравнения
второго порядка с двумя неизвестными -
20 слайд
Примеры решения задач
-
-
-
-
-
-
-
-
-
29 слайд
Примеры решения задач
-
-
-
-
-
-
-
-
-
-
-
40 слайд
Примеры решения задач
-
-
-
-
-
45 слайд
Примеры решения задач
-
-
47 слайд
Спасибо за внимание!
-
48 слайд
Список используемой литературы:
Андреева А.О. ЕГЭ по математике. Практическая подготовка. – СПб.: БХВ-Петербург, 2014. – 256 с.
Вольфсон Г.И. ЕГЭ 2018. Математика. Арифметика и алгебра. Задача 19 (профильный уровень) / Под ред. И.В. Ященко. – М.: МЦНМО, 2018. – 112 с.
Ерина Т.М. ЕГЭ 2020. 100 баллов. Математика. Профильный уровень. Практическое руководство / Т.М. Ерина. – М.: Издательство «Экзамен», 2020. – 350 с.
Лаппо Л.Д. ЕГЭ 2020. Эксперт. Математика. Профильный уровень / Л.Д. Лаппо, М.А. Попов. – М.: Издательство «Экзамен», 2020. – 350 с.
Мордкович А.Г. Математика: Полный справочник / А.Г. Мордкович, В.И. Глизбург, Н.Ю. Лаврентьева. – М.: АСТ: Астрель, 2016. – 335 с.
Семенов А.В. Основной государственный экзамен. Математика. Комплекс материалов для подготовки учащихся. Учебное пособие. / А.В. Семенов, А.С. Трепалин, И.В. Ященко, П.И. Захарова, И.Р. Высоцкий; под ред. И.В. Ященко; Московский Центр непрерывного образования. – М.: Интеллект-Центр, 2017. – 248 с.
Садовничий Ю.В. ЕГЭ. Математика. Профильный уровень. Задания с развернутым ответом / Ю.В. Садовничий. – М.: Издательство «Экзамен», 2020. – 654 с.
Третьяк И.В. ОГЭ. Математика: универсальный справочник / И.В. Третьяк. — Москва : Эксмо, 2016. – 352 с.
Краткое описание документа:
Презентация «Диофантовы уравнения: подготовка к ЕГЭ» предназначена для подготовки решения задачи 19. Теоретический и практический материал включает: диофантовы уравнения первого порядка с двумя неизвестными, диофантовы уравнения второго порядка с двумя неизвестными. Материал полезен для профильной подготовки к ЕГЭ по математике.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 587 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра и начала математического анализа», Муравин Г.К., Муравина О.В
Тема
ГЛАВА 5. Уравнения, неравенства и их системы
Больше материалов по этой теме
-
«Алгебра и начала математического анализа. Учебник (базовый и углублённый уровни)», Мордкович А.Г., Семенов П.В.
Тема
Глава 6. Уравнения и неравенства. Системы уравнений и неравенств
Больше материалов по этой теме
-
«Алгебра и начала математического анализа», Колягин Ю.М., Ткачёва М.В. и др.
Тема
Глава 8. Уравнения и неравенства с двумя переменными
Больше материалов по этой теме
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни)», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.
Тема
Глава 2. Уравнения. Неравенства. Системы
Больше материалов по этой теме
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Пратусевич М.Я., Столбов К.М., Головин А.Н.
Тема
Глава XIII. Уравнения и неравенства
Больше материалов по этой теме
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Базовый и углублённый уровни», Рубин А.Г., Чулков П.В.
Тема
Глава III. Решение уравнений, неравенств и систем
Больше материалов по этой теме
Другие материалы
Презентация по теме «Показательные неравенства»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни)», Алимов Ш.А., Колягин Ю.М., Ткачёва М.В. и др.
- Тема: Показательные неравенства
- 18.12.2020
- 214
- 6

Касательная к графику функции
- Учебник: «Алгебра и начала математического анализа», Колягин Ю.М., Ткачёва М.В. и др.
- Тема: § 8. Геометрический смысл производной
- 18.12.2020
- 567
- 5





- 18.12.2020
- 276
- 5

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Этика делового общения»
-
Курс профессиональной переподготовки «Организация менеджмента в туризме»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Организация маркетинга в туризме»
-
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Осуществление и координация продаж»
-
Курс профессиональной переподготовки «Управление качеством»
-
Скачать материал
-
18.12.2020
19506
-
PPTX
3.4 мбайт -
36
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Яковлева Татьяна Петровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 6 месяцев
- Подписчики: 117
- Всего просмотров: 2125827
-
Всего материалов:
95
Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»
Диофантовы уравнения, типы и способы решения
Выполнила:
учащаяся 10 класса «А»
Лаврентьева Елизавета Андреевна
Научный руководитель:
учитель математики
Сухненко Ирина Александровна
Тамбов, 2022
Оглавление
Введение 3
Глава 1. Диофант и история диофантовых уравнений 4
Глава 2. О диофантовых уравнениях 6
Глава 2.1. Определение. Диофантовый анализ 6
Глава 2.3. Диофантовы уравнения второго порядка с двумя неизвестными 14
Глава 2.4. Другие уравнения в целых числах 20
Глава 2.5. Текстовые задачи, использующие уравнения в целых числах. 22
Глава 2.6. Оценки переменных. Организация перебора 24
Глава 2.7. Неравенства в целых числах. Графические иллюстрации 26
Глава 2.8. Задачи математических олимпиад 29
Заключение 31
Введение
В последние годы значительно возрос интерес к задачам, при решении которых используются свойства целых чисел. Это определено, в первую очередь, тем, что такие задачи часто встречаются на вступительных экзаменах в высшие учебные заведения и на олимпиадах по математике.
Диофантовы уравнения (задачи на целые числа) всегда считались одними из наиболее сложных задач, предлагаемых учащимся старших классов. Это объясняется отсутствием единого метода их решения.
Гипотеза: умение решать диофантовы уравнения позволяет оптимизировать многие процессы, найти остроумные и сравнительно простые решения «неразрешимых» задач, а в практической деятельности значительно сэкономит затраты средств и времени.
Объект исследования — диофантовы уравнения.
Предмет исследования — методы решения уравнений в целых числах.
Уравнения в математике занимают важное место. Большее количество задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений.
Актуальность данной темы обусловлена тем, что умение решать уравнения в целых числах окажется полезным при решении задач, выходящих за рамки школьной программы, олимпиадных заданий, а также задач с практическим содержанием в реальной жизни.
Глава 1. Диофант и история диофантовых уравнений
«Достопочтеннейший Дионисий, зная, что ты ревностно хочешь научиться решению задач, касающихся чисел, я попытался изложить природу их и могущество, начиная с тех оснований, на которых покоится эта наука.
Может быть, этот предмет покажется тебе затруднительным, поскольку ты еще с ним незнаком, а начинающие не склонны надеяться на успех. Но он станет тебе удобопонятным благодаря твоему усердию и моим пояснениям, ибо страстная любовь к науке помогает быстро воспринять учение»
Таким посвящением открывается «Арифметика» Диофанта Александрийского.
Диофант представляет одну из занимательных загадок в истории математики. Мы не знаем, кем был Диофант, точные года его жизни; полагают, что он жил в III в. н. э. На могиле Диофанта есть стихотворение — задача, решая которую нетрудно подсчитать, сколько лет прожил великий математик.
«Прах Диофанта гробница покоит; дивись ей — и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком,
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей».
Решение задачи сводится к решению уравнения первой степени с одним неизвестным.
Пусть x — количество лет, прожитых Диофантом, тогда 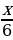
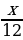
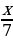
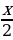
Составим и решим уравнение:
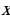
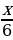
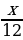
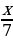
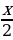
откуда 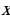
Эта головоломка служит примером тех задач, которые решал Диофант. Он специализировался на решении задач в целых числах. Такие задачи в настоящее время известны под названием диофантовых.
Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные и придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». «Арифметика» Диофанта — это сборник 189 задач с решениями, сводящимися к определенным уравнениям первой и второй степеней и неопределенным. Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения.
Глава 2. О диофантовых уравнениях Глава 2.1. Определение. Диофантовый анализ
Диофантовыми уравнениями называют алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях должно быть не менее двух (если не ограничиваться только целыми числами).
К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величин могут быть только целыми числами.
Рассмотрим одну задачу: За покупку нужно уплатить 1700 р. У покупателя имеются купюры только по 200 и 500 р. Какими способами он может расплатиться?
Для ответа на этот вопрос достаточно решить уравнение 2х +5у = 17 с двумя неизвестными х и у. Такие уравнения имеют бесконечное множество решений. В частности, полученному уравнению отвечает любая пара чисел вида 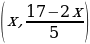
Таким образом, особенности диофантовых задач заключаются в том, что:
1) они сводятся к уравнениям или системам уравнений с целыми коэффициентами;
2) решения требуется найти только целые, часто натуральные.
Диофантовыми уравнениями называются уравнения вида
P(x1, x2, …, xn) = 0,
где P(x1, …, xn) — многочлен с целыми коэффициентами.
Проблема решения уравнений в целых числах решена до конца только для уравнений первой степени и для уравнений второй степени с двумя неизвестными. Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача существования целочисленных решений. Например, не известно, имеет ли уравнение
x3 + y3 + z3 = 30
хотя бы одно целочисленное решение. Более того, доказано, что в принципе не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения.
Уравнение x2 + y2 = z2, связывающее стороны x, y, z прямоугольного треугольника, всегда вызывало большой интерес. Натуральные числа x, y и z, являющиеся решениями этого уравнения, называются «пифагоровыми тройками».
Неопределенное уравнение Ферма (уравнение Пелля). К работам Диофанта имеют непосредственное отношение и математические исследования французского математика Пьера Ферма. Считается, что именно с работ Ферма началась новая волна в развитии теории чисел.
x2 — ay2 = 1, где a — целое положительное число, не являющееся полным квадратом.
В 1630 г. французский математик Пьер Ферма сформулировал гипотезу, которую называют великой теоремой Ферма: «Уравнение xn + yn = zn для натурального n ≥ 3 не имеет решений в натуральных числах».
Глава 2.2. Диофантовы уравнения первого порядка с двумя неизвестными
Диофантовым уравнением первого порядка с двумя неизвестными x, y будем называть уравнение вида ax + by = c, где a, b, c, x, y 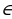
ax = c – by.
Левая часть полученного выражения делится нацело на a. Значит, должна делиться нацело на a и правая часть этого уравнения. Рассматривая всевозможные остатки l от деления y на a; l = 0, 1, …, a -1, получим, что при одном значении l из указанного промежутка будет делиться на a и правая часть. Поскольку число a не велико по модулю, то и перебор вариантов будет тоже невелик.
Теоремы о числе целых решений диофантового уравнения первого порядка с двумя неизвестными.
Теорема 1. Если свободный член c диофантового уравнения ax + by = c не делится на НОД(a, b), то уравнение не имеет целых решений.
Теорема 2. Если коэффициенты a и b неопределенного уравнения ax + by = c являются взаимно простыми числами, то уравнение имеет по крайней мере одно целое решение.
Теорема 3. Если в уравнении ax + by = с, НОД(a, b) = 1, то все целые решения этого уравнения заключены в формулах:
x = x0 + b * t, y = y0 – a * t,
где (x0 ; y0 ) – некоторое решение уравнения ax + by = с, a t – произвольное целое число.
Посмотрим на практике, как работает метод подбора для решения уравнений в целых числах.
Пример 1. Решить уравнение 3х — 4у = 1 в целых числах.
Решение. Перепишем уравнение в виде 3х = 4у + 1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмотрим три случая.
-
Если у = 3t; t
Z, то 4у + 1 = 12t + 1 не делится на 3.
-
Если у = 3t + 1, то 4у + 1= 4(3t + 1) + 1 = 12t + 5 не делится на 3.
-
Если у = 3t + 2, то 4у + 1 = 4(3t + 2) +1 = 12t + 9 делится на 3, поэтому 3х = 12t + 9, т.е. x = 4t + 3.
Ответ: {(4t + 3, 3t + 2)}; t ∈ Z.
Рассмотренный метод становится неэффективным, если числа 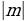
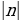
Алгоритм:
-
Выбор наибольшего по модулю коэффициента (пусть
).
-
Проведение процедуры уменьшения коэффициентов. Это делается с помощью деления с остатком. Пусть n = l
+ q, где 0 q ≤
, тогда mx + ny = k
mx + (l
y = k
mx + l
Левая часть последнего уравнения делится на m и правая часть: k – qy = mt, где t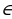
-
Повторение процедуры уменьшения коэффициентов. Новое уравнение отличается от старого только тем, что его коэффициенты по модулю меньше коэффициентов старого. За конечное число шагов добьемся того, что коэффициент при одном из новых неизвестных будет равен 1.
-
Возврат к исходным переменным.
Пример 2. Решить уравнение 79y – 23x = 1 в целых числах.
Решение. Проведем деление с остатком: 79 = 23*3 + 10 и перепишем исходное уравнение в виде 23x = 79y — 1 = (23*3 + 10)y – 1 = 69y + 10y — 1
Левая часть уравнения делится нацело на 23, поэтому должна делиться на 23 и правая часть: 10y – 1 = 23t или 10y = 23t + 1; t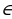
Полученное новое уравнение по типу точно такое же, как исходное. Однако коэффициенты при неизвестных в нем уменьшились по модулю. Повторим процедуру уменьшения коэффициентов еще раз: 10y = 23t + 1 = (10*2 + 3)t + 1
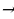
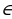

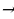
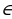
Осталось выразить x и y через v. Поскольку u = 3v + 1, то
-
3t = 10u – 1 = 10(3v + 1) — 1 = 30v + 9
t = 10v + 3.
-
10y = 23t +1 = 23(10v + 3) + 1 = 230v + 70
y = 23v + 7.
-
23x = 79y – 1 = 79(23v + 7) — 1=79*23v + 552
x = 79v + 24.
Ответ: {(79v + 24, 23v + 7)}; v ∈ Z.
Пример 3. Решить уравнение 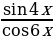
Решение. Преобразуем данное уравнение следующим образом:
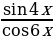

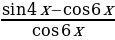

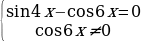

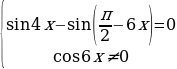

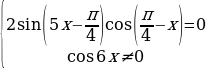

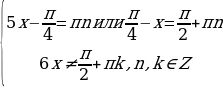

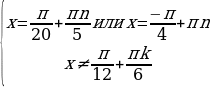
Решим два уравнения в целых числах. Рассмотрим сначала первое уравнение:
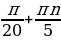
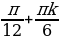

Перебирая все возможные остатки при делении n на 5, находим, что решением последнего уравнения являются n = 5l + 1; l 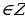
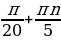
n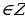
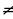
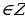
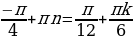

Ясно, что любое целое n является решением этого уравнения. Таким образом, ни одно значение x из серии x = 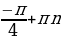
Ответ: 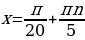
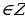
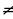
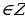
Решение диофантового уравнения с помощью алгоритма Евклида.
Сам метод Евклида относится к другой математической задаче — нахождению наибольшего общего делителя: вместо исходной пары чисел записывают новую пару — меньшее число и разность между меньшим и большим числом исходной пары. Это действие продолжают до тех пор, пока числа в паре не уравняются — это и будет наибольший общий множитель. Разновидность алгоритма используется и при решении диофантовых уравнений.
Пример 4. Решить в целых числах уравнение 2х + 7y = 4.
Решение. 2х + 7y = 4
2(x + 3y) + y = 4
Введем новую неизвестную z = x + 3y, тогда уравнение запишется так:
2z + y = 4.
Мы получили уравнение с коэффициентом один! Тогда z — любое число, y = 4 − 2z.
Осталось найти x: x = z − 3y = z − 3(4 − 2z) = 7z − 12.
Пусть z = 1. Тогда y = 2, x = -5. 2 * (-5) + 7 * 2 = 4
Пусть z = 5. Тогда y = -6, x = 23. 2 * 23 + 7 * (-6) = 4
Ответ: {(-5, 2); (23, -6)}.
В этом примере важно понять, как мы перешли от уравнения с коэффициентами 2 и 7 к уравнению с коэффициентами 2 и 1. В данном случае (и всегда!) новый коэффициент (в данном случае — единица) это остаток от деления исходных коэффициентов друг на друга (7 на 2).
Здесь нам повезло, мы сразу после первой замены получили уравнение с коэффициентом 1. Такое бывает не всегда, но и мы можем повторять предыдущий трюк, вводя новые неизвестные и выписывая новые уравнения. Рано или поздно после таких замен получится уравнение с коэффициентом 1.
Пример 5. Решить уравнение в целых числах 13х – 36у = 2.
36 / 13 = 2 (10 в остатке). Таким образом, исходное уравнение можно переписать следующим образом:
13x – 13 * 2y — 10y = 2.
13(x — 2y) — 10y = 2.
Введем новую переменную z = x — 2y.
Теперь мы получили уравнение: 13z — 10y = 2.
13 / 10 = 1 (3 в остатке). Исходное уравнение 13z — 10y = 2 можно переписать следующим образом:
10z — 10y + 3z = 2.
10(z — y) + 3z = 2.
Введем новую переменную m = z — y.
Теперь мы получили уравнение: 10m + 3z = 2.
10 / 3 = 3 (1 в остатке). Исходное уравнение 10m + 3z = 2 можно переписать следующим образом:
3*3m + 3z + m = 2.
3(3m + z) + m = 2.
Введем новую переменную t = 3m + z. Теперь мы получили уравнение:
3t + m = 2.
Мы получили уравнение с коэффициентом единица!
m = 2 – 3t, причем t может быть любым числом. Однако нам нужно найти x и y. Проведем замену переменных в обратном порядке. Помните, мы должны выразить x и y через t, которое может быть любым числом.
y = z — m; z = t — 3m, m = 2 – 3t ⇒ z = t — 3*(2 – 3t), y = t — 3*(2 – 3t) — (2 – 3t) = 13t — 8; y = 13t — 8
x = 2y + z ⇒ x = 2(13t – 
Пусть t = 1. Тогда y = 5, x = 24. 13*14 — 36*5 = 2
Пусть t = 5. Тогда y = 57, x = 158. 13*158 — 36*57 = 2
Ответ: {(24, 5); (158, 57)}.
Глава 2.3. Диофантовы уравнения второго порядка с двумя неизвестными
Диофантовым уравнением второго порядка с двумя неизвестными x, y будем называть уравнение вида
Ax2 + Bxy + Cy2 + Dx + Ey = F,
где A, B, C, D, E, F, x, y 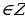
Рассмотрим основные методы решения данных уравнений.
Разложение на множители. Этот метод состоит в том, что левая часть данного уравнения каким-либо образом раскладывается на множители (чаще всего путем нахождения дискриминанта), и задача сводится к перебору конечного числа вариантов.
Пример 1. Найти все пары целых чисел (x, y), каждая из которых удовлетворяет уравнению 2x2 + 5 = 3y2 + 5xy.
Решение. Преобразуем данное уравнение следующим образом:
2x2 + 5 = 3y2 + 5xy 


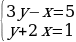
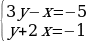
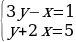
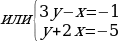
Первые две системы не имеют решений в целых числах, третья и четвертая имеют решением пары (x, y) = (2, 1) и (x, y) = (-2, -1) соответственно.
Ответ: {(2,1); (-2, -1)}.
Пример 2. Найти все тройки чисел (x, y, z), удовлетворяющие системе уравнений 
Решение. Рассмотрим второе уравнение системы как квадратное относительно x. Это уравнение будет иметь решение тогда и только тогда, когда его дискриминант больше либо равен нулю. Имеем:
D = 3(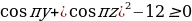
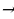
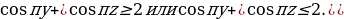
В первом случае 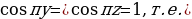
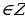
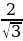
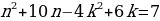
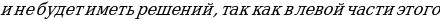
Во втором случае 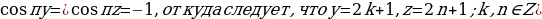
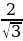
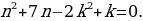
Дискриминант этого уравнения (которое мы рассматриваем как квадратное относительно n) равен D = 49 + 16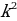
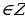
Разность первого и второго чисел, стоящих в скобках, равна 8k — 2, т.е. дает остаток 6 при делении на 8. В соответствии с этим получаем четыре варианта:
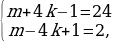
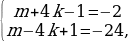
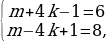
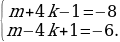
В первых двух случаях получаем k = 3, n = — 5, откуда y = 7, z = — 9; в третьем и четвертом случаях находим, что k = n = 0 и y = z = 1.
Ответ: {(- 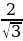
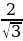
Если в уравнении отсутствует член, содержащий 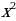
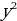
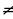
Bxy + Cy2 + Dx + Ey = F 


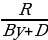
где P, Q, R – рациональные числа. Подобрав, при необходимости, целое число T и домножив на него обе части уравнения
x = Py + Q + 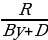
получим уравнение
Tx = P’y + Q’ + 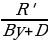
где P’, Q’ и R’ уже являются целыми числами. Дальнейшее решение сводится к перебору всех делителей числа R’ (если R’ = 0, то уравнение становится линейным).
Пример 3. Решить в целых числах уравнение 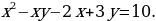
Решение. Выразим в данном уравнении y через x:
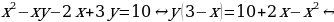
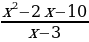
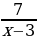
Из полученного равенства видно, что дробь 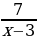
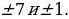
Ответ: {(10, 10); (-4, -2); (4, -2); (2, 10)}.
Если диофантово уравнение второго порядка каким-либо образом (например, выделением полных квадратов) приводится к виду Ax2 + Cy2 = F, где A, C и F – целые, отличные от нуля, числа, то метод решения зависит от знаков коэффициентов при переменных. Если А и С имеют один и тот же знак, то используются следующие оценки (пусть A, C, F 0):
Ax2 + Cy2 = F 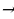
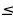
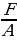

Далее задача сводится к перебору конечного числа вариантов. Если же А и С имеют разные знаки, то в общем виде решение уравнения достаточно сложно, но в некоторых случаях можно, например, перебором остатков доказать, что уравнение не имеет решений в целых числах.
Пример 4. Найти целочисленные решения уравнения 14x4 – 5y4 – 3x2y2 + 82y2 – 125x2 + 51 = 0.
Решение. Рассмотрим данное уравнение как квадратное относительно x2. Имеем: 14x4 – 5y4 – 3x2y2 + 82y2 – 125x2 + 51 = 0 
Дискриминант этого уравнения равен D = (3y2 + 125)2 + 56(5y4 — 82y2 – 51) = 289y4 — 3842y2 + 12769 = (17y2 — 113)2.
Корни уравнения равны
x2 = 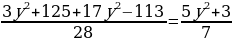
или
x2 = 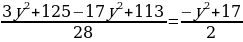
Таким образом, левая часть исходного уравнения раскладывается на множители следующим образом:
(7x2 – 5y2 – 3)(2x2 + y2 – 17) = 0,
и задача сводится к решению двух уравнений в целых числах.
Докажем сначала, что уравнение 7x2 = 5y2 + 3 не имеет целочисленных решений. Для этого посмотрим, какие остатки могут давать при делении на 3 левая и правая части этого уравнения. Так как любой полный квадрат дает при делении на 3 остаток 0 или остаток 1, число 7x2 также дает при делении на 3 остатки 0 и 1. Остатки от деления на 3 числа 5y2 + 3 могут быть равны 0 или 2. Таким образом, равенство может иметь место только в том случае, когда x и y кратны 3. Но в этом случае числа x2 и 5y2 делятся без остатка на 9, поэтому равенство также не может иметь место (поскольку 3 не делится на 9).
Рассмотрим теперь уравнение 2x2 + y2 – 17. Из оценки x2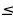
Ответ: {(2, 3); (-2, 3); (-2, -3); (2, -3)}.
Наконец, рассмотрим уравнение вида Ax2 + Dx + Ey = F, где A, D, E, F – целые числа и А, и Е отличны от нуля. Это уравнение решается перебором остатков при делении на Е числа F – Dx — Ax2. Но в отличие уравнений первого порядка разрешимость данного уравнения может быть и при нескольких значениях остатка q. Кроме того, может оказаться, что такое уравнение и вовсе не имеет решений.
Пример 5. Решить в целых числах уравнение 3x2 + 2x + 3y = 2.
Решение. Перепишем исходное уравнение в виде 3y = 2 – 2x — 3x2.
Левая часть полученного уравнения делится на 3, значит, должна делиться на 3 и его правая часть. Рассмотрим три случая.
-
Если x = 3k; k
, то 2 – 2x — 3x2 = 2 – 6k – 27k2 не делится на 3.
-
Если x = 3k + 1, то 2 – 2x — 3x2 = 2 – 2(3k + 1) – 3(3k + 1)2 = — 27k2 — 24k – 3 делится на 3.
-
Если x = 3k + 2, то 2 – 2x — 3x2 = 2 – 2(3k + 2) – 3(3k + 2)2 = — 27k2 — 42k – 14 не делится на 3.
Итак, x = 3k + 1, откуда y = — 9k2 — 8k – 1, где k 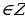
Ответ: {(3k + 1, — 9k2 — 8k – 1)}; k 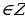
Рассмотрим на примере метод выделения полного квадрата.
Пример 6. Найти целочисленные решения 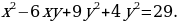
Решение.
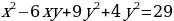
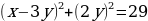
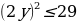
Значит, y = 0; 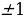
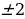
Перебрав все варианты значений y, и найдя соответствующие значения x, запишем ответ.
Ответ: {(2, -1); (-2; 1); (8; 1); (-8; -1)}.
Глава 2.4. Другие уравнения в целых числах
Все описанные в предыдущем разделе методы применимы для решения не только диофантовых уравнений второго порядка с двумя неизвестными, но и других уравнений в целых числах. К таким уравнениям относятся уравнения второго порядка с тремя и более переменными, уравнения более высокого, чем второго, порядка. Выбор нужного метода при решении подобного уравнения порой является определяющим условием для успешного решения задачи. Рассмотрим несколько примеров.
Пример 1. Решить в целых числах уравнение x2 + 5y2 + 34z2 + 2xy – 10xz – 22yz = 0.
Решение. Преобразуем данное уравнение следующим образом:
x2 + 5y2 + 34z2 + 2xy – 10xz – 22yz = 0 
(x2 + 2x(y — 5z) + y2 – 10yz + 25z2) + 4y2 — 12yz + 9z2 = 0 
(x + y – 5z)2 + (2y – 3z)2 = 0 
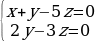

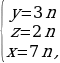
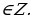
Ответ: x = 7n, y = 3n, z = 2n; n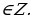
Пример 2. Найти все пары целых чисел (x, y), каждая из которых удовлетворяет уравнению (x2 + y2)(x + y – 3) = 2xy.
Решение. Ясно, что пара (0, 0) является решением данного уравнения. Предположим теперь, что хотя бы одно из чисел x и y отлично от нуля. Имеем
(x2 + y2)(x + y – 3) = 2xy 
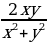
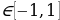
-
Если x + y – 3 = — 1, то x = — y, нет решений.
-
Если x + y – 3 = 0, то либо x = 0, y = 3, либо x = 3, y = 0.
-
Если x + y – 3 = 1, то x = y, следовательно, x = 2 и y = 2.
Таким образом, решением данного уравнения будут служить следующие пары чисел:
(x, y) = {(2, 2); (3, 0); (0, 3); (0, 0)}.
Ответ: {(2, 2); (3, 0); (0, 3); (0, 0)}.
Глава 2.5. Текстовые задачи, использующие уравнения в целых числах.
В завершение тем предыдущих глав рассмотрим несколько текстовых задач, при решении которых возникают уравнения в целых числах. В таких задачах необходимым условием их решения является правильная формализация задачи, т.е. введение нужных переменных и составление уравнения (или системы уравнений), содержащего эти переменные.
Пример 1. Длина дороги, соединяющей пункты А и В, равна 2 км. По этой дороге курсируют два автобуса. Достигнув пункта А или пункта В, каждый из автобусов немедленно разворачивается и следует без остановок к другому пункту. Первый автобус движется со скоростью 51 км/час, а второй – 42 км/час. Сколько раз за 8 часов движения автобусы встретятся в пункте В, если известно, что первый стартует из пункта А, а второй – из пункта В?
Решение. Первый автобус проезжает путь между А и В за 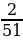
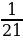
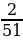
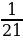
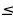
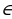

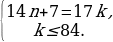
Из последнего уравнения видно, что k нечетно и кратно 7. Таких чисел в интервале от 1 до 84 шесть, это 7, 21, 35, 49, 63 и 77. Каждому такому k соответствует целое значение n. Таким образом, за 8 часов движения автобусы встретятся в пункте В шесть раз.
Ответ: 6 раз.
Пример 2. Мастер делает за 1 час целое число деталей, большее 5, а ученик – на 2 детали меньше. Один мастер выполняет заказ за целое число часов, а два ученика вместе – на 1 час быстрее. Из какого количества деталей состоит заказ?
Решение. Пусть х 5 деталей делает мастер за 1 час, тогда ученик за один час делает х – 2 детали. Пусть также мастер выполняет заказ за t часов, где t – целое число. Согласно условиям задачи имеем уравнение
xt = 2(x – 2)(t – 1) 
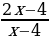
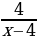
Дробь 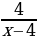
Ответ: Из 24 деталей.
Глава 2.6. Оценки переменных. Организация перебора
Один из самых распространенных приемов при решении задач в целых числах – это заключение целочисленной переменной в интервал с последующим перебором всех целых значений из этого интервала. Иногда для этого приходится складывать неравенства, полученные согласно условиям задачи. Также возможен переход от двойного неравенства к одинарному путем исключения центральной части двойного неравенства. Надо понимать, что оба этих преобразования не являются равносильными, а осуществляют переход к следствию, т.е. при их применении возможно появление посторонних решений. В связи с вышесказанным после применения данных преобразований необходима проверка. Рассмотрим несколько примеров.
Пример 1. В двух ящиках находится более 29 одинаковых деталей. Число деталей в первом ящике, уменьшенное на 2, более чем в три раза превышает число деталей во втором ящике. Утроенное число деталей в первом ящике превышает удвоенное число деталей во втором ящике, но менее чем на 60. Сколько деталей в каждом ящике?
Решение. Обозначим через x число деталей в первом ящике, а через y – число деталей во втором. Тогда, согласно условию, имеет место система неравенств
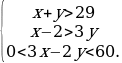
Перепишем эту систему в виде
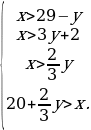
Отсюда следует, что справедливы неравенства
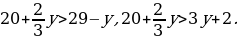
Первое из них можно переписать в виде 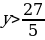
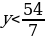
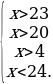
Ясно, что нет натуральных чисел x, удовлетворяющих ей. Значит, y = 7. Тогда исходная система перепишется в виде
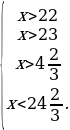
Отсюда вытекает, что существует единственное натуральное число x = 24, ей удовлетворяющее. Следовательно, в первом ящике 24 детали, а во втором – 7 деталей.
Ответ: 24 детали и 7 деталей.
Глава 2.7. Неравенства в целых числах. Графические иллюстрации
Часто при решении уравнений, неравенств, систем, а также текстовых задач, связанных с целыми числами, удобно пользоваться графической иллюстрацией. Иногда удается достаточно несложно изобразить множество решений на координатной плоскости, и возникает необходимость выделить из этого множества точки с целочисленными координатами. Рассмотрим примеры.
Пример 1. Найти все целочисленные решения системы
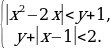
Решение. Пусть t = x – 1, тогда данная система примет следующий вид:
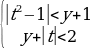

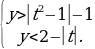
На координатной плоскости Oty полученная система определяет множество точек.
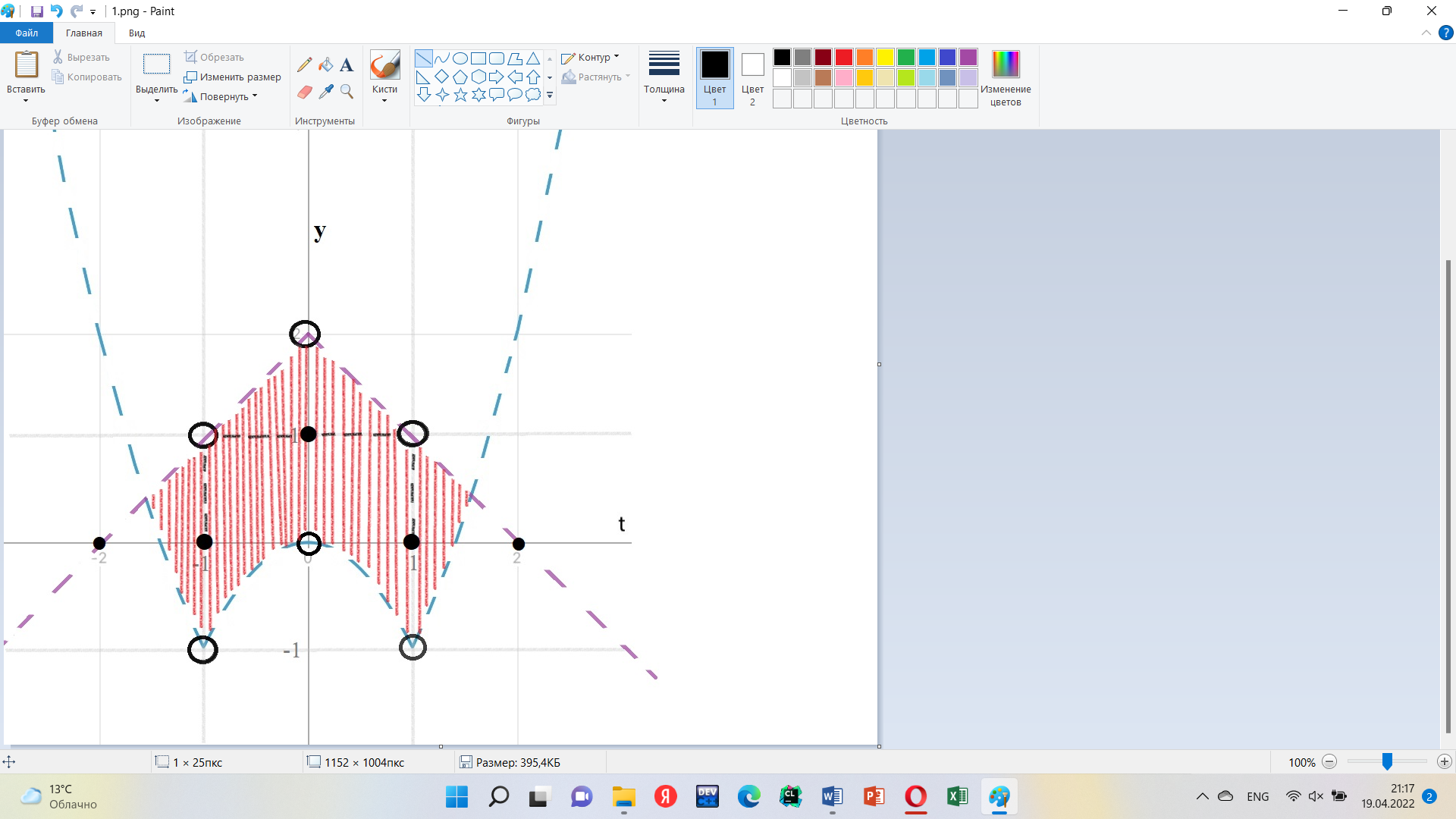
Из рисунка видно, что в полученном множестве содержатся только три точки с целочисленными координатами – это (t, y) = {(-1, 0); (1, 0); (1, 1)}. Таким образом, ответом к задаче будут служить пары чисел (x, y) = {(0, 0); (2, 0); (1, 1)}.
Ответ: {(0, 0); (2, 0); (1, 1)}.
Пример 2. Найти все пары целых чисел x, y, удовлетворяющих системе
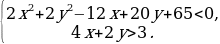
Решение. Преобразуем данную систему следующим образом:
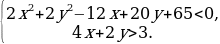

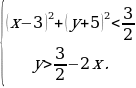
На координатной плоскости Oxy полученная система определяет множество точек.
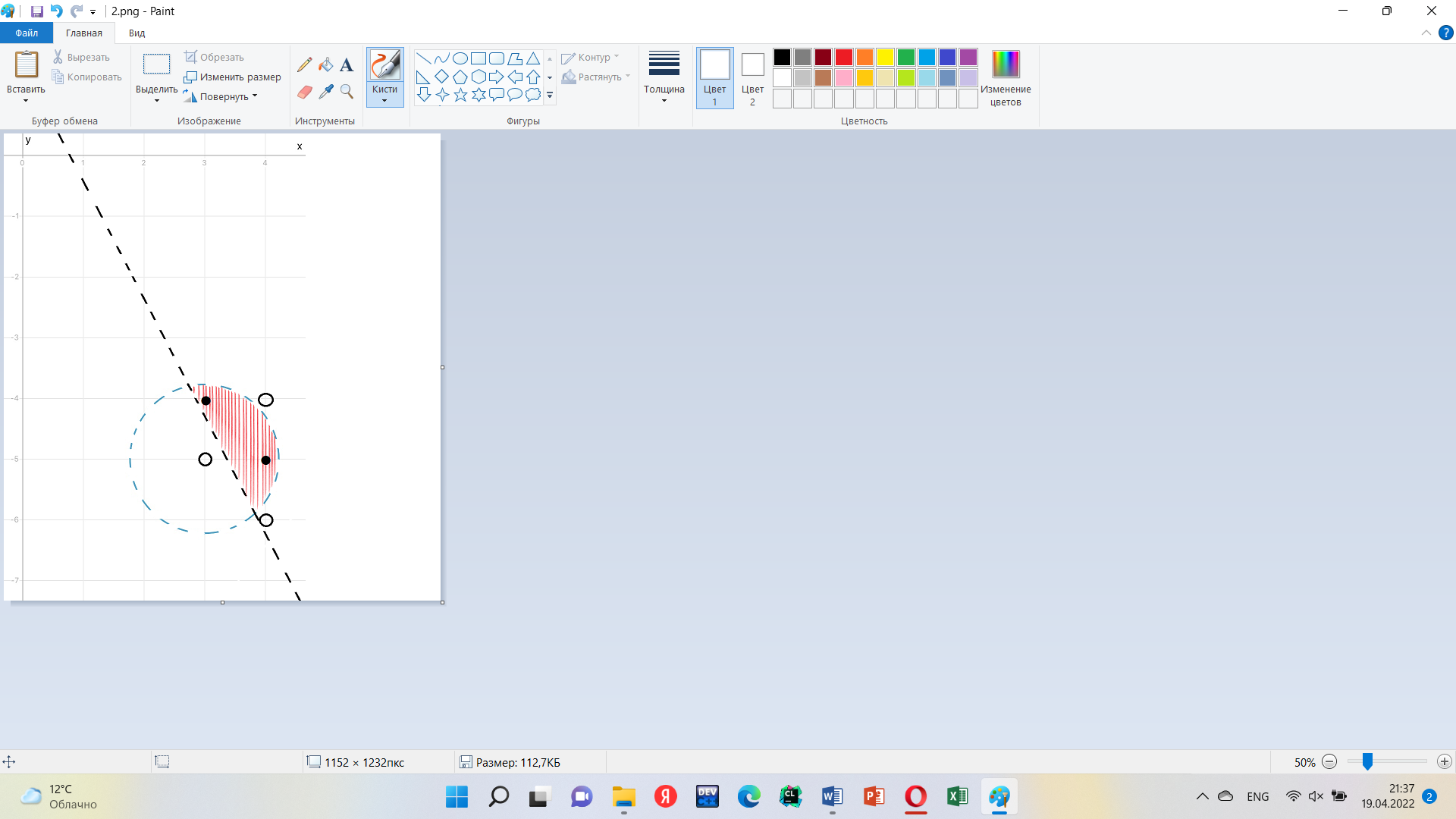
Из рисунка видно, что этому множеству принадлежат только две точки с целочисленными координатами – это точки (3, -4) и (4, -5).
Ответ: {(3, -4); (4, -5)}.
Глава 2.8. Задачи математических олимпиад
Пример 1. Каким может быть наибольший общий делитель натуральных чисел m и n, если при увеличении числа m на 6 он увеличивается в 9 раз?
Решение. Пусть d – наибольший общий делитель чисел m и n, тогда 9d – наибольший общий делитель чисел m + 6 и n. Так как d – делитель m и m + 6, то d – делитель разности этих чисел, т.е. делитель числа 6. Следовательно, d = 1, d = 2, d = 3 или d = 6. Так как числа m + 6 и n делятся на 9, то числа m и n делятся на 3, следовательно, d делится на 3. Таким образом, d = 3 или d = 6. Осталось проверить, что оба случая имеют место. Если d = 3, то, например, m = 21, n = 27; если d = 6, то m = 48, n = 54.
Ответ: 3 или 6.
Пример 2. На клетчатой бумаге отмечен прямоугольник m * n клеток, причем числа m и n взаимно просты и m n. Диагональ этого прямоугольника не пересекает ровно 116 его клеток. Найти все возможные значения m и n при денных условиях.
Решение. Диагональ прямоугольника не может проходить через узлы клеток, лежащие внутри прямоугольника. Действительно, если бы это было не так, то существовал бы прямоугольник меньшего размера m1 * n1 клеток, причем m = km1 и n = kn1 (k, m1 и n1 – натуральные числа). Тогда числа m и n не являлись бы взаимно простыми, что противоречит условию задачи.
Далее диагональ прямоугольника, пересекая каждую новую клетку, пересекает либо вертикальную, либо горизонтальную линию клетчатой бумаги, находящуюся внутри этого прямоугольника. Это значит, что число пересекаемых ею клеток, уменьшенное на единицу (не рассматривается клетка, прилегающая к той вершине прямоугольника, из которой выходит данная диагональ), равно суммарному количеству вертикальных и горизонтальных линий, лежащих внутри прямоугольника, т.е. (m — 1) + (n — 1). Итак, число пересекаемых клеток равно m + n – 1, и из условия задачи получаем уравнение
mn – 116 = m + n – 1 
Поскольку m n, пара (m — 1, n — 1) равна либо (1, 116), либо (2, 58), либо (4, 29). Первые две пары приводят к ответу, в последнем случае получаются числа m = 5 и n = 30, не являющиеся взаимно простыми.
Ответ: {(2, 117); (3, 59)}.
Заключение
Решение уравнений в целых числах – один из самых красивых и интересных разделов математики, именно поэтому изучение данной темы показалось мне по-настоящему полезным и не скучным. Эта тема многогранна и практически необъятна. Недаром над ней ломали голову ученые с мировым именем на протяжении всей истории развития математики. Знания о диофантовых уравнениях, как мне кажется, никогда не будут исчерпывающими.
Надеюсь, что многих заинтересует данная тема и они захотят познакомиться с ней поближе.
1
Основные понятия
Решением линейных уравнений начали заниматься ещё в Древнем Вавилоне и Греции. Особого успеха в их вычислении смог добиться древнегреческий философ и математик правителя Греции — Диофант Александрийский. В третьем веке до нашей эры он издал свой труд под названием «Арифметика», в котором описал возможные решения различных математических задач. Большая часть их была посвящена уравнениям, которые и были позже названы в его честь.
Диофантовыми уравнениями принято называть линейные выражения вида: a1x1 + a2x2 + … + anxn = c. В этих равенствах икс обозначает искомое неизвестное, а коэффициенты a и c являются целыми числами. Греческий учёный предложил несколько способов решения таких уравнений:
- полный перебор;
- разложение на множители;
- выражение одной переменной через другую с выделением целой части при решении системы;
- поиск частного решения;
- алгоритм Евклида;
- геометрический метод.
Методы решения диофантовых уравнений позволяют найти целые или рациональные решения для алгебраических равенств или их систем. Но при этом число переменных в выражении не должно превышать двух. Как правило, такие уравнения имеют несколько решений, поэтому их другое популярное название — неопределённые.
Чтобы воспользоваться способами, предложенными математиком при рассмотрении задач, нужно попробовать проанализировать исходные данные и свести их к линейному равенству или системе уравнений. При этом коэффициенты, как стоящие возле неизвестных, так и свободные, должны быть целыми. Ответом же должно получиться тоже целое число, обычно натуральное.
Чтобы понимать возможности применения уравнений в тех или иных исследовательских вычислениях, необходимо предварительно ответить на два вопроса: могут ли быть у задания целочисленные решения и ограничено ли число действительных ответов. Поэтому использование способов подходит только для простейших уравнений первой и второй степени. Для выражений высших порядков, например, 4x 3 + 6Y 3 — 2z 4 = 23, определить, является ли решением целое число, довольно проблематично.
Методы решения
Для начала следует рассмотреть однородное линейное уравнение вида: ax + by = 0. Это простой многочлен первой степени. Для него характерно то, что если для коэффициентов можно подобрать один делитель, то обе части возможно сократить на его величину не нарушив принципы записи. Наиболее простым способом определить этот делитель является метод разработанный великим математиком своего времени Евклидом.
Решение диофантовых уравнений по алгоритму Евклида заключается в нахождении общего делителя натуральных чисел с использованием деления с остатком. Для этого нужно взять большее число и просто разделить его на наименьшее. Затем полученный остаток нужно снова разделить на меньшее из чисел. Это действие необходимо повторять до тех пор, пока результатом операции не станет единица, то есть выполнится деление без остатка. Последнее полученное число и будет являться наибольшим общим делителем (НОД).
Существует три теоремы, которые используются при решении уравнений первой степени:
- В случае, когда НОД равняется единице, выражение будет обязательно иметь хотя бы одну пару целого решения.
- Если коэффициенты выражения больше единицы, и при этом свободный член нельзя нацело разделить на них, то корни равенства не имеют целого значения.
- Когда коэффициенты равняются единице, все решения, состоящие из целых чисел, находятся с помощью формул: x = x0c + bt и y = y0c — at, где: х0, y0 — целые ответы, t — множество чисел.
Например, пусть есть равенство вида 54x + 37y = 1. Используя то, что a = 54, а b =37, можно записать: 54 — 37 *1 = 17. Теперь можно выполнить следующие вычисления:
- 37 — 17 * 2 = 3;
- 71 — 3 * 5 = 2;
- 3 — 2 * 1 = 1.
Далее нужно выразить значения коэффициентов через остаток:
- 3 — (17 — 3 * 5) = 1;
- 1 = 17 — 3 * 4;
- 1 = 17 — (37- 17 * 2) * 4;
- 1 = 17 — 37 * 4+17 * 8;
- 1 = 17 * 9 — 37 * 4;
- 1 = (54 — 37 * 1) * 9 — 37 * 4;
- 1 = 54 * 9 — 37 * 9 — 37 * 4;
- 1 = 54 * 9 — 37 * 13;
- 1 = 54х + 37у.
Исходя из приведённого следует, что x0 равняется девяти, а игрек нулевой — минус тринадцать. Таким образом, рассматриваемое уравнение будет иметь вид:
{x = 9 + 37t;
{y = -13 — 54t.
Этим же способом можно и определить, что целых решений в выражении быть не может, как, например, для равенства 17x + 36y = 7. В этом случае НОД не делится на два, поэтому и целых решений нет.
Способ подбора и разложения
Метод подбора используется для нахождения корней простых уравнений. Пожалуй, это самый простой способ, но вместе с тем и требующий повышенного внимания и большого количества операций. Его суть заключается в полном переборе всех допустимых значений переменных, входящих в равенство. Например, эта задача которая будет интересна и школьникам, только знакомящимся с уравнениями.
Пусть имеется зоопарк, в котором находятся птицы и млекопитающие. Всего у животных двадцать лап. Определить, какое количество может быть птиц, а какое — млекопитающих. Для нахождения ответа методом перебора следует принять число одних животных, равное x (пусть это будут четырёхпалые), а других — y (птицы). Таким образом, получится уравнение: 2x + 4 y = 20. Для простоты выражение можно упростить, сократив на два: x + 2y = 10.
Полученное выражение нужно преобразовать, разделив неизвестные знаком равно: x = 10 — 2y. Зная, что ответом могут быть только целые числа, вместо y нужно пробовать подставлять возможные варианты: 1 — 8; 2 — 6; 3 — 4; 4 — 2; 5 — 0. Это и есть все возможные ответы на поставленную задачу.
Разложение выражения на множители можно выполнять различными способами. Вот основные из них:
- вынесение общего множителя: если каждый член многочлена можно разделить на одно и то же число, то его можно вынести за скобку;
- использование формулы сокращённого умножения: оно выполняется по формуле: an — bn = (a-b) * (an-1 + an-2 * b +… a2bn-3 + abn-2 + bn-1);
- применение свойства полного квадрата: это самый эффективный способ, заключающийся в вынесении полного квадрата за скобку с последующим использованием формул разности квадратов;
- группировкой — в его основе лежит вынесение общего множителя таким образом, чтобы появилась возможность перегруппировки выражения, после которой получится значение, присутствующее во всех членах равенства.
Например, пусть имеется нелинейное уравнение вида: 8×4 + 32×2 = 8. Все его члены можно перенести в одну сторону, а равенство приравнять к нулю, при этом сократив каждый член на восемь: x4 + 4×2 — 1 = 0. Для преобразования такого выражения удобнее всего применить метод квадратов. Таким образом, уравнение можно расписать следующим образом: x4 + 2 * 2 * x2 + 4 — 4 — 1 = (x2 + 2)2 — 5 = (x2 + 2 — √5) * (x2 + 2 +√5).
Геометрический подход
Этот метод удобно применять для системы уравнений. Его принцип построен на изображении графиков уравнений и определения их точки пересечения. При этом координаты этой точки и будут являться корнями рассматриваемой системы.
Из этого утверждения можно сделать следующие выводы:
- если графики уравнений представляют пересекающиеся прямые, то решением будет только одно число;
- когда графики уравнений не имеют общих точек, то решения у системы уравнений нет;
- в случае, когда графики совпадают, система будет иметь бесконечное множество корней.
Применять этот метод можно для уравнений, порядок которых не превышает единицы. В равенствах высшего порядка построить график обычно сложно. Например, дана система:
{2x — y = -9;
{3x + 2y = 4.
Из первого и второго равенства можно выразить одно неизвестное через другое, используя несколько произвольных чисел. Затем, подставляя их вместо неизвестного, можно построить график. Как только две прямые будут построены, можно будет определить, что точка их пересечения имеет координаты -2; 5. Эти значения и будут искомыми корнями.
Занимательная задача
На самом деле примеры диофантовых уравнений можно встретить в повседневной жизни. Например, при покупке чего-либо в магазине. На эту тему математики смогли придумать интересные задачи, обычно предлагающиеся ученикам на дополнительных занятиях.
Вот одна из них, появившаяся из реальной истории. Однажды математик пришёл в магазин приобрести свитер. Его цена составляла 19 рублей. У учёного же были с собой только купюры номиналом три рубля, а у кассира — пятирублёвки. Задача состоит в том, чтобы выяснить, сможет ли состояться сделка. Иными словами, необходимо найти, сколько нужно математику дать купюр, и какое их количество он получит от кассира.
Рассуждать нужно следующим образом. В задачи есть два неизвестных: количество трёхрублёвых и пятирублёвых купюр. Поэтому можно составить уравнение: 3x — 5y = 19. По сути, уравнение с двумя неизвестными может иметь бесчисленное число решений, но не всегда из них может найтись хотя бы одно целое положительное.
Итак, зная, что неизвестные должны быть целыми положительными числами, нужно выразить неизвестное с меньшим коэффициентом через остальные члены. Получится равенство: 3 x = 19 + 5 y. Левую и правую часть можно разделить на три, а после выполнить простейшие преобразования: x = (19 + 5y) / 3 = 6 + y + (1 + 2y) / 3. Учитывая, что неизвестные и свободный член это целые числа, выражение (1 + 2y) / 3 можно заменить буквой r, также являющимся каким-то целым числом.
Тогда уравнение можно переписать как x = 6 + y + t. Отсюда t = (1 + 2y) / 3 или y = t + (t — 1) / 2. Снова можно сделать вывод, что (t — 1) / 2 — какое-то целое число. Если заменить его на t1, выражение примет вид: y = t + t1.
Подставив t = 2t1 + l в равенство можно получить, что x = 8 + 5t1, а y = 1 + 3t1. Таким образом, решением уравнения будут полученные равенства. Исходя из того, что результат должен быть положительным, равенства можно переписать в неравенства вида:8 + 5t1> 0, 1 + 3t1 > 0. Отсюда определить диапазон, ограничивающий t1. Беря во внимание только плюсовую часть диапазона, можно сделать заключение, что возможные варианты решения лежать в пределе от нуля до плюс бесконечности.
Подставляя по очереди числа, можно определить значения x и y. Искомый ряд будет выглядеть следующим образом: {x = 8 + 5t} 1 = 8, 13, 18, 23, …, n; {у = 1 + 3t} 1 = 1, 4, 7, 10,…, m. То есть математик, дав восемь купюр, получит одну на сдачу, а если он отдаст 13 купюр, то продавец должен будет ему выдать четыре пятирублёвки. Этот ряд можно продолжать до бесконечности.
Использование онлайн-калькулятора
Существуют сайты, рассчитывающие линейные уравнения в автоматическом режиме. Они называются математическими онлайн-калькуляторами. Пользователю, желающему воспользоваться их услугами, нужно иметь лишь подключение к интернету и любой веб-браузер.
Свои услуги сервисы предоставляют бесплатно. При этом часто на их страницах содержится краткий теоретический материал, посвящённый решению диофантовых уравнений. Кроме того, пользователю предоставляется возможность ознакомиться с решением типовых примеров.
Из нескольких десятков таких сайтов на русском языке можно отметить следующие:
- HostCiti;
- PocketTeacher;
- Upbyte;
- Planetcalc;
- Math24.
Все приведённые сайты имеют интуитивно понятный интерфейс и бесплатны. После того как пользователь введёт в предложенную форму нужные уравнения и запустит расчётчик, онлайн-сервисы не только выдадут ответ, но и выведут на экран пошаговое решение с объяснениями. Таким образом, эти сервисы помогают не только быстро и верно найти решение, но и дают возможность пользователю понять принципы вычисления, проверить самостоятельно выполненный расчёт.
Диофантовы уравнения задачи с решениями и пояснениями
Задача 1. Допустим, в аквариуме живут осьминоги и морские звёзды. У осьминогов по 8 ног, а у морских звёзд – по 5. Всего конечностей насчитывается 39. Сколько в аквариуме животных?
Решение. Пусть х — количество морских звёзд, у – количество осьминогов. Тогда у всех осьминогов по 8у ног, а у всех звёзд 5х ног. Составим уравнение: 5х + 8у = 39.
Заметим, что количество животных не может выражаться нецелым или отрицательным числами. Следовательно, если х – целое неотрицательное число, то и у=(39 – 5х)/8 должно быть целым и неотрицательным, а, значит, нужно, чтобы выражение 39 – 5х без остатка делилось на 8. Простой перебор вариантов показывает, что это возможно только при х = 3, тогда у = 3. Ответ: (3; 3).
Уравнения, вида ах+bу=с, называются диофантовыми, по имени древнегреческого математика Диофанта Александрийского. Жил Диофант, по-видимому, в 3 в. н. э., остальные известные нам факты его биографии исчерпываются таким стихотворением-загадкой, по преданию выгравированным на его надгробии:
Прах Диофанта гробница покоит; дивись ей и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругой он обручился.
С нею, пять лет, проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Сколько же лет прожил Диофант Александрийский?
Задача 2. На складе имеются гвозди в ящиках по 16,17 и 40 кг. Может ли кладовщик выдать 100 кг гвоздей, не вскрывая ящики? (метод прямого перебора)
Разберем метод решения относительно одного неизвестного.
Задача 3. В каталоге картинной галереи всего 96 картин. На каких-то страницах расположено 4 картины, а на каких-то 6. Сколько страниц каждого вида есть в каталоге?
Решение. Пусть х – количество страниц с четырьмя картинами,
у – количество страниц с шестью картинами,
тогда по условию этой задачи можно составить уравнение:
Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. В нашем случае это 4х, то есть:
Делим все уравнение на этот коэффициент:
Остатки при делении на 4: 1,2,3. Подставим вместо у эти числа.
Если у=1, то х=(96-6∙1):4=90:4 — Не походит, решение не в целых числах.
Если у=2, то х=(96-6∙2):4=21 – Подходит.
Если у=3, то х=(96-6∙3):4=78:4 — Не походит, решение не в целых числах.
Итак, частным решением является пара (21;2), а это значит, что на 21 странице расположено по 4 картины, а на 2 страницах по 6 картин.
Разберем метод решения с использованием алгоритма Евклида.
Задача 4. В магазине продаётся шоколад двух видов: молочный и горький. Весь шоколад хранится в коробках. Молочного шоколада на складе имеется 7 коробок, а горького 4. Известно, что горького шоколада было на одну плитку больше. Сколько плиток шоколада находятся в коробках каждого вида?
Решение. Пусть х – количество плиток молочного шоколада в одной коробке,
у – количество плиток горького шоколада в одной коробке,
тогда по условию этой задачи можно составить уравнение:
Решим это уравнение, используя алгоритм Евклида.
Выразим 7=4∙1+3, => 3=7-4∙1.
Выразим 4=3∙1+1, => 1=4-3∙1=4-(7-4∙1)=4-7+4∙1=4∙2-7∙1=1.
Итак, получается х=1; у=2.
А это значит, что молочный шоколад лежит в коробке по 1 штуке, а горький по 2 штуки.
Разберем метод поиска частного решения и общей формулы решений.
Задача 5. В африканском племени Тумбе-Юмбе два аборигена Тумба и Юмба работают парикмахерами, причем Тумба всегда заплетает своим клиентам по 7 косичек, а Юмба по 4 косички. Сколько клиентов обслужили мастера по отдельности за смену, если известно, что вместе они заплели 53 косички?
Решение. Пусть х – количество клиентов Тумбы,
у – количество клиентов Юмбы,
Теперь чтобы найти частные решения уравнения ( , ), заменим данную нам сумму чисел на 1. Это заметно упростит поиск подходящих чисел. Получим:
Решим это уравнение методом подстановки.
Остатки при делении на 4: 1, 2, 3. Подставим вместо х эти числа:
Если х=1, то у=(1-7):4 – не подходит, т.к. решение не в целых числах.
Если х=2, то у=(1-7∙2):4 – не подходит, т.к. решение не в целых числах.
Если х=3, то у=(1-7∙3):4=-5 – подходит.
Затем умножим получившиеся значения на начальное значение суммы, которую мы заменяли на 1, т.е.
Мы нашли частное решение уравнения(1). Проверим его, подставив начальное уравнение:
Ответ сошелся. Если бы, мы решали абстрактное уравнение, то можно было бы на этом остановиться. Однако мы решаем задачу, а поскольку Тумба не мог заплести отрицательное число косичек, нам необходимо продолжать решение. Теперь составим формулы для общего решения. Чтобы это сделать вычтем из начального уравнения(1) уравнение с подставленными значениями (3). Получим:
Вынесем общие множители за скобки:
Перенесем одно из слагаемых из одной части уравнения в другую:
Теперь стало видно, что чтобы уравнение решалось (х-159) должно делиться на -4, а (у+265) должно делиться на 7. Введем переменную n, которая будет отображать это наше наблюдение:
Перенесем слагаемые из одной части уравнения в другую:
Мы получили общее решение данного уравнения, теперь в него можно подставлять различные числа и получать соответствующие ответы.
Например, пусть n=39, тогда
А это значит, что Тумба заплел косички 3 клиентам, а Юмба 8 клиентам.
Решите задачи различными методами.
Задача 6: Вовочка купил ручки по 8 рублей и карандаши по 5 рублей. Причем за все карандаши он заплатил на 19 рублей больше, чем за все ручки. Сколько ручек и сколько карандашей купил Вовочка? (метод поиска общего решения, решение относительно одного не известного, использование алгоритма Евклида).
Задача 7. Куплены фломастеры по 7 рублей и карандаши по 4 рубля за штуку, всего на сумму 53 рубля. Сколько куплено фломастеров и карандашей?
Задача 8.(муниципальный тур ВОШ 2014-2015 г.) : на планете С в ходу два вида монет: по 16 тугриков и по 27 тугриков. Можно ли с их помощью купить товар, ценой в 1 тугрик?
Задача 9. Шехерезада рассказывает свои сказки великому правителю. Всего она должна рассказать 1001 сказку. Сколько ночей потребуется Шехерезаде, чтобы рассказать все свои сказки, если в какие-то ночи она будет рассказывать по 3 сказки, а в какие-то по 5? За сколько ночей Шехерезада расскажет все свои сказки, если хочет сделать это как можно быстрее? Сколько ночей понадобится Шехерезаде, если ей утомительно рассказывать по пять сказок за ночь, поэтому таких ночей должно быть как можно меньше?
Задача10. (вспомним «Водолея») Как налить 3 литра воды, имея 9-литровую и 5-литровую емкости?
Задача 11. Вовочка отлично успевает по математике. В дневнике у него только пятерки и четверки, причем пятерок больше. Сумма всех Вовочкиных оценок по математике равна 47. Сколько Вовочка получил пятерок и сколько четверок?
Задача 12. Кощей Бессмертный устроил питомник по разведению Змеев Горынычей. В последнем выводке у него есть Змеи о 17-ти головах и о 19-ти головах. Всего этот выводок насчитывает 339 голов. Сколько 17-тиголовых и сколько 19-тиголовых Змеев вывелось у Кощея?
Ответы: Диофант прожил 84 года;
задача 2: 4 ящика по 17 кг и 2 ящика по 16 кг;
задача 6: куплено 7 карандашей и 8 ручек, то есть (7,2) – частное решение и у = 2 + 5n, х = 7 + 8n, где nє Z – общее решение;
задача 7: (-53; 106) – частное решение, х=4n-53, у=-7n+106 – общие решения, при n=14, х=3, у=8, то есть куплено 3фломастера и 8 карандашей;
задача 8: например, заплатить 3 монеты по 27 тугриков и получить сдачу 5 монет по 16 тугриков;
задача 9: (2002; -1001) – частное решение, х=-5 n+2002, у=3n-1001 – общее решение, при n=350, у=49, х=252, то есть 252 ночи по 3 сказки и 49 ночей по 5 сказок — всего 301 ночь; самый быстрый вариант: 2 ночи по три сказки и 199 ночей по 5 сказок — всего 201 ночь; самый долгий вариант: 332 ночи по 3 сказки и 1 ночь 5 сказок — всего 333 ночи.
задача 10: например, 2 раза налить воду 9-тилитровой банкой и 3 раза вычерпать ее 5-тилитровой банкой;
задача 11: Вовочка получил 7 пятерок и 4 четверки;
задача 12: 11 Змеев о 17-ти головах и 8 Змеев о 19-ти головах.
Линейное диофантово уравнение и 4 способа его решения
Разделы: Математика
Првило 1. Если с не делится на d, то уравнение ах + ву = с не имеет решений в целых числах. Н.О.Д.(а,в) = d.
Правило 2. Чтобы найти решение уравнения ах + ву = с при взаимно-простых а и в, нужно сначала найти решение (Хо ; уо) уравнения ах + ву = 1; числа СХо , Суо составляют решение уравнения ах + ву = с.
Решить в целых числах (х,у) уравнение
Первый способ. Нахождение частного решения методом подбора и запись общего решения.
Знаем, что если Н.О.Д.(а;в) =1, т.е. а и в взаимно-простые числа, то уравнение (1)
имеет решение в целых числах х и у. Н.О.Д.(5;8) =1. Методом подбора находим частное решение: Хо = 7; уо =2.
Итак, пара чисел (7;2) — частное решение уравнения (1).
Значит, выполняется равенство: 5 x 7 – 8 x 2 = 19 … (2)
Вопрос: Как имея одно решение записать все остальные решения?
Вычтем из уравнения (1) равенство (2) и получим: 5(х -7) – 8(у — 2) =0.
Отсюда х – 7 = 

Тем самым все целые решения исходного уравнения можно записать в таком виде:


Второй способ. Решение уравнения относительно одного неизвестного.
Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х — 8у = 19 


Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.
Если у = 0, то х = 

Если у =1, то х = 

Если у = 2, то х = 


Если у =3, то х = 

Если у = 4 то х = 

Итак, частным решением является пара (7;2).
Тогда общее решение: 

Третий способ. Универсальный способ поиска частного решения.
Для решения применим алгоритм Евклида. Мы знаем, что для любых двух натуральных чисел а, в, таких, что Н.О.Д.(а,в) = 1 существуют целые числа х,у такие, что ах + ву = 1.
1. Сначала решим уравнение 5m – 8n = 1 используя алгоритм Евклида.
2. Затем найдем частное решение уравнения (1)по правилу 2.
3. Запишем общее решение данного уравнения (1).
1. Найдем представление: 1 = 5m – 8n. Для этого используем алгоритм Евклида.
8 = 5 
5 = 3
3 = 2 
Из этого равенства выразим 1. 1 = 3 — 2 


= 3 — 5 




= 5
2. Частное решение уравнения (1): Хо = 19m; уо =19n.
Отсюда получим: Хо =19

Пара (-57; -38)- частное решение (1).
3. Общее решение уравнения (1): 

Четвертый способ. Геометрический.
1. Решим уравнение 5х – 8у = 1 геометрически.
2. Запишем частное решение уравнения (1).
3. Запишем общее решение данного уравнения (1).
Отложим на окружности последовательно друг за другом равные дуги, составляющие

На 5 – ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли 



Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1.
2. Частное решение уравнения (1): Хо = 19 
3. Общее решение уравнения (1): 

Алгебра. 7 класс
Конспект урока
Линейные диофантовы уравнения
Перечень рассматриваемых вопросов:
- Диофантово уравнение.
- Разрешимость диофантова уравнения.
- Решение задач с помощью диофантова уравнения.
Диофантовым уравнением называется уравнение вида ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с, х и у – целые числа.
Если c делится на НОД(а; b), то уравнение ах + bу = с имеет решение в целых числах. Если c не делится на НОД (а; b), то уравнение ах + bу = с не имеет решений в целых числах.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Определение диофантова уравнения.
Пусть дано уравнение ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с – целые числа. Если поставлена задача найти только такие его решения (х0; у0), где х0, у0 – целые числа, то это уравнение называют линейным диофантовым уравнением.
Диофантовы уравнения связаны с именем древнегреческого математика Диофанта Александрийского. О подробностях жизни Диофанта Александрийского практически ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век до нашей эры); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года нашей эры). Откуда можно сделать вывод, что жил он приблизительно в III веке нашей эры.
Решение диофантовых уравнений.
Решим линейное диофантово уравнение
Выразим у через х:
Из этого равенства видно, что у будет целым только тогда, когда целое число х делится на 3, т.е. х = 3х1, где х1 – некоторое целое число. Тогда у = 2 -2х1.
Таким образом, решениями уравнения являются все пары чисел (3х1;2 -2х1).
Приведём некоторые частные решения этого уравнения.
Если х1 = 0, то х = 3х1 = 0, а у = 2 — 2 х1 = 2; решением уравнения является пара (0;2).
Если х1 = 1, то х = 3х1 = 3, а у = 2 — 2 х1 = 0;
решением уравнения является пара (3; 0)
Аналогично можно найти и другие частные решения, их бесконечно много.
Решение задач при помощи линейных диофантовых уравнений.
Линейные диофантовы уравнения возникают при решении некоторых задач.
У покупателя и продавца имеются монеты только по 2р. и 5р. Сможет ли покупатель заплатить за покупку стоимостью 1р.?
Если покупатель даст х монет по 2р. и у монет по 5 р., то он заплатит (2х + 5у) р. А по условию задачи это 1р. Составим уравнение:
Выразим х через у из уравнения:
Из равенства видно, что х будет целым только тогда, когда у будет нечетным числом: у = 2m + 1, где m – целое число.
Таким образом, решением уравнения являются все пары чисел (-5m – 2; 2m + 1), где m – любое целое число.
Таким образом, способов оплаты товара стоимостью 1р. Бесконечно много. Если х окажется отрицательным, то это означает, что покупатель должен получить сдачу: х монет по 2р.
Например, пара (-2; 1) является решением уравнения. Это означает, что покупатель далодну монету по 5 р. и получил сдачу 2 монеты по 2р.
Разрешимость диофантова уравнения.
Не каждое диофантово уравнение имеет решение в целых числах.
Рассмотрим на примере уравнения
3х + 6у = 2 алгоритм, с помощью которого можно определить, имеет оно решение в целых числах.
1 шаг. Надо найти наибольший общий делитель чисел 3 и 6. НОД(3; 6) = 3.
2 шаг. Определить, делится ли 2 на НОД(3; 6).
3 шаг. Если 2 делится на НОД(3; 6), то уравнение имеет решение в целых числах.
Если 2 не делится на НОД (3; 6), то уравнение не имеет решений в целых числах.
Расширенный алгоритм Евклида для решения диофантовых уравнений.
Для нахождения наибольшего общего делителя двух целых неотрицательных чисел используют алгоритм Евклида. Рассмотрим его реализацию на примере чисел 24 и 17.
Разделим большее из этих чисел на меньшее, то есть 24 на 17.
Получаем 24 : 17 = 1 (ост. 7), что можно записать в виде равенства:
Теперь разделим делитель на остаток, то есть 17 на 7, получим:
Снова разделим делитель на остаток:
Выполним деление еще раз:
Мы получили остаток, равный нулю, так как 3 делится на 1 без остатка.
В представленной последовательности действий мы получали остатки: 7, 3, 1, 0. Последний остаток, не считая 0, является наибольшим общим делителем чисел 24 и 17. То есть, НОД(24; 17) = 1.
Рассмотрим еще один пример: НОД(612; 342)?
612 = 342 ∙ 1 + 270,
342 = 270 ∙ 1 + 72,
Теперь выполним действия «в обратном направлении», то есть выразим 18 (остаток) через числа 612 и 342.
Для этого в каждой строчке последовательности Евклида выразим остатки через делимое и делитель (второй столбик таблицы):
612 = 342 ∙ 1 + 270
342 = 270 ∙ 1 + 72
270 = 612 – 342 ∙ 1
72 = 342 – 270 ∙ 1
Получаем, 18 = 72 – 54 ∙ 1 = 72 – (270 – 72 ∙ 3) = 342 – 270 ∙ 1 – (270 – (342 — 270 ∙ 1) ∙3) =
342 – ((612 – 342 ∙1) ∙ 1) – (612 – 342 ∙ 1 – (342 – (612 – 342 ∙ 1)) ∙3) = 342 – 612 + 342 – 612 + 342 + 342 ∙ 3 – 612 ∙ 3 + 342 ∙ 3 = 342 ∙ 9 – 612 ∙ 5 = 342 ∙ 9 + 612 ∙ (-5).
То есть 18 = 9 ∙ 342 + (-5) ∙ 612.
Умение выполнять действия алгоритма «в обратном направлении» понадобится нам в решении диофантовых уравнений при помощи расширенного алгоритма Евклида.
Пример: решите уравнение 24x−17y=2.
Найдем при помощи алгоритма Евклида НОД(24, 17):
Выполним действия «в обратном направлении»:
1 = 7 – 3 · 2 = 7 − (17 – 7 · 2) · 2 = 7 – 17 · 2 + 7 · 4 + 5 · 7 – 2 · 17 = 5 · (24 – 17 · 1) – 2 · 17 = 5 · 24 – 5 · 17 – 2 · 17 = 5 · 24 – 7 · 17 = 24 · 5 – 17 · 7.
24 · 5 – 17 · 7 = 1; В исходном уравнении в правой части стоит число 2. Поэтому умножим обе части уравнения на 2. Получим:
24 · 10 – 17 · 14 = 2.
То есть, x0 = 10, y0 = 14 – частные решения уравнения 24x −17y = 2.Если уравнение имеет одно решение в целых числах, то оно имеет бесконечное множество других решений.
Прибавим коэффициент b к значению х.
Чтобы значение исходного уравнения не изменилось, при прибавлении одного числа к х нужно вычесть другое число изу:
(-7; -10) – еще одно решение уравнения.
Значения x будут равны сумме исходного решения (х0) и любого кратного коэффициента b. То есть х = 10 + (-17t), где t – целое число.
А значение у – равны разности у0 и любого кратного коэффициента а. То есть у = 14 – 24t.
Ответ: (10 − 17t, 14 − 24t), t ∈ Z.
Разбор заданий тренировочного модуля.
1. Решите задачу:
Некий чиновник купил ослов и быков за 1770 талеров. За каждого осла он уплатил по 31 талеру, а за каждого быка – по 21 талеру. Сколько ослов и быков купил чиновник?
Пусть чиновник купил х ослов и у быков. Тогда 31х + 21у = 1770.
По смыслу задачи х и у – натуральные числа. Так как 21 и 1770 делятся на 3, то 31х делится на 3, т. е. х делится на 3: х = 3n, где n – натуральное число. Тогда 31n + 7у = 590. Откуда n =
Очевидно, что n будет целым, если 7у – 1 делится на 31.
Наименьшее натуральное у, при котором это произойдет, равно 9. При этом n = 17, х = 51. Первое решение найдено: (51; 9).
Заметим, что следующие целые n будут получаться в результате увеличения у = 9 на число, кратное 31.
При у = 9 + 21 = 40 имеем n = 10, х = 30.
При у = 40 + 9 имеем n = 3, х = 9.
При следующих значениях у значения n отрицательны. Таким образом, исходное уравнение имеет 3 решения: (51, 9), (30, 40), (9, 71).
Ответ: (51, 9), (30, 40), (9, 71).
2. Решение уравнения.
Разделите уравнения на 2 группы: уравнение имеет решение в целых числах, уравнение не имеет решений в целых числах.
1) НОД(7; 5) = 1, 2 делится на 1, следовательно, 7х – 5у = 2 имеет решение в целых числах.
2) НОД(3; 5) = 1, 10 делится на 1, следовательно, 3х + 5у = 10 имеет решение в целых числах.
3) НОД(2; 4) = 2, -1 не делится на 2, следовательно, 2х + 4у = -1 не имеет решений в целых числах.
4) НОД(3; 9) = 3, 10 не делится на 3, следовательно, 3х – 9у = 10 не имеет решений в целых числах.
5) НОД(6; 9) = 3, 2 не делится на 3, следовательно, 6х + 9у = 2 не имеет решений в целых числах.
6) НОД(2; 5) = 1, 15 делится на 1, следовательно, 2х – 5у = 15 имеет решение в целых числах.
источники:
http://urok.1sept.ru/articles/501260
http://resh.edu.ru/subject/lesson/7275/conspect/
Пример 16. Диофантовы уравнения в задаче реального ЕГЭ
Главная /Курс по свойствам чисел (Задание 18) /Пример 16. Диофантовы уравнения в задаче реального ЕГЭ
Чтобы получить доступ к бесплатным материалам, пожалуйста зарегистрируйтесь.
Извините, у Вас нет прав просматривать контент!
Регистрация
Войти
Следующий урок























































































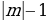 , тогда mx + ny = k
, тогда mx + ny = k 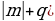 y = k
y = k