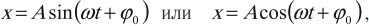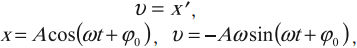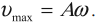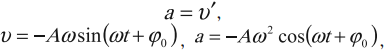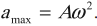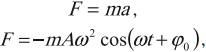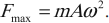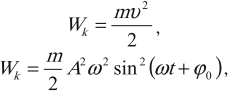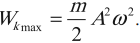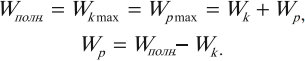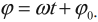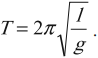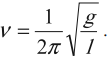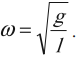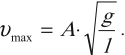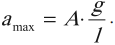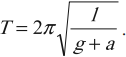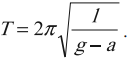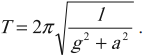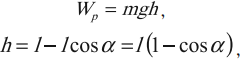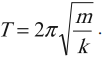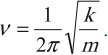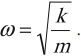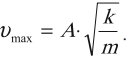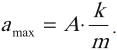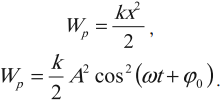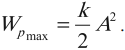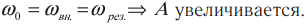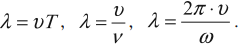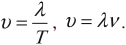Каталог заданий.
Волны
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 3 № 621
Диапазон голоса мужского баса занимает частоты от до
Каково отношение граничных длин звуковых волн
этого диапазона?
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.5.5 Звук. Скорость звука
Решение
·
·
2 комментария · Сообщить об ошибке · Помощь
2
Тип 3 № 622
Диапазон звуков скрипки занимает частотный интервал от до
Каково отношение граничных длин звуковых волн
этого интервала?
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.5.5 Звук. Скорость звука
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 3 № 623
Диапазон звуков фортепиано занимает частотный интервал от до
Каково отношение граничных длин звуковых волн
этого интервала?
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.5.5 Звук. Скорость звука
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 3 № 624
Диапазон частот ультразвуковых волн, применяемых в физиотерапии, занимает частотный интервал от до
Каково отношение граничных длин звуковых волн
этого интервала?
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.5.5 Звук. Скорость звука
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 3 № 625
Средняя частота звуковых волн мужского голоса а женского
Каково отношение средних длин звуковых волн
мужского и женского голоса?
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.5.5 Звук. Скорость звука
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
Механические волны.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: механические волны, длина волны, звук.
Механические волны — это процесс распространения в пространстве колебаний частиц упругой среды (твёрдой, жидкой или газообразной).
Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.
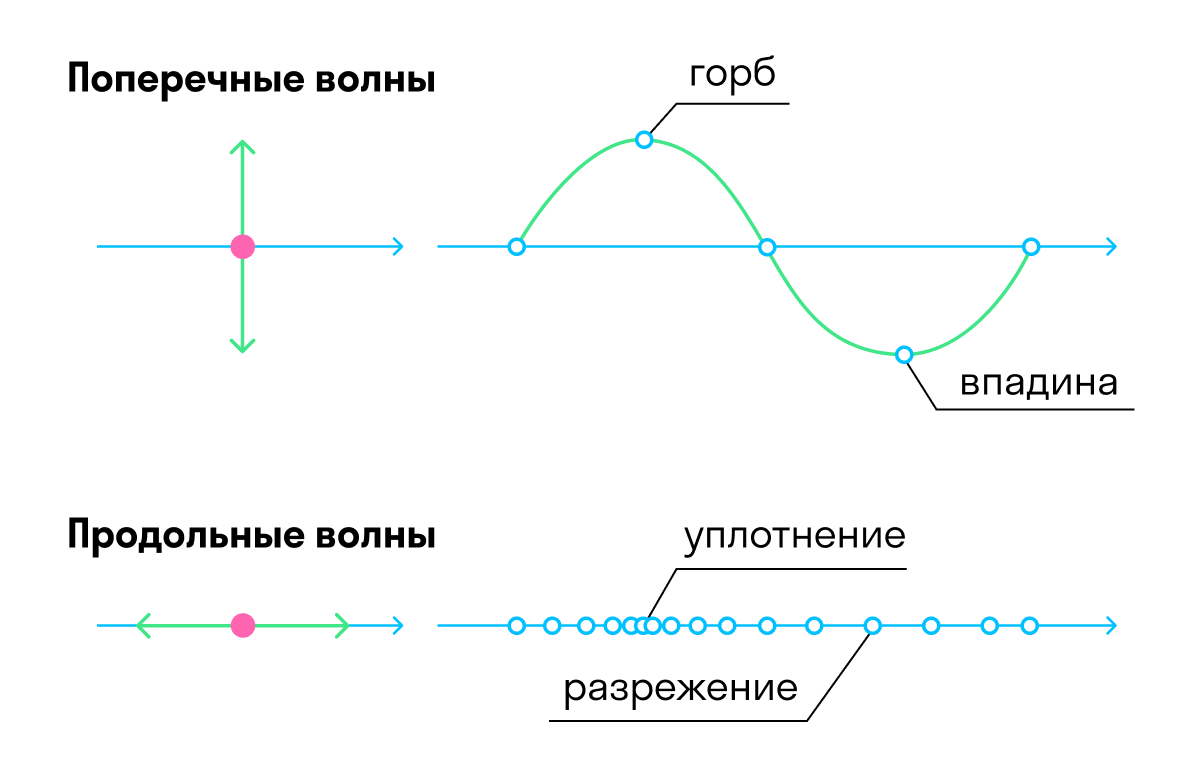
Продольные и поперечные волны.
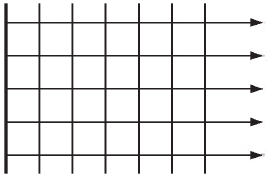
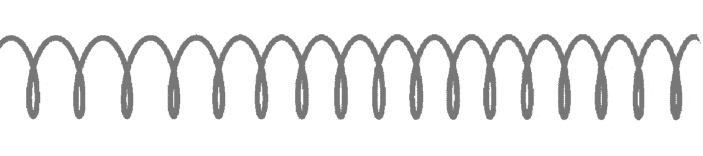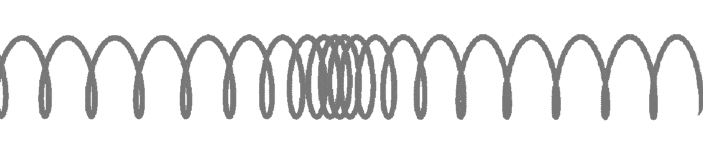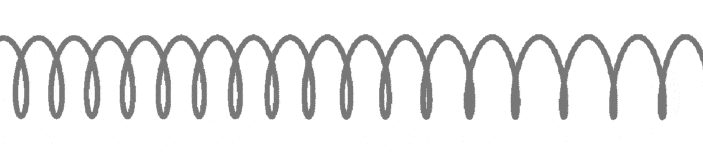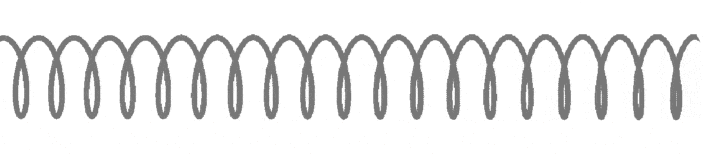
Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия. На рис. 1 показана продольная волна, представляющая собой колебания плоских слоёв среды; направление, вдоль которого колеблются слои, совпадает с направлением распространения волны (т. е. перпендикулярно слоям).
 |
| Рис. 1. Продольная волна |
Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого. На рис. 2 каждый слой колеблется вдоль самого себя, а волна идёт перпендикулярно слоям.
 |
| Рис. 2. Поперечная волна |
Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.
Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов*.
Важно отметить, что частицы среды при прохождении волны совершают колебания вблизи неизменных положений равновесия, т. е. в среднем остаются на своих местах. Волна, таким образом, осуществляет
перенос энергии, не сопровождающийся переносом вещества.
Наиболее просты для изучения гармонические волны. Они вызываются внешним воздействием на среду, меняющимся по гармоническому закону. При распространении гармонической волны частицы среды совершают гармонические колебания с частотой, равной частоте внешнего воздействия. Гармоническими волнами мы в дальнейшем и ограничимся.
Рассмотрим процесс распространения волны более подробно. Допустим, что некоторая частица среды (частица ) начала совершать колебания с периодом
. Действуя на соседнюю частицу
она потянет её за собой. Частица
в свою очередь, потянет за собой частицу
и т. д. Так возникнет волна, в которой все частицы будут совершать колебания с периодом
.
Однако частицы имеют массу, т. е. обладают инертностью. На изменение их скорости требуется некоторое время. Следовательно, частица в своём движении будет несколько отставать от частицы
, частица
будет отставать от частицы
и т. д. Когда частица
пустя время
завершит первое колебание и начнёт второе, своё первое колебание начнёт частица
, находящаяся от частицы
на некотором расстоянии
.
Итак, за время, равное периоду колебаний частиц, возмущение среды распространяется на расстояние . Это расстояние называется длиной волны. Колебания частицы
будут идентичны колебаниям частицы
колебания следующей частицы
будут идентичны колебаниям частицы
и т. д. Колебания как бы воспроизводят себя на расстоянии
можно назвать пространственным периодом колебаний; наряду с временным периодом
она является важнейшей характеристикой волнового процесса. В продольной волне длина волны равна расстоянию между соседними сжатиями или разрежениями (рис. 1). В поперечной — расстоянию между соседними горбами или впадинами (рис. 2). Вообще, длина волны равна расстоянию (вдоль направления распространения волны) между двумя ближайшими частицами среды, колеблющимися одинаково (т. е. с разностью фаз, равной
).
Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:
.
Частотой волны называется частота колебаний частиц:
.
Отсюда получаем связь скорости волны, длины волны и частоты:
. (1)
| На поверхности жидкости могут существовать волны особого типа, похожие на поперечные — так называемые поверхностные волны. Они возникают под действием силы тяжести и силы поверхностного натяжения. |
Звук.
Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше — область ультразвука.
К основным характеристикам звука относятся громкость и высота.
Громкость звука определяется амплитудой колебаний давления в звуковой волне и измеряется в специальных единицах —децибелах (дБ). Так, громкость 0 дБ является порогом слышимости, 10 дБ — тиканье часов, 50 дБ — обычный разговор, 80 дБ — крик, 130 дБ — верхняя граница слышимости (так называемый болевой порог).
Тон — это звук, который издаёт тело, совершающее гармонические колебания (например, камертон или струна). Высота тона определяется частотой этих колебаний: чем выше частота, тем выше нам кажется звук. Так, натягивая струну, мы увеличиваем частоту её колебаний и, соответственно, высоту звука.
Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах — больше, чем в жидкостях.
Например, скорость звука в воздухе при равна примерно 340 м/с (её удобно запомнить как «треть километра в секунду»)*. В воде звук распространяется со скоростью около 1500 м/с, а в стали — около 5000 м/с.
Заметим, что частота звука от данного источника во всех средах одна и та же: частицы среды совершают вынужденные колебания с частотой источника звука. Согласно формуле (1) заключаем тогда, что при переходе из одной среды в другую наряду со скоростью звука изменяется длина звуковой волны.
| Если хочешь найти расстояние до грозовых туч в километрах, посчитай, через сколько секунд после молнии придёт гром, и раздели полученное число на три. |
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Механические волны.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Фаза колебаний
Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс.
Для гармонических колебаний
$X(t)=Acos(ωt+φ_0)$
где $φ=ωt+φ_0$ — фаза колебания, $А$ — амплитуда, $ω$ — круговая частота, $t$ — время, $φ_0$ — начальная (фиксированная) фаза колебания: в момент времени $t=0$ $φ=φ_0$. Фаза выражается в радианах.
Фаза гармонического колебания при постоянной амплитуде определяет не только координату колеблющегося тела в любой момент времени, но и скорость и ускорение, которые тоже изменяются по гармоническому закону (скорость и ускорение гармонических колебаний — это первая и вторая производные по времени функции $X(t)=Acos(ωt+φ_0)$, которые, как известно, снова дают синус и косинус). Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени.
Два колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами. Так как $ω={2π}/{T}$, то
$φ-φ_0=ωt={2πt}/{T}$
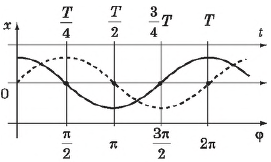
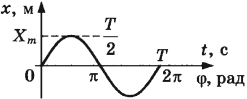
Отношение ${t}/{T}$ показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженной в радианах. Сплошная кривая — это зависимость координаты от времени и одновременно от фазы колебаний (верхние и нижние значения на оси абсцисс соответственно) для точки, совершающей гармонические колебания по закону:
$x=x_{m}cosω_{0}t$
Здесь начальная фаза равна нулю $φ_0=0$. В начальный момент времени амплитуда максимальна. Это соответствует случаю колебаний тела, прикрепленного к пружине (или маятника), которое в начальный момент времени отвели от положения равновесия и отпустили. Описание колебаний, начинающихся из положения равновесия (например, при кратковременном толчке покоящегося шарика), удобнее вести с помощью функции синуса:
$x=sinω_{0}t$
Как известно, $cosφ=sin(φ+{π}/{2})$, поэтому колебания, описываемые уравнениями $x=x_{m}cosω_{0}t$ и $x=sinω_{0}t$, отличаются друг от друга только фазами. Разность фаз, или сдвиг фаз, составляет ${π}/{2}$. Чтобы определить сдвиг фаз, нужно колеблющуюся величину выразить через одну и ту же тригонометрическую функцию — косинус или синус. Пунктирная кривая сдвинута относительно сплошной на ${π}/{2}$.
Сравнивая уравнения свободных колебаний, координаты, скорости и ускорения материальной точки, находим, что колебания скорости опережают по фазе на ${π}/{2}$, а колебания ускорения — на $π$ колебания смещения (координаты).
Затухающие колебания
Затухание колебаний — это уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Свободные колебания всегда являются затухающими колебаниями.
Потери энергии колебаний в механических системах связаны с превращением ее в теплоту вследствие трения и сопротивления окружающей среды.
Так, механическая энергия колебаний маятника расходуется на преодоление сил трения и сопротивления воздуха, переходя при этом во внутреннюю энергию.
Амплитуда колебаний постепенно уменьшается, и через некоторое время колебания прекращаются. Такие колебания называются затухающими.
Чем больше силы сопротивления движению, тем быстрее прекращаются колебания. Например, в воде колебания прекращаются быстрее, чем в воздухе.
Упругие волны (механические волны)
Возмущения, распространяющиеся в пространстве, удаляясь от места их возникновения, называют волнами.
Упругие волны — это возмущения, распространяющиеся в твердой, жидкой и газообразной средах благодаря действию в них сил упругости.
Сами эти среды называют упругими. Возмущение упругой среды — это любое отклонение частиц этой среды от своего положения равновесия.
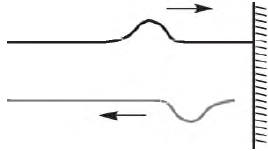
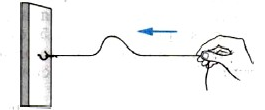
Возьмем, например, длинную веревку (или резиновую трубку) и прикрепим один из ее концов к стене. Туго натянув веревку, резким боковым движением руки создадим на ее незакрепленном конце кратковременное возмущение. Мы увидим, что это возмущение побежит вдоль веревки и, дойдя до стены, отразится назад.
Начальное возмущение среды, приводящее к появлению в ней волны, вызывается действием в ней какого-нибудь инородного тела, которое называют источником волны. Это может быть рука человека, ударившего по веревке, камешек, упавший в воду, и т. д.
Если действие источника носит кратковременный характер, то в среде возникает так называемая одиночная волна. Если же источник волны совершает длительное колебательное движение, то волны в среде начинают идти одна за другой. Подобную картину можно увидеть, поместив над ванной с водой вибрирующую пластину, имеющую наконечник, опущенный в воду.
Необходимым условием возникновения упругой волны является появление в момент возникновения возмущения сил упругости, препятствующих этому возмущению. Эти силы стремятся сблизить соседние частицы среды, если они расходятся, и отдалить их, когда они сближаются. Действуя на все более удаленные от источника частицы среды, силы упругости начинают выводить их из положения равновесия. Постепенно все частицы среды одна за другой вовлекаются в колебательное движение. Распространение этих колебаний и проявляется в виде волны.
В любой упругой среде одновременно существуют два вида движения: колебания частиц среды и распространение возмущения. Волна, в которой частицы среды колеблются вдоль направления ее распространения, называется продольной, а волна, в которой частицы среды колеблются поперек направления ее распространения, называется поперечной.
Продольная волна
Волна, в которой колебания происходят вдоль направления распространения волны, называется продольной.
В упругой продольной волне возмущения представляют собой сжатия и разрежения среды. Деформация сжатия сопровождается возникновением сил упругости в любой среде. Поэтому продольные волны могут распространяться во всех средах (и в жидких, и в твердых, и в газообразных).
Пример распространения продольной упругой волны изображен на рисунке. По левому концу длинной пружины, подвешенной на нитях, ударяют рукой. От удара несколько витков сближаются, возникает сила упругости, под действием которой эти витки начинают расходиться. Продолжая движение по инерции, они будут продолжать расходиться, минуя положение равновесия и образуя в этом месте разрежение. При ритмичном воздействии витки на конце пружины будут то сближаться, то отходить друг от друга, т. е. колебаться возле своего положения равновесия. Эти колебания постепенно передадутся от витка к витку вдоль всей пружины. По пружине распространятся сгущения и разрежения витков, или упругая волна.
Поперечная волна
Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными.
В поперечной упругой волне возмущения представляют собой смещения (сдвиги) одних слоев среды относительно других. Деформация сдвига приводит к появлению сил упругости только в твердых телах: сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому поперечные волны могут распространяться только в твердых телах.
Плоская волна
Плоская волна — это волна, у которой направление распространения одинаково во всех точках пространства.
В такой волне амплитуда не меняется со временем (по мере удаления от источника). Получить такую волну можно, если большую пластину, находящуюся в сплошной однородной упругой среде, заставить колебаться перпендикулярно плоскости. Тогда все точки среды, примыкающей к пластине, будут колебаться с одинаковыми амплитудами и одинаковыми фазами. Распространяться эти колебания будут в виде волн в направлении нормали к пластине, причем все частицы среды, лежащие в плоскостях, параллельных пластине, будут колебаться с одинаковыми фазами.
Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называется волновой поверхностью, или фронтом волны.
С этой точки зрения плоской волне можно дать и следующее определение.
Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Линия, нормальная к волновой поверхности, называется лучом. Вдоль лучей происходит перенос энергии волны. Для плоских волн лучи — это параллельные прямые.
Уравнение плоской синусоидальной волны имеет вид:
$s=s_{m}sin[ω(t-{x}/{υ})+φ_0]$
где $s$ — смещение колеблющейся точки, $s_m$ — амплитуда колебаний, $ω$ — циклическая частота, $t$ — время, $х$ — текущая координата, $υ$ — скорость распространения колебаний или скорость волны, $φ_0$ — начальная фаза колебаний.
Сферическая волна
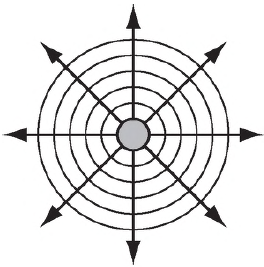
Сферической называется волна, волновые поверхности которой имеют вид концентрических сфер. Центр этих сфер называется центром волны.
Лучи в такой волне направлены вдоль радиусов, расходящихся от центра волны. На рисунке источником волны является пульсирующая сфера.
Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны. Уравнение сферической волны имеет вид:
$s={a_0}/{r}sin[ω(t-{r}/{υ})+φ_0]$
В отличие от плоской волны, где $s_m=A$ — амплитуда волны постоянная величина, в сферической волне она убывает с расстоянием от центра волны.
Длина и скорость волны
Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около $5$ км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
$λ=υT$
где $υ$ — скорость волны, $Т$ — период колебаний в волне, $λ$ (греческая буква лямбда) — длина волны.
Формула $λ=υT$ выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте $v$, т. е. $T={1}/{v}$, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
$λ=υT=υ{1}/{v}$
откуда
$υ=λv$
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
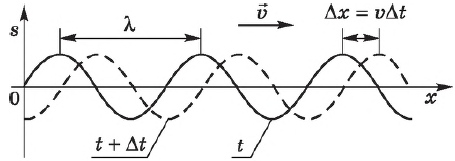
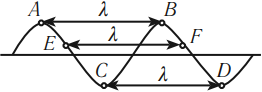
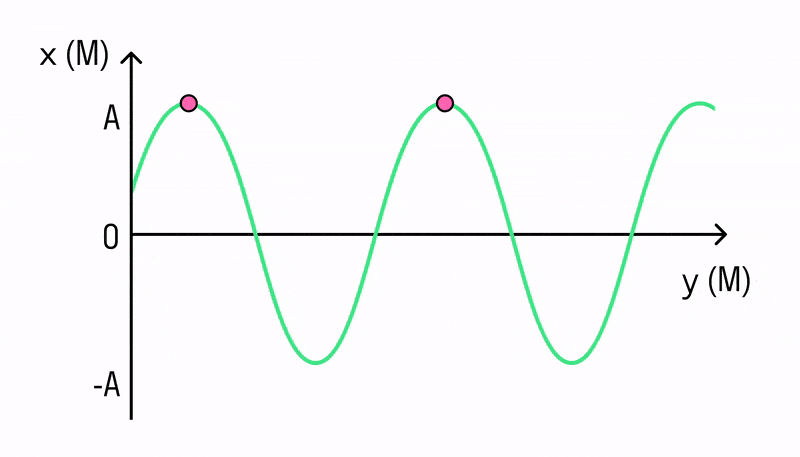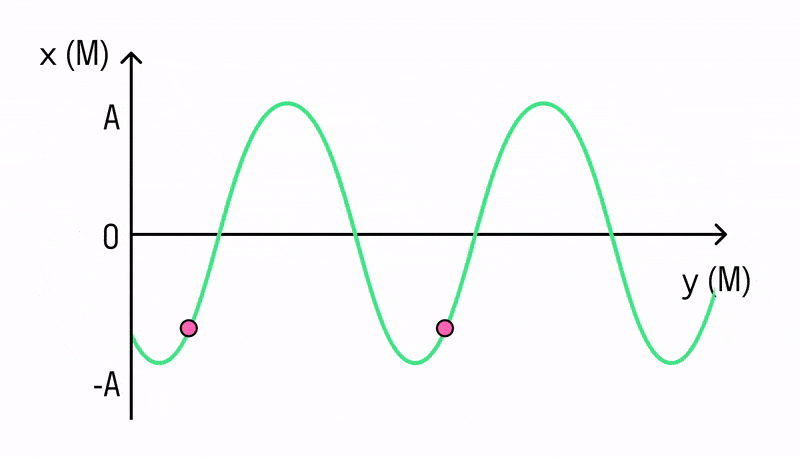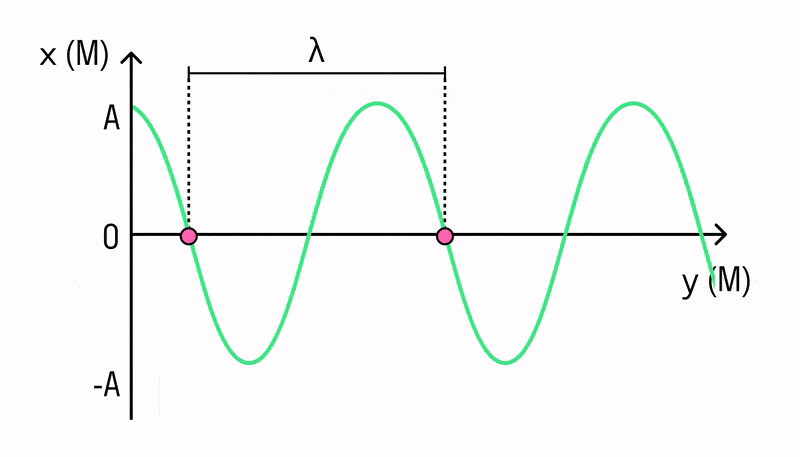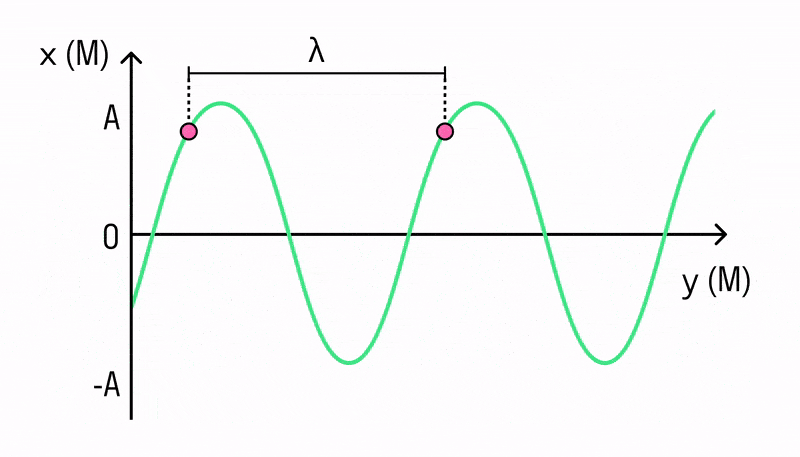
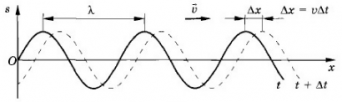
Длина волны — это пространственный период волны. На графике волны длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Рисунок — это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени $t$ и $t+∆t$. Ось $х$ совпадает с направлением распространения волны, на оси ординат отложены смещения $s$ колеблющихся частиц среды.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
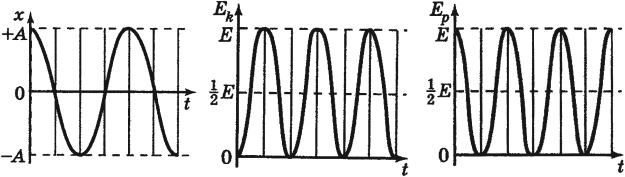
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
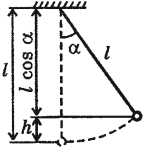
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
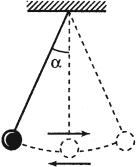
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
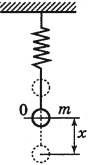
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
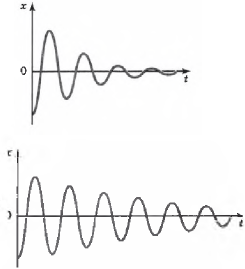
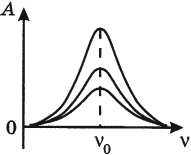
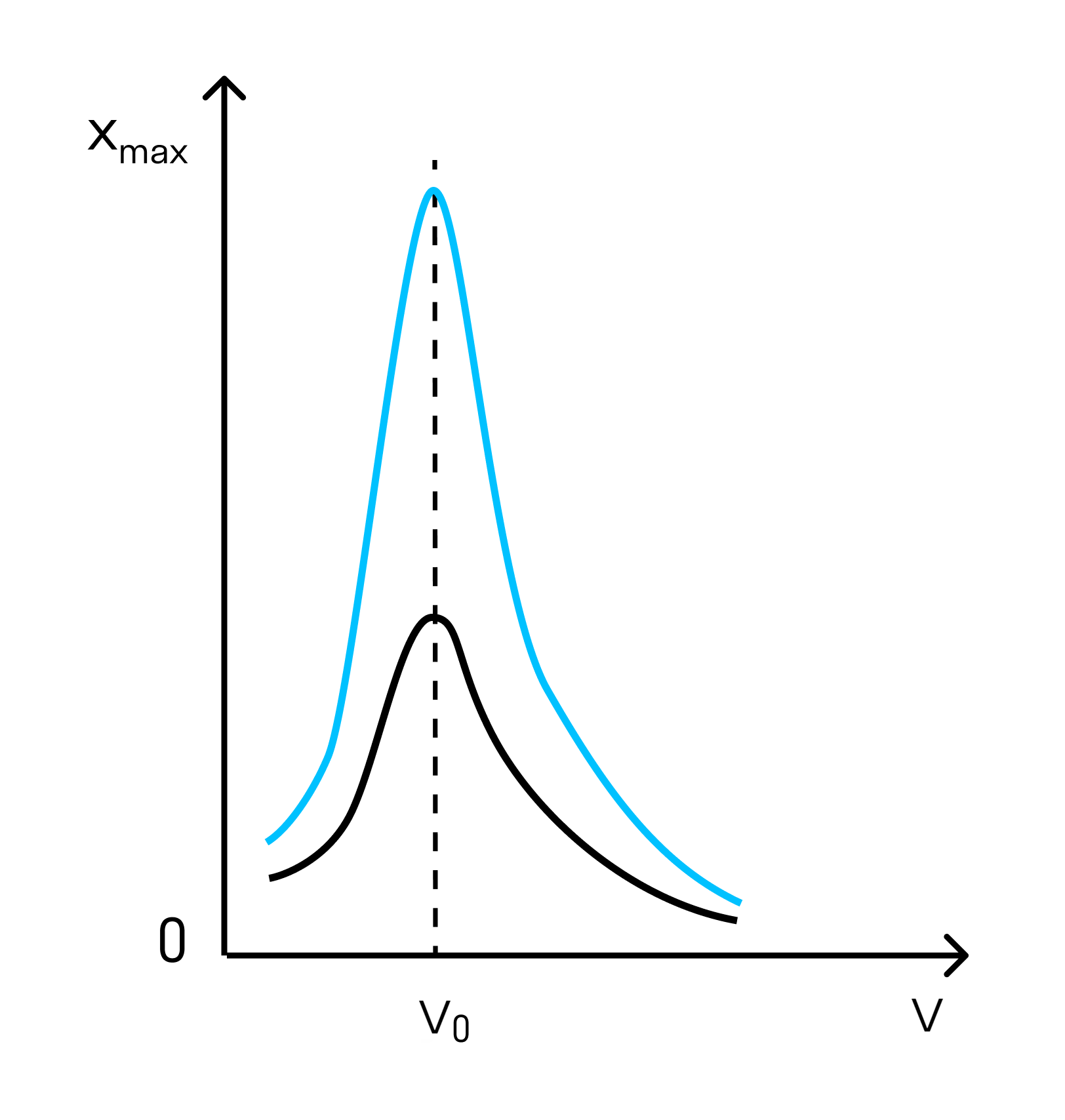
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
2.9 (58.03%) 132 votes
Волна: продольная и поперечная
Начнем с того, что волна — это распространение колебания в пространстве.
Волны бывают механическими и электромагнитными.
Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.
- Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.
Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.
Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.
Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.
Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.
Электромагнитные волны — это те волны, которые мы потрогать не можем.
- Например, радиоволны, Wi-Fi и свет.
Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 108 м/с. И источники у них разные.
Волны также принято делить на продольные и поперечные:
Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.
- Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.
Поперечные — волны, у которых колебание происходит поперек направления распространения волны.
- Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
- Видимый свет и дрожание гитарной струны — тоже поперечные волны.
Морская волна — продольная или поперечная?
На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Длина волны: определение и расчет
Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.
- λ — длина волны [м]
Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».
Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.
Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.
Формула периода колебания волны
T = t/N
T — период [с]
t — время [с]
N — количество колебаний [—]
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Формула скорости
𝑣 = S/t
𝑣 — скорость [м/с]
S — путь [м]
t — время [с]
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
Формула скорости волны
𝑣 = λ/T
𝑣 — скорость [м/с]
λ — длина волны [м]
T — период [с]
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
- Возьмем формулу скорости:
- Нам известна длина волны, но не дан период. Период вычисляется по формуле:
- Теперь подставляем величины в формулу
𝑣 = λ/T
T = t/N
T = 40/10 = 4 с
𝑣 = λ/T
𝑣 = ¼ = 0,25 м/с
Ответ: 𝑣 = 0,25 м/с
Резонанс
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
Формула частоты
ν = N/t
ν — частота [Гц]
t — время [с]
N — количество колебаний [—]
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
Отдельные частицы любого тела — твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-то частица начинает колебаться, то благодаря взаимодействию между частицами это движение с некоторой скоростью начинает распространяться во все стороны.
Определение
Волна — колебания, распространяющиеся в пространстве с течение времени.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря силам упругости. Эти силы осуществляют связь между отдельными частями тела. В образовании волн на поверхности воды играют роль сила тяжести и сила поверхностного натяжения. Такие волны позволяют наиболее наглядно рассмотреть главные особенности волнового движения.
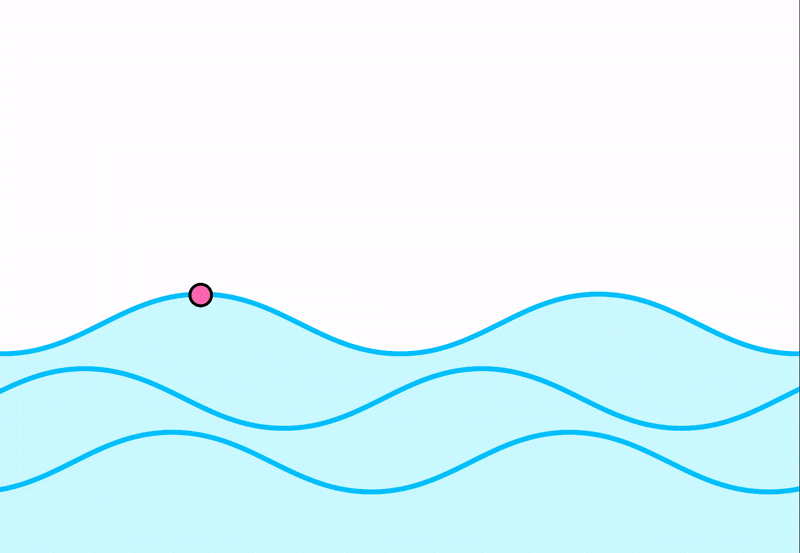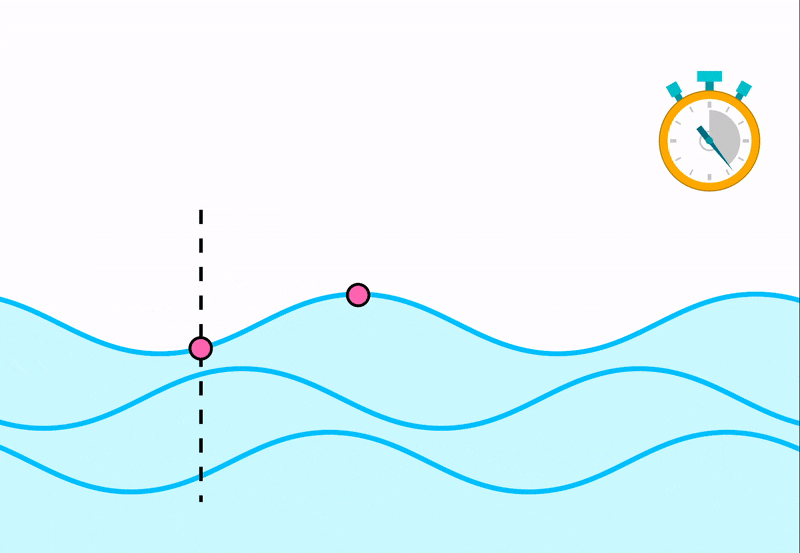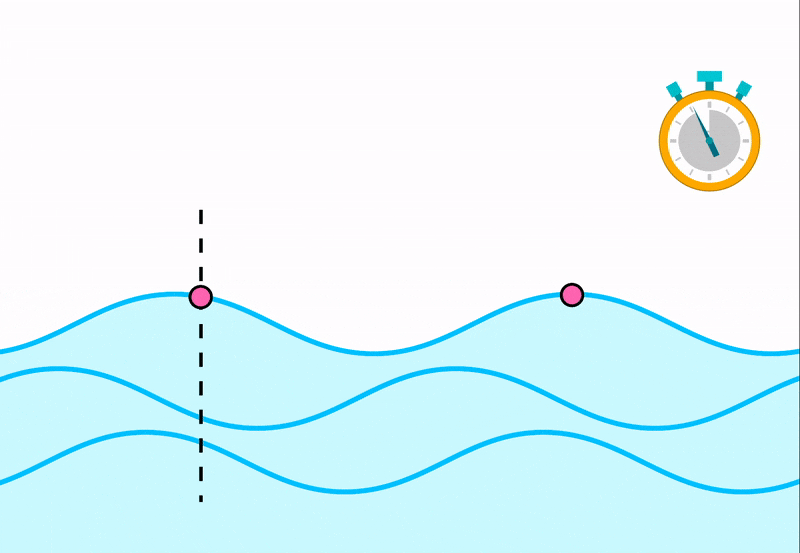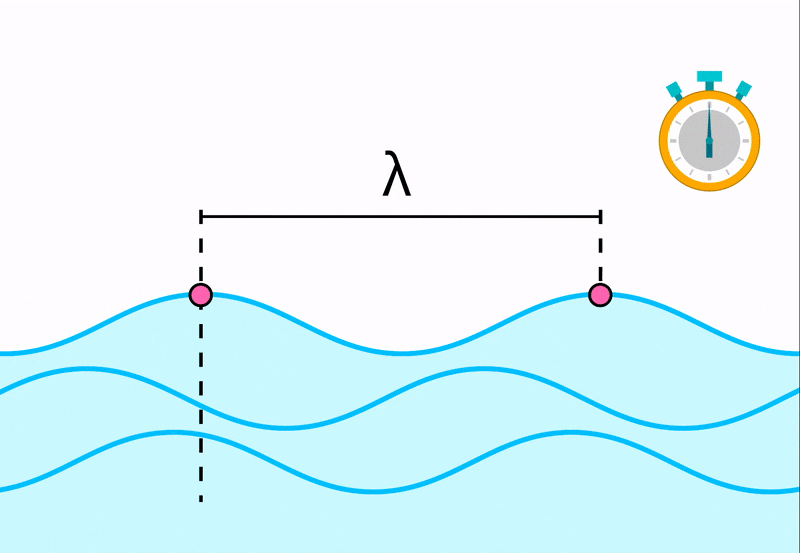
Волна на поверхности воды представляет собой бегущие вперед валы округлой формы. Расстояние между валами, которые также называют гребнями, примерно одинаковы. Волны распространяются в среде с определенной скоростью. Так, если чайка летит вперед, а по ней в любой момент времени оказывается один и тот же гребень, то скорость распространения волны можно принять равной скорости полета чайки. Волны на воде наблюдать удобно потому, что скорость их распространения невелика.
Если бросить в воду легкий предмет, он не будет увлекаться волной, а начнет совершать колебания вверх и вниз, оставаясь примерно на одном месте, как поплавок. Это говорит о том, что частицы воды остаются на месте в то время, как волна распространяется на большие расстояния.
Если же резко толкнуть горизонтальную пружину, можно будет наблюдать, как в одних местах она разрежается, в других — уплотняется. Это тоже волна. Видно, что энергия, полученная от толчка руки, переносится через пружину, хотя ее частицы остаются на месте.
Примеры с поплавком на воде и горизонтальной пружиной позволяют сделать вывод, что волна переносит энергию, но не переносит вещество среды.
Виды механических волн
По характеру колебаний частиц среды относительно положения равновесия различают два вида волн:
Определения
- Поперечная волна — волна, при которой частицы среды колеблются перпендикулярно направлению распространения этой волны.
- Продольная волна — волна, при которой частицы среды колеблются параллельно направлению распространения этой волны.
Волны, распространяющиеся вдоль резинового шнура, являются поперечными (см. рисунок ниже). Чтобы появилась волна, нужно взять конец шнура, прикрепленного к вертикальной опоре, и дернуть его. При этом волна побежит к вертикальной опоре, а сам шнур будет менять свою форму. Каждая частица шнура станет совершать колебания относительно своего неизмененного положения равновесия сверху вниз (перпендикулярно направлению распространения волны).
Рассмотрим поперечные волны подробнее. Каждый участок шнура обладает массой и упругостью. При деформации шнура в любом его сечении появляются силы упругости. Эти силы стремятся возвратить шнур в исходное положение. Благодаря инертности участок колеблющегося шнура не останавливается в положении равновесия, а проходит его, продолжая двигаться до тех пор, пока силы упругости не остановят этот участок в момент максимального отклонения от положения равновесия.
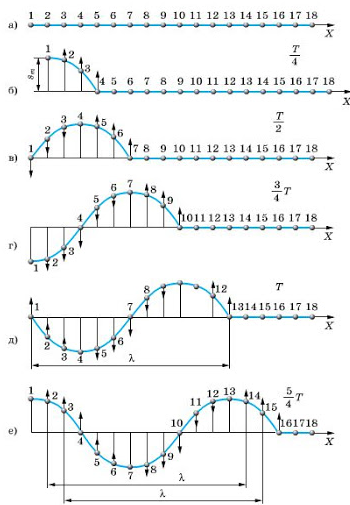
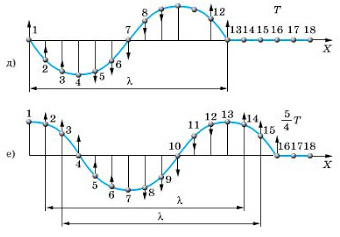
На рисунках а, б, в, г, д и е изображен процесс распространения поперечной волны. На них показаны положения частиц среды в последовательные моменты времени.
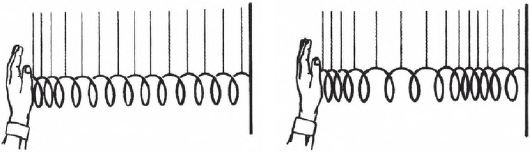
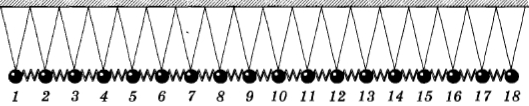
Теперь рассмотрим распространение в среде продольной волны. Такую волну можно наблюдать, собрав установку из цепочки массивных шариков, связанных пружинками. Шары подвешены так, чтобы они могли колебаться только вдоль цепочки (см. рисунок ниже).
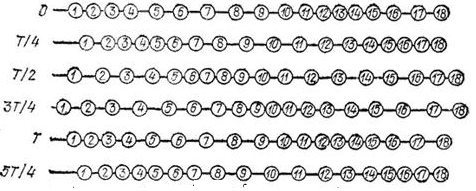
Если первый шар привести в колебательное движение, то вдоль цепочки побежит продольная волна, состоящая из чередующихся уплотнений и разрежений шаров. Уплотнения и разрежения (см. рисунок ниже) появляются вследствие горизонтальных колебаний шаров у положения равновесия. Волна также распространяется горизонтально.
Физические характеристики волны
Обратимся к рисункам д, е еще раз. Видно, что когда частица 1 находится в положении равновесия и движется вверх, частица 13 тоже находится в положении равновесия и движется вверх. Спустя четверть период частица 1 будет максимально отклонена от положения равновесия, ровно, как и частица 13. Так как частицы 1 и 13 движутся одинаково, говорят, что колебания этих частиц происходят в одинаковых фазах. Расстояние между этими частицами называют длиной волны.
Внимание! В действительности частица 13 отстает по фазе от частицы 1 на 2π. Но поскольку такая разница фаз не приводит к различию в состояниях колеблющихся частиц, можно считать, что частицы колеблются в одинаковых фазах.
Определение
Длина волны — расстояние между двумя ближайшими точками волны, колеблющимися в одинаковых фазах.
Длина волны обозначается как λ (лямбда). Единица измерения длины волны — метр (м).
Согласно рисунку е, в одинаковых фазах колеблются частицы 1 и 13, 2 и 14, 3 и 15, 4 и 16. Поэтому расстояния между этими частицами равно длине волны. Но частицы 1 и 7, находящиеся на расстоянии λ2, колеблются в противоположных фазах. Посмотрите на рисунок д: когда 1 частица находится в положении равновесия и движется вверх, частица 7 находится в положении равновесия и движется низ. На рисунке е обе частицы максимально отклонены от положения равновесия, но в противоположных направлениях.
Волна распространяется на расстояние λ за время, равное периоду колебаний частиц вещества. Зная расстояние, на которое распространилась волна, и время, в течение которого это распространение происходило, можно найти скорость волны:
v=λT
Но мы знаем, что период равен величине, обратной частоте колебаний:
T=1ν
Тогда скорость распространения волны равна:
v=λν
Скорость волны равна произведению длины волны на частоту колебаний.
При распространении волны мы имеем дело с периодичностью двоякого рода:
- Во-первых, каждая частица среды совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по синусоидальному или косинусоидальному закону) частота постоянна и амплитуда одинакова во всех точках. Колебания отличаются только фазами.
- Во-вторых, в данный момент времени форма волны повторяется в пространстве через отрезки длиной λ вдоль линии распространения волны. На рисунке ниже показан профиль волны в определенный момент времени (сплошная линия). С течением времени вся эта картина перемещается со скоростью v направо. Спустя промежуток времени ∆t волна будет иметь вид, изображенный на том же рисунке прерывистой линией.
Пример №1. Определите скорость распространение волны на поверхности воды, если расстояние между ее гребнями равно 1 метру. Учитывайте, что мимо наблюдателя за 5 секунд прошло 10 волн.
Обычно под волной на воде люди понимают гребни — частицы воды, максимально отклоненные от положения равновесия. Расстояние между гребнями равно длине волны. Чтобы найти скорость распространения волны, нужно знать частоту колебания молекул воды. Ее можно вычислить по следующей формуле:
ν=nt
где n — количество «волн», прошедших мимо наблюдателя.
Тогда скорость волны равна:
v=λν=λnt=1·105=2 (мс)
Уравнение бегущей волны
Определение
Бегущая волна — волна, распространяющаяся в пространстве.
Колебания гармонической волны в любой точке происходят по гармоническому закону с одной и той же амплитудой. Найдем уравнение, описывающее колебательный процесс в любой точке пространства при распространении гармонической волны.
Будем рассматривать волну, бегущую по длинному тонкому резиновому шнуру. Ось Ox направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса необходимо знать значение s в любой точке шнура в любой момент времени. Следовательно, нужно знать вид функции:
s = s(x, t)
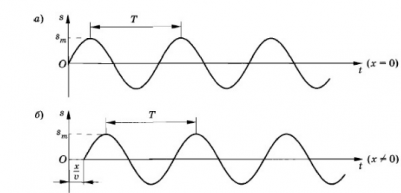
Заставим конец шнура (точка х = 0) совершать гармонические колебания с частотой ω. Если начальную фазу колебаний считать равной 0, то колебания этой точки будут происходить по закону:
s = smaxsin ωt
smax — амплитуда колебаний (рис. а).
Колебания распространяются вдоль шнура (оси Ox) со скоростью v и в произвольную точку шнура с координатой х придут спустя время, которое можно определить следующим выражением:
τ=xv
Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой smax, но с другой фазой:
Уравнение бегущей волны
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Это уравнение называется уравнением бегущей волны, распространяющейся в положительном направлении оси Ox.
Пример №2. Уравнение бегущей волны имеет вид s(x, t)=0,1sin(2πt−xπ2). Найдите частоту волны, скорость её распространения и длину.
Запишем уравнение бегущей волны:
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Сопоставляя эти два уравнения можно определить, что циклическая частота и скорость распространения соответственно равны:
ω=2π (радс)
v=4 (мс)
Циклическую частоту также можно рассчитать по формуле:
ω=2πν
Тогда частота волны равна:
ν=ω2π=2π2π=1 (Гц)
Тогда длина волны равна:
λ=vν=41=4 (м)
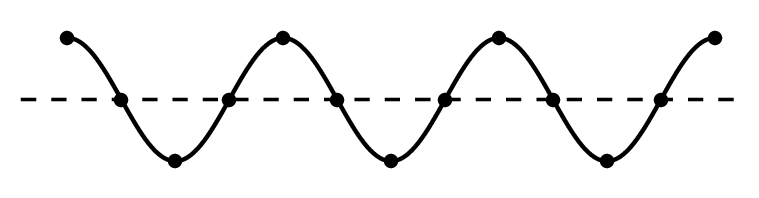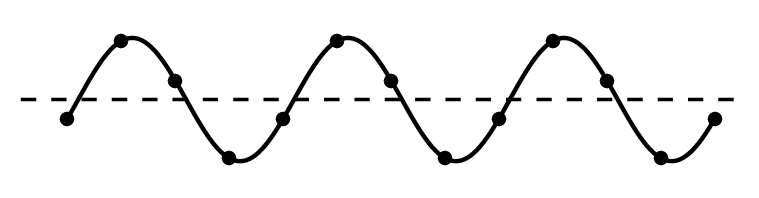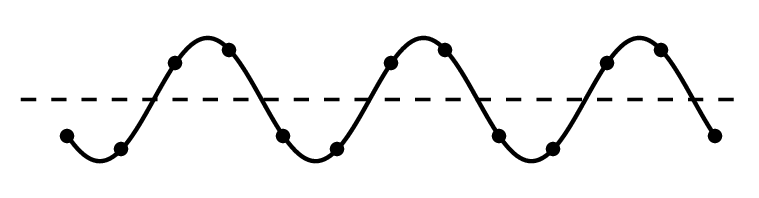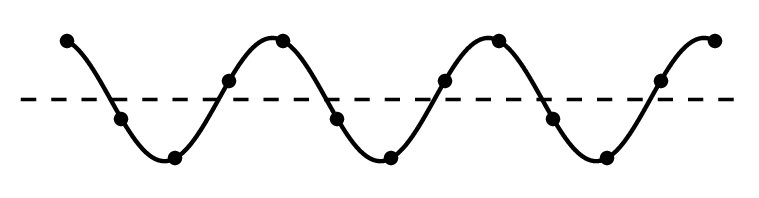
Задание EF18242
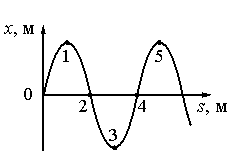
Ответ:
а) π/3
б) π/2
в) π
г) 2π
Алгоритм решения
- Определить характер движения указанных точек.
- По характеру движения точек определить их разность фаз.
Решение
Точки 1 и 5 соответствуют максимальной амплитуде колебаний. В этот момент они меняют направление движения (до этого двигались вверх, теперь меняют направление в противоположную сторону). Поскольку точки 1 и 5 движутся одинаково, можно считать, что они колеблются в одинаковых фазах. Это возможно, если разность фаз кратна 2π.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22628
Какова скорость звуковых волн в среде, если при частоте 400 Гц длина волны λ = 4 м?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу, которая связывает скорость волны с ее частотой и длиной.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Частота звуковой волны: ν = 400 Гц.
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν=4·400=1600 (мс)
Ответ: 1600
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18803
На расстоянии 510 м от наблюдателя рабочие вбивают сваи с помощью копра. Какое время пройдёт от момента, когда наблюдатель увидит удар копра, до момента, когда он услышит звук удара? Скорость звука в воздухе равна 340 м/с.
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение задачи в общем виде.
3.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Скорость распространения звука в воздухе: v = 340 м/с.
• Расстояние наблюдателя до источника звука: s = 510 м.
Звук от удара проделает путь, равный одинарному расстоянию от наблюдателя до источника звука. Следовательно, для нахождения времени, через которое наблюдатель услышит звук, нужно разделить этот путь на скорость звука в воздухе:
t=sv=510340=1,5 (с)
Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 2.8k
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Волны
Волновой процесс — любое изменение состояния сплошной среды, распространяющееся со скоростью и несущее энергию.
Поперечные волны — волны, при распространении которых смещение частиц среды происходит в направлении, перпендикулярном распространению волны.
— волна, при распространении которой смещение частиц среды происходит в направлении распространения волны.
Длина волны (lambda) — расстояние между двумя ближайшими друг другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Единицы измерения: (displaystyle [text{м}])
Скорость распространения волны
[displaystyle v=dfrac{lambda}{T}=hnu]
где (T) — период колебаний, (nu) — частота колебаний.
Поскольку для всех электромагнитных волн скорость в вакууме ((c)) одинакова, по частоте легко определить длину волны (lambda):
[lambda=dfrac{c}{nu}]
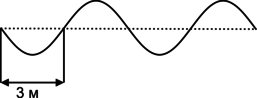
Канатоходец заметил, что, когда он наступает на канат, то он выглядит так, как показано на рисунке, а скорость распространения волны 3 м/с. Найдите частоту колебаний.
По рисунку видно, что половина длины волны равна 3 метра, значит длина волны равна 6 м.
По формуле найдем частоту: [displaystyle nu=frac{upsilon}{lambda}=frac {3text{ м/с}}{6text{ м}}=0,5text{ Гц}]
Ответ: 0,5
Струна гитары издает звуковые волны с максимальной частотой (nu_1=40) Гц, а струна балалайки (nu_2=120) Гц. Найдите отношение длин волн (dfrac{lambda_1}{lambda_2}).
Частота находится по формуле: [nu=dfrac{upsilon}{lambda}]
Выразим (lambda): [lambda=frac{upsilon}{nu}]
Значит, [dfrac{lambda_1}{lambda_2}=dfrac{dfrac{upsilon_1}{nu_1}}{dfrac{upsilon_2}{nu_2}}]
Так как звук в одной среде распространяется с одинаковой скоростью, то (upsilon_1=upsilon_2), следовательно [frac{lambda_1}{lambda_2}=frac{nu_2}{nu_1}=frac{120text{ Гц}}{40text{ Гц}}=3]
Ответ: 3
Пчела совершает 600 взмахов крыльев в минуту. Найдите период колебания крыльев. (Ответ дайте в секундах)
Период найдем по формуле: [T=dfrac{1}{nu}]
Где (nu) — частота колебаний.
Частоту колебаний найдем по формуле: [displaystyle nu=dfrac{n}{t}]
где (n) – количество взмахов, (t) – время, за которое совершается данное количество взмахов.
Переведем взмахи/минуту в взмахи/секунду [600text{ взмах/минут}=10text{ взмах/секунд}Rightarrow]
Частота колебаний равна 10 Гц. Найдем период: [T=dfrac{1}{nu}=frac{1}{ 10 text{ Гц}}=0,1text{ с}]
Ответ: 0,1
Отношение длин волн в средах 1 и 2 (dfrac{lambda_1}{lambda_2}=2), а отношение частот (dfrac{nu_1}{nu_2}=1). Найдите отношение времен (dfrac{t_1}{t_2}), за которые звуковые волны проходят расстояние (S)?
Время рассчитыватся по формуле (displaystyle t=frac{S}{upsilon}), где (upsilon) – скорость. Значит: [frac{t_1}{t_2}=dfrac{dfrac{S}{upsilon_1}}{dfrac{S}{upsilon_2}}=frac{upsilon_2}{upsilon_1} quad (1)]
Формула для нахождение скорости: [displaystyle upsilon=lambda cdot nu]
Значит, [displaystyle upsilon_1=lambda_1 cdot nu_1 quad(2)] [displaystyle upsilon_2=lambda_2 cdot nu_2 quad(3)]
Подставим (2) и (3) в (1) [frac{t_1}{t_2}=frac{lambda_2 cdot nu_2}{lambda_1 cdot nu_1}=0,5]
Ответ: 0,5
Муха крыльями совершает 300 колебаний за 2 минуты. Найдите частоту колебания крыльев. (Ответ дайте в Гц)
Формула для расчета частоты: [nu=frac{n}{t}]
Где (n) – количество колебаний, а (t) – время за которое совершили данное количество колебаний.
Переведем время в СИ: 2 минуты=120 секунд.
Посчитаем частоту: [nu=frac{n}{t}=frac{300}{120text{ с}}=2,5text{ Гц }]
Ответ: 2,5
Колеблющаяся струна издает звук с длиной волны (lambda=2,72) м. Найдите частоту колебаний, если скорость звука (upsilon=340) м/с. (Ответ дайте в Гц)
Формула для расчета частоты [nu=frac{upsilon}{lambda}=frac{340text{ м/c}}{2,72text{ м}}=125text{ Гц }]
Ответ: 125
Петя стоит на расстоянии (S=165) м от горы и говорит в громкоговоритель. Найдите время, через которое Петя вновь услышит себя. Скорость звука принять 330 м/c. (Ответ дайте в секундах.)
Звук сначала дойдет до горы, потом отразится от горы и вновь дойдет до Пети. Значит он пройдет (2S), обозначим это расстояние (S_text{полн}), а двигаться будет равномерно. Чтобы посчитать время будем использовать формулу [t=frac{S_text{полн}}{upsilon}]
Где (upsilon) – скорость звука
[t=frac{S_text{полн}}{upsilon}=frac{2S}{upsilon}=frac{2cdot 165 text{ м}}{330text{ м/с}}=1 text{ с}]
Ответ: 1

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ