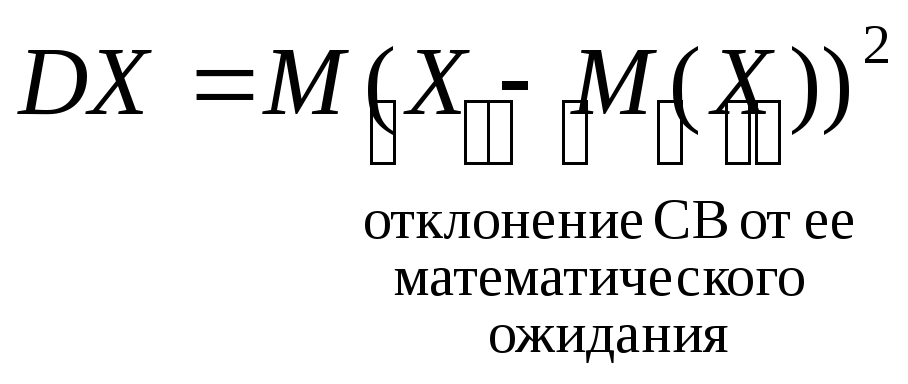СВ является непрерывной, если
ее функция распределения непрерывна.
Для НСВ наряду с функцией распределения
вводится еще 1 закон распределения –
плотность вероятности.
Определение 4.6:
Плотностью вероятностей хназывается производная ее функции
распределения, т.е.
(плотность вероятностей может быть
обозначена
)
Свойства плотностей вероятности:
1.
2.
3.
4.
— условие нормировки
4.5. Числовые характеристики cb
Определение 4.7:
Математическим ожиданием ДСВназывается число.
Определение 4.8:
Математическим ожиданием НСВназывается число.
математическое
ожидание
Свойства математического ожидания:
1. X = с
= const,
M(C) = C
2. Постоянный множитель выносится за
знак математического ожидания, т.е.:
3. Математическое ожидание суммы СВ
равно сумме математических ожиданий
4.6. Дисперсия случайной величины
Определение 4.9:
Дисперсией СВназывается число:
Свойства дисперсии:
1. Дисперсию можно найти по формуле:
2.
3. Если X = с=const,
тоD(C)
= 0
4. Если
,
то
Формулы:
для ДСВ:
1.
2.
для НСВ:
1.
2.
Средним квадратичным отклонением
СВ Хназывается число:.
Законы распределения СВ (стр.19):
-
Биноминальное распределение.
-
Распределение Пуассона
-
Равномерное распределение
-
Показательное распределение
-
Нормальное распределение
Практическая работа № 2
№ 1.
Для данного студента вероятность
успешной сдачи первого экзамена равна
0,9, второго – 0,8, третьего – 0,7. Случайная
величина х – число успешно
сданных экзаменов. Найти: ряд распределения
ДСВ, математическое ожидание М(Х);
дисперсию D(X);
среднеквадратичное отклонение
.
Решение:
Случайная величина принимает значения:
0, 1, 2, 3
Пусть р1– вероятность
сдачи первого экзамена.
р2– вероятность сдачи
второго экзамена.
р3– вероятность сдачи
третьего экзамена.
q1– вероятность
несдачи первого экзамена.
q2– вероятность
несдачи второго экзамена.
q3– вероятность
несдачи третьего экзамена.
-
Х
0
1
2
3
Р
0,006
0,092
0,398
0,504
(методичка, стр.25, формула для доверительного
интервала)
Нормальное распределение – стр.21
П.6 зад.7 для решения к.р.
№ 2.
На сборку поступили детали с 3 конвейеров.
Первый дает 25%, второй – 30%, третий – 45%
деталей, поступающих на сборку. С первого
конвейера в среднем поступает 2% брака,
со второго – 3%, с третьего – 1%. Найти
вероятность того, что:
-
На сборку поступила бракованная
деталь. -
Поступившая бракованная деталь со
второго конвейера.
Решение:
Пункт 1.
Пусть событие А– поступившая деталь
на сборку – бракованная.
Н1– деталь с первого конвейера.
Н2– деталь со второго конвейера.
Н1– деталь с третьего конвейера.
Пункт 2.
№ 3.
Монету бросают 10 раз. Найти вероятность
того, что герб выпадет:
-
2 Раза.
-
Менее 2 раз.
-
Не менее 2 раз.
Решение:
1:
Вероятность того, что выпадет герб,
;n = 10, k
= 2
Формула Бернулли:
2:
По формуле Бернулли:
3:
Тел. кафедры – 60-27-71
Надежда Николаевна
1. Пусть Х – число сданных экзаменов. Составим ряд распределения Х. Возможные значения Х: 0, 1, 2, 3. Вычислим вероятности этих значений: Р(Х=0) = 0.1, Р(Х=1) = 0.9*0.2 = 0.18, Р(Х=2) = 0.9*0.8*0.3=0.216, Р(Х=3) = 0.9*0.8*0.7=0.504.
Математическое ожидание. М[X] = 0*0.1 + 1*0.18 2*0.216 + 3*0.504 = 2.124
2. Пусть Х – прибыль от инвестиций. Далее, решение можно оформить различными способами. Сначала находим все значения Х и их вероятности, а потом математическое ожидание Х. Можно немного ” повеселее”. Введём две случайные величины: Y – доход от инвестиций в фирму А, Z – доход от инвестиций в фирму В.
Значения Y: 0 , 0.5 с вероятностями 0.2 и 0.8 соответственно. M[Y] = 0.5*0.8 = 0.4.
Значения Z: 0 , 0.4 с вероятностями 0.15 и 0.85 соответственно. M[Y] = 0.4*0.85 = 0.34.
Тогда X = 10*Y + 15*Z. Поэтому М[X] = 10*M[Y] + 15*M[Z] = 9.1
Однако закон распределения Х надо найти.
Значения Х: 0, 5, 6, 11, с вероятностями 0.03, 0.12, 0.17, 0.68.
2 / 2 / 1
Регистрация: 05.08.2013
Сообщений: 122
1
Составить закон распределения дискретной случайной величины
09.02.2017, 11:46. Показов 5608. Ответов 2
Вероятность успешной сдачи по первому, второму, третьему экзамену предметам для данного студента соответственно равны 0.8; 0.5; 0,7. Составить закон распределения СВ X — числа элементов, успешно сданных студентом. Найти MX, DX, С.К.О, ф-ция распределения F(x). Построить график F(x) и многоугольник распределения.
————————
Возможных вариантов успешно сданных экзаменов могут быть: 0,1,2,3
P(0) = 0.2*0.5*0.3 = 0,03 — успешно сданных 0 экзаменов
P(1) = 0.8*0,5*0,3+0,8*0,5*0,7+0,2*0,5*0,7= 0,47
P(2) = 0.8*0.5*0.3+0.2*0.5*0.3+0.2*0.5*0.7=0.22
P(3) = 0.8*0.5*0.7=0.28
———————-
Кликните здесь для просмотра всего текста
| x(i) | 0 | 1 | 2 | 3 |
| p(i) | 0.03 | 0.47 | 0.22 | 0.28 |
Правильный ход решения?
Добавлено через 4 минуты
Если правильно, то:
MX=1.75
DX=[MX]^2 — MX^2 = 3.96 — 1.75^2 = 0.8975
С.К.О = 0.9474
———
Добавлено через 6 минут
И тогда:
F(x)=P(X<x)
если x<=0, F(x) = P(X<0) = 0; тогда 0
если x<=1, F(x) = P(0<x<=1) = 0+0.03; тогда 0.03
если x<=2, F(x) = P(1<x<=2) = 0+0,03+0,47; тогда 0.5
если x<=3, F(x) = P(2<x<=3) = 0+0.03+0.47+0.22; тогда 0.72
если x<=4, F(x) = P(x>3) = 1; тогда 1
————-
0, x<=0
0.03, 0<x<=1
F(x) =0.5, 1<x<=2
0.75, 2<x<=3
1, x>3
Не знаю как тут графики сделать, поэтому постарался нарисовать в paint
Миниатюры
__________________
Помощь в написании контрольных, курсовых и дипломных работ, диссертаций здесь
0
Вероятность успешной сдачи первого экзамена для данного студента равна 0, 9 , втрого экзамена 0, 8.
Найти закон распределения дискретной случайной величины х — число успешно сданных экзаменов .
Если вам необходимо получить ответ на вопрос Вероятность успешной сдачи первого экзамена для данного студента равна 0, 9 , втрого экзамена 0, 8?, относящийся
к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу.
В категории Математика вы также найдете ответы на похожие вопросы по
интересующей теме, с помощью автоматического «умного» поиска. Если после
ознакомления со всеми вариантами ответа у вас остались сомнения, или
полученная информация не полностью освещает тематику, создайте свой вопрос с
помощью кнопки, которая находится вверху страницы, или обсудите вопрос с
посетителями этой страницы.
Подборка по базе: Контрольная работа.docx, Лабораторная работа № 2.docx, Лабораторная работа №9 _Расчет основных характеристик силовых тр, Курсовая работа (Копрлексное изучение личности).DOC, практическая работа.7.2.docx, Практическая работа № 1 Лучшие модели и практики наставничества , Контрольная работа №2 .doc, Лабораторная работа 3.docx, практическая работа 10.docx, Лабораторная работа № 7. Измерение сопротивления проводника при
Контрольная работа по математике
Задание 1
1.10
Из 10 кандидатов на одну и ту же должность должно быть выбрано 3. Определить все возможные варианты результатов выборов?
Сочетаниями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m в каждом обозначается символом Cnm
Задание 2
2.10
Десять студентов условились ехать определенным рейсом электропоезда с 10 вагонами, но не договорились о номере вагона. Какова вероятность того, что ни одним из них не встретиться с другим, если возможности в размещении студентов по вагонам равновероятны?
Пусть А — событие, что все студенты окажутся в разных вагонах.
Общее количество способов разместить 10 студентов по 10 вагонам равно числу размещений с повторениями. В каждом вагоне может оказаться от 0 до 10 студентов.
n = A`(10,10) = 10^10.
Количество благоприятных вариантов размещения по одному студенту в вагоне равно числу перестановок из 10 элементов.
m = P = 10!.
Первый студент может выбирать из 10 вагонов, второй из 9, третий из 8 и т.д.
Вероятность, что ни один из них не встретится с другим:
P(A) = m/n = 10!/10^10 = 0,000363.
Ответ: Вероятность события А: P(A) = 0,000363.
Задание 3
3.10
Первый станок-автомат дает 1 % брака, второй – 1,5 %, а третий – 2 %. Случайным образом отобрали по одной детали с каждого станка. Какова вероятность того, что стандартными окажутся: а) три детали; б) две детали; в) хотя бы одна деталь?
Процент выхода стандартных деталей — 99%, 98,5% и 98%.
а) Вероятность, что со всех 3 станков все 3 детали окажутся стандартными
p1 = 0,99*0,985*0,98 = 0,955647
95,6%
в) Вероятность, что все три детали окажутся бракованными
q3 = 0,01*0,015*0,02 = 0,000003
Вероятность, что хотя бы одна деталь окажется стандартной
p3 = 1 — q3 = 0,999997
б) Самый трудный случай.
Вероятность, что с 1 и 2 станка детали будут стандарт, а с 3 браком
q1 = 0,99*0,985*0,02 = 0,019503
Вероятность, что с 1 и 3 станка детали будут стандарт, а со 2 браком
q2 = 0,99*0,015*0,98 = 0,014553
Вероятность, что со 2 и 3 станка детали будут стандарт, а с 1 браком
q3 = 0,01*0,985*0,98 = 0,009653
Вероятность, что только 2 каких-то детали будут стандарт, а третья браком
p2 = q1 + q2 + q3 = 0,019503 + 0,014553 + 0,009653 = 0,043709
Задание 4
4.10
По линии связи передано два сигнала типов А и В с вероятностями соответственно 0,8 и 0,2. В среднем принимается 60 % сигналов типа А и 70 % типа В. Найти вероятность того, что: а) посланный сигнал будет принят; б) принятый сигнал – типа А.
Пусть событие А — посланный сигнал будет принят. Рассмотрим гипотезы :
связь передается сигналом А;
связь передается сигналом B.
Условные вероятности:
a) По формуле полной вероятности, вероятность того, что посланный сигнал будет принят, равна
б) Посланный сигнал был принят, вероятность того, что это сигнал А, по формуле Байеса, равна
Задание 5
5.10
Вероятность поражения мишени для данного стрелка в среднем составляет 80 %. Стрелок произвел 6 выстрелов по мишени. Найти вероятность того, что мишень была поражена: а) пять раз; б) не менее пяти раз; в) не более пяти раз.
Вероятность сдачи экзамена для каждого из шести студентов равна 0,8. Найти вероятность того, что экзамен сдадут: а) пять студентов; б) не менее пяти студентов.
а) вероятность попадания 5 раз из шести составляет %
б) вероятность попадания не менее шести раз — т.е. пять раз или шесть %
в) не более пяти раз, т.е вероятность того, что он НЕ попадёт шесть раз в цель %
Задание 6
6.10
Вероятность успешной сдачи первого экзамена для данного студента равна 0,9, второго экзамена – 0,8, третьего – 0,7; СВ Х – число сданных экзаменов.
Случайная величина X может принимать такие значения:
X = 0 — студент не сдал ни одного экзамена;
X = 1 — студент сдал один экзамен;
X = 2 — студент сдал 2 экзамена.
P(0) = (1 — 0,9)(1 — 0,8) = 0,1 · 0,2 = 0,02;
P(1) = 0,9 · (1 — 0,8) + (1 — 0,9) · 0,8 = 0,26;
P(2) = 0,9 · 0,8 = 0,72.
X 0 1 2;
P(X) 0,02 0,26 0,72;
Задание 7
7.10