Доказательство от противного в сочинении

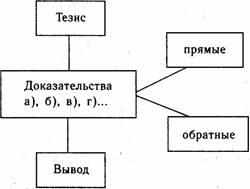
Рассуждение

      В VII классе
продолжается обучение рассуждению на
дискуссионные темы.

      В рассуждениях,
которые писали дети в V и VI классах,
они пользовались так называемыми прямыми
доказательствами, т. е. такими доводами,
которые непосредственно обосновывали
справедливость выдвинутого тезиса:
«Моряком быть хорошо, потому что…»; «Я
считаю, что Миша поступил правильно,
так как…» и пр.

      Рассуждения на
дискуссионные темы дают возможность
познакомить учащихся с новым для них
способом доказательства — «обратным»
доказательством, доказательством от
противного. С подобным способом
доказательства учащиеся встречаются
в курсе геометрии. В этом случае для
доказательства приводится положение,
противоположное доказываемому. Это
положение развивается для того, чтобы
стала очевидной его абсурдность. А если
оно несостоятельно, абсурдно, значит,
истинно другое утверждение, которое и
доказывает автор.

      Умения, приобретенные
учащимися в процессе работы над
сочинениями-рассуждениями на дискуссионные
темы, имеют большое значение для их
дальнейшей самостоятельной деятельности.
Практическое участие в производстве
материальных ценностей и в общественной
жизни невозможно без умения вести спор,
доказывать справедливость своих суждений
или убедительно и тактично опровергать
противоположные суждения. Воспитание
этих умений и является целью обучения
рассуждению на дискуссионные темы.

      Учебник дает
возможность провести следующую работу
над сочинениями-рассуждениями:

      1. Закрепление
приобретенных ранее умений. Анализ
текстов, представляющих собой
рассуждения.
      2. Знакомство
с «обратным» доказательством в
сочинении-рассуждении на дискуссионную
тему.
        

Знакомство с «обратным» доказательством в рассуждении на дискуссионную тему

      Цели
урока:
1) повторить практическим путем то,
что ученики знают об особенностях
сочинений-рассуждений; 2) познакомить
учащихся с приемом доказательства от
противного; 3) подготовить учащихся
к самостоятельной работе (к
сочинению — упр. 343 или к сжатому
изложению с дополнительным заданием).

      1. Проверка
домашнего задания. Повторение.
Запись в форме свободного диктанта
(упр. 21, с. 11).

      Этот отрывок-рассуждение,
в котором ученики выделяют тезис
(«Издаваемые нами звуки — это
звуки речи»), доказательства и вывод
(«Значит, для человеческой речи важны…»).

      2. Сообщение
целей урока. Знакомство с «обратным»
доказательством.
Учитель предлагает найти в учебнике
геометрии теорему-рассуждение на научную
тему. Строится это рассуждение как любое
другое; в нем есть тезис, то, что
утверждается, сама теорема; доказательства
и вывод. Рассмотрим последние две части:
какими словами начинается доказательство?
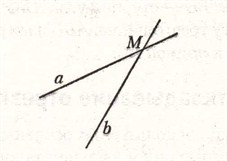
(«Допустим противное».) А именно? («Прямые
а и
б
не параллельны».) Как развивается дальше
это предположение, допущение? («Это
значит, что…») Это развертывание
доказательств приводит к абсурду:
делается ясным, что «допущение невозможно»
(по аксиоме параллельных). Отсюда вывод:
«Значит, допущение неверно, и потому
а || б».
Вывод введен словом значит.

      При доказательстве
этой теоремы был использован не прямой,
а обратный способ доказательства, иногда
его называют доказательством от
противного. Найдем еще такого же типа
доказательство. Какими словами оно
вводится? Какие языковые средства
используются при переходе к выводу?
«Предположим противоположное тому, что
требуется доказать, т. е. что…», «что
противоречит условию…», «следовательно,
предложение о… неверно». «Значит,
более…» Такого типа доказательства
используются и в рассуждениях на
жизненные темы. При этом, в отличие от
геометрических доказательств, нередко
ставится задача не только доказать
правильность какого-либо суждения, но
и воздействовать на чувства своих
читателей (слушателей). Поэтому
используются иные языковые средства.

      Проведенная работа
позволяет возобновить в памяти учащихся
сведения об особенностях сочинений-рассуждений
и уже знакомую детям схему композиции
сочинения-рассуждения, в которую вносятся
необходимые коррективы.

      3. Упражнения
в использовании приема доказательства
от противного.

      Учитель
записывает на доске одну-две темы,
например: «Что важнее в учебе — трудолюбие
или способности?», «Верно ли, что главное
для спортсмена — это вежливость?».
Ученики должны дать устно или письменно
ответ на поставленный в теме вопрос.
Так, на вопрос первой темы ученики могут
дать такие ответы: 1) важнее трудолюбие;
2) важнее способности; 3) одинаково
важно и то и другое. Учитель установит,
как его ученики собираются ответить на
дискуссионный вопрос, затем предложит
каждому обосновать свой ответ в форме
доказательства от противного и записать
это доказательство. Какими словами
может оно начинаться? Допустим,
что… Предположим противное… Если бы…
Представим, что… и
т. д. (Желательно записать эти выражения
на доске.)

      Два-три доказательства
(различных по содержанию) обсуждаются.
Например:

      1. Я
считаю, что важнее в учебе — трудолюбие.
Допустим, что это не так, что важнее —
способности. Тогда почему я учусь плохо?
Ведь все учителя говорят, что я способный,
и правда, я быстро схватываю, все могу
повторить за учителем. А часто получаю
двойки. Что толку от моих способностей?
Знаний-то настоящих у меня нет. Значит,
трудолюбие важнее.
      2. Мое
мнение: важнее всего в
учебе — способности.
      Если
бы способности не имели значения, тогда
все усидчивые ученики учились бы на «4»
и «5». И мало того, по всем предметам. А
это не так. Я делаю все уроки, а по физике
больше «3» не получаю. (В данном случае
предположение введено с помощью союза
если.)

      Обсуждая подобные
доказательства, учитель обращает
внимание на их развернутость,
убедительность, логичность, речевое
оформление. Приведенные выше доказательства,
построенные на анализе своего школьного
опыта, убедительны, хотя второе из них
больше доказывает выдвинутый тезис,
что в учебе важны и трудолюбие, и
способности.

      В целях подготовки
к сочинению о спортсменах, а также для
тренировки учащихся в умении строить
доказательства (в том числе и обратные)
можно использовать упражнения на
редактирование. Так, разбирая недостатки
сочинения, учитель предложит привести
пример, соответствующий тезису («грубиянов
в команду не берем») и иллюстрирующий
грубое поведение игроков во время игры
в ручной мяч (именно грубость, а не
разболтанность), а затем пусть ученики
воспользуются обратным доказательством:
предположим (допустим) противное, что
команда состояла бы сплошь из грубиянов
(или что в команде завелся хотя бы один
грубиян и т. п.).

      4. Работа
учащихся над сочинением
(упр. 343).

      Ученики знакомятся
с текстом упражнения и с темой рассуждения
«Правильно ли, что чтение — роскошь?».
Затем учитель предлагает подумать над
тем, как можно начать это сочинение? (С
прямого ответа на вопрос; с мнения одного
из героев романа И. А. Гончарова — именно
оно приведено в тексте упражнения; с
«выдуманного» диалога о пользе чтения
между ребятами и т. д.)

      Во всех случаях,
подчеркнет учитель, важно: 1) определить
основную мысль (тезис) своего рассуждения;
2) подобрать убедительные доказательства
и определить последовательность их
использования; 3) подумать о том, нужен
ли вывод, и сформулировать его (если он
нужен). Главное — уметь привести
веские доказательства в пользу своего
мнения, при этом они могут быть различными
по существу и по форме (не только
обратные — от противного). «Что
же это могут быть за доказательства?» — спросит
учитель. (Примеры из своей жизни и жизни
других людей; примеры из книг; высказывания
авторитетных людей по затронутому
вопросу; пословицы; различные рассуждения.)
Сочинение должно быть написано так,
чтобы читатель почувствовал
заинтересованность автора, проникся
его убежденностью.

      Вместо
этого сочинения учитель может предложить
другое, более актуальное по тематике
для данного конкретного коллектива,
например: «Может ли жадный человек быть
хорошим товарищем?», «Можно ли человека,
не умеющего грамотно говорить и писать,
считать образованным?», «Живой как жизнь
(о русском языке)» (упр. 6), «Большой
красивый человек — как я его себе
представляю» (упр. 358), «Прозвища
опасны или не опасны?» (упр. 217).

      На основе этих
сочинений может быть выпущена стенная
газета, если учитель предложит актуальную
для класса тему и ученикам полезно будет
узнать мнение друг друга. Назначенная
учителем редколлегия отберет самые
интересные сочинения или отрывки из
них, заменит невыразительные заголовки
яркими, броскими и подведет итоги (от
редакции), если в этом будет необходимость.
Таким образом, работа над рассуждениями
дискуссионного характера может научить
школьников быстро, оперативно выпускать
бюллетени, стенгазеты, откликаться на
темы, злободневные для классного
коллектива.
        

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ДОКАЗАТЕЛЬСТВО ОТ ПРОТИВНОГО

Полезное

Как писать сочинение-рассуждение

Начнём с определений, что же такое «рассуждение»:

• умозаключение, ряд мыслей, изложенных в логически последовательной форме («Словарь русского языка» Ожегова С.И.);
• один из трех элементов сочинения, определяемый как развёртывание мысли по определенной схеме; доказательное развитие какого-нибудь отвлеченного положения до степени его очевидной ясности («Литературная энциклопедия»);
• функционально-смысловой тип речи, выполняющий особое коммуникативное задание – придать речи аргументированный характер (прийти логическим путем к новому суждению или аргументировать высказанное ранее) и оформляемый с помощью лексико-грамматических средств причинно-следственной семантики («Стилистический энциклопедический словарь русского языка»).

Итак, рассуждение – это мысли, изложенные в соответствии с логикой, подкрепленные доказательствами, связанные цепью аргументов и перерастающие в убедительные выводы.

Рассуждение выявляет и описывает причины и взаимосвязь каких-либо явлений. В его начале, как правило, помещается тезис — утверждение, истинность которого необходимо доказать с помощью аргументов, веских и убедительных доводов. Сочинение может быть основано как на рассуждениях-утверждениях (доказывается истинность выдвинутого тезиса), так и на рассуждениях-опровержениях (доказывается ложность выдвинутого основного положения). Пишущему предоставляется возможность использовать не только прямые факты, но иногда и доказательства от противного. Выстраивая доказательства, автор сочинения может опираться на личный опыт, газетные и журнальные публикации, фильмы, приводить примеры из жизни и литературы.

Перед началом работы над сочинением нужно чётко сформулировать мысль, которую потребуется доказать. Затем уже, исходя из утверждения, требующего аргументации, составляется план будущей творческой работы.

Схема сочинения-рассуждения

1. Вступление.
2. Тезис.
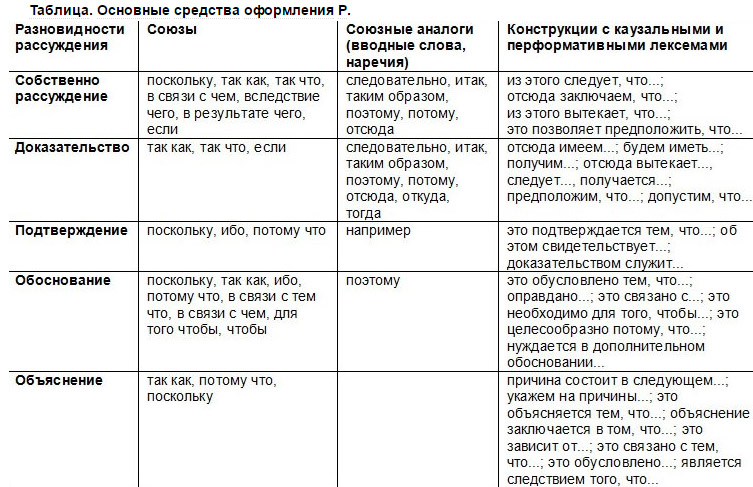
3. Аргументы: доводы, доказательства, объяснения, обоснования; примеры, случаи, факты, цифры; мнения авторитетных людей, утверждения, цитаты…
4. Вывод.

Вступление в сочинении-рассуждении – это небольшое по объему введение в тему. Оно может быть сформулировано в виде вопроса или содержать цитату. Выдвигаемый тезис станет отправной точкой для последующих рассуждений, а бОльшую часть сочинения составит аргументация – не менее 2/3 всего объёма текста. Считается, что оптимальное количество аргументов для сочинения-рассуждения – три.

В роли аргументов могут выступать:

• исторические факты;
• статистические данные;
• эпизоды, сюжетные линии литературных произведений, подтверждающие доказываемую мысль;
• пословицы и поговорки, афоризмы;
• мнения авторитетных людей… 

Самый убедительный, на Ваш взгляд, аргумент лучше всего располагать последним.

Приводить аргументы в доказательство своей позиции можно при помощи следующих слов и словосочетаний:

Обратимся к (факту, воспоминаниям кого-либо, научным данным…)

Достаточно привести такой пример…

Это можно доказать следующим образом…

Подтверждением сказанному может служит следующий факт…

Приведу ещё один пример, доказывающий мою точку зрения, …

В этом легко убедиться, обратившись к…

Например… 

Допустим…

По свидетельству (кого-либо)…

Предположим…

Так как; потому что…

Во-первых, во-вторых и т.д.

В представленной ниже таблице из «Стилистического словаря русского языка» можно увидеть и другие лексические средства, пригодные для различных видов рассуждения.

Вывод завершает ваше сочинение. Он должен быть убедительным, т.к.  это умозаключение, итог, следствие ваших рассуждений. Он почти дублирует тезис, но выводит его на новый (более глубокий) уровень за счет обобщений и, возможно, прогнозов. Вывод можно формулировать, используя следующие слова и выражения: итак, обобщая сказанное, таким образом, исходя из наших рассуждений, следовательно…

Сочинение-рассуждение станет более убедительным при следующих условиях:

• основной тезис соответствует теме сочинения,
• отобранные доказательства достаточно весомы,
• между частями сочинения тесная логическая связь,
• выводы четко сформулированы.

Форма вывода (в частности, доказательства) правильна, если в нём не нарушено ни одно правило логики.

Материалы, использованные при подготовке рубрики:

1. Алиев Г. Учимся рассуждать [Текст] : школьное сочинение и проблемы его написания / Г. Алиев // Начальная школа : прил. к газ. «Первое сент.». — 2001. — № 30.
2. Литневская Е.И., Багрянцева В. А. Методика преподавания русского языка в средней школе: Учебное пособие для студентов высших учебных заведений / Под ред. Е. И. Литневской. — М.: Академический проект, 2006. — 590 с.
3. Никитина Н. Н. Алгоритм написания сочинения-рассуждения (части С) при подготовке к ЕГЭ. 11-й класс.
4. Статья «Рассуждение» в «Стилистическом словаре русского языка».

Часто при доказательстве теорем пользуются методом доказательства от противного. Суть этого метода помогает понять загадка. Попробуйте её разгадать.

Представьте себе страну, в которой приговорённому к казни предлагается выбрать одну из двух одинаковых на вид бумаг: на одной написано «смерть», на другой — «жизнь». Враги оклеветали одного жителя этой страны. И, чтобы у него не осталось никаких шансов спастись, сделали так, что на обороте обоих бумажек, из которых он должен выбрать одну, было написано «смерть». Друзья узнали об этом и сообщили осуждённому. Он попросил никому об этом не рассказывать. Вытащил одну из бумажек. И остался жить. Как ему это удалось?

Ответ. Осуждённый проглотил выбранную им бумажку. Чтобы установить, какой жребий ему выпал, судьи заглянули в оставшуюся бумажку. На ней было написано: «смерть». Это доказывало, что ему повезло, он вытащил бумажку, на которой было написано: «жизнь».

Как в случае, о котором рассказывает загадка, при доказательстве возможны только два случая: можно… или нельзя… Если удастся убедится, что первое невозможно (на бумажке, которая досталась судьям, написано: «смерть»), то сразу можно сделать вывод, что справедлива вторая возможность (на второй бумажке написано: «жизнь»).

Доказательство методом «от противного» осуществляется так.

1) Устанавливают, какие варианты в принципе возможны при решении задачи или доказательстве теоремы. Вариантов может быть два (например, перпендикулярны ли не перпендикулярны рассматриваемые прямые); вариантов ответа может быть три и больше (например, какой получается угол: острый, прямой или тупой).

2) Доказывают. Что не может выполняться ни один из тех вариантов, которые нам необходимо отбросит. (Например, если надо доказать, что прямые перпендикулярные, смотрим, что получается, если рассматривать не перпендикулярные прямые. Как правило, удаётся установить, что в этом случае какой-либо из выводов противоречит тому, что дано в условии, а потому невозможен.

3) На основании того, что все нежелательные выводы отброшены и только один (желательный) остался нерассмотренным, делаем вывод, что именно он верный.

Пример.

Решим задачу, используя доказательство от противного.

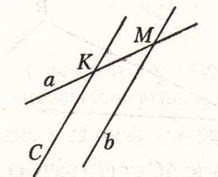
Дано: прямые а и b такие, что любая прямая, которая пересекает а, пересекает и b.

Используя метод доказательства «от противного», доказать, что а ll b.

Доказательство.

Возможны только два случая:

1) прямые а и b параллельны (жизнь);

2) прямые а и b не параллельны (смерть).

Если удастся исключить нежелательный случай, то останется сделать вывод, что имеет место второй из двух возможных. Чтобы отбросить нежелательный случай, давайте подумаем, что произойдёт, если прямые а и b пересекаются:

По условию любая прямая, которая пересекает а, пересекает и b. Поэтому, если удастся найти хотя бы одну прямую, которая пересекает а, но не пересекает b, этот случай надо будет отбросить. Таких прямых можно найти сколько угодно: достаточно провести через любую точку К прямой а, кроме точки М прямую КС, параллельную b:

Поскольку отброшен один из двух возможных случаев, можно сразу сделать вывод, что а ll b.

 Остались вопросы? Не знаете, как доказать теорему?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Доказательство от противного

(лат. reductio ad absurdum) — вид доказательства, при кром истинность суждения (тезиса) достигается или демонстрируется через опровержение противоречащего ему суждения — антитезиса. Опровержение антитезиса достигается путем установления его несовместимости с заведомо истинным суждением.

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
   карточек