Доклад по егэ математика

ДОКЛАД

Эффективные приемы и методы подготовки учащихся к успешной сдаче ЕГЭ по математики.

В основу построения рекомендаций положены принципы развития математического образования, определение приоритетных и перспективных направлений, а также анализ наиболее типичных ошибок, допущенных в решении заданий базового и профильного экзамена.

Возрастание роли математики в современной жизни привело к тому, что для адаптации в современном обществе и активному участию в нем необходимо быть   математически   грамотным   человеком.   В   связи   со   стратегическими направлениями   социально — ­экономического   развития   России   до   2020   года: «Приоритетной   государственной   задачей   является   обеспечение   качественного базового уровня математических и  естественнонаучных знаний у всех выпускниковшколы, не только будущих ученых, но и будущих квалифицированных рабочих…»           Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам.           Формула успеха хорошо сдать экзамен ЕГЭ и ОГЭ по математике: Высокая степень восприимчивости + мотивация + компетентный педагог.

Практика показывает, что прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта. Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего разбора. После удачного разбора в классе домашний вариант не представляет большого труда, и у обучающегося и учителя складывается ложное впечатление, что подготовка идет эффективно и цель достигнута. Многократное повторение этих манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант, он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные ранее варианты часто идет во вред обучению.

Правильным подходом является систематическое изучение материала, решение большого числа задач по каждой теме – от простых к сложным, изучение отдельных методов решения задач. Разумеется, варианты подготовительных сборников, открытые варианты можно и нужно использовать в качестве источника заданий, но их решение не должно становиться главной целью; они должны давать возможность иллюстрировать и отрабатывать те или иные методы. В любом случае, при проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.

Компенсирующее обучение в старших классах.

Часто мы сталкиваемся с ситуацией, когда главенствующим методическим принципом оказывается принцип «прохождения программы», – то есть программа должна быть пройдена во что бы то ни стало, невзирая на то, что содержание этой программы может не отвечать реальным возможностям и подготовке обучающихся.

С введением нового ФГОС, реализацией Концепции развития математического образования, принятием федеральных примерных образовательных программ по математике принцип прохождения программы приобретает новый смысл – обучающийся должен участвовать в посильной интеллектуальной математической деятельности, дающей осязаемые плоды обучения.

Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность  эффективно  подготовить   обучающихся  к решению 8 – 10 заданий профильного ЕГЭ.

Практико-ориентированная математика.

Важной частью ЕГЭ по математике и современных программ являются задачи на применение математических знаний в быту, в реальных жизненных ситуациях. Это задачи на проценты, оптимальный выбор из предложенных вариантов, чтение данных, представленных в виде диаграмм, графиков или таблиц, вычисление площадей или других геометрических величин по рисунку, задачи на вычисление по формулам и т.п.

Круг практико-ориентированных задач в ЕГЭ постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.

Сложилась практика, когда к практическим задачам учитель приступает только в последний год перед сдачей ЕГЭ. К этому времени обучающиеся успели прочно забыть, как вычислять проценты, как находить площади фигур с помощью палетки или на клетчатой бумаге – все эти задачи для них оказываются новыми.

На протяжении всего периода обучения математике не следует отрываться от простых практических задач; их следует включать в блоки повторения в начале и конце учебного года, в текущий, внутришкольный контроль. Задачи на вычисление сумм налогов, процентов по банковскому вкладу или кредиту, другие задачи финансового характера должны стать постоянным инструментом на уроках математики, поскольку эти задачи связывают наш предмет с окружающим миром и повседневной жизнью.

Практико-ориентированные задачи по финансовой грамотности, геометрического плана, чтение таблиц и графиков нужно включать в изучение математики в средней и старшей школе. При этом характер и трудность задач могут меняться со временем, более того, это необходимо для органического вплетения практических тем в изучение теоретических вопросов. Например, задачи на вклады и кредиты органично возникают при изучении прогрессий, показательной функции и производных. Вычисление площадей по клеточкам очень часто помогает при изучении совершенно абстрактной, казалось бы, темы «первообразная и интеграл». Чтение простых графиков помогает понять и грамотно на качественном уровне применять производную.

Отдельную важную роль в сближении школьной математики с задачами окружающего мира играют вопросы вероятностей и статистики.

Теория вероятности и статистика.

В Концепции развития математического образования ТВ и статистика названы в числе перспективных и важных направлений развития школьной математики. С 2012 года задачи по ТВ формально включаются в КИМ ОГЭ и ЕГЭ. При этом учителя понимают, что те задачи, которые сейчас есть в открытом банке заданий и те, что включены в экзамен, в большинстве случаев сводятся к перечислению равновозможных исходов.

Ясно, что роль ТВ и статистики в школьной математике будет расти. Одновременно будет расширяться круг тем, подлежащих контролю.

При обучении математике следует больше внимания уделять темам вероятности и статистики, постепенно нарабатывая опыт преподавания этих разделов, которые оказываются наиболее практически направленными. Изучение вероятности и статистики требуется вести в тесной привязке к темам алгебры и геометрии, поскольку систематический подход к вопросам ТВ требует от обучающихся знаний о свойствах геометрической прогрессии преобразованиях многочленов, корнях и степенях, площадях фигур.

Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив, поддерживает изучение традиционных разделов школьной математики. В 2012 – 2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент медиана выполнения задания 4 – около 90%.

Некоторые эффективные приёмы обучения математике.

Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.

1) При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче.

Условие. Каждый из двух друзей одновременно показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 8?

Решение. Общее число исходов равно: 25. Благоприятными событию «получится в сумме число 8» будут исходы: 3 + 5, 5 + 3, 4 + 4. Вероятность события равна: 3/25 = 0,12. Ответ: 0,12.

Комментарий. Следует различать две комбинации, когда один из друзей показывает 3 пальца, а другой – 5 пальцев. Ответ можно записать как обыкновенной дробью, так и десятичной.

Задание для самостоятельного решения. Каждый из двух друзей показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 7?

Описанный приём может использоваться применительно к отдельному заданию, однако из таких заданий – с решениями и комментариями – можно составить тематическую проверочную работу, которую можно использовать и в рамках подготовки к экзамену. Решения могут быть написаны учителем самостоятельно, могут быть взяты из публикуемых сборников для подготовки к ЕГЭ, а также из материалов журнала «Математика» или других источников.

2) Весьма эффективно использование при решении задач подсказок,  то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка,  тем больше  из нее можно  извлечь.  Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.

Пример. Решите уравнение.

Подсказка. Можно применить формулу синуса суммы двух углов. Подсказкой может быть похожая задача, которая решалась недавно, указание на конкретный метод. Всегда полезно использовать результаты, методы уже решённых задач, а также опыт, приобретенный при решении. Это широко используется в школьном курсе геометрии, где многие важные геометрические факты, которыми целесообразно пользоваться при решении других задач, даны не в виде утверждений (теорем), а в виде задач. Кроме того, это возможность использования еще одного метода – аналогии.

При решении тригонометрических уравнений подсказкой может быть определённая формула, а при решении логарифмического уравнения – свойство логарифма. Полезно учить пользоваться подсказками, искать их самостоятельно, а также учить давать подсказки.

3) При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма – мозговой штурм. Основные принципы мозгового штурма: на первом этапе – предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором – анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема – в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.

4) При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины. Ниже приводится пример такой задачи из варианта профильного экзамена.

«Задание 11. Заказ на изготовление 323 деталей первый рабочий выполняет на 2 ч быстрее, чем второй. Сколько деталей изготавливает первый рабочий, если известно, что он изготавливает на 2 детали больше второго?»

Данную задачу экзаменуемые решили существенно хуже, чем аналогичную задачу с более привычной и хорошо отработанной фабулой, связанной с движением двух велосипедистов.

Умение переформулировать условие важно и при решении нестандартных  задач,  то  есть  таких,  метод  решения  которых   ученику   не известен, не изучался и не отрабатывался на уроках.

Ещё более актуально это умение при решении практико- ориентированных задач, представляющих собой некоторую ситуацию из реальной жизни, которую необходимо преобразовать и описать на языке математики (то есть самостоятельно сформулировать задачу). В самом простом случае основа задачи будет следующая: за лестницей, которую прислонили к стене дома, надо распознать прямоугольный треугольник, гипотенузой которого и будет данная лестница.

5).В связи с введением обязательного ЕГЭ и ОГЭ по математике возникает необходимость научить учащихся решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных

 вычислений, так как   на   экзамене   не   разрешается   использовать   калькулятор   и   таблицы.   Можно научить   учащихся   выполнять простейшие (и   не   очень)   преобразования   устно. Конечно,  для   этого   потребуется   организовать   отработку   такого   навыка   до автоматизма,

 на каждом уроке необходимо отводить 5 — ­7 минут для проведения упражнений устных вычислений, предусмотренных программой каждого

класса. Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении

 развивается память, речь, внимание, быстрота реакции.

Если в 5 — ­6 классах устный счет – это выполнение действий с числами:

 натуральные числа, обыкновенные дроби, десятичные дроби, то в старших

 классах – это могут быть:

7 класс:   Формулы   сокращенного   умножения.   Решение   простейших   ЛУР.   Действия со степенью. График линейной

 функции.

8 класс:   Линейные неравенства и числовые промежутки. 

Решение простейших линейных неравенств. Решение КВУР с помощью

 теоремы Виета и частных случаев.  Решение КВУР   рациональными   способами.   Арифметический   квадратный   корень   и   его свойства. 9 класс: Решение неравенств 2 степени. Преобразование графиков функций.  Формулы приведения. Значения тригонометрических функций.

10 — 11 классах: Вычисление   производных.   Простейшие   тригонометрические   неравенства. Тригонометрические   формулы.   Простейшие   тригонометрические   уравнения. Функции,   обратные  тригонометрическим.   Преобразование   графиков   функций. Вычисление   первообразных.   Свойства   логарифмов.   Простейшие   показательные уравнения

 и неравенства. Простейшие логарифмические уравнения и неравенства. Практика   показала,   что   систематическая   работа   с   устным   счетом способствует   значительному   повышению   продуктивности   вычислений   и преобразований.   Сокращается   время   на   выполнение   таких   операций,   что переводит   их   из   разряда   самостоятельной   задачи   в   разряд   вспомогательной   и становится инструментом (“таблицей

 умножения”) для решения более сложных задач.                         Учитель по математике, знающий, с чем придется столкнуться школьнику на экзамене,   кроме   фундамента   уделяет   большую   часть   времени   на   занятии отработке вопросов специфики ЕГЭ и ОГЭ.                Правильность оформления заданий,  тактика   и  стратегия   решения   в условиях  дефицита   выделенного   времени  на   экзамене,   а   также   банальная невнимательность. Эти и масса других особенностей составляют

 суть специфики.          Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и еще раз тренировка. Довести решение задач до автоматизма.

Развитие геометрических представлений

Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. Одна из основных причин – недостатки в формировании пространственного мышления учащихся. Массово эта проблема проявилась с уходом из общего образования такого учебного предмета, как черчение, и вряд ли стоит ожидать его возвращения – профессия конструктора перестала быть столь массово востребованной с приходом компьютерных технологий.

Эта проблема легла на плечи учителей математики, однако решение её известно: непрерывное развитие геометрических представлений и геометрического воображения обучающихся с 1 по 11 класс; наглядная геометрия в 1–6 классах; больше внимания геометрическому моделированию и конструированию (из плоских и пространственных фигур), геометрическим чертежам, построениям, изображениям от руки и с помощью различных чертёжных инструментов, на нелинованной и клетчатой бумаге.

Это отнюдь не означает, что всю геометрию надо свести к наглядности и к работе руками. Определения и доказательства, логика и аксиоматика важны для современного человека и для изучения геометрии не менее, но надо понимать, что в развитии человека всему отводится свое время, а несформированное наглядно-образное мышление, которое должно быть основой и этапом на пути формирования логического мышления, просто мешает его формированию.

Если вернуться к этапу обучения в старшей школе, то целесообразно использовать любые приёмы и средства, которые способствовали бы визуализации предлагаемых обучающимся задач. Это не только построение чертежей по условию задачи (что непросто сделать при проблемах с пространственным воображением), это прежде всего различные предметные модели (полезно для каждой решаемой задачи иметь соответствующую ей модель-подсказку, чтобы использовать её для визуализации условия, поиска и проверки решения), компьютерные программы, позволяющие выполнять стереометрические чертежи.

Полезно выделить эту работу в отдельный тематический практикум, на котором обучающиеся тренировались бы в изображении и моделировании пространственных тел, построении чертежей по условию задачи (в различных ракурсах, выбирая наиболее удобный для поиска решения), можно также организовать данную работу в рамках проекта.

Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.

Работает ли эта стратегия?

Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!

Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.

1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Учить наизусть.

Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике

2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.

3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем.

4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы.

5.) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится.

6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.

7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).

 Саморегуляция и обратная связь «ученик-учитель».

Известно, что эффективность обучения возрастает в случае самооценивания, поскольку ученик самостоятельно получает информацию о своих результатах, сам её анализирует, делает выводы о своем прогрессе, корректирует цели в случае необходимости. Но для этого необходимы критерии оценивания работы, которые должны быть у ученика не просто до начала выполнения конкретной работы, но желательно и в самом начале изучения темы. К сожалению, на практике более распространена ситуация, когда работа выдаётся ученику без критериев ее выполнения.

К саморегуляции относятся также вопросы, связанные с осознанностью знания и незнания. Объяснение учителя сродни лекционной форме предъявления новых знаний. В связи с этим подчеркнём важность обратной связи. Учитель должен получать сигналы от обучающихся: «Я понимаю, могу объяснить», «Я не уверен, правильно ли я понимаю», «Я не понимаю». Учитель может прервать своё объяснение вопросом к тем, кто  ещё не понял, предложением высказать свои сомнения тем, кто не уверен в понимании, предоставлением слова тем, кто всё понял.

Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку, как «рациональное решение», «интересная идея», «грамотная запись». Может быть отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных» мест и т.п.

Обратная связь эффективна в случае, если она конкретна, то есть связана с известными ученику результатами и действиями, подлежащими усвоению. Важное значение имеет информированность ученика относительно того, чему он должен научиться, какие задания должен научиться решать, а какие может научиться решать для того, чтобы получить желаемое количество баллов на экзамене. Если ученик фиксирует и отслеживает сам, умеет ли он выполнять требуемое задание или нет, то минимизируется время на выполнение заданий, при этом работа становится более эффективной и рациональной. Отсюда необходимость в открытости предъявляемых требований к результатам обучения, а на этапе подготовки к экзамену – в ориентации на конечный запланированный результат.

И еще об одном факторе следует упомянуть – это повторяющееся тестирование. Уже имеющийся опыт российской школы и более продолжительный зарубежный опыт не позволяют говорить о нём, как об эффективном факторе. Положительные эффекты возникают только в тех случаях, когда учитель учитывает результаты тестирования для корректировки процесса обучения и приспосабливает методы обучения к возможностям конкретного ученика, учитывая его сильные и слабые стороны, или при условии содержательной обратной связи, с которой ученик может работать самостоятельно, то есть имеет возможность учиться на тестах.

Завершающие рекомендации.

Необходимо отметить, что создание ЕГЭ по математике базового уровня и появление акцента на использование математических знаний в реальных ситуациях были неверно истолкованы некоторыми учителями в качестве генеральной идеи обучения, что привело к поверхностному освоению обучающимися программы старшей школы. В частности, это зафиксировано и результатами экзамена: результаты выполнения заданий по темам курса старшей школы ниже результатов выполнения заданий из «реальной математики».

Для того чтобы успешно сдать ЕГЭ по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.

Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий базового уровня в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.

Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6–7 часов в неделю.

В первую очередь нужно выработать у обучающихся быстрое и правильное выполнение заданий части 1, используя, в том числе и банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.

Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля.

В записи решений к заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность  пояснений, доказательность рассуждений.

И в завершение необходимо отметить, что еще одним важным фактором является психологический климат в учебном коллективе: дружеские отношения среди одноклассников, спокойная рабочая атмосфера на уроке, методичная, прозрачная и последовательная подготовка к экзамену, доверительные отношения учителя с учениками, вера в достижение более высоких результатов и эмоциональная поддержка.

 На занятиях стараюсь создать атмосферу комфортности, 

взаимопонимания. На своих уроках я делаю   установку   на   то,   чтобы   любой   ребенок   должен   быть   понят   и   услышан учителем   и   соучеником:   учение   должно   проходить   в   «атмосфере непринужденности,   чтобы   дети   и   учитель   свободно   дышали   на   уроках».   От учителя   требуется   и   мастерство,   и   большое   терпение,   и   любовь к   учащимся. Доброжелательное отношение к ученикам снимает у них страх перед трудностями обучения: ребенок не должен бояться 

ошибиться, спросить учителя, если он что­ то прослушал   или   не   понял.   Психологическая   подготовка   учащихся, может заключается в следующем:

 отработка поведения в период подготовки к экзамену; обучение навыкам 

саморегуляции, самоконтроля, повышение уверенности в себе, в   своих   силах.   Методы   проведения   занятий   по   психологической   подготовке учащихся   разнообразны:   групповая   дискуссия,   игровые   методы,   медитативные техники,   Содержание   занятий   должно ориентироваться   на следующие   вопросы:   как   подготовиться   к   экзаменам, поведение   на   экзамене,   способы   снятия   нервно­психического   напряжения,   как противостоять стрессу. 

Литература:

Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике, подготовленные ФГБНУ «ФИПИ».

Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2020 года по математике, подготовленные ФГБНУ «ФИПИ».

Бабанский Ю.К. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский ­ М., Педагогика, 1989.

Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. – М., 1989.

Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педагогика. – 1989. ­ №5.

Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченко.­М., 1989.

Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И. ­ М., 1979.  

25

АНО ВПО

«Европейский Университет «Бизнес Треугольник»

Реферат

по дополнительной профессиональной образовательной программе

профессиональной переподготовки

Тема:

«Основные трудности при подготовке старшеклассников к сдаче ЕГЭ

по математике»

Реферат подготовил:

Захарова Ирина Николаевна

Должность:

учитель математики

Место работы:

Муниципальное бюджетное общеобразовательное

учреждение «Никольская средняя общеобразовательная

школа имени А.С. Жадова»

Номер и дата договора:

март 2018 г.

Содержание

стр

Введение………………………………………………………………………….. 3

1. Теоретические аспекты методики подготовки к ЕГЭ ……………………….5

2. Трудности в подготовке к ЕГЭ поматематике…………………………………6

Заключение……………………………………………………………………….18

Список литературы………………………………………………………………24

Введение

Актуальность темы определяется тем, что:

1. Введение ЕГЭ требует корректировки в учебно-методической и организационной деятельности, что абсолютно невозможно без создания учителем новых целей общего образования, новых форм и новых критериев.

2. Тестовая форма аттестации обладает весьма существенными особенностями. Несмотря на довольно простые по содержанию вопросы, около 20% тестируемых ощущают большую психологическую нагрузку от калейдоскопичности тем заданий – мгновенный переход от тригонометрии к логарифмам и т.п. Школа не готовит учащихся к таким нагрузкам – традиционно в российской школе основной упор делается на качество и логику решения, но не скорость заполнения бланковой документации — это тоже одна из новых форм работы, по которой у выпускников нет необходимых навыков и к которой нужно специально готовиться.

3. Кроме подготовки по предмету, технике выполнения задания заданий разных типов и записи ответов на те же задания, очень важно обеспечить правильную мотивацию учащихся к участию в ЕГЭ.

4. Психологическая подготовка к ЕГЭ учащихся и их родителей – существенный фактор, влияющий на результаты ЕГЭ.

Подготовка к успешному выполнению ЕГЭ отличается от привычной нам методики обучения школьников математике вообще.

При положительной мотивации учащихся к участию в ЕГЭ, при овладении ими техникой выполнения текста, полноценном повторении изученного материала можно обеспечить высокие результаты в соответствии с возможностями каждого ученика.

Таким образом, исходя из вышеизложенного, ввиду многоплановости темы, в работе сосредоточено внимание на исследовании узловых проблем, характеризующих деятельность учителя математики при подготовке к ЕГЭ, и поставлены следующие задачи:

— обеспечить правильную мотивацию учащихся к участию в ЕГЭ;

— реализовать сбалансированное сочетание традиционных и новых методов контроля заданий; разработать методику обучения технике выполнения текста;

— разработать планирование обобщающего повторения курса алгебры и начал анализа с учетом основных содержательных линий курса, структурой и содержанием КИМов;

— обеспечить достижение конкретным учеником возможных для него результатов на ЕГЭ.

1. Теоретические аспекты методики подготовки к ЕГЭ

Проблемы подготовки учащихся к сдаче ЕГЭ по математике, который стал обязательным для всех выпускников средней школы и включен в перечень вступительных испытаний вызваны многими факторами современного образовательного пространства. Происходящие в последние годы значительные изменения в российской системе образования, связаны не только с демократизацией общества и переходом страны к рыночным отношениям, но и созданием условий для развития разнообразных типов и видов образовательных учреждений, внедрением в практику вариативных образовательных программ, учебников, методик и технологий обучения. Сегодня мы говорим об актуальности введения единого государственного экзамена как элемента инновационной педагогической технологии оценки и контроля качества знаний и умений выпускников школ. Модернизация высшего образования в нашей стране, вызванная в том числе и фактом присоединения в июне 2003 Российской Федерации к Болонскому процессу, повлекла за собой переход от парадигмы знаний к личностно-ориентированной парадигме. Изначально ЕГЭ был задуман и экспериментально внедрен в большинстве регионов России с целью обеспечения государственных гарантий реализации конституционных прав и свобод граждан на образование и, прежде всего, для обеспечения равного доступа молодых людей к полноценному образованию независимо от уровня доходов семьи, места проживания, национальной принадлежности и состояния здоровья. Придание с 2009 года единому государственному экзамену по математике статуса обязательного испытания на выпускном и вступительном этапах выявляет ряд проблем в подготовке учащихся в форме ЕГЭ. Прежде всего, неоднозначное отношение к тестовому контролю по математике со стороны учащихся, родителей, учителей и вузовских преподавателей. Тест как метод изучения индивидуальных различий обучающихся возник сравнительно недавно и находится в нашей стране в стадии развития. Проблема любого тестирования как формы контроля знаний школьников сдают компьютерным тестом имеет ряд плюсов и минусов. При контроле знаний тестирование, на наш взгляд, оправдано в качестве первой ступени оценки знаний, когда происходит выявление учеников и, особенно, студентов, подготовленных плохо. Любое тестирование позволяет в какой — то мере исключить субъективный фактор при оценке знаний учащегося, а также дает возможность проверить знания обучающегося не по отдельным случайно выбранным вопросам билета, а по всему изученному материалу. Под сомнением у преподавателей математики традиционно остается глубина и качество усвоения данного раздела: «дрессировка и натасканность» выходят на первый план в целевой подготовке к испытанию в виде тестов, в то время как из устного ответа учащегося можно выявить те моменты, которые он не понял, или понял неправильно, или понял не до конца и в процессе собеседования устранить обнаруженные пробелы в знаниях и др.

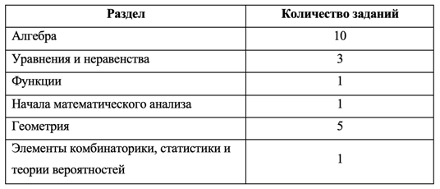
При проведении ЕГЭ проверяется владение материалом не только курса «Алгебра и начала анализа», но материалом курсов «Планиметрия 7-9» и «Стереометрия 10-11 (многогранники и тела вращения)», а также некоторых разделов курса математики основной и средней школы: проценты (основные задачи на проценты); пропорции (основное свойство пропорции, задачи на составление и решение пропорций); арифметические и геометрические прогрессии.

При этом содержание проверочных заданий не выходит за рамки тех

вопросов, которые включены в минимум содержания основной и средней школы по математике. Содержание заданий связано со следующими разделами курсов основной и средней школы:

1. Выражения и преобразования.

2. Уравнения и неравенства.

3. Функции (функционально-графические представления).

4. Числа и вычисления.

5. Геометрические фигуры и их свойства. Измерение геометрических

величин.

2 Трудности в подготовке к ЕГЭ по математике

Проблемами современного этапа математической подготовки учащихся к выпускным и вступительным экзаменам в форме ЕГЭ являются и сложность самой математики как науки, и психофизиологические основы формирования готовности старшеклассников к выпускным экзаменам по предмету, и интеграция содержания и методов преподавания алгебраического и геометрического материала с целью подготовки учащихся к ЕГЭ, и противоречие между осуществлением обязательного всеобщего среднего образования и реализацией принципа индивидуализации усвоения знаний, учебной деятельности при подготовке к экзаменам, а также осуществление соответствующей подготовки учителей математики к работе с учащимися в условиях обязательного ЕГЭ. Организация промежуточных тестирований, использование информационных технологий, проведение выпускных экзаменов за курс основной школы в режиме пропедевтики ЕГЭ позволяет, на наш взгляд, формировать систему общеучебных умений и навыков, прежде всего, умений и навыков самоконтроля, самоанализа и рефлексии, самообразования, выработки знаний о самом себе, об особенностях познавательного процесса при усвоении знаний. Многолетний опыт работы с учителями и учащимися старших классов по подготовке к экзаменам в том числе и в форме ЕГЭ позволяет утверждать, что в современных условиях совершенствование учебного процесса должно затрагивать не только выпускные классы, но и всю среднюю школу, все методические службы, системы повышения квалификации учителей математики, авторские коллективы по написанию учебников, пособий и рекомендаций для учащихся. Важным аспектом работы с учителями по подготовке к ЕГЭ является формирование позитивного отношения к тестовому итоговому контролю, как к одной из форм оценки результатов обучения. Тесты в форме ЕГЭ являются наиболее сложными, поскольку представляют собой комбинацию тестов, ориентированных на критерий и норму. К сожалению, работать в полной мере с тестами школьники могут только в последней четверти одиннадцатого класса.
Результаты ЕГЭ выявили ряд нерешенных проблем, характерных для подготовки различных категорий выпускников. Что позволяют высказать некоторые общие рекомендации, направленные на совершенствование процесса преподавания и подготовки учащихся средней школы.

1. Необходимо совершенствовать методику формирования базовых умений, составляющих основу математической подготовки выпускников средней школы.

2. Анализ результатов выполнения базовых заданий по курсу алгебры и начал анализа показал наличие положительной динамики в овладении материалом раздела «Тригонометрия»». В настоящее время вызывают тревогу низкие результаты выполнения заданий на решение иррациональных уравнений и логарифмических неравенств. Следует обратить внимание на обеспечение более прочного усвоения учащимися стандартных алгоритмов решения этих уравнений и неравенств.

3. Геометрическая подготовка выпускников школы продолжает оставаться невысокой, поэтому по-прежнему необходимо усиленное внимание учителей к преподаванию курса геометрии в основной и старшей школе, чтобы в процессе обучения учащиеся не только овладевали теоретическими фактами курса, но и приобретали умения проводить обоснованные рассуждения при решении геометрических задач и математически грамотно записывать полученное решение

4. Самые низкие результаты учащиеся показали при решении задач, которые труднее всего поддаются алгоритмизации: задачи по геометрии, задачи прикладного содержания (где требуется применить умение читать графики, решать сюжетные задачи), задачи, для решения которых требуется применить элементарные навыки исследовательской работы.

5. слабая подготовка учащихся по математике за курс основной школы по вопросам: выполнение совместных действий над обыкновенными и десятичными дробями; преобразование многочленов; преобразование алгебраических дробей; преобразование выражений, содержащих степень с целым показателем; преобразование иррациональных выражений; решение линейных, квадратных, дробно-рациональных уравнений и неравенств; определение свойств функции с помощью графика и аналитически;

6. неосознанное усвоение знаний по отдельным темам, например, «Логарифмы», «Решение иррациональных уравнений»;

7. неумение преобразовать ситуацию, описанную в задаче, к типовой     ситуации на основе анализа и переформулирования условия задачи;

8. неумение самостоятельно разрабатывать план решения;

9. неумение построить логически грамотную цепочку рассуждений, приводящую к более рациональному, нестандартному решению задачи.

1.  Когнитивные трудности — это трудности, связанные с особенностями переработки информации в ходе ЕГЭ, со спецификой работы с тестовыми заданиями. Причем если для педагога важен объем знаний, то с психологической точки зрения важнее умение пользоваться этими знаниями.

• психогимнастические упражнения, развивающие переключаемость в целом (работа с таблицами Шульте и т.п.);

• игры и задания, основанные на материале школьных предметов, причем не столько акцентируются фактические знания, сколько развиваются навыки оперирования понятиями и переключения. Пример такого упражнения — модификация известной игры «Ассоциации», где в качестве ассоциируемых понятий используются термины из школьных курсов биологии, физики и др. Инструкция имеет следующий вид: «У ведущего в руках мяч. Он может бросить его любому игроку и назвать любое понятие из… (называется предмет). Задача игрока — поймать мяч и назвать ассоциацию с этим понятием, после чего игрок становится ведущим». Игру можно усложнить, используя штрафные очки за ассоциации, не связанные с предметом, или вводя бонусы за тематические ассоциации.

  1.  Личностные трудности обусловлены особенностями восприятия учеником ситуации экзамена, его субъективными реакциями и состояниями.

• Трудности, связанные с ролью взрослого. Обычно на экзамене педагог, особенно работающий в данном классе, совмещает функции поддержки и оценки. В ситуации ЕГЭ присутствующие педагоги — это только наблюдатели, что также может повышать тревогу у выпускников.

•  

  Трудности, связанные с критериями оценки. Контраст с привычными проверочными процедурами действительно велик (обычно — личный контакт с экзаменатором, здесь — отсутствие такового, обычно — развернутый цветистый ответ, здесь — лаконичный и т.п.).
  Процедура ЕГЭ требует особой стратегии деятельности: ученику необходимо определить для себя, какие задания и в каком соотношении он будет выполнять. И здесь мы сталкиваемся еще с одной специфической проблемой, о которой мы уже упоминали. При традиционной форме проведения экзамена способы подготовки и организации деятельности во время экзамена более или менее одинаковы: на письменном экзамене ученики имеют стандартный набор заданий, с которым они должны справиться, на устном — изложить заранее выученное содержание экзаменационного билета. А в случае ЕГЭ определение стратегии деятельности становится ключевым моментом, поскольку это во многом определяет экзаменационную оценку. Следование какой-то рекомендуемой, а не индивидуальной, эффективной для себя стратегии работы может привести к тому, что человек делает не то, что ему удобно, и это в конечном счете приводит к снижению результата. На выбор стратегии оказывает влияние множество факторов. Например, он может зависеть от уровня притязаний. Неумение адекватно оценивать свои возможности (завышенный или заниженный уровень притязаний), отсутствие информации о том, как будет оцениваться работа, может привести к выбору неэффективной для себя стратегии.
  Таким образом, процессуальные трудности связаны с недостаточным знакомством с процедурой экзамена и отсутствием четкой стратегии деятельности.
  Чем может помочь психолог? Преодоление процессуальных трудностей должно ориентироваться на овладение специфическими особенностями процедуры ЕГЭ. Хороший поддерживающий эффект оказывает не просто рассказ о процедуре ЕГЭ, но ее проигрывание, причем в юмористической форме. Комическое представление пугающей ситуации способствует снижению у детей напряжения и тревоги. Такое проигрывание может также включать совместное с детьми сочинение комических вопросов и подготовку юмористических заданий друг для друга.
  Кроме того, психолог может помочь в выработке индивидуальной стратегии деятельности для каждого старшеклассника.

  Приемы, мобилизующие интеллектуальные возможности школьников при подготовке и сдаче экзаменов

Заключение

Таким образом, обеспечив правильную мотивацию учащихся к участию в ЕГЭ, сбалансировав сочетание традиционных и новых методов контроля знаний, обучив учащихся технике выполнения теста, организовав повторение курса алгебры и начал анализа с учетом содержательных линий курса, структуры и содержания КИМов можно получить достижение каждым конкретным учеником возможных для него результатов ЕГЭ.

Итоги ЕГЭ 2017 г. выявляют ключевые проблемы, определяющие

недостаточное число выпускников с уровнем подготовки, подходящим для успешного продолжения образования в профильных вузах:

• несформированность базовой логической культуры;

• недостаточные геометрические знания, графическая культура;

• неумение проводить анализ условия, искать пути решения, применять

известные алгоритмы в измененной ситуации;

• неразвитость регулятивных умений: находить и исправлять

собственные ошибки.

Как видно из проделанного анализа типичных и массовых неверных ответов, самой большой проблемой является неверное понимание, неполное или невнимательное чтение условия. Это относится практически ко всем заданиям практико-ориентированного направления. Наверняка это же верно и в отношении текстовых задач повышенного уровня, но эта ошибка там проявляется не так открыто, как в базовых задачах.

Потеря знака остается массовой ошибкой, на это нужно обращать особое внимание, выявляя «группы риска» – тех учащихся, кто допускает эту ошибку регулярно.

Заметно снизилось количество ошибок, полученных из-за того, что

участник экзамена не сопоставляет свой ответ с реально возможными значениями величины. Раньше таких ошибок было намного больше. Возможно, снижение их числа связано с тем, что в базовом ЕГЭ на протяжении трех лет дается задача, назначение которой – проверить ответ на здравый смысл и соответствие реальности. Так или иначе, учителя больше стали обращать внимание на правдоподобность полученных ответов. Здесь уже сыграла свою положительную роль практическая ориентированность многих задач ЕГЭ.

Общая рекомендация при подготовке учащихся к ЕГЭ – следование простым правилам.

1. Для каждого из обучающихся определить задачи, которые он или она решает уверенно (1 тип), задачи, которые решаются хорошо, но часто бывают случайные ошибки (2 тип), и задачи, которые решаются плохо или вовсе не поняты (3 тип).

2. Обратить особое внимание на задачи 2-го типа: занимаясь ими, учащийся не только эффективно готовится к задачам этого типа, но и, незаметно для себя, повышает общую культуру, которая потребуется для решения прочих задач.

3. Доводя до совершенства решение понятных задач, не следует забывать задачи 1-го типа – к ним нужно постоянно возвращаться.

4. Задачи, трудные для обучающегося (3-й тип), следует добавлять в варианты понемногу, следя за тем, чтобы они не стали преобладающими, иначе мотивация может снизиться (ничего не получается), а понятные и привычные задачи забудутся. Лучше, если обучающийся, выполняя свои подготовительные задания, решит почти все сам и уже после этого будет с учителем разбираться в одной-двух непонятных задачах. Это экономит время также и учителю, а школьнику придает уверенности в том, что большинство задач он решить может.

5. Нельзя забывать о том, что подготовка к ЕГЭ может быть успешной только на фоне хорошего общего знания математики. Поэтому, повторим, сводить обучение в последние год-два к прорешиванию вариантов чревато провалом на ЕГЭ. Подготовка к ЕГЭ, как и ко всякому экзамену, – заключительная часть этапа обучения, а не цель обучения.

Органам управления образования, администрациям образовательных

организаций, учителям необходимо усилить разъяснительную работу среди обучающихся и родителей, направляя и поощряя их сознательный выбор требуемого и необходимого уровня математического образования и уровня итоговой аттестации.

На ступени основной и средней (полной) общей школы при организации преподавания математики приобретают еще большую актуальность следующие меры.

1. Выделение направлений математической подготовки:

 математика, необходимая для успешной жизни в современном обществе;

 математика, необходимая для прикладного использования в дальнейшей учебе и профессиональной деятельности;

 математика как подготовка к творческой работе в математике и других научных областях.

2. Для каждого направления необходимо определить меры по реализации содержания образования на базе ФГОС и примерных образовательных программ, в частности актуализированное общедоступными базами учебных и контрольных заданий.

3. Требуется дальнейшее увеличение доли геометрии, статистики, теории вероятностей и логики в преподавании математики.

4. Для эффективной реализации программы уровневого обучения

необходим мониторинг индивидуальных учебных траекторий школьников

начиная с первого года обучения.

5. Необходимо внедрение механизмов компенсирующего математического образования как в виде очных занятий, так и через сеть интернет-курсов, позволяющих своевременно ликвидировать пробелы, незнание.

6. Необходимо внедрение эффективных механизмов текущего и рубежного контроля – на школьном, региональном и федеральном уровнях.

7. Для учащихся, достигших базового уровня и не претендующих на достижение профильного уровня и выполнение экзаменационной работы профильного уровня, на ступени старшей школы должна быть предусмотрена возможность развивающего обучения математике.

8. Для учащихся, не достигших базового уровня математической

подготовки к окончанию основной школы, дальнейшее математическое образование на старшей ступени средней школы должно проводиться по специально разработанным интенсивным программам, направленным на освоение базовых математических умений и позволяющим подготовиться к итоговой аттестации на базовом уровне. Система внутреннего промежуточного контроля и итоговой аттестации по математике должна быть нацелена не на оценку абсолютной подготовки учащегося, а на оценку результата освоения математики учащимся с учетом выбранного направления математической подготовки.

9. Необходимо заменить «принцип прохождения программы» качественным усвоением знаний и умений на выбранном ими направлении подготовки.

10. Для организации повторения необходимо использовать для работы на уроке комплекты материалов для подготовки учащихся к итоговой аттестации.

Рекомендации по работе с учащимися, планирующими выполнение экзаменационной работы на профильном уровне.

Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий базового уровня, в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.

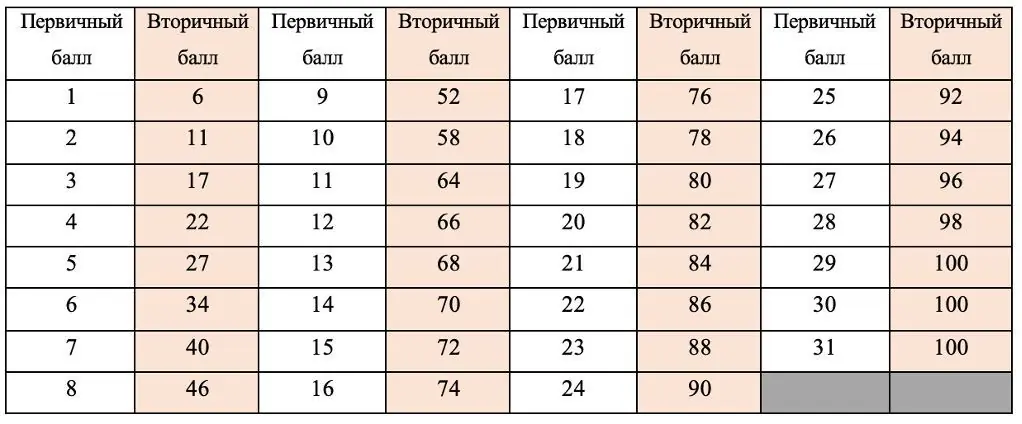
Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6–7 часов в неделю. В первую очередь нужно выработать у обучающихся быстрое и правильное выполнение заданий части 1, используя в том числе открытый банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.

Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля. В записи решений к заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений.

Рекомендации по работе с учащимися, планирующими выполнение экзаменационной работы на базовом уровне

Для учащихся, слабо овладевших или фактически не овладевших

математическими компетенциями, требуемыми в повседневной жизни, и допускающих значительное количество ошибок в вычислениях, при чтении условия задачи, образовательный акцент должен быть сделан на формировании базовых математических компетентностей. В этой группе учебный материал старшей школы может изучаться обзорно. Дополнительно потребуется не менее 2–3 часов в неделю для ликвидации проблем в базовых предметных компетенциях. Общее количество часов математики должно быть не менее 5 часов в неделю.

Для подготовки к ЕГЭ учащихся этой категории следует различными диагностическими процедурами выявить 9–12 заданий экзамена базового уровня, которые учащийся может выполнить, возможно, с ошибками, и в процессе обучения добиться уверенного выполнения этих заданий. Расширять круг этих заданий следует поэтапно. Эта работа может быть организована для различных групп учащихся одного класса на разных уровнях в урочной и внеурочной работе.

В обучении учащихся, имеющих значительные пробелы в знаниях и слабые вычислительные навыки, программа обучения должна быть компенсирующей. Для учащихся, которые имеют достаточно высокий уровень подготовки, но не планируют сдачу экзамена профильного уровня, при подготовке к экзамену базового уровня следует делать больший акцент на решение задач 18–20 в целях развития математического мышления, а также уделять внимание формированию представления об общекультурной роли математики, развитию наглядных геометрических представлений.

Следует обратить особое внимание на выбор уровня экзамена, рекомендуя учащимся, которые неуверенно решают 6 заданий с кратким ответом, базовый экзамен вместо профильного, а тем, кто решает 6–10 заданий, – базовый экзамен наряду с профильным. При подготовке к профильному экзамену следует обратить дополнительное внимание на задания с полным решением. В частности учащимся с не очень высоким уровнем подготовки, следует обратить особое внимание на задание 13, и первые пункты заданий 14, 16 и 19.

В заключение хотелось бы подчеркнуть, что главной основой успешной задачей сдачи экзамена по математике является качественное системное изучение математики, отсутствие пробелов в базовых математических знаниях.

Список литературы:

1. Директор школы // 2004 г — № 1-6, 2005 г. — № 3, 5, 6.

2. Квант // 2001 г. — № 5, 6.

3. Математика в школе // 2014 г. — № 1, 2; 2012 г. — № 2.

4. Народное образование // 2013 г. — № 2; 2014 г. — № 1; 2010 г. — № 2.

5. Первое сентября. Математика. // 2002 г. — № 3, 23, 27, 28, 39; 2003 г. —

№ 14, 21; 2004 г. — № 21, 27, 28;

«Система подготовки учащихся к ЕГЭ по математике».

Повышение качества образования всегда было и остается

приоритетным направлением в работе любого

общеобразовательного учреждения.

Основными целями данной работы являются:

-грамотная организация действий каждого учителя в режиме

подготовки учащихся к итоговой аттестации;

— обеспечение методическим сопровождением процесса

подготовки с учетом учебных возможностей и способностей

учащихся;

— своевременное информирование учащихся и их родителей по

всем аспектам итоговой аттестации.

Мы, математики, пришли к выводу о том, что только комплексный

подход к деятельности по подготовке учащихся к ЕГЭ способствует

повышению эффективности и качества результатов экзамена в

тестовой форме. Под комплексным подходом мы понимаем

целенаправленное сотрудничество администрации, учителей-

предметников, учащихся и их родителей.

Вот уже много лет в нашей стране введен новый формат

оценки уровня качества образования выпускников – Единый

государственный экзамен (ЕГЭ). Практика показывает, что для

большинства учащихся 11-х классов и их родителей, многих

педагогов, а особенно молодых и малоопытных, «камнем

преткновения» является ЕГЭ по математике. С одной стороны, ЕГЭ

по математике является обязательным. С другой стороны,

математика, как учебный предмет, относится к первой степени

сложности.

В нашей школе сложилась определенная система подготовки к

экзамену в форме ЕГЭ, так и к ОГЭ. Система-это целое, состоящее

из частей, связанных между собой.

С годами совершенствуется экзамен, совершенствуется и

методика подготовки учащихся. Поэтому очень важным является то,

чтобы сам учитель был готов к экзамену:

-представлял его структуру,

— количество заданий по разделам математики и по типам заданий,

-знал перечень элементов содержания,

-понимал принципы оценивания.

Только в этом случае учитель эффективно может выстроить

подготовку к экзамену.

Учителя-математики нашей школы имеют достаточный опыт

подготовки учащихся к выпускным экзаменам.

Подготовка к сдаче

ОГЭ и ЕГЭ по математике идет через приобретение и освоение

конкретных математических знаний. Только это обеспечит

выпускнику успешную сдачу экзамена.

В своей работе применяем следующие принципы подготовки к

экзаменам

Первый принцип – тематический. Позволяет эффективнее

выстраивать подготовку, соблюдая принцип от простых типовых

заданий к более сложным.

Второй принцип – логический. На этапе освоения знаний

подбираем материал в виде логически взаимосвязанной системы,

где из одного следует другое. На следующих занятиях полученные

знания способствуют пониманию нового материала.

Третий принцип – тренировочный. На консультациях учащимся

предлагаются тренировочные тесты, выполняя которые дети могут

оценить степень подготовленности к экзаменам.

Четвёртый принцип – индивидуальный. На консультациях ученик

может не только выполнить тест, но и получить ответы на вопросы,

которые вызвали затруднение.

Пятый принцип – временной. Все тренировочные тесты проводим

с ограничением времени, чтобы учащиеся могли контролировать

себя — за какое время сколько заданий они успевают решить.

Шестой принцип – контролирующий. Максимализация нагрузки

по содержанию и по времени для всех учащихся одинакова. Это

необходимо, поскольку тест по своему назначению ставит всех в

равные условия и предполагает объективный контроль результатов.

И надо отметить, что систематическая планомерная работа по

данному направлению, которую из года в год мы совершенствуем с

учетом новых образовательных методик и технологий, сказывается

только положительным образом на конечный результат.

Я расскажу о тех главных, на мой взгляд, составляющих, которые

обеспечивают подготовку к выпускному экзамену по математике за

курс основной и средней школы. Подготовленность к чему-либо

понимается как комплекс приобретенных знаний, навыков, умений,

качеств, позволяющих успешно выполнять определенную

деятельность. В готовности учащихся к сдаче экзамена в форме ОГЭ

и ЕГЭ можно выделить следующие составляющие:

— информационная готовность (информированность о правилах

поведения на экзамене, информированность о правилах

заполнения бланков и т.д.);

— предметная готовность или содержательная (готовность по

определенному предмету, умение решать тестовые задания);

— психологическая готовность (состояние готовности – «настрой»,

внутренняя настроенность на определенное поведение,

ориентированность на целесообразные действия, актуализация и

приспособление возможностей личности для успешных действий в

ситуации сдачи экзамена).

Содержание информационной работы с учащимися.

1) Организация информационной работы в форме инструктажа

учащихся:

— правила поведения на экзамене;

— правила заполнения бланков;

— расписание работы кабинета информатики (часы свободного

доступа к ресурсам Интернет).

2) Информационный стенд для учащихся: нормативные документы,

бланки, правила заполнения бланков, ресурсы Интернет по

вопросам ОГЭ и ЕГЭ

3) Проведение занятий по тренировке заполнения бланков.

4) Пробные внутри школьные ОГЭ и ЕГЭ

Содержание информационной работы с родителями учащихся.

1) Родительские собрания:

— информирование родителей о процедуре проведения экзамена

об особенностях подготовки к тестовой форме сдачи экзаменов.

Информирование о ресурсах Интернет;

— информирование о результатах пробного внутри школьного ОГЭ и

ЕГЭ;

— пункт проведения экзамена.

2) Индивидуальное консультирование родителей.

Психологическая подготовка к ОГЭ.

Психологическая подготовка учащихся заключается в следующем:

отработка стратегии и тактики поведения в период подготовки к

экзамену; обучение навыкам саморегуляции, самоконтроля,

повышение уверенности в себе, в своих силах. Психологом нашей

школы рассматриваются следующие вопросы:

— как подготовиться к экзаменам,

— поведение на экзамене,

-способы снятия нервно-психического напряжения,

— как противостоять стрессу.

Работа с учащимися проводится со всем классом и выборочно,

кто пожелает, индивидуально.

Предметная готовность или содержательная

Именно на этом я остановлюсь подробнее.

Предметная готовность к сдаче экзамена складывается в

процессе всего периода обучения с 1 по 11 класс. И здесь трудно

переоценить роль учителей начальных классов. В результатах ОГЭ

есть и их вклад: либо положительный, либо со знаком минус.

Так же большую роль играет количество часов по предмету.

В общем, факторов, которые влияют на предметную подготовку

большое количество.

Я хочу рассказать о тех элементах системы подготовки к

экзаменам,

которые,

по

моему

мнению,

являются

наиболее

значимыми.

Устный счет – один из важных приемов при подготовке учащихся

к ОГЭ и ЕГЭ по математике.

В методике математики различают устные и письменные

приемы вычисления. Устная работа на уроках имеет большое

значение – это и беседы учителя с классом или отдельными

учениками, и рассуждения учащихся при выполнении тех или иных

заданий и т.п. Среди этих видов устной работы можно выделить так

называемые устные упражнения. В начальной школе они

сводились в основном к вычислениям, поэтому за ними

закрепилось название “устный счет”, хотя в современных

программах содержание устных упражнений весьма разнообразно

и велико за счет введения алгебраического и геометрического

материала, а также за счет большого внимания к свойствам

действий над числами и величинами.

Важность и необходимость устных упражнений велика в

формировании вычислительных навыков и в совершенствовании

знаний по нумерации, и в развитии личностных качеств ученика.

Создание определённой системы повторения ранее изученного

материала дает учащимся возможность усвоения знаний на уровне

автоматического навыка. В связи с введением обязательной ОГЭ по

математике возникает необходимость научить учащихся старших

классов решать быстро и качественно задачи базового уровня. При

этом необыкновенно возрастает роль устных вычислений и

вычислений вообще, так как на экзамене не разрешается

использовать калькулятор и таблицы. Для достижения

правильности и беглости устных вычислений, преобразований,

решения задач в течение всех лет обучения в среднем звене на

каждом уроке отводим 5-7 минут для проведения упражнений в

устных вычислениях, предусмотренных программой каждого

класса.

Устные упражнения активизируют мыслительную деятельность

учащихся, требуют осознанного усвоения учебного материала; при

их выполнении развивается память, речь, внимание, быстрота

реакции.

Устные упражнения как этап урока имеют свои задачи:

1) воспроизводство и корректировка знаний, умений и навыков

учащихся, необходимых для их самостоятельной деятельности на

уроке или осознанного восприятия объяснения учителя;

2) контроль состояния знаний учащихся;

3) автоматизация навыков простейших вычислений и

преобразований.

Если в 5-6 классах устный счет – это выполнение действий с

числами: натуральные числа, обыкновенные дроби, десятичные

дроби, то в старших классах – это могут быть совершенно

различные операции, навык выполнения которых стараемся

довести до автоматизма. Например, на уроках математики мы

используем УС по темам:

7 класс:

1) Запись чисел в стандартном виде и действия с ними.

2) Формулы сокращенного умножения.

3) Решение простейших ЛУР.

4) Действия со степенью.

5) График линейной функции.

8 класс:

1) Линейные неравенства и числовые промежутки.

2) Решение простейших линейных неравенств.

3) Решение КВУР с помощью теоремы Виета и частных случаев.

4) Решение КВУР рациональными способами.

5) Арифметический квадратный корень и его свойства.

9 -10 класс-:

1) Решение неравенств 2 степени.

2) Преобразование графиков функций.

3) Формулы приведения.

4) Тригонометрические формулы.

5) Значения тригонометрических функций.

Устный счёт на каждом уроке стараемся строить на основе

упражнений ЕГЭ и ОГЭ. Практика показала, что систематическая

работа с УС способствует значительному повышению

продуктивности вычислений и преобразований. Сокращается

время на выполнение таких операций, как решение КВУР, линейных

неравенств и неравенств 2-ой степени, разложение на множители,

построение графиков функций, преобразования иррациональных

выражений и другие. Эти операции переходят из разряда

самостоятельной задачи в разряд вспомогательной и становятся

инструментом (“таблицей умножения”) для решения более

сложных задач.

Виды устного счёта, которые мы используем:



Математический диктант



Презентация



Раздаточные таблицы

Основные задачи по подготовке детей к ЕГЭ:

1. Начинать подготовку к ЕГЭ с 5 класса;

2. Создавать учебный материал (по типу ЕГЭ) для обучающих

программ,

тренингов

и

использовать

готовые

печатные

и

электронные пособия;

3. Учить школьников «технике сдачи теста»;

4.Через систему дополнительных занятий (элективных курсов,

индивидуальных консультаций) повышать интерес к предмету и

личную ответственность школьника за результаты обучения.

Как мы решаем поставленные задачи? С чего начинаем эту

работу?

Во-первых, с первых же дней учёбы убеждаем детей в том, что

если

очень

постараться,

то

можно

получить

вполне

приличный

балл. Главное не упустить время.

Во-вторых, в течение всего учебного года знакомим детей с

материалами ОГЭ и ЕГЭ.

Кроме этого, систематически на уроках

каждому раздаем тест ЕГЭ: в 7- 9 классах – за основную школу, в

10-11 классах – за полную среднюю школу. Просим ребят найти в

тесте те задания, с которыми они могут справиться уже сегодня и

решить их. Стараемся выслушать все подходы к решению каждой

задачи и только потом раскрываем секрет, как можно было решить

задачу рациональнее, чтобы сэкономить время.

В-третьих, когда уже удалось заинтересовать детей, знакомим

их

с

особенностями

новой

формы

итоговой

аттестации:

со

структурой

теста,

временными

рамками,

нормами

оценивания

экзаменационной

работы,

условиями

проведения

экзамена

и

начинаем обучать «технике сдачи теста»:



обучаем строгому самоконтролю времени;



учим определять трудность заданий;



знакомим

с

приёмом

«прикидки»

р е зул ьт а т а

подстановкой;



знакомим с приёмом «спирального движения по тесту»



.

Начну

с

первого

пункта.

Говорим

ученикам,

чтобы

успешно

выполнить тест, на каждое задание первой части надо затрачивать

не более 5

минут. И из урока в урок отрабатываем

тесты на

скорость: например, за 12 минут школьникам необходимо решить 4

– 6 заданий теста. При этом даем настоящие тесты ОГЭ или ЕГЭ с

отмеченными в нём заданиями, посильными на данный момент

обучения.

Обязательно

отмечаем

количество

человек

уложившихся во времени, и сразу анализируем ситуацию и опять

даем совет,

какое задание

можно было решить рациональнее.

Постепенно

приучаем

ребят

к

методу

«пристального

взгляда»

—

внимательно посмотри: «Нет ли короткого пути решения? Так как

ты

ограничен

во

времени».

Поверьте,

если

разбирать

тест,

над

которым

ученик

уже

потрудился,

то

заинтересованность

и

внимание 100%. Все рекомендации учителя воспринимаются более

осознанно.

Как

учим

определять

трудность

заданий?

Сначала

просим

учеников

просмотреть

тест

от

начала

до

конца

и

отметить

карандашом те задания, которые кажутся им простыми и лёгкими и

выполнить их в «режиме скорости». Затем, отметить 2-3 задания,

которые

им

понятны

по

формулировке,

но

требуют

большего

времени и выполнить их; и только после этого, если останется

время, можно поразмышлять над остальными.

Двигаясь

по

тесту,

дети

знают,

что

сложность

заданий

нарастает, поэтому всегда советуем настойчиво и добросовестно

отрабатывать

первую

часть,

только

затем

можно

приступать

ко

второй части – это и есть принцип «спирального движения» по

тесту.

С введением новой формы аттестации у нас появилось ещё

несколько методических приёмов и хитростей. Чтобы

работу по

подготовке к экзамену проводить в течение всего учебного года в

кабинете

имеется

огромное

количество

тестового

материала,

кроме

этого

11классники

работают

с

сайтом

Ларина.

Решают

выложенные

варианты

с

понедельника,

в

четверг

сдают

на

проверку. Это очень трудоемко, но зато эффективно Отдельно хочу

сказать о консультациях.

Консультации индивидуальные. Ребята

знают, что с вопросами по первой, части, можно подойти в любое

время,

но

вопросы

второй

части

подают

заранее

и

приходят

в

назначенное

время.

Консультации

проводим

по

своей

инициативе, труд этот не оплачивается, я просто рассказываю о

нашей,

годами

сложившейся

традиции.

Ребята

знают,

что

проконсультироваться можно на любой большой перемене и после

уроков, если учитель свободен.

Коротко расскажу ещё о некоторых факторах успешности на

ЕГЭ.

Для

хорошей

подготовки

к

экзамену

необходимо

целенаправленное

повторение. Во втором полугодии начинаем

тематическое повторение. Готовясь к уроку, учителю приходится

искать задания по каждой теме в разных источниках, что занимает

много

времени.

Кроме

того,

повторять

материал

темы

удобно,

когда задания расположены в одном месте. Наиболее оптимальное

решение — это тематические и комплексные тесты, учим ребят

оценивать итоги работы над тестом в целом. Ребята проходят в

течении

года

предварительное

тестирование

в

системе

работы

Стат-Град. Это тестирование становится генеральной репетицией по

заполнению бланков, сдачи экзамена.

Преимущества тематического теста:

-в нём собраны разные задания по одной теме;

-на уроках можно рассматривать отдельные задания из теста;

-по такому тесту удобно проводить повторение;

-осуществлять контроль знаний и умений учащихся по данной теме.

Итоговое повторение строим исключительно на отработке

умений и навыков, требующихся для получения положительной

отметки на экзамене.

Примерные экзаменационные работы берем из различных

сборников для подготовки к ЕГЭ

Кроме этого ребята могут проверить свои знания, решая

примерные работы в режиме on-lain (См. сайт Савченко Е.М.), а так-

ж

е работы, размещённые на сайте Стат-Града.

Применение ИКТ на уроках математики при подготовке к ЕГЭ.

для повторения теоретического материала проводим

обобщающие уроки с применением компьютерных технологий.

Уроки с применением презентаций зрелищны и эффективны в

работе над информацией. Особенно, если это уроки повторения и

обобщения материала определённой темы.

Презентация обладает наглядностью и выразительностью, это

прекрасное дидактическое и мотивационное средство,

способствующее лучшему запоминанию учебного материала.

При её систематическом использовании увеличивается

продуктивность обучения. С помощью презентации можно

повысить объём повторяемого материала и выполняемой работы.

В работе используем свои презентации и презентации,

созданные коллегами и представленные на различных

образовательных сайтах в Интернете:

-Интернет-сообщество учителей

-Сеть творческих учителей

-Фестиваль педагогических идей «Открытый урок»

-Информационно-методический сайт

Хорошие презентации с сайта Каратановой Марии

Николаевны. Эти презентации помогли нам построить

систематическое повторение и отработку навыков. (показать

презентации).

Можно использовать презентации, сделанные другими

учителями. Но не всегда они содержат всю нужную информацию

для реализации задумок учителя, но почти всегда их можно

отредактировать. С этой целью полезно посещать сайты

-«Интернет – сообщество учителей»,

-«Сеть творческих учителей»,

-«Фестиваль педагогических идей

-«Открытый урок»,

-«Информационно методический сайт» и другие.

В работе мы часто используем презентации Савченко Елены

Михайловны, учителя математики МОУ гимназии №1, г. Полярные

Зори. Как сделала это она, я думаю, лучше никому не сделать. И

тогда .почему бы не использовать в работе этот образовательный

продукт?!

Использование компьютерных презентаций на уроках

математики и при подготовке к итоговой аттестации

открывает огромные возможности:

-компьютер может взять на себя функцию контроля знаний,

-поможет сэкономить время на уроке для решения

экзаменационных задач,

-богато иллюстрировать материал,

-трудные для понимания моменты показать в динамике,

-повторить то, что вызвало затруднения,

-дифференцировать урок в соответствии с индивидуальными

особенностями учащихся,

-быстро повторить теоретический материал.

Особенно эти презентации помогли при итоговом повторении

теоретического материала по геометрии.

Мы стали экономить время на теории, чтобы использовать его

на практику. Всегда стараемся выдать теорию по теме за 1-2 урока и

лекцию

построить

так,

чтобы

она

содержала

все

необходимые

сведения

для

решения

текущей

контрольной

работы

и

экзаменационного

материала.

Остальные

уроки

посвящаем

практике.

Уроки-практикумы

попутно

дополняем

недостающим

теоретическим материалом. И еще учителя математики знают, что

учебники

почти

не

готовят

детей

к

ЕГЭ,

в

них

по-прежнему

традиционные

формулировки

заданий.

Какой

мы

нашла

выход:

сразу

после

объяснения

нового

материала

и

его

первичного

закрепления показываем, как эта тема вышла на ЕГЭ. Стараемся

при

этом

продемонстрировать

всё

разнообразие

заданий

из

первой и второй части, используя сборники с материалами ЕГЭ

разных лет. Иногда прошу найти подобные задания в учебнике.

Убедившись,

что

таких

заданий

почти

нет,

ученики

осознают

значимость, приобретённых материалов для подготовки к экзамену

и

уже

практически

не

расстаются

с

ними.

Регулярно

проводим

диагностические

работы

для

определения

пробелов

в

знаниях.

Полученные

результаты

определяют

индивидуальную

и

дифференцированную

работу.

Мониторинг

и

диагностику

планируем на основе экзаменационных

материалов.

Работая с

КИМами

с

5

класса,

ребята

привыкают

к

структуре

теста,

к

необычности

формулировок

заданий,

разнообразию

методов

и

приёмов

при

решении

задач,

систематическому

пополнению

копилки по теории (набору шпаргалок те опорным конспектам). У

них

постепенно

исчезает

чувство

растерянности

и

полной

безнадёжности,

появляется

уверенность

и

психологическая

готовность к новой форме аттестации.

Конечно,

максимально

используем

урочное

время

для

подготовки

к

экзамену,

но

этого

недостаточно,

поэтому

в

8-11

классах

систематически

проводим

углублённую

факультативную

работу по предмету. Элективные курсы:

«Модуль»,

«Квадратный трёхчлен и его приложения»,

«Дробно-рациональные и линейные уравнения и неравенства с

параметрами»,

«Самый простой способ решения непростых неравенств».

-«Решение уравнений и неравенств с параметрами».

— «Нестандартные методы решения неравенств и их систем».

Программы

курсов

рассматривают

ключевые

и

сложные

темы

школьной

математики,

помогают

расширить

спектр

задач,

п о с и л ь н ы х

д л я

у ч а щ и х с я

и

р е а л и з о в а т ь

п р и н ц и п ы

дифференцированного обучения.

Ежегодно

пополняем

кабинет

математики

новыми

дидактическими

материалами

для

урочной

и

внеурочной

деятельности, способствующими развитию у школьников интереса

к

математике,

активизации

мыслительной

деятельности,

выявлению детей, проявляющих особый интерес к предмету и в

первую очередь повышению качества знаний по подготовке к ЕГЭ.

Разработали и систематизировали тестовый материал, создали

подборку

текстовых

задач

по

подготовке

к

промежуточным

аттестациям,

ОГЭ

и

ЕГЭ.

Приобрели

для

кабинета

большое

количество

методической

и

математической

литературы

по

ключевым

вопросам

ЕГЭ.

Конечно,

очень

важен

позитивный

настрой детей на серьёзный самостоятельный труд по подготовке к

экзамену,

поэтому

в

начале

каждого

учебного

года

с

большим

удовольствием

сообщаем

им

информацию

о

том,

что

снова,

практически все наши выпускники поступили в высшие и средние

учебные заведения и обучаются на бюджетной основе.

В заключении хочу сказать, что такая система подготовки детей

к итоговой аттестации помогла нам в течение четырёх лет получить

результаты

ЕГЭ

по

математике

значительно

выше

средних

по

району

и

области

и

выше

средних

по

России. Ну

и

следует

добавить,

что

работа

проводимая

учителем

в

ходе

подготовки

выпускников

к

итоговой

аттестации

достаточно

объемная

и

тяжелая.

Но

если

она

грамотно

спланирована,

то

многие

проблемные моменты можно избежать еще на начальной стадии и

в

результате

получить

достойную

оценку

качества

образования

собственных учеников.

P.

S.

После

сдачи

ЕГЭ

выпускники

перебивая

друг

друга,

с

огромным волнением рассказывают, что было на экзамене. И как

приятно слышать от детей, что все задания экзамена

им были

знакомы. А потом долгое ожидание результатов, переживание и,

наконец, радость со слезами на глазах – ЕГЭ успешно сдали все.

Это самая большая награда учителю!

ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.

Какие темы важно знать для ЕГЭ по математике 2023?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.

Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

План успешной подготовки к ЕГЭ по математике 2023

Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.

Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:

• Алгебра
• Уравнения и неравенства
• Элементы комбинаторики, статистики и теории вероятностей
• Функции
• Начала математического анализа
• Геометрия

Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.

Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».

Как решать часть с кратким ответом

Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.

Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.

Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.

Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.

Задания с развернутым ответом: немного статистики

Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.

Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

В ЕГЭ по математике базового уровня 6 тематических блоков:

Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

Структура ЕГЭ по математике 2023

Часть 1:

• Приносит 11 баллов, то есть 35% всего экзамена
• 11 заданий с кратким ответом

Часть 2:

• Приносит 20 баллов, то есть 65% всего экзамена
• 7 заданий с развернутым ответом

Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.

В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.

ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.

Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:

Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.

Разделы ЕГЭ по математике

• Алгебра и начала анализа — 8 заданий, 13 первичных баллов
• Геометрия — 4 задания, 8 первичных баллов
• Реальная математика — 6 заданий, 10 первичных баллов

Какие задания входят в ЕГЭ по математике?

Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.

• Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.

  Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.

• Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
• Спецификация — это документ, описывающий структуру экзамена и разбалловку.

Что в итоге

Доклад на тему:
учащихся
«Подготовка
к ЕГЭ и ОГЭ по
математике» Возрастание роли математики в современной жизни привело к тому, что
для адаптации в современном обществе и активному участию в нем необходимо
быть   математически   грамотным   человеком.   В   связи   со   стратегическими
направлениями   социально­экономического   развития   России   до   2020   года:
«Приоритетной   государственной   задачей   является   обеспечение   качественного
базового уровня математических и естественнонаучных знаний у всех выпускников
школы, не только будущих ученых, но и будущих квалифицированных рабочих…»
          Каждый школьник в процессе обучения должен иметь возможность получить
полноценную подготовку к выпускным экзаменам.
          Формула успеха хорошо сдать экзамен ЕГЭ и ОГЭ по математике:
Высокая степень восприимчивости + мотивация + компетентный педагог.
          В любом случае натаскивание на варианты ЕГЭ и ОГЭ необходимо, но его
нужно сочетать с фундаментальной подготовкой, формируя системные знания и
навыки. В готовности  учащихся  к  сдаче   экзамена  в форме  ЕГЭ  и ОГЭ  можно
выделить следующие составляющие:
­информационная готовность;
­предметная готовность;
­психологическая.
         Ориентируясь на данные компоненты, актуальными вопросами в подготовке
к экзамену являются следующие:
1. Организация информационной работы:
­ по подготовке учащихся к экзамену в форме инструктажа (содержание ­ правила
поведения на экзамене; правила заполнения бланков);
­ информирование родителей о процедуре ЕГЭ и ОГЭ, особенностях подготовки к
тестовой форме сдачи экзаменов. Информирование о ресурсах Интернет;
­  информирование   о  результатах   пробного  внутри  школьного  диагностического
тестирования;
­ индивидуальное консультирование родителей.
2. Психологическая подготовка к ОГЭ и ЕГЭ.
                Состояние   готовности   –   «настрой»,   внутренняя   настроенность   на
 
определенное   поведение,   ориентированность   на   целесообразные   действия,
актуализация и приспособление возможностей личности для успешных действий в
ситуации сдачи экзамена.
         Являясь классным руководителем учащихся 9 класса, провожу внеклассные
мероприятия,   которые   помогают   преодолеть   страхи   учеников   перед   ОГЭ   и
правильно подготовиться к экзамену. Как можно заставить ребенка поверить в мини­лекции.
  анкетирование,
свои силы, в то, что всегда есть надежда на разрешимость любой ситуации? Да
просто показать ему то, что данные задания он способен выполнить, если будет
использовать определенный алгоритм или логические рассуждения. На занятиях
стараюсь создать атмосферу комфортности, взаимопонимания. На своих уроках я
делаю   установку   на   то,   чтобы   любой   ребенок   должен   быть   понят   и   услышан
учителем   и   соучеником:
  учение   должно   проходить   в   «атмосфере
непринужденности,   чтобы   дети   и   учитель   свободно   дышали   на   уроках».   От
учителя   требуется   и   мастерство,   и   большое   терпение,   и   любовь   к   учащимся.
Доброжелательное отношение к ученикам снимает у них страх перед трудностями
обучения: ребенок не должен бояться ошибиться, спросить учителя, если он что­то
прослушал   или   не   понял.   Психологическая   подготовка   учащихся,   может
заключается в следующем: отработка поведения в период подготовки к экзамену;
обучение навыкам само регуляции, самоконтроля, повышение уверенности в себе,
в   своих   силах.   Методы   проведения   занятий   по   психологической   подготовке
учащихся   разнообразны:   групповая   дискуссия,   игровые   методы,   медитативные
техники,
  Содержание   занятий   должно
ориентироваться   на   следующие   вопросы:   как   подготовиться   к   экзаменам,
поведение   на   экзамене,   способы   снятия   нервно­психического   напряжения,   как
противостоять стрессу. Работа с учащимися проводится по желанию учащихся –
со всем классом или выборочно.
3. Организация работы по предмету:
 Организация правильной, ответственной самоорганизации у обучающегося:
­ ведение отдельной тетради для прорешивания тестовых заданий ОГЭ или ЕГЭ;
­   справочника,   который   мы   начинаем   вести   с   восьмого   класса,   записывая   и
повторяя основные формулы и правила по математике, алгебре и геометрии;
­ наличие сборников разных авторов для самостоятельной подготовки к экзамену
(например  ­ 8  класс работаем  со сборником  под редакцией  Ященко, 9 класс ­
сборник под редакцией Мальцева)
 Устный счет – один из важных приемов при подготовке учащихся к ЕГЭ и ОГЭ
по математике.  В связи с введением обязательного ЕГЭ и ОГЭ по математике
возникает необходимость научить учащихся решать быстро и качественно задачи
базового уровня. При этом необыкновенно возрастает роль устных вычислений, так
как   на   экзамене   не   разрешается   использовать   калькулятор   и   таблицы.   Можно
научить   учащихся   выполнять   простейшие   (и   не   очень)   преобразования   устно.
Конечно,   для   этого   потребуется   организовать   отработку   такого   навыка   до
автоматизма, на каждом уроке необходимо отводить 5­7 минут для проведения
упражнений устных вычислений, предусмотренных программой каждого класса.
Устные упражнения активизируют мыслительную деятельность учащихся, требуют
осознанного усвоения учебного материала; при их выполнении развивается память,
речь, внимание, быстрота реакции. Если в 5­6 классах устный счет – это выполнение действий с числами: натуральные
числа, обыкновенные дроби, десятичные дроби, то в старших классах – это могут
быть:
7 класс:
  Формулы   сокращенного   умножения.   Решение   простейших   ЛУР.   Действия   со
степенью. График линейной функции.
8 класс:
  Линейные неравенства и числовые промежутки. Решение простейших линейных
неравенств. Решение КВУР с помощью теоремы Виета и частных случаев.  Решение
КВУР   рациональными   способами.   Арифметический   квадратный   корень   и   его
свойства.
9 класс: Решение неравенств 2 степени. Преобразование графиков функций. 
Формулы приведения. Значения тригонометрических функций.
10­11 классах:
Вычисление   производных.
  Простейшие   тригонометрические   неравенства.
Тригонометрические   формулы.   Простейшие   тригонометрические   уравнения.
Функции,   обратные   тригонометрическим.   Преобразование   графиков   функций.
Вычисление   первообразных.   Свойства   логарифмов.   Простейшие   показательные
уравнения и неравенства. Простейшие логарифмические уравнения и неравенства.
                    Практика   показала,   что   систематическая   работа   с   устным   счетом
способствует   значительному   повышению   продуктивности   вычислений   и
преобразований.   Сокращается   время   на   выполнение   таких   операций,   что
переводит   их   из   разряда   самостоятельной   задачи   в   разряд   вспомогательной   и
становится инструментом (“таблицей умножения”) для решения более сложных
задач.              
          Учитель по математике, знающий, с чем придется столкнуться школьнику на
экзамене,   кроме   фундамента   уделяет   большую   часть   времени   на   занятии
отработке вопросов специфики ЕГЭ и ОГЭ.
               Правильность оформления заданий,  тактика   и  стратегия   решения   в
условиях  дефицита   выделенного   времени  на   экзамене,   а   также   банальная
невнимательность. Эти и масса других особенностей составляют суть специфики.
         Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и
еще раз тренировка. Довести решение задач до автоматизма.
Применение ИКТ на уроках математики при подготовке к ЕГЭ и ОГЭ.
          Поскольку наглядно­образные компоненты мышления играют исключительно
важную   роль   в   жизни   человека,   то   использование   их   в   изучении   материала   с
использованием ИКТ повышают эффективность обучения:
­ графика и мультипликация помогают ученикам понимать сложные логические
математические построения;
– повышение мотивации учащихся;
– экономия времени при выполнении заданий;
– формированию навыков самоконтроля, взаимоконтроля и самообучения; диагностика,
– включению у учащихся всех каналов восприятия информации.
                   Использую   интернет­ресурсы, открытый банк математических задач,
обеспечивающий   цель   поддержки   работы   учителя   и   самостоятельной   работы
учащихся по подготовке к сдаче экзамена.
        Мониторинг качества.
        Особое внимание в процессе деятельности по подготовке учащихся к ЕГЭ и
ОГЭ   занимает   мониторинг   качества   обученности   по   предмету.   Мониторинг   –
отслеживание,
  прогнозирование   результатов   деятельности.
Мониторинг   качества   должен   быть   системным   и   комплексным.   Он   должен
включать следующие параметры: контроль текущих оценок по предмету, оценок по
контрольным и самостоятельным работам, результаты пробного внутри школьного
диагностического   тестирования   в  форме   ЕГЭ   и   ОГЭ.  Учитель   анализирует   их,
выносит   на   обсуждение,   доводит   до   сведения   родителей.   Мониторинг
обеспечивает возможность прогнозирования оценок на выпускном ЕГЭ и ОГЭ.
       Использование дифференцированного подхода при подготовке к ОГЭ.
        На каждого ученика 9 класса есть мониторинг выполнения диагностических
работ по каждому заданию. Для организации подготовки школьников к экзамену
по результатам первой диагностической работы определены 3 группы учащихся:
первая группа  – учащиеся, которые поставили перед собой  цель  – преодоление
нижнего рубежа (8 заданий);
вторая группа – учащиеся, которые поставили перед собой цель – сдать экзамен
на оценку «4».
третья   группа  –   учащиеся,   которые   поставили   перед   собой  цель  –   получить
высокие баллы.
Для каждой группы были определены принципы организации подготовки к ОГЭ.
Первая   группа.   Для   этой   группы   необходимо   преодолеть   рубеж 8   баллов.
Выявляем   сильные   и   слабые   позиции   математической   подготовки   каждого   и
работаем с сильными позициями (закрепляем то, что уже получается), добавляя
посильные задания из слабых позиций. Цель  такой работы – отработать решение
выбранных заданий и вселить уверенность в учащихся, что нижний рубеж им по
силам.
Вторая группа. Для этой группы необходимо уверенно получить 16­22 баллов.
Работаем   со   слабыми   позициями,   постоянно   держа   под   контролем   сильные
позиции выполнением соответствующих задач (добиваемся выполнения того, что
не получается). Цель  работы – сформировать навыки самопроверки и добиться
устойчивого результата (на уровне ожидаемого) по работе с задачами в которых
ученик более успешен, повторить темы, дающие возможность решения наиболее
сложных заданий.
Третья   группа.  Для   этой   группы   вырабатываем   умение   уверенно   выполнять
задания   части   2,чтобы   набрать   23­38   баллов.     Регулярно   решаем,   задания, развивающие   творческие   способности   учащихся   к   решению   задач   повышенного
уровня сложности. Цель  работы ­ сформировать умения и навыки, позволяющие
получить наивысшие баллы.
При дифференцированной работе каждый ученик имеет возможность овладевать
учебным   материалом   в   зависимости   от   его   способностей   и   индивидуальных
особенностей
Принцип   Парето:   «20%   усилий   дают   80%   результата,   а   остальные   80%
усилий —   лишь   20%   результата».   Как   же   не   распыляться   и   направить   20%
усилий в нужное русло и достигнуть 80% результата? Предлагаю инструкцию:
1. Поставь цель – какой балл ты хочешь получить по экзамену?
2. Пройди пробный экзамен и посмотри, сколько баллов ты набрал, и сколько 
тебе не хватило.
3. Определи, какие задания ты:
a)  всегда решаешь,
b)  решаешь, но иногда допускаешь ошибки,
c)  обычно не решаешь, но уверен, что сможешь быстро и легко в них разобраться.
4. Тренировка по типам заданий, которые ты отметил в пунктах b) и с), а так же 
не забывай повторять задачи из пункта a).
                 Мы работаем в простой школе, наши ученики имеют средние учебные
возможности   и   понятно,   что   без   прочного   усвоения   базовых   знаний   детьми
невозможно   дальнейшее   обучение.  Уделяю   внимание   технике   выполнения
экзаменационной работы:
В своей работе применяю следующие принципы для эффективной подготовки к
ОГЭ и ЕГЭ.
1. Эффективнее  выстраивать  такую подготовку, соблюдая принцип от простых
типовых заданий к сложным.
2. На этапе освоения знаний необходимо подбирать материал в виде логически
взаимосвязанной системы, где из одного следует другое.
3.   На   консультациях   учащимся   предлагаются   тренировочные   тесты,   выполняя
которые дети могут оценить степень подготовленности к экзаменам.
4.   На   консультациях   ученик   может   не   только   выполнить   тест,   но   и   получить
ответы на вопросы, которые вызвали затруднение.
5. Все тренировочные тесты следует проводить с ограничением времени, чтобы
учащиеся   могли   контролировать   себя   ­   за   какое   время   сколько   заданий   они
успевают решить.
6.   Максимализация   нагрузки   по   содержанию   и   по   времени   для   всех   учащихся
одинакова. Это необходимо, поскольку тест по своему назначению ставит всех в
равные условия и предполагает объективный контроль результатов.
            Следуя этим принципам, формирую у учеников навыки самообразования,
критического   мышления,
  самоорганизации   и
самоконтроля.
  самостоятельной   работы, Моя цель состоит в том, чтобы помочь каждому школьнику научиться
быстро решать задачи, оформлять их чётко и компактно. Развиваю способность
мыслить свободно, без страха, творчески. Стараюсь давать возможность каждому
школьнику расти настолько, насколько он способен.
              
Литература:
1 Бабанский Ю.К. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский ­ М., Педагогика,
1989.
1. Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. – М., 1989.
2. Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педагогика. – 1989. ­
№5.
3. Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченко.­М., 1989.
4. Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И. ­ М., 1979.
5. http://nsportal.ru/shkola/algebra/library/2015/02/08/podgotovka­uchashchikhsya­k­ege­i­oge­po­matematike
6. http://youclever.org/matematika/effektivnaya­podgotovka­k­ege/
7. https://infourok.ru/sistema­raboti­uchitelya­matematiki­po­podgotovki­k­ege­i­oge­748992.html

МБОУ СОШ №22

п. Пересыпь, муниципального образования Темрюкский район Краснодарский край.

Опыт работы

учителя математики

Лисицыной Т.П.

«Из опыта работы по подготовке учащихся к сдаче ЕГЭ по математике»

Ведущей целью школьного математического образования является интеллектуальное развитие и формирование качеств мышления учащихся, необходимых для полноценной жизни в обществе. Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам, освоить тот объём знаний, умений и навыков, который необходим для успешной сдачи ЕГЭ и дальнейшего обучения в вузе. Развитие  ЕГЭ по математике определяется основными задачами, которые стоят перед образованием в связи со стратегическими направлениями социально-экономического развития России до 2020 года: «Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускников школы, не только будущих ученых, но и будущих квалифицированных рабочих. Сильное математическое и естественнонаучное образование, его фундаментальность являются конкурентным преимуществом России. В обучении математике и естественным наукам мы должны максимально использовать существующий потенциал и российские традиции, дополняя их последними научными достижениями, современными образовательными технологиями».

         В своей работе в качестве средств формирования таких качеств у учащихся я использую различные формы и методы проведения учебных занятий. Владею такими   образовательными   технологиями, как  технология проблемного диалога, технология  развития  критического мышления,  применяю сетевые  технологии в  учебной  и во внеурочной  деятельности,  использую  цифровые образовательные ресурсы  Единой коллекции цифровых  образовательных ресурсов, социального сайта работников образования «nsportal.ru», «Учительского портала», «Решу ЕГЭ»,  что позволяет обеспечивать  стопроцентный  уровень сдачи ЕГЭ  по математике моими выпускниками.  

         Единый государственный экзамен является новой формой итоговой аттестации. Для успешной его сдачи учащийся должен быть подготовлен не только практически, но и психологически. Прежде всего, выполняя  типовые задания на уроках, подчёркиваю возможность их решения каждым учеником, создавая ситуацию успеха. Являясь классным  руководителем, провожу внеклассные мероприятия, которые помогают преодолеть страхи учеников перед предстоящими экзаменами ГИА и ЕГЭ уже заранее.

    Можно ли заставить ребёнка поверить в свои силы, в то, что всегда есть надежда на успех? Оказывается можно. Показать ему то, что данные задания он способен выполнить, если будет использовать определенный алгоритм сначала с помощью учителя, потом сам с некоторой подсказкой, консультацией, а в дальнейшем и самостоятельно. На занятиях стараюсь создать атмосферу комфортности, взаимопонимания. Использую сотрудничество «учитель – ученик» и «ученик — ученик». На своих уроках я делаю установку на то, чтобы любой ребёнок должен быть понят и услышан учителем: учение должно проходить в атмосфере деловитости, непринужденности, чтобы и дети и учитель чувствовали себя свободно на уроках. Но увеличение умственной нагрузки на уроках математики заставляет задуматься ещё и над тем, как поддержать у детей интерес к изучаемому материалу и их активность на протяжении всего урока. Для решения этой задачи в своей работе использую различные виды и формы деятельности учащихся на уроке, нетрадиционные формы проведения учебных занятий.

Нестандартные формы организации уроков позволяют мне стимулировать активность учащихся, раскрывать творческие силы, скрытые возможности каждого школьника. Познавательный интерес  к предмету формирую у детей через  использование разнообразных форм, приёмов и методов обучения, влияющих на личность ученика. Положительный учебный эффект достигается сочетанием интеллектуальности содержания с новизной формы ведения урока: уроки взаимного обучения, уроки-консультации, уроки-лекции, уроки  разбора ошибок и другие. В процессе обучения добиваюсь осознанного восприятия учащимися изучаемого материала, приобретения навыков логического мышления, развития воображения и интуиции, понимания взаимосвязи усваиваемых знаний, механизма ошибок и их преодоление. Развиваю наблюдательность, мышление и практические действия, а не только конкретные операции и приёмы.

Повысить эффективность уроков и интерес учащихся к ним позволяет применение информационно-коммуникационных технологий: самостоятельно разработанных мною и учащимися слайдовых презентаций, цифровых образовательных ресурсов, возможностей Интернет. Использую  «Открытый банк математических задач», обеспечивающий поддержку работы учителя и самостоятельной работы  учащихся по подготовке к сдаче экзамена на базовом уровне.

Так же на своих уроках использую сервисы образовательного портала «РЕШУ ЕГЭ». Дистанционная обучающая система для подготовки к экзамену «РЕШУ ЕГЭ» (http://решуегэ.рф) создана творческим объединением «Центр интеллектуальных инициатив». Руководитель — учитель математики гимназии № 261 Санкт-Петербурга, Почетный работник общего образования РФ, Учитель года России — 2007, член Федеральной комиссии по разработке контрольно-измерительных материалов по математике для проведения единого государственного экзамена по математике Гущин Д. Д.

Этот информационный ресурс можно использовать:

• для организации тематического повторения. Разработан классификатор экзаменационных заданий, позволяющий последовательно повторять те или иные небольшие темы и сразу же проверять свои знания по ним.
• для организации текущего контроля знаний предоставляется возможность включения в тренировочные варианты работ произвольного количества заданий каждого экзаменационного типа.
• для проведения итоговых контрольных работ предусмотрено прохождение тестирования в формате ЕГЭ 2013 года по одному из предустановленных в системе вариантов или по индивидуальному случайно сгенерированному варианту.
• для контроля уровня подготовки система ведет статистику изученных тем и решенных задач.
• для ознакомления с правилами проверки экзаменационных работ дана возможность узнать критерии проверки заданий части С и проверить в соответствии с ними задания с открытым ответом.
• для предварительной оценки уровня подготовки после прохождения тестирования сообщается прогноз тестового экзаменационного балла по стобалльной шкале.

 Все задания базовой части ЕГЭ по математике взяты из открытого банка экзаменационных заданий (http://mathege.ru) и представляют собой модельные задачи, на основе которых путем изменения конкретных числовых данных составляются реальные экзаменационные работы ЕГЭ. Задания повышенного и высокого уровня сложности ЕГЭ по математике, а также все задания по другим предметам были специально составлены для портала «РЕШУ ЕГЭ» или предлагались в официальных сборниках для подготовки к экзамену.

 Все используемые в системе задачи снабжены ответами и подробными решениями, что, конечно же, очень удобно для индивидуальной подготовки выпускника.

Подготовка к ЕГЭ требует индивидуального, личностно ориентированного подхода. Для реализации такого подхода в учебном плане 11 класса есть обязательные предметы  «Алгебра и начала анализа», «Геометрия», «Практикум по математике». Кроме того приказом по школе определены часы индивидуальных и групповых консультаций по математике для выпускников 11 класса. Как и уроки, мною контролируется посещаемость консультаций учащимися 11 класса с обязательной отметкой в специальном журнале. Информация о посещаемости доводится до сведения классного руководителя незамедлительно, а родители выпускников узнают о пропусках в течение 1-2 дней. Обязательно выясняю причины отсутствия ученика на занятии.

Повысить уровень обученности и качество знаний учащихся позволяет использование мониторинга знаний умений и навыков, применение самодиагностики, самооценки, проведение  индивидуальной работы с учениками по ликвидации пробелов в знаниях. Хороший результат отслеживания показателей обучения каждого выпускника дают диагностические карты учебных достижений каждого ученика по результатам КДР (контрольные диагностические работы, предлагаемые ККИДППО ежемесячно с ноября по апрель в 9-11 классах у нас, в Краснодарском крае) и других значимых работ, в том числе и индивидуальных.

Этот нелёгкий процесс более эффективен в случае, когда сами учащиеся осознанно прогнозируют результаты своего обучения. Я доверяю своим ученикам заполнять такие карты не только после краевых контрольных работ, но и после самостоятельных работ или тестов по определенным темам программы. Диагностические карты регулярно доводятся до сведения учащихся и их родителей, классного руководителя.

Определив типологию пробелов в знаниях учащихся по итогам очередной тестовой диагностической работы, я вношу корректировку в календарно-тематическое планирование, организую уроки разноуровнего обобщающего повторения. Сейчас издано огромное количество сборников тестов для подготовки в ЕГЭ. По таким сборникам мы работаем в течение уже пяти лет.

Хорошим подспорьем в разработке таких уроков является необходимая методическая литература, прежде всего — это книги серии «Готовимся к ЕГЭ по математике. Обобщающее повторение курса алгебры и начал анализа» под редакцией Е.А. Семенко, а также различные КИМы и тренировочные тематические задания, разработанные ФИПИ, информационные ресурсы Интернета.

После разделения ЕГЭ на два разных уровня – базового и профильного, возникла ещё одна важная задача: правильно сориентировать учащихся и их родителей в выборе уровня, убедить их (а иногда это бывает очень и очень непросто) двигаться в правильном направлении. Когда этот этап выбора уже пройден, наступает техническая сторона подготовки к ЕГЭ: работа, работа и ещё раз работа, результатом которой будет либо оценка по базе, или набранные баллы профильного ЕГЭ.

Для качественной подготовки школьников к экзамену определены три группы учащихся:

первая группа – учащиеся, которые имеют минимум знаний и рассчитывают лишь преодолеть порог успешности  (5-6 заданий);

вторая группа – учащиеся, которые поставили перед собой цель – получить не очень высокие баллы (на уровне 45-60 баллов по 100-балльной шкале), но достаточные для поступления в вуз, не предъявляющий высоких требований к уровню математической подготовки;

третья группа – учащиеся, которые хотят получить высокие баллы (больше 60 баллов по 100 балльной шкале), необходимые для поступления в технические вузы.

Для каждой группы  определена своя линия подготовки к ЕГЭ.

Учащимся первой группы необходимо преодолеть рубеж 5 – 6 заданий части В. Выявляются сильные и слабые стороны математической подготовки каждого ученика, и работаем с теми заданиями, которые уже получаются, добавляя посильные задания из уже усвоенного материала. Выполняем  осмысленную отработку базовых математических навыков, не забывая попутно о критическом мышлении.

 Для второй группы необходимо уверенно выполнять 9-12 заданий части В. Желательно и 13, 14, 15 задания второй части КИМов ЕГЭ. Цель работы – сформировать навыки самопроверки и добиться устойчивого результата по работе с задачами первой части (на уровне – 9-12 заданий), повторить темы, дающие возможность решения определенных заданий части С.

           С третьей группой  вырабатываю  умение  уверенно выполнять 13-14 заданий части В, задания 1,2 части С, определяю его возможности относительно заданий С3-С6. С такими учащимися регулярно решаем задания, развивающие творческие способности учащихся к решению задач повышенного уровня сложности.

           В каждодневной работе использую указанную  уровневую дифференциацию. При таком подходе  каждый ученик имеет возможность овладевать учебным материалом в зависимости от его способностей и индивидуальных особенностей личности. Для реализации принципа дифференциации мною собран банк упражнений  по определенным  заданиям первой и второй частей контрольно-измерительных материалов с образцами решений, рекомендациями по их выполнению.

Ежемесячно провожу проверку вычислительных навыков, начиная с простейших математических действий: сложения, вычитания, умножения и деления.

Уделяю внимание технике выполнения экзаменационной работы:

• обучение постоянному жесткому контролю времени;
• обучение оценке объективной и субъективной трудности заданий и, конечно, разумному выбору этих заданий;
• обучение прикидке границ результатов и минимальной подстановке как приёму проверки, проводимой сразу после решения задания.

        Одним из немаловажных факторов качественной подготовки к ЕГЭ, на мой взгляд, является работа кабинета математики, где мною оформлен информационный стенд, отражающий общую информацию, связанную с ЕГЭ.  Отдельно собраны  также материалы ЕГЭ по математике: демонстрационный вариант КИМ, инструкция по выполнению работы, инструкция по заполнению бланков, спецификация экзаменационной работы по математике единого государственного экзамена, методические и психолого-педагогические особенности подготовки к сдаче ЕГЭ по математике (рекомендации для выпускников),  список литературы и адреса полезных сайтов, график проведения КДР.

Считаю важным доверительные отношения между учителем и каждым учеником, потому, что почти в каждой семье есть свои психологические проблемы, которые отвлекают внимание ребёнка и не дают ему сосредоточиться на достижении главной цели на данный период времени – успешной сдаче ЕГЭ.

  Сегодня школы поставлены перед необходимостью подготовить ученика к проверке знаний в форме ЕГЭ. Использование информационных технологий здесь оказывает огромную помощь. Тестирование – это один из видов контроля знаний, который в последнее время всё больше входит в жизнь современной школы. Высокая эффективность контролирующих программ определяется тем, что они укрепляют обратную связь в системе «учитель – ученик». Тестовые программы позволяют быстро оценивать результат работы, точно определить темы, в которых имеются пробелы в знаниях. Так, решая тесты по всем темам, учащиеся ведут личный диагностический контроль, где отмечают всякий раз «неподдающиеся» темы с тем, чтобы повторить теорию, получить консультацию учителя, пройти тестирование по этой же теме снова. И так до тех пор, пока тема не будет совершенно освоена.