Дополнительные построения в геометрии егэ

Дополнительные построения занимают важное место среди различных методов решения геометрических задач. Например, теорема о площади треугольника, теорема Пифагора, теорема о пересечении высот треугольника и многие другие. При подготовке к экзамену по математике большинство задач по планиметрии не решается с помощью строгих алгоритмов, почти каждая геометрическая задача требует своего подхода.

Искусство решать задачи основывается на хорошем знании теории, на знании достаточного количества геометрических фактов и в овладении приёмами и методами решения.

Эти методы обладают некоторыми особенностями:

большое разнообразие, трудность формального описания, взаимозаменяемость, отсутствие чётких границ области применения.

При решении геометрических задач используются три основных метода:

• геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем;
• алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений;
• комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других — алгебраическим.

Во многих случаях решать задачи помогает введение в чертеж дополнительных линий — так называемые дополнительные построения. Такие дополнительные построения, вводящие новые углы и новые отрезки, иногда приводят к появлению геометрических фигур, облегчающих решение задачи. Представленные данные говорят об актуальности изучения метода дополнительных построений.

Объект исследования: планиметрические задачи

Предмет исследования: метод дополнительных построений

Цель работы:

·выяснить, в чем состоит суть метода дополнительных построений;

• узнать, при   решении каких задач   целесообразно   использовать метод дополнительных построений.

Задачи:

• выявить, при решении каких задач метод дополнительных построений является наиболее эффективным;
• изучить разнообразные методы, которые могут быть успешно применены при решении многих геометрических задач;
• провести группировку различных видов дополнительного построения;

В процессе работы я использовала следующие методы исследования:

• анализ математической и методической литературы;
• анализ геометрических задач, которые предлагались на ЕГЭ и ОГЭ;
• классификация дополнительных построений;
• математическое моделирование;

-поиск рационального способа решения задачи методом дополнительного построения.

Теоретическая значимость: исследовательская работа позволяет расширить знания о методе дополнительных построений при решении геометрических задач.

Практическая    значимость    работы    заключается    в    возможности    использования    ее результатов учениками, учителями математики.

Глава 1. Дополнительное построение как метод решения планиметрических задач

1. Приёмы дополнительного построения

Решение геометрической задачи начинается с работы над чертежом. Часто на чертеже, особенно в геометрических задачах, которые предлагаются на различных олимпиадах, трудно заметить связи между данными и искомыми величинами. В подобных ситуациях решить задачу помогают дополнительные линии, которые проводятся для того, чтобы свести задачу к ранее решенной или более простой задаче. Они позволяют включить в задачу новые фигуры с их свойствами, тем самым увеличить число теорем, которые можно использовать при решении задачи.

Приёмы дополнительного построения, которые используются при решении геометрических задач можно разделить на два вида — это разбиение фигур и дополнение.

Разбиение фигур:

• проведение в многоугольнике прямой, параллельной одной из имеющихся (или параллельных прямых), что позволяет применять подобие;
• разбиение фигуры на части с целью получения треугольника и параллелограмма (в том числе ромба, квадрата), что позволяет применять свойства этих фигур;
• проведение перпендикуляров, радиусов окружности в точки касания, высот в трапеции позволяют получить прямоугольные треугольники.

Дополнение фигур:

• построение параллелограмма, с помощью продления медианы треугольника, что позволяет применять свойства параллелограмма;
• построение дополнительного треугольника;
• построение вспомогательной окружности с целью применения свойств хорд, касательных и углов, связанных с окружностью.

Рассмотрим дополнительные построения, использование которых целесообразно при решении планиметрических задач, связанных с треугольниками и четырёхугольниками [4].

Результатом этих дополнительных построений является прямоугольный треугольник. В треугольнике вершины острых углов совпадают с центрами данных окружностей, один из катетов равен половине отрезка секущей, расположенного внутри окружностей (или отрезку касательной, заключенному между точками касания), а другой сумме (для случая с внутренней касательной) или — разности (для случая с внешней касательной) радиусов этих окружностей. В случае касания данных окружностей (рис. 15) гипотенуза O1O2  ?O1O2В равна сумме радиусов этих окружностей (r1 и r2), поэтому расстояния между точками касания окружностей с их общей внешней касательной можно найти по формуле А1А2=2

1. Прямоугольный треугольник достраивается до равнобедренного треугольника/

Если дан прямоугольный треугольник, то он достраивается до равнобедренного треугольника. Один из катетов данного треугольника становится, медианой, биссектрисой и высотой, а другой – половиной основания.

1. Если дана трапеция, то с помощью продолжения боковых сторон она достраивается до треугольника.
2. Если в треугольнике, параллелограмме или трапеции дана биссектриса одного из внутренних углов, то проводится дополнительное построение треугольника, одна из   сторон

которого содержит эту биссектрису, вторая совпадает со стороной данной фигуры, а третья или параллельна другой стороне этой фигуры, или получается при ее продолжении (рис. 17– рис. 20). Построенный треугольник является равнобедренным.

 

1.3.3. Построение дополнительной окружности

Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы.

Если дан четырехугольник, у которого суммы противоположных углов равны, то вокруг него описывается окружность. Признаком существования для четырехугольника описанной окружности обладают квадрат, прямоугольник и равнобедренная трапеция.

Если дан четырехугольник, у которого суммы противоположных сторон равны, то в него вписывается окружность.

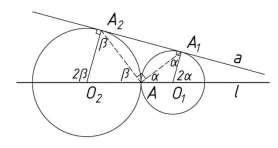
Если даны две окружности с общей внешней касательной, касающиеся друг друга внешним образом, то в рассмотрение вводится треугольник, вершинами которого служат три точки касания данных фигур (рис.21).

Рис.21

Треугольник АА1А2 является прямоугольным с прямым углом А (А – точка касания окружностей). Докажем, что угол A1AA2 = 90°.

?O1AA1 и ?O2AA2 – равнобедренные. Пусть α и β углы при основаниях этих треугольников; тогда 2α – внешний угол при вершине O1, 2β   – внешний угол при   вершине O2. 2α и 2β — односторонние углы при O1A1 || O2A2 и секущей O1O2, значит 2α + 2β = 180°, поэтому α + β =90°. ?A1AA2  = 180° – (LA1AO1  +LA2AO2) = 180° – (α + β) = 180° – 90°, что и требовалось доказать.

Глава 2 Практическое применение метода дополнительных построений.

2.1. Решение задач методом дополнительных построений

Задача 1. Построение прямой параллельной одной из имеющихся (или параллельных прямых)

Две стороны треугольника равны 10см и 15см, угол между ними равен 600. Найти длину биссектрисы, проведённой из данного угла.       

Δ АВС, АВ= 10см,  АС = 15см,  < А = 600

АМ – биссектриса -?

Проведём MN ? АВ

< ВАМ = < MAN = < AMN = 300

Δ ANM – равнобедренный

AN = x,   NC = 15 – x

Δ ABC ~ Δ NMC,

NC : АС = MN : АВ

(15 – х) : 15 = х : 10

10( 15 – х) = 15х

х = 6

AN = NC = 6

< ANM = 1800 – 600 =1200

 По теореме косинусов:

АМ2 = AN2 + NM2 – 2 • AN • NM • cos 1200

АМ2 = 36 + 36 – 2 • 36 • cos 1200

АМ2 = 72 + 2 • 36 • cos 600

АМ2 = 72 + 36 = 108

АМ = √108

Ответ: √108

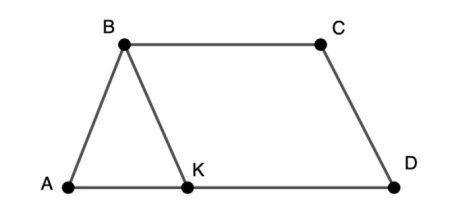
Задача 2. Построение прямой параллельной одной из имеющихся (или параллельных прямых)

В треугольнике АВС высота АМ равна медиане BN. Найти < NBC.

Проведём NK ? AM 

AN = NC, AM ? NK, тогда по теореме Фалеса МК = КС.

NK – средняя линия Δ АМС,

NK =   АМ

Δ BNK – прямоугольный

NK =   АМ =  = BN

Катет, лежащий против угла в 300 равен половине гипотенузы

< NBC = 300

Ответ: 300

Задача 3.Разбиение фигуры на части для получения треугольника и параллелограмма

Доказать, что если диагонали трапеции равны, то она равнобедренная.

АBСD – трапеция, BD = AC

Доказать: АВ = СD

                                  Доказательство:

BD ? CM, DC = DM

< BDA = < CMA как соответственные угла при параллельных прямых.

BD = CM, BD = AC, тогда АС = СМ,

Δ АСМ – равнобедренный,

< САМ = < СМА

Δ ABD = Δ DCA ( II признак равенства треугольников), тогда AB = CD,

 ABCD – равнобокая трапеция.

Задача 4. Разбиение фигуры на части для получения треугольника и параллелограмма

Биссектриса острого угла равнобокой трапеции делит боковую сторону на отрезки длиной 20см и 30см, считая от меньшего основания, которое равно 6см. Найти площадь трапеции.

ABCD – трапеция, < ВАМ = < MAD, BC = 6 см, СМ = 20 см, MD = 30 см

S ABCD -?

Решение:

BN ? AD , BN ∩ AN = N

Δ ABN – равнобедренный

< BAN = < BNA ( накрест лежащие, BN ? AD)

AB =BN = 50 см,

CN = BN – BC = 50 – 6 = 44 см

Δ AMD ~ Δ NCM

AD : 44 = 30 : 20

AD : CN = DM : СM

20 AD = 1320

   AD = 66 cм

S =  ( AD + ВС) • ВЕ

АЕ =  ( AD — ВС) = 30 см

Δ АЕВ – прямоугольный

ВЕ2 = АВ2 – АЕ2

ВЕ2 = 2500 – 900 = 1600

ВЕ = 40

S =  (66 + 6) • 40 = 1440 см2

Ответ: 1440 см2

Задача 5. Дополнительное построение окружности

На стороне АВ треугольника АВС построен равносторонний треугольник АВD. Найти расстояние от центра этого треугольника до вершины С, если АВ = 5√3, < АВС = 1200.

Решение:

Опишем около четырёхугольника ABCD окружность.

< С + < D = 1800 (сумма противолежащих углов)

< А + < В = 3600 – 1800 = 1800

Δ АВС – вписанный в окружность. ОС = R

             Ответ: 5 см

Задача 6.

Даны две окружности, касающиеся между собой внешним образом в точке С. Прямая а касается обеих окружностей. Найти расстояние от точки С до общей касательной а данных окружностей, если известны их радиусы R1 = 10 см, R2 = 8см.

Найти: CD

Решение:

АВ = 10 см, MN = 8 см

a– касательная к окружностям   АВ  ?   а, MN  ?  a, CD  ?  a, построим отрезки СВ и СN

Δ ВСN – прямоугольный,   BN – гипотенуза, CD – высота, проведённая к гипотенузе

CD2 = BD • DN

Так как AB ? CD ? MN, то по теореме Фалеса

BD : DN = AC : СМ

BD : DN = 5 : 4, BN = 2√АВ • MN

BN = 2√10 • 8 = 8√5

Ответ:

2.2. Применение метода дополнительный построений в решении задачи из ОГЭ и ЕГЭ

Пример (из открытого банка заданий ОГЭ ФИПИ) В трапеции АВСD с основаниями АD и ВС угол АВD равен углу АСD. Доказать, что АВСD – равнобедренная трапеция.

Решение:

Точки В и С лежат по одну сторону от АD и углы < АВD = < АСD, то точки А, В, С,D лежат на окружности. Так как хорды ВС ¦ AD , то дуга АВ равна дуге СD. Поскольку равные дуги стягивают равны хорды, то АВ = СD.

Задачи с несколькими вариантами дополнительного построения

 В условиях задания № 16 ЕГЭ пункт «б» может подсказать, какое решение задачи будет более удачным. Пример (из открытого банка заданий ЕГЭ ФИПИ)

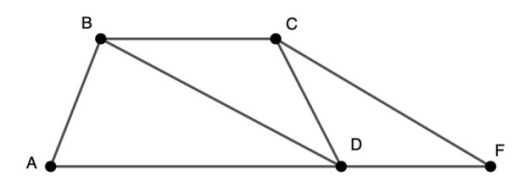
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O. а) Докажите, что CO=KO. б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD.

Решение: Первый вариант построения. Продлеваем ВС и АЕ, вследствие чего появляются равные треугольники АЕD и ZЕC. Так как АЕ=EZ, то ВЕ — это медиана треугольника АВZ. КС и АZ параллельны. Медиана хороша тем, что она делит пополам не только сторону треугольника, но и любой отрезок, который этой стороне параллелен. Поэтому CO=KO. Площадь треугольника ABZ такая же, как площадь трапеции ABCD за счет равенства треугольников АЕD и ZЕC. Треугольник КВС подобен треугольнику ABZ. Как известно, отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Отрезок BC, деленый на отрезок BZ, равен 3:10. На отрезок СZ приходится 7 частей. Ответ в пункте «б»: 3:7.

Второй вариант построения. Продолжим стороны AB и CD. Используя теорему, обратную теореме Фалеса, доказываем, что KB относится к BY так же, как YE к ED, и что отрезок KD параллелен BE. В треугольнике KCD видна середина CD. Отрезок OE параллелен KD и проходит через середину — следовательно, является средней линией и проходит через середину KC. Пункт «а» задания выполнен. Разобраться с пунктом «б» при данном дополнительном построении сложнее. К ответу 3:7 приводит то, что KB с BY соотносятся так же, как ED с YE.
Задачи с разрозненными данными

Пример (из всероссийской олимпиады школьников по математике, 8 класс, 2017 год, II этап)

Точки M и N — середины сторон BC и AD четырехугольника ABCD. Известно, что ∠В = 150°, ∠С = 90° и AB = CD. Найдите угол между прямыми MN и BC.

Программа динамической геометрии GeoGebra позволяет строить чертежи к геометрическим задачам. В стандартных ситуациях ее использование методически не всегда оправдано, а в некоторых задачах инструменты программы действительно помогают найти идею решения.

Рассмотрим пример геометрической задачи, входящей в материалы ОГЭ по математике (в спецификации ОГЭ — задача №24), для поиска решения которой действительно удобно использовать возможности программы GeoGebra:

Задача. В выпуклом четырехугольнике ABCD длина отрезка, соединяющего середины сторон АВ и CD, равна одному метру. Прямые ВС и AD перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей АС и BD.

Сначала просто трудно сделать чертеж на бумаге. Поэтому выполним построение в среде GeoGebra.

Алгоритм построения:
— построить прямую АD
— построить прямую ВС перпендикулярно AD
— построить середины отрезков AВ и CD — точки E и F соответственно, построить отрезок EF
— построить отрезки AC и BD — диагонали четырехугольника ABCD
— построить середины отрезков AC и BD — точки H и G, построить отрезок HG

Перемещение исходных точек позволяет сформулировать гипотезу, что середины образуют прямоугольник. Гипотеза проверяется перемещением исходных точек.
Вопросы:
— чем является отрезок EG в треугольнике ABD?
— отрезки EG и HF равны?
— прямая EG перпендикулярна прямой BC? и т.д.
Решение и обоснование становится очевидным.

Вывод: программа помогает провести анализ задачи, самостоятельно найти идею решения, проводя манипуляции с чертежом. Без программы нужно много раз выполнить построение или быть достаточно опытным или просто должно повезти.

Дополнительные построения в планиметрии

Проанализируем экзаменационные и олимпиадные задачи, чтобы понять, как использовать нетривиальные, неочевидные подходы.

28 марта 2019

Задачи с окружностями

С помощью дополнительного построения окружности часто решаются задания № 24 и № 26 ОГЭ, а также № 16 ЕГЭ.

Пример (из открытого банка заданий ОГЭ ФИПИ)

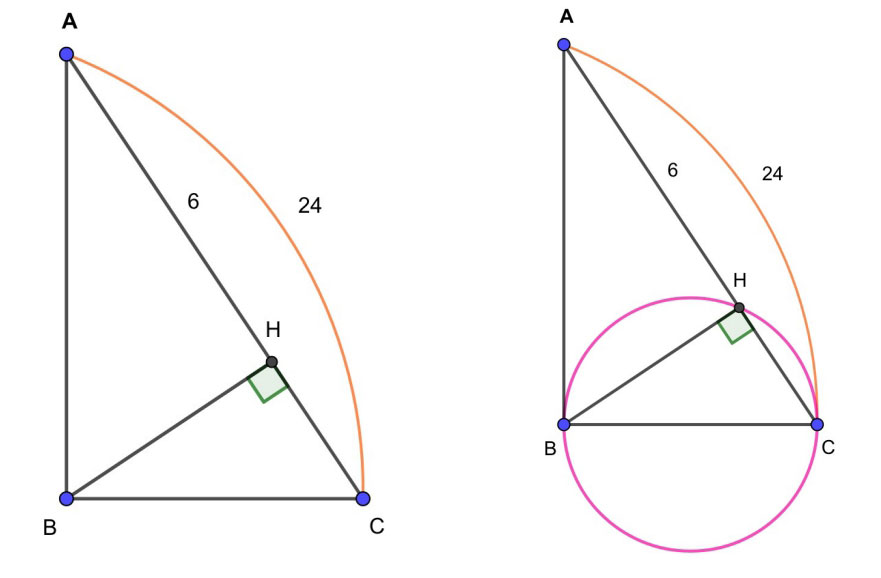
Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.

Строим окружность вокруг треугольника ВНС. Центр этой окружности является и серединой ВС. ВС — диаметр. АС по отношению к данной окружности — секущая. АВ — отрезок касательной. АН — внешняя часть секущей. Все это подводит к теореме о квадрате касательной.

АВ² — произведение секущей на ее внешнюю часть. Следовательно, нужно умножить AH на AC. 6×24 = 144 (это АВ в квадрате). АВ=12. Больше заданий для подготовки к ОГЭ вы найдёте в учебнике «Геометрия. 9 класс».

Задачи с несколькими вариантами дополнительного построения

В условиях задания № 16 ЕГЭ пункт «б» может подсказать, какое решение задачи будет более удачным.

Пример (из открытого банка заданий ЕГЭ ФИПИ)

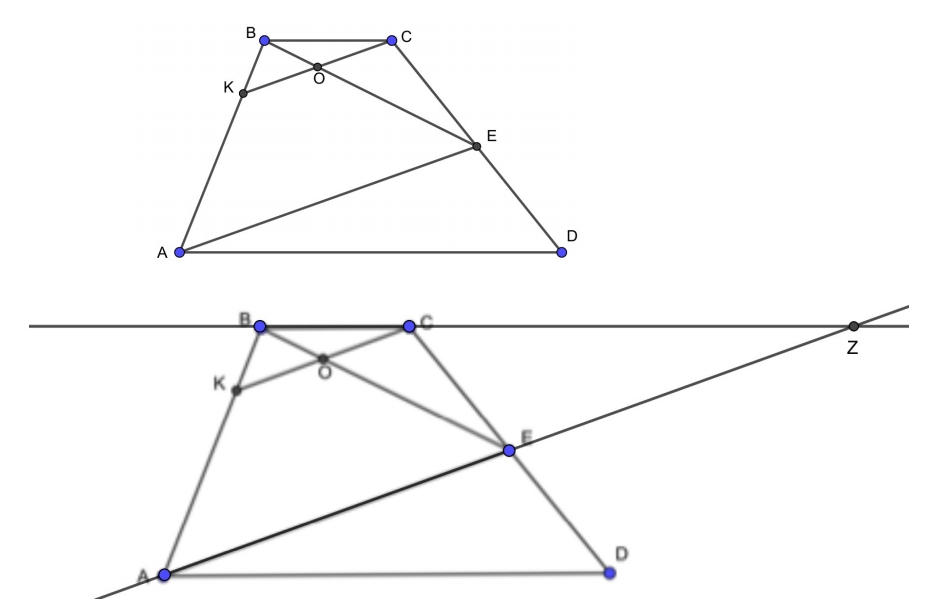
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а) Докажите, что CO=KO.

б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD.

Первый вариант построения. Продлеваем ВС и АЕ, вследствие чего появляются равные треугольники АЕD и ZЕC. Так как АЕ=EZ, то ВЕ — это медиана треугольника АВZ. КС и АZ параллельны. Медиана хороша тем, что она делит пополам не только сторону треугольника, но и любой отрезок, который этой стороне параллелен. Поэтому CO=KO.

Площадь треугольника ABZ такая же, как площадь трапеции ABCD за счет равенства треугольников АЕD и ZЕC. Треугольник КВС подобен треугольнику ABZ. Как известно, отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Отрезок BC, деленый на отрезок BZ, равен 3:10. На отрезок СZ приходится 7 частей. Ответ в пункте «б»: 3:7.

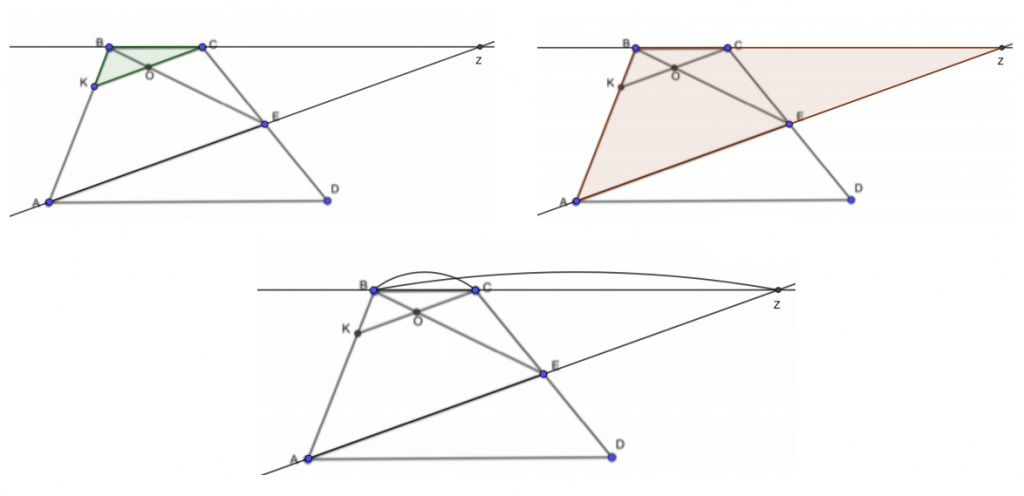
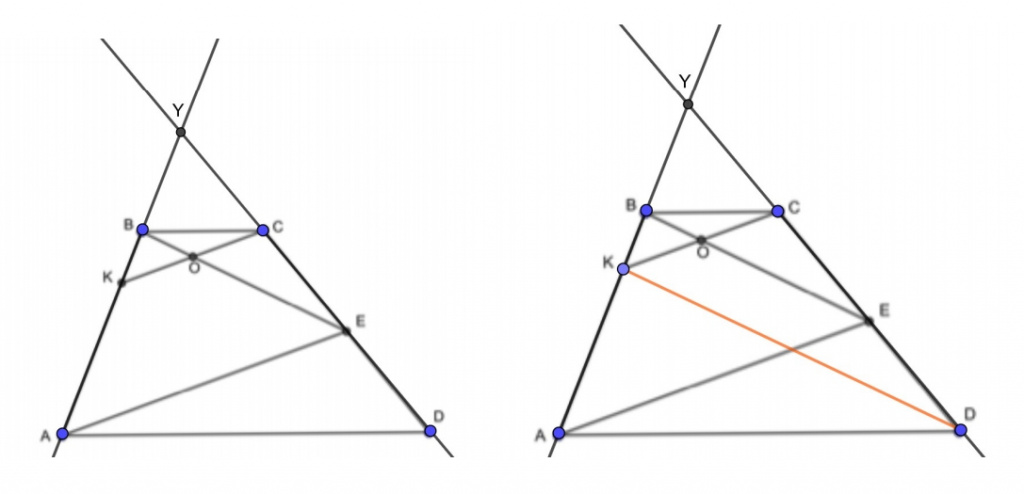
Второй вариант построения. Продолжим стороны AB и CD. Используя теорему, обратную теореме Фалеса, доказываем, что KB относится к BY так же, как YE к ED, и что отрезок KD параллелен BE. В треугольнике KCD видна середина CD. Отрезок OE параллелен KD и проходит через середину — следовательно, является средней линией и проходит через середину KC. Пункт «а» задания выполнен. Разобраться с пунктом «б» при данном дополнительном построении сложнее. К ответу 3:7 приводит то, что KB с BY соотносятся так же, как ED с YE.

Задачи с разрозненными данными

Пример (из всероссийской олимпиады школьников по математике, 8 класс, 2017 год, II этап)

Точки M и N — середины сторон BC и AD четырехугольника ABCD. Известно, что ∠В = 150°, ∠С = 90° и AB = CD. Найдите угол между прямыми MN и BC.

Начинаем компоновку данных с точки М и проводим через нее две прямые, параллельные АВ и CD. Далее от точки М откладываем отрезки, равные АВ и, соответственно, CD. Так получается заготовка для равнобедренного треугольника. Нужно понять, будет ли точка N лежать на отрезке, соединяющем две новые точки. Строятся новые отрезки, равные и параллельные ВМ и МС — получается четырехугольник-параллелограмм. AD является диагональю этого параллелограмма, а N — серединой диагонали. Также N лежит и на другой диагонали. Равнобедренный треугольник готов. Угол с вершиной M в нем равен 60°. Треугольник равносторонний, MN является медианой и биссектрисой. MN, пресекаясь с BC, образует угол, равный 60°.

Чтобы ученики прочно запоминали формулы и теоремы, лучше как можно чаще давать им решать подобные задачи. К слову, задачи с трапециями оптимально подходят для отработки навыка дополнительного построения: две параллельные стороны открывают широкие возможности для создания разных геометрических фигур. Об этом – в учебнике «Геометрия. 7-9 классы».

Один мудрец сказал: “ Высшее проявление духа – это разум.

Высшее проявление разума – это геометрия.

Клетка геометрии – треугольник. Он так же неисчерпаем,

 как и Вселенная. Окружность – душа геометрии.

Познайте окружность, и вы не только познаете душу геометрии,

но и возвысите душу свою”.

Дополнительные построения при решении

сложных геометрических задач.

Введение

В структуру выпускного экзамена ЕГЭ по математике профильного уровня входит геометрическая задача на доказательство повышенной сложности, требующая от обучающихся всестороннего знания планиметрии. Важнейшей особенностью является отсутствие единых алгоритмов решения таких задач, успех во многом зависит от накопленного учащимися опыта решения комбинированных планиметрических задач. Тем не менее, практика решения позволила выделить некоторые геометрические структуры, являющиеся вспомогательными ключами к поиску правильного решения. Метод вспомогательной окружности является одним из ключей к поиску правильного решения геометрических задач.  Сформулируем теоретические аспекты, лежащие в основе применения метода вспомогательной окружности, и покажем, как он используется для решения различных геометрических задач.  

Данная тема является дополнением и углублением изученных в курсе геометрии свойств окружности.  

Теоремы и следствия, изучаемые в курсе 8-9 класса

Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Вспомогательная окружность — одно из наиболее эстетичных дополнительных построений. Суть метода вспомогательной окружности заключается в том, что на чертежи к задаче вводится окружность, которую можно вписать или описать около треугольника, четырёхугольника или многоугольника. После этого связи между данными и искомыми величинами становятся очевидными. Использование вспомогательной окружности связано с характерными признаками фигуры, рассматриваемой в задаче. В процессе изучения метода вспомогательной окружности необходимо научиться выделять и использовать

эти признаки, наличие которых в задаче приводит к построению вспомогательной окружности. Они основаны на теоремах и их следствиях, изучаемых в курсе геометрии 8, 9 классов.

Углы, связанные с окружностью.

 

1. Градусная мера дуги окружности равна величине центрального угла:  

2.Вписанный угол измеряется половиной дуги, на которую он опирается:  

 

1. Вписанный угол, опирающийся на диаметр окружности, прямой: α = 90°

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны: α =  β 

1. Угол с вершиной внутри круга измеряется полусуммой двух дуг, одна из которых между его сторонами, а другая между их продолжениями :  

6.Угол с вершиной вне круга измеряется полуразностью дуг, заключённых между её сторонами:  

1. Угол, составленный касательной и хордой, проведённой в точку касания, равен половине дуги, заключённой внутри этого угла.  

Вписанные и описанные окружности.

 

1. Около любого треугольника можно описать единственную окружность, центр — точка

пересечения серединных перпендикуляров.

1. В треугольник можно вписать окружность и притом единственную. Центр окружности — точка пересечения

                                                    биссектрис.                

 

1. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Центр — точка пересечения диагоналей.

4.Только около равнобедренной трапеции  

                                        Можно описать окружность.                                                               

1. Если в четырехугольнике сумма длин его противоположных сторон равны, то в четырёхугольник можно вписать окружность.  AB + DC = AD + BC 

1. Если сумма противоположных углов четырехугольника равна 180, то около него можно

описать окружность.  

Свойства окружности, пересекающихся хорд, секущих и касательных.

1. Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на ее внешнюю часть равно квадрату касательной.  

AD2 = AC·AB

1. Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть, равно произведению другой секущей на ее внешнюю часть. 

AB · АС = AE · AD

1. Если две хорды окружности пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды 

AE · EB = CE · ED

 Признаки вспомогательной окружности

Метод вспомогательной окружности заключается в том, что если геометрическая   фигура (многоугольник, треугольник, квадрат и т.п.) имеет ряд конкретных признаков, то вокруг неё можно описать окружность. 

Если около геометрической фигуры можно описать вспомогательную окружность, то в некоторых случаях это облегчит решение некоторых геометрических задач.  Связь между данными и искомыми величинами становятся более ощутимыми или

 даже очевидными. К построению вспомогательной окружности приводит наличие

некоторых признаков.

 То есть критерием применимости метода вспомогательной окружности служит возможность использования в задаче следующих утверждений.

        Первый признак

Если можно указать точку, равноудалённую от             рассматриваемых четырех точек, то эти четыре точки

будут лежать на одной окружности.

BO = CO = DO = AO

    Второй  признак

Если точки A и B лежат на одной стороне неразвернутого угла с вершиной O, точки C и D на другой, и при этом OA · OB = OC · OD, то четыре точки A, B, C и D лежат на одной окружности.

Третий признак

    а)Если в четырехугольнике сумма        противоположных углов равна 180°, то вокруг него можно описать окружность.

 б) частным случаем является ситуация, в которой два противоположных угла

равны 90°.                   

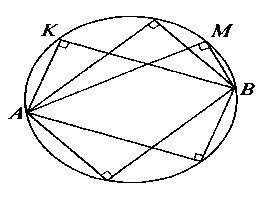
Четвертый признак

А) Если отрезок CD из точек E и F  виден под равными углами, то четыре точки E, F, C и D лежат на одной окружности (рис.2а).

Б) частным случаем является ситуация, когда концы отрезка видны под прямым углом(рис.2б).

  Заметим, что рассмотренные частные случаи можно объединить в конструкцию с общим названием: «прямоугольные треугольники с общей гипотенузой». В данных условиях явно определяется положение центра вспомогательной окружности – он лежит в середине гипотенузы, а радиус равен медиане, проведенной к гипотенузе этого треугольника.

Обобщим.

   Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:

а) точки М и К расположены по одну сторону от прямой АВ и при этом <АМВ = <АКВ;

б) точки М и К расположены по разные стороны от прямой АВ и при этом <АМВ+<АКВ = 180 ,

то точки А, В, М, К лежат на одной окружности

Пятый признак

Если отрезки AB и CD пересекаются в точке О и при этом OA·OB=OC·OD, TO четыре точки A, B,

C и D лежат на одной окружности.

Шестой признак

В задачах, условие которых подразумевает построение серединных перпендикуляров, часто сводится к построению окружности.

Седьмой признак

Если дан квадрат, прямоугольник, правильный n-угольник, равнобедренная трапеция, то вокруг них описывается окружность

Этапы решения задач методом вспомогательной окружности.

1.  Анализ условия («первый взгляд на задачу»).  Ещё при анализе условия  

  можно задуматься о возможности применить метод вспомогательной окружности. В качестве «сигналов» могут выступать следующие фразы:

«опущены перпендикуляры…», «проведены высоты…», «стороны (или прямые)

перпендикулярны…». Как правило, в задачах идёт речь о двух перпендикулярностях. В контексте условия речь также может идти о двух углах, сумма заданных градусных мер которых равна 180°.

2.  Построение чертежа («конкретизация»). На данном этапе выполняется построение в соответствии с условием, одновременно конкретизируя и подводя под чертеж свои догадки относительно применения метода вспомогательной окружности. Отыскать удачное вспомогательное построение часто бывает нелегко.

 Чертёж, как  модель,  является  ключевым  элементом  на  пути  решения  задачи и, следовательно, его незаменимой частью, поэтому качество выполнения чертежа играет значимую роль.

3.  Анализ чертежа и выбор метода. На данном этапе происходит выявление

соответствующей ситуации (общей или частной из описанных выше), позво-

ляющей   обоснованно применить метод вспомогательной окружности.  

4.  Обоснование метода. После выбора конкретного случая проводится его теоре-

тическое обоснование, опираясь на  общую  возможность  построения  окружности  

по двум вписанным равным углам или же по вписанному в неё четырёхугольнику.

5.  Дополнительное построение. Здесь непосредственно строят вспомогательную окружность.

6.  Цепочка следствий. Окружность, как новый элемент позволяет расширить

область возможных умозаключений, привнося видимость новых особенностей

чертежа.  Работая далее с углами в окружности в связи со всем чертежом зада-

чи, выполняя  поиск  новых  отношений,  приходим  к  истинности  

доказываемого суждения.

                       Применение вспомогательной окружности.  

Рассмотрим  применение  данного  метода  при  решении  задач  ЕГЭ  на  доказательство, предлагаемых в открытом банке заданий, а также сборниках типовых задач.  К  каждой  задаче  мы  предложим  два  чертежа:  первый,  который  строит сам обучающийся  – после первичного понимания условия задачи, и второй, который получается из первого чертежа  – после применения метода вспомогательной окружности.

Задача 1. В треугольнике АВС проведена высота BК. Найти длину отрезка, соединяющего точку К с серединой АB, если АB = 10см.

Решение:

Проведем высоту АМ, тогда углы АКВ и АМВ равны по 900 , значит точки А, К, М, В лежат на одной окружности и АВ – диаметр.(На рисунке окружность изображена штриховой линией, хотя ее можно и вообще не изображать, а “представлять               в уме”).  Точка О – середина АВ по условию.  Следовательно, АО = ОВ = КО = =r = 5 см. (рис. 3)

Ответ: 5см

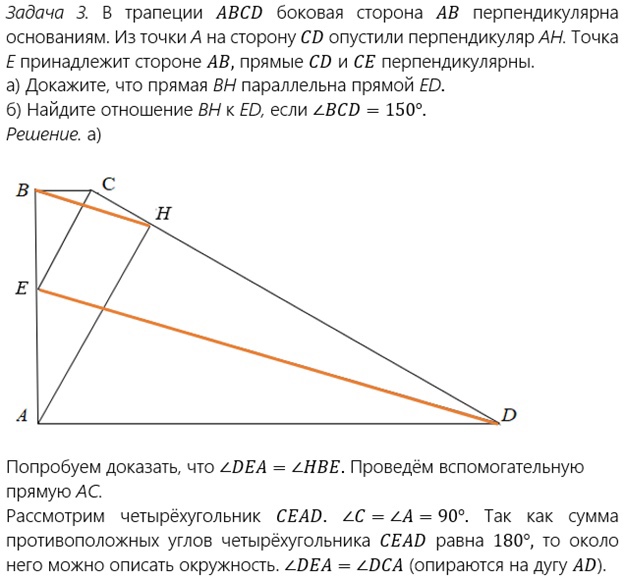
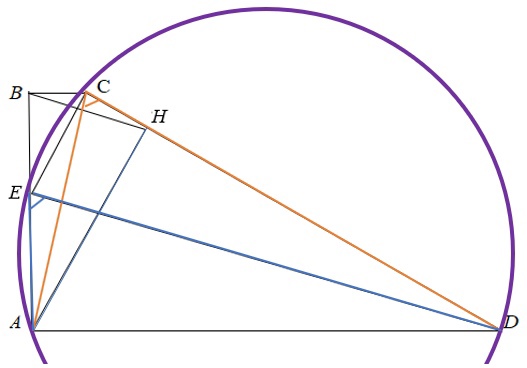
Задача 2 (2017 г.). В трапеции АВСD боковая сторона AB перпендикулярна осонованиям. Из точки А на сторону СD опустили перпендикуляр АН. Точка Е принадлежит стороне АВ, прямые CD и CE перпендикулярны. Докажите, что прямая ВН параллельна прямой ED.

Доказательство.

 1) В четырёхугольнике ABCH два противолежащих угла – прямые, ∠ABC + +∠AHC = 180°, значит, четырёхугольник – вписанный, точки A, B, C, H лежат на одной окружности. Построим эту вспомогательную окружность. Её центр – середина АС.

2) ∠ABH = ∠ACH как вписанные, опирающиеся на дугу AH.

3) Аналогично, четырёхуг-к AECD – вписанный. Центр окружности – середина ED.

4) ∠AED = ∠ACD как вписанные, опирающиеся на дугу AD.

5) Из пунктов 2 и 4 следует равенство: ∠AED = ∠ABH. Значит, равны соответственные углы при прямых BH, ED и секущей AB. Следовательно, BH || ED, что и требовалось доказать.

Задача 3 (2018 г.) В равнобедренном треугольнике АВС, где угол В – тупой, на

продолжение ВС опущена высота АН. Из точки Н на стороны АВ и АС опущены

перпендикуляры НК и НМ, соответственно. Докажите, что АМ = МК.

Доказательство. 

1) ∆AMH, ∆AKH – прямоугольные, с общей гипотенузой AH. Значит, точки A, M, K, H – лежат на одной окружности, центр которой – середина AH.                   2) ∠KAM = ∠KHM = α как вписанные, опирающиеся на дугу MK.                                                  3) ∠BAC = ∠BCA = α по свойству углов при основании р/б ∆ ABC.

4) ∠HBA = ∠BAC + ∠BCA = α + α = 2α как внешний угол ∆ABC.

5) Из прямоугольного ∆ABH имеем:  ∠HAB = 90° – 2α.

 6) Из прямоугольного ∆AKH имеем: ∠AHK = 2α.

7) ∠AHM = ∠AHK – ∠KHM = 2α – α = α.

∠AHM = ∠AKM = α как вписанные, опирающиеся на дугу AM.

9) Из пунктов 2 и 8 имеем: ∠KAM = ∠AKM = α, следовательно, ∆AMK – равнобедренный (по признаку), т. е. AM = MK (по определению), что и требовалось доказать.

Заключение.

В статье рассмотрен один из интересных приёмов решения геометрических задач, который состоит в том, что в чертёж вводится вспомогательная окружность. Построение вспомогательной окружности позволяет увеличить число теорем, которыми можно пользоваться при решении задач, и благодаря этому отыскивать зависимость между элементами фигуры. В статье выделены наиболее типичные ситуации, в которых можно применить вспомогательную окружность, рассмотрены задачи различных уровней сложности.

Данная статья помогает «увидеть» окружность там, где ее нет. Помогает описать окружность там, где это возможно, что значительно облегчает решение задач. Вспомогательная окружность- ключ к решению ряда геометрических задач.

Статья может быть использована для практических занятий и элективных курсов в 9-11 классах при подготовке к ОГЭ и ЕГЭ, успешному участию в математических конкурсах и олимпиадах.

Список литературы

1. Гордин Р.К. «ЕГЭ 2011. Математика. Задача С4» под редакцией А.Л.

Семёнова и И.В. Ященко.- М.: МЦНМО, 2011 г.

1. Мерзляк А.Г. «Учимся решать задачи по геометрии».

1. Погорелов А.В.  «Геометрия: учебник для 7-9 классов общеобразовательных учреждений».- М.: Просвещение, 2018 г.

1. Ященко И. В.  ЕГЭ. Математика. Профильный уровень: типовые

     экзаменационные варианты: 36 вариантов / под ред. И. В. Ященко. М.:

Издательство «Национальное образование», 2021.

 5.   Казаков Н. А., Кузнецова Т. И. Метод вспомогательной окружности в       планиметрических задачах ЕГЭ // Вестник Московского государственного областного университета. Серия: Физика-Математика. 2019. № 1

Использование метода дополнительных построений при решении геометрических задач

Астахова Вера Григорьевна,

учитель математики МБОУ «Гимназия №3»

Большинство задач по геометрии, как планиметрических, так и стереометрических, не решаются по алгоритму, каждая требует своего подхода, но всё-таки можно при решении задач выделить общие идеи. Рассмотрим решение планиметрических задач. Решение геометрической задачи всегда начинается с построения чертежа, который выполняется с условием задачи, учитывается пропорциональность отрезков, углов, параллельности, перпендикулярности прямых и т.п. Аккуратное выполнение чертежа позволяет найти связь между элементами фигуры и наметить план решения. В ряде случаев решить задачу помогают дополнительные построения: отрезки, прямые, углы, треугольники, окружности и т.п. Дополнительные линии чаще всего проводятся для того, чтобы свести задачу к ранее решенной или просто более простой задаче, так как появляются другие фигуры, свойства которых известны учащимся, увеличивается число теорем, которые можно использовать. Метод дополнительных построений при решении геометрических задач является непростым, так как нужное дополнительное построение не всегда удается определить с первого взгляда. Иногда условие задачи подсказывает выбор дополнительного построения. Однако увидеть нужное дополнительное построение увидеть трудно. В одних случаях построения очевидны, в других требуют большого опыта того, кто решает задачу. Вместе с тем существуют достаточно типичные дополнительные построения, к выполнению которых учащихся можно подготовить. Для этого необходимо знать различные способы дополнительных построений, при которых решение геометрической задачи становится намного проще.

Приёмы дополнительного построения, которые используются при решении
геометрических задач можно разделить на два вида – это разбиение фигур и дополнение.
Разбиение фигур:

 проведение в многоугольнике прямой, параллельной одной из имеющихся (или
параллельных прямых), что позволяет применять подобие;

 разбиение фигуры на части с целью получения треугольника и параллелограмма (в том числе ромба, квадрата), что позволяет применять свойства этих фигур;

 проведение перпендикуляров, радиусов окружности в точки касания, высот в
трапеции позволяют получить прямоугольные треугольники.

Дополнение фигур:

 построение параллелограмма, с помощью продления медианы треугольника, что
позволяет применять свойства параллелограмма;

 построение дополнительного треугольника;

 построение вспомогательной окружности с целью применения свойств углов, хорд, касательных, связанных с окружностью.

Дополнительные построения встречаются по всему курсу планиметрии с 7 по 9 классы. В учебнике геометрии Л.С. Атанасяна имеются задачи, теоремы, при решении, доказательстве, которых применяются различные дополнительные построения, например, в темах: «Треугольники», «Параллельные прямые», «Соотношения между сторонами и углами треугольника», «Четырехугольники», «Площадь», «Подобные треугольники», «Окружность». В 7 классе вводится метод дополнительного построения при изучении темы «Свойства равнобедренного треугольника», при доказательстве признаков параллельности прямых, и теорем, обратных этим теоремам. В 8 классе при изучении темы «Четырехугольники», «Площади», «Теорема Пифагора» можно ознакомить обучающихся с удвоением медианы треугольника с последующим достраиванием треугольника до
параллелограмма, рассмотреть стандартные дополнительные построения в задачах на трапецию. При изучении планиметрии в 7-8 классах особое внимание
нужно уделять построению отрезков (соединение отрезком каких-либо точек, лежащих на
сторонах многоугольника, построение высот треугольника или четырехугольника,
радиусов или хорд окружности, диагоналей многоугольника, продолжение отрезков до
взаимного пересечения между собой и т.д.), при доказательстве теоремы о
сумме углов треугольника, неравенства треугольника. При этом общее представление о разновидностях дополнительных построений при решении геометрических задач у школьников не формируется, в учебниках нет систематизации разновидностей дополнительных построений.

Приведем некоторую квалификацию дополнительных построений.

1. Выделение элементов чертежа или фрагментальный чертеж.

Цель: более подробное рассмотрение нужной части чертежа.

1. Построение вспомогательной окружности, описанной около многоугольника.

Цель: получение вписанных, центральных углов, опирающихся на одну и ту же или равные дуги.

1. Построение боковых сторон трапеции до их пресечения.

Цель: получение треугольника и использование его свойств, использование замечательного свойства трапеции.

1. Удвоение медианы.

Цель: получение параллелограмма и использование его свойств.

1. Построение дополнительных прямых в треугольниках и многоугольниках, пересекающих их стороны или вершины, в частности, высот, медиан, биссектрис.

Цель: 1) получение равных ил подобных треугольников,

2) получение углов с соответственно параллельными или перпендикулярными сторонами,

3) перенос соотношений длин отрезков с одной стороны угла на другую.

1. Проведение дополнительных прямых в окружностях, в частности, радиусов, диаметров, хорд, секущих, касательных.

Цель: 1) получение вписанных и центральных углов,

2) получение углов между касательной и хордой,

3) использование теоремы о касательной и секущей.

Рассмотрим некоторые основные дополнительные построения, которые необходимо знать обучающимся.

Например, дополнительные построения в трапеции.

1) Проведение двух диагоналей.

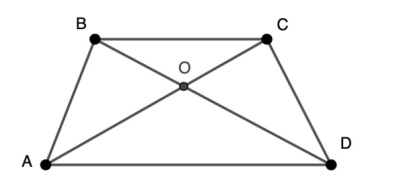
При проведении двух диагоналей образуются подобные треугольники, с которыми дальше можно работать.

В нашем случае это треугольники АОD и COB. В этих треугольниках можно отметить равные вертикальные углы, а также равные накрест лежащие углы при двух параллельных прямых AD и BC и секущей (на выбор берем одну из диагоналей).

2) Проведение двух высот.

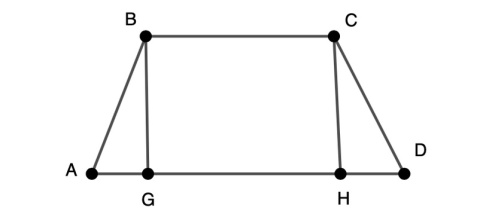
Проведя две высоты из вершин меньшего основания, мы делим трапецию на прямоугольник и два прямоугольных треугольника, имеющих одинаковые катеты (одинаковая высота трапеции).

Если такое дополнительное построение сделать в равнобедренной трапеции, то в этом случае мы получим два равных друг другу прямоугольных треугольника.

3) Продление боковых сторон до пересечения.

Продлеваем AB и DC до пересечения в точке Е. Если продлить боковые стороны до пересечения, мы получим треугольник, в котором проведена прямая, параллельная основанию.

За счет параллельных прямых мы снова получаем подобные треугольники (треугольники АЕD и BEC).

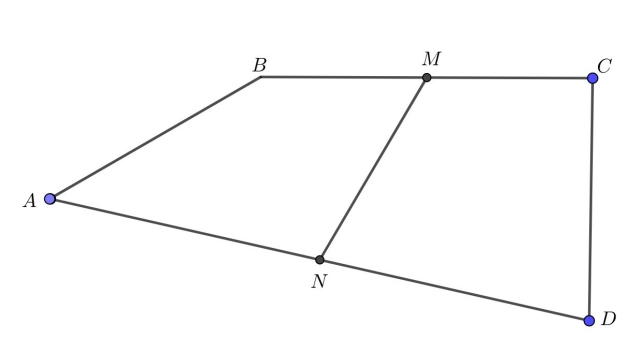
4) Из вершины малого основания внутри трапеции проводим прямую параллельно одной из боковых сторон.

ВК параллельно CD. За счет параллельности мы отсекаем параллелограмм.

Особенно полезным данное дополнительное построение будет в том случае, когда мы знаем все стороны трапеции и нам необходимо найти какой-то угол в трапеции. Угол мы будем искать через теорему косинусов в треугольнике, который здесь образуется.

5) Из одной из вершин основания проводим прямую, параллельную одной из диагоналей до пересечении с прямой, которая содержит другое основание.

Проводим CF параллельно BD. Здесь мы также получаем параллелограмм, но дополнительно мы получаем сторону, которая равна сумме длин оснований исходной трапеции, что может пригодится в задачах на подобные идеи.

Построение вспомогательной окружности.

1. Если дан прямоугольный треугольник, то вокруг него описывается окружность,
   центром которой является середина гипотенузы.

2. Если дан четырехугольник, у которого суммы противоположных углов равны, то
   вокруг него описывается окружность. Признаком существования для четырехугольника
   описанной окружности обладают квадрат, прямоугольник и равнобедренная трапеция.

3. Если дан четырехугольник, у которого суммы противоположных сторон равны, то в него можно вписать окружность.

4. Если даны две окружности с общей внешней касательной, касающиеся друг друга
   внешним образом, то целесообразно рассмотреть треугольник, вершинами которого
   служат три точки касания данных фигур. Треугольник A₁AA₂ является прямоугольным с прямым углом А (А – точка касания окружностей).

Вспомогательные окружности часто облегчают вычисление углов в задачах о
«некруглых» фигурах.

Теорема (условие принадлежности четырех точек окружности).

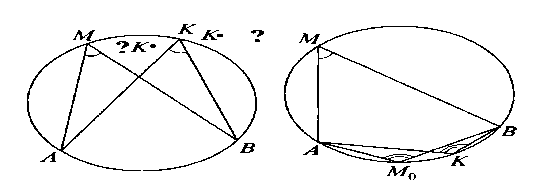
Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:
а) точки М и К расположены по одну сторону от прямой АВ и при этом угол АМВ равен углу АКВ, то точки А, В, М и К лежат на одной окружности
б) точки М и К расположены по разные стороны от прямой АВ и при этом
АМВ + АКВ = 1800, то точки А, В, М и К лежат на одной окружности
Особенно важную роль играет частный случай.

Теорема. Если АМВ = АКВ= 90⁰, то точки А, В, М, К расположены на окружности с диаметром АВ (здесь два случая слились в один: точки М и К могут располагаться как по одну, так и по разные стороны от прямой АВ)

Для примера рассмотрим решение геометрической задачи №16 ЕГЭ, где применяются дополнительные построения.

Задача. В трапеции АВСD боковая сторона АВ перпендикулярна основаниям. Из точки А на сторону СD опустили перпендикуляр АН. Точка Е принадлежит стороне АВ, прямые СD и СЕ перпендикулярны.

а) Докажите, что прямая ВН параллельна прямой ЕD.

б) Найдите отношение ВН к ЕD, если ВСD=150°.

Решение.

а) Докажем, что DЕА=НВЕ.

Для этого проведем вспомогательную прямую АС.

Рассмотрим четырехугольник СЕАD. С=А=90°. Так как сумма противоположных углов четырехугольника СЕАD равна 180°, то около него можно описать окружность. DЕА=DСА (опираются на дугу АС).

Рассмотрим четырехугольник АВСН. В=Н=90°. Так как сумма противоположных углов четырехугольника АВСН равна 180°, то около него можно описать окружность. НСА=НВА (опираются на дугу АН).

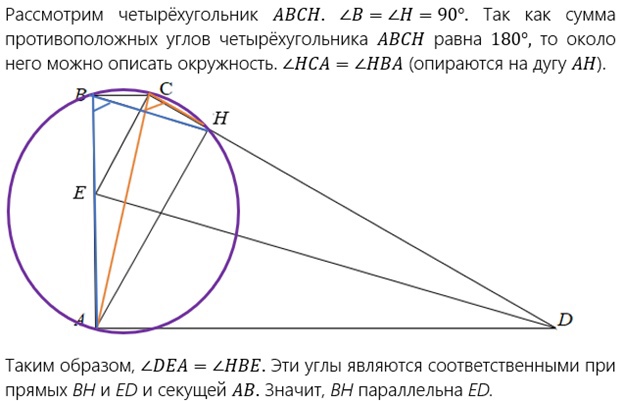
Таким образом, DЕА=НВЕ. Эти углы являются соответственными при прямых ВН и ЕD и секущей АВ. Значит, ВН параллельна ЕD.

б) Достроим трапецию АВСD до треугольника АМD продолжением боковых сторон.

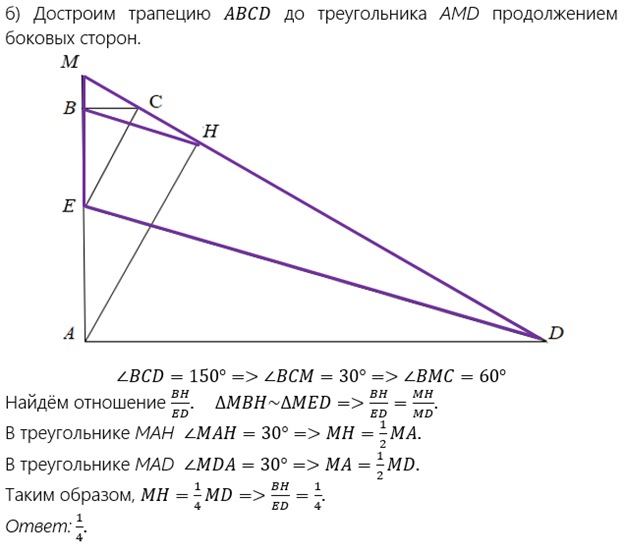
ВСD=150° = ВСМ=30° = ВМС=60°.

Найдем отношение ВН /ВD.

ΔМВН~ΔМЕD = ВН/ЕD=МН/МD.

В ΔМАН МАН=30° = МН=1/2МА.

В ΔМАD МDА=30° = МА=1/2МD.

Таким образом, МН=1/4МD = ВН/ЕD=1/4.

Ответ: ¼.

Балганова О. И.

ГБОУ РХ «Хакасская национальная гимназия – интернат имени Н. Ф. Катанова», г. Абакан.

Дополнительные построения при решении геометрических задач.

«Если вы хотите научиться плавать, то смело входите в воду,

а если хотите научиться решать задачи, то решайте их!»

Д.Пойа 

При решении геометрических задач традиционные методы иногда приводят к громозким решениям, поэтому важной составной частью геометрических методов решения являются дополнительные построения.

Дополнительные построения используются для:

— появления новых фигур и возможность использовать формулы, свойства и теоремы, связанные с ними;

— появление подобных или равновеликих фигур;

— появление пропорциональных отрезков.

Наиболее распространненые дополнительные построения:

Если в треугольнике задана медиана, то достраиваем до параллелограмма с центром в основании этой медианы.

Задача 1.

Определить площадь треугольника, если две стороны и медиана, выходящая из общей вершины этих сторон, имеют длины 3, 7 и 4 (соответственно).

Дано: АВС, , , , ВО – медиана.

Найти: .

Решение.

Достроим АВС до параллелограмма ABCD (рис. 1).

Найдем площадь АВD по формуле Герона: S=; где , SАВD = = 6 , так как , то = = 6 . .

Ответ: 6

Если в треугольнике задан отрезок прямой, проведенный через его вершину, заключенный внутри треугольника, то через ее основание внутрь треугольника проводится луч, параллельный стороне, до его пересечения с другой стороной.

Задача 2.

В треугольнике ABC проведена высота ВВ1 и медиана СС1. Известно, что их точка пересечения О отстоит от стороны АС на расстоянии 1см. Определите АВ, если ВВ1 =6; СС1 = 5.

Дано: АВС, ВВ1 – высота, СС1 –медиана, ВВ1 СС1 = О, ОВ1 = 1см, ВВ1 = 6см,

СС1 = 5см.

Найти: АВ

Решение: Построим С1С2║АС ВВ2 = В2В1 т.к. ОВ1 = 1, то ОВ2 = 2,

ОВ1С ОВ2С1 = CC1 = 3х = 5 х =; ∆ОВ1С: В1С = = ; АВ1 = 4В1С = 4 =

∆АВВ1: АВ = = =

Ответ:

Если в треугольнике заданы медиана и высота или биссектриса или вторая медиана, проведенные из разных вершин, то через основание медианы внутрь треугольника проводится луч, параллельный данной высоте, биссектрисе или медиане, до его пересечения со стороной треугольника.

Задача 3.

В треугольнике MNK высота MM1 равна медиане NN1. Найти величину угла N1NK

Дано: MNK, MM1 – высота, NN1 – медиана, MM1 = NN1.

Найти:N

Решение:

Построим N1N2 II MM1 (рис.3), тогда M1N1 = N1т.е. N1N2 — средняя линия ∆MM1K N1N2 = MM1 ; MM1 = NN1 N1N2= NN1 = 300

Ответ: 300

Если в треугольнике заданы два отезока прямых проведенные из разных вершин, то через начало одной из них (вершину треугольника) проводится прямая, параллельная стороне треугольника, до пересечения с продолжением другой прямой.

Задача 4.

Точка В1 взята на стороне АС треугольника АВС так, что = n. В каком отношении медиана АА1 делит отрезок ВВ1?

Дано: АВС, В1 АС, = n.

Найти:

Решение:

Построим ВА2 параллельно АС (рис.4), продолжим АА1 до пересечения с прямой ВА2 . ∆АОВ1 ∆А2ОВ = = = = (B =

Ответ:

Если в треугольнике заданы отрезок с концами на двух сторонах треугольника и высота (медиана, биссектриса), пересекающий эту высоту (медиану, биссектрису), и не параллельный третьей стороне, то данный отрезок продолжается в обе стороны до пересечения с продолжением третьей стороны и с прямой, параллельной этой стороне и проходящей через вершину, из которой выходит высота (медиана, биссектриса).

Задача 5.

Точки R и L лежат на боковых сторонах АВ и ВС равнобедренного треугольника АВС так, что АR = АВ; CL = BC. Определите, в каком отношении отрезок RL делит высоту ВВ1

Дано: АВС, АВ = ВС, R АВ, L BC, АR = АВ; CL = BC.

Найти:

Решение:

Построим ВR1 АС (рис. 5), продолжим RL до пересечения с BR1 и АС в точках R1 и L1 ∆ВRR1 ∆АRL1 = = == = ;

∆BLK1 ∆CLL1 = = = 3;

AL1 = 3СL1 AL1 = 6CL1 АС = 5CL1 B1C = AC = CL1; B1L1 = CL1 + CL1 = CL1 = AL1 ∆BGR1 ∆В1GL1 = = = .

Ответ: =

Есди дана трапеция, то ее диагональ или боковая сторона переносится на вектор, определяемый одним из оснований

Задача 6. Основание AD трапеции ABCD вдвое длиннее боковой стороны АВ и верхнего основания ВС. Диагональ АС = a, CD = b. Найти площадь трапеции.

Дано: ABCD – трапеция, AD = 2AB=2BC, АС = a, CD = b

Найти:

Решение:

Построим СМ и соединим точки В и М (рис. 6); АВСМ – ромб (АВ СМ,

АМ ВС, АВ = ВС); SABCD = SACD + SABC = AC CD + AC BM = + ab = =

Ответ: SABCD =

Задачи для самостоятельного решения.

Найти площадь треугольника, медианы которого равны 12, 15 и 21.

Точки А1 и В1 делят стороны ВС и АС треугольника АВС в отношениях ВА1 А1С = 1 р и АВ1 В1С = 1 ԛ. В каком отношении точка пересечения АА1 и ВВ1 делит каждую из них.

Высота, проведенная к гипотенузе прямоугольного треугольника, делит ее на части длиной 9 см. и 16см. Из вершины большего острого угла треугольника проведена прямая, проходящая через середину высоты. Найлите длину отрезка этой прямой, заключенной внутри данного треугольника.

Равнобедренный треугольник АВС вписан в окружность и его медиана АА1 продолжена до пересечения с окружностью в точке А2. Определите стороны треугольника, если АА1 = 27, А1А2 = .

Докажите, что сумма медиан в любом треугольнике меньше его периметра.

Литература:

М. А. Иванов Математика без репетитора. Москва, «Вентана – Граф», 2002

ж. Математика № 39, 2001

Доп построения в треугольнике

Дополнительные построения занимают важное место среди различных методов решения геометрических задач. Например, теорема о площади треугольника, теорема Пифагора, теорема о пересечении высот треугольника и многие другие. При подготовке к экзамену по математике большинство задач по планиметрии не решается с помощью строгих алгоритмов, почти каждая геометрическая задача требует своего подхода.

Искусство решать задачи основывается на хорошем знании теории, на знании достаточного количества геометрических фактов и в овладении приёмами и методами решения.

Эти методы обладают некоторыми особенностями:

большое разнообразие, трудность формального описания, взаимозаменяемость, отсутствие чётких границ области применения.

При решении геометрических задач используются три основных метода:

• геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем;
• алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений;
• комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других — алгебраическим.

Во многих случаях решать задачи помогает введение в чертеж дополнительных линий — так называемые дополнительные построения. Такие дополнительные построения, вводящие новые углы и новые отрезки, иногда приводят к появлению геометрических фигур, облегчающих решение задачи. Представленные данные говорят об актуальности изучения метода дополнительных построений.

Объект исследования: планиметрические задачи

Предмет исследования: метод дополнительных построений

·выяснить, в чем состоит суть метода дополнительных построений;

• узнать, при решении каких задач целесообразно использовать метод дополнительных построений.

• выявить, при решении каких задач метод дополнительных построений является наиболее эффективным;
• изучить разнообразные методы, которые могут быть успешно применены при решении многих геометрических задач;
• провести группировку различных видов дополнительного построения;

В процессе работы я использовала следующие методы исследования:

• анализ математической и методической литературы;
• анализ геометрических задач, которые предлагались на ЕГЭ и ОГЭ;
• классификация дополнительных построений;
• математическое моделирование;

-поиск рационального способа решения задачи методом дополнительного построения.

Теоретическая значимость: исследовательская работа позволяет расширить знания о методе дополнительных построений при решении геометрических задач.

Практическая значимость работы заключается в возможности использования ее результатов учениками, учителями математики.

Глава 1. Дополнительное построение как метод решения планиметрических задач

1. Приёмы дополнительного построения

Решение геометрической задачи начинается с работы над чертежом. Часто на чертеже, особенно в геометрических задачах, которые предлагаются на различных олимпиадах, трудно заметить связи между данными и искомыми величинами. В подобных ситуациях решить задачу помогают дополнительные линии, которые проводятся для того, чтобы свести задачу к ранее решенной или более простой задаче. Они позволяют включить в задачу новые фигуры с их свойствами, тем самым увеличить число теорем, которые можно использовать при решении задачи.

Приёмы дополнительного построения, которые используются при решении геометрических задач можно разделить на два вида — это разбиение фигур и дополнение.

• проведение в многоугольнике прямой, параллельной одной из имеющихся (или параллельных прямых), что позволяет применять подобие;
• разбиение фигуры на части с целью получения треугольника и параллелограмма (в том числе ромба, квадрата), что позволяет применять свойства этих фигур;
• проведение перпендикуляров, радиусов окружности в точки касания, высот в трапеции позволяют получить прямоугольные треугольники.

• построение параллелограмма, с помощью продления медианы треугольника, что позволяет применять свойства параллелограмма;
• построение дополнительного треугольника;
• построение вспомогательной окружности с целью применения свойств хорд, касательных и углов, связанных с окружностью.

Рассмотрим дополнительные построения, использование которых целесообразно при решении планиметрических задач, связанных с треугольниками и четырёхугольниками [4].

1.2.1.Построение прямой параллельной одной из имеющихся (или параллельных прямых)

Если в треугольнике известен отрезок АА1, то через точку А1 проводится прямая, параллельная стороне АВ, до её пересечения со стороной АС (рис.1). По теореме о пропорциональных отрезках получаем . Если отрезок АА1 является медианой, то по теореме Фалеса А2 – середина стороны АС.

Если в треугольнике известны два отрезка, проведённые из разных вершин, в том числе биссектриса, высота, или медиана, то через основание одного из них проводится прямая, параллельная данному отрезку, до её пересечения со стороной треугольника (рис. 2, рис.3). Так на рис. 2 прямая КB2 отсекает от треугольника AA1A2 подобный ему треугольник AКB2, а прямая A1A2 – треугольник CA1A2, подобный треугольнику CBB2.

1.2.2.Разбиение фигуры на части для получения треугольника и параллелограмма

Если в треугольнике (рис. 4), параллелограмме (рис. 5) или трапеции (рис. 6, рис. 7) дана биссектриса одного из внутренних углов, то можно построить ромб, две стороны которого лежат на сторонах данного треугольника или четырехугольника, а биссектриса является диагональю. Такое построение позволяет использовать свойства этих фигур.

Проведённые перпендикуляры позволяют получить прямоугольные треугольники и использовать теорему Пифагора, теоремы о подобии треугольников.

Часто в задачах используются такие дополнительные построения как проведение радиусов окружности в точки касания, высот в трапеции.

Так, если в условии задачи известна медиана треугольника, то удвоив её, мы получим параллелограмм (рис.8), что позволит использовать его свойства [8].

В зависимости от содержания задачи такое дополнительное построение можно выполнять и для двух, и для трёх медиан; использовать не весь параллелограмм, а только его части Например, треугольника АА2С (рис. 8).

1.3.2.Дополнительное построение треугольника

1. В результате построения, выполненного на рис. 9 (АВ2 ||ВС) и рис. 10 (АС||ВА2), появляются две пары подобных треугольников. Так, на рисунке 9 ?AКB2 и ?A1КB; ?AB1B2 и ?CB1B; на рис. 10 ?AКB1 и ?A2КВ; ?AA1C и ?A2A1B подобны.

На рис. 11 и рис 12 (АМ1|| ВС, L1=КМ∩ВС) ? ALМ1 подобен ? BLL1, ? AMM1 подобен ?CML1, ? AКM1 подобен ?КA1L1.

Если даны две окружности разных радиусов (не имеющие общих точек, пересекающиеся в двух точках или касающиеся внешним образом) с секущей, проходящей через одну из точек пересечения окружностей (или общей касательной), то через центр меньшей окружности проводится прямая, параллельная данной секущей (или касательной). Находится точка пересечения с радиусом большей окружности, проведённым в точку касания, или с его продолжением (рис. 13, рис. 15, рис. 14, рис. 16).

Результатом этих дополнительных построений является прямоугольный треугольник. В треугольнике вершины острых углов совпадают с центрами данных окружностей, один из катетов равен половине отрезка секущей, расположенного внутри окружностей (или отрезку касательной, заключенному между точками касания), а другой сумме (для случая с внутренней касательной) или — разности (для случая с внешней касательной) радиусов этих окружностей. В случае касания данных окружностей (рис. 15) гипотенуза O1O2 ?O1O2В равна сумме радиусов этих окружностей (r1 и r2), поэтому расстояния между точками касания окружностей с их общей внешней касательной можно найти по формуле А1А2=2

1. Прямоугольный треугольник достраивается до равнобедренного треугольника/

Если дан прямоугольный треугольник, то он достраивается до равнобедренного треугольника. Один из катетов данного треугольника становится, медианой, биссектрисой и высотой, а другой – половиной основания.

1. Если дана трапеция, то с помощью продолжения боковых сторон она достраивается до треугольника.
2. Если в треугольнике, параллелограмме или трапеции дана биссектриса одного из внутренних углов, то проводится дополнительное построение треугольника, одна из сторон

которого содержит эту биссектрису, вторая совпадает со стороной данной фигуры, а третья или параллельна другой стороне этой фигуры, или получается при ее продолжении (рис. 17– рис. 20). Построенный треугольник является равнобедренным.

1.3.3. Построение дополнительной окружности

Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы.

Если дан четырехугольник, у которого суммы противоположных углов равны, то вокруг него описывается окружность. Признаком существования для четырехугольника описанной окружности обладают квадрат, прямоугольник и равнобедренная трапеция.

Если дан четырехугольник, у которого суммы противоположных сторон равны, то в него вписывается окружность.

Если даны две окружности с общей внешней касательной, касающиеся друг друга внешним образом, то в рассмотрение вводится треугольник, вершинами которого служат три точки касания данных фигур (рис.21).

Треугольник АА1А2 является прямоугольным с прямым углом А (А – точка касания окружностей). Докажем, что угол A1AA2 = 90°.

?O1AA1 и ?O2AA2 – равнобедренные. Пусть α и β углы при основаниях этих треугольников; тогда 2α – внешний угол при вершине O1, 2β – внешний угол при вершине O2. 2α и 2β — односторонние углы при O1A1 || O2A2 и секущей O1O2, значит 2α + 2β = 180°, поэтому α + β =90°. ?A1AA2 = 180° – (LA1AO1 +LA2AO2) = 180° – (α + β) = 180° – 90°, что и требовалось доказать.

Глава 2 Практическое применение метода дополнительных построений.

2.1. Решение задач методом дополнительных построений

Задача 1. Построение прямой параллельной одной из имеющихся (или параллельных прямых)

Две стороны треугольника равны 10см и 15см, угол между ними равен 600. Найти длину биссектрисы, проведённой из данного угла.

Δ АВС, АВ= 10см, АС = 15см,

Старт в науке

Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».

Дополнительные построения в планиметрии

Задачи с окружностями

С помощью дополнительного построения окружности часто решаются задания № 24 и № 26 ОГЭ, а также № 16 ЕГЭ.

Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.

Строим окружность вокруг треугольника ВНС. Центр этой окружности является и серединой ВС. ВС — диаметр. АС по отношению к данной окружности — секущая. АВ — отрезок касательной. АН — внешняя часть секущей. Все это подводит к теореме о квадрате касательной.

АВ 2 — произведение секущей на ее внешнюю часть. Следовательно, нужно умножить AH на AC. 6×24 = 144 (это АВ в квадрате). АВ=12. Больше заданий для подготовки к ОГЭ вы найдёте в учебнике «Геометрия. 9 класс».

Задачи с несколькими вариантами дополнительного построения

В условиях задания № 16 ЕГЭ пункт «б» может подсказать, какое решение задачи будет более удачным.

Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а) Докажите, что CO=KO.

б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD.

Первый вариант построения. Продлеваем ВС и АЕ, вследствие чего появляются равные треугольники АЕD и ZЕC. Так как АЕ=EZ, то ВЕ — это медиана треугольника АВZ. КС и АZ параллельны. Медиана хороша тем, что она делит пополам не только сторону треугольника, но и любой отрезок, который этой стороне параллелен. Поэтому CO=KO.

Площадь треугольника ABZ такая же, как площадь трапеции ABCD за счет равенства треугольников АЕD и ZЕC. Треугольник КВС подобен треугольнику ABZ. Как известно, отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Отрезок BC, деленый на отрезок BZ, равен 3:10. На отрезок СZ приходится 7 частей. Ответ в пункте «б»: 3:7.

Второй вариант построения. Продолжим стороны AB и CD. Используя теорему, обратную теореме Фалеса, доказываем, что KB относится к BY так же, как YE к ED, и что отрезок KD параллелен BE. В треугольнике KCD видна середина CD. Отрезок OE параллелен KD и проходит через середину — следовательно, является средней линией и проходит через середину KC. Пункт «а» задания выполнен. Разобраться с пунктом «б» при данном дополнительном построении сложнее. К ответу 3:7 приводит то, что KB с BY соотносятся так же, как ED с YE.

Задачи с разрозненными данными

Пример (из всероссийской олимпиады школьников по математике, 8 класс, 2017 год, II этап)

Точки M и N — середины сторон BC и AD четырехугольника ABCD. Известно, что ∠В = 150°, ∠С = 90° и AB = CD. Найдите угол между прямыми MN и BC.

Начинаем компоновку данных с точки М и проводим через нее две прямые, параллельные АВ и CD. Далее от точки М откладываем отрезки, равные АВ и, соответственно, CD. Так получается заготовка для равнобедренного треугольника. Нужно понять, будет ли точка N лежать на отрезке, соединяющем две новые точки. Строятся новые отрезки, равные и параллельные ВМ и МС — получается четырехугольник-параллелограмм. AD является диагональю этого параллелограмма, а N — серединой диагонали. Также N лежит и на другой диагонали. Равнобедренный треугольник готов. Угол с вершиной M в нем равен 60°. Треугольник равносторонний, MN является медианой и биссектрисой. MN, пресекаясь с BC, образует угол, равный 60°.

Чтобы ученики прочно запоминали формулы и теоремы, лучше как можно чаще давать им решать подобные задачи. К слову, задачи с трапециями оптимально подходят для отработки навыка дополнительного построения: две параллельные стороны открывают широкие возможности для создания разных геометрических фигур. Об этом – в учебнике «Геометрия. 7-9 классы».

исследовательская работа «Решение задач по геометрии методом дополнительных построений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Объект исследования: стереометрические задачи по геометрии

Предмет исследования: геометрия

Цель исследования: выявление способа, позволяющего решать задачи нетрадиционным методом.

Изучить литературу по теме исследования.

Проанализировать способы решения задач и выбрать более эффективный.

Для каждой фигуры найти рациональный метод построения.

Показать практическое применение данного метода.

Подобрать примеры для решения задач предложенным мной методом.

Классификация дополнительных построений……………………4-21

Практическое применение приёма метода дополнительных построений………………………………………………………….22-30

Задачи на доказательство………………………………………….31-32

Задачи на вычисление……………………………………………. 33-35

Список использованной литературы……………………………….37

В геометрии существуют задачи к которым традиционные методы(методы геометрических треугольников, векторный метод, метод равных треугольников) или не применимы, или дают сложные и громоздкие решения. При решении задач такого вида помогает введение в чертёж дополнительных линий или проведение дополнительных построений. В таких задачах это единственный способ её решения. Так как чертёж данной в задаче фигуры можно достроить до фигуры другого типа, то всегда с многоугольной фигурой можно связать окружность и можно на чертеже выделить равные и подобные фигуры.

Суть данного метода дополнительных построений заключается в том, что чертёж и задача, на котором трудно заметить связь между данными и искомыми величинами, дополняется новыми элементами, после чего эти связи становятся очевидными.

Анализ решений задач показал, что для каждой фигуры существуют характерные признаки, которые можно классифицировать. Предлагаю классификацию, которую мне удалось выделить для некоторых фигур.

Классификация дополнительных построений.

Если в треугольнике задана медиана, то его можно достроить до параллелограмма, где основание медианы это точка пересечения диагоналей.

Если в треугольнике создан отрезок, соединяющий вершину с противоположной стороной, то через основание отрезка проводим прямую параллельную стороне треугольника.

М N ‖ АВ или прямую параллельную АС

В результате данного построения получаются подобные треугольники ΔАВС

ΔМ N С или по теореме Фалеса получаются пропорциональные отрезки:

=

что позволяет определить неизвестные стороны треугольника. Если АМ – медиана Δ АВС, тогда N всегда будет серединой отрезка АС.

Если в треугольнике задана медиана и отрезок, соединяющий вершину с противоположной стороной, то через основание медианы проводим прямую, параллельную данному отрезку.

=

ДК – средняя линия Δ В N С

3) NK = KC , К – середина NC

Если в треугольнике заданы два отрезка, проведённых из разных вершин, то проводится а) через основание одного отрезка прямая, параллельная другому отрезку

б) прямая, проходящая через вершину треугольника параллельная стороне до пересечения с прямой, содержащей один из отрезков

Если в треугольнике задан отрезок, проведённый из вершины до противоположной стороны и отрезок, соединяющий две другие стороны, но не параллелен его стороне, то данный отрезок продолжается в обе стороны до пересечения с продолжением третьей стороны и с прямой, параллельной этой стороне и проходящей через вершину, из которой выходит отрезок.

Если в треугольнике задан отрезок с концами на его сторонах и если продолжение этого отрезка пересекает прямую, содержащую третью сторону треугольника, то:

а) продолжаем отрезок до пресечения с прямой, проведённой через вершину треугольника параллельно третьей стороне.

б) проводим прямую, параллельную одной из сторон до пересечения с другой стороной.

а)

б)

Если дан прямоугольный треугольник, то он достраивается до равнобедренного треугольника, в котором один из катетов данного треугольника становится высотой ( медианой и биссектрисой), а другой – половиной основания.

Если дана трапеция, то её диагональ или боковая сторона переносятся на вектор, определяемый одним из оснований.

Если в треугольнике, параллелограмме или трапеции задана биссектриса одного из внутренних углов, то в чертёж вводится ромб, две стороны которого направлены по сторонам данной фигуры, а эта биссектриса является одной из диагоналей.

Если в треугольнике, параллелограмма или трапеции задана биссектриса одного из внутренних углов, то в чертёж вводится треугольник, одна из сторон которого содержит эту биссектрису, вторая совпадает со стороной исходной фигуры, а третья либо параллельна другой стороне этой фигуры, либо получается при её продолжении.

Если дана трапеция, то посредством продолжения боковых сторон она достраивается до треугольника.

Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы.

Если дан четырёхугольник, у которого суммы противоположных углов равны, то вокруг него описывается окружность.

Если в треугольнике заданы биссектриса и медиана или биссектриса и серединный перпендикуляр, проведённые к одной и той же стороне, то около треугольника описывается окружность, а биссектриса продолжается до пересечения с нею.

Если даны две окружности разных радиусов с общей касательной, то через центр меньшей окружности проводится прямая, параллельная данной касательной, до пересечения с радиусом большей окружности, идущим в точку касания, или с его продолжением.

Если даны две окружности с общей внешней касательной, касающиеся друг друга внешним образом, то в рассмотрение вводится треугольник, вершинами которого служат три точки касания данных фигур.

Практическое применение метода дополнительных построений.

Две стороны треугольника равны 10см и 15см, угол между ними равен 60 0 . Найти длину биссектрисы, проведённой из данного угла.

проведём MN ‖ АВ

Δ ANM – равнобедренный

AN = x, NC = 15 – x

(15 – х) : 15 = х : 10

По теореме косинусов:

АМ 2 = AN 2 + NM 2 – 2 ∙ AN ∙ NM ∙ cos 120 0

АМ 2 = 36 + 36 – 2 ∙ 36 ∙ cos 120 0

АМ 2 = 72 + 2 ∙ 36 ∙ cos 60 0

АМ 2 = 72 + 36 = 108

В треугольнике АВС высота АМ равна медиане BN . Найти NBC .

проведём NK ‖ AM

AN = NC , AM ‖ NK , тогда по теореме Фалеса МК = КС.

NK – средняя линия Δ АМС,

NK = АМ

Δ BNK – прямоугольный

NK = АМ = = BN

Катет, лежащий против угла в 30 0 равен половине гипотенузы

Доказать, что если диагонали трапеции равны, то она равнобокая.

Дано: А B С D – трапеция

Доказать: АВ = С D

BDA = CMA как соответственные угла при параллельных прямых.

BD = CM , BD = AC , тогда АС = СМ,

Δ АСМ – равнобедренный,

Δ ABD = Δ DCA ( II признак равенства треугольников), тогда AB = CD ,

ABCD – равнобокая трапеция.

Биссектриса острого угла равнобокой трапеции делит боковую сторону на отрезки длиной 20см и 30см, считая от меньшего основания, которое равно 6см. Найти площадь трапеции.

Дано: ABCD – трапеция

BN ‖ AD BN ∩ AN = N

Δ ABN – равнобедренный

накрестлежащие , BN ‖ AD)

CN = BN – BC = 50 – 6 = 44 см

AD : CN = DM : С M

S = ( AD + ВС ) ∙ ВЕ

АЕ = ( AD — ВС) = 30 см

Δ АЕВ – прямоугольный

ВЕ 2 = АВ 2 – АЕ 2

ВЕ 2 = 2500 – 900 = 1600

S = ( 66 + 6 ) ∙ 40 = 1440 см 2

Ответ: 1440 см 2

На стороне АВ треугольника АВС построен равносторонний треугольник АВ D . Найти расстояние от центра этого треугольника до вершины С, если АВ = 5√3, 0 .

Опишем около четырёхугольника ABCD окружность.

D = 180 0 (сумма противолежащих углов)

0 – 180 0 = 180 0

Δ АВС – вписанный в окружность. ОС = R

Ответ: 5 см

Даны две окружности, касающиеся между собой внешним образом в точке С. Прямая а касается обеих окружностей. Найти расстояние от точки С до общей касательной а данных окружностей, если известны их радиусы R ₁ = 10 см, R ₂ = 8см.

а – касательная к окружностям АВ а, MN a , CD a

построим отрезки СВ и С N

Δ ВС N – прямоугольный, BN – гипотенуза, CD – высота, проведённая к гипотенузе

Так как AB ‖ CD ‖ MN , то по теореме Фалеса

BD : DN = 5 : 4, BN = 2√ АВ ∙ MN

Ответ:

Задачи на доказательство.

Доказать, что в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.

На сторонах АВ и ВС треугольника АВС построены вне его квадраты. Доказать, что отрезок, соединяющий вершины квадратов, в два раза больше медианы, проведённой из вершины В.

В треугольнике АВС луч, выходящий из вершины А, делит медиану ВВ₁ в отношении 1: 2. Доказать, что этот луч делит противоположную сторону треугольника в отношении 1: 4.

Доказать, что если в прямоугольном треугольнике один острый угол равен 30 0 , то противолежащий ему катет равен половине гипотенузы.

Катеты прямоугольного треугольника равны a и b . Доказать, что биссектриса прямого угла этого треугольника равна .

Через середину О гипотенузы АВ прямоугольного треугольника АВС проведена прямая, перпендикулярная АВ, и на этой прямой в обе стороны от точки О отложены отрезки О D и ОЕ, равные половине гипотенузы. Доказать, что [ CD ) и [ CE ) – биссектрисы внутреннего и внешнего углов треугольника АВС при вершине С.

Доказать, что прямая, соединяющая основания двух высот остроугольного треугольника, отсекает от него треугольник, подобный данному.

Точка D лежит на стороне АС правильного треугольника АВС, а точка Е – середина отрезка А D . Прямые, перпендикулярные сторонам АВ и ВС данного треугольника и проходящие соответственно через точки D и С, пересекаются в точке F . Доказать, что треугольник ВЕ F прямоугольный с острыми углами 30 0 и 60 0 .

Окружность радиусов R и r ( R > r ) касаются друг друга внешним образом. Доказать, что радиус третьей окружности, касающейся двух данных окружностей и их общей внешней касательной, равен

Две окружности радиусов R и r ( R > r ) касаются друг друга и сторон данного угла. Доказать, что радиус третьей окружности, касающейся сторон того же угла, центр которой находится в точке касания между собой двух данных окружностей, равен