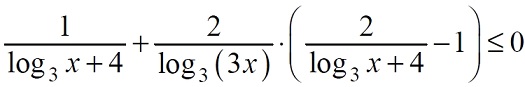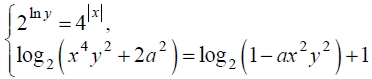ЕГЭ по математике 2021 года. Досрочная волна.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 21 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см.
Ответ:
2
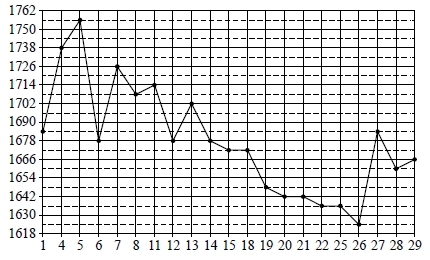
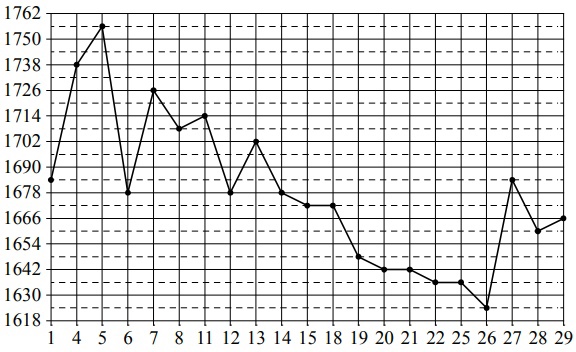
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2011 года. По горизонтали указываются числа месяца, по вертикали — цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода цена золота была равна 1678 рублям за грамм.
Ответ:
3
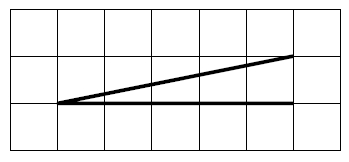
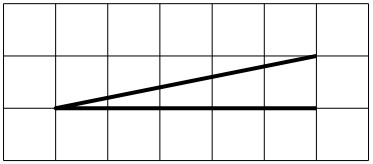
На клетчатой бумаге с размером клетки 1 × 1 изображён острый угол. Найдите тангенс этого угла.
Ответ:
4
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 12, но не дойдя до отметки 3.
Ответ:
5
Найдите корень уравнения
Ответ:
6
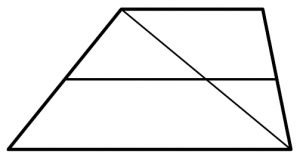
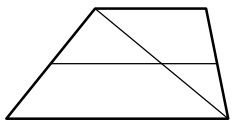
Основания трапеции равны 5 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Ответ:
7
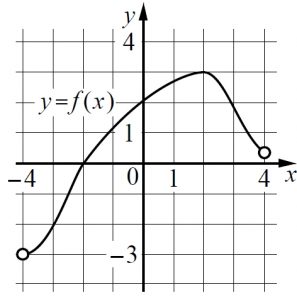
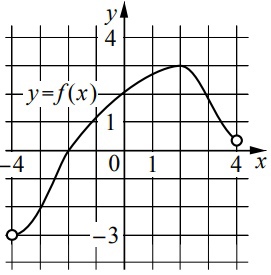
На рисунке изображён график функции y = f(x), определённой на интервале (−4; 4). Найдите корень уравнения f ’(x) = 0.
Ответ:
8
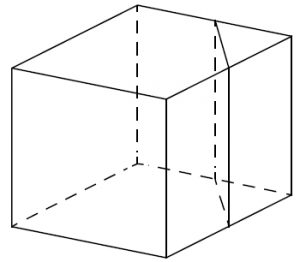
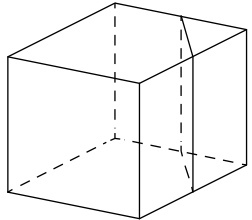
Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Ответ:
9
Найдите значение выражения
Ответ:
10
11
Расстояние между пристанями A и B равно 165 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Ответ:
12
Найдите наименьшее значение функции на отрезке
Ответ:
13
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
Точка E лежит на высоте SO, а точка F — на боковом ребре SC правильной четырёхугольной пирамиды SABCD, причём SE : EO = SF : FC = 2 : 1.
а) Докажите, что плоскость BEF пересекает ребро SD в его середине.
б) Найдите площадь сечения пирамиды плоскостью BEF, если AB = 8, SO = 14.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. Отрезок AP — диаметр окружности, описанной около треугольника ABC.
а) Докажите, что прямая HP пересекает отрезок BC в его середине.
б) Луч PH вторично пересекает окружность, описанную около треугольника ABC, в точке M. Найдите длину отрезка MC1, если расстояние от центра этой окружности до прямой BC равно 4, ∠BPH = 120°.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,25 млн рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Известно, что значение параметра а таково, что система уравнений
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
В последовательности из 80 целых чисел каждое число (кроме первого и последнего) больше среднего арифметического соседних чисел. Первый и последний члены последовательности равны 0.
а) Может ли второй член такой последовательности быть отрицательным?
б) Может ли второй член такой последовательности быть равным 20?
в) Найдите наименьшее значение второго члена такой последовательности.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Решение заданий варианта досрочного периода ЕГЭ 2021 по математике (профильный уровень). Открытый вариант КИМ.
Задание 1.
Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 21 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см.
Задание 2.
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2011 года. По горизонтали указываются числа месяца, по вертикали – цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода цена золота была равна 1678 рублям за грамм.
Задание 3.
На клетчатой бумаге с размером клетки 1×1 изображён острый угол. Найдите тангенс этого угла.
Задание 4.
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 12, но не дойдя до отметки 3.
Задание 5.
Найдите корень уравнения
Задание 6.
Основания трапеции равны 5 и 9. Найдите бо́льший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Задание 7.
На рисунке изображён график функции y = f(x), определённой на интервале (−4; 4). Найдите корень уравнения f ‘(x) = 0.
Задание 8.
Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Задание 9.
Найдите значение выражения
Задание 10.
Коэффициент полезного действия (КПД) некоторого двигателя вычисляется по формуле , где T1 – температура нагревателя (в кельвинах), T2 – температура холодильника (в кельвинах). При какой температуре нагревателя T1 КПД этого двигателя будет 20%, если температура холодильника T2 = 336 К? Ответ дайте в кельвинах.
Задание 11.
Расстояние между пристанями A и B равно 165 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Задание 12.
Найдите наименьшее значение функции
y = 8tg x − 8x − 2π +13
на отрезке .
Задание 13.
а) Решите уравнение
3⋅9x+1 − 5⋅ 6x+1 + 8⋅ 22x = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку .
Задание 15.
Решите неравенство
Задание 17.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,25 млн рублей.
Задание 18.
Найдите все значения a, при каждом из которых система уравнений
имеет единственное решение.
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 21 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2011 года. По горизонтали указываются числа месяца, по вертикали — цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько рабочих дней из данного периода цена золота была равна 1678 рублям за грамм.
На клетчатой бумаге с размером клетки 1×1 изображён острый угол. Найдите тангенс этого угла.
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 12, но не дойдя до отметки 3.
Найдите корень уравнения (sqrt[3]{x-5}=3)
Основания трапеции равны 5 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
На рисунке изображён график функции (y=f(x)), определённой на интервале ((-4;4) ). Найдите корень уравнения (f'(x)=0 )
Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Найдите значение выражения (16log_{10}{sqrt[4]{10}})
Коэффициент полезного действия (КПД) некоторого двигателя вычисляется по формуле (η=dfrac{T_1 — T_2}{T_1}cdot 100% ), где (T_1) — температура нагревателя (в кельвинах), (T_2) — температура холодильника (в кельвинах). При какой температуре нагревателя (T_1) КПД этого двигателя будет 20%, если температура холодильника (T_2 = 336) K? Ответ дайте в кельвинах.
Расстояние между пристанями A и B равно 165 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Найдите наименьшее значение функции (y=8mathrm{tg,}{x}-8x-2pi+13) на отрезке (left[-dfrac{pi}{4};dfrac{pi}{4}right])
а) Решите уравнение (3cdot 9^{x+1}-5cdot 6^{x+1}+8cdot 2^{2x}=0)
б) Укажите корни этого уравнения, принадлежащие отрезку (left[-dfrac{pi}{2};piright])
В ответ запишите корни без пробелов через точку с запятой в порядке возрастания. Сначала на пункт А, затем на пункт Б. Например, «8;13;8»
Точка E лежит на высоте SO, а точка F — на боковом ребре SC правильной четырёхугольной пирамиды SABCD, причём SE:EO=SF:FC=2:1.
а) Докажите, что плоскость BEF пересекает ребро SD в его середине
б) Найдите площадь сечения пирамиды плоскостью, BEF если AB = 8, SO =14
Решите неравенство (dfrac{1}{log_{3}{x}+4}+dfrac{2}{log_{3}{(3x)}} cdot left(dfrac{2}{log_{3}{x}+4}-1right)leqslant 0 )
Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H. Отрезок AP — диаметр окружности, описанной около треугольника ABC.
а) Докажите, что прямая HP пересекает отрезок BC в его середине.
б) Луч PH вторично пересекает окружность, описанную около треугольника ABC, в точке M. Найдите длину отрезка MC₁, если расстояние от центра этой окружности до прямой BC равно 4, ∠BPH=120°.
В ответ введите квадрат длины этого отрезка.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) |
1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,25 млн рублей.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases}2^{ln y}=4^{|x|}\log_{2}(x^4y^2+2a^2)=log_{2}{(1-ax^2y^2)+1}end{cases}) имеет единственное решение.
В последовательности из 80 целых чисел каждое число (кроме первого и последнего) больше среднего арифметического соседних чисел. Первый и последний члены последовательности равны 0.
а) Может ли второй член такой последовательности быть отрицательным?
б) Может ли второй член такой последовательности быть равным 20?
в) Найдите наименьшее значение второго члена такой последовательности.
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Досрочный ЕГЭ 2021
- 01.05.2021
Постараемся объяснить как обстоят дела с вариантами досрочного ЕГЭ в 2021 году.
- Реальные задания ЕГЭ 2021 по всем предметам
Во-первых
Не прошел даром коронавирус. В связи с пандемией расписание ЕГЭ в 2021 году очень сильно и много раз менялось. Да, кстати, актуальное расписание находится здесь. Последний раз оно обновлялось в феврале 2021 года.
- Результаты ЕГЭ 2021
Во-вторых
Досрочный ЕГЭ в 2021 году ОТМЕНИЛИ. А что вместо него?
А вместо него ФИПИ придумал очень хитрую штуку. Она называется — ОТКРЫТЫЕ ВАРИАНТЫ.
Что это такое? Это такие «аля варианты досрочного ЕГЭ 2021 года.». Аля — потому что досрочную волну отменили. Но называть эти варианты досрочными мы вполне можем. Есть основания предполагать, что эти варианты предназначались именно для этой волны.
В-третьих
По многим предметам изменений в 2021 году не было. Поэтому вы смело можете ориентироваться на досрочные варианты ЕГЭ 2020 года. Всё аналогично + там видеоразборы, ответы и прочие радости подготовки. Если вы не знаете какие изменения произошли в ЕГЭ в 2021 году, то посмотрите «Изменения по всем предметам в 2021 году».
Что дальше?
А дальше берём и решаем открытые варианты как варианты досрочного ЕГЭ 2021. Выбираем предмет и прорешиваем.
Кстати, к каждому такому открытому варианту досрочного ЕГЭ 2021 мы подготовили подробный видеоразбор.
Выберите нужный предмет
Обязательные предметы
- Русский язык
- Математика (профиль)
Предметы по выбору
- Английский язык
- Биология
- География
- Информатика
- Испанский язык
- История
- Китайский язык
- Литература
- Немецкий язык
- Обществознание
- Физика
- Французский язык
- Химия
Что ещё?
Обязательно просмотрите разделы с тренировочными и реальными вариантами ЕГЭ по предметам. Там мы собрали и тренировочные варианты 2021 года, и реальные варианты прошлых лет.
- Реальные варианты ЕГЭ 2020
Да, ещё очень круто разобрать все тренировочные работы Статграда за 2020-2021 учебный год. Для вашего удобства мы сделали супер подборку по всем предметам и всем датам. Смотрите здесь.
И не забывайте. ЕГЭ по базовой математике в 2021 году НЕ БУДЕТ. Всю актуальную для вас информацию по ЕГЭ в 2021 году мы собрали здесь.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2021 из различных источников.
Тренировочные варианты ЕГЭ 2021 по математике (профиль)
| Реальный вариант (по материалам из открытых источников) | скачать |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 (ЕГЭ 100БАЛЛОВ) | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| Вариант 11 | скачать |
| Вариант 12 | скачать |
| Вариант 13 | скачать |
| alexlarin.net (без ответов) | |
| Вариант 331 | скачать |
| Вариант 332 | скачать |
| Вариант 333 | скачать |
| Вариант 334 | скачать |
| Вариант 335 | скачать |
| math100.ru (с ответами) | |
| Вариант 110 | скачать |
| Вариант 111 | скачать |
| Вариант 112 | скачать |
| Вариант 113 | скачать |
| Вариант 114 | скачать |
| Ягубов РФ | |
| Вариант 11 | скачать |
| Вариант 19 | скачать |
| На основе реального (дальний восток) | скачать |
| На основе реального (Москва) | скачать |
Связанные страницы:
Тренировочные варианты ЕГЭ 2021 по математике базового уровня
Разбор задания 13 ЕГЭ по математике (профильный уровень)
Решение задания № 14 ЕГЭ по математике
Разбор задания 2 ЕГЭ математика профильный уровень
Решение задачи №19 ЕГЭ по профильной математике