Досрочный егэ 2016 математика 2016 - Помощь в подготовке к экзаменам и поступлению

Категория: ЕГЭ (диагностич. работы)

1. Бегун пробежал метров за секунд. Найдите среднюю скорость бегуна. Ответ выразите в километрах в час.

Решение: + показать

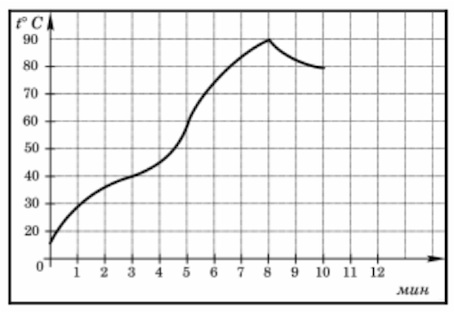
2. На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси – температура двигателя в градусах Цельсия. Определите по графику, до скольких градусов Цельсия двигатель нагрелся за первые минут с момента запуска.

Решение: + показать

3. Найдите длину средней линии трапеции, изображенной на рисунке. Сторона каждой клетки равна см. Ответ выразите в сантиметрах.

Решение: + показать

4. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна . Вероятность того, что это вопрос на тему «Параллелограмм», равна . Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение: + показать

5. Найдите корень уравнения

Решение: + показать

6. У треугольника со сторонами и проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна . Найдите длину высоты, проведенной ко второй стороне.

Решение: + показать

7. На рисунке изображён график производной функции и шесть точек на оси абсцисс: В скольких из этих точек функция возрастает?

Решение: + показать

8. Шар вписан в цилиндр объемом . Найдите объем шара.

Решение: + показать

8. Найдите значение выражения $0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}}.$

Решение: + показать

10. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной км с постоянным ускорением км/ч, вычисляется по формуле . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав километра, приобрести скорость не менее км/ч. Ответ выразите в км/ч.

Решение: + показать

11. Первая труба заполняет бассейн за часов, а две трубы вместе ‐ за часов минут. За сколько часов заполняет бассейн одна вторая труба?

Решение: + показать

12. Найдите точку максимума функции на промежутке $(0;frac{pi}{2}).$

Решение: + показать

Часть С

13. а) Решите уравнение $8^x-7cdot 4^x-2^{x+4}+112=0;$

б) Укажите корни этого уравнения, принадлежащие отрезку

Решение: + показать

14. В правильной четырехугольной призме сторона основания равна а боковое ребро равно На ребрах и отмечены точки и соответственно, причем

а) Пусть – точка пересечения плоскости с ребром . Докажите, что – квадрат.

б) Найдите площадь сечения призмы плоскостью

Решение: + показать

15. Решите неравенство: $(5x-13)log_{2x-5}(x^2-6x+10)geq 0.$

Видеорешение

Решение: + показать

16. Точка – центр окружности, описанной около остроугольного треугольника , ‐ центр вписанной в него окружности, ‐ точка пересечения высот. Известно, что

а) Докажите, что точка лежит на окружности, описанной около треугольника .

б) Найдите угол , если $angle ABC=55^{circ}.$

Решение: + показать

17. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на % по сравнению с его размером в начале года, а, кроме того, в начале третьего и четвертого годов вклад ежегодно пополняется на млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше млн рублей.

Решение: + показать

18. Найдите все значения параметра при каждом из которых система уравнений

$begin{cases} frac{xy^2-3xy-3y+9}{sqrt{x+3}}=0,& &y=ax;& end{cases}$

имеет ровно два различных решения.

Решение: + показать

19. Множество чисел назовем хорошим, если его можно разбить на два подмножества с одинаковой суммой чисел.

а) Является ли множество {} хорошим?
б) Является ли множество { $2;4;8;...;2^{100}$ } хорошим?
в) Сколько хороших четырехэлементных подмножеств у множества

{}?

Решение: + показать

Источник

11.04.2016

Два варианта с реального ЕГЭ 2016 по математике профильного уровня с досрочной волны.

Профильный уровень по математике (в досрочной волне) проходил 28 марта 2016 года.

Оба варианта имеют правильные ответы, которые указаны в конце вариантов.

Обсудить задания вы можете в комментариях ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Комментарии

+1

#1
Svetlana
14.04.2016 08:21

В задаче 17 варианта 2 исправьте арендную плату на 14.000 руб.

Цитировать

+1

#2
Роза
19.04.2016 12:28

Почему во втором варианте 4 задание ответ 0,86??? Я решала так: 50/57 ответ 0,877…
Что не так??

Цитировать

+1

#3
Нина
23.04.2016 08:45

Ребята, помогите хотя бы начать решать неравенство задание №
15. Я не могу.

Цитировать

0

#4
Нина
23.04.2016 08:47

Ребята,как хотя бы начать решать неравенство № 17?

Цитировать

-1

#5
Кирилл
24.04.2016 18:16

Перевести второй множитель к новому основанию и решать, могу решить, если надо)

Цитировать

+1

#6
Любовь
02.05.2016 06:46

Кирилл, реши, пожалуйста.

Цитировать

-1

#7
Андрей
05.05.2016 13:03

Да совершенно не понятно неравенство №15

Кирилл решите пожалуйста!

Цитирую Кирилл:

Перевести второй множитель к новому основанию и решать, могу решить, если надо)

Цитировать

+2

#8
Наталья
10.05.2016 17:22

Кто-нибудь решил 15 неравенство?

Цитировать

+2

#9
Илья
13.05.2016 16:23

В 1 варианте в 8 задании разве не 102 должно быть?

Цитировать

+1

#10
Илья
13.05.2016 16:26

И в 13 а) задании 1-ого варианта не хватает еще одного корня x=pi + 2*pi*n, n принадлежит z

Цитировать

-1

#11
Ардалион
15.05.2016 18:13

Да кто-нибудь, решите 15-ое неравенство

Цитировать

0

#12
Павел
27.05.2016 14:44

Пишите на мэйл vemmy124gmail.com, пришлю решение 15ого задания первого варианта

Цитировать

0

#13
Marfusha
03.06.2016 11:38

Цитирую Роза:

Почему во втором варианте 4 задание ответ 0,86??? Я решала так: 50/57 ответ 0,877…
Что не так??

50/50-7/50=0.86

Цитировать

0

#14
Ринат
03.06.2016 17:41

Изи 15 , вы чего ребята , учитесь :lol:

Цитировать

0

#15
моя
04.06.2016 06:24

сомовосска взрывается очень классно

Цитировать

-1

#16
АНЯ
04.06.2016 10:41

Цитирую Илья:

И в 13 а) задании 1-ого варианта не хватает еще одного корня x=pi + 2*pi*n, n принадлежит z

он не принадлежит ,т.к в одз синус не равен нулю.

Цитировать

0

#17
Тимофей
04.06.2016 11:02

Цитирую Роза:

Почему во втором варианте 4 задание ответ 0,86??? Я решала так: 50/57 ответ 0,877…
Что не так??

не правильно считали.
Там написано 7 ИЗ 50 кепок.
Т.е. 43 — без дефектов.
43/50=0.86.
В первом варианте такая же схема.

Как вы решают в задачах, где пишут: «на каждые 50 кепок приходится 7 с дефектами…» и т.п. тогда уже складывать надо.

Цитировать

0

#18
Надежда
05.06.2016 18:04

Я не пойму, а как в 1м варианте номер 12 делали?

Цитировать

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Источник

ЕГЭ по математике 2016. Досрочная волна, резервная волна (часть С)

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

а)  Решите уравнение

б)  Укажите корни этого уравнения на интервале

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

Решите неравенство

Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а)  Докажите, что ∠ABM = ∠DBC = ∠MBD.

б)  Найдите расстояние от точки О, точки пересечения диагоналей, до отрезка СМ, если BC  =  42.

В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия возврата таковы:

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года.

— с февраля по июнь необходимо выплатить часть долга.

— в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6 млн. рублей.

При каком значении параметра a система имеет ровно три решения?

Верно ли, что для любого набора положительных чисел, каждое из которых не превосходит 10, а сумма которых больше 90, всегда можно выбрать несколько чисел так, чтобы их сумма была не больше 90, но больше:

а)  80;

б)  82;

в)  81.

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

ЕГЭ 2016, Математика, Досрочный экзамен, Профильный уровень, Реальный вариант №107.

При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, за сколько часов напряжение упадёт с 1,4 вольта до 1 вольта.

Примеры.
Вероятность того, что новый сканер прослужит больше года, равна 0,94.
Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 1 млн рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 10 млн рублей.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу ЕГЭ 2016, Математика, Досрочный экзамен, Профильный уровень, Реальный вариант №107 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать
— pdf — Яндекс.Диск.

Дата публикации: 21.07.2016 17:29 UTC

Теги:

ЕГЭ по математике :: математика

Следующие учебники и книги:

ЕГЭ 2016, Математика, 11 класс, Тренировочная работа, Вариант МА10101
ЕГЭ 2016, Математика, Экзаменационные тесты, Базовый уровень, Практикум, Лаппо Л.Д., Попов М.А.
Математика в формате ЕГЭ, Базовый уровень, Вычисления и преобразования, Клово А.Г., 2016
ЕГЭ 2016, Математика, Тренировочный вариант №1-19

Предыдущие статьи:

ЕГЭ 2016, Математика, Досрочный экзамен, Базовый уровень, Реальный вариант
ЕГЭ 2016, Математика, Досрочный экзамен, Тренировочный вариант №1-17, Профильный уровень
ЕГЭ, Математика, Ляшко М.А., Ляшко С.А., Муравина О.В., 2011
ЕГЭ 2016, Математика, 30 вариантов типовых тестовых заданий и 800 заданий части 2, Ященко И.В., Волчкевич М.А.

Источник

Варианты досрочного профильного ЕГЭ по математике 26.03.2016 можно скачать здесь.

Ответы на досрочный профильный ЕГЭ по математике скачать бесплатно можно здесь.

Реальные варианты КИМ ЕГЭ по математике 2016 досрочного периода, опубликованные на портале fipi.ru: профильный и базовый.

Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровня сложности с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1.

Баллы за задания с развернутым ответом:

2016	#13	#14	#15	#16	#17	#18	#19	Общ.балл
Балл	2	2	2	3	3	4	4	20

Admin

Источник