Досрочный вариант по математике ЕГЭ Профиль 28.03.2022 с видео-разбором
Скачать досрочный вариант в формате pdf.
Подробный видео-разбор первой и второй части:
Решение заданий варианта досрочного периода ЕГЭ 2022 от 28 марта 2022 по математике (профильный уровень). Досрочник КИМ. Досрочная волна 2022. Полный разбор. ГДЗ профиль решебник для 11 класса. Ответы с решением.

Задание 1.
Найдите корень уравнения log2(7 – x) = 5.
Задание 2.
В чемпионате по гимнастике участвуют 4 спортсменки из Аргентины, 7 из Бразилии, 5 из Германии и 4 из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Бразилии.
ИЛИ
В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Задание 3.
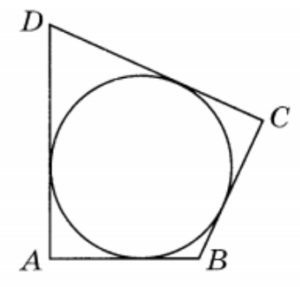
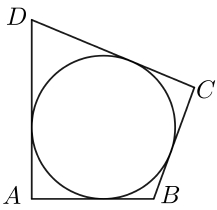
В четырёхугольник ABCD вписана окружность, AB = 8, BC = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.
ИЛИ
В четырехугольник ABCD, периметр которого равен 56, вписана окружность. Найдите AB, если CD = 13.
Задание 4.
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}
ИЛИ
Найдите значение выражения frac{5^{3,7}cdot 6^{4,7}}{30^{2,7}}
Задание 5.
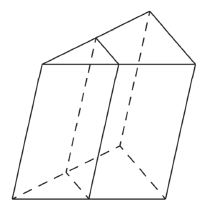
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.
Задание 6.
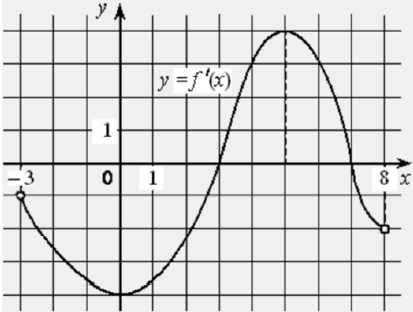
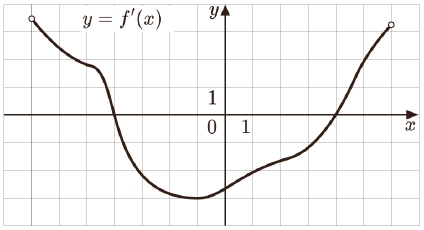
На рисунке изображён график функции y = f ′(x) − производной функции f(x), определённой на интервале (−3; 8). Найдите точку максимума функции f(x).
ИЛИ
На рисунке изображён график y = f ′(x) – производной функции f(x), определённой на интервале (−7; 6). Найдите точку минимума функции f(x).
Задание 7.
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле: f=f_{0}cdot frac{c+u}{c-v}, где f0 = 170 Гц – частота исходного сигнала, c – скорость распространения сигнала в среде (в м/с), а u = 2 м/с и v = 17 м/с – скорости приёмника и источника относительно среды. При какой скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.
ИЛИ
В розетку электросети подключены приборы, общее сопротивление которых составляет R1 = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 Ом и R2 Ом их общее сопротивление дается формулой R_{общ}=frac{R_{1}R_{2}}{R_{1}+R_{2}} (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.
Задание 8.
Имеется два сплава. Первый содержит 50% никеля, второй – 15% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
ИЛИ
Имеется два сплава. Первый сплав содержит 5 % меди, второй – 14 % меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Задание 9.
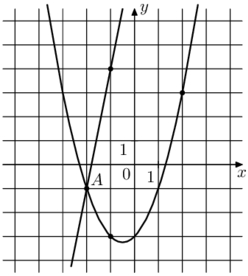
На рисунке изображён график функции f(x) = 5x + 9 и g(x) = ax2 + bx + c, которые пересекаются в точках А и В. Найдите абсциссу точки В.
ИЛИ
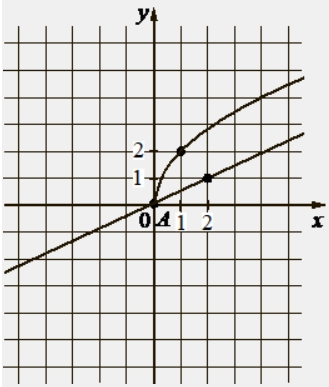
На рисунке изображены графики функций видов f(x) = a√x и g(x) = kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.
Задание 10.
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
ИЛИ
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Задание 11.
Найдите точку минимума функции y = frac{4}{3}xsqrt{x}-5x+4.
Задание 12.
а) Решите уравнение 4sin x + 4sin(x + π) = frac{5}{2}.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].
Задание 13.
Вне плоскости правильного треугольника ABC взята точка D так, что cos∠DAB = cos∠DAC = 0, 2.
а) Докажите, что прямые AD и BC перпендикулярны.
б) Найдите расстояние между прямыми AD и BC, если известно, что AB = 2.
Задание 14.
Решите неравенство frac{log_{2}^{}(32x)-1}{log_{2}^{2}x-log_{2}^{}x^{5}}ge -1
Задание 15.
15-го декабря планируется взять кредит размером 600 тыс. рублей в банке на 26 месяцев. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 25-й долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 691 тысяч рублей?
Задание 16.
В треугольник ABC вписана окружность, которая касается AB в точке P. Точка М середина стороны AB.
а) Докажите, что MP=frac{|BC-AC|}{2}.
б) Найдите углы треугольника ABC, если известно, что отрезок MP равен половине радиуса окружности вписанной в треугольник ABC, BC > AC, отрезки MC и MA равны.
Задание 17.
Найдите всe значения параметра a, при каждом их которых система
begin{cases} frac{xy^{2}-2xy-4y+8}{sqrt{4-y}}=0, \ y=ax. end{cases}
имеет ровно 3 различных решения.
Задание 18.
Каждое из четырех последовательных натуральных чисел поделили на его первую цифру и сложили все полученные числа, а полученную сумму обозначили за S.
а) Может ли S = 41frac{11}{24}?
б) Может ли S = 569frac{29}{72}?
в) Какое наибольшее целое значение может принимать S, если известно, что 4 исходных числа не меньше 400 и не больше 999?
Источники заданий варианта: школа Пифагора, Профиматика, беседы vk.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 19
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
29 марта 2022
В закладки
Обсудить
Жалоба
Вариант профильного уровня от группы «Профиматика» с подробным разбором.
28_03_22.pdf
- 29.03.2022
Собираем варианты реального досрочного ЕГЭ 2022 по математике профильного уровня. ЕГЭ проходил 28 марта 2022 года.
- Все реальные варианты ЕГЭ 2022 по математике
На сегодня 01.05.2022 уже есть несколько вариантов с досрочного. С разборами, решениями и ответами. Сопровождаем варианты видеоразборами. Плюс открытый вариант от ФИПИ (в конце).
- Реальные варианты ЕГЭ 2022 по всем предметам
Вариант ОТ ПИФАГОРА! Реальный преподаватель, кто сдал досрочный ЕГЭ 2022
Вариант досрочного ЕГЭ от Школково
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Вариант досрочного от Профиматики
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Вариант №3
Вариант №4
Вариант №5
Задания с 1 по 11
Задания с 12 по 17
Вариант №6
Вариант №7
Вариант №8
Вариант №9
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
ЕГЭ по математике 28.03.2022. Досрочная волна. Москва. Вариант 1
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Найдите корень уравнения
Ответ:
2
В соревнованиях участвуют 40 спортсменов, из которых 6 — из Румынии. Найдите вероятность того, что первым на соревнованиях будет выступать спортсмен из Румынии.
Ответ:
3
В четырёхугольник ABCD, периметр которого равен 54, вписана окружность, AB = 18. Найдите длину стороны CD.
Ответ:
4
Найдите значение выражения
Ответ:
5
Площадь боковой поверхности треугольной призмы равна 36. Через среднюю линию основания этой призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсечённой треугольной призмы.
Ответ:
6
7
8
Имеется два сплава. Первый сплав содержит 35% меди, второй — 5% меди. Масса первого сплава больше массы второго на 80 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Ответ:
9
10
Биатлонист четыре раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые два раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Ответ:
11
Найдите точку минимума функции
Ответ:
12
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
13
Дан правильный треугольник ABC. Точка D лежит вне плоскости ABC,
а) Докажите, что прямые AD и BC перпендикулярны.
б) Найдите расстояние между прямыми AD и BC, если AC = 6.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
15-го декабря планируется взять кредит в банке на 900 000 рублей на 13 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
− cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа с 1 по 12 месяц долг должен уменьшаться на одну и ту же сумму;
− 15-го числа 13 месяца долг должен быть погашен.
Сколько тысяч рублей составляет долг на 15 число 12 месяца, если всего было выплачено 1134 тысяч рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
Окружность вписана в треугольник ABC, P — точка касания окружности со стороной AB, точка M — середина AB.
а) Докажите, что
б) Найдите углы треугольника, если MC = MA, AC > BC,
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
Найдите все значения параметра a, при каждом из которых система
имеет три различных решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Каждое из четырёх подряд идущих натуральных чисел разделили на их первые цифры и результаты сложили в сумму S.
а) Может ли быть ?
б) Может ли быть ?
в) Найдите наибольшее целое S, если все четыре числа лежат в отрезке от 400 до 999 включительно.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
ФИПИ опубликовал досрочные варианты КИМ единого государственного экзамена 2022 года по математике профильного уровня.
→ скачать вариант
Примеры заданий:
2. На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 7 спортсменов из Германии и 9 спортсменов из США. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать спортсмен из Германии.
Ответ:
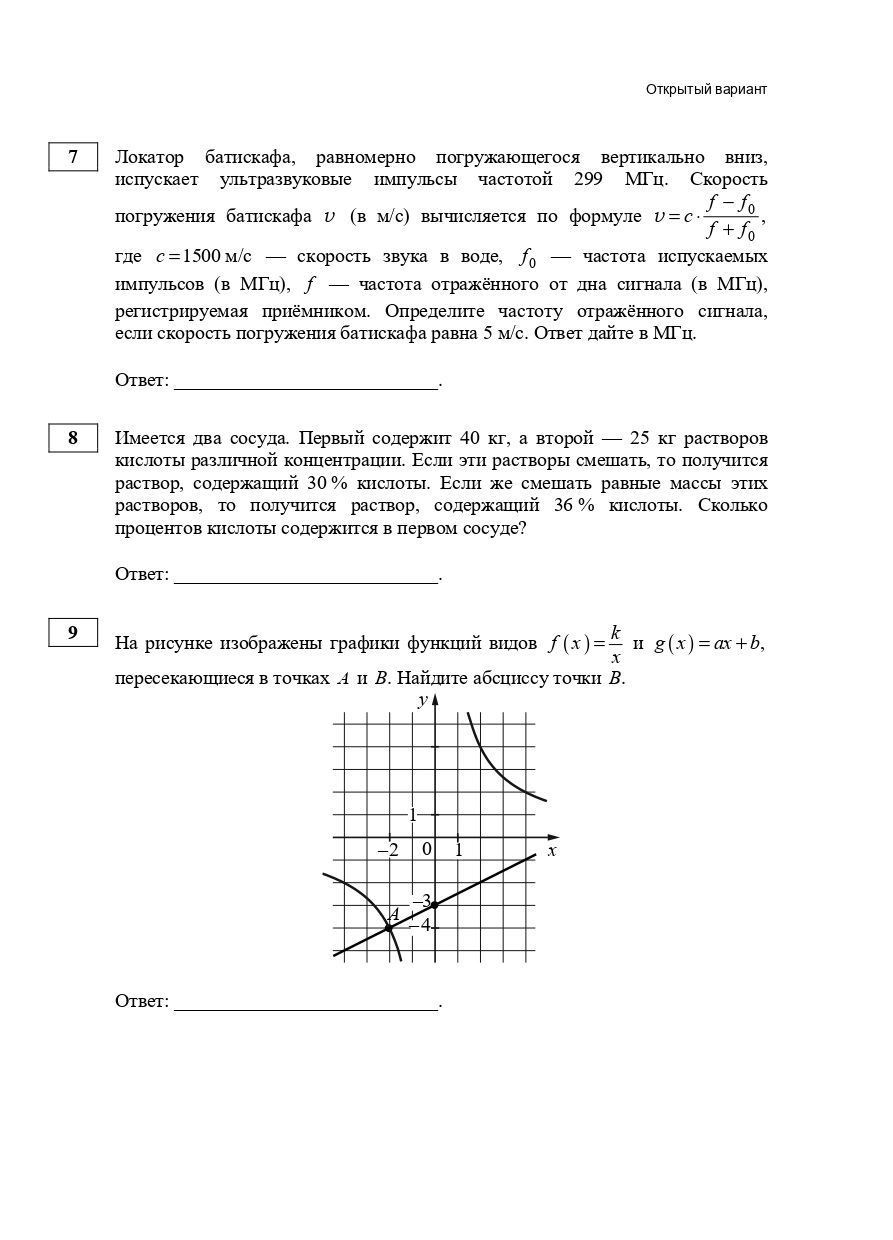
8. Имеется два сосуда. Первый содержит 40 кг, а второй — 25 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько процентов кислоты содержится в первом сосуде?
Ответ:
10. Имеется два сосуда. Первый содержит 40 кг, а второй — 25 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько процентов кислоты содержится в первом сосуде?
Ответ:
15. 15 декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 16 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг будет возрастать на r % по сравнению с концом предыдущего месяца (r — целое число); — со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга; — 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; — 15-го числа 15-го месяца долг должен быть равен 500 тысяч рублей; — к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что сумма всех платежей после полного погашения кредита будет составлять 1228 тысяч рублей.
18. Каждое из четырёх последовательных натуральных чисел, последние цифры которых не равны нулю, поделили на его последнюю цифру. Сумма получившихся чисел равна . S
а) Может ли S быть равной 5 16 6 ?
б) Может ли S быть равной 29 569126 ?
в) Найдите наибольшее целое значение S, если каждое из исходных чисел было трёхзначным.
Связанные страницы:
Курсы ЕГЭ Lancman School подготовили для вас подробную информацию о заданиях ЕГЭ по профильной математике досрочного периода 2022 года.
Приглашаем всех прокачать свои знания накануне ЕГЭ-2022 с лучшими преподавателями Lancman School. Поскольку выпускники 2022 года не сдавали ОГЭ в 2020-м и у них нет опыта сдачи государственных экзаменов, пройтись по всем сложным темам ЕГЭ будет очень полезно. Наши марафоны рассчитаны на 8 занятий (по 90 минут каждое). Старт майских интенсивов — 2 мая. Все свои вопросы смело пишите сюда.
Подробно с программами можно ознакомиться по ссылке. Накопленная статистика показывает, что все ученики, прошедшие курс наших майских интенсивов, прибавляют за месяц в среднем 15-20 первичных баллов.
Разбор досрочного ЕГЭ по профильной математике 2022 года с сайта ФИПИ
Источник: ФИПИ
Если материал показался интересным, подписывайтесь на обновления нашего блога. Мы знаем о поступлении в вузы всё (и даже больше). Кнопку подписки вы найдёте прямо под постом.