Древо фано егэ информатика

Привет! Сегодня узнаем, как решать 4 задание из ЕГЭ по информатике нового формата 2021.

Четвёртое задание из ЕГЭ по информатике раскрывает тему кодирование информации. Одним из центральных приёмов при решении задач подобного типа является построение дерева Фано. Рассмотрим на примерах этот метод.

Задача (стандартная)

По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу.

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование

Решение:

Т.к. код букв должен удовлетворять условию Фано (т.е. однозначно декодироваться), то
расположим буквы, которые уже имеют код (A, B, C), на Дереве Фано.

Дерево Фано для двоичного кодирования начинается с двух направлений, которые означают 0(ноль) и 1(единицу) (цифры двоичного кодирования).

От каждого направления можно также рисовать только два направления: 0(ноль) и 1(единицу) и т.д. Для удобства будем рисовать 1(единицу) только вправо, а 0(ноль) только влево.

Получается структура похожая на дерево!

В конце каждой ветки можно располагать букву, которую мы хотим закодировать, но если мы расположили букву, от этой ветки больше нельзя делать новых ответвлений.

Такой подход позволяет однозначно декодировать сообщение, состоящее из этих букв.

Буква C заблокировала левую ветку, поэтому будем работать с правой частью нашего дерева.

Если мы расположим какую-нибудь букву на оставшуюся ветку (100), то эта ветка заблокируется, и нам некуда будет писать остальные 2 буквы. Поэтому продолжаем ветку (100) дальше.

Теперь свободно уже две ветки, а нам нужно закодировать ещё три буквы. Поэтому должны ещё раз продолжить дерево от какой-нибудь ветки.

Но уже видно, что букве F будет правильно присвоить код 1000, т.к. нам в условии сказано, что код буквы F должен соответствовать наименьшему возможному двоичному числу. Как расположить буквы D и E в данной задаче не принципиально.

Ответ: 1000.

Ещё один важный тип задания 4 из ЕГЭ по информатике нового формата 2021.

Задача (стандартная)

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, С, Ц. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 00, К — 010, Л — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова АБСЦИССА?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

Решение:

Коды букв должны удовлетворять условию Фано. Некоторые буквы уже имеют заданные коды (Б, К, Л). Нам нужно, чтобы слово АБСЦИССА имело как можно меньше двоичных знаков. Заметим, что буква C встречается три раза, а буква A два раза, значит, этим буквам стараемся присвоить как можно меньшую длину!

Отметим на дереве Фано уже известные буквы (Б, К, Л).

У нас осталось 4 (четыре) буквы, а свободных веток 3(три), поэтому мы должны продолжить дерево. но какую ветку продолжить ?

1 вариант

Если продолжить линию 1-0, то получится такая картина :

Теперь получились 4(четыре) свободные ветки равной длины (3(трём) двоичным символам). Т.к. ветки равной длины, то не важно на какую ветку какую букву расположим.

Посчитаем общую длину слова АБСЦИССА.

3 + 2 + 3 + 3 + 3 + 3 + 3 + 3 = 23.

2 вариант

С мы присваиваем 1-0, т.к. это буква повторяется в сообщении самое большое количество раз, значит, ей присваиваем самый маленький код, чтобы всё сообщение имело наименьшую длину.

Из этих же соображений букве А присваиваем код из трёх двоичных символов 0-1-1.

Подсчитаем общее количество символов в сообщении.

3 + 2 + 2 + 4 + 4 + 2 + 2 + 3 = 22

Длина получилась меньше, чем в первом варианте. Других вариантов нет, поэтому ответ будет 22.

Ответ: 22.

Задача (не сложная)

Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется неравномерный (по длине) код: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в восьмеричный вид.

Решение:

В этой задаче ничего не сказано про условие Фано. Здесь уже все буквы закодированы, осталось написать сам код.

Задача сводится к переводу из двоичной системы в восьмеричную систему. На эту тему был урок на моём сайте.

Ответ: 151646.

На этом всё! Увидимся на следующих занятиях по подготовке к ЕГЭ по информатике.

Всего: 97    1–20 | 21–40 | 41–60 | 61–80 | 81–97

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 97    1–20 | 21–40 | 41–60 | 61–80 | 81–97

Представление чисел в компьютере

Формат с фиксированной запятой

В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно

1 ⋅ 2⁷ + 1 ⋅ 2⁶ + 1 ⋅ 2⁵ + 1 ⋅ 2⁴ + 1 ⋅ 2³ + 1 ⋅ 2² + 1 ⋅ 2¹ + 1 ⋅ 2⁰ = 255₁₀.

Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.

Для п-разрядного представления диапазон будет составлять от 0 до 2ⁿ – 1.

Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.

Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2ⁿ − |А|.

Алгоритм получения дополнительного кода отрицательного числа:

1. Записать прямой код числа в п двоичных разрядах.

2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)

3. Прибавить единицу к полученному обратному коду.

Например, получим дополнительный код числа –2014₁₀ для шестнадцатиразрядного представления:

Прямой код	Двоичный код числа 201410 со знаковым разрядом	1000011111011110
Обратный код	Инвертирование (исключая знаковый разряд)	1111100000100001
	Прибавление единицы	1111100000100001 + 0000000000000001
Дополнительный код		1111100000100010

При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.

Например:

1) Найдем разность 13₁₀ – 12₁₀ для восьмибитного представления. Представим заданные числа в двоичной системе счисления:

13₁₀ = 1101₂ и 12₁₀ = 1100₂.

Запишем прямой, обратный и дополнительный коды для числа –12₁₀ и прямой код для числа 13₁₀ в восьми битах:

	1310	–1210
Прямой код	00001101	10001100
Обратный код	—	11110011
Дополнительный код	—	11110100

Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):

Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.

2) Найдем разность 8₁₀ – 13₁₀ для восьмибитного представления.

Запишем прямой, обратный и дополнительный коды для числа –13₁₀ и прямой код для числа 8₁₀ в восьми битах:

	810	–1310
Прямой код	00001000	10001101
Обратный код	—	11110010
Дополнительный код	—	11110011

Вычитание заменим сложением:

В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:

11111011 – 00000001 = 11111010.

Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –5₁₀.

Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2^n–1, а максимальное: |А| = 2^n–1 или А = –2^n–1 – 1.

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно

А = –2³¹ = –2147483648₁₀.

Максимальное положительное число равно

А = 2³¹ – 1 = 2147483647₁₀.

Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.

Формат с плавающей запятой

Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.

Число в экспоненциальном формате представляется в таком виде:

$A=m·q^n$,

где $m$ — мантисса числа (правильная отличная от нуля дробь);

$q$ — основание системы счисления;

$n$ — порядок числа.

Например, десятичное число 2674,381 в экспоненциальной форме запишется так:

2674,381 = 0,2674381 ⋅ 10⁴.

Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.

Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.

Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 1111111₂ = 127₁₀. Так как числа представляются в двоичной системе счисления, то

$q^n = 2^{127}≈ 1.7 · 10^{38}$.

Аналогично, максимальное значение мантиссы равно

$m = 2^{23} — 1 ≈ 2^{23} = 2^{(10 · 2.3)} ≈ 1000^{2.3} = 10^{(3 · 2.3)} ≈ 10^7$.

Таким образом, диапазон чисел обычной точности составляет $±1.7 · 10^{38}$.

Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы

Соответствие между набором символов и набором числовых значений называется кодировкой символа. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение.

Присвоенный каждому символу конкретный числовой код фиксируется в кодовых таблицах. Одному и тому же символу в разных кодовых таблицах могут соответствовать разные числовые коды. Необходимые перекодировки текста обычно выполняют специальные программы-конверторы, встроенные в большинство приложений.

Как правило, для хранения кода символа используется один байт (восемь битов), поэтому коды символов могут принимать значение от 0 до 255. Такие кодировки называют однобайтными. Они позволяют использовать 256 символов ( N = 2^I = 2⁸ = 256 ). Таблица однобайтных кодов символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Первая часть таблицы ASCII-кодов (от 0 до 127) одинакова для всех IBM-PC совместимых компьютеров и содержит:

• коды управляющих символов;
• коды цифр, арифметических операций, знаков препинания;
• некоторые специальные символы;
• коды больших и маленьких латинских букв.

Вторая часть таблицы (коды от 128 до 255) бывает различной в различных компьютерах. Она содержит коды букв национального алфавита, коды некоторых математических символов, коды символов псевдографики. Для русских букв в настоящее время используется пять различных кодовых таблиц: КОИ-8, СР1251, СР866, Мас, ISO.

В последнее время широкое распространение получил новый международный стандарт Unicode. В нем отводится по два байта (16 битов) для кодирования каждого символа, поэтому с его помощью можно закодировать 65536 различных символов ( N = 2¹⁶ = 65536 ). Коды символов могут принимать значение от 0 до 65535.

Примеры решения задач

Пример. С помощью кодировки Unicode закодирована следующая фраза:

Я хочу поступить в университет!

Оценить информационный объем этой фразы.

Решение. В данной фразе содержится 31 символ (включая пробелы и знак препинания). Поскольку в кодировке Unicode каждому символу отводится 2 байта памяти, для всей фразы понадобится 31 ⋅ 2 = 62 байта или 31 ⋅ 2 ⋅ 8 = 496 битов.

Ответ: 32 байта или 496 битов.

ЕГЭ по информатике 2022 — Задание 4 (Кодирование и декодирование информации)

В этом уроке мы поговорим о задании 4 из ЕГЭ по информатике 2022.

Задание 4 включает в себя понятие кодирование и декодирование информации.

Приступим к тренировочным заданиям из ЕГЭ по информатике 2022.

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е. решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 00, 01, 100, 110. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

Используем приём Дерево Фано. Расставим на этом дереве те буквы, для которых уже известны кодовые слова.

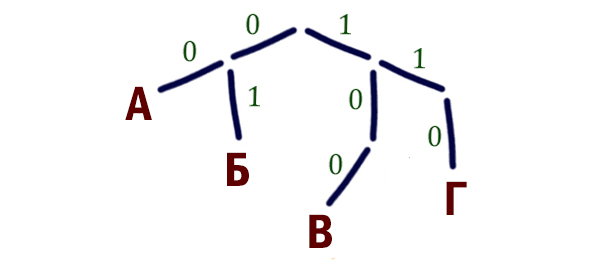
Дерево рисуется обычно сверху вниз. В начале от дерева рисуются две ветки: ветка 0 и ветка 1. От каждой ветки можно нарисовать ещё две ветки, так же 0 и 1, и т. д.

Для удобства ветки с 1 будем направлять вправо, а ветки с 0 будем направлять влево.

В конце каждой ветки можно размещать буквы, но если мы разместили букву, то эта ветка блокируется, и от этой ветки больше нельзя делать новые ответвления.

Нам осталось закодировать (расположить на дереве) две буквы: Д и Е.

Мы можем нарастить ещё две ветки от точки 1-1. Тогда получится код 111. И от точки 1-0. Тогда получится код 101.

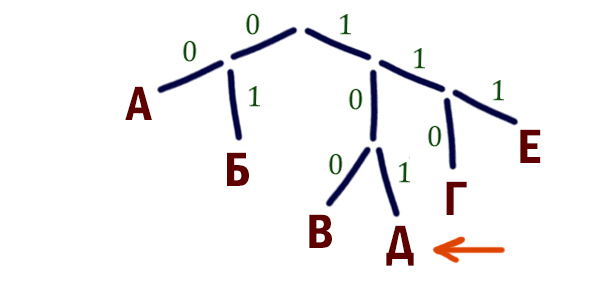
Для буквы Д нужно выбрать код с наименьшим числовым значением. Значит, для буквы Д выбираем код 101, а для буквы Е выбираем код 111.

Закрепим приём дерево Фано на ещё одной примерной задаче из ЕГЭ по информатике 2022.

Для кодирования некоторой последовательности, состоящей из букв Н, О, П, Р, С, Т, У, Ф решили использовать неравномерный двоичный код, удовлетворяющий условию, что ни одно кодовое слово не является началом другого кодового слова. Для букв Н, О, П, Р, С, Т использовали соответственно кодовые слова 10, 110, 010, 0110, 111, 0111. Укажите кратчайшее возможное кодовое слово для буквы У, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Здесь код так же должен удовлетворять Условию Фано, т.к. сказано, что ни одно кодовое слово не является началом другого кодового слова .

Значит, можем воспользоваться Деревом Фано . Расположим на Дереве Фано буквы, для которых уже известны кодовые слова.

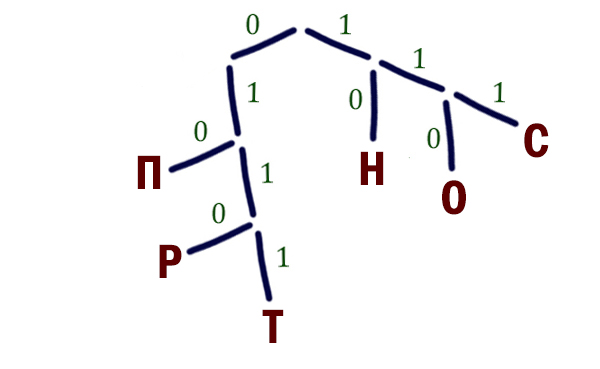
Нам нужно закодировать ещё две буквы: У, Ф. У нас единственная возможность осталась прорастить ветку от точки 0. От этой точки проращиваем ветку 0 и от этой ветки проращиваем ещё две ветки 0 и 1.

Букву У размещаем на позиции 000, потому что для этой буквы нужно выбрать код с наименьшим числовым значением.

Ещё одна примерная задача из ЕГЭ по информатике 2022 является частым гостем в различных тренировочных вариантах.

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Д, Л, Е, И, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 110, Б – 01, И – 000. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ?

Расставим на дереве Фано буквы, для которых известны коды.

Нам осталось расположить 4 буквы: Д, Л, E, Н.

Буква Е встречается три раза в слове ДЕЛЕНИЕ, значит, ей нужно постараться присвоить самый короткий код. По дереву видно, что можно букве Е присвоить код 10.

Буквы Д, Л, Н встречаются в слове ДЕЛЕНИЕ 1 раз. Одну букву можно разместить на позицию 111. Так же можно продлить ветку из точки 00, а затем от позиции 001 сделать два отростка. У нас получатся ещё два свободных места: 0011 и 0010.

Можно оставшиеся буквы разместить следующим образом:

Подсчитаем какое количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ.

3+2+4+2+4+3+2=20
Ответ: 20

Далее решим непростую задачу из тренировочных вариантов ЕГЭ по информатике 2022. Похожая задача была в сборнике С. С. Крылова в 2021 году.

По каналу связи передаются сообщения, содержащие только четыре буквы: М, Н, Р, Т; для передачи используется двоичный код, допускающий однозначное декодирование.

Для букв М, Н, Р используются такие кодовые слова: М: 00011, Н: 1001, Р: 01100.

Укажите кратчайшее кодовое слово для буквы Т, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Нужно, чтобы код декодировался однозначно. Чтобы код декодировался однозначно, можно использовать условие Фано. Мы видим, что в уже известных кода не нарушается условие Фано. Узнаем код для буквы Т по дереву Фано. Отметим известные буквы.

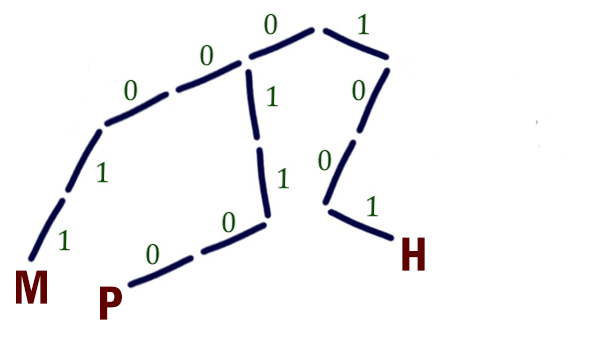
Куда разместить букву Т? Чтобы кодовое слово было кратчайшее, разместим букву Т на позицию 11.

Сложность этой задачи заключается в том, что явно не указано, что нужно использовать условие Фано. Так же однозначное декодирование будет, если используется обратное условие Фано.

Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.

Т. е. сообщения нужно такие раскодировать справа налево. Здесь про то, как будут раскодировать сообщения, ничего не сказано, поэтому мы должны проверить, какой код получится для буквы Т, если здесь используется обратное условие Фано.

Кодовое слово 0 мы использовать не можем, потому что 0 — это окончание кодового слова буквы Р. Кодовое слово 1 — это окончание кодовых слов букв М и Н. Кодовое слово 00 — это окончание кодового слова буквы Р. А вот 10 подходит для буквы Т.

Получилась следующая ситуация. Если кодовые слова будут удовлетворяют условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 11 с минимальным числовым значением. Если кодовые слова будут удовлетворяют обратному условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 10 с минимальным числовым значением.

И в том и в другом случае будет однозначное декодирование. Но мы выбираем тот случай, когда кодовое слово будет наименьшим числовым значением. Таким образом, в ответе напишем 10.

Разберём ещё один нюанс в подобных задах из ЕГЭ по информатике.

Задача (Ещё раз про однозначное декодирование)

По каналу связи передаются сообщения, содержащие только четыре буквы: М, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, М используются такие кодовые слова: Т: 111, О: 0, М: 100. Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Здесь условие похоже на то, которое было в предыдущей задаче. Но обратное условие Фано здесь не применимо, т.к. код для буквы О является окончанием для кода буквы М.

Значит, у нас остаётся единственный инструмент, чтобы сообщения декодировались однозначно — это условие Фано. Теперь задачу решаем как обычно по дереву Фано.

Выбираем из двух вариантов: 110 и 101. Но останавливаемся на 101, т.к. это кодовое слово с наименьшим числовым значением.

Решим задачу, которая часто встречается в бумажных сборниках по подготовке к ЕГЭ по информатике.

Задача (код не удовлетворяет условию Фано)

По каналу связи передаются шифрованные сообщения, содержащие только пять латинских букв: A, B, С, D, E. Для передачи используется неравномерный двоичный код. Для некоторых букв известны кодовые слова: A: 01, B: 10, C: 11, D: 000.

Укажите самое короткое кодовое слово для буквы E, при котором код не будет удовлетворять условию Фано, при этом в записи самого этого слова должно использоваться более одного символа, а само слово не должно совпадать ни с одним из используемых слов для букв с известными кодами.

Если таких слов несколько, то укажите слово с наименьшим числовым значением.

Здесь код не должен однозначно декодироваться.

Подходит код 00, т.к. длина этого кодового слова больше чем 1 символ. Этот код не совпадает ни с одним кодом для известных букв. Этот код нарушает принцип условия Фано, видно, что он является началом кодового слова буквы D. И этот код имеет самое маленькое числовое значение.

В 4 задании из ЕГЭ по информатике 2022 не обязательно может попасться задача, связанная с условием Фано. Может просто быть задача на кодирование и декодирование информации.

Для кодирования букв X, К, Л, О, Д решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ХОЛОДОК таким способом и результат запишите шестнадцатеричным кодом.

Распишем, как кодируются все буквы в двоичной системе. Ноль и один кодируются одним разрядом, поэтому к ним слева приписывается ноль, как написано в условии.

Буква	Десятичное Представление	Двоичное Представление
Х		00
К	1	01
Л	2	10
О	3	11
Д	4	100

Выписываем слово ХОЛОДОК и под ним кодовые слова букв.

Чтобы перевести из двоичной системы число в шестнадцатиричную систему, мы должны двоичные цифры разбить по четвёркам, начиная с правого края. Каждая четвёрка превращается в цифру в шестандцатиричной системе. Таблицу перевода четвёрок двоичных цифр в шестнадцатиричную систему можно посмотреть в этой статье.

Т.к. ЕГЭ по информатике сдаётся в компьютерной форме, то можно воспользоваться стандартным калькулятором в режиме программист.

На этом всё! Пусть Вам повезёт на ЕГЭ по информатике 2022.

Источник

ЕГЭ по информатике 2021 — Задание 4 (Условие Фано)

Привет! Сегодня узнаем, как решать 4 задание из ЕГЭ по информатике нового формата 2021.

Четвёртое задание из ЕГЭ по информатике раскрывает тему кодирование информации. Одним из центральных приёмов при решении задач подобного типа является построение дерева Фано. Рассмотрим на примерах этот метод.

По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу.

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование

Т.к. код букв должен удовлетворять условию Фано (т.е. однозначно декодироваться), то расположим буквы, которые уже имеют код (A, B, C), на Дереве Фано.

Дерево Фано для двоичного кодирования начинается с двух направлений, которые означают 0(ноль) и 1(единицу) (цифры двоичного кодирования).

От каждого направления можно также рисовать только два направления: 0(ноль) и 1(единицу) и т.д. Для удобства будем рисовать 1(единицу) только вправо, а 0(ноль) только влево.

Получается структура похожая на дерево!

В конце каждой ветки можно располагать букву, которую мы хотим закодировать, но если мы расположили букву, от этой ветки больше нельзя делать новых ответвлений.

Такой подход позволяет однозначно декодировать сообщение, состоящее из этих букв.

Буква C заблокировала левую ветку, поэтому будем работать с правой частью нашего дерева.

Если мы расположим какую-нибудь букву на оставшуюся ветку (100), то эта ветка заблокируется, и нам некуда будет писать остальные 2 буквы. Поэтому продолжаем ветку (100) дальше.

Теперь свободно уже две ветки, а нам нужно закодировать ещё три буквы. Поэтому должны ещё раз продолжить дерево от какой-нибудь ветки.

Но уже видно, что букве F будет правильно присвоить код 1000, т.к. нам в условии сказано, что код буквы F должен соответствовать наименьшему возможному двоичному числу. Как расположить буквы D и E в данной задаче не принципиально.

Ещё один важный тип задания 4 из ЕГЭ по информатике нового формата 2021.

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, С, Ц. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 00, К — 010, Л — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова АБСЦИССА?

Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.

Коды букв должны удовлетворять условию Фано. Некоторые буквы уже имеют заданные коды (Б, К, Л). Нам нужно, чтобы слово АБСЦИССА имело как можно меньше двоичных знаков. Заметим, что буква C встречается три раза, а буква A два раза, значит, этим буквам стараемся присвоить как можно меньшую длину!

Отметим на дереве Фано уже известные буквы (Б, К, Л).

У нас осталось 4 (четыре) буквы, а свободных веток 3(три), поэтому мы должны продолжить дерево. но какую ветку продолжить ?

Если продолжить линию 1-0, то получится такая картина :

Теперь получились 4(четыре) свободные ветки равной длины (3(трём) двоичным символам). Т.к. ветки равной длины, то не важно на какую ветку какую букву расположим.

Посчитаем общую длину слова АБСЦИССА.

3 + 2 + 3 + 3 + 3 + 3 + 3 + 3 = 23.

Продлим линию 1-1-0 (можно и 0-1-1, не принципиально, т.к. эти ветки имеют одинаковую длину.), то получится:

С мы присваиваем 1-0, т.к. это буква повторяется в сообщении самое большое количество раз, значит, ей присваиваем самый маленький код, чтобы всё сообщение имело наименьшую длину.

Из этих же соображений букве А присваиваем код из трёх двоичных символов 0-1-1.

Подсчитаем общее количество символов в сообщении.

3 + 2 + 2 + 4 + 4 + 2 + 2 + 3 = 22

Длина получилась меньше, чем в первом варианте. Других вариантов нет, поэтому ответ будет 22.

Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется неравномерный (по длине) код: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в восьмеричный вид.

В этой задаче ничего не сказано про условие Фано. Здесь уже все буквы закодированы, осталось написать сам код.

Задача сводится к переводу из двоичной системы в восьмеричную систему. На эту тему был урок на моём сайте.

На этом всё! Увидимся на следующих занятиях по подготовке к ЕГЭ по информатике.

Источник