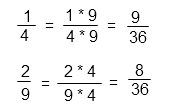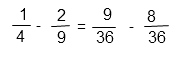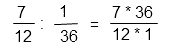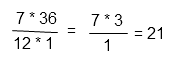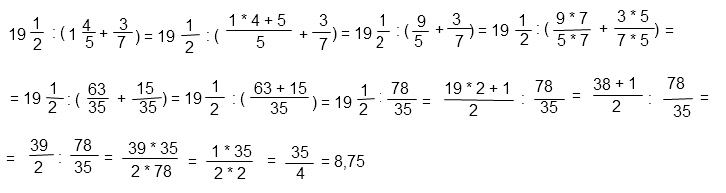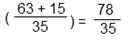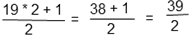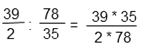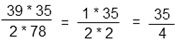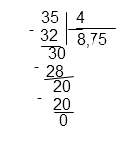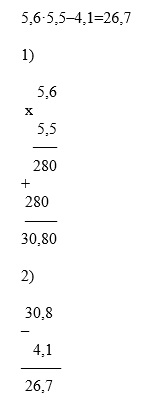6.1. Округление с недостатком (Скачать)
6.2. Округление с избытком (Скачать)
6.3. Разные задачи (Скачать)
7.1. Линейные, квадратные, кубические уравнения (Скачать)
7.2. Рациональные уравнения (Скачать)
7.3. Иррациональные уравнения (Скачать)
7.4. Показательные уравнения (Скачать)
7.5. Логарифмические уравнения (Скачать)
7.6. Тригонометрические уравнения (Скачать)
8. Многоугольники (Скачать)
10.1. Классическое определение вероятности (Скачать)
10.2. Теоремы о вероятностях событий (Скачать)
12.1. Подбор комплекта или комбинации (Скачать)
12.2. Выбор варианта из двух возможных (Скачать)
12.3. Выбор варианта из трех возможных (Скачать)
12.4. Выборварианта из четырех возможных (Скачать)
13.1. Куб (Скачать)
13.2. Прямоугольный параллелепипед (Скачать)
13.3. Призма (Скачать)
13.4. Пирамида (Скачать)
13.5. Элементы составных многогранников (Скачать)
13.6. Площадьповерзности составного многогранника (Скачать)
13.7. Объем составного многогранника (Скачать)
13.8. Комбинации тел (Скачать)
13.9. Цилиндр (Скачать)
13.10. Конус (Скачать)
13.11. Шар (Скачать)
14. Скорость изменения величин (Скачать)
15.1. Треугольник (Скачать)
15.2. Прямоугольник: длины и площади (Скачать)
15.3. Параллелограмм: длины и площади (Скачать)
15.4. Ромб: длины и площади (Скачать)
15.5. Трапеция: длины и площади (Скачать)
15.6. Произвольный четырехугольник (Скачать)
15.7. Задачина квадратной решетке (Скачать)
15.8. Круг и его элементы (Скачать)
15.9. Векторы (Скачать)
15.10. Координатная плоскость (Скачать)
15.11. Прямоугольный треугольник: вычисление углов (Скачать)
15.12. Прямоугольный треугольник: вычисление внешних углов (Скачать)
15.13. Прямоугольный треугольник:вычисление элементов (Скачать)
15.14. Равнобедренный треугольник: вычисление углов (Скачать)
15.15. Равнобедренный треугольник: вычисление элементов (Скачать)
15.16. Треугольники общего вида (Скачать)
15.17. Параллелограмм: углы (Скачать)
15.18. Ромб: углы (Скачать)
15.19. Трапеция: углы (Скачать)
15.20. Центральные и вписанные углы (Скачать)
15.21. Окружность описанная около треугольника (Скачать)
15.22. Окружность описанная около четырехугольника (Скачать)
15.23. Многоугольник (Скачать)
16.1. Прямоугольный параллелепипед (Скачать)
16.2. Призма (Скачать)
16.3. Пирамида (Скачать)
16.4. Цилиндр (Скачать)
16.5. Конус (Скачать)
16.6. Куб (Скачать)
17. Числовая ось, числовые промежутки (Скачать)
18. Анализ утверждений (Скачать)
19. Цифровая запись числа (Скачать)
20. Задачина смекалку (Скачать)
Разное
Найдите значения выражений
| 1 | frac{7}{2} cdot frac{5}{4} — frac{3}{8} | Смотреть видеоразбор >> |
| 2 | frac{22}{3}:frac{2}{15} cdot frac{6}{5} | Смотреть видеоразбор >> |
| 3 | (frac{9}{14}-frac{10}{21}) cdot 42 | Смотреть видеоразбор >> |
| 4 | (frac{11}{10}+frac{11}{13}):frac{22}{39} | Смотреть видеоразбор >> |
| 5 | (frac{11}{10}-frac{13}{15}):frac{7}{60} | Смотреть видеоразбор >> |
| 6 | frac{19}{6}:(frac{5}{6}+frac{3}{4}) | Смотреть видеоразбор >> |
| 7 | frac{0,9+0,7}{3,2} | Смотреть видеоразбор >> |
| 8 | frac{3,2-5,7}{2,5} | Смотреть видеоразбор >> |
| 9 | frac{4,7-1,4}{7,5} | Смотреть видеоразбор >> |
| 10 | frac{2,4}{1,2-0,4} | Смотреть видеоразбор >> |
| 11 | frac{5,6}{1,9-7,5} | Смотреть видеоразбор >> |
| 12 | (1,7+2,8) cdot 4,8 | Смотреть видеоразбор >> |
| 13 | 4,1 cdot 7,7 + 0,86 | Смотреть видеоразбор >> |
| 14 | 1,2 : 0,6 cdot 1,5 | Смотреть видеоразбор >> |
| 15 | 1 + frac{1}{7} cdot 0,77 | Смотреть видеоразбор >> |
| 16 | frac{5}{3}:frac{2}{7}-frac{11}{6} | Смотреть видеоразбор >> |
| 17 | frac{5}{6}+frac{5}{2} cdot frac{2}{3} | Смотреть видеоразбор >> |
| 18 | (frac{5}{12}-frac{3}{20}) cdot frac{45}{2} | Смотреть видеоразбор >> |
| 19 | (frac{17}{35}+frac{3}{8}):frac{5}{28} | Смотреть видеоразбор >> |
| 20 | (frac{11}{5}-frac{13}{6}):frac{1}{90} | Смотреть видеоразбор >> |
| 21 | frac{12}{7}:(frac{6}{7}-frac{3}{4}) | Смотреть видеоразбор >> |
| 22 | frac{7,9+3,4}{0,2} | Смотреть видеоразбор >> |
| 23 | frac{2,6-8,4}{2,5} | Смотреть видеоразбор >> |
| 24 | frac{2,6-2,6}{7,8} | Смотреть видеоразбор >> |
| 25 | frac{5,6}{1,7-1,6} | Смотреть видеоразбор >> |
| 26 | frac{9,2}{0,5-2,8} | Смотреть видеоразбор >> |
| 27 | (1,7+2,8) cdot 24 | Смотреть видеоразбор >> |
| 28 | 5,6 cdot 5,5 — 4,1 | Смотреть видеоразбор >> |
| 29 | frac{1}{4} cdot 0,48 + 1 | Смотреть видеоразбор >> |
| 30 | frac{1}{frac{1}{5}-frac{1}{30}} | Смотреть видеоразбор >> |
| 31 | frac{14}{9} cdot frac{3}{2}:frac{7}{6} | Смотреть видеоразбор >> |
| 32 | frac{5}{4}+frac{7}{6}:frac{2}{3} | Смотреть видеоразбор >> |
| 33 | (frac{11}{9}+frac{4}{9}):frac{5}{36} | Смотреть видеоразбор >> |
| 34 | (frac{5}{7}-frac{3}{7}):frac{2}{21} | Смотреть видеоразбор >> |
| 35 | (frac{8}{25}-frac{13}{38}):frac{6}{19} | Смотреть видеоразбор >> |
| 36 | 3:(frac{6}{7}-frac{3}{4}) | Смотреть видеоразбор >> |
| 37 | frac{6,9+4,1}{0,2} | Смотреть видеоразбор >> |
| 38 | frac{0,5-1,5}{0,8} | Смотреть видеоразбор >> |
| 39 | frac{3,8}{2,6+1,2} | Смотреть видеоразбор >> |
| 40 | frac{2,6}{3,1-0,6} | Смотреть видеоразбор >> |
| 41 | frac{6,9}{3,2-5,7} | Смотреть видеоразбор >> |
| 42 | (6,9-3,4) cdot 8,4 | Смотреть видеоразбор >> |
| 43 | 5,4 cdot 1,9 — 2,15 | Смотреть видеоразбор >> |
| 44 | frac{1}{6} cdot 9,6 — 1 | Смотреть видеоразбор >> |
| 45 | frac{1}{frac{1}{2}+frac{1}{3}} | Смотреть видеоразбор >> |
| 46 | frac{18}{7} cdot frac{14}{3} : frac{4}{5} | Смотреть видеоразбор >> |
| 47 | (frac{5}{6}+frac{7}{15}) cdot frac{30}{13} | Смотреть видеоразбор >> |
| 48 | (frac{3}{22}+frac{2}{11}):frac{5}{33} | Смотреть видеоразбор >> |
| 49 | (frac{13}{6}-frac{11}{6}):frac{1}{90} | Смотреть видеоразбор >> |
| 50 | frac{13}{7}:(frac{1}{3}+frac{2}{7}) | Смотреть видеоразбор >> |
| 51 | frac{1,8+1,9}{3,7} | Смотреть видеоразбор >> |
| 52 | frac{7,5+3,5}{2,5} | Смотреть видеоразбор >> |
| 53 | frac{7,3-2,5}{1,2} | Смотреть видеоразбор >> |
| 54 | frac{9,4}{2,1+2,6} | Смотреть видеоразбор >> |
| 55 | frac{4,4}{5,8-5,3} | Смотреть видеоразбор >> |
| 56 | frac{0,6}{1,7-2,9} | Смотреть видеоразбор >> |
| 57 | (5,3-2,8)cdot38 | Смотреть видеоразбор >> |
| 58 | 1,32:1,2-0,8 | Смотреть видеоразбор >> |
| 59 | 3-frac{1}{4}cdot5,6 | Смотреть видеоразбор >> |
| 60 | frac{1}{frac{1}{4}-frac{1}{5}} | Смотреть видеоразбор >> |
| 61 | frac{15}{2}:frac{5}{21}cdotfrac{4}{3} | Смотреть видеоразбор >> |
| 62 | (frac{4}{15}+frac{1}{20})cdot60 | Смотреть видеоразбор >> |
| 63 | (frac{13}{21}+frac{3}{14}):frac{10}{27} | Смотреть видеоразбор >> |
| 64 | (frac{17}{8}-frac{1}{16}):frac{11}{48} | Смотреть видеоразбор >> |
| 65 | 13:(frac{1}{3}+frac{2}{7}) | Смотреть видеоразбор >> |
| 66 | frac{4,2+3,3}{0,3} | Смотреть видеоразбор >> |
| 67 | frac{2,7+5,8}{6,8} | Смотреть видеоразбор >> |
| 68 | (frac{6,8-4,7}{1,4}) | Смотреть видеоразбор >> |
| 69 | frac{5,6}{8,5-2,9} | Смотреть видеоразбор >> |
| 70 | frac{2,1}{6,6-2,4} | Смотреть видеоразбор >> |
| 71 | frac{7,7}{3,7-8,7} | Смотреть видеоразбор >> |
| 72 | 3,5cdot6,6+1,6 | Смотреть видеоразбор >> |
| 73 | 2,7+1,32:1,2 | Смотреть видеоразбор >> |
| 74 | 0,15:frac{3}{7}+1 | Смотреть видеоразбор >> |
| 75 | frac{1}{frac{1}{10}-frac{1}{15}} | Смотреть видеоразбор >> |
Вариант 1 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значения выражения:
8. Найдите значение выражения
9. Найдите значение выражения
10. Найдите значение выражения .
Вариант 2 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения .
3. Найдите значение выражения
4. Найдите значение выражения .
5. Найдите значение выражения
6. Найдите значение выражения
7. Найдите значение выражения .
8. Найдите значение выражения .
9. Найдите значение выражения .
10. Найдите значение выражения:
Вариант 3 1. Вычисления. Действия с дробями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения .
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения 10.Найдите значение выражения .
Вариант 4 1. Вычисления. Действия с дробями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения .
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения 10. Найдите значение выражения .
Вариант 5 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения
10. Найдите значение выражения
Вариант 6 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения .
10. Вычислите
Вариант 7 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения .
7. Найдите значение выражения .
8. Найдите значение выражения (3,9 − 2,4) · 8,2.
9. Найдите значение выражения
10. Найдите значение выражения .
Вариант 8 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения .
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения .
9. Найдите значение выражения 1000 − 35 · 20 − 43.
10. Найдите значение выражения
Вариант 9 1. Вычисления. Действия с дробями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения:
5. Найдите значение выражения .
6. Вычислите:
7. Найдите значение выражения .
8. Найдите значение выражения
9. Найдите значение выражения 1000 − 35 · 20 − 43.
10. Найдите значение выражения
Вариант 10 1. Вычисления. Действия с дробями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Вычислите
6. Найдите значение выражения
7. Найдите значение выражения (3,9 − 2,4) · 8,2.
8. Найдите значение выражения
9. Найдите значение выражения .
10. Найдите значение выражения
|
Вычисления. Действия с дробями. |
||||
|
Вариант 1 1. 0,5 2. 14,49 3. -0,43 4. 20,4 5. 1 6. 26,25 7. 0,4 8. -3 9. 3,5 10. -0,1 |
Вариант 2 1. -4,375 2. 31 3. 27,75 4. 56 5. 2,65 6. 4 7. -1,05 8. 10 9. 80,625 10. -500 |
Вариант 3 1.-2,5 2. 1,25 3. -4,9 4. 1 5. 49 6. 56 7. 27,75 8. 45 9. 1,8 10.1 |
Вариант 4 1. -2,5 2. 1,25 3. -4,9 4. 1 5. 49 6. 56 7. 27,75 8. 45 9. 1,8 10. 1 |
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
Практика по заданию №1 ЕГЭ по математике базового уровня — вычисления (действия с дробями).
Для выполнения задания №1 необходимо уметь выполнять вычисления и преобразования
Практика
| time4math.ru | Скачать задания |
| math100.ru | Действия с дробями |
| vk.com/math.studying | Задания + ответы |
Коды проверяемых элементов содержания (по кодификатору) — 1.1.1, 1.1.3, 1.4.1
Уровень сложности задания — базовый
Максимальный балл за выполнение задания — 1
Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 5
Связанные страницы:
Задание 14 ЕГЭ по математике профильный уровень — неравенства
Решение 17 задания ЕГЭ по профильной математике
Задание 5 ЕГЭ по математике профильный уровень — стереометрия
Задание 4 ЕГЭ по математике (профиль) — вычисления и преобразования
Задание 11 ЕГЭ 2022 по математике: «Наибольшее и наименьшее значения функции»
Описание презентации по отдельным слайдам:
-
1 слайд
Степанюк Елена Александровна
Учитель математики
Готовимся к ЕГЭ
Базовый уровень
Задание 1
«Вычисления»
МОАУ СОШ № 2 с. Возжаевка
Действия с дробями -
2 слайд
Единый государственный экзамен по математике базового уровня состоит из 20 заданий.
В задании 1 проверяются навыки вычисления значения выражений с обыкновенными и десятичнымиЕсли задание выполнено правильно получишь 1 первичный балл.
На решение отводится примерно 5 минут. -
3 слайд
порядок проведения арифметических операций:
действия в скобках,
возведение в степень или извлечение корня,
умножения и деления,
вычитания и сложения.Для выполнения задания 1 по математике базового уровня необходимо знать:
правила умножения и деления в столбик
правила вычисления обыкновенных дробей -
4 слайд
Вспомним обыкновенные дроби
-
-
-
7 слайд
Вспомним десятичные дроби
сложение
вычитание
умножение
деление -
-
-
10 слайд
Самостоятельная работа
1)
2)
3)4)
5)
6) -
11 слайд
Проверь себя
1) −4,375.
2) 0,4
3) 2,33
4) 12,3
5) 2,28
6)0,2 -
12 слайд
Демоверсия 1 задания
(2019 год. ФИПИ) -
13 слайд
Удачи на экзамене
-
14 слайд
РЕСУРС:
1. Фон http://img10.proshkolu.ru/content/media/pic/std/4000000/3495000/3494889-fa45b6e66e31cba7.png
2. Учитель
http://detskiy1972sad.caduk.ru/images/11.pnghttps://ege.sdamgia.ru/
3. Сайт решу ЕГЭ
4. Сайт Бингоскул
https://bingoschool.ru/ege/maths-base/tasks/1/
https://fipi.ru/ege/demoversii-specifikacii-kodifikatory
5. Сайт ФИПИ -
15 слайд
Автор шаблона:
Бурдейная Наталья Викторовна
воспитатель МКДОУ «Улыбка»
г. Бородино, Красноярский крайСайт: http://medea.ucoz.ru/
В задании №1 ЕГЭ по математике базового уровня необходимо провести элементарные вычисления — сложение, вычитание, деление и умножение дробей. Ответом в первом задании является целое число или конечная десятичная дробь.
Примерное время выполнения: 3 мин.
Разбор типовых вариантов заданий №1 ЕГЭ по математике базового уровня
Во всех заданиях необходимо найти значение выражения.
Вариант 1МБ1
Алгоритм решения:
- Определить порядок действий.
- Выполнить действия в скобках.
- Преобразовать смешанное число в неправильную дробь.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Произвести действия в числителе.
- Знаменатель оставить наименьший общий.
- Умножить числитель получившейся дроби на 9.
- Полученный результат сократить и преобразовать в десятичную дробь.
Решение в общем виде:
Пояснения к решению:
Первым всегда выполняется действие в скобках, в данном случае вычитание.
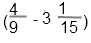
в неправильную дробь. Для этого умножим целую часть на знаменатель, и прибавим числитель
3 • 15 + 1 = 46
Запишем результат в числитель, знаменатель оставим без изменения.
Действие в скобках примет вид:
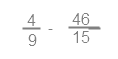
Приводим дроби к общему знаменателю – 45. Для этого по основному свойству дроби необходимо и числитель и знаменатель дроби умножить на одно и то же число, чтобы дробь не изменилась. Это число называется дополнительным множителем. Дополнительный множитель к первой дроби — 5 (9*5=45). Чтобы получить в знаменателе первой дроби 45 необходимо умножить на 5 и числитель и знаменатель.
Вторую дробь умножим на 3 (15 • 3=45)
Действие в скобках после преобразования будет выглядеть так:
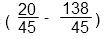
Выполним действие за скобками, в данном случае умножение на целое число. Для этого умножим числитель дроби на 9, а знаменатель оставим без изменений. Числитель и знаменатель полученной дроби сократим на 9, то есть разделим и числитель и знаменатель дроби на 9. По основному свойству дроби дробь не изменится.
Минус в числителе выносится за дробную черту.
Полученную дробь преобразуем в десятичную, поделив в столбик.
Не забудьте о знаке «минус» в ответе.
Ответ: 23,6
Вариант 1МБ2
Алгоритм решения:
- Определить порядок действий.
- Выполнить действие в скобках.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Выполнить вычитание числителей, знаменатель оставить без изменений.
- Выполнить деление. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Решение в общем виде:
 Пояснения к решению:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае вычитание.
Для того чтобы выполнить вычитание дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 4, и на 9. 9 на 4 не делится. Удвоим больший знаменатель: 18 не делится на 4. Утроим больший знаменатель: 27 не делится на 4. Увеличим больший знаменатель в 4 раза: 36 делится и на 9, и на 4 одновременно. Следовательно, 36 – наименьший общий знаменатель для дробей 1/4 и 2/9.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 1/4 и 2/9. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 1/4 нужно умножить на 9(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36. Дробь 2/9 нужно умножить на 4 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36.
В результате получим:
Действие в скобках примет вид:
Выполним вычитание дробей с одинаковыми знаменателями. Для этого вычтем из числителя первой дроби числитель второй, результат запишем в числитель. Знаменатель оставим прежним.

Сократим (разделим и числитель и знаменатель) полученную дробь на 12.
Ответ: 21
Вариант 1МБ3
Алгоритм решения:
- Определить порядок действий.
- Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
- Перевести смешанное число в неправильную дробь.
- Привести полученные дроби к наименьшему общему знаменателю.
- Выполните сложение дробей с одинаковыми знаменателями. Для этого сложить числители, результат записать в числитель, знаменатель оставить без изменений.
- Выполнить деление.
- Перевести смешанное число в неправильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
- Числитель первой дроби умножить на знаменатель второй – записать в числитель. Знаменатель первой дроби умножить на числитель второй результат записать в знаменатель.
- Сократить получившуюся дробь.
- Привести результат к десятичному виду.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
Нужно сложить смешанное число и правильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним. Переведем смешанное число в неправильную дробь:
Действие в скобках примет вид:
Для того, чтобы выполнить сложение дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 5, и на 7. 7 на 5 не делится. Удвоим больший знаменатель: 14 не делится на 5. Утроим больший знаменатель: 21 не делится на 5. Увеличим больший знаменатель в 4 раза: 28 не делится 5. Увеличим больший знаменатель в 5 раз: 35 делится одновременно и на 5, и на 7. Следовательно, 35 – наименьший общий знаменатель для дробей 9/5 и 3/7.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 9/5 и 3/7. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 9/5 нужно умножить на 7(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35. Дробь 3/7 нужно умножить на 5 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35.
В результате получим:
Действие в скобках примет вид:
Выполним сложение дробей с одинаковыми знаменателями. Для этого сложим числители, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Переведем смешанное число в неправильную дробь, для этого целую часть нужно умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
Выполнить деление дробей. Числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель, и знаменатель на одно и то же число) полученную дробь на 39.
Переведем полученную дробь в десятинную.
Ответ: 8,75
Вариант 1МБ4
(6,7 − 3,2) ⋅ 2,4
В данном случае первым действием мы выполняем вычитание в скобках, а затем производим умножение:
6,7 − 3,2 = 3,5
3,5⋅ 2,4 = 8,4
Отдельно остановлюсь на последнем действии. Его можно вычислить умножением в столбик, либо посчитать устно, воспользовавшись следующими логическими операциями:
2,4 ⋅ 3 + 2,4 ⋅ 0,5 = 2 ⋅ 3 + 0,4 ⋅ 3 + 2,4/2 = 6 + 1,2 +1,2 = 8,4
Ответ: 8,4
Вариант 1МБ5
В данном случае необходимо выполнить сложение обыкновенных дробей. Общий знаменатель для дробей в скобках — 15 (если вы забыли как определять общий знаменатель, смотрите здесь). Первую дробь домножаем на 5, вторую на 3. Получаем:
(5 + 3)/15
После сложения:
8/15
Теперь выполняем умножение:
8•6/15 = 48/15
В таком варианте дробь в ответ записать мы не можем, выделяем сначала целую часть, это 3 (45/15=3), в остатке получим:
3/15
После сокращения на 3:
1/5
и перевода в десятичный вид:
1/5 = 20/100 = 2/10 = 0,2
Не забываем про целую часть и получаем ответ:
3,2
Ответ: 3,2
Вариант 1МБ6
- Если представить черту дроби в виде знака деления, то получим выражение: (2,7+5,8):6,8. Отсюда получаем приоритет действий: 1) сложение в скобках; 2) деление. Поэтому сначала выполняем действие в числителе.
- Избавляемся от десятичных запятых в числителе и знаменателе. Для этого применяем основное свойство дроби и умножаем числитель и знаменатель на 10.
- Делим 85 на 68 в столбик.
Решение
Ответ: 1,25
Вариант 1МБ7
- Учитываем приоритетность операций. Здесь 1-м действием выполняется умножение, а затем вычитание.
- При умножении числа записываем друг под другом, выровняв их по последней цифре. В результирующем числе отделяем столько знаков после запятой, сколько имеется суммарно в обоих множителях. В данном случае нужно отделить 2 знака.
- При выполнении вычитания в столбик числа располагают так, чтобы десят.запятые располагались на друг под другом.
Решение
Ответ: 26,7
Вариант 1МБ8
- Умножаем 1/5 на 5,5. При этом 5,5 переходит в числитель дроби.
- Выполняем сокращение полученной дроби на 5. Получаем десят.дробь
- Находим конечную разность.
Решение
Ответ:0,1
Вариант 1МБ9
- Находим разность в скобках. Для этого находим НОК (25, 38) и приводим дроби к общему знаменателю.
- Делим результат в скобках на дробь 6/19. Для этого переходим к умножению дробей, перевернув 9/16 и получив 16/9. Далее сокращаем множители в числителе и знаменателе и находим результирующую дробь.
- Полученную дробь записываем в десят.виде.
















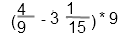
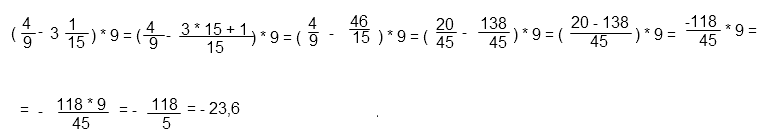
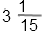
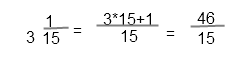
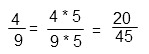
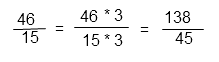
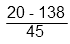
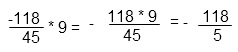
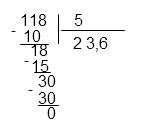
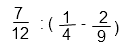
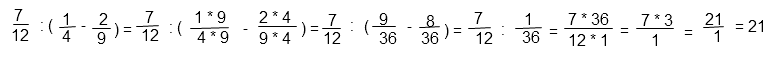 Пояснения к решению:
Пояснения к решению: