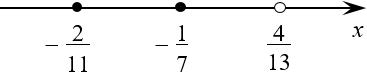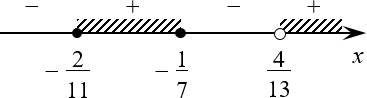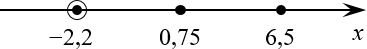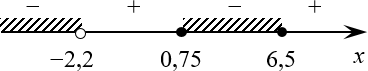Дробно рациональные неравенства егэ профиль

(blacktriangleright) Рациональное неравенство – это неравенство, которое можно свести к виду [large{dfrac{P(x)}{Q(x)}geqslant 0}
quad (*)] где (P(x), Q(x)) – многочлены.
(на месте знака (geqslant) может стоять любой из знаков (leqslant,
>,
<))

Способы решения данного неравенства:

1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство ((*)) равносильно совокупности:

[{large{left[begin{gathered}
begin{aligned}
&begin{cases} P(x)geqslant 0\ Q(x)>0 end{cases}\
&begin{cases} P(x)leqslant 0\ Q(x)<0 end{cases}
end{aligned}
end{gathered}
right.}}]

2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере):

1 ШАГ. Разложим на множители числитель и знаменатель дроби.

Пусть после разложения неравенство примет вид [dfrac{x^2(x-1)^3(x+1)(2x^2+3x+5)(2x-x^2-3)}{(x+1)^3(3-x)(2-3x)^2} geqslant0] Помним, что если квадратное уравнение:

(sim) имеет два корня (x_1) и (x_2) (дискриминант (D>0)), то (ax^2+bx+c=a(x-x_1)(x-x_2)).

(sim) имеет один корень (x_1) ((D=0)), то (ax^2+bx+c=a(x-x_1)^2).

(sim) не имеет корней ((D<0)), то квадратный трехчлен (ax^2+bc+c) никогда не может быть равен нулю, соответственно, не разлагается на линейные множители.

2 ШАГ. Рассмотрим скобки, в которых находится квадратный трехчлен с (D<0).

Если при (x^2) находится положительный коэффициент, то эти скобки можно вычеркнуть (в нашем неравенстве это ((2x^2+3x+5))).

Если при (x^2) находится отрицательный коэффициент, то при вычеркивании такой скобки знак неравенства меняем на противоположный (в нашем неравенстве это ((2x-x^2-3))).
Заметим, что если таких скобок несколько, то вычеркиваем их последовательно по одной, каждый раз меняя знак неравенства на противоположный.

Таким образом, неравенство примет вид [dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(3-x)(2-3x)^2}
leqslant0]

3 ШАГ. Рассмотрим линейные скобки.

Назовем скобку хорошей, если при (x) находится положительный коэффициент (такие скобки не трогаем), и плохой, если при (x) находится отрицательный коэффициент (в таких скобках меняем все знаки на противоположные, т.е. делаем их хорошими).

Если плохих скобок было четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.

В нашем неравенстве одна скобка ((3-x)) и две скобки ((2-3x)) (т.к. ((2-3x)^2=(2-3x)(2-3x))), т.е. всего три плохих скобки, следовательно, неравенство примет вид: [dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(x-3)(3x-2)^2}
geqslant0quad (**)]

4 ШАГ. Отметим нули каждой скобки на числовой прямой, причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как у нас) или выколотые (если знак неравенства строгий).

Если мы отметили (n) точек, то числовая прямая разобьется на (n+1) промежутков.

Расставим знак на каждом промежутке справа налево.

Т.к. все скобки – хорошие, то первый знак всегда будет («+»). Если какая-то точка входит в четное количество скобок, то при переходе через нее (справа налево!) знак меняться не будет (например, точка (-1) входит в четное количество скобок: одна в числителе и три в знаменателе);

5 ШАГ. Запишем ответ. В нашем случае, т.к. знак преобразованного ((**)) неравенства (geqslant 0), то в ответ пойдут промежутки со знаком («+») и закрашенные точки: [xin
(-infty;-1)cup left(-1;frac23right)cup
left(dfrac23;1right]cup(3;+infty)]

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

^New 

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов 

Уравнения и неравенства с модулем 

Иррациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства 

1. Решите неравенство:

Сделаем замену

Тогда , а

Получим:

Решим неравенство относительно t методом интервалов:

Получим:

Вернемся к переменной x:

Ответ:

Показательные неравенства

2. Решите неравенство

Сделаем замену Получим:

Умножим неравенство на

Дискриминант квадратного уравнения

Значит, корни этого уравнения:

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

Ответ:

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.

3. Решите неравенство

Сделаем замену Получим:

Вернемся к переменной

Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х?

Оценим Для этого рассмотрим функцию

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда , и это значит, что Значение не достигается ни при каких х.

Но если и , то

Мы получили:

Ответ:

Логарифмические неравенства

4. Решите неравенство

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

Ответ:

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство

ОДЗ:

Замена

Ответ:

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство:

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,

Поскольку

Согласно методу замены множителя, выражение заменим на

Получим систему:

Решить ее легко.

Ответ: .

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

ОДЗ:

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Ответ:

Дробно-рациональные неравенства

25 января 2018

Этот урок будет жёстким. Настолько жёстким, что до конца его дойдут лишь Избранные. Поэтому перед началом чтения рекомендую убрать от экранов женщин, кошек, беременных детей и…

Да ладно, на самом деле всё просто. Допустим, вы освоили метод интервалов (если не освоили — рекомендую вернуться и прочитать) и научились решать неравенства вида $Pleft( x right) gt 0$, где $Pleft( x right)$ — какой-нибудь многочлен или произведение многочленов.

Полагаю, что для вас не составит труда решить, например, вот такую дичь (кстати, попробуйте для разминки):

[begin{align} & left( 2{{x}^{2}}+3x+4 right)left( 4x+25 right) gt 0; \ & xleft( 2{{x}^{2}}-3x-20 right)left( x-1 right)ge 0; \ & left( 8x-{{x}^{4}} right){{left( x-5 right)}^{6}}le 0. \ end{align}]

Теперь немного усложним задачу и рассмотрим не просто многочлены, а так называемые рациональные дроби вида:

[frac{Pleft( x right)}{Qleft( x right)} gt 0]

где $Pleft( x right)$ и $Qleft( x right)$ — всё те же многочлены вида ${{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+…+{{a}_{0}}$, либо произведение таких многочленов.

Это и будет рациональное неравенство. Принципиальным моментом является наличие переменной $x$ в знаменателе. Например, вот это — рациональные неравенства:

[begin{align} & frac{x-3}{x+7} lt 0; \ & frac{left( 7x+1 right)left( 11x+2 right)}{13x-4}ge 0; \ & frac{3{{x}^{2}}+10x+3}{{{left( 3-x right)}^{2}}left( 4-{{x}^{2}} right)}ge 0. \ end{align}]

А это — не рациональное, а самое обычное неравенство, которое решается методом интервалов:

[frac{{{x}^{2}}+6x+9}{5}ge 0]

Забегая вперёд, сразу скажу: существует как минимум два способа решения рациональных неравенств, но все они так или иначе сводятся к уже известному нам методу интервалов. Поэтому прежде чем разбирать эти способы, давайте вспомним старые факты, иначе толку от нового материла не будет никакого.

Что уже нужно знать

Важных фактов не бывает много. Действительно потребуются нам всего четыре.

Формулы сокращённого умножения

Да, да: они будут преследовать нас на протяжении всей школьной программы математики. И в университете тоже. Этих формул довольно много, но нам потребуются лишь следующие:

[begin{align} & {{a}^{2}}pm 2ab+{{b}^{2}}={{left( apm b right)}^{2}}; \ & {{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right); \ & {{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right); \ & {{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right). \ end{align}]

Обратите внимание на последние две формулы — это сумма и разность кубов (а не куб суммы или разности!). Их легко запомнить, если заметить, что знак в первой скобке совпадает со знаком в исходном выражении, а во второй — противоположен знаку исходного выражения.

Линейные уравнения

Это самые простые уравнения вида $ax+b=0$, где $a$ и $b$ — это обычные числа, причём $ane 0$. Такое уравнение решается просто:

[begin{align} & ax+b=0; \ & ax=-b; \ & x=-frac{b}{a}. \ end{align}]

Отмечу, что мы имеем право делить на коэффициент $a$, ведь $ane 0$. Это требование вполне логично, поскольку при $a=0$ мы получим вот что:

[b=0]

Во-первых, в этом уравнении нет переменной $x$. Это, вообще говоря, не должно нас смущать (такое случается, скажем, в геометрии, причём довольно часто), но всё же перед нами уже не линейное уравнение.

Во-вторых, решение этого уравнения зависит исключительно от коэффициента $b$. Если $b$ — тоже ноль, то наше уравнение имеет вид $0=0$. Данное равенство верно всегда; значит, $x$ — любое число (обычно это записывается так: $xin mathbb{R}$). Если же коэффициент $b$ не равен нулю, то равенство $b=0$ никогда не выполняется, т.е. ответов нет (записывается $xin varnothing $ и читается «множество решений пусто»).

Чтобы избежать всех этих сложностей, просто полагают $ane 0$, что нисколько не ограничивает нас в дальнейших размышлениях.

Квадратные уравнения

Напомню, что квадратным уравнением называется вот это:

[a{{x}^{2}}+bx+c=0]

Здесь слева многочлен второй степени, причём снова $ane 0$ (в противном случае вместо квадратного уравнения мы получим линейное). Решаются такие уравнения через дискриминант:

[D={{b}^{2}}-4ac]

Дальше всё зависит от знака дискриминанта:

1. Если $D gt 0$, мы получим два различных корня;
2. Если $D=0$, то корень будет один, но второй кратности (что это за кратность и как её учитывать — об этом чуть позже). Либо можно сказать, что уравнение имеет два одинаковых корня;
3. При $D lt 0$ корней вообще нет, а знак многочлена $a{{x}^{2}}+bx+c$ при любом $x$ совпадает со знаком коэффициента $a$. Это, кстати, очень полезный факт, о котором почему-то забывают рассказать на уроках алгебры.

Сами корни считаются по всем известной формуле:

[{{x}_{1,2}}=frac{-bpm sqrt{D}}{2a}]

Отсюда, кстати, и ограничения на дискриминант. Ведь квадратный корень из отрицательного числа не существует. По поводу корней у многих учеников жуткая каша в голове, поэтому я специально записал целый урок: что такое корень в алгебре и как его считать — очень рекомендую почитать.:)

Действия с рациональными дробями

Всё, что было написано выше, вы и так знаете, если изучали метод интервалов. А вот то, что мы разберём сейчас, не имеет аналогов в прошлом — это совершенно новый факт.

Определение. Рациональная дробь — это выражение вида

[frac{Pleft( x right)}{Qleft( x right)}]

где $Pleft( x right)$ и $Qleft( x right)$ — многочлены.

Очевидно, что из такой дроби легко получить неравенство — достаточно лишь приписать знак «больше» или «меньше» справа. И чуть дальше мы обнаружим, что решать такие задачи — одно удовольствие, там всё очень просто.

Проблемы начинаются тогда, когда в одном выражении находятся несколько таких дробей. Их приходится приводить к общему знаменателю — и именно в этот момент допускается большое количество обидных ошибок.

Поэтому для успешного решения рациональных уравнений необходимо твёрдо усвоить два навыка:

1. Разложение многочлена $Pleft( x right)$ на множители;
2. Собственно, приведение дробей к общему знаменателю.

Как разложить многочлен на множители? Очень просто. Пусть у нас есть многочлена вида

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+…+{{a}_{1}}x+{{a}_{0}}]

Приравниваем его к нулю. Получим уравнение $n$-й степени:

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+…+{{a}_{1}}x+{{a}_{0}}=0]

Допустим, мы решили это уравнение и получили корни ${{x}_{1}}, …, {{x}_{n}}$ (не пугайтесь: в большинстве случаев этих корней будет не более двух). В таком случае наш исходный многочлен можно переписать так:

[begin{align} & Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+…+{{a}_{1}}x+{{a}_{0}}= \ & ={{a}_{n}}left( x-{{x}_{1}} right)cdot left( x-{{x}_{2}} right)cdot …cdot left( x-{{x}_{n}} right) end{align}]

Вот и всё! Обратите внимание: старший коэффициент ${{a}_{n}}$ никуда не исчез — он будет отдельным множителем перед скобками, и при необходимости его можно внести в любую из этих скобок (практика показывает, что при ${{a}_{n}}ne pm 1$ среди корней почти всегда есть дроби).

Задача. Упростите выражение:

[frac{{{x}^{2}}+x-20}{x-4}-frac{2{{x}^{2}}-5x+3}{2x-3}-frac{4-8x-5{{x}^{2}}}{x+2}]

Решение. Для начала посмотрим на знаменатели: все они — линейные двучлены, и раскладывать на множители тут нечего. Поэтому давайте разложим на множители числители:

[begin{align} & {{x}^{2}}+x-20=left( x+5 right)left( x-4 right); \ & 2{{x}^{2}}-5x+3=2left( x-frac{3}{2} right)left( x-1 right)=left( 2x-3 right)left( x-1 right); \ & 4-8x-5{{x}^{2}}=-5left( x+2 right)left( x-frac{2}{5} right)=left( x+2 right)left( 2-5x right). \end{align}]

Обратите внимание: во втором многочлене старший коэффициент «2» в полном соответствии с нашей схемой сначала оказался перед скобкой, а затем был внесён в первую скобку, поскольку там вылезла дробь.

То же самое произошло и в третьем многочлене, только там ещё и порядок слагаемых перепутан. Однако коэффициент «−5» в итоге оказался внесён во вторую скобку (помните: вносить множитель можно в одну и только в одну скобку!), что избавило нас от неудобств, связанных с дробными корнями.

Что касается первого многочлена, там всё просто: его корни ищутся либо стандартно через дискриминант, либо по теореме Виета.

Вернёмся к исходному выражению и перепишем его с разложенными на множители числителями:

[begin{matrix} frac{left( x+5 right)left( x-4 right)}{x-4}-frac{left( 2x-3 right)left( x-1 right)}{2x-3}-frac{left( x+2 right)left( 2-5x right)}{x+2}= \ =left( x+5 right)-left( x-1 right)-left( 2-5x right)= \ =x+5-x+1-2+5x= \ =5x+4. \ end{matrix}]

Ответ: $5x+4$.

Как видите, ничего сложного. Немного математики 7—8 класса — и всё. Смысл всех преобразований в том и состоит, чтобы получить из сложного и страшного выражения что-нибудь простое, с чем легко работать.

Однако так будет не всегда. Поэтому сейчас мы рассмотрим более серьёзную задачу.

Но сначала разберёмся с тем, как привести две дроби к общему знаменателю. Алгоритм предельно прост:

1. Разложить на множители оба знаменателя;
2. Рассмотреть первый знаменатель и добавить к нему множители, имеющиеся во втором знаменателе, однако отсутствующие в первом. Полученное произведение и будет общим знаменателем;
3. Выяснить, каких множителей не хватает каждой из исходных дробей, чтобы знаменатели стали равны общему.

Возможно, этот алгоритм вам покажется просто текстом, в котором «много букв». Поэтому разберём всё на конкретном примере.

Задача. Упростите выражение:

[left( frac{x}{{{x}^{2}}+2x+4}+frac{{{x}^{2}}+8}{{{x}^{3}}-8}-frac{1}{x-2} right)cdot left( frac{{{x}^{2}}}{{{x}^{2}}-4}-frac{2}{2-x} right)]

Решение. Такие объёмные задачи лучше решать по частям. Выпишем то, что стоит в первой скобке:

[frac{x}{{{x}^{2}}+2x+4}+frac{{{x}^{2}}+8}{{{x}^{3}}-8}-frac{1}{x-2}]

В отличие от предыдущей задачи, тут со знаменателями всё не так просто. Разложим на множители каждый из них.

Квадратный трёхчлен ${{x}^{2}}+2x+4$ на множители не раскладывается, поскольку уравнение ${{x}^{2}}+2x+4=0$ не имеет корней (дискриминант отрицательный). Оставляем его без изменений.

Второй знаменатель — кубический многочлен ${{x}^{3}}-8$ — при внимательном рассмотрении является разностью кубов и легко раскладывается по формулам сокращённого умножения:

[{{x}^{3}}-8={{x}^{3}}-{{2}^{3}}=left( x-2 right)left( {{x}^{2}}+2x+4 right)]

Больше ничего разложить на множители нельзя, поскольку в первой скобке стоит линейный двучлен, а во второй — уже знакомая нам конструкция, которая не имеет действительных корней.

Наконец, третий знаменатель представляет собой линейный двучлен, который нельзя разложить. Таким образом, наше уравнение примет вид:

[frac{x}{{{x}^{2}}+2x+4}+frac{{{x}^{2}}+8}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}-frac{1}{x-2}]

Совершенно очевидно, что общим знаменателем будет именно $left( x-2 right)left( {{x}^{2}}+2x+4 right)$, и для приведения к нему всех дробей необходимо первую дробь домножить на $left( x-2 right)$, а последнюю — на $left( {{x}^{2}}+2x+4 right)$. Затем останется лишь привести подобные:

[begin{matrix} frac{xcdot left( x-2 right)}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}+frac{{{x}^{2}}+8}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}-frac{1cdot left( {{x}^{2}}+2x+4 right)}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}= \ =frac{xcdot left( x-2 right)+left( {{x}^{2}}+8 right)-left( {{x}^{2}}+2x+4 right)}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}= \ =frac{{{x}^{2}}-2x+{{x}^{2}}+8-{{x}^{2}}-2x-4}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}= \ =frac{{{x}^{2}}-4x+4}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}. \ end{matrix}]

Обратите внимание на вторую строчку: когда знаменатель уже общий, т.е. вместо трёх отдельных дробей мы написали одну большую, не стоит сразу избавляться от скобок. Лучше напишите лишнюю строчку и отметьте, что, скажем, перед третьей дробью стоял минус — и он никуда не денется, а будет «висеть» в числителе перед скобкой. Это избавит вас от множества ошибок.

Ну и в последней строчке полезно разложить на множители числитель. Тем более что это точный квадрат, и нам на помощь вновь приходят формулы сокращённого умножения. Имеем:

[frac{{{x}^{2}}-4x+4}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}=frac{{{left( x-2 right)}^{2}}}{left( x-2 right)left( {{x}^{2}}+2x+4 right)}=frac{x-2}{{{x}^{2}}+2x+4}]

Теперь точно так же разберёмся со второй скобкой. Тут я просто напишу цепочку равенств:

[begin{matrix} frac{{{x}^{2}}}{{{x}^{2}}-4}-frac{2}{2-x}=frac{{{x}^{2}}}{left( x-2 right)left( x+2 right)}-frac{2}{2-x}= \ =frac{{{x}^{2}}}{left( x-2 right)left( x+2 right)}+frac{2}{x-2}= \ =frac{{{x}^{2}}}{left( x-2 right)left( x+2 right)}+frac{2cdot left( x+2 right)}{left( x-2 right)cdot left( x+2 right)}= \ =frac{{{x}^{2}}+2cdot left( x+2 right)}{left( x-2 right)left( x+2 right)}=frac{{{x}^{2}}+2x+4}{left( x-2 right)left( x+2 right)}. \ end{matrix}]

Возвращаемся к исходной задачи и смотрим на произведение:

[frac{x-2}{{{x}^{2}}+2x+4}cdot frac{{{x}^{2}}+2x+4}{left( x-2 right)left( x+2 right)}=frac{1}{x+2}]

Ответ: [frac{1}{x+2}].

Смысл этой задачи такой же, как и у предыдущей: показать, насколько могут упрощаться рациональные выражения, если подойти к их преобразованию с умом.

И вот теперь, когда вы всё это знаете, давайте перейдём к основной теме сегодняшнего урока — решению дробно-рациональных неравенств. Тем более что после такой подготовки сами неравенства вы будете щёлкать как орешки.:)

Основной способ решения рациональных неравенств

Существует как минимум два подхода к решению рациональных неравенств. Сейчас мы рассмотрим один из них — тот, который является общепринятым в школьном курсе математики.

Но для начала отметим важную деталь. Все неравенства делятся на два типа:

1. Строгие: $fleft( x right) gt 0$ или $fleft( x right) lt 0$;
2. Нестрогие: $fleft( x right)ge 0$ или $fleft( x right)le 0$.

Неравенства второго типа легко сводятся к первому, а также уравнению:

[fleft( x right)ge 0Leftrightarrow left[ begin{align} & fleft( x right) gt 0, \ & fleft( x right)=0. \ end{align} right.]

Это небольшое «дополнение» $fleft( x right)=0$ приводит к такой неприятной штуке как закрашенные точки — мы познакомились с ними ещё в методе интервалов. В остальном никаких отличий между строгими и нестрогими неравенствами нет, поэтому давайте разберём универсальный алгоритм:

1. Собрать все ненулевые элементы с одной стороны от знака неравенства. Например, слева;
2. Привести все дроби к общему знаменателю (если таких дробей окажется несколько), привести подобные. Затем по возможности разложить на числитель и знаменатель на множители. Так или иначе мы получим неравенство вида $frac{Pleft( x right)}{Qleft( x right)}vee 0$, где «галочка» — знак неравенства.
3. Приравниваем числитель к нулю: $Pleft( x right)=0$. Решаем это уравнение и получаем корни ${{x}_{1}}$, ${{x}_{2}}$, ${{x}_{3}}$, … Затем требуем, чтобы знаменатель был не равен нулю: $Qleft( x right)ne 0$. Разумеется, по сути приходится решить уравнение $Qleft( x right)=0$, и мы получим корни $x_{1}^{*}$, $x_{2}^{*}$, $x_{3}^{*}$, … (в настоящих задачах таких корней вряд ли будет больше трёх).
4. Отмечаем все эти корни (и со звёздочками, и без) на единой числовой прямой, причём корни без звёзд закрашены, а со звёздами — выколоты.
5. Расставляем знаки «плюс» и «минус», выбираем те интервалы, которые нам нужны. Если неравенство имеет вид $fleft( x right) gt 0$, то в ответ пойдут интервалы, отмеченные «плюсом». Если $fleft( x right) lt 0$, то смотрим на интервалы с «минусами».

Практика показывает, что наибольшие трудности вызывают пункты 2 и 4 — грамотные преобразования и правильная расстановка чисел в порядке возрастания. Ну, и на последнем шаге будьте предельно внимательны: мы всегда расставляем знаки, опираясь на самое последнее неравенство, записанное перед переходом к уравнениям. Это универсальное правило, унаследованное ещё от метода интервалов.

Итак, схема есть. Давайте потренируемся.

Задача. Решите неравенство:

[frac{x-3}{x+7} lt 0]

Решение. Перед нами строгое неравенство вида $fleft( x right) lt 0$. Очевидно, пункты 1 и 2 из нашей схемы уже выполнены: все элементы неравенства собраны слева, к общему знаменателю ничего приводить не надо. Поэтому переходим сразу к третьему пункту.

Приравниваем к нулю числитель:

[begin{align} & x-3=0; \ & x=3. end{align}]

И знаменатель:

[begin{align} & x+7=0; \ & {{x}^{*}}=-7. \ end{align}]

В этом месте многие залипают, ведь по идее нужно записать $x+7ne 0$, как того требует ОДЗ (на ноль делить нельзя, вот это вот всё). Но ведь в дальнейшем мы будем выкалывать точки, пришедшие из знаменателя, поэтому лишний раз усложнять свои выкладки не стоит — пишите везде знак равенства и не парьтесь. Никто за это баллы не снизит.:)

Четвёртый пункт. Отмечаем полученные корни на числовой прямой:

Обратите внимание: все точки выколоты, поскольку исходное неравенство строгое. И тут уже неважно: из числителя эти точки пришли или из знаменателя.

Ну и смотрим знаки. Возьмём любое число ${{x}_{0}} gt 3$. Например, ${{x}_{0}}=100$ (но с тем же успехом можно было взять ${{x}_{0}}=3,1$ или ${{x}_{0}}=1 000 000$). Получим:

[fleft( x right)=frac{x-3}{x+7}Rightarrow fleft( 100 right)=frac{100-3}{100+7}=frac{97}{107} gt 0]

Итак, справа от всех корней у нас положительная область. А при переходе через каждый корень знак меняется (так будет не всегда, но об это позже). Поэтому переходим к пятому пункту: расставляем знаки и выбираем нужное:

Возвращаемся к последнему неравенству, которое было перед решением уравнений. Собственно, оно совпадает с исходным, ведь никаких преобразований в этой задаче мы не выполняли.

Поскольку требуется решить неравенство вида $fleft( x right) lt 0$, я заштриховал интервал $xin left( -7;3 right)$ — он единственный отмечен знаком «минус». Это и есть ответ.

Ответ: $xin left( -7;3 right)$

Вот и всё! Разве сложно? Нет, не сложно. Правда, и задачка была лёгкая. Сейчас чуть усложним миссию и рассмотрим более «навороченное» неравенство. При его решении я уже не буду давать столь подробных выкладок — просто обозначу ключевые моменты. В общим, оформим его так, как оформляли бы на самостоятельной работе или экзамене.:)

Задача. Решите неравенство:

[frac{left( 7x+1 right)left( 11x+2 right)}{13x-4}ge 0]

Решение. Это нестрогое неравенство вида $fleft( x right)ge 0$. Все ненулевые элементы собраны слева, разных знаменателей нет. Переходим к уравнениям.

Числитель:

[begin{align} & left( 7x+1 right)left( 11x+2 right)=0 \ & 7x+1=0Rightarrow {{x}_{1}}=-frac{1}{7}; \ & 11x+2=0Rightarrow {{x}_{2}}=-frac{2}{11}. \ end{align}]

Знаменатель:

[begin{align} & 13x-4=0; \ & 13x=4; \ & {{x}^{*}}=frac{4}{13}. \ end{align}]

Не знаю, что за извращенец составлял эту задачу, но корни получились не очень: их будет трудно расставить на числовой прямой. И если с корнем ${{x}^{*}}={4}/{13};$ всё более-менее ясно (это единственное положительное число — оно будет справа), то ${{x}_{1}}=-{1}/{7};$ и ${{x}_{2}}=-{2}/{11};$ требуют дополнительного исследования: какое из них больше?

Выяснить это можно, например, так:

[{{x}_{1}}=-frac{1}{7}=-frac{2}{14} gt -frac{2}{11}={{x}_{2}}]

Надеюсь, не нужно объяснять, почему числовая дробь $-{2}/{14}; gt -{2}/{11};$? Если нужно, рекомендую вспомнить, как выполнять действия с дробями.

А мы отмечаем все три корня на числовой прямой:

Расставляем знаки. Например, можно взять ${{x}_{0}}=1$ и выяснить знак в этой точке:

[begin{align} & fleft( x right)=frac{left( 7x+1 right)left( 11x+2 right)}{13x-4}; \ & fleft( 1 right)=frac{left( 7cdot 1+1 right)left( 11cdot 1+2 right)}{13cdot 1-4}=frac{8cdot 13}{9} gt 0. \end{align}]

Последним неравенством перед уравнениями было $fleft( x right)ge 0$, поэтому нас интересует знак «плюс».

Получили два множества: один — обычный отрезок, а другой — открытый луч на числовой прямой.

Ответ: $xin left[ -frac{2}{11};-frac{1}{7} right]bigcup left( frac{4}{13};+infty right)$

Важное замечание по поводу чисел, которые мы подставляем для выяснения знака на самом правом интервале. Совершенно необязательно подставлять число, близкое к самому правому корню. Можно брать миллиарды или даже «плюс-бесконечность» — в этом случае знак многочлена стоящего в скобке, числителе или знаменателе, определяется исключительно знаком старшего коэффициента.

Давайте ещё раз посмотрим на функцию $fleft( x right)$ из последнего неравенства:

[fleft( x right)=frac{left( 7x+1 right)left( 11x+2 right)}{13x-4}]

В её записи присутствуют три многочлена:

[begin{align} & {{P}_{1}}left( x right)=7x+1; \ & {{P}_{2}}left( x right)=11x+2; \ & Qleft( x right)=13x-4. end{align}]

Все они являются линейными двучленами, и у всех старшие коэффициенты (числа 7, 11 и 13) положительны. Следовательно, при подстановке очень больших чисел сами многочлены тоже будут положительны.:)

Это правило может показаться чрезмерно сложным, но только поначалу, когда мы разбираем совсем лёгкие задачи. В серьёзных неравенствах подстановка «плюс-бесконечности» позволит нам выяснить знаки намного быстрее, нежели стандартное ${{x}_{0}}=100$.

Мы очень скоро столкнёмся с такими задачами. Но сначала разберём альтернативный способ решения дробно-рациональных неравенств.

Альтернативный способ

Этот приём мне подсказала одна из моих учениц. Сам я никогда им не пользовался, однако практика показала, что многим ученикам действительно удобнее решать неравенства именно таким способом.

Итак, исходные данные те же. Нужно решить дробно-рациональное неравенство:

[frac{Pleft( x right)}{Qleft( x right)} gt 0]

Давайте подумаем: чем многочлен $Qleft( x right)$ «хуже» многочлена $Pleft( x right)$? Из-за чего нам приходится рассматривать отдельные группы корней (со звёздочкой и без), думать о выколотых точках и т.д.? Всё просто: у дроби есть область определения, согласной которой дробь имеет смысл только тогда, когда её знаменатель отличен от нуля.

В остальном никаких отличий между числителем и знаменателем не прослеживается: мы так же приравниваем его к нулю, ищем корни, затем отмечаем их на числовой прямой. Так почему бы не заменить дробную черту (фактически — знак деления) обычным умножением, а все требования ОДЗ прописать в виде отдельного неравенства? Например, так:

[frac{Pleft( x right)}{Qleft( x right)} gt 0Rightarrow left{ begin{align} & Pleft( x right)cdot Qleft( x right) gt 0, \ & Qleft( x right)ne 0. \ end{align} right.]

Обратите внимание: такой подход позволит свести задачу к методу интервалов, но при этом нисколько не усложнит решение. Ведь всё равно мы будем приравнивать многочлен $Qleft( x right)$ к нулю.

Давайте посмотрим, как это работает на реальных задачах.

Задача. Решите неравенство:

[frac{x+8}{x-11} gt 0]

Решение. Итак, переходим к методу интервалов:

[frac{x+8}{x-11} gt 0Rightarrow left{ begin{align} & left( x+8 right)left( x-11 right) gt 0, \ & x-11ne 0. \ end{align} right.]

Первое неравенство решается элементарно. Просто приравниваем каждую скобку к нулю:

[begin{align} & x+8=0Rightarrow {{x}_{1}}=-8; \ & x-11=0Rightarrow {{x}_{2}}=11. \ end{align}]

Со вторым неравенством тоже всё просто:

[x-11ne 0Rightarrow xne 11.]

Отмечаем точки ${{x}_{1}}$ и ${{x}_{2}}$ на числовой прямой. Все они выколоты, поскольку неравенство строгое:

Обратите внимание на точку $x=11$. Получается, что она «дважды выколота»: с одной стороны, мы выкалываем её из-за строгости неравенства, с другой — из-за дополнительного требования ОДЗ.

В любом случае, это будет просто выколотая точка. Поэтому расставляем знаки для неравенства $left( x+8 right)left( x-11 right) gt 0$ — последнего, которое мы видели перед тем, как начали решать уравнения:

Нас интересуют положительные области, поскольку мы решаем неравенство вида $fleft( x right) gt 0$ — их и закрасим. Осталось лишь записать ответ.

Ответ. $xin left( -infty ;-8 right)bigcup left( 11;+infty right)$

На примере этого решения хотел бы предостеречь вас от распространённой ошибки среди начинающих учеников. А именно: никогда не раскрывайте скобки в неравенствах! Наоборот, старайтесь всё разложить на множители — это упростит решение и избавит вас от множества проблем.

Теперь попробуем кое-что посложнее.

Задача. Решите неравенство:

[frac{left( 2x-13 right)left( 12x-9 right)}{15x+33}le 0]

Решение. Это нестрогое неравенство вида $fleft( x right)le 0$, поэтому здесь нужно внимательно следить за закрашенными точками.

Переходим к методу интервалов:

[left{ begin{align} & left( 2x-13 right)left( 12x-9 right)left( 15x+33 right)le 0, \ & 15x+33ne 0. \ end{align} right.]

Переходим к уравнению:

[begin{align} & left( 2x-13 right)left( 12x-9 right)left( 15x+33 right)=0 \ & 2x-13=0Rightarrow {{x}_{1}}=6,5; \ & 12x-9=0Rightarrow {{x}_{2}}=0,75; \ & 15x+33=0Rightarrow {{x}_{3}}=-2,2. \ end{align}]

Учитываем дополнительное требование:

[15x+33ne 0Rightarrow xne -2,2.]

Отмечаем все полученные корни на числовой прямой:

Опять две точки «накладываются» друг на друга — это нормально, так будет всегда. Важно лишь понимать, что точка, отмеченная одновременно выколотой и закрашенной, на самом деле является выколотой. Т.е. «выкалывание» — более сильное действие, чем «закрашивание».

Это абсолютно логично, ведь выкалыванием мы отмечаем точки, которые влияют на знак функции, но сами не участвуют в ответе. И если в какой-то момент число перестаёт нас устраивать (например, не попадает в ОДЗ), мы вычёркиваем его из рассмотрения до самого конца задачи.

В общем, хватит философствовать. Расставляем знаки и закрашиваем те интервалы, которые отмечены знаком «минус»:

Ответ. $xin left( -infty ;-2,2 right)bigcup left[ 0,75;6,5 right]$.

И снова хотел обратить ваше внимание вот на это уравнение:

[left( 2x-13 right)left( 12x-9 right)left( 15x+33 right)=0]

Ещё раз: никогда не раскрывайте скобки в таких уравнениях! Вы только усложните себе задачу. Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Следовательно, данное уравнение просто «разваливается» на несколько более мелких, которые мы и решали в предыдущей задаче.

Учёт кратности корней

Из предыдущих задач легко заметить, что наибольшую сложность представляют именно нестрогие неравенства, потому как в них приходится следить за закрашенными точками.

Но в мире есть ещё большее зло — это кратные корни в неравенствах. Тут уже приходится следить не за какими-то там закрашенными точками — тут знак неравенства может внезапно не поменяться при переходе через эти самые точки.

Ничего подобного мы в этом уроке ещё не рассматривали (хотя аналогичная проблема часто встречалась в методе интервалов). Поэтому введём новое определение:

Определение. Корень уравнения ${{left( x-a right)}^{n}}=0$ равен $x=a$ и называется корнем $n$-й кратности.

Собственно, нас не особо интересует точное значение кратности. Важно лишь то, чётным или нечётным является это самое число $n$. Потому что:

1. Если $x=a$ — корень чётной кратности, то знак функции при переходе через него не меняется;
2. И наоборот, если $x=a$ — корень нечётной кратности, то знак функции поменяется.

Частным случаем корня нечётной кратности являются все предыдущие задачи, рассмотренные в этом уроке: там везде кратность равна единице.

И ещё. Перед тем, как мы начнём решать задачи, хотел бы обратить ваше внимание на одну тонкость, которая покажется очевидной для опытного ученика, но вгоняет в ступор многих начинающих. А именно:

Корень кратности $n$ возникает только в том случае, когда в эту степень возводится всё выражение: ${{left( x-a right)}^{n}}$, а никак не $left( {{x}^{n}}-a right)$.

Ещё раз: скобка ${{left( x-a right)}^{n}}$ даёт нам корень $x=a$ кратности $n$, а вот скобка $left( {{x}^{n}}-a right)$ или, как часто бывает, $(a-{{x}^{n}})$ даёт нам корень (или два корня, если $n$ — чётное) первой кратности вне зависимости от того, чему равно $n$.

Сравните:

[{{left( x-3 right)}^{5}}=0Rightarrow x=3left( 5k right)]

Здесь всё чётко: вся скобка возводилась в пятую степень, поэтому на выходе мы получили корень пятой степени. А теперь:

[left( {{x}^{2}}-4 right)=0Rightarrow {{x}^{2}}=4Rightarrow x=pm 2]

Мы получили два корня, но оба они имеют первую кратность. Или вот ещё:

[left( {{x}^{10}}-1024 right)=0Rightarrow {{x}^{10}}=1024Rightarrow x=pm 2]

И пусть вас не смущает десятая степень. Главное, что 10 — это чётное число, поэтому на выходе имеем два корня, и оба они вновь имеют первую кратность.

В общем будьте внимательны: кратность возникает только тогда, когда степень относится ко всей скобке, а не только к переменной.

Задача. Решите неравенство:

[frac{{{x}^{2}}{{left( 6-x right)}^{3}}left( x+4 right)}{{{left( x+7 right)}^{5}}}ge 0]

Решение. Попробуем решить её альтернативным способом — через переход от частного к произведению:

[left{ begin{align} & {{x}^{2}}{{left( 6-x right)}^{3}}left( x+4 right)cdot {{left( x+7 right)}^{5}}ge 0, \ & {{left( x+7 right)}^{5}}ne 0. \ end{align} right.]

Разбираемся с первым неравенством методом интервалов:

[begin{align} & {{x}^{2}}{{left( 6-x right)}^{3}}left( x+4 right)cdot {{left( x+7 right)}^{5}}=0; \ & {{x}^{2}}=0Rightarrow x=0left( 2k right); \ & {{left( 6-x right)}^{3}}=0Rightarrow x=6left( 3k right); \ & x+4=0Rightarrow x=-4; \ & {{left( x+7 right)}^{5}}=0Rightarrow x=-7left( 5k right). \ end{align}]

Дополнительно решаем второе неравенство. На самом деле мы уже решали его, но чтобы проверяющие не придрались к решению, лучше решить его ещё раз:

[{{left( x+7 right)}^{5}}ne 0Rightarrow xne -7]

Обратите внимание: никаких кратностей в последнем неравенстве нет. В самом деле: какая разница, сколько раз вычёркивать точку $x=-7$ на числовой прямой? Хоть один раз, хоть пять — результат будет один и тот же: выколотая точка.

Отметим всё, что мы получили, на числовой прямой:

Как я и говорил, точка $x=-7$ в итоге будет выколота. Кратности расставлены исходя из решения неравенства методом интервалов.

Осталось расставить знаки:

Поскольку точка $x=0$ является корнем чётной кратности, знак при переходе через неё не меняется. Остальные точки имеют нечётную кратность, и с ними всё просто.

Ответ. $xin left( -infty ;-7 right)bigcup left[ -4;6 right]$

Ещё раз обратите внимание на $x=0$. Из-за чётной кратности возникает интересный эффект: слева от неё всё закрашено, справа — тоже, да и сама точка вполне себе закрашена.

Как следствие, её не нужно обособлять при записи ответа. Т.е. не надо писать что-нибудь в духе $xin left[ -4;0 right]bigcup left[ 0;6 right]$ (хотя формально такой ответ тоже будет правильным). Вместо этого сразу пишем $xin left[ -4;6 right]$.

Такие эффекты возможны только при корнях чётной кратности. И в следующей задаче мы столкнёмся с обратным «проявлением» этого эффекта. Готовы?

Задача. Решите неравенство:

[frac{{{left( x-3 right)}^{4}}left( x-4 right)}{{{left( x-1 right)}^{2}}left( 7x-10-{{x}^{2}} right)}ge 0]

Решение. В этот раз пойдём по стандартной схеме. Приравниваем к нулю числитель:

[begin{align} & {{left( x-3 right)}^{4}}left( x-4 right)=0; \ & {{left( x-3 right)}^{4}}=0Rightarrow {{x}_{1}}=3left( 4k right); \ & x-4=0Rightarrow {{x}_{2}}=4. \ end{align}]

И знаменатель:

[begin{align} & {{left( x-1 right)}^{2}}left( 7x-10-{{x}^{2}} right)=0; \ & {{left( x-1 right)}^{2}}=0Rightarrow x_{1}^{*}=1left( 2k right); \ & 7x-10-{{x}^{2}}=0Rightarrow x_{2}^{*}=5; x_{3}^{*}=2. \ end{align}]

Поскольку мы решаем нестрогое неравенство вида $fleft( x right)ge 0$, корни из знаменателя (которые со звёздочками) будут выколоты, а из числителя — закрашены.

Расставляем знаки и штрихуем области, отмеченные «плюсом»:

Перед тем, как записать окончательный ответ, внимательно посмотрим на картинку:

1. Точка $x=1$ имеет чётную кратность, но сама выколота. Следовательно, её придётся обособить в ответе: нужно записать $xin left( -infty ;1 right)bigcup left( 1;2 right)$, а никак не $xin left( -infty ;2 right)$.
2. Точка $x=3$ тоже имеет чётную кратность и при этом закрашена. Расстановка знаков свидетельствует, что сама точка нас устраивает, но шаг влево-вправо — и мы попадаем в область, которая нас точно не устраивает. Такие точки называются изолированными и записываются в виде $xin left{ 3 right}$.

Объединяем все полученные кусочки в общее множество и записываем ответ.

Ответ: $xin left( -infty ;1 right)bigcup left( 1;2 right)bigcup left{ 3 right}bigcup left[ 4;5 right)$

Прежде чем мы пойдём дальше, хотелось бы ещё раз напомнить, что означает термин «решить неравенство» (любое — не обязательно дробно-рациональное). А означает он буквально следующее:

Определение. Решить неравенство — значит найти множество всех его решений, либо доказать, что это множество пусто.

Казалось бы: что тут может быть непонятны? Да в том-то и дело, что множества можно задавать по-разному. Давайте ещё раз выпишем ответ к последней задаче:

[xin left( -infty ;1 right)bigcup left( 1;2 right)bigcup left{ 3 right}bigcup left[ 4;5 right)]

Читаем буквально, что написано. Переменная «икс» принадлежит некому множеству, которое получается объединением (значок «U») четырёх отдельных множеств:

• Интервал $left( -infty ;1 right)$, который буквально означает «все числа, меньшие единицы, но не сама единица»;
• Интервал $left( 1;2 right)$, т.е. «все числа в пределах от 1 до 2, но не сами числа 1 и 2»;
• Множество $left{ 3 right}$, состоящее из одного-единственного числа — тройки;
• Интервал $left[ 4;5 right)$, содержащий все числа в пределах от 4 до 5, а также саму четвёрку, но не пятёрку.

Интерес здесь представляет третий пункт. В отличие от интервалов, которые задают бесконечные наборы чисел и лишь обозначают лишь границы этих наборов, множество $left{ 3 right}$ задаёт строго одно число путём перечисления.

Чтобы понять, что мы именно перечисляем конкретные числа, входящие в множество (а не задаём границы или что-либо ещё), используются фигурные скобки. Например, запись $left{ 1;2 right}$ означает именно «множество, состоящее из двух чисел: 1 и 2», но никак не отрезок от 1 до 2. Ни в коем случае не путайте эти понятия.

Правило сложения кратностей

Ну и в заключение сегодняшнего урока немного жести от Павла Бердова.:)

Внимательные ученики уже наверняка задались вопросом: а что будет, если в числителе и знаменателе обнаружатся одинаковые корни? Так вот, работает следующее правило:

Кратности одинаковых корней складываются. Всегда. Даже если этот корень встречается и в числителе, и в знаменателе.

Иногда лучше решать, чем говорить. Поэтому решаем следующую задачу:

Задача. Решите неравенство:

[frac{{{x}^{2}}+6x+8}{left( {{x}^{2}}-16 right)left( {{x}^{2}}+9x+14 right)}ge 0]

Решение. Приравниваем к нулю числитель:

[begin{align} & {{x}^{2}}+6x+8=0 \ & {{x}_{1}}=-2; {{x}_{2}}=-4. \ end{align}]

Пока ничего особенного. Приравниваем к нулю знаменатель:

[begin{align} & left( {{x}^{2}}-16 right)left( {{x}^{2}}+9x+14 right)=0 \ & {{x}^{2}}-16=0Rightarrow x_{1}^{*}=4; x_{2}^{*}=-4; \ & {{x}^{2}}+9x+14=0Rightarrow x_{3}^{*}=-7; x_{4}^{*}=-2. \ end{align}]

Обнаружены два одинаковых корня: ${{x}_{1}}=-2$ и $x_{4}^{*}=-2$. Оба имеют первую кратность. Следовательно заменяем их одним корнем $x_{4}^{*}=-2$, но уже с кратностью 1+1=2.

Кроме того, есть ещё одинаковые корни: ${{x}_{2}}=-4$ и $x_{2}^{*}=-4$. Они тоже первой кратности, поэтому останется лишь $x_{2}^{*}=-4$ кратности 1+1=2.

Обратите внимание: в обоих случаях мы оставили именно «выколотый» корень, а «закрашенный» выкинули из рассмотрения. Потому что ещё в начале урока договорились: если точка одновременно и выколотая, и закрашенная, то мы всё равно считаем её выколотой.

В итоге у нас есть четыре корня, причём все оказались выколоты:

[begin{align} & x_{1}^{*}=4; \ & x_{2}^{*}=-4left( 2k right); \ & x_{3}^{*}=-7; \ & x_{4}^{*}=-2left( 2k right). \ end{align}]

Отмечаем их на числовой прямой с учётом кратности:

Расставляем знаки и закрашиваем интересующие нас области:

Всё. Никаких изолированных точек и прочих извращений. Можно записывать ответ.

Ответ. $xin left( -infty ;-7 right)bigcup left( 4;+infty right)$.

Правило умножения кратностей

Иногда встречается ещё более неприятная ситуация: уравнение, имеющее кратные корни, само возводится в некоторую степень. При этом меняются кратности всех исходных корней.

Такое встречается редко, поэтому большинство учеников не имеют опыта решения подобных задач. А правило здесь следующее:

При возведении уравнения в степень $n$ кратности всех его корней тоже увеличиваются в $n$ раз.

Другими словами, возведение в степень приводит к умножению кратностей на эту же степень. Рассмотрим это правило на примере:

Задача. Решите неравенство:

[frac{x{{left( {{x}^{2}}-6x+9 right)}^{2}}{{left( x-4 right)}^{5}}}{{{left( 2-x right)}^{3}}{{left( x-1 right)}^{2}}}le 0]

Решение. Приравниваем к нулю числитель:

[x{{left( {{x}^{2}}-6x+9 right)}^{2}}{{left( x-4 right)}^{5}}=0]

Произведение равно нулю, когда хотя бы один из множителей равен нулю. С первым множителем всё понятно: $x=0$. А вот дальше начинаются проблемы:

[begin{align} & {{left( {{x}^{2}}-6x+9 right)}^{2}}=0; \ & {{x}^{2}}-6x+9=0left( 2k right); \ & D={{6}^{3}}-4cdot 9=0 \ & {{x}_{2}}=3left( 2k right)left( 2k right) \ & {{x}_{2}}=3left( 4k right) \ end{align}]

Как видим, уравнение ${{x}^{2}}-6x+9=0$ имеет единственный корень второй кратности: $x=3$. Затем всё это уравнение возводится в квадрат. Следовательно, кратность корня составит $2cdot 2=4$, что мы в итоге и записали.

Дальше — стандартно:

[{{left( x-4 right)}^{5}}=0Rightarrow x=4left( 5k right)]

Со знаменателем тоже никаких проблем:

[begin{align} & {{left( 2-x right)}^{3}}{{left( x-1 right)}^{2}}=0; \ & {{left( 2-x right)}^{3}}=0Rightarrow x_{1}^{*}=2left( 3k right); \ & {{left( x-1 right)}^{2}}=0Rightarrow x_{2}^{*}=1left( 2k right). \ end{align}]

В сумме у нас получилось пять точек: две выколотых и три закрашенных. Совпадающих корней в числителе и знаменателе не наблюдается, поэтому просто отмечаем их на числовой прямой:

Расставляем знаки с учётом кратностей и закрашиваем интересующие нас интервалы:

Из-за корней чётной кратности вновь получили парочку «нестандартных» элементов. Это $xin left[ 0;1 right)bigcup left( 1;2 right)$, а никак не $xin left[ 0;2 right)$, а также изолированная точка $xin left{ 3 right}$.

Ответ. $xin left[ 0;1 right)bigcup left( 1;2 right)bigcup left{ 3 right}bigcup left[ 4;+infty right)$

Как видите, всё не так сложно. Главное — внимательность. Последний раздел этого урока посвящён преобразованиям — тем самым, которые мы обсуждали в самом начале.

Предварительные преобразования

Неравенства, которые мы разберём в этом разделе, нельзя назвать сложными. Однако в отличие от предыдущих задач здесь придётся применить навыки из теории рациональных дробей — разложение на множители и приведение к общему знаменателю.

Мы детально обсуждали этот вопрос в самом начале сегодняшнего урока. Если вы не уверены, что понимаете, о чём речь — настоятельно рекомендую вернуться и повторить. Потому что нет никакого смысла зубрить методы решения неравенств, если вы «плаваете» в преобразовании дробей.

В домашней работе, кстати, тоже будет много подобных задач. Они вынесены в отдельный подраздел. И там вас ждут весьма нетривиальные примеры. Но это будет в домашке, а сейчас давайте разберём парочку таких неравенств.

Задача. Решите неравенство:

[frac{x}{x-1}le frac{x-2}{x}]

Решение. Переносим всё влево:

[frac{x}{x-1}-frac{x-2}{x}le 0]

Приводим к общему знаменателю, раскрываем скобки, приводим подобные слагаемые в числителе:

[begin{align} & frac{xcdot x}{left( x-1 right)cdot x}-frac{left( x-2 right)left( x-1 right)}{xcdot left( x-1 right)}le 0; \ & frac{{{x}^{2}}-left( {{x}^{2}}-2x-x+2 right)}{xleft( x-1 right)}le 0; \ & frac{{{x}^{2}}-{{x}^{2}}+3x-2}{xleft( x-1 right)}le 0; \ & frac{3x-2}{xleft( x-1 right)}le 0. \end{align}]

Теперь перед нами классическое дробно-рациональное неравенство, решение которого уже не представляет трудности. Предлагаю решить его альтернативным методом — через метод интервалов:

[begin{align} & left( 3x-2 right)cdot xcdot left( x-1 right)=0; \ & {{x}_{1}}=frac{2}{3}; {{x}_{2}}=0; {{x}_{3}}=1. \ end{align}]

Не забываем ограничение, пришедшее из знаменателя:

[xleft( x-1 right)ne 0Rightarrow xne 0;xne 1]

Отмечаем все числа и ограничения на числовой прямой:

Все корни имеют первую кратность. Никаких проблем. Просто расставляем знаки и закрашиваем нужные нам области:

Это всё. Можно записывать ответ.

Ответ. $xin left( -infty ;0 right)bigcup left[ {2}/{3};;1 right)$.

Разумеется, это был совсем уж просто пример. Поэтому сейчас рассмотрим задачу посерьёзнее. И кстати, уровень этой задачи вполне соответствует самостоятельным и контрольным работам по этой теме в 8 классе.

Задача. Решите неравенство:

[frac{1}{{{x}^{2}}+8x-9}ge frac{1}{3{{x}^{2}}-5x+2}]

Решение. Переносим всё влево:

[frac{1}{{{x}^{2}}+8x-9}-frac{1}{3{{x}^{2}}-5x+2}ge 0]

Перед тем как приводить обе дроби к общему знаменателю, разложим эти знаменатели на множители. Вдруг вылезут одинаковы скобки? С первым знаменателем легко:

[{{x}^{2}}+8x-9=left( x-1 right)left( x+9 right)]

Со вторым чуть сложнее. Не стесняйтесь вносить множитель-константу в ту скобку, где обнаружилась дробь. Помните: исходный многочлен имел целые коэффициенты, поэтому велика вероятность, что и разложение на множители будет иметь целые коэффициенты (на самом деле так будет всегда, за исключением случаев, когда дискриминант иррационален).

[begin{align} & 3{{x}^{2}}-5x+2=3left( x-1 right)left( x-frac{2}{3} right)= \ & =left( x-1 right)left( 3x-2 right) end{align}]

Как видим, есть общая скобка: $left( x-1 right)$. Возвращаемся к неравенству и приводим обе дроби к общему знаменателю:

[begin{align} & frac{1}{left( x-1 right)left( x+9 right)}-frac{1}{left( x-1 right)left( 3x-2 right)}ge 0; \ & frac{1cdot left( 3x-2 right)-1cdot left( x+9 right)}{left( x-1 right)left( x+9 right)left( 3x-2 right)}ge 0; \ & frac{3x-2-x-9}{left( x-1 right)left( x+9 right)left( 3x-2 right)}ge 0; \ & frac{2x-11}{left( x-1 right)left( x+9 right)left( 3x-2 right)}ge 0; \ end{align}]

Дальше легко. Приравниваем к нулю числитель.

[2x-11=0Rightarrow x=5,5]

Приравниваем к нулю знаменатель:

[begin{align} & left( x-1 right)left( x+9 right)left( 3x-2 right)=0; \ & x_{1}^{*}=1; x_{2}^{*}=-9; x_{3}^{*}=frac{2}{3} \ end{align}]

Никаких кратностей и совпадающих корней. Отмечаем четыре числа на прямой:

Расставляем знаки:

Записываем ответ.

Ответ: $xin left( -infty ;-9 right)bigcup left( {2}/{3};;1 right)bigcup left[ 5,5;+infty right)$.

Всё! Лайк тому, то дочитал до этой строчки.:)

Смотрите также:

1. Тест по методу интервалов для строгих неравенств
2. Особенности решения неравенств с радикалами
3. Комбинаторика в задаче B6: легкий тест
4. Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
5. Задача B2: лекарство и таблетки
6. ЕГЭ 2022, задание 6. Касательная к графику функции