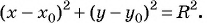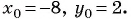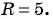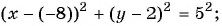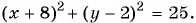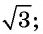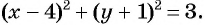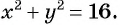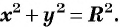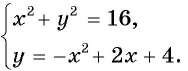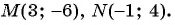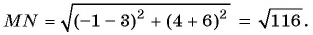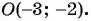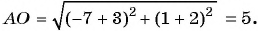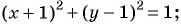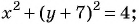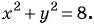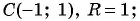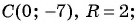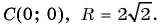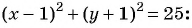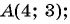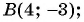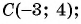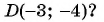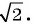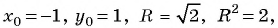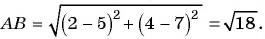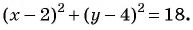Тип 8 № 27967
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: где l − длина ребра куба в метрах,
кг/м3 − плотность воды, а g − ускорение свободного падения (считайте
Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
ЕГЭ Профиль №13. Рациональные уравнения
«Решение целых и дробно рациональных уравнений.»
материал для подготовки к егэ (гиа) по алгебре (11 класс)
Использованный материал можно применять для подготовки к ЕГЭ в 11 классе
Скачать:
| Вложение | Размер |
|---|---|
| dlya_podgotovki_k_ege_po_matematike_10-11klass.docx | 62.17 КБ |
Предварительный просмотр:
Тема «Решение целых и дробно рациональных уравнений.»
Учитель: Незнамова Н.И
( Использовать при подготовке к ЕГЭ в 11 классе)
Рациональные уравнения – это уравнения, в которых и левая, и правая части рациональные выражения.
Этапы решения рационального уравнения.
- Определить ОДЗ (ни один знаменатель не может равняться нулю).
- Найти наименьший общий знаменатель всех дробей.
- Умножить уравнение на этот знаменатель и решить полученное целое уравнение.
- Включить в ответ только те корни, которые входят в ОДЗ.
Решение целых уравнений
Решение таких уравнений обычно сводится к преобразованию их в равносильные алгебраические уравнения. Достичь этого можно путем проведения равносильных преобразований уравнений в соответствии со следующим алгоритмом:
- сначала получим ноль в правой части уравнения, для этого на необходимо перенести выражение, которое находится в правой части уравнения, в его левую часть и поменять знак;
- затем преобразуем выражение в левой части уравнения в многочлен стандартного вида.
Мы должны получить алгебраическое уравнение. Это уравнение будет равносильным по отношению к исходному уравнению. Легкие случаи позволяют нам для решения задачи свести целое уравнение с линейному или квадратному. В общем случае мы решаем алгебраическое уравнение степени n
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Дробь равна 0 тогда и только тогда, когда ее числитель равен 0, а знаменатель не равен 0.
Получаем следующую систему:
Первое уравнение системы – это квадратное уравнение. Прежде чем его решать, поделим все его коэффициенты на 3. Получим:
Коэффициенты данного уравнения: . Вычисляем дискриминант:
Далее, по формуле корней квадратного уравнения находим:
Получаем два корня: ; .
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Поскольку 2 никогда не равно 0, то необходимо, чтобы выполнялись два условия: . Поскольку ни один из полученных выше корней уравнения не совпадает с недопустимыми значениями переменной, которые получились при решении второго неравенства, они оба являются решениями данного уравнения.
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе:
Первое уравнение системы – это квадратное уравнение.
Коэффициенты данного уравнения: . Вычисляем дискриминант:
Далее, по формуле корней квадратного уравнения находим:
Получаем два корня: ; .
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия: . Получаем, что из двух корней первого уравнения подходит только один – 3.
Раскрыв скобки в знаменателях, получаем уравнение:
Полагая, что x 2 + 3х + 2 = t ,приходим к системе уравнений
Решив первое уравнение системы, получаем корни t 1 = 2, t 2 = 18. Далее, из второго уравнения системы, получаем корни исходного уравнения: .
Прибавим к числителю второй дроби выражение 2 х — 2 х , тождественно равное нулю:
Решив первое уравнение системы, получаем корни: t 1 = -1, t 2 = 2. Из второго уравнения системы, получаем корни исходного уравнения:
По теме: методические разработки, презентации и конспекты
Урок алгебры 8 класс «Решение дробно-рациональных уравнений»
Приводится конспект урока по алгебре в 8 классе по теме «Решение дробно-рациональных уравнений».
Решение дробных рациональных уравнений
Презентация содержит демонстрационный материал к обяснению нового материала по теме «Решение дробных рациональных уравнений». Учебник Макарычева Ю.Н. и др. «Алгебра 8».
Решение дробно — рациональных уравнений с модулем.
Данная презентация разработана для подготовки учащихся 10 классса к КДР, может быть полезна для подготовки учащихся 11 класса к ЕГЭ.
Урок алгебры в 8-м классе «Решение дробно-рациональных уравнений»
Урок закрепления изученного материала проводится в форме игры «Лабиринт». Задания в лабиринте дифференцированы по уровням сложности, что позволяет учащимся выбрать наиболее походящий для себя режим ра.
Урок в 8 классе»Решение дробных рациональных уравнений»
Урок формирования умений и навыков.
урок алгебры в 8 классе по теме «Решение задач с помощью дробных рациональных уравнений»
урок — путешествие по городам Белгородской области (с презентацией).
Алгебра. 8 класс. Решение задач с дробно рациональными уравнениями, которые сводятся к квадратным уравнениям.
Алгебра. 8 класс. Решение задач с дробно рациональными уравнениями, которые сводятся к квадратным уравнениям.
Рациональные уравнения
Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.
Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.
$<2>/+5x=7$ – рациональное уравнение
$3x+√x=7$ — иррациональное уравнение (содержит корень)
Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль общий знаменатель.
Решить уравнение: $4x+1-<3>/=0$
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
3. решаем полученное уравнение
Решим вторым устным способом, т.к. $а+с=b$
4. исключаем те корни, при которых общий знаменатель равен нулю
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
Воспользуемся основным свойством пропорции
Раскроем скобки и соберем все слагаемые в левой стороне
Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$
В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Дробно рациональные уравнения
Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .
Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .
Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.
ОДЗ – область допустимых значений переменной.
В выражении вида f ( x ) g ( x ) = 0
ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).
Алгоритм решения дробно рационального уравнения:
- Привести выражение к виду f ( x ) g ( x ) = 0 .
- Выписать ОДЗ: g ( x ) ≠ 0.
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Пример решения дробного рационального уравнения:
Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.
Решение:
Будем действовать в соответствии с алгоритмом.
- Привести выражение к виду f ( x ) g ( x ) = 0 .
Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:
x 2 − 4 2 − x − 1 2 − x = 0
x 2 − 4 2 − x − 2 − x 2 − x = 0
x 2 − 4 − ( 2 − x ) 2 − x = 0
x 2 − 4 − 2 + x 2 − x = 0
x 2 + x − 6 2 − x = 0
Первый шаг алгоритма выполнен успешно.
Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:
x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.
a = 1, b = 1, c = − 6
D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25
D > 0 – будет два различных корня.
x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Корни, полученные на предыдущем шаге:
Значит, в ответ идет только один корень, x = − 3.
Задания для самостоятельного решения
№1. Решите уравнение: 3 x − 19 = 19 x − 3 .
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
3 x − 19 = 19 x − 3
[ x − 19 ≠ 0 x − 3 ≠ 0 ⇒ [ x ≠ 19 x ≠ 3
Приводим обе дроби к общему знаменателю, записываем дополнительные множители к числителям:
3 ( x − 3 ) x − 19 − 19 ( x − 19 ) x − 3 = 0
3 ( x − 3 ) − 19 ( x − 19 ) ( x − 19 ) ( x − 3 ) = 0
В соответствии с алгоритмом, приравниваем числитель к нулю:
3 x − 9 − 19 x + 361 = 0
x = − 352 − 16 = − 352 16 = 22
Полученный корень не входит в ОДЗ, так что смело можем его включать в ответ.
№2. Решите уравнение x − 4 x − 6 = 2.
Решение:
Можно решать эту задачу способом, который использовался при решении задачи №8. Но сейчас мы используем еще один способ решения таких уравнений.
Представим число 2 в виде дроби со знаменателем 1 .
Воспользуемся основным свойством пропорции :
произведение крайних членов равно произведению средних (правило «креста»):
a b = c d ⇒ a ⋅ d = b ⋅ c
x − 4 x − 6 = 2 1 ⇒ ( x − 4 ) ⋅ 1 = ( x − 6 ) ⋅ 2
Полученный корень не входит в ОДЗ, так что смело можем его включать в ответ.
источники:
http://examer.ru/ege_po_matematike/teoriya/racionalnye_uravneniya
http://epmat.ru/drobno-racionalnye-uravnenija/
Целые рациональные уравнения
Важно знать, что рациональные уравнения в свою очередь тоже разные бывают.
Если в дроби нет деления на переменную (то есть на ( displaystyle x), ( displaystyle y) и т.д.), тогда рациональное уравнение будет называться целым (или линейным) уравнением, вот примеры:
( displaystyle begin{array}{l}frac{2x}{3}=13-frac{3x}{2};\4(2y-3)=y-9.end{array})
Умеешь такие решать? – конечно, умеешь, упрощаешь и находишь неизвестное, тема-то 5-ого или 6-ого класса.
Ну, рассмотрим первый из примеров на всякий случай и по порядочку. Все неизвестные переносим влево, все известные вправо:
( displaystyle frac{2x}{3}+frac{3x}{2}=13);
Какой наименьший общий знаменатель будет?
Правильно ( displaystyle 6)!
Чтоб к нему привести домножаем и числитель и знаменатель первого слагаемое на ( displaystyle 2), а второго на ( displaystyle 3), этого делать не запрещено, если и числитель и знаменатель дроби умножить на одно и то же значение, то дробь от этого не изменится, т.к. ее можно будет сократить на то же число.
А ( displaystyle 13) не трогаем, оно нам не мешает, имеем:
( displaystyle frac{4x}{6}+frac{9x}{6}=13)
( displaystyle frac{13x}{6}=13),
А теперь делим обе части на ( displaystyle 13):
( displaystyle begin{array}{l}frac{x}{6}=1\x=6end{array})
Тут все просто?
Поскольку уравнение целое, что мы уже определили, то и ограничений никаких нет, ( displaystyle 6), так ( displaystyle 6), ну можно для верности подставить этот ответ в исходное уравнение, получим ( displaystyle 0=0), значит все верно и ответ подходит (ты можешь пересчитать, а вообще должно сойтись).
Дробно-рациональные уравнения
А вот еще одно уравнение ( displaystyle frac{5}{x+1}+frac{4{x}-6}{(x+1)cdot (x+3)}=3).
Это уравнение целое? НЕТ!!! Тут есть деление на переменную ( displaystyle x), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.
Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.
Для начала найдем наименьший общий знаменатель, это будет ( displaystyle (x+1)cdot (x+3)).
Важный момент!
В предыдущем примере, где было целое уравнение мы не стали свободный член ( displaystyle 13) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель ( displaystyle (x+1)cdot (x+3)).
А это тебе не шутки, переменная в знаменателе!
Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!
Это надеюсь, ты запомнишь, но давай посмотрим что вышло:
( displaystyle frac{5(x+1)cdot (x+3)}{x+1}+frac{(4{x}-6)cdot (x+1)cdot (x+3)}{(x+1)cdot (x+3)}=3cdot (x+1)cdot (x+3)).
Что-то оно огромное получилось, надо все посокращать:
( displaystyle 5(x+3)+(4{x}-6)=3cdot (x+1)cdot (x+3)).
Раскроем скобки и приведем подобные члены:
( displaystyle begin{array}{l}9x+9=3{{x}^{2}}+12x+9\3{{x}^{2}}+3x=0.end{array})
Ну как, это уже попроще выглядит, чем в начале было?
Выносим за скобку общий множитель: ( displaystyle 3xcdot (x+1)=0)
У этого уравнения два решения, его левая сторона принимает нулевое значение при ( displaystyle x=0) и ( displaystyle x=-1).
Вроде бы все, ну ладно давайте напоследок подставим корни ( displaystyle x=0) и ( displaystyle x=-1) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим ( displaystyle 0), получается ( displaystyle 3=3) –нет претензий?
С ним все нормально. А теперь ( displaystyle -1), и тут же видим в знаменателе первого члена ( displaystyle -1+1)!
Но ведь это же будет ноль!
На ноль делить нельзя, это все знают, в чем же дело???
Дело в ОДЗ – Области Допустимых Значений!
(если забыл что это, повтори тему «ОДЗ – область допустимых значений»!)
Всякий раз когда ты видишь уравнение, где есть переменные (( displaystyle x,y) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс.
Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.
Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:
ОДЗ: ( displaystyle x+1ne 0) и ( displaystyle x+3ne 0) ( displaystyle Rightarrow xne -1) и ( displaystyle xne -3).
Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами ( displaystyle x=0) и ( displaystyle x=-1) мы смело исключаем ( displaystyle x=-1), т.к. он противоречит ОДЗ.
Значит, какой ответ будет у решенного уравнения?
В ответ стоит написать только один корень, ( displaystyle x=0).
Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.
Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,
ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!
Рациональные выражения, уравнения и дробно-рациональные уравнения
Повторим еще раз то, что прошил в предыдущих разделах, больше используя язык математики.
Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной ( displaystyle x) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Ну а рациональное уравнение – это равенство двух рациональных выражений.
Дробно-рациональные уравнения – рациональные (без знака корня) уравнения, в которых левая или правая части являются дробными выражениями.
Например:
( displaystyle frac{{{x}^{2}}-2{x}-3}{{x}-1}-frac{x+1}{{x}-3}={{x}^{2}}-1) (чаще всего мы встречаем именно дробно рациональные уравнения).
В общем случае при решении рациональных уравнений мы стремимся преобразовать его к виду: Произведение = “( displaystyle 0)” или Дробь = “( displaystyle 0)“, например:
( displaystyle frac{left( {x}-2 right)left( x+3 right)left( {{x}^{2}}+1 right)}{xcdot left( {x}-3 right)}=0).
Тогда мы сможем сказать, что любой из множителей числителя может быть равен нулю, но знаменатель при этом нулю не равен.
Для этого нам нужно сначала всё перенести в левую часть уравнения (не забываем при этом поменять знаки между слагаемыми: “( displaystyle +)” на “( displaystyle –)” и наоборот).
Затем мы обычно приводим все к общему знаменателю, и пишем систему:
( displaystyle left{ begin{array}{l}Числитель=0,\Знаменательne 0.end{array} right.)
Например:
( displaystyle begin{array}{l}frac{{x}-2}{{{x}^{2}}+2{x}-3}-frac{x+1}{{{x}^{2}}+5x+6}=frac{3}{x+3}Leftrightarrow \Leftrightarrow frac{{x}-2}{left( {x}-1 right)left( x+3 right)}-frac{x+1}{left( x+2 right)left( x+3 right)}-frac{3}{x+3}=0Leftrightarrow end{array})
( displaystyle Leftrightarrow frac{{{x}^{2}}-4-left( {{x}^{2}}-1 right)-3left( {{x}^{2}}+{x}-2 right)}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow frac{-3{{x}^{2}}-3x+3}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow )
( displaystyle Leftrightarrow left{ begin{array}{l}{{x}^{2}}+{x}-1=0\left( {x}-1 right)left( x+2 right)left( x+3 right)ne 0end{array} right.Leftrightarrow left{ begin{array}{l}left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}end{array} right.\xne 1\xne -2\xne -3end{array} right.Leftrightarrow left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}.end{array} right.)
Если знаменателя нет, или он является числом, – тем лучше, не придется решать неравенство.
Как бы то ни было, в ЕГЭ все рациональные выражения степени больше ( displaystyle 2) легко преобразуются в произведение более простых выражений при помощи либо перегруппировки, либо замены переменных (см. раздел «Разложение многочлена на множители»).
Дробно-рациональные уравнения — это уравнения c одной переменной.
Содержание:
Определение дробно-рационального уравнения
Определение дробно-рационального уравнения:
Например, уравнения
являются дробно-рациональными.
Рассмотрим дробно-рациональное уравнение 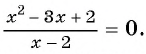
Рациональная дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю.
Таким образом, получим:
Ответ: 1.
Вернемся к уравнению 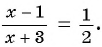
1) Перенесем все слагаемые из правой части уравнения в левую:
2) Преобразуем левую часть уравнения к рациональной дроби:
3) Применим условие равенства дроби нулю:
Ответ: 5.
Что нужно для решения дробно-рационального уравнения
Чтобы решить дробно-рациональное уравнение, нужно:
- Перенести все слагаемые из правой части уравнения в левую.
- Преобразовать левую часть уравнения к рациональной дроби.
- Применить условие равенства дроби нулю.
- Записать ответ.
Рассмотрим задачу: В дроби числитель на 2 больше знаменателя. Если числитель этой дроби уменьшить на 3, а знаменатель увеличить на 3, то новая дробь будет равна 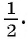
Решение:
Обозначим знаменатель первоначальной дроби через х, тогда ее числитель равен
Если числитель дроби уменьшить на 3, то получится числитель новой дроби: 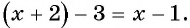
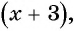
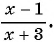
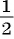
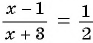
Решение многих задач приводит к уравнениям, у которых в левой или правой (или в той и другой) частях записаны дробные рациональные выражения. Такие уравнения называют дробно-рациональными уравнениями.
Пример №1
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ:
Пример №2
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ:
Пример №3
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ: -2; 6.
Пример №4
Решите уравнение
Решение:
Выполним замену переменной 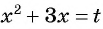
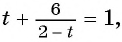
Подставим найденные значения 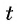
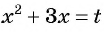
Ответ:
Дробно-рациональные уравнения используются как математические модели для решения задач, описывающих реальные ситуации.
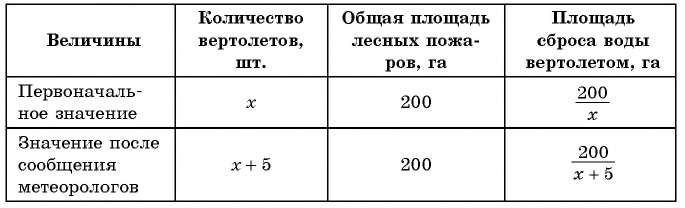
Например, рассмотрим задачу. На тушение лесных пожаров площадью 200 га отправлено несколько вертолетов с водосливными устройствами. По информации метеорологов предполагается усиление ветра, поэтому было выделено еще 5 вертолетов, в связи с чем площадь для сброса воды каждым вертолетом уменьшилась на 20 га. Сколько вертолетов участвовало в тушении пожаров первоначально?
Решение:
(1) Выясним, о каких величинах и зависимостях между ними в задаче идет речь. В задаче речь идет о площади лесных пожаров и количестве вертолетов для тушения пожаров.
(2) Выясним, какие значения, величин и зависимости между ними, известны. Известна зависимость между количеством вертолетов и площадью для сброса воды.
(3) Выясним, какие значения величин и зависимости между ними не известны. Неизвестно, сколько потребовалось вертолетов.
(4) Обозначим неизвестное значение одной величины через х, а остальные выразим через х и зависимости между величинами. Обозначим через 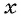
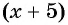
(5) Используя зависимости между известными и неизвестными значениями величин, составим уравнение (математическую модель задачи) и решим его.
По условию задачи 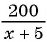
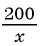
(6) Запишем ответ в соответствии со смыслом задачи. Поскольку 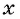
Ответ: 5 вертолетов.
Многие задачи, описывающие реальные процессы, имеют одну и ту же математическую модель. К таким относятся, например, задачи на движение, работу и т. п.
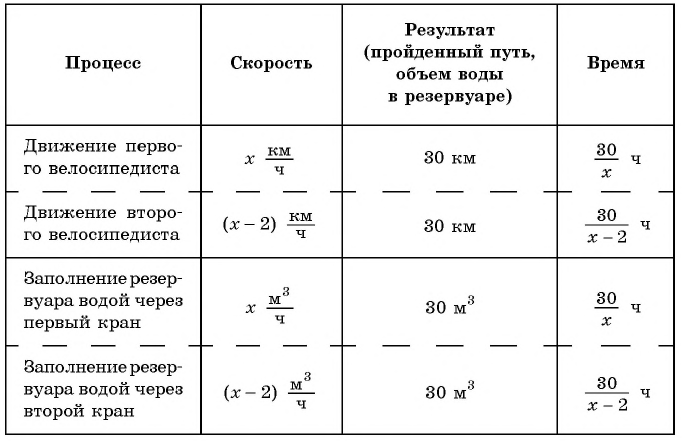
Рассмотрим две задачи:
Задача 1. Два велосипедиста выехали одновременно из поселка 
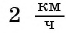
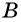
Задача 2. Для заполнения водой резервуара объемом 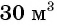
В обеих задачах речь идет о процессах: в первой — о процессе движения, во второй — о процессе заполнения резервуара водой.
Составим таблицу зависимостей между величинами.
Поскольку первый велосипедист прибыл в поселок на 0,5 ч раньше второго, а один кран заполняет резервуар на 0,5 ч быстрее другого, то уравнение 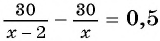
Решим полученное уравнение:
По условию каждой задачи подходит число 12.
Ответ задачи 1: скорость первого велосипедиста 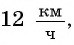
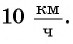
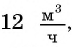
Пример №5
Является ли дробно-рациональным уравнение:
а)
б)
в)
г)
Решение:
Уравнение а) не является дробно-рациональным, так как его левая и правая части — целые рациональные выражения. Уравнения б)—г) являются дробно-рациональными, так как левые части этих уравнений — дробно-рациональные выражения.
Пример №6
Решите уравнение, используя условие равенства дроби нулю:
а)
б)
в)
г)
Решение:
а)
Ответ: 6.
б)
Ответ: -6.
в)
Ответ: 0; 6.
г)
Ответ: нет корней.
Пример №7
Какие из уравнений:
а)
б)
в)
г) 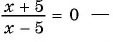
Решение:
а)
б)
в)
г)
Ответ: уравнения а), в), г) имеют один и тот же корень (уравнения равносильны).
Пример №8
Решите уравнение:
а)
б)
Решение:
а) (1)
(2)
(3)
(4) Ответ: 1; 2.
б)
Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
Ответ: 2,5.
Пример №9
Найдите нули функции
Решение:
Так как нули функции — это значения аргумента, при которых значение функции равно нулю, то для решения задачи нужно решить уравнение
Используем условие равенства дроби нулю:
Ответ: 0; 3.
Пример №10
Найдите корни уравнения
Решение:
Выполним замену переменной в данном уравнении: 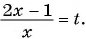
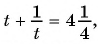
Решим его:
Выполним подстановку найденных значений переменной 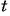
Ответ:
Моделирование реальных процессов с помощью дробно-рациональных уравнении
Задача:
Катер прошел 15 км по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Чему равна скорость катера при движении по озеру, если скорость течения реки 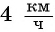
Решение:
В задаче идет речь о процессах движения катера по реке и по озеру. Составим таблицу зависимостей между величинами.
Так как по условию задачи на весь путь затрачен 1 ч, то составим уравнение: 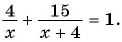
По условию подходит число 16.
Ответ: 16
Системы нелинейных уравнений для решения дробно-рациональных уравнений
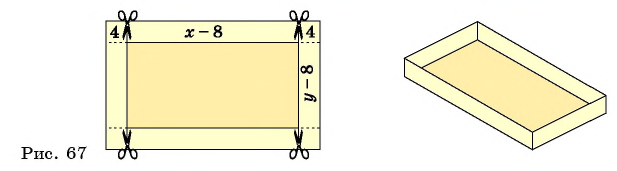
Рассмотрим задачу. Из листа картона прямоугольной формы нужно изготовить коробку без крышки, сделав надрезы в углах длиной 4 см (рис. 67). Найдите длину и ширину листа, зная, что его периметр равен 60 см, а объем коробки должен быть равен
Решение:
Обозначим длину и ширину листа соответственно 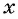
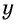
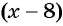

По условию задачи периметр листа прямоугольной формы равен 60 см, а объем коробки равен 160 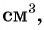
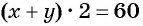
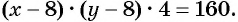
Полученная система уравнений содержит нелинейное рациональное уравнение 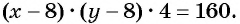
Способ подстановки
Решим полученную в задаче систему уравнений способом подстановки:
Из первого уравнения системы выразим переменную 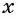
Заменим во втором уравнении переменную 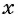
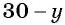
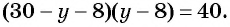
Найденные значения 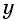
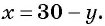
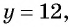
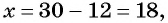
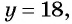
Решениями системы уравнений являются пары чисел 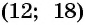
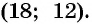
Чтобы решить систему уравнений способом подстановки, нужно:
- Из одного уравнения системы выразить одну из переменных.
- Заменить в другом уравнении эту переменную на ее выражение.
- Решить полученное уравнение.
- Найденные значения одной переменной подставить в выражение для другой переменной и найти значение другой переменной.
- В виде упорядоченных пар чисел записать ответ.
Решите систему уравнений
Решение:
(1) Из второго уравнения системы выразим переменную
(2) Заменим в первом уравнении переменную 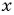
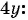
(3) Решим уравнение 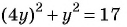
(4) Найденные значения 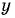
Если 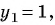
Если 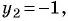
(5) Ответ: (4; 1), (-4; -1).
Способ сложения
Чтобы решить систему уравнений способом сложения, нужно:
- Одно из уравнений системы оставить без изменения, а другое заменить суммой уравнений системы.
- Из полученного уравнения (суммы) найти значения одной из переменных.
- Подставить эти значения переменной в оставленное без изменения уравнение системы и найти значения другой переменной.
- Записать ответ.
Решите систему уравнений
Решение:
(1)
(2)
(3) При 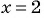
При 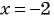
(4) Ответ: (2;1), (2;-1), (-2;1), (-2;-1).
- Заказать решение задач по высшей математике
Графический метод решения систем нелинейных уравнений
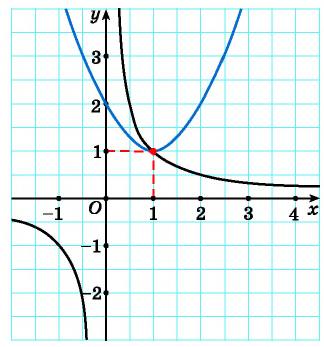
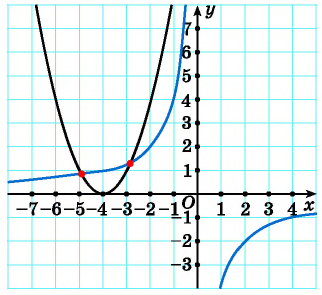
Решим систему уравнений 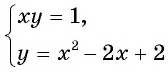
Первое уравнение системы равносильно уравнению 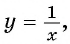
Графиком второго уравнения системы 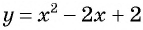
Единственная точка пересечения гиперболы 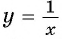
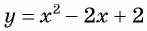
Рис. 68
Поскольку графический метод решения систем уравнений не является точным, то полученный результат необходимо проверить.
Подставим пару чисел (1; 1) в каждое из уравнений системы 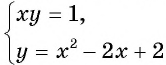
В рассмотренной системе решением оказалась пара целых чисел, которую легко было найти с помощью построенных графиков. В других случаях найти точные значения переменных по графику может оказаться затруднительно. Но, как правило, с помощью графического метода можно определить число решений системы уравнений.
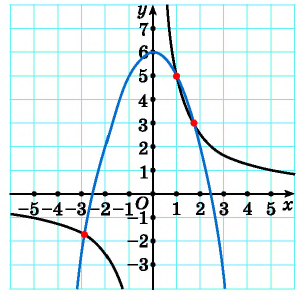
Например, определим число решений системы уравнений 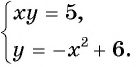
Рис. 69
Моделирование реальных процессов с помощью систем нелинейных уравнений
Системы нелинейных уравнений также являются математическими моделями при решении задач.
Задача:
Лечебными травами было решено засеять прямоугольный участок площадью 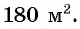
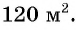
Решение:
В задаче речь идет о длине и ширине прямоугольного участка и его площади.
Если одну сторону участка обозначить через 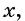
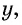
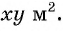
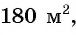
После уменьшения размеров участка площадь станет равной 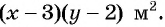
Объединим оба уравнения в систему
Получили математическую модель задачи в виде системы нелинейных уравнений. Решим ее, используя способ подстановки.
Условию задачи удовлетворяют найденные решения системы: стороны участка равны либо 15 м и 12 м, либо 18 м и 10 м.
Ответ: 15 м, 12 м или 18 м, 10 м.
Пример №11
Решите систему уравнений:
а)
б)
Решение:
а) Решим систему способом подстановки:
Ответ: (3; 0), (0; 3).
б) Применим способ сложения. Умножим первое уравнение на 2, сложим со вторым и получим:
Ответ:
Пример №12
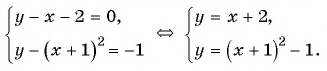
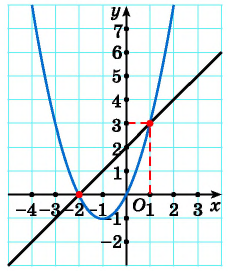
Решите графически систему уравнений
Решение:
Построим графики уравнений системы
График первого уравнения — прямая, проходящая через точки (-2; 0), (1; 3). График второго уравнения — парабола с вершиной в точке (-1; -1), пересекающая ось абсцисс в точках (-2; 0) и (0; 0), проходящая через точку (1; 3).
Прямая пересекается с параболой в точках с координатами (-2; 0), (1; 3). С помощью проверки убеждаемся, что пары чисел (-2; 0) и (1; 3) являются решениями данной системы.
Ответ: (-2; 0), (1; 3).
Пример №13
Сколько решений имеет система уравнений
Решение:
Построим в одной системе координат графики уравнений системы. Графиком первого уравнения системы является гипербола, проходящая через точки (-1; 4), (-4; 1). График второго уравнения — парабола с вершиной в точке (-4; 0), пересекающая ось ординат в точке (0; 16).
На рисунке видны только две точки пересечения графиков. Но, учитывая то, что парабола пересекает ось ординат, а гипербола не пересекает, делаем вывод, что графики пересекаются еще в одной точке. Таким образом, графики пересекаются в трех точках, а, значит, система имеет три решения.
Пример №14
Решите систему уравнений
Решение:
Решим систему методом замены переменных. Введем новые переменные: 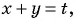
Тогда система примет вид
Решим ее способом подстановки:
Подставим 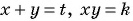
Решив каждую из двух систем совокупности способом подстановки, получим следующие решения исходной системы уравнений: (-5; 1); (1; -5); (4; 1); (1; 4).
Ответ: (-5; 1); (1; -5); (4; 1); (1; 4).
Задача:
Сумма квадратов цифр двузначного числа равна 13. Если из этого числа вычесть 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.
Решение:
Обозначим цифру десятков данного числа через 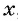
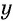
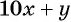
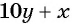
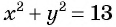
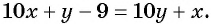
По условию задачи подходит только
Ответ: 32.
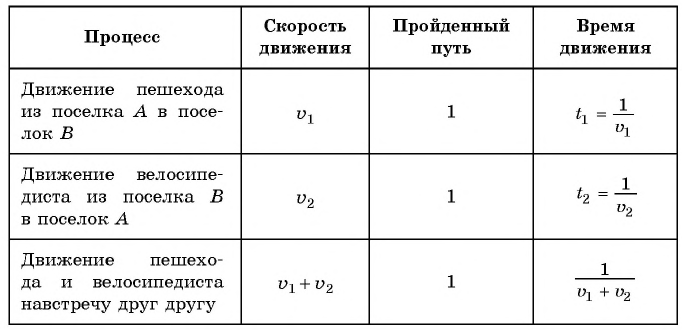
Задача:
Из поселка 
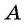
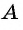
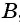
Решение:
Составим таблицу зависимостей между величинами.
По условию задачи велосипедист проделал бы тот же путь на 4 ч быстрее пешехода, поэтому получим уравнение
При движении навстречу друг другу пешеход и велосипедист встретились через 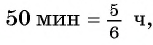
Составим и решим систему уравнений:
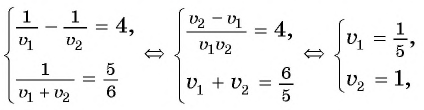
Ответ: 5 ч.
Задача:
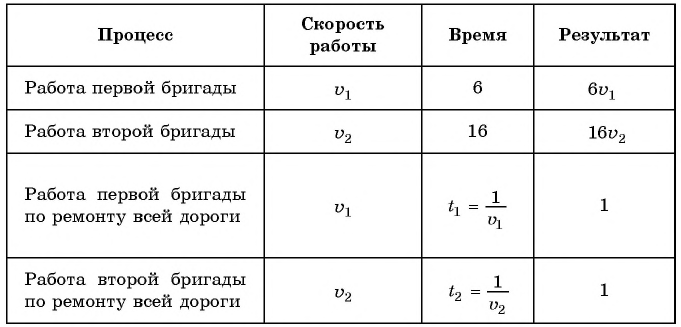
Две бригады, работая вместе, ремонтировали дорогу в течение б дней, а затем одна вторая бригада закончила ремонт за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на б дней быстрее, чем одна вторая?
Решение:
Составим таблицу зависимостей между величинами.
Обозначим объем всей работы через 1, тогда получим уравнение
Зная, что одна первая бригада может выполнить эту работу на б дней быстрее, чем одна вторая, составим уравнение
Составим и решим систему уравнений:
Ответ: 18 ч.
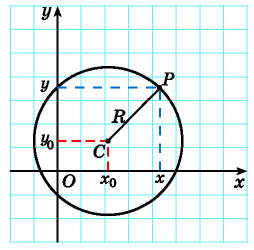
Формула длины отрезка с заданными координатами его концов. Уравнение окружности
Для применения графического метода решения систем необходимо знать графики различных уравнений. Многие из них вам уже знакомы. Это, например, прямая, гипербола, парабола.
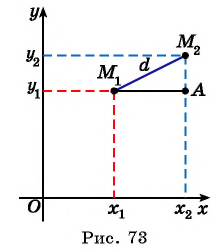
Расширим возможности использования графического метода решения систем нелинейных уравнений и выведем уравнение окружности с центром в заданной точке с заданным радиусом. Для этого сначала выведем формулу для вычисления длины отрезка с заданными координатами его концов, т. е. для вычисления расстояния между двумя точками, заданными своими координатами.
Рассмотрим точки 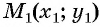
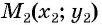
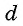
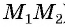
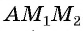
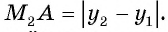
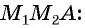
Получили формулу длины отрезка с заданными координатами его концов, или формулу расстояния между двумя точками с координатами
Пример №15
Найдите расстояние между точками А(-1; 3) и В(2; 5).
Решение:
Подставим координаты точек А(-1; 3) и В(2; 5) в формулу расстояния между двумя точками 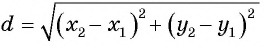
Рассмотрим окружность на координатной плоскости. Окружность — это множество точек плоскости, расстояние от каждой из которых до одной данной точки (центра окружности) является величиной постоянной, равной радиусу окружности
По формуле расстояния между двумя точками найдем расстояние от данной точки 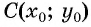
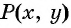
Рис. 74
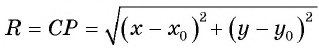
Таким образом, если точка принадлежит окружности с центром 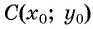
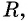
Уравнение 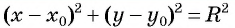
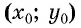
Если координаты точки удовлетворяют уравнению 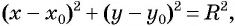
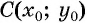
Покажем, что если точка 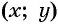
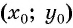
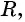
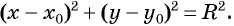
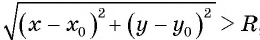
т. е.
Чтобы составить уравнение окружности, нужно:
- Определить координаты центра окружности
- Определить радиус окружности
- Подставить найденные значения
и
в уравнение окружности
Составьте уравнение окружности с центром в точке (-8; 2) и радиусом 5.
Решение:
(1)
(2)
(3)
Пример №16
Составьте уравнение окружности:
а) с центром в точке (4; -1) и радиусом
б) с центром в точке (0; 0) и радиусом 4.
Решение:
а) Подставим координаты центра окружности 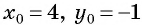
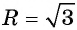
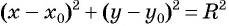
б) Координаты центра окружности: 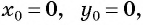
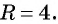
Если центром окружности радиуса 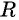
Пример №17
Определите количество решений системы уравнений
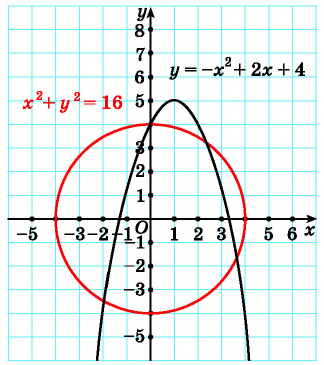
Решение:
Рис. 75
Построим графики уравнений системы. Первое уравнение — это уравнение окружности с центром в начале координат и радиусом, равным 4. Графиком второго уравнения является парабола с вершиной в точке (1; 5), пересекающая ось ординат в точке (0; 4).
Построенные графики пересекаются в четырех точках (рис. 75). Значит, данная система уравнений имеет 4 решения.
Ответ: 4 решения.
Пример №18
Найдите длину отрезка 
Решение:
По формуле длины отрезка 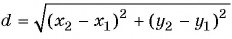
Пример №19
Найдите длину диагонали прямоугольника, если заданы его вершина 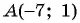
Решение:
Найдем длину отрезка
Длина отрезка 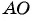
Пример №20
Определите координаты центра и радиус окружности:
а)
б)
в)
Решение:
а)
б)
в)
Пример №21
Какие из данных точек лежат на окружности
а)
б)
в)
г)
Решение:
Подставим координаты точек в уравнение окружности:
а) 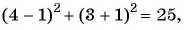
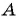
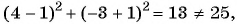
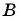
в) 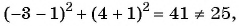
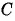
г) 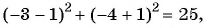
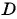
Пример №22
Запишите уравнение окружности с центром в точке (-1; 1) и радиусом
Решение:
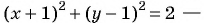
Пример №23
Запишите уравнение окружности с центром в точке 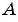
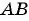
Решение:
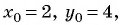
Уравнение окружности
Пример №24
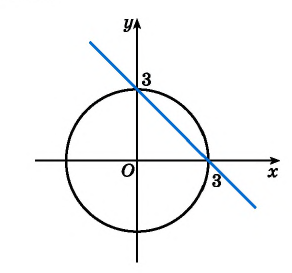
Решите систему уравнений 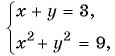
Решение:
График первого уравнения — прямая, проходящая через точки (3; 0), (0; 3). График второго уравнения — окружность с центром в начале координат и радиусом, равным 3.
Координаты точек пересечения (3; 0), (0; 3) — решения системы.
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Рациональная дробь
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
«Рациональные уравнения с многочленами» — одна из самых часто встречающихся тем в тестовых заданиях ЕГЭ по математике. По этой причине их повторению стоит уделить особое внимание. Многие ученики сталкиваются с проблемой нахождения дискриминанта, перенесения показателей из правой части в левую и приведения уравнения к общему знаменателю, из-за чего выполнение подобных заданий вызывает трудности. Решение рациональных уравнений при подготовке к ЕГЭ на нашем сайте поможет вам быстро справляться с задачами любой сложности и сдать тестирование на отлично.
Выбирайте образовательный портал «Школково» для успешной подготовки к единому экзамену по математике!
Чтобы знать правила вычисления неизвестных и легко получать правильные результаты, воспользуйтесь нашим онлайн-сервисом. Портал «Школково» — это единственная в своем роде площадка, где собраны необходимые для подготовки к ЕГЭ материалы. Наши преподаватели систематизировали и изложили в понятной форме все математические правила. Кроме того, мы предлагаем школьникам попробовать силы в решении типовых рациональных уравнений, база которых постоянно обновляется и дополняется.
Для более результативной подготовки к тестированию рекомендуем следовать нашему особому методу и начать с повторения правил и решения простых задач, постепенно переходя к более сложным. Таким образом, выпускник сможет выделить для себя самые трудные темы и сделать акцент на их изучении.
Начните подготовку к итоговому тестированию со «Школково» уже сегодня, и результат не заставит себя ждать! Выберите самый легкий пример из предложенных. Если вы быстро справились с выражением, переходите к более сложной задаче. Так вы сможете подтянуть свои знания вплоть до решения заданий ЕГЭ по математике профильного уровня.
Обучение доступно не только выпускникам из Москвы, но и школьникам из других городов. Уделяйте пару часов в день занятиям на нашем портале, например, решению кубических уравнений и совсем скоро вы сможете справиться с уравнениями любой сложности!
План-конспект занятия №1
Занятие обобщающего повторения при подготовке к ЕГЭ по теме:
«Решение рациональных уравнений. Базовые задания»
Цель занятия:
- формирование учебно-познавательной компетенции: обобщить теоретический материал по теме «Решение уравнений», рассмотреть решения типичных задач;
- формирование математической компетенции: использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
- формирование оценочной компетенции: развивать умение оценивать свой уровень знаний и стремление его повышать.
I этап занятия (5 минут) – организационный момент.
Учитель сообщает тему занятия, его цель, структуру занятия, необходимость его проведения.
На экране появляются слайды №1,2,3.
II этап занятия (10 минут) — повторение основных теоретических знаний.
Повторение проходит в виде презентации, во время которой учащимся предлагается вспомнить типы уравнений, формулы для их решения, разобрать примеры решенных заданий. Данный этап проводится для всех учащихся класса. По ходу появления объектов слайда учитель ведет диалог с классом. Каждый новый объект слайда выводится по щелчку, поэтому темп прохождения материала задает учитель.
Учитель: Какие уравнения называются линейными? Какие значения могут принимать коэффициенты к и b? (На экране слайд №4). Что называется корнем уравнения? Как его найти?
(На экране слайд №5). Рассматривая примеры решенных заданий, учитель повторяет с учащимися равносильные преобразования уравнений.
(На экране слайд №6). Учитель: Какие уравнения называются квадратными? Какие значения могут принимать коэффициенты а, b, с?
Повторяются формулы корней квадратного уравнения, теорема Виета.
(На экране слайд №7).Рассматривая решенные уравнения, учитель обращает внимание учащихся на целесообразность использования того или иного способа решения.
(На экране слайд №8). Учитель: Какие уравнения называются рациональными? Решение рационального уравнения сводится к решению системы: числитель равен нулю, знаменатель не равен нулю.
(На экране слайды №9,10).Разбирая решение уравнений, учитель обращает внимание учащихся на возможность появления посторонних корней и необходимость проверки найденных корней на условие: знаменатель не равен нулю.
III этап занятия (30 минут) — решение типичных задач.
Учащиеся получают приложение с заданиями и раздатку с теорией.
На обычной классной доске решаются типичные базовые задачи, используя запись на слайде как справочный материал, дается теоретическое обоснование способа решения.
- Линейные уравнения — №4, 10,14,18
- Квадратные уравнения — №5,8,13,16,19
- Рациональные — №5, 7,10,13, 16
IV этап занятия (25 мин) — самостоятельная работа.
Учащиеся выполняют самостоятельную работу по вариантам (зад. из приложения).
В1: 1. №5,11; 2. №1, 11,15; 3. №1 ,8, 11
В2:1. №6,12; 2. №2, 12,17; 3. №2, 9,12
V этап занятия (5 мин) — проверка работ.
По окончании работы учащиеся сверяют свои ответы с правильными. (На экране слайд №11). Самостоятельно оценивают свой уровень:
«3» — 4-5 зад., «4» — 6-7 зад., «5» — 8 зад.
VI этап занятия (5 минут) — подведение итогов.
Учитель оценивает работу учащихся на занятии, обращает их внимание на необходимость знания теоретического материала для успешного решения уравнений, дает домашнее задание – выполнить нерешенные уравнения из приложения.




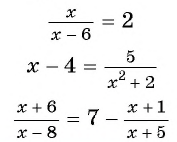
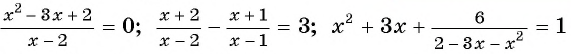
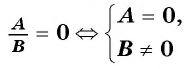
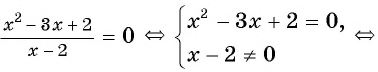
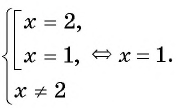
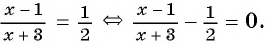
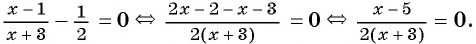
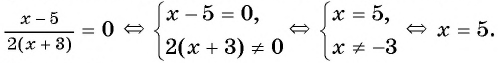
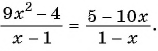
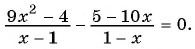
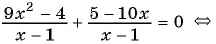
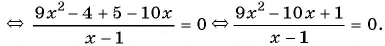
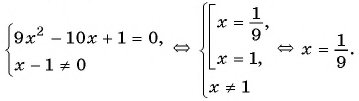
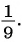
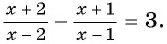
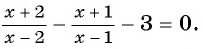
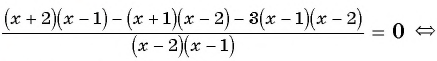
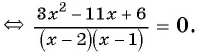
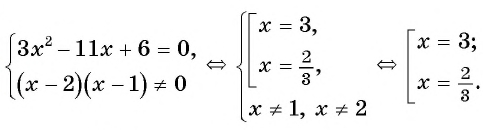
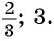
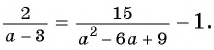
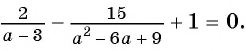
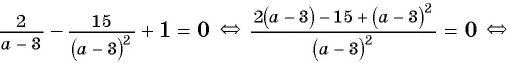
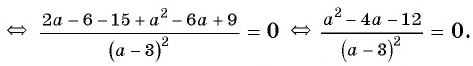
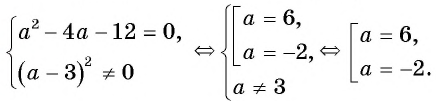
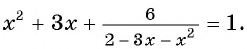
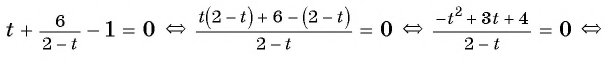
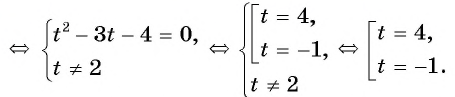
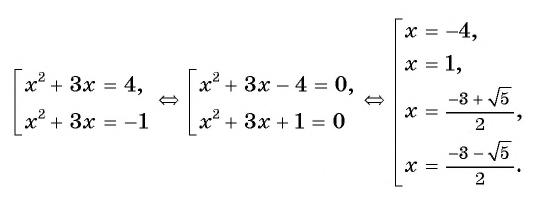

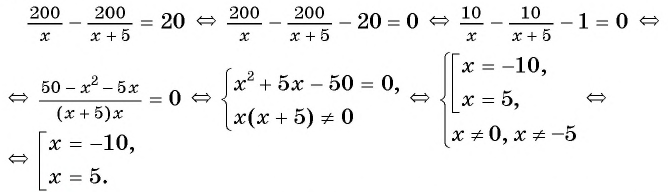
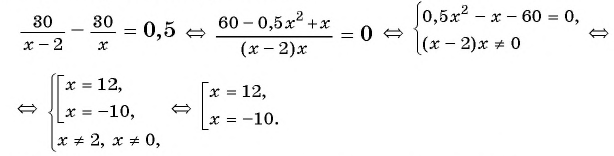
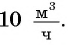
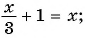
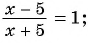
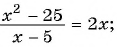
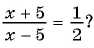
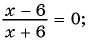
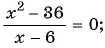
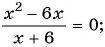
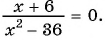
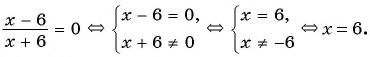
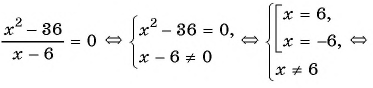
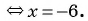
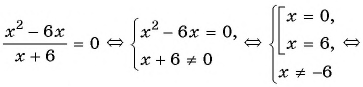
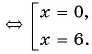
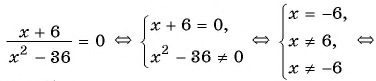
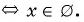
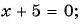
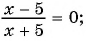
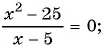
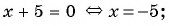
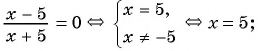
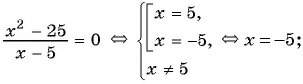
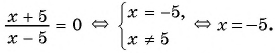
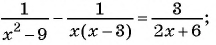
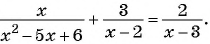
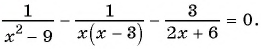
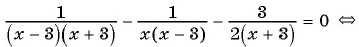
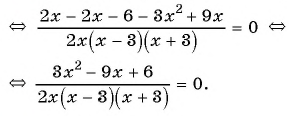
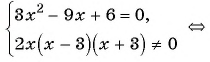
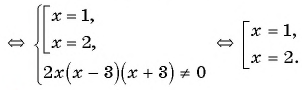
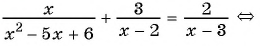
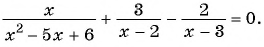
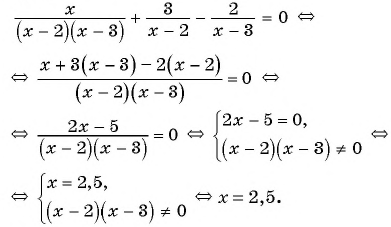
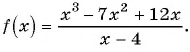
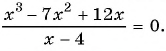
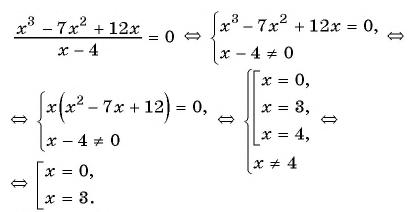
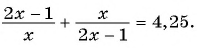
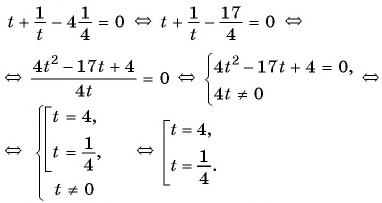
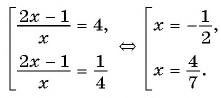

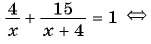
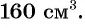
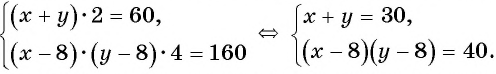
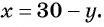
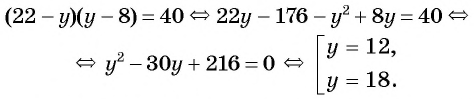
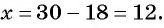
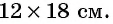
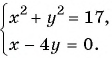
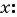
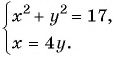
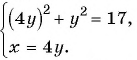
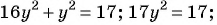
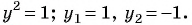
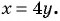
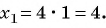
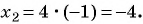
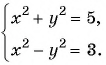
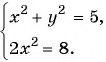
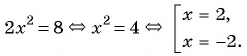
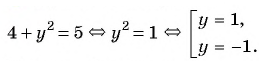
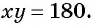
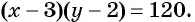
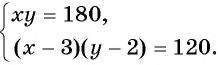
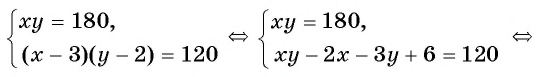
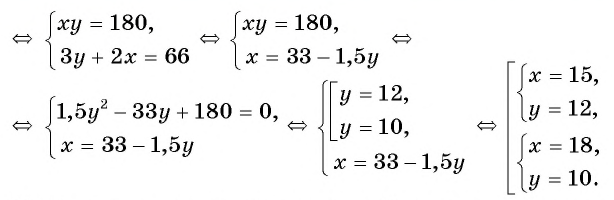
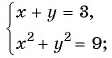
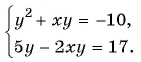
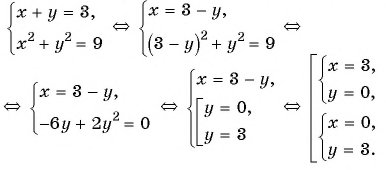
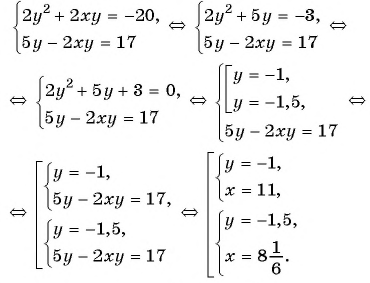
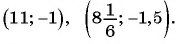
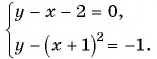
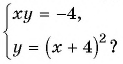
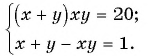
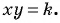
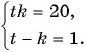
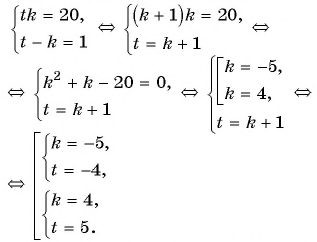
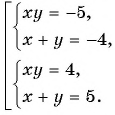
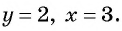
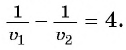
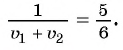
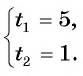
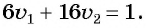
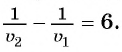
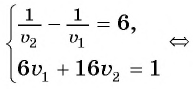
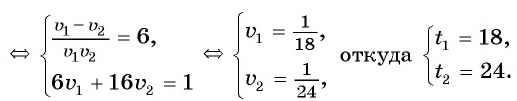
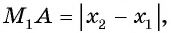
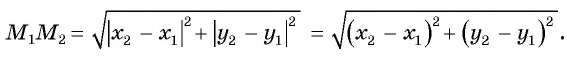
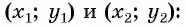
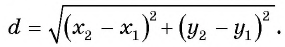
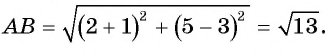
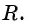
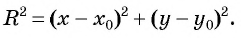
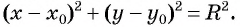
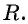
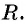
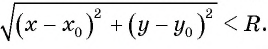
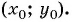
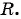
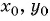 и
и 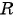 в уравнение окружности
в уравнение окружности