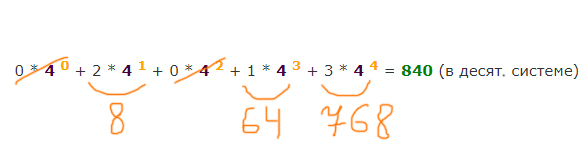Типичные ошибки.
1.Ошибка при склонении числительных.
Запомните, что у количественных числительных (отвечают на вопрос СКОЛЬКО?) изменяются обе части слова и каждое слово в сложном числительном, а в порядковом— только последнее слово.
Примеры.
- Он заканчивал школу в двух тысяч девятнадцатом году. (Две тысячи девятнадцатый — какой? Это порядковое числительное, изменяется только последнее слово).
Верно.
Он заканчивал школу в две тысячи девятнадцатом году.
- С семистами работниками завода был продлён трудовой договор. (Неверная форма творительного падежа числительного «семьсот»).
Верно.
С семьюстами работниками завода был продлён трудовой договор.
2.Числительные ОБА, ОБЕ имеют род.
Пример.
По обоим сторонам дороги росли сосны. (Слово «сторона»- женского рода).
Верно.
По обеим сторонам дороги росли сосны.
3.Собирательные числительные (двое, трое, четверо и т.д.) НЕ употребляются с существительными женского рода, со словами, обозначающими взрослых животных (только детёнышей). Они также употребляются со словами, имеющими только множественное число.
Примеры.
- Трое подростков, среди которых были двое девушек, о чём-то шумно спорили. (ТРОЕ подростков – это верно, так ка сущ. мужского рода; а вот ДВОЕ девушек- нет.)
Верно.
Трое подростков, среди которых были ТРИ девушки, о чём-то шумно спорили.
- Двое огромных волков перебежали дорогу. (ДВОЕ волков – неверно , так как сущ. обозначает взрослых животных).
Верно.
Два огромных волка перебежали дорогу.
- К школе родители купили двое пар брюк и пару рубашек, из которых я вырос буквально за два месяца. (Слово «пара»- женского рода, а с сущ. женского рода собирательное числительное не употребляется)
Верно.
К школе родители купили две пары брюк и пару рубашек, из которых я вырос буквально за два месяца.
4.Неверное сочетание числительных ДВА, ТРИ, ЧЕТЫРЕ, а также составных, заканчивающихся на них, с существительными.
Запомните, данные числительные НЕ сочетаются с сущ. имеющими только множественное число.
Пример.
Для выполнения работы нам дали двадцать двое суток.
Верно.
Для выполнения работы нам дали двадцать два дня.
5.Ошибка в склонении числительных, оканчивающихся на -СТА,-СТО,-СОТ.
Запомните: двумстам, четырёмстам, нет двухсот, четырёхсот, любуюсь двумястами, четырьмястами. Восьмисот, восьмьюстами.
Пример.
Команда вышла в финал турнира с семистами баллами.
Верно.
Команда вышла в финал турнира с семьюстами баллами.
6.Ошибка при склонении числительных СОРОК, ДЕВЯНОСТО, СТО, ПОЛТОРА, ПОЛТОРАСТА.
Запомните, что в косвенных падежах (кроме винительного) они имеют всего одну форму: СОРОКА, ДЕВЯНОСТА, СТА, ПОЛУТОРА, ПОЛУТОРАСТА.
Пример.
Он прочитал не более полтораста страниц.
Верно.
Он прочитал не более полутораста страниц.
ПРИМЕРЫ.
| Пример № 1. | Комментарий. |
| В этом году город отметил свое шестьсотлетие. | В этом году город отметил свое шестьсотлетие.
Верно. В этом году город отметил свое шестисотлетие. (Склоняются оба корня числительного «шестьсот»). |
| Пример № 2. | Комментарий. |
| Среди депутатов было пятеро женщин. | Среди депутатов было пятеро женщин.
Верно. Среди депутатов было пять женщин. (Собирательные числительные НЕ употребляются с сущ. женского рода). |
| Пример № 3. | Комментарий. |
| Мы опоздали всего на полторы сутки. | Мы опоздали всего на полторы сутки.
Числительное «полторы» в косвенном падеже имеет форму «полутора». Верно. Мы опоздали всего на полутора суток. |
Таковы типичные ошибки в предложениях с числительными. Запомните их, научитесь находить такие предложения.
Материал подготовила: Мельникова Вера Александровна.
Вернутьсяк списку тестов по русскому языку ЕГЭ
Сегодня на повестке дня 8 задание из ЕГЭ по информатике 2021. Данный тип заданий включает в себя нахождение количества вариантов, элементы комбинаторики и другие математические понятия.
Перейдём к практике решения задач задания 8 ЕГЭ по информатике 2021.
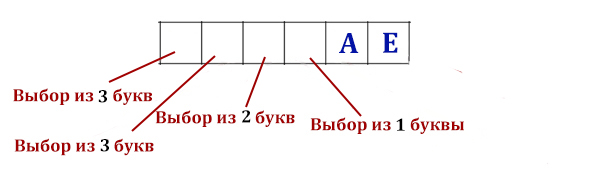
Задача (Классика)
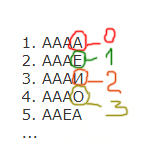
Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…
Запишите слово, стоящее на 248-м месте от начала списка.
Решение:
Обозначим условно А — 0, Е — 1, И — 2, О — 3.
Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.
Теперь запишем список с помощью цифр.
1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…
Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.
Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.
Переведём число 247 в четверичную систему!
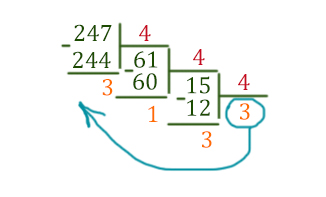
Получилось число 33134 в четверичной системе. Сделаем обратное декодирование в буквы. Таким образом, ответ будет ООЕО.
Ответы: ООЕО
Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике, но другой вариации.
Задача (Классика, Другая вариация)
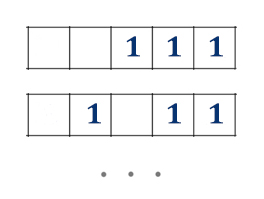
Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА
Решение:
Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.
У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.
1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……
Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!

Получили число в четверичной системе 310204. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 310204 из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.
Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу 840 нужно прибавить 1, и в ответе будет 841
Ответ: 841
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)
Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И,
записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…
Под каким номером в списке идёт первое слово, которое начинается
с буквы О?
Решение:
Закодируем буквы цифрами.
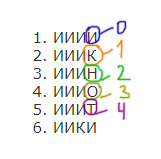
Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.
Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 30005. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.
Теперь, как в предыдущей задаче, переведём число 30005 из пятеричной системы в десятичную.
0 * 5 0 + 0 * 5 1 + 0 * 5 2 +
3 * 5 3 = 375 (в десят. системе)
Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.
Ответ: 376
Задача (Досрочная волна 2020 ЕГЭ по информатике, вариант 1)
Вася составляет 5-буквенные слова, в которых есть только буквы В, О, Л, К,
причём буква В используется в каждом слове ровно 1 раз. Каждая из других
допустимых букв может встречаться в слове любое количество раз или
не встречаться совсем. Словом считается любая допустимая
последовательность букв, не обязательно осмысленная. Сколько существует
таких слов, которые может написать Вася?
Решение:
Для начала решим вводную подзадачу.
Пусть у нас есть те же буквы В, О, Л, К, каждая из букв может встречаться в слове любое количество раз или
не встречаться совсем. Сколько можно составить 5-буквенных слов ?
Т.е буквы могут повторяться!
Например
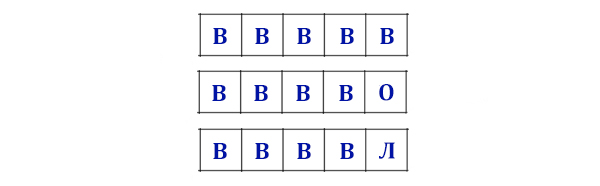
Такая конструкция сильно напоминает перебор чисел, где вместо цифр используются буквы.
Рассмотрим перебор трёхразрядных чисел. Вместо 5 букв теперь можно использовать 10 цифр ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). Цифры так же могут повторяться. Сколько получится вариантов ?
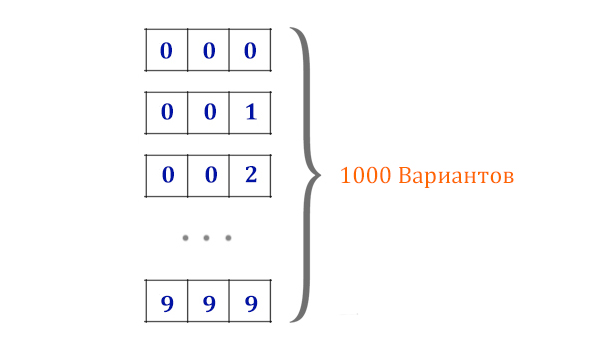
Выведем общую формулу для количества вариантов, когда символы могут повторяться!
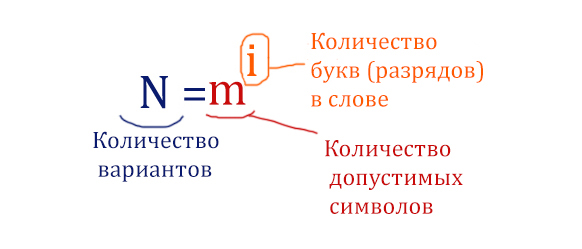
Для трёхразрядных чисел от 000 до 999:
N = 103 = 1000 вариантов.
Вернёмся к пятибуквенным словам и нашей подзадаче. Здесь количество букв (разрядов) в слове равно 5, количество допустимых символов равно 4 ( В, О, Л, К ).
N = 45 = 1024 вариантов.
Вернёмся к изначальной задаче. Сначала найдём количество вариантов, когда буква В находится в самой левой ячейке!
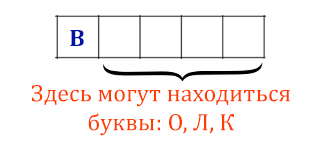
Применим формулу! Здесь слово сократилось до четырёхразрядного. А количество букв для использования 3 (О, Л, К).
N = 34 = 81 комбинация.
Но буква В так же может стоять во второй ячейке слева. Этот случай тоже даст 81 других комбинаций. Буква В может стоять в каждой из 5-ти ячеек, и везде будет получатся 81 комбинация.
Таким образом, окончательный ответ будет:
N = 81 * 5 = 405 различных вариантов.
Ответ: 405
Разобравшись с этой задачей, больше половины тренировочных задач десятого задания из различных книг и сайтов по подготовке к ЕГЭ по информатике будут решаться, как по маслу!
Задача(Закрепление формулы)
Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?
Решение:
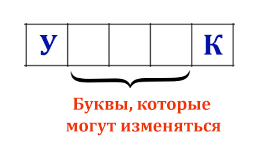
Применим главную формулу 8 задания из ЕГЭ по информатике
N = mi = 63 = 216
Здесь буквы могут изменяться на 3 ячейках! Значит, в формуле i=3. Количество допустимых символов, которые можно поставить в каждую ячейку равно 6. Значит, в формуле m=6.
В ответе будет 216.
Примечание: Здесь можно использовать все буквы в каждой ячейке, включая У и К. В некоторых задачах их уже использовать нельзя, т.е. сказано, что буквы У и К используются один раз в слове. Тогда в формуле m, будет на 2 единицы меньше. Нужно внимательно читать задачу!
Ответ: 216
Задача (Демонстрационный вариант ЕГЭ по информатике, 2019)
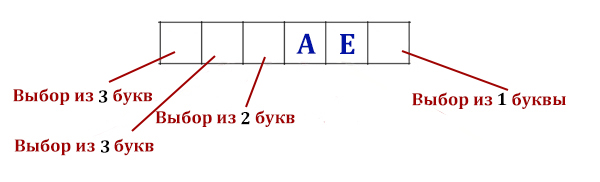
Вася составляет 5-буквенные слова, в которых есть только буквы З, И, М, А,
причём в каждом слове есть ровно одна гласная буква и она встречается
ровно 1 раз. Каждая из допустимых согласных букв может встречаться
в слове любое количество раз или не встречаться совсем. Словом считается
любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Вася?
Решение:
Рассмотрим количество вариантов, когда гласная И стоит в первом месте!
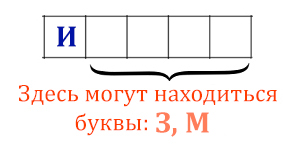
Подсчитаем количество слов с помощью супер-формулы
N = mi = 24 = 16
Длина изменяющихся ячеек равна 4, а количество допустимых букв равно 2.
Но буква И может стоять не только на первом месте. Она так же может стоять и на 2, и на 3, и на 4, и на 5 месте. Каждый такое случай добавляет столько же новых слов.
Значит, при использовании только буквы И будет количество слов 16 * 5 = 80. Ещё столько же слов добавится, если в словах вместо буквы И будет использоваться буква А. Поэтому окончательный ответ будет 80 * 2 = 160
Ответ: 160
Отработаем главную формулу 8 задания из ЕГЭ по информатике.
Задача (Развиваем понимание формулы!)
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Решение:
Рассмотрим, какие варианты могут быть, если у нас на первом месте стоит согласная, а на последнем месте гласная
Получилось 4 разных случая. Подсчитаем, сколько слов можно составить при одном случае.
N = mi = 43 = 64
Длина изменяющихся ячеек равна 3, а количество возможных букв 4.
Но т.к. таких случая у нас четыре, то ответ будет 4 * 64 = 256
Ответ: 256
Рассмотрим важнейший «метод умножения» при решении 8 задания из ЕГЭ по информатике.
Задача (Другой метод решения!!)
Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз , при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?
Решение:
Эта задача отличается от уже разобранных тем, что каждую букву можно использовать один раз. В этой задаче удобнее воспользоваться немного другим методом решения! «Методом умножения»!
Решим вводную подзадачу (без дополнительных ограничений).
Сколькими способами можно составить 6-x буквенное слово из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз .
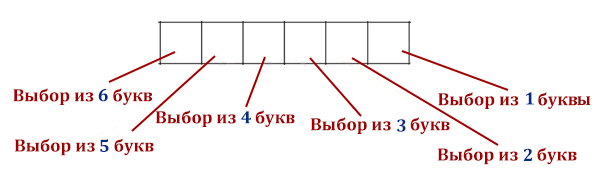
Чтобы найти возможные варианты, перемножаем для каждой ячейки количество букв из которых у нас есть выбор!
N = 6 * 5 * 4 * 3 * 2 * 1 = 720
Вернёмся к изначальной задаче!
В начале подсчитаем «методом умножения» количество слов, не обращая внимание, на условие, в котором сказано, что слово не может содержать сочетание АЕ.
N = 5 * 5 * 4 * 3 * 2 * 1 = 600
В формуле стоят почти все те же самые числа, как и в вводном примере, только первый множитель не 6, а 5. Это произошло из-за того, что у нас в задаче слово не может начинаться на букву Й. Значит, выбор на первую позицию будет не из 6 букв, а из 5.
Но в 600 комбинаций входят и те случаи, когда в слове присутствует сочетание АЕ. Теперь найдём сколько таких слов, где присутствует сочетание АЕ
Узнаем количество вариантов в каждом таком случае.
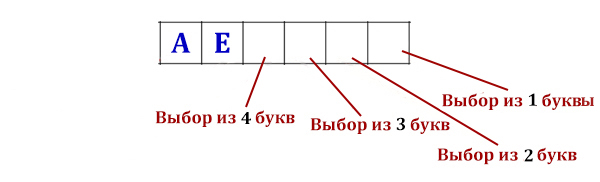
N1 = 4 * 3 * 2 * 1 = 24
На первом месте мы не можем использовать букву Й, поэтому мы на первом месте выбираем из 3 букв.
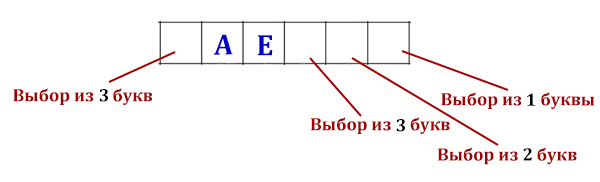
N2 = 3 * 3 * 2 * 1 = 18
Аналогично предыдущему случаю.
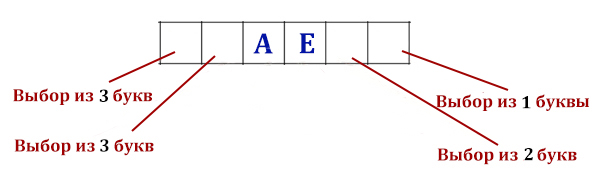
N3 = 3 * 3 * 2 * 1 = 18
N4 = 3 * 3 * 2 * 1 = 18
N5 = 3 * 3 * 2 * 1 = 18
Всего слов с сочетанием АЕ будет
24 + 18 + 18 + 18 + 18 = 96
Значит, всего слов, которые удовлетворяют условию задаче будет
N = 600 — 96 = 504
Примечание: Метод умножения можно было использовать и в задачах, которые мы рассмотрели ранее. Например, в задаче «Закрепление формулы» в первой свободной ячейке выбираем из 6 букв, во второй свободной ячейке тоже из 6 букв, и в третий свободной ячейке тоже можно использовать 6 букв. Значит, по методу умножения получается N = 6 * 6 * 6 = 63 = 216
Ответ: 504
Задача (Закрепления «метода умножения»)
Полина составляет 6-буквенные коды из букв П, О, Л, И, Н, А. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Полина?
Решение:
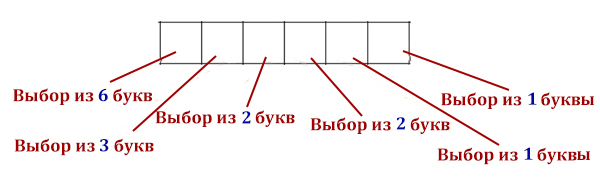
Опять сказано, что каждая буква используется 1 раз, следовательно, нужно применять «метод умножения».
На первое место можно выбрать из 6 букв, предположим, мы выберем согласную. Тогда на второе место нужно выбирать из 3 гласных. Потом опять должна идти согласная, но их у нас осталось только 2. Далее, на следующее место выбираем из 2 гласных букв. И на предпоследнее место выбирается 1 согласная, а на последнее место остаётся 1 гласная.
Т.к. количество гласных букв и согласных одинаковое, и равно трём, то если мы бы начали делать «метод умножения» с гласной буквы, количество вариантов бы не поменялось.
N = 6 * 3 * 2 * 2 * 1 * 1 = 72
Ответ: 72
Задача (Азбука Морзе)
Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее трёх и не более четырёх сигналов (точек и тире) ?
Решение:
Зная формулу, без проблем решим данную примерную задачу из ЕГЭ по информатике.
У нас есть 2 символа, которые можно использовать: точка и тире. Фраза, что сообщение может иметь «не менее трёх и не более четырёх сигналов», означает, что сообщения могут быть длиною 3 символа и длиною 4 символа.
Подсчитаем общее количество вариантов.
N = 23 + 24 = 8 + 16 = 24 комбинаций.
Значит, для 24 различных символов (цифр, букв, знаков пунктуации и т.д.) мы найдём различные комбинации, чтобы их закодировать
Ответ: 24
Задача (Обратная предыдущей)
Световое табло состоит из цветных индикаторов. Каждый индикатор может окрашиваться в четыре цвета: белый, черный, желтый и красный. Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 300 различных сигналов?
Решение:
Нам нужно закодировать 300 различных вариантов! Имеются 4 различных лампочки! (Они имеют смысл, как количество допустимых символов!) На этот раз нужно узнать количество лампочек (количество разрядов, «длину слова»). Применяем формулу.
N = 4x = 300
Не найдётся такое целое x, чтобы равенство стало верным. Поэтому берём целое минимальное x такое, чтобы 4x больше 300.
45 = 1024
Пять лампочек на табло хватит, чтобы закодировать 300 сигналов, но, к сожалению, много комбинаций просто не пригодится!
Ответ: 5
Задача (Важная!)
Нужно выбрать в подарок 3 книги из 5. Сколькими способами можно выбрать ?
Решение:
На рисунке показано две комбинации, как можно выбрать в подарок 3 книги из 5.

Данную задачку нужно решать используя формулу сочетаний из раздела комбинаторика.
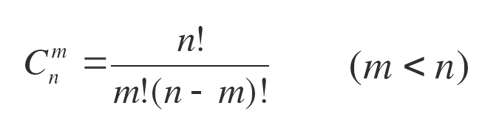
n — количество книг, из которых мы выбираем подарок, m — количество книг, которое мы хотим выбрать, C — количество вариантов (способов).
Восклицательный знак — это факториал!
Факториалом числа «n» (условное обозначение n!- читается как «эн» — факториал) называется произведение чисел от 1 до «n»
Примечание: При использовании формулы сочетаний, не важен порядок, в котором мы выбираем одни и те же книги. Это будет один и тот же вариант.
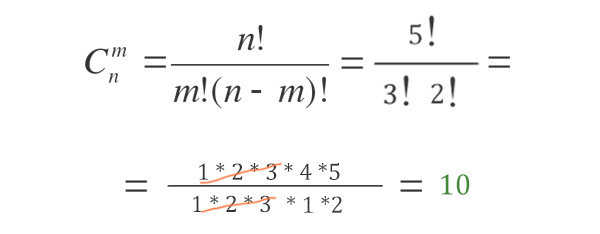
Ответ: 10
Следующая задача часто встречается в книгах по подготовке к ЕГЭ по информатике.
Задача (Главная формула + сочетания)
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно три раза, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Решение:
В начале нужно посчитать, сколькими способами на 5-ти ячейках можно расположить 3 единицы!
Обратите внимание, как будто мы выбираем 3 книги в подарок из 5 возможных! Значит, опять применяем формулу сочетаний из комбинаторики. Мы вычисляли уже её точно с такими же числами в прошлой задаче, количество вариантов равно 10.
Подсчитаем, сколько вариантов кодового замка можно составить при одном определённом расположении трёх единиц.
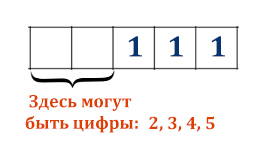
Применим формулу, есть две ячейки, в которых изменяются цифры, а в каждой ячейке может быть одна из 4 цифр.
N = mi = 42 = 16
Т.к. различных вариантов, как расположить единицы на 5 ячейках равно 10, то ответ будет 16 * 10 = 160
Ответ: 160
Ещё одна задача из примерных вариантов по подготовке к ЕГЭ по информатике.
Задача (Таблица соревнований)
Для записи результатов соревнований используется таблица, в которой для каждой из 20-ти команд по каждому из 10-ти видов состязаний записано 1, 2 или 3 (если команда заняла соответствующее место в этом состязании) или прочерк (если не заняла призовое место или не участвовала). Какое количество информации (бит) содержит таблица ?
Решение:
Есть таблица с 20 командами и для каждой команды есть результат по 10-ти видам состязаний.
| 1 команда | 2 команда | 3 команда | … | 20 команда | |
| 1 дисциплина | 1 | — | 1 | … | 3 |
| 2 дисциплина | — | 2 | 1 | … | 2 |
| … | … | … | … | … | … |
| 10 дисциплина | 1 | 1 | 2 | … | — |
В каждой ячейке может быть 4 различных значения ( 1, 2, 3, — ). Нужно узнать, сколько бит занимает одна ячейка таблицы. Один бит может быть либо единицей, либо нулём.
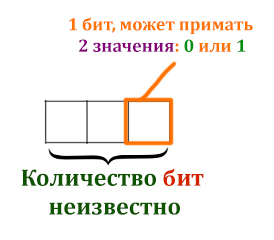
Сделав рисунок, задача обрела привычные очертания.
Как будто мы решаем задачу с перебором слов. Но здесь длина слова неизвестна, а количество вариантов, которое должно получится уже дано и равно 4 (четырём). Применим главную формулу из 10 задания из ЕГЭ по информатике.
N = mi = 2i = 4
i=2 бита (длина равна «2 буквам», если воспринимать задачу, как со словами.)
Одна ячейка таблицы весит 2 бита. Найдём количество ячеек во всей таблице соревнований.
Всего ячеек = 20 * 10 = 200
Тогда вся таблица будет весит:
V = 2 бита * 200 = 400 бит.
Ответ: 400
Формула Шеннона
Задача (Формула Шеннона)
В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?
Решение:
Данную задачу нужно решать по формуле Шеннона
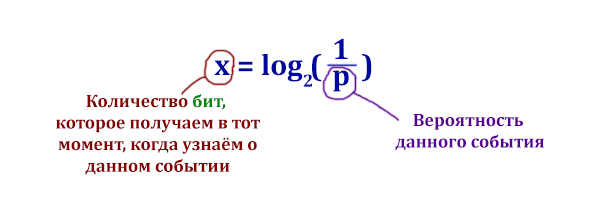
Найдём вероятность p того, что вытащили чёрный шарик.
p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + = 8 / 32 = 1 /4
p = 1 / 4
Применим формулу Шеннона.
x = log2(4)
2x = 4
x = 2 бита
Ответ: 2
Задание 8
Установите соответствие между грамматическими ошибками и предложениями, в которых они допущены: к каждой позиции первого столбца подберите соответствующую позицию из второго столбца.
ГРАММАТИЧЕСКИЕ ОШИБКИ
А) ошибка в построении предложения с однородными членами.
Б) нарушение связи между подлежащим и сказуемым
В) неправильное построение предложения с косвенной речью.
Г) нарушение видовременной соотнесённости глагольных форм
Д) ошибка в употреблении имени числительного
ПРЕДЛОЖЕНИЯ
1) По длине—три тысячи шестьсот восемьдесят километров—Волга занимает первое место среди рек Европы.
2) Вопреки первоначальным планам, экспедиция затянулась на целых двадцать двое суток.
3) Сад отцветал, осыпАлся, но зато продолжал буйно густеть и темнеть.
4) Все, кто безрезультатно выступал раньше против назначения Ермолова, теперь вновь поднял голову.
5) Елизавета, воспитанная в строгих правилах, очень любила и восхищалась своей матерью.
6) Только поздней осенью, когда опадёт с деревьев пожелтевший и покрасневший лист, nрижмут первые осенние заморозки, ягоды рябины становятся сладкими.
7) Когда римский император Веспасиан не успевал сделать за день ни одного доброго дела, он говорил с горечью, что «Друзья, я потерял день».

9) Затем я встретил бабушку, и она сказала мне, что скоро у меня будет новый отец.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г | Д |
Пояснение.
А) ошибка в построении предложения с однородными членами в предложении 5 вызвана тем, что к двум сказуемым «любила» и «восхищалась» относится одно дополнение «матерью». Если восхищаться матерью можно, то любить матерью нельзя никак.
Приведём верное написание:
Елизавета, воспитанная в строгих правилах, очень любила свою мать и восхищалась ею.
Пункт правила 7.6.1
Читать правило
Б) нарушение связи между подлежащим и сказуемым в предложении 4. Подлежащее ВСЕ требует сказуемого во множественном числе.
Приведём верное написание:
Все, кто безрезультатно выступал раньше против назначения Ермолова, теперь вновь поднялИ голову.
Пункт правила 7.3.1
Читать правило
В) неправильное построение предложения с косвенной речью —в предложении 7.
Нельзя при косвенной речи оставлять местоимения 1 и 2 лица. Их нужно менять на 3 лицо.
Приведём верное написание:
Когда римский император Веспасиан не успевал сделать за день ни одного доброго дела, он говорил с горечью, обращаясь к друзьям, что он потерял день.
Пункт правила 7.9.2
Читать правило
Г) нарушение видовременной соотнесённости глагольных форм 8 вызвана тем, что из трёх сказуемых одно стоит в настоящем времени и имеет несовершенный вид, а два—в прошедшем, совершенного вида. Сказуемые должны соотноситься с друг другом по времени и виду.
Приведём верное написание:
Взошло солнце, позолотило перила веранды и открыЛО вокруг необыкновенную чистоту и свежесть.
Пункт правила 7.5.1
Читать правило
Д) ошибка в употреблении имени числительного 2 вызвана тем, что нельзя сказать ни «двадцать два сутки», ни «двадцать две сутки», и остаётся, как «жест отчаяния», — «двадцать двое суток», но это не соответствует литературной норме. В нормативной речи эту грамматическую несочетаемость числительных 22, 23, 24
и т.п. с существительными, не имеющими формы единственного числа, мы преодолеваем или заменой таких существительных:
поход продолжался 22 дня , или изменением конструкции:
поход продолжался в течение двадцати двух суток.
Приведём верное (примерное) написание:
Вопреки первоначальным планам, экспедиция затянулась на целых двадцать два дня.
Пункт правила 7.10.2
Читать правило
Ответ: 54782
Задание № 8 (ЕГЭ)
I). Причастный оборот:
а). Проверяем окончание причастия, задав вопрос определяемого существительного;
б). Смотрим место определяемого слова по отношению к причастному обороту;
Ошибка!
Я взял книгу, лежащего на столе.
Лежащая книга на столе.
II). Несогласованное приложение:
Если в предложении есть определяемое слово «книга», «роман», «кинотеатр», «машина» и т. д., то название, занесенное в кавычки должно стоять в Им. п.
Но в «Войне и мире»
Ошибка!
В романе «Войне и мире».
III). Подлежащее и сказуемое:
Сказуемое должно согласовываться с подлежащим в роде и числе.
а). собирательное существительное «молодежь», «народ», «студенчество» всегда в ед. числе
б). диван-кровать (удобный)
кресло-качалка (удобное)
стол-тумба (удобный)
в). МГУ (университет) пригласил
ООН (организация) пригласила
г). несклоняемые существительные
Сочи (город) удивил
Салями (колбаса) понравилась
Онтарио (озеро) разлилось
д). в СПП рядом могут оказаться подлежащее главного и придаточного предложения
Сказуемое придаточного будет находиться рядом, а сказуемое главного будет оторвано
нужно согласовать каждое сказуемое со своим подлежащим
после слова «кто» глагол всегда в ед. числе;
Ошибка!
[Все, (кто знают этого человека), понимает нелепость обвинений].
IV). Нарушение в построении СП:
а). проверять, чтобы придаточное с союзным словом «который» находилось после определяемого слова;
Ошибка!
Мне понравилась книга о девочке, которую подарила мне мама.
б). в СПП может оказаться лишнее указательное слово или подчинительный союз;
Ошибка!
Он рассказал, что как ему было тяжело.
Мы постановили о том, что работать будем в воскресенье
V). Видовременная соотнесенность:
Все глагольные формы в предложении должны стоять в одном времени и быть одного вида.
Ошибка!
Артисты вышли на сцену и кланяются
VI). Однородные члены:
смотреть на сочинительные союзы (!и!)
а). союзом «и» не должны соединяться слово и предложение;
Ошибка!
Он рассказал о приключении, и как мы охотились.
б). при двух сказуемых может быть общее дополнение. Оно должно согласовываться в падеже с каждым из сказуемых;
Ошибка!
Он любил и увлекался чтением.
в). Нельзя связывать союзом «и» слова разных частей речи;
Ошибка!
Он любил пение и читать.
г). нельзя менять вторую часть союза;
не только…, но и
как…, так и
если не…, то
не столько…, сколько
Ошибка!
не только…, а так же
первая часть союза может находиться не на своем месте (не перед однородными членами);
Ошибка!
Он не только любил заниматься спортом, но и шахматами.
VII). Неправильное употребление падежной формы существительного с предлогом (управление):
по приезде ошибка
по приходе по завершению фильма ребята его обсудили
по прилете
по истечении
по завершении
благодаря
согласно чему
вопреки
Ошибка!
Согласно приказа.
в — из Ошибка!
на — с Я пришел со школы.
VIII). Деепричастный оборот:
Действие, названное сказуемым и деепричастием должно выполняться одним лицом. Оно должно быть подлежащим.
Ошибка!
Изучая историю, она увлекла меня.
Поднимаясь по лестнице, старику приходилось останавливаться.
IX). Косвенная речь: ищи глагол говорения
1)союз «что», «чтобы», «как»; Ошибка!
2) лицо 2 или 3; Мама сказала, что я скоро приду.
3). нет кавычек;
X). Числительное:
Собирательные числительные (двое, трое, десятеро) не употребляются с женским родом;
Ошибка!
Двое подруг
а). Собирательные числительные не входят в составные;
Ошибка!
Двадцать двое суток.
Оба берега обеих рек.
Ошибка!
Обоих подруг
НО:
Полтора; полтораста книг;
Полутора; полутораста книгами.