Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
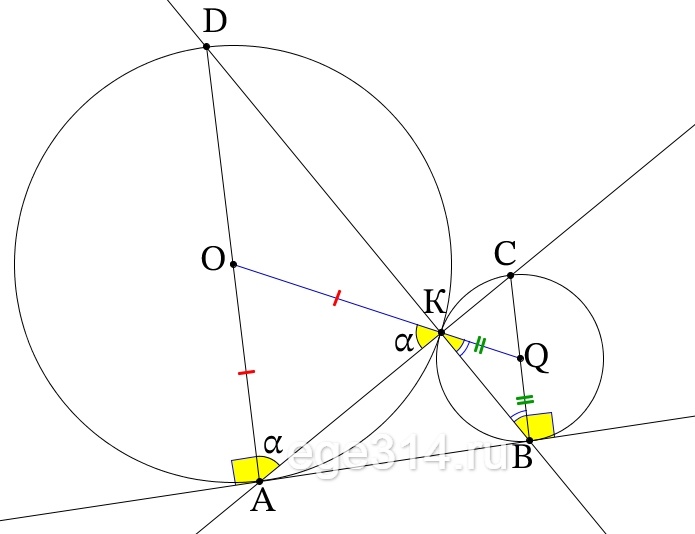
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Источник: Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Проект демонстрационной версии ЕГЭ—2014 по математике., Демонстрационная версия ЕГЭ—2020 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2015 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень.
2
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 4 и 1.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 3. (Часть C).
3
Хорды AD, BE и CF окружности делят друг друга на три равные части.
а) Докажите, что эти хорды равны.
б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D, E, F последовательно расположены на окружности, а радиус окружности равен
4
Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L — точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Источник: ЕГЭ — 2015 по математике. Основная волна 04.06.2015. Вариант 1 (Часть С)., Задания 16 (С4) ЕГЭ 2015
5
Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке A, а вторую — в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке B, а вторую — в точке C.
а) Докажите, что четырёхугольник ABCD — параллелограмм.
б) Найдите отношение CP : PB, если радиус первой окружности втрое больше радиуса второй.
Раздел: Планиметрия
Пройти тестирование по этим заданиям
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
а) Другими словами, в пункте (а) надо доказать, что точка D лежит на прямой , а точка C — на прямой
.
— прямоугольная трапеция, поскольку
(как радиусы, проведенные в точку касания),
.
Если , то
(как односторонние углы),
тогда
и
.
— прямоугольный,
.
Тогда — диаметр первой окружности;
— диаметр второй окружности, так как вписанный угол, опирающийся на диаметр, — прямой.
Значит,
б) Найдем
AK — высота в , где
Рассмотрев прямоугольную трапецию , где
, найдем, что
.
Из по теореме Пифагора
.
Задание 16 Профильного ЕГЭ по математике. Планиметрия
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16 Профильного ЕГЭ по математике. Планиметрия. Задача 3» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Решение:
а)
ОА и QB радиусы к касательной АВ, значит ОА⊥АВ, QB⊥АВ, отсюда ОА||QB. Соединим центры окружностей ОQ, точка касания окружностей К∈ОQ.
ОАВQ – прямоугольная трапеция. Треугольник АОК равнобедренный, т.к. АО = ОК, как радиусы, углы при основании равны, обозначим их как α, ∠ОАК = ∠АКО = α, зная, что сумма углов треугольника равна 180°, найдём третий угол треугольника:
∠АОК = 180° – α – α = 180° – 2α
∠АОК и ∠ВQО углы при боковой стороны трапеции их сумма равна 180°, найдём ∠ВQО:
∠ВQО = 180 – (180° – 2α) = 180 – 180° + 2α = 2α
Треугольник КQB равнобедренный KQ = QB, как радиусы, углы при основании равны, найдём ∠QKB:
angle QKB=frac{180°-2alpha}{2}=frac{2(90°-alpha)}{2}=90°-alpha
Угол ОКQ развёрнутый он равен 180°, состоит из трёх углов, найдём ∠АКВ:
∠АКВ = 180° – α – (90 – α) = 180° – α – 90° + α = 90°
∠АКВ = 90°, тогда ∠АКD тоже равен 90°, как смежный ему. Треугольник АКD прямоугольный, вписанный в окружность, значит АD – диаметр окружности с центром О.
∠АКD = ∠ВКС = 90°, как вертикальные, тогда ΔСКВ прямоугольный вписанный в окружность с центром Q, значит ВС – диаметр.
Т.к. радиусы ОА||QB, являющиеся частью диаметров АD и ВС, значит АD||ВС.
Что и требовалось доказать.
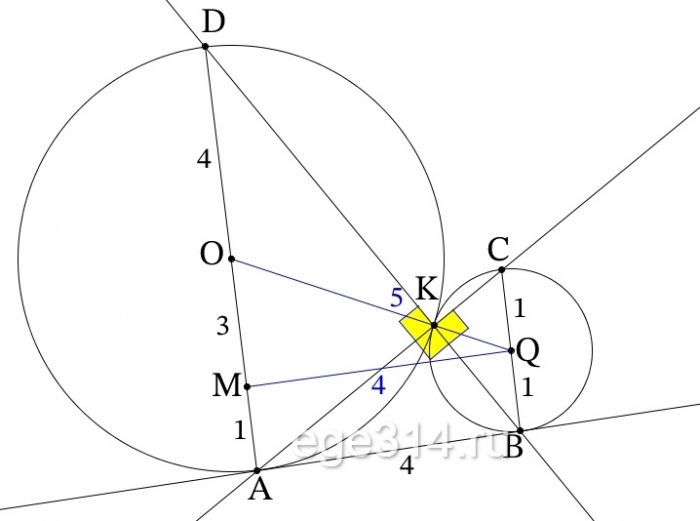
б) Проведём высоту QM прямоугольной трапеции, QM||AB, M∈DА.
QB = QK = 1, как радиусы меньшей окружности. ОК = ОА = 4, как радиусы большей окружности. Рассмотрим ΔОQM, он прямоугольный, ОQ = OK + KQ = 4 + 1 = 5, QB = MA = 1, как противоположные стороны прямоугольника. ОМ = ОА – МА = 4 – 1 = 3. Тогда MQ = 4, как сторона египетского треугольника (или по т. Пифагора). MQ = AB = 4, как противоположные стороны прямоугольника.
ΔАКD подобен ΔВСК (∠АКD = ∠ВКС = 90°, ∠АDK = ∠KBC, как накрест лежащие углы) с коэффициентом подобия:
k=frac{DA}{CB}=frac{4+4}{1+1}=frac{8}{2}=4
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
frac{S_{Delta AKD}}{S_{Delta BCK}}=k^{2}
Обозначим SΔBCK как S, тогда:
frac{S_{Delta AKD}}{S}=4^{2}\frac{S_{Delta AKD}}{S}=16
SΔAKD = 16S
ΔАКD подобен ΔАКB (АК высота в прямоугольном ΔВАD, делит его на два подобных треугольника) с коэффициентом подобия:
k=frac{AD}{AB}=frac{8}{4}=2\frac{S_{Delta AKD}}{S_{Delta AKB}}=k^{2}\frac{16S}{S_{Delta AKB}}=2^{2}\frac{16S}{S_{Delta AKB}}=4\S_{Delta AKB}=frac{16S}{4}=4S
Найдём SΔАВС:
S_{Delta ABC}=frac{1}{2}cdot ABcdot CB=frac{1}{2}cdot 4cdot 2=4
SΔАKB = 4S, SΔBCK = S, тогда SΔABC = SΔАKB + SΔBCK = 4S + S = 5S:
4 = 5S
S=frac{4}{5}=0,8
SΔАKB = 4S = 4·0,8 = 3,2
Ответ: 3,2.
25
Дек 2014
Категория: 16 (С5) Планиметр. задачиПланиметрияТ/P A. Ларина
2014-12-25
2015-09-04
В новом формате ЕГЭ по математике задание значится как «Задание №16»
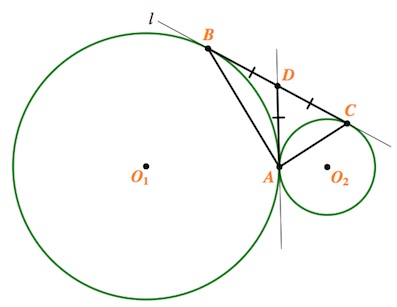
Две окружности касаются внешним образом в точке . Прямая
касается первой окружности в точке
, а второй – в точке
.
a) Докажите, что треугольник прямоугольный.
б) Найдите площадь треугольника , если радиусы окружностей 8 и 2.
Решение:
a) Проведем общую касательную к окружностям через точку . Пусть она пересекает прямую
в точке
.
По свойству отрезков касательных имеем: и
, то есть точка
равноудалена от всех вершин треугольника
.
Итак, точка – центр описанной окружности около треугольника
, при этом
– диаметр этой окружности. Угол
, опирающийся на диаметр, – прямой.
б) Пусть – центры большой и малой окружностей соответственно.
Заметим, и
.
Проведем через центр меньшей окружности прямую, параллельную . Пусть она пересекает
в точке
.
Треугольник – прямоугольный, известны его гипотенуза и один из катетов. Тогда
Заметим, , так как
.
.
Заметим, , так как в четырехугольнике
на сумму углов
и
, а значит и на сумму углов
и
, приходится
Из треугольника
Итак,
Ответ: 12,8.
Автор: egeMax |
Один комментарий
Тренировочная работа 20.09.2018 СтатГрад
пробный ЕГЭ 11 класс Задание 16 (Вариант МА10110)
№ задачи в базе 1143
Две окружности касаются внешним образом в точке С. Прямая касается меньшей окружности в точке A, а большей — в точке B, отличной от A. Прямая AC вторично пересекает большую окружность в точке D, прямая BC вторично пересекает меньшую окружность в точке E. а) Докажите, что прямая AE параллельна прямой BD. б) Пусть L — отличная от D точка пересечения отрезка DE с большей окружностью. Найдите
EL
, если радиусы окружностей равны
1
и
3
Ответ:
2/sqrt7
ФИПИ 2023 🔥 …
Примечание: Тренировочная работа 20.09.2018 СтатГрад
пробный ЕГЭ 11 класс Задание 16 (Вариант МА10110) # Задача-аналог 209
Рейтинг сложности задачи:
Задание 10938
Две окружности разных радиусов касаются внешним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите ВС, если радиусы окружностей равны $$sqrt{15}$$ и 15.
Ответ: 7,5
Скрыть
а) $$angle ACD=angle BCE$$ — вертикальные, $$angle ACD=180{}^circ -angle ACB=90{}^circ to AD$$ и $$BE$$ — диаметры. Пусть LC — общая касательная: $$angle LCB=alpha to angle CEB=alpha $$ (вписанный и м/у хордой и касательной, опирающиеся на одну дугу). $$angle ACL=90-alpha =angle ADCto angle DAC=alpha =angle CEBto ADparallel BE$$ и $$triangle ADCsim triangle CEB$$.
б) $$frac{AD}{BE}=frac{2sqrt{15}}{2cdot 15}=frac{1}{sqrt{15}}=frac{AC}{CE}$$, но $$AC=CBto frac{CB}{CE}=frac{1}{sqrt{15}}$$. Пусть $$CB=xto CE=sqrt{15}xto $$ по теореме Пифагора: $$CB^2+CE^2=BE^2leftrightarrow x^2+15x^2={left(15cdot 2right)}^2to x^2=frac{{15}^2cdot 2^2}{16}to x=7,5$$.
Две окружности касаются внешним образом…
Задание:
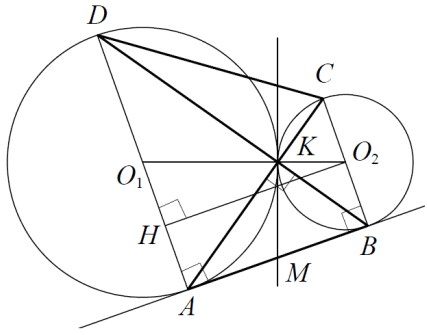
Две окружности касаются внешним образом в точке K. Прямая АВ касается первой окружности в точке А, а второй – в точке В. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке С.
а) Докажите, что прямые AD и BCпараллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решение:
а) Обозначим центры окружностей О1 и О2 соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает АВ в точке М. По свойству касательных, проведенных из одной точки, АМ = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный.
Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD⊥AB. Аналогично, получаем, что BC⊥ AB. Следовательно, прямые AD и BC параллельны.
б) Пусть, для определенности, первая окружность имеет радиус 4, а вторая – радиус 1.
Треугольники ВKC и AKD подобны, AD/BC = 4. Пусть SBKC = S, тогда SAKD = 16S.