Слайд 1
Движение по окружности (замкнутой трассе) Савченко Елена Михайловна, учитель математики высшей квалификационной категории. Муниципальное общеобразовательное учреждение гимназия №1, г. Полярные Зори, Мурманская обл. Государственная (итоговая) аттестация Обучающие модули для дистанционной самоподготовки X IV Всероссийский конкурс методических разработок «Сто друзей»
Слайд 2
Е сли два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v 1 и v 2 соответственно (v 1 > v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 . В момент, когда 1-й велосипедист в первый раз догоняет 2-го , он проходит расстояние на один круг больше. Продолжить Показать В момент, когда 1-й велосипедист в о второй раз догоняет 2-го , он проходит расстояние на два круг а больше и т.д .
Слайд 3
1 2 1. Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг? 1 красный 2 зеленый 60 80 v, км/ч на 15 км меньше (1 круг) Уравнение: Ответ: 45 х получим в часах. Не забудь перевести в минуты. t , ч х х S, км 60х 80х Показать
Слайд 4
2 1 2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. 1 автомоб. 2 автомоб. 90 х v, км/ч на 10 км больше (1 круг) Ответ: 75 t , ч 2 3 2 3 S, км 2 3 90 2 3 х Уравнение: Показать
Слайд 5
3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? 1 красный 2 синий х х+21 v, км/ч на 7 км меньше (половина круга) Уравнение: Ответ: 20 t получим в часах. Не забудь перевести в минуты. t , ч t t S, км t х t( х +21) Сколько кругов проехал каждый мотоциклист нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км. Еще способ в комментариях. Показать
Слайд 6
старт финиш 2 1 2 1 1 2 2 1 1 2 Пусть полный круг – 1 часть. 4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг? Показать
Слайд 7
4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг? на 1 круг больше Ответ: 10 1 лыжник 2 лыжник v, круг/мин t , мин 60 60 S, км х х+2 1 1 t , мин 1 лыжник 2 лыжник S, часть v, часть/мин 1 х+2 1 х 1 х+2 1 х 60 х 60 х+2 Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2. 60 х 60 х+2 – = 1 Это условие поможет ввести х …
Слайд 8
5. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч , и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. 1 желтый 2 синий S, км 80 х v, км/ч t , ч 2 3 2 3 2 3 80 2 3 х на 14 км больше (1 круг) Уравнение: Можно было сначала найти скорость вдогонку: 80 – х Тогда уравнение будет выглядеть так: v S t Ответ: 59 Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км. Показать 1 2
Слайд 9
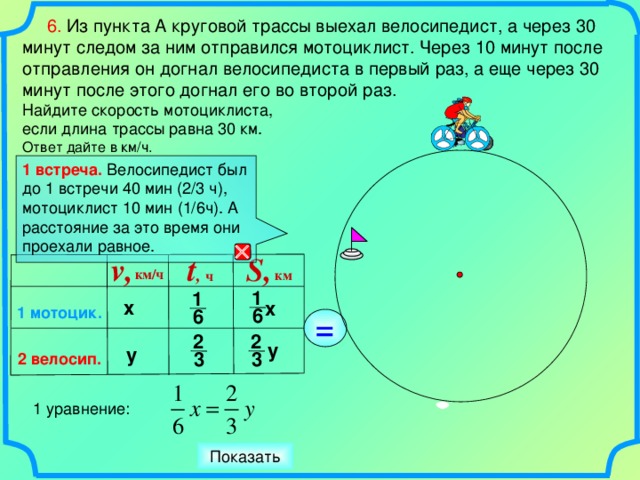
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. 1 мотоцик. 2 велосип. S, км х у v, км/ч t , ч 1 6 2 3 2 3 у 1 уравнение: 1 6 х = Показать 1 встреча. Велосипедист был до 1 встречи 40 мин (2/3 ч), мотоциклист 10 мин (1/6ч). А расстояние за это время они проехали равное.
Слайд 10
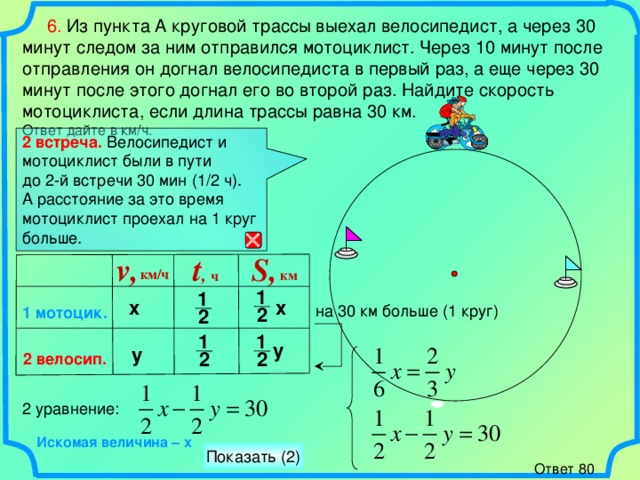
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. 1 мотоцик. 2 велосип. S, км х у v, км/ч t , ч 1 2 1 2 1 2 у на 30 км больше (1 круг) 2 уравнение: Ответ 80 1 2 х Искомая величина – х Показать (2) 2 встреча. Велосипедист и мотоциклист были в пути до 2-й встречи 30 мин (1/2 ч). А расстояние за это время мотоциклист проехал на 1 круг больше.
Слайд 11
7. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой? минутная часовая х S, круг v, круг/ч t , ч 1 1 12 х 1х 1 12 х на круга больше 2 3 3 1х – = 1 12 х 2 3 3 Ответ: 240 мин 2 3 1 3 В первый раз минутной стрелке надо пройти на круга больше, чтобы догнать минутную стрелку. Во 2-й раз – еще на 1 круг больше. В 3-й раз – еще на 1 круг больше. В 4-й раз – еще на 1 круг больше. Всего 2 3 на круга больше 2 3 3
Слайд 12
6 12 1 2 9 11 10 8 7 4 5 3 Показать (4) В первый раз минутной стрелке надо пройти на круга больше, чтобы догнать минутную стрелку. Во 2-й раз – еще на 1 круг больше. В 3-й раз – еще на 1 круг больше. В 4-й раз – еще на 1 круг больше. Всего 2 3 на круга больше 2 3 3 Проверка Другой способ – в комментариях.
Слайд 13
ЕГЭ 2010. Математика. Задача В12. Под редакцией А. Л. Семенова и И. В. Ященко http://www.2x2abc.com/forum/users/2010/B12.pdf Открытый банк заданий по математике. ЕГЭ 2011 http://mathege.ru/or/ege/Main.html Рисунки автора http://le-savchen.ucoz.ru/index/0-67 Лыжник http://officeimg.vo.msecnd.net/en-us/images/MH900282779.gif Материалы опубликованы на сайте автора «Сайт учителя математики» Раздел «Подготовка к ЕГЭ». Задание В12. http://le-savchen.ucoz.ru/publ/17
Движение
по окружности
Гусак Е.И.
МАОУ «Обдорская гимназия»
г. Салехард
В задачах ЕГЭ на круговое движение перемещение могут осуществлять 2 объекта. В этом случае следует учитывать их скорость сближения или удаления.
Пусть два тела начали движение из одной точки в одном направлении со скоростями .
— длина круга, — время, через которое они окажутся в одной точке в первый раз.
=
Если время, через которое они в n–ый раз окажутся в одной точке, то
Пусть два тела начали движение из разных точек в одном направлении со скоростями .
Нужно найти сначала время , через которое они окажутся в одной точке в первый раз, а дальше все сводится к предыдущей задаче.
=
и соответственно и
t – время их встречи, а S – длина круга, то
1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
∙ 60 мин=20 мин.
2. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
С
3. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
.
.
4. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
.
.
.
5. Автобус и мотоциклист выезжают одновременно из поселка, расположенного на кольцевой дороге. Время, которое затрачивает мотоциклист на то, чтобы обогнать автобус при движении в одном направлении, в три раза больше времени, которое нужно для того, чтобы они встретились при движении в разных направлениях. Найдите скорость автобуса, если скорость мотоциклиста равна 80 км/ч.
.
.
.
6. Автобус Две точки движутся по окружности длиной 1,2 м с постоянными скоростями. При движении в разных направлениях они встречаются через каждые 15 с. При движении в одном направлении одна точка догоняет другую через каждую минуту. Найдите скорость движения каждой точки.
.
.
.
.
7. По сигналу тренера два бегуна побежали по круговому маршруту в противоположных направлениях. Первый бегун пробежал к месту их встречи на 500 м больше, чем второй. Продолжая бежать по кругу в том же направлении, первый пришел к месту старта через 9 минут после встречи со вторым бегуном, а второй – через 16 минут после встречи. Какова длина кругового маршрута?
∙ = 3500 м.
8. Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?
.
.
ч.
ч, где — время второй и каждой следующей встречи. Таких встреч 9.
1) Статья
2) Шолково.
shkolkovo.net/catalog/syuzhetnye_tekstovye_
zadachi/krugovoe_dvizhenie
3) Математика? Легко!!!
https://matematikalegko.ru/dvigenie/zadachi-na-krugovoe-
dvizhenie.html
4) ЕГЭ. Профиль. Задачи на движение по окружности.
5) Открытый банк задач ЕГЭ по математике.
http://prof.mathege.ru/prototypes/?position=12
6) Фотография на тему Horse racing PressFoto
https://yandex.ru/images/search?pos=127&p=4&img_url=https%3A%2F%2Fs
7) Статья
https://yandex.ru/images/search?text=бегуны%20бегут%20по%20кругу%20в%20разных%20направлениях

https://yandex.ru/images/search?text=часы%20без%20стрелок&lr=58
9) Гоночные машины на треке.
https://yandex.ru/images/search?text=езда%20машин%20по%20круговой%20трассе%20фото
ЕГЭ-2014 Решение задач
Движение по окружности (замкнутой трассе)
Школа
ЕГЭ
Фабер Галина Николаевна –
учитель математики высшей категории
КМОУ «Гимназия имени Горького А.М.»
Москаленского муниципального района Омской области
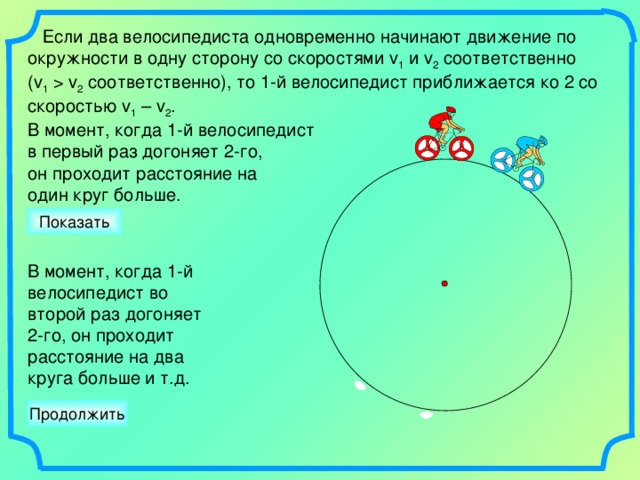
Если два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v 1 и v 2 соответственно
(v 1 v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 .
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние на
один круг больше.
Показать
В момент, когда 1-й
велосипедист во
второй раз догоняет
2-го, он проходит
расстояние на два
круга больше и т.д.
Продолжить
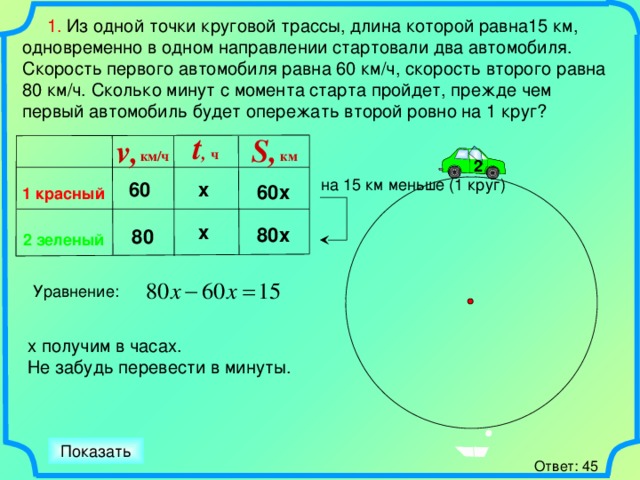
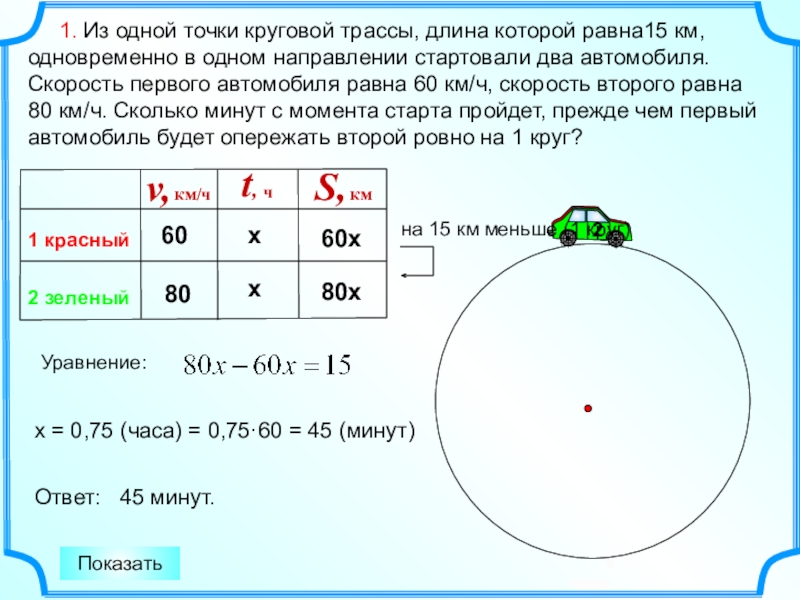
1. Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг?
t ,
S,
v,
ч
км
км/ч
1
2
на 15 км меньше (1 круг)
60
х
60х
1 красный
х
80х
80
2 зеленый
Уравнение:
На слайде приводится алгебраический способ решения. Хотя можно решить задачу и арифметическим способом.
1) 80 – 60 = 20 (км/ч) скорость вдогонку. С этой скоростью 2-й автомобиль должен преодолеть расстояние в 1 круг (15 км).
2) 15:20 = 3/4(ч) = 45 (мин).
х получим в часах.
Не забудь перевести в минуты.
Показать
Ответ: 45
3
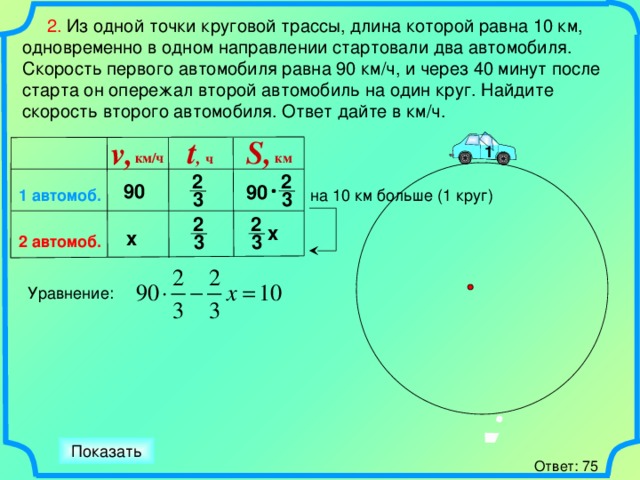
2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
t ,
S,
v,
1
2
км
км/ч
ч
2
2
90
90
1 автомоб.
на 10 км больше (1 круг)
3
3
2
2
х
х
3
3
2 автомоб.
Уравнение:
Задачу можно решить другим способом.
1) 90*(2/3) = 60 (км) проехал первый автомобиль за 40 мин. Это на 1 круг больше, чем расстояние, которое прошел второй автомобиль.
2) 60 – 10 = 50 (км) проехал второй автомобиль за 40 мин.
Чтобы найти скорость второго автомобиля разделим пройденный им путь 50 км на время 40 мин (ч).
3) 50 : (2/3) = 75 (км/ч)
Ответ: 75 км/ч скорость второго автомобиля.
Показать
Ответ: 75
4
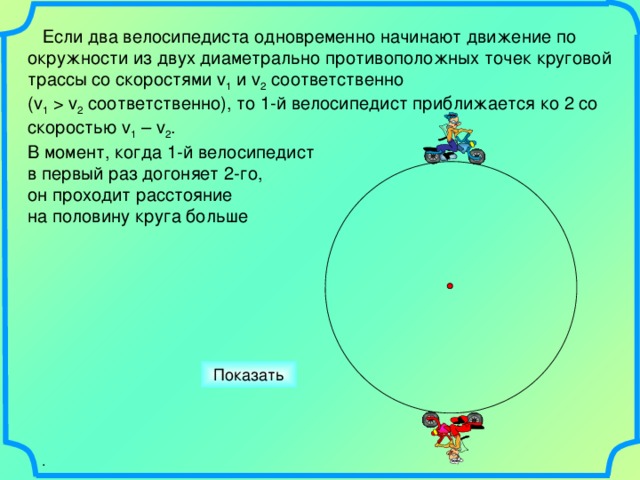
Если два велосипедиста одновременно начинают движение по окружности из двух диаметрально противоположных точек круговой трассы со скоростями v 1 и v 2 соответственно
(v 1 v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 .
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние
на половину круга больше
Скорость одного на 21 км/ч больше скорости второго – это означает, что скорость в вдогонку 21 км/ч.
Узнаем, за какое время он ликвидирует разницу в 7 км (именно такое расстояние между ними изначально – пол круга от 14 км всей трассы).
7 : 21 = 1/3 (ч)
Осталось перевести 1/3 ч в минуты – это 20 мин.
Надо понимать, что за эти 20 минут мотоциклист проедет не 7 км(!), а может больше круга.
Показать
.
4
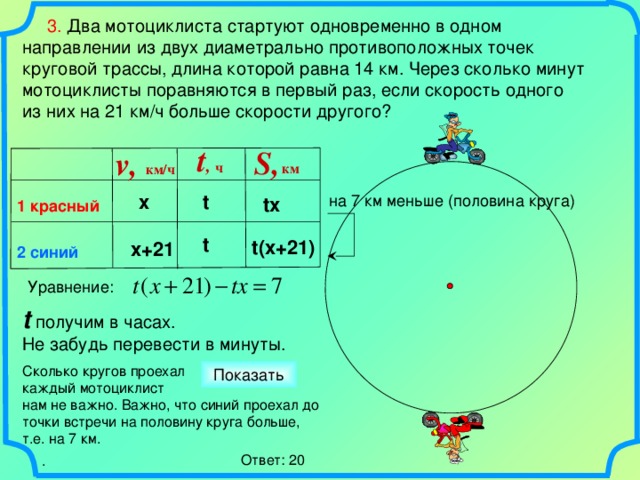
3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного
из них на 21 км/ч больше скорости другого?
t ,
S,
v,
ч
км
км/ч
х
t
на 7 км меньше (половина круга)
tх
1 красный
t
t(х+21)
х+21
2 синий
Уравнение:
t получим в часах.
Не забудь перевести в минуты.
Скорость одного на 21 км/ч больше скорости второго – это означает, что скорость в вдогонку 21 км/ч.
Узнаем, за какое время он ликвидирует разницу в 7 км (именно такое расстояние между ними изначально – пол круга от 14 км всей трассы).
7 : 21 = 1/3 (ч)
Осталось перевести 1/3 ч в минуты – это 20 мин.
Надо понимать, что за эти 20 минут мотоциклист проедет не 7 км(!), а может больше круга.
Сколько кругов проехал
каждый мотоциклист
нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км.
Показать
Ответ: 20
.
6
старт
финиш
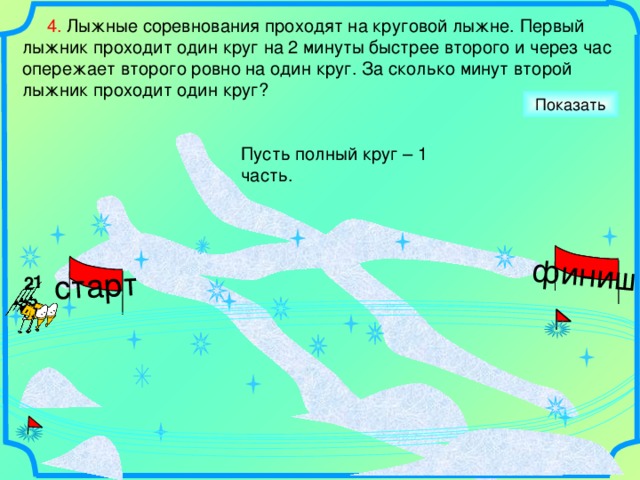
4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Показать
Пусть полный круг – 1 часть.
1
2
1
2
1
2
1
2
2
1
7
4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Это условие поможет ввести х …
t ,
v,
S,
Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2.
мин
часть/мин
часть
1
х
1
1 лыжник
х
1
х+2
1
2 лыжник
х+2
t ,
S,
v,
мин
км
круг/мин
1
60
на 1 круг больше
60
1 лыжник
х
х
1
60
60
2 лыжник
х+2
х+2
60
60
– = 1
х
х+2
Ответ: 10
8
5. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч , и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1
2
S,
t ,
v,
км/ч
км
ч
2
2
на 14 км больше (1 круг)
80
80
1 желтый
3
3
2
2
х
х
3
3
2 синий
Уравнение:
1) 80 *(2/3)= 160/3=53(1/3) (км) проехал первый автомобиль за 40 мин. Это на 1 круг больше, чем расстояние, которое прошел второй автомобиль, т.е. на 14 км.
2) 53(1/3) – 14 = 39(1/3) (км) проехал второй автомобиль за 40 мин.
Чтобы найти скорость второго автомобиля разделим пройденный им путь 50 км на время 40 мин (ч).
3) 39(1/3) : (2/3) = 59 (км/ч)
Ответ: 59 км/ч скорость второго автомобиля.
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
t
=
v
S
Показать
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.
Ответ: 59
9
5. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч , и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1
2
S,
t ,
v,
км/ч
км
ч
2
2
на 14 км больше (1 круг)
80
80
1 желтый
3
3
2
2
х
х
3
3
2 синий
Уравнение:
1) 80 *(2/3)= 160/3=53(1/3) (км) проехал первый автомобиль за 40 мин. Это на 1 круг больше, чем расстояние, которое прошел второй автомобиль, т.е. на 14 км.
2) 53(1/3) – 14 = 39(1/3) (км) проехал второй автомобиль за 40 мин.
Чтобы найти скорость второго автомобиля разделим пройденный им путь 50 км на время 40 мин (ч).
3) 39(1/3) : (2/3) = 59 (км/ч)
Ответ: 59 км/ч скорость второго автомобиля.
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
t
=
v
S
Показать
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.
Ответ: 59
10
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз.
Найдите скорость мотоциклиста,
если длина трассы равна 30 км.
Ответ дайте в км/ч.
1 встреча. Велосипедист был до 1 встречи 40 мин (2/3 ч), мотоциклист 10 мин (1/6ч). А расстояние за это время они проехали равное.
v,
t ,
S,
км/ч
км
ч
1
1
х
х
1 мотоцик.
6
6
=
Можно составить уравнение и иначе.
2
2
у
у
3
3
2 велосип.
1 уравнение:
Показать
11
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км.
Ответ дайте в км/ч.
2 встреча. Велосипедист и мотоциклист были в пути
до 2-й встречи 30 мин (1/2 ч).
А расстояние за это время мотоциклист проехал на 1 круг больше.
v,
S,
t ,
км/ч
км
ч
1
1
х
х
на 30 км больше (1 круг)
1 мотоцик.
2
2
Можно составить уравнение и иначе.
1
1
у
у
2
2
2 велосип.
2 уравнение:
Искомая величина – х
Показать (2)
Ответ 80
12
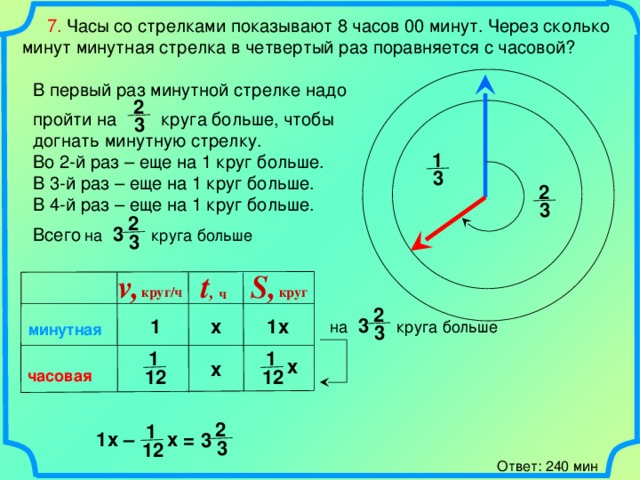
7. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
В первый раз минутной стрелке надо
пройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.
Всего
2
3
1
3
2
3
2
3
на круга больше
3
t ,
S,
v,
круг/ч
круг
ч
2
Минутная стрелка догоняет часовую один раз в час. Последний, четвертый раз догонит в 12:00, т.е. через 4 часа, или 240 минут.
3
1х
х
1
на круга больше
минутная
3
1
1
х
х
12
12
часовая
2
1
1х – =
х
3
3
12
Ответ: 240 мин
13
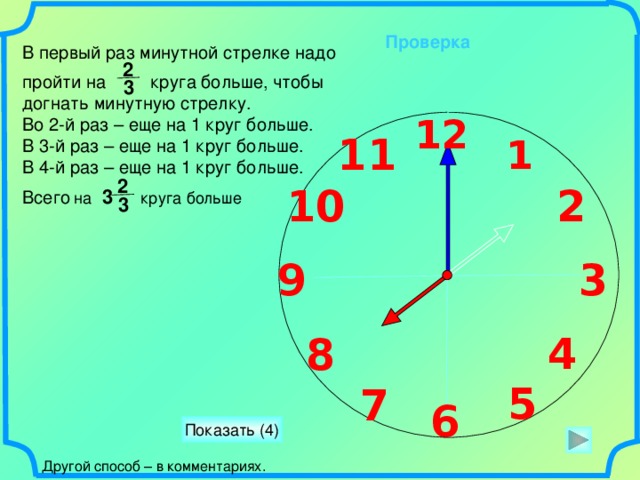
Проверка
В первый раз минутной стрелке надо
пройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.
Всего
2
3
12
11
1
2
10
2
3
на круга больше
3
3
9
Минутная стрелка догоняет часовую один раз в час. Последний, четвертый раз догонит в 12:00, т.е. через 4 часа, или 240 минут.
4
8
5
7
6
Показать (4)
Другой способ – в комментариях.
14
№ 99599.
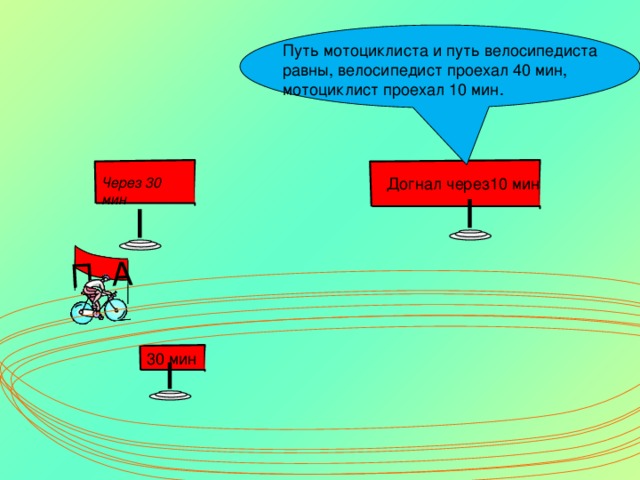
Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
П. А
Путь мотоциклиста и путь велосипедиста
равны, велосипедист проехал 40 мин,
мотоциклист проехал 10 мин.
Догнал через10 мин
Через 30 мин
30 мин
Решение.
Так как мотоциклист догнал велосипедиста через 10 минут, то их пути равны.
x км/ч – скорость вел., y км/ч – скорость мот.
Длина трассы 30 км, т.к. мотоциклист догнал второй раз велосипедиста , то они за 30 мин прошли S км, тогда путь мотоциклиста за 0,5 ч –( S+30), а у велосипедиста S км.
Значит путь мотоциклиста равен 30+10=40 км .
v(мот)= 40:0,5=80 км/ч
Ответ: 80 км/ч
№ 99596.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Один из них проехал на половину круга
больше, то есть на 7 км больше.
Через сколько минут они
Поравняются в первый раз?
Решение.
Один из них проехал на половину круга больше, то есть
Ответ: 20 минут
Слайд 1Задание
№6
Ответы:
№1 – 500 м
№2 – 400 м
№3 –
88 км/ч
№4 – 70 км/ч
№5 – 72 км/ч
Проверка домашнего задания

Слайд 3Задание
№6
Ответы:
Проверка самостоятельной работы
1-вариант
№1 – 120 км/ч
№2 – 400
м
2-вариант
№1 – 35 км/ч
№2 – 450 м

Слайд 4ЕГЭ МАТЕМАТИКА-2017
Задачи на движение
Задание
№6

Слайд 5
Движение по окружности (замкнутой трассе)
Слайд 6 Если два велосипедиста одновременно начинают движение по окружности в
одну сторону со скоростями v1 и v2 соответственно
(v1 > v2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v1 – v2.
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние на
один круг больше.
Продолжить
Показать
В момент, когда 1-й
велосипедист во
второй раз догоняет
2-го, он проходит
расстояние на два
круга больше и т.д.

Слайд 7 1. Из одной точки круговой трассы, длина которой
равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг?
х = 0,75 (часа) = 0,75·60 = 45 (минут)
Ответ: 45 минут.
Показать
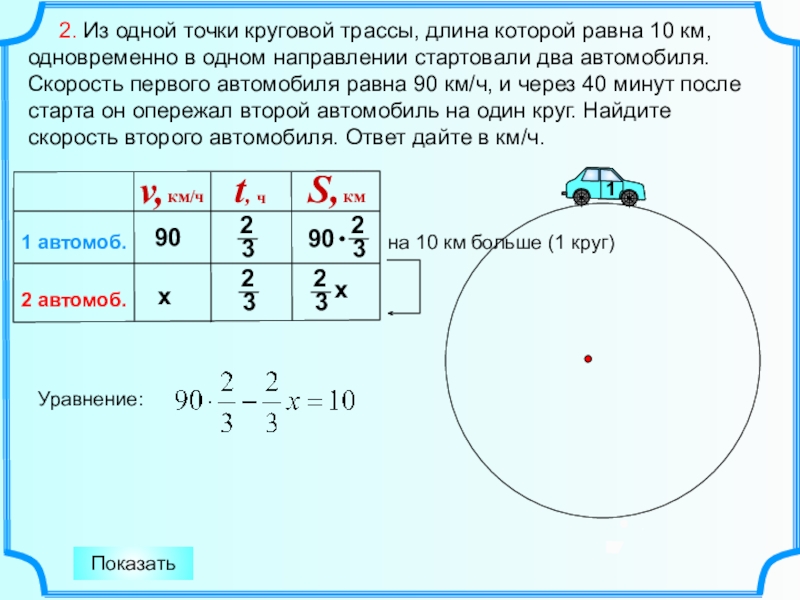
Слайд 8 2. Из одной точки круговой трассы, длина которой
равна 10 км, одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Показать
Слайд 9
Пусть полный круг – 1 часть.
3. Лыжные
соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Показать

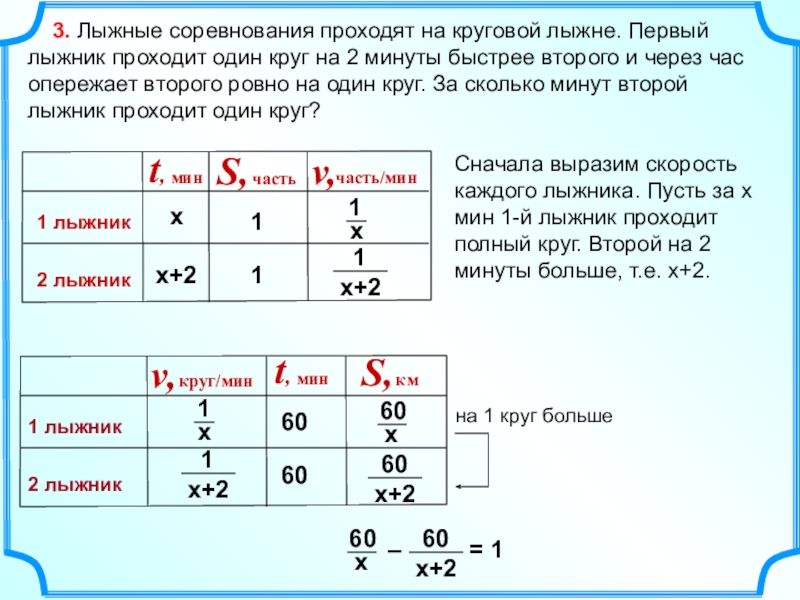
Слайд 10 3. Лыжные соревнования проходят на круговой лыжне. Первый лыжник
проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
х
х+2
Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2.
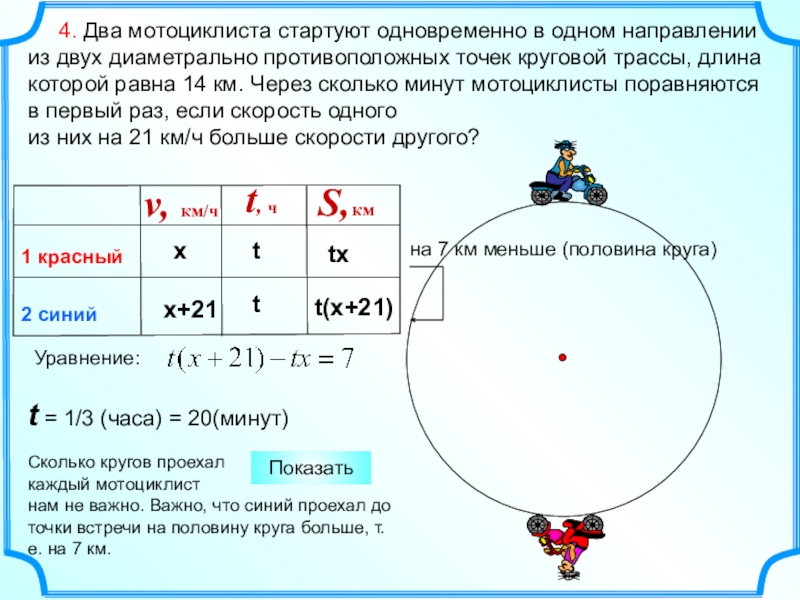
Слайд 11 4. Два мотоциклиста стартуют одновременно в одном направлении
из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного
из них на 21 км/ч больше скорости другого?
t = 1/3 (часа) = 20(минут)
Сколько кругов проехал
каждый мотоциклист
нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км.
Показать
Слайд 12Домашнее задание
Решить задачи по теме «Движение по окружности»
(карточка)

Слайд 13Итог урока
всё понял
Не всё понял, надо поработать
Ничего не понятно
Презентация на тему «Движение по окружности» 11 класс
-
Скачать презентацию (0.4 Мб)
-
7 загрузок -
0.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Скачать презентацию (0.4 Мб). Тема: «Движение по окружности». Предмет: математика. 13 слайдов. Для учеников 11 класса. Добавлена в 2021 году.
-
Формат
pptx (powerpoint)
-
Количество слайдов
13
-
Аудитория
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Движение по окружности
(замкнутой трассе)
Савченко Елена Михайловна,
учитель математики высшей квалификационной категории.
Муниципальное общеобразовательное учреждение гимназия №1,
г. Полярные Зори, Мурманская обл.
Государственная (итоговая) аттестация
Обучающие модули для дистанционной самоподготовки
XIV Всероссийский конкурс методических разработок «Сто друзей» -
Слайд 2
Если два велосипедиста одновременно начинают движение поокружности в одну сторону со скоростями v1 и v2 соответственно
(v1 > v2 соответственно), то 1-й велосипедист приближаетсяко 2 со скоростью v1 –v2.
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние на
один круг больше.Продолжить
Показать
В момент, когда 1-й
велосипедист во
второй раз догоняет
2-го, он проходит
расстояние на два
круга больше и т.д. -
Слайд 3
1
2
1.Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг?
1 красный
2 зеленый
60
80
v,
км/чна 15 км меньше (1 круг)
Уравнение:
Ответ: 45
х получим в часах.
Не забудь перевести в минуты.
t,
ч
х
х
S,
км
60х
80хПоказать
-
Слайд 4
2
1
2.Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.1 автомоб.
2 автомоб.
90
х
v,
км/чна 10 км больше (1 круг)
Ответ: 75
t,
ч
23
23
S,
км
23
902
3
х
Уравнение:Показать
-
Слайд 5
3.Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного
из них на 21 км/ч больше скорости другого?1 красный
2 синий
х
х+21
v,
км/чна 7 км меньше (половина круга)
Уравнение:
Ответ: 20
tполучим в часах.
Не забудь перевести в минуты.
t,
ч
t
t
S,
км
tх
t(х+21)
Сколько кругов проехал
каждый мотоциклист
нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км.
Еще способ в комментариях.Показать
-
Слайд 6
старт
финиш
2
1
2
11
22
1
1
2Пусть полный круг – 1 часть.
4.Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Показать -
Слайд 7
4.Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
на 1 круг больше
Ответ: 101 лыжник
2 лыжник
v,
круг/мин
t,
мин
60
60
S,
км
х
х+2
1
1
t,
мин1 лыжник
2 лыжник
S,
часть
v,
часть/мин
1х+2
1х
1х+2
1х
60х
60х+2
Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2.
60х
60х+2
– = 1Это условие поможет ввести х …
-
Слайд 8
5.Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1 желтый
2 синий
S,
км
80
х
v,
км/ч
t,
ч
23
23
23
802
3
хна 14 км больше (1 круг)
Уравнение:
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
v
S
=
tОтвет: 59
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.Показать
1
2
-
Слайд 9
6.Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз.
Найдите скорость мотоциклиста,
если длина трассы равна 30 км.
Ответ дайте в км/ч.1 мотоцик.
2 велосип.
S,
км
х
у
v,
км/ч
t,
ч
16
23
23
у
1 уравнение:
16
х=
Показать
1 встреча. Велосипедист был до 1 встречи 40 мин (2/3 ч), мотоциклист 10 мин (1/6ч). А расстояние за это время они проехали равное.
-
Слайд 10
6.Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км.
Ответ дайте в км/ч.1 мотоцик.
2 велосип.
S,
км
х
у
v,
км/ч
t,
ч
12
12
12
уна 30 км больше (1 круг)
2 уравнение:
Ответ 80
12
хИскомая величина – х
Показать (2)
2 встреча. Велосипедист и мотоциклист были в пути
до 2-й встречи 30 мин (1/2 ч).
А расстояние за это время мотоциклист проехал на 1 круг больше.
-
Слайд 11
7.Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
минутная
часовая
х
S,
круг
v,
круг/ч
t,
ч
1
112
х
1х
112
хна круга больше
23
3
1х – =
112
х
23
3
Ответ: 240 мин2
3
13
В первый раз минутной стрелке надопройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.Всего
23
на круга больше
23
3 -
Слайд 12
6
121
2
9
11
10
8
7
4
5
3Показать (4)
В первый раз минутной стрелке надо
пройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.Всего
23
на круга больше
23
3
ПроверкаДругой способ – в комментариях.
-
Слайд 13
ЕГЭ 2010. Математика. Задача В12.
Под редакцией А. Л. Семенова и И. В. Ященко
http://www.2x2abc.com/forum/users/2010/B12.pdf
Открытый банк заданий по математике. ЕГЭ 2011
http://mathege.ru/or/ege/Main.html
Рисунки автора http://le-savchen.ucoz.ru/index/0-67Лыжник
http://officeimg.vo.msecnd.net/en-us/images/MH900282779.gif
Материалы опубликованы на сайте автора «Сайт учителя математики»
Раздел «Подготовка к ЕГЭ». Задание В12.
http://le-savchen.ucoz.ru/publ/17
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации










Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
Презентация по математике «Подготовка к ЕГЭ» (задачи на движение по окружности)
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Описание презентации по отдельным слайдам:
Ответы: №1 – 500 м №2 – 400 м №3 – 88 км/ч №4 – 70 км/ч №5 – 72 км/ч Проверка домашнего задания
Самостоятельная работа 1 вариант 2 вариант 1. Первую половину пути путешественник ехал на машине со скоростью 100 км/ч, а вторую – со скоростью 150 км/ч. Определите среднюю скорость путешественника на протяжении всего пути. 2. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 60 км/ч и 80 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 3 минуты. Ответ дайте в метрах. 1. Путешественник плыл по морю на яхте со скоростью 20 км/ч, а возвратился обратно на самолёте со скоростью 140 км/ч. Определите среднюю скорость путешественника на протяжении всего пути. 2. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 85 км/ч и 65 км/ч. Длина пассажирского поезда равна 550 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 24 секундам. Ответ дайте в метрах.
Ответы: Проверка самостоятельной работы 1-вариант №1 – 120 км/ч №2 – 400 м 2-вариант №1 – 35 км/ч №2 – 450 м
Презентация «Движение по окружности»
презентация к уроку по алгебре (9, 11 класс) на тему
Презентация содержит примеры решения задач на движение по круговой трассе. Ресурс окажет существенную помощь при подготовке к итоговой аттестации учащимся 9 и 11 классов.
Скачать:
| Вложение | Размер |
|---|---|
| dvizhenie_po_krugovoy_trasse.ppt | 912 КБ |
Предварительный просмотр:
Подписи к слайдам:
Движение по окружности (замкнутой трассе) Савченко Елена Михайловна, учитель математики высшей квалификационной категории. Муниципальное общеобразовательное учреждение гимназия №1, г. Полярные Зори, Мурманская обл. Государственная (итоговая) аттестация Обучающие модули для дистанционной самоподготовки X IV Всероссийский конкурс методических разработок «Сто друзей»
Е сли два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v 1 и v 2 соответственно (v 1 > v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 . В момент, когда 1-й велосипедист в первый раз догоняет 2-го , он проходит расстояние на один круг больше. Продолжить Показать В момент, когда 1-й велосипедист в о второй раз догоняет 2-го , он проходит расстояние на два круг а больше и т.д .
1 2 1. Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг? 1 красный 2 зеленый 60 80 v, км/ч на 15 км меньше (1 круг) Уравнение: Ответ: 45 х получим в часах. Не забудь перевести в минуты. t , ч х х S, км 60х 80х Показать
2 1 2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. 1 автомоб. 2 автомоб. 90 х v, км/ч на 10 км больше (1 круг) Ответ: 75 t , ч 2 3 2 3 S, км 2 3 90 2 3 х Уравнение: Показать
3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? 1 красный 2 синий х х+21 v, км/ч на 7 км меньше (половина круга) Уравнение: Ответ: 20 t получим в часах. Не забудь перевести в минуты. t , ч t t S, км t х t( х +21) Сколько кругов проехал каждый мотоциклист нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км. Еще способ в комментариях. Показать
старт финиш 2 1 2 1 1 2 2 1 1 2 Пусть полный круг – 1 часть. 4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг? Показать
4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг? на 1 круг больше Ответ: 10 1 лыжник 2 лыжник v, круг/мин t , мин 60 60 S, км х х+2 1 1 t , мин 1 лыжник 2 лыжник S, часть v, часть/мин 1 х+2 1 х 1 х+2 1 х 60 х 60 х+2 Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2. 60 х 60 х+2 – = 1 Это условие поможет ввести х …
5. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч , и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. 1 желтый 2 синий S, км 80 х v, км/ч t , ч 2 3 2 3 2 3 80 2 3 х на 14 км больше (1 круг) Уравнение: Можно было сначала найти скорость вдогонку: 80 – х Тогда уравнение будет выглядеть так: v S t Ответ: 59 Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км. Показать 1 2
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. 1 мотоцик. 2 велосип. S, км х у v, км/ч t , ч 1 6 2 3 2 3 у 1 уравнение: 1 6 х = Показать 1 встреча. Велосипедист был до 1 встречи 40 мин (2/3 ч), мотоциклист 10 мин (1/6ч). А расстояние за это время они проехали равное.
6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. 1 мотоцик. 2 велосип. S, км х у v, км/ч t , ч 1 2 1 2 1 2 у на 30 км больше (1 круг) 2 уравнение: Ответ 80 1 2 х Искомая величина – х Показать (2) 2 встреча. Велосипедист и мотоциклист были в пути до 2-й встречи 30 мин (1/2 ч). А расстояние за это время мотоциклист проехал на 1 круг больше.
7. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой? минутная часовая х S, круг v, круг/ч t , ч 1 1 12 х 1х 1 12 х на круга больше 2 3 3 1х – = 1 12 х 2 3 3 Ответ: 240 мин 2 3 1 3 В первый раз минутной стрелке надо пройти на круга больше, чтобы догнать минутную стрелку. Во 2-й раз – еще на 1 круг больше. В 3-й раз – еще на 1 круг больше. В 4-й раз – еще на 1 круг больше. Всего 2 3 на круга больше 2 3 3
6 12 1 2 9 11 10 8 7 4 5 3 Показать (4) В первый раз минутной стрелке надо пройти на круга больше, чтобы догнать минутную стрелку. Во 2-й раз – еще на 1 круг больше. В 3-й раз – еще на 1 круг больше. В 4-й раз – еще на 1 круг больше. Всего 2 3 на круга больше 2 3 3 Проверка Другой способ – в комментариях.
Презентация «Движение по окружности»
Код для использования на сайте:
Скопируйте этот код и вставьте себе на сайт
Для скачивания поделитесь материалом в соцсетях
После того как вы поделитесь материалом внизу появится ссылка для скачивания.
Подписи к слайдам:
В задачах ЕГЭ на круговое движение перемещение могут осуществлять 2 объекта. В этом случае следует учитывать их скорость сближения или удаления.
Пусть два тела начали движение из одной точки в одном направлении со скоростями .
— длина круга, — время, через которое они окажутся в одной точке в первый раз.
Если время, через которое они в n–ый раз окажутся в одной точке, то
Пусть два тела начали движение из разных точек в одном направлении со скоростями .
Нужно найти сначала время , через которое они окажутся в одной точке в первый раз, а дальше все сводится к предыдущей задаче.
и соответственно и
t – время их встречи, а S – длина круга, то
1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
2. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
3. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
4. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
5. Автобус и мотоциклист выезжают одновременно из поселка, расположенного на кольцевой дороге. Время, которое затрачивает мотоциклист на то, чтобы обогнать автобус при движении в одном направлении, в три раза больше времени, которое нужно для того, чтобы они встретились при движении в разных направлениях. Найдите скорость автобуса, если скорость мотоциклиста равна 80 км/ч.
источники:
http://nsportal.ru/shkola/algebra/library/2017/12/25/prezentatsiya-dvizhenie-po-okruzhnosti
http://uchitelya.com/matematika/163166-prezentaciya-dvizhenie-po-okruzhnosti.html