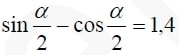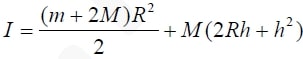Задание 1
Найдите значение выражения $$frac{1,8}{1+frac{1}{11}}$$
Ответ: 1,65
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{1,8}{1+frac{1}{11}}=$$$$frac{18}{10}*frac{11}{12}=$$$$frac{33}{20}=1,65$$
Задание 2
В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты:
| Команда | 1 эстафета, мин. | 2 эстафета, мин. | 3 эстафета, мин | 4 эстафета, мин |
| Ласточка | 3,4 | 4,9 | 2,9 | 5,8 |
| Чайка | 4,5 | 4,3 | 3,2 | 5,4 |
| Буревестник | 4,9 | 4,8 | 2,7 | 6,3 |
| Альбатрос | 3,7 | 4,5 | 2,4 | 5,1 |
За каждую эстафету команда получает количество баллов, равное занятому в этой эстафете месту, затем баллы по всем эстафетам суммируются. Какое итоговое место заняла команда «Буревестник», если победителем считается команда, набравшая наименьшее количество очков?
Варианты ответа
1. 1
2. 2
3. 3
4. 4
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
| Команда | 1 эстафета, место | 2 эстафета, место | 3 эстафета, место | 4 эстафета, место | итоговый бал |
| Ласточка | 1 | 4 | 3 | 3 | 11 |
| Чайка | 3 | 1 | 4 | 2 | 10 |
| Буревестник | 4 | 3 | 2 | 4 | 13 |
| Альбатрос | 2 | 2 | 1 | 1 | 6 |
В итоге команда Буревестник займет 4 место, что соответствует 4 варианту ответа
Задание 3
Между какими числами заключено число $$2sqrt{3}$$ Варианты ответа 1)12 и 13 2)3 и 4 3)5 и 6 4)6 и 7
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$2sqrt{3}=sqrt{2^{2}*3}=sqrt{12}Leftrightarrow$$$$sqrt{9}<sqrt{12}<sqrt{16}$$, что соответствует $$3<2sqrt{3}<4$$ и является 2 вариантом ответа
Задание 4
Представьте выражение $$frac{(c^{-9})^{2}}{c^{-4}}$$ в виде степени с основанием с Варианты ответа: 1) $$c^{-22}$$ 2) $$c^{-72}$$ 3) $$c^{68}$$ 4) $$c^{-14}$$
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Воспользуемся свойствами степени: $$frac{(c^{-9})^{2}}{c^{-4}}=$$$$frac{c^{-18}}{c^{-4}}=c^{-18-(-4)}=$$$$c^{-14}$$, что соответствует 4 варианту ответа
Задание 5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры с 6:00 до 18:00. Ответ дайте в градусах Цельсия.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
min=12 (6:00) , max=24 (12:00-15:00), тогда max-min=24-12=12
Задание 6
Решите уравнение $$3(2-3x)-(2x+1)=27$$
Ответ: -2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$3(2-3x)-(2x+1)=27Leftrightarrow$$$$6-9x-2x-12-27=0Leftrightarrow$$$$-11x=22|:-11Leftrightarrow$$$$x=-2$$
Задание 7
Рабочий выточил за смену 920 деталей, превысив план на 15%. Сколько деталей предполагало выточить?
Ответ: 800
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть первоначально планировалось выточить х деталей, тогда мы можем принять эту величину за 100%: x-100% 920-115% Тогда: $$x=frac{920*100}{115}=800$$ деталей
Задание 8
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 8 млн пользователей.
Какие из следующих утверждений неверны?
1. пользователей из России больше, чем пользователей из Украины;
2. больше трети пользователей сети — из Украины;
3. пользователей из Беларуси больше, чем пользователей из Украины;
4. пользователей из России больше 4 миллионов человек.
Ответ: 23
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1. пользователей из России больше, чем пользователей из Украины — верно 2. больше трети пользователей сети — из Украины — неверно (так как сегмент Украины менее трети всей окружности) 3. пользователей из Беларуси больше, чем пользователей из Украины — неверно (так как сегмент Беларуси меньше сегмента Украины) 4. пользователей из России больше 4 миллионов человек — верно. Ответом будут 2 и 3 варианты
Задание 9
В корзинке у Красной Шапочки 20 пирожков, 4 из которых с мясом, 7 с картошкой, а остальные с капустой. Бабушка наугад взяла один пирожок. Какова вероятность того, что бабушка взяла пирожок с капустой?
Ответ: 0,45
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Количество пирожков с капустой: 20-4-7=9. Тогда вероятность взять пирожок с капустой составляет: $$P=frac{9}{20}=0,45$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают
ФОРМУЛЫ
1) $$y=2x$$
2) $$y=x^{2}-2$$
3) $$y=-frac{2}{x}$$
Ответ: 213
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) $$y=2x$$ — линейная функция, графиком является прямая, что соответствует пункту Б 2) $$y=x^{2}-2$$ — квадратичная функция, графиком является парабола, что соответствует пункту А 3) $$y=-frac{2}{x}$$ — обратная пропорциональность, графиком является гипербола, что соответствует пункту В В итоге ответ будет 213
Задание 11
Укажите номер первого отрицательного члена арифметической прогрессии: 9,5; 9; 8,5; …
Ответ: 21
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем разность арифметической прогрессии: $$d=a_{n+1}-a_{n}=9-9,5=-0,5$$, $$a_{1}=9,5$$. По формуле N-ый член арифметической прогрессии вычисляется как: $$a_{n}=a_{1}+d(n-1)$$. Тогда $$9,5-0,5(n-1)<0 Leftrightarrow$$$$9,5-0,5n+0,5<0Leftrightarrow$$$$10<0,5n|:0,5Leftrightarrow$$$$n>20$$. Так как неравенство строгое, и n — порядковый номер, то первый отрицательный член будет под номером 21
Задание 12
Найдите значение выражения $$(frac{2}{a}+frac{1}{b})cdot frac{1}{a^{2}+4b^{2}+4ab} cdot (a^{2}-4b^{2})$$
Ответ: 0,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(frac{2}{a}+frac{1}{b})cdot frac{1}{a^{2}+4b^{2}+4ab} cdot (a^{2}-4b^{2})=$$$$frac{2b+a}{ab}cdot frac{1}{(a+2b)^{2}} cdot ((a-2b)(a+2b)=$$$$frac{a-2b}{ab}=$$$$frac{2sqrt{5}+2-2(sqrt{2}-1)}{(2sqrt{5}+2)(sqrt{5}-1)}=$$$$frac{2sqrt{5}+2-2sqrt{5}+2}{2(sqrt{5}+1)(sqrt{5}-1)}=$$$$frac{4}{2(5-1)}=frac{1}{2}=0,5$$
Задание 13
Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула $$F=1,8C+32$$ , где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует $$186^{circ}$$ по шкале Фаренгейта? Ответ округлите до десятых.
Ответ: 85,6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим в формулу известные значения: $$186=1,8C+32Leftrightarrow$$$$1,8C=154|:1,8Leftrightarrow$$$$C=85,(5)$$. Так как дробь бесконечная десятичная, то если округлить до десятых получим: $$85,555…=85,6$$
Задание 14
На каком рисунке изображено множество решений неравенства $$2x-x^{2}+3 leq 0$$
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$2x-x^{2}+3 leq 0|*(-1) Leftrightarrow$$$$x^{2}-2x-3 geq 0$$
Найдем корни уравнения $$x^{2}-2x-3 =0$$. По теореме Виета: $$left[begin{matrix}x_{1}+x_{2}=2\ x_{1}*x_{2}=-3end{matrix}right.Leftrightarrow $$$$left[begin{matrix}x_{1}=-1\ x_{2}=3end{matrix}right.$$
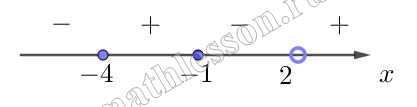
Отметим полученные корни и расставим знаки, которые принимает выражение $$x^{2}-2x-3$$ на полученных промежутках:
Нам необходимы значения, которые больше нуля (те, где отмечен +), следовательно, ответом будет пункт под номером 2
Задание 15
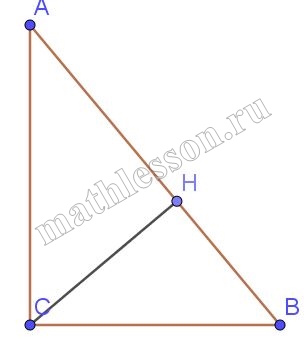
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Опустим перпендикуляр из точки C как показано на рисунке. BC=DE=8, BD-CE=3, тогда из треугольника ABC: $$AB=sqrt{AC^{2}-BC^{2}}=sqrt{10^{2}-8^{2}}=6$$. Тогда AD=6+3=9 метров
Задание 16
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 48° и 74°. Найдите меньший угол параллелограмма. Ответ дайте в градусах
Ответ: 58
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Весь угол в таком случае составляет: 48+74=122. Тогда меньший острый по свойству углов параллелограмма составляет: 180-122=58.
Задание 17
В треугольнике ABC известно, что AC=24, BC= $$sqrt{265}$$ , угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
Ответ: 14,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
По теореме Пифагора: $$AB=sqrt{AC^{2}+BC^{2}}=sqrt{576+265}=29$$. По свойству радиуса описанной окружности около прямоугольного треугольника : $$R=frac{AB}{2}=14,5$$
Задание 18
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Ответ: 30
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть a,b — стороны прямоугольника и параллелограмма. Площадь прямоугольника: $$S_{1}=ab$$, площадь параллелограмма: $$S_{2}=absinalpha$$, где $$alpha$$ — острый угол между сторонами параллелограмма, тогда: $$frac{1}{2}ab=absinalphaLeftrightarrow$$$$sinalpha=frac{1}{2}Leftrightarrow$$$$alpha=30^{circ}$$
Задание 19
В треугольнике ABC угол C равен 90°, СН – высота, AВ = 16, sin A = 3/4 . Найдите BН.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Из треугольника ABC: $$CB=ABsin A=16*frac{3}{4}=12$$.
Из треугольника CHB: $$HB=CBsin BCH$$. Но из подобия прямоугольных треугольников при проведении высоты из прямого угла получаем, что $$sin BCH=sin A$$, тогда $$HB=CBsin A=12*frac{3}{4}=9$$
Задание 20
Какие из следующих утверждений верны?
1. Диагонали любого прямоугольника равны.
2. Существует прямоугольник, который не является параллелограммом.
3. Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Ответ: 13
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1. Диагонали любого прямоугольника равны — верно 2. Существует прямоугольник, который не является параллелограммом — неверно, так как прямоугольник сам по себе и есть параллелограмм, у которого все углы прямые 3. Площадь треугольника меньше произведения двух его сторон — верно, так как равна половине произведения его сторон на синус угла между ними Правильными являются ответы под номерами 1 и 3
Задание 21
Найдите сумму целых отрицательных решений неравенства $$frac{x^{2}+2x+10}{x-2} geq -3$$
Ответ: -10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{x^{2}+2x+10}{x-2} geq -3Leftrightarrow$$$$frac{x^{2}+2x+10}{x-2}+3 geq 0Leftrightarrow$$$$frac{x^{2}+2x+10}{x-2}+frac{3(x-2)}{x-2} geq 0Leftrightarrow$$$$frac{x^{2}+2x+10+3x-6}{x-2} geq 0Leftrightarrow$$$$frac{x^{2}+5x+4}{x-2} geq 0$$
Найдем при каких значениях x числитель дроби равен нулю и отметим эти значения (закрашенные, так как неравенство нестрогое), а так же значение, когда знаменатель равен нулю (пустое, так как мы должны исключить данное значение из ОДЗ) на координатной прямой и расставим знаки значений, которые принимает дробь на полученных промежутках:
Нам необходимо выбрать те промежутки, где дробь принимает положительные значения, а так же из данных промежутков найти сумму всех целых отрицательных значений: $$-4+(-3)+(-2)+(-1)=-10$$
Задание 22
В сплаве олова с медью содержалось 11 кг меди. После того, как в сплав добавили 7,5 кг олова, содержание олова повысилось на 33%. Какова была первоначальная масса сплава?
Ответ: 12,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x кг — масса сплава, тогда x — 11 кг — масса олова в нем, а доля олова : $$frac{x-11}{x}*100$$%. Добавили 7,5 кг олова, тогда масса олова стала : x — 11 + 7,5 = x — 3,5 кг , масса сплава при этом стала: x + 7,5 кг, следовательно, доля олова : $$frac{x-3,5}{x+7,5}*100$$%. Тогда:
$$frac{x-3,5}{x+7,5}*100-frac{x-11}{x}*100=33|*x(x+7,5)Leftrightarrow$$$$100x(x-3,5)-100(x-11)(x+7,5)=33x(x+7,5)Leftrightarrow$$$$100x^{2}-350x-100x^{2}+350x+8250=33x^{2}+247,5xLeftrightarrow$$$$33x^{2}+247,5x-82550=0|:16,5Leftrightarrow$$$$2x^{2}+15x-500=0$$
$$D=225+4000=65^{2}Leftrightarrow$$$$x_{1}=frac{-15+65}{4}=12,5 ; x_{2}<0$$. Следовательно, первоначальная масса сплава составляла 12,5 кг.
Задание 23
Постройте график функции $$y=|x^{2}+6x+5|$$ и определите, при каких значениях а прямая $$y=a$$ имеет с графиком три общие точки.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Рассмотрим график функции $$y_{1}=x^{2}+6x+5$$. Искомый будет отличаться от данного тем, что та часть параболы, которая находится под осью Ох симметрично отобразиться относительно оси Ох (в силу того, что модуль все отрицательные значения сделает положительными). Найдем вершину параболы: $$x_{0}=-frac{b}{2a}=-frac{6}{2}=-3$$ , $$y_{1}(3)=(-3)^{2}+6*(-3)+5=-4$$. Найдем еще несколько значений для функции $$y_{1}$$: $$y_{1}(-2)=-3 ; y_{1}(-1)=0 ; y_{1}(0)=5$$.
График квадратичной функции симметричен относительно оси $$x=x_{0}$$, в нашем случае относительно $$x=-3$$. Начертим график функции $$y_{1}$$:
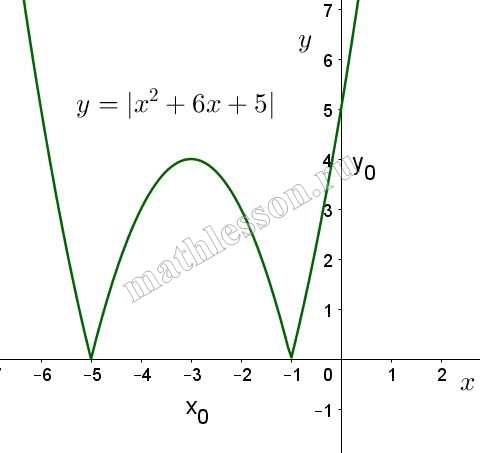
Отобразим симметрично относительно оси Ох ту часть параболы, которая располагается под осью Ох и получим график функции $$y=|x^{2}+6x+5|$$:
Очевидно, что прямая параллельная оси Оу будет иметь три точки пересечения с графиком данной функции при $$a=4$$:
Задание 24
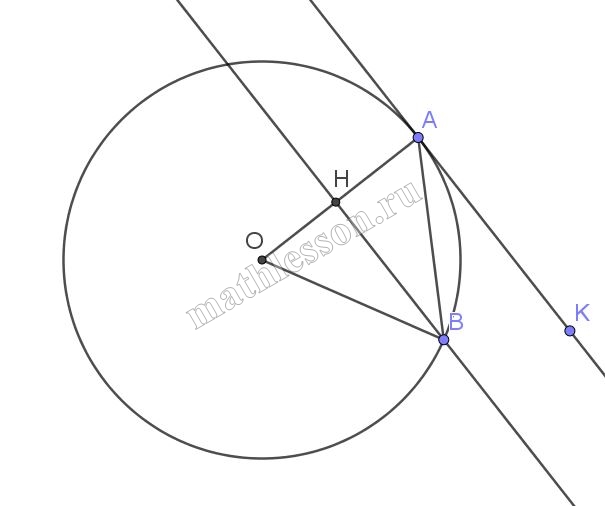
В окружности радиуса 16 см проведена хорда длиной, равной 8 см. через один конец хорды проведена касательная, а через другой – секущая, параллельная касательной. Найдите расстояние между касательной и секущей.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1)Из треугольника AOB: по теореме косинусов $$cos OAB = frac{OA^{2}+AB^{2}-OB^{2}}{2OA*OB}=frac{16^{2}+8^{2}-16^{2}}{2*16*8}=frac{1}{4}$$
2)По свойству касательной и радиуса, проведенного в точку касания получаем, что $$AOperp AK$$, но из параллельности AK и BH получаем, что $$AOperp BH$$
3)Из треугольника ABH: $$AH=ABcos OAB=8*frac{1}{4}=2$$
Задание 25
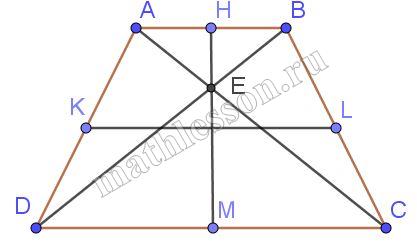
Докажите, что если в равнобедренной трапеции диагонали взаимно перпендикулярны, то высота трапеции равна средней линии.
Ответ:
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) Треугольники ABE и CDE прямоугольные (по условию), $$AB parallel DC$$ (свойство трапеции), тогда треугольник $$ABEsim CDE$$. Следовательно, $$frac{EC}{AE}=frac{ED}{BE}=k$$. Пусть AE=x, тогда EC=kx, пусть BE=y, тогда ED=ky
2) Треугольники ABD и ABC равны (AD=BC и $$angle DAB=angle ABC$$ т.к. трапеция равнобедренная, AB — общая), тогда AC=BD и x+kx=y=ky, следовательно x=y, тогда треугольники ABE и CDE — равнобедерненные
3)HE — высота и медиана, тогда, по свойству медианы в прямоугольном треугольнике: $$HE=frac{1}{2}AB$$, аналогично $$EM=frac{1}{2}CD$$, тогда $$HE+EM=frac{1}{2}(AB+CD)=KL$$
ч.т.д.
Задание 26
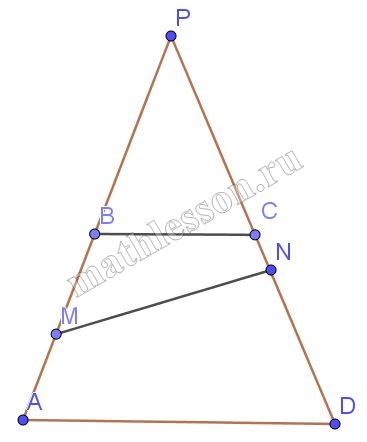
На боковой стороне АВ трапеции АВСD взята точка М таким образом, что АМ : МВ = 2 : 3. На противоположной стороне СD взята такая точка N, что отрезок MN делит трапецию на части, одна из которых по площади втрое больше другой. Найдите отношение CN : ND, если известно, что BC : AD = 1 : 2
Ответ: $$frac{3}{29}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1)Продолжим боковые стороны до пересечения в точке P: $$frac{BC}{AD}=frac{1}{2}$$, тогда BC — средняя линия в треугольнике APD
2)Пусть $$S_{MBCN}=S$$, тогда $$S_{AMND}=3S$$, тогда $$S_{ABCD}=4S$$
3)Из подобия треугольников PBC и APD и свойства средней линии треугольника : $$frac{S_{BPC}}{S_{ABCD}}=frac{1}{3}$$, следовательно, $$S_{BPC}=frac{4S}{3}$$
4)Пусть AM=2x, тогда MB=3x ; AB=5x=BP. Пусть CN=q, CD=PC=z. Тогда $$frac{S_{BMN}}{S_{PAD}}=$$$$frac{frac{4s}{3}+S}{frac{4s}{3}+4S}=$$$$frac{PM*PN}{PA*PD}=$$$$frac{8x*(z+q)}{10x*2x}$$. Получаем, что $$frac{35z}{32}=z+q Leftrightarrow$$$$q=frac{3}{32}z=CNLeftrightarrow$$$$z-q=frac{29}{32}z=NDLeftrightarrow$$$$frac{CN}{ND}=frac{3}{29}$$
Примечание: возможен вариант построения точки N ближе к D, чтобы распределение площадей получилось противоположным $$S_{MBCN}=3S$$, тогда $$S_{AMND}=S$$, но при подобном приведенному решению мы получим невозможность существования подобного разбиения площадей (точка N будет лежать вне стороны CD) — попробуйте решить самостоятельно.
№181-185 Тренировочные варианты ОГЭ по математике от Alexlarin. Основной государственный экзамен. Варианты с актуальными заданиями и ответами от сайта alexlarin.net, а также видео решениями от канала MrMathlesson. Ниже прикрепляем ссылки для скачивания и сами видео.
Вариант №181: скачать
Ответы: скачать
Видео решения варианта №181 задания 1-20:
Видео решения варианта №181 задания 21-26:
Вариант №182: скачать
Ответы: скачать
Видео решения варианта №182 задания 1-20:
Видео решения варианта №182 задания 21-26:
Вариант №183: скачать
Ответы: скачать
Видео решения варианта №183 задания 1-20:
Видео решения варианта №183 задания 21-26:
Вариант №184: скачать
Ответы: скачать
Видео решения варианта №184 задания 1-20:
Видео решения варианта №184 задания 21-26:
Вариант №185: скачать
Ответы: скачать
Видео решения варианта №185 задания 1-20:
Видео решения варианта №185 задания 21-26:
Поделиться с друзьями:
Задание 1
Тимофей на день рождения Ангелине купил флеш карту объемом 64 Гб за 850 рублей, после чего увидел флеш карту объемом 128 Гб. И хотя она стоила на 90% дороже уже купленной, Тимофей взял в подарок ее, решив флеш карту меньшей емкости оставить себе. Не меньше какой суммы в рублях было у Тимофея с собой изначально?
Ответ: 2465
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Стоимость на 128 Гб: $$850cdot 1,9=1615$$ рублей. Соответственно, было не менее: $$850+1615=2465$$ рублей.
Задание 2
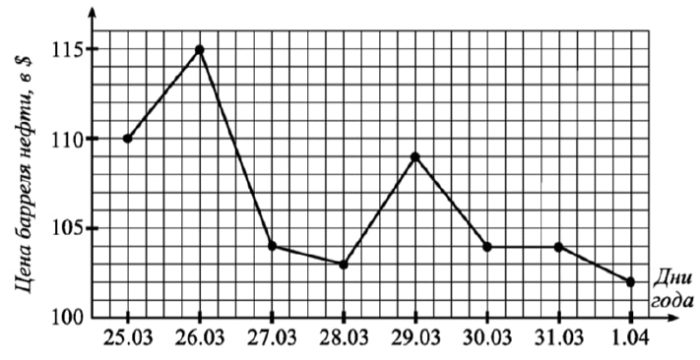
На графике жирными точками показана цена барреля нефти в течение восьми дней 2011 года на международных рынках. По оси абсцисс отмечена дата, по оси ординат — цена барреля нефти в долларах на данный период. Для наглядности жирные точки соединены линиями. Определите по графику разницу (в долларах) между наибольшей и наименьшей ценами барреля нефти за указанный период.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Наибольшая: 115.
Наименьшая: 102.
$$max-min=115-102=13$$
Задание 3
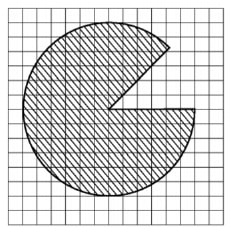
Найдите (в см$${}^{2}$$) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1см х 1см (см. рис.). В ответе запишите $$frac{S}{pi }.$$
Ответ: 31,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Центральный угол $$left(alpha right)=360-45=315{}^circ .$$ Площадь сектора: $$S=frac{pi R^2alpha }{360}=frac{pi cdot 6^2cdot 315}{360}=31,5pi to 31,5$$
Задание 4
Вероятность того, что Гриша сдаст первый экзамен, равна 0,9; второй — 0,9; третий — 0,8. Найдите вероятность того, что Гришей будут сданы по крайней мере два экзамена.
Ответ: 0,954
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Сдаст по крайней мере 2: сдаст два или три. Распишем таблицу («+» — сдал, «-» — не сдал)
| событие | 1 | 2 | 3 | вероятность |
| + + — | 0,9 | 0,9 | 0,2 | $$0,9times 0,9times 0,2=0,162$$ |
| + — + | 0,9 | 0,1 | 0,8 | $$0,9times 0,1times 0,8=0,072$$ |
| — + + | 0,1 | 0,9 | 0,8 | $$0,1times 0,9times 0,8=0,072$$ |
| + + + | 0,9 | 0,9 | 0,8 | $$0,9times 0,9times 0,8=0,648$$ |
Тогда вероятность не менее 2-х сдать: $$P(A)=0,162+0,072+0,072+0,648=0,954$$
Задание 5
Решить уравнение $$3sqrt{2x-3}-sqrt{48x-272}=5$$
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$3sqrt{2x-3}-sqrt{48x-272}=5$$
$$3sqrt{2x-3}-4sqrt{3x-17}=5$$
$$3sqrt{2x-3}=5+4sqrt{3x-17}$$
$$9left(2x-3right)=25+left(48x-272right)+8sqrt{3x-17}$$
$$-30x+220=40sqrt{3x-17}$$ $$22-3x=4sqrt{3x-17}$$
$$484-132x+9x^2-16left(3x-17right)=0$$
$$x^2-20+84=0to left[ begin{array}{c} x_1=14 x_2=6 end{array} right.$$
Подставим в первоначальное: 14 — посторонний корень.
Задание 6
Точки $$Aleft(-3;1right), Bleft(2;-1right), C(4;4)$$ являются вершинами треугольника АВС с биссектрисой ВК. Найдите $$16AK^2.$$
Ответ: 232
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$AB=sqrt{{left(2-left(-3right)right)}^2+{left(1-left(-1right)right)}^2}=sqrt{29}$$
$$BC=sqrt{{left(4-2right)}^2+{left(4-left(-1right)right)}^2}=sqrt{29}$$
$$AC=sqrt{{left(4-left(-3right)right)}^2+{left(4-1right)}^2}=sqrt{58}$$
$$AB=BCto BK$$ — биссектриса и медиана $$to AK=frac{AC}{2}=frac{sqrt{58}}{2}to 16AK^2=frac{16cdot 58}{4}=232$$
Задание 7
В точке А графика функции $$y=x^3+4x+2$$ проведена касательная к нему, параллельная прямой $$y=4x+5.$$ Найдите сумму координат точки А.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$${left(x^3+4x+2right)}’={left(4x+5right)}’leftrightarrow 3x^2+4=4to x=0.$$
$$yleft(0right)=0^3+4cdot 0+2=2to x+y=0+2=2.$$
Задание 8
Цилиндрическая кастрюля, диаметр дна которой равен 36 см, наполнена водой. Какое минимальное число кастрюль той же высоты и с диаметром дна, равным 12 см, потребуется для того, чтобы перелить в них эту воду?
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$frac{V_1}{V_2}=frac{S_1cdot h}{S_2cdot h}=frac{pi R^2_1h}{pi R^2_2h}={left(frac{R_1}{R_2}right)}^2={left(frac{18}{6}right)}^2=9$$
Задание 9
Вычислите $${sin alpha },$$ если $${sin frac{alpha }{2} }-{cos frac{alpha }{2}=1,4 }$$
Ответ: -0,96
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$${sin frac{alpha }{2} }-{cos frac{alpha }{2}=1,4 }to {cos frac{alpha }{2} }={sin frac{alpha }{2} }-1,4.$$
$${{sin }^{{rm 2}} frac{alpha }{2} }-{{cos }^{{rm 2}} frac{alpha }{2} }=1to {{sin }^{{rm 2}} frac{alpha }{2} }+{{sin }^{{rm 2}} frac{alpha }{2} }-2,8{sin frac{alpha }{2} }+1,96=1.$$
$${{{rm 2sin}}^{{rm 2}} frac{alpha }{2} }-2,8{sin frac{alpha }{2} }+0,96=0to {{sin }^{{rm 2}} frac{alpha }{2} }-1,4{sin frac{alpha }{2} }+0,48=0.$$
$$D=1,96-1,92=0,04$$
$$left[ begin{array}{c} {sin frac{alpha }{2} }=frac{1,4+0,2}{2}=0,8 {sin frac{alpha }{2} }=frac{1,4-0,2}{2}=0,6 end{array} leftrightarrow right.left[ begin{array}{c} {cos frac{alpha }{2} }=0,6 {cos frac{alpha }{2} }=-0,8 end{array} right.$$ $${sin alpha }=2{sin frac{alpha }{2} }{cos frac{alpha }{2} }=2cdot 0,8cdot left(-0,6right)=-0,96$$
Задание 10
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных соосных цилиндров: центрального массой $$m=5$$ кг и радиуса $$R=8$$ см и двух боковых с массами $$M=2$$ кг и с радиусами $$R+h.$$ При этом момент инерции катушки относительно оси вращения, выражаемый в кг•см$${}^{2}$$, дается формулой $$I=frac{left(m+2Mright)R^2}{2}+Mleft(2Rh+h^2right).$$ При каком максимальном значении момент инерции катушки не превышает предельного значения 402 кг•см$${}^{2}$$? Ответ выразите в сантиметрах.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$402ge frac{left(5+2cdot 2right)8^2}{2}+2left(2cdot 8h+h^2right)leftrightarrow 2h^2+32h+288-402le 0.$$
$$h^2+16h-57le 0leftrightarrow left(h+19right)left(h-3right)le 0leftrightarrow left{ begin{array}{c}hin left[-19;3right] h>0 end{array}right.leftrightarrow h=3$$
Задание 11
Два садовника вместе стригут кусты за 5 часов. Если бы первый садовник подстригал кусты один 3 часа, то второму понадобилось бы 7,5 часов, чтобы доделать работу до конца. За сколько часов второй садовник может один подстричь все кусты?
Ответ: 11,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Пусть $$x$$ частей работы в час — производительность первого, $$y$$ — второго; 1 — объем всей работы: $$left{ begin{array}{c}
5left(x+yright)=1
3x+7,5y=1 end{array}
leftrightarrow left{ begin{array}{c}
7,5x+7,5y=1,5
3x+7,5y=1 end{array}
right.right..$$
$$4,5x=1,5-1=0,5to x=frac{0,5}{4,5}=frac{1}{9}.$$ $$frac{1}{9}+y=frac{1}{5}to y=frac{9-5}{45}=frac{4}{45}to t_2=frac{frac{1}{4}}{45}=frac{45}{4}=11,25.$$
Задание 12
Найдите наибольшее значение функции $$y={{log }_{frac{1}{3}} sqrt{x^3} }$$ на отрезке $$[frac{1}{3};3]$$
Ответ: 1,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$y={{log }_{frac{1}{3}} sqrt{x^3} }$$ т.к. $$fleft(xright)=x^3$$ — возрастает, то $$y={{log }_{frac{1}{3}} f(x) }$$ — убывает на $$left[frac{1}{3};3right]to y_{max}=yleft(frac{1}{3}right)={{log }_{frac{1}{3}} sqrt{{left(frac{1}{3}right)}^3} }=frac{3}{2}{{log }_{frac{1}{3}} frac{1}{3} }=1,5.$$
Задание 13
а) Решите уравнение $$2{{sin }^{{rm 3}} x }-{{sin }^{{rm 2}} x }cdot {cos x }-13{sin x }cdot {{cos }^{{rm 2}} x }-6{{cos }^{{rm 3}} x }={sin left(frac{pi }{3}+xright) }-{cos (frac{pi }{6}-x) }$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{pi }{2};frac{pi }{2}]$$
Ответ: а) $$arctg3+pi n;-arctgfrac{1}{2}+pi k;$$ $$-arctg2+pi m,n,k,min Z$$; б) $$-arctg2;-arctgfrac{1}{2}; arctg3$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
а)
$$2{{sin }^{{rm 3}} x }-{{sin }^{{rm 2}} x }cdot {cos x }-13{sin x }cdot {{cos }^{{rm 2}} x }-6{{cos }^{{rm 3}} x }={sin left(frac{pi }{3}+xright) }-{cos left(frac{pi }{6}-xright) }.$$
Учтем, что $${sin (frac{pi }{3}+x) }=left({sin frac{pi }{2} }-left(frac{pi }{6}-xright)right)={cos (frac{pi }{6}-x) }.$$
Получим: $$2{{sin }^{{rm 3}} x }-{{sin }^{{rm 2}} x }cdot {cos x }-13{sin x }cdot {{cos }^{{rm 2}} x }-6{{cos }^{{rm 3}} x }=0|:{{cos }^{{rm 3}} x }ne 0.$$
$$2{{tan }^{{rm 3}} x }-{{tan }^{{rm 2}} x }-13{tan x }-6=0.$$
Пусть $${tan x }=y:$$ $$2y^3-y^2-13y-6=0leftrightarrow left(y-3right)left(2y^2+5y+2right)=0leftrightarrow$$ $$leftrightarrow left[ begin{array}{c} y=3 y=-frac{1}{2} y=-2 end{array} right.leftrightarrow left[ begin{array}{c} {tan x }=3 {tan x }=-frac{1}{2} {tan x }=-2 end{array} right.leftrightarrow left[ begin{array}{c} x=arctg3+pi n x=-arctgfrac{1}{2}+pi k x=-arctg2+pi m,n,k,min Z end{array} right.$$
б) с помощью единичной окружности отберем корни: $$1)-arctg2;2)-arctgfrac{1}{2};3) arctg3$$
Задание 14
В основании прямой призмы $$ABCDA_1B_1C_1D_1$$ лежит равнобедренная трапеция АВСD c основаниями AD и ВС. Известно, что $$AD:BC = 2:1$$ и $$АВ = ВС.$$
а) Докажите, что $$DB_1bot A_1B_1$$.
б) Найдите угол между прямыми $$CD_1$$ и $$DB_1$$, если боковая грань $$AA_1D_1D$$ — квадрат.
Ответ: $$arccosfrac{sqrt{35}}{14}$$
Задание 15
Решите неравенство: $$x^2{{log }_{4096} (3-x) }ge {{log }_8 (x^2-6x+9) }$$
Ответ: $$(-infty ;-sqrt{8}];[2;sqrt{8}]$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
$$x^2{{log }_{4096} (3-x) }ge {{log }_8 left(x^2-6x+9right) }leftrightarrow $$
$$frac{x^2}{12}{{log }_2 left(3-xright) }-frac{1}{3}{{log }_2 {left(3-xright)}^2 }ge 0leftrightarrow$$
$$leftrightarrow x^2{{log }_2 left(3-xright) }-8{{log }_2 left|3-xright| }ge 0leftrightarrow$$
$$left{ begin{array}{c}(x^2-8)(3-x-1)(2-1)ge 0 3-x>0 end{array}right.leftrightarrow$$
$$left{ begin{array}{c}(x-2)(x+sqrt{8})(x-sqrt{8})le 0 x<3 end{array}right.$$
Задание 16
Окружность с центром О, вписанная в треугольник АВС, касается его сторон ВС, АВ и АС в точках K, L и М соответственно. Прямая КМ вторично пересекает в точке Р окружность радиуса АМ с центром А.
а) Докажите, что прямая АР параллельна прямой ВС
б) Пусть $$angle ABC=90{}^circ , AM=3, CM=2, Q$$ — точка пересечения прямых КМ и АВ, а Т — такая точка на отрезке РQ, что $$angle OAT=45{}^circ .$$ Найдите QT.
Ответ: $$frac{12sqrt{5}}{5}$$
Задание 17
В распоряжении прораба имеется бригада рабочих в составе 35 человек. Их нужно распределить на строительство двух частных домов, находящихся в разных городах. Если на строительстве первого дома работает $$t$$ человек, то их суточная зарплата составляет $$7t^2$$ д.е. Если на строительстве второго дома работает $$t$$ человек, то их суточная зарплата составляет $$3t^2$$ д.е. Какое минимальное количество денежных единиц придётся выплатить рабочим за сутки?
Ответ: 2575
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
Пусть на 1-ом объекте $$x$$ рабочих, тогда из з/п $$7x^2$$, на втором $$35-x$$ рабочих, их з/п $$3{left(35-xright)}^2.$$ Получим функцию з/п:
$$fleft(xright)=7x^2+3{left(35-xright)}^2to min.$$
$$f’left(xright)=14x+6left(35-xright)left(-1right)=0to 14x+6x=6cdot 35to x=frac{210}{20}=10,5.$$
Тогда: $$fleft(10right)=7cdot {10}^2+3{left(35-10right)}^2=700+1875=2575;$$
$$fleft(11right)=7cdot {11}^2+3{left(35-11right)}^2=847+1728=2575.$$
Минимальная з/п: 2575 д.е.
Задание 18
Найдите все значения параметра $$a$$ при каждом из которых множество решений неравенства $$2+sqrt{x^2+ax}>x$$ содержит отрезок $$[4;7]$$
Ответ: (-3;$$infty $$)
Задание 19
Последовательность $$a_1,a_2,a_3,dots $$ состоит из натуральных чисел, причем $$a_{n+2}=a_{n+1}+a_n$$ при всех натуральных $$n$$.
а) Может ли выполняться равенство $$frac{a_5}{a_4}=frac{9}{5}$$
б) Может ли выполняться равенство $$frac{a_5}{a_4}=frac{7}{5}$$
в) При каком наибольшем натуральном $$n$$ может выполняться равенство $$6na_{n+1}=(2n^2-2)a_n$$?
Ответ: а) да; б) нет; в) 5
А. Ларин. Тренировочный вариант № 326. (часть C).
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В основании прямой призмы АВСDA1В1С1D1 лежит равнобедренная трапеция АВСD c основаниями AD и ВС. Известно, что AD : BC = 2 : 1 и АВ = ВС.
а) Докажите, что прямые DB1 и A1B1 перпендикулярны.
б) Найдите угол между прямыми CD1 и DB1, если боковая грань AA1D1D — квадрат.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Окружность с центром О, вписанная в треугольник АВС, касается его сторон ВС, АВ и АС в точках K, L и М соответственно. Прямая КМ вторично пересекает в точке Р окружность радиуса АМ с центром А.
а) Докажите, что прямая АР параллельна прямой ВС.
б) Пусть AM = 3, CM = 2, Q — точка пересечения прямых КМ и АВ, а Т — такая точка на отрезке РQ, что
Найдите QT.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В распоряжении прораба имеется бригада рабочих в составе 35 человек. Их нужно распределить на строительство двух частных домов, находящихся в разных городах. Если на строительстве первого дома работает t человек, то их суточная зарплата составляет 7t2 д. е. Если на строительстве второго дома работает t человек, то их суточная зарплата составляет 3t2 д. е. Какое минимальное количество денежных единиц придется выплатить рабочим за сутки?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых множество решений неравенства
содержит отрезок [4; 7].
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Последовательность a1, a2, a3, … состоит из натуральных чисел, причем an+2 = an+1 + an при всех натуральных n.
а) Может ли выполняться равенство
б) Может ли выполняться равенство
в) При каком наибольшем натуральном n может выполняться равенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
|
Заголовок сообщения: Re: Тренировочный вариант №326
|
|||||||
Зарегистрирован: 18 апр 2012, 17:33 |
Kirill Kolokolcev писал(а): 13 Подробности: Что-то, вроде, с 13-й не так… |
||||||
  |
|||||||
|
rgg |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 29 окт 2014, 22:13 |
Kirill Kolokolcev писал(а): 13 Подробности: У меня ответы такие же, как и у Кирилла Юрьевича. |
||||||
  |
|||||||
|
lavrik |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 18 апр 2012, 17:33 |
Да, мне показалось, что 13-я задача чуть интереснее. |
||||||
  |
|||||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 08 май 2015, 03:53 |
Решение задачи 18 Подробности: Решение задачи 19 Подробности:
|
||||||
  |
|||||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 08 мар 2017, 23:11 |
Задача 19 Подробности:
|
||||||
  |
|||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 20 мар 2011, 22:29 |
Всем здравствуйте! Решение заданий 13 и 15. Подробности: Решение задания 18. Подробности:
|
||||||
  |
|||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 20 мар 2011, 22:29 |
Решение задания 14. Вложение:
скрин решения Подробности: |
||||||
  |
|||||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 23 янв 2014, 20:36 |
Всем доброй ночи! Подробности: Решение задачи 14. Подробности:
|
||||||
  |
|||||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 23 янв 2014, 20:36 |
Решение задач 16, 17. Подробности:
|
||||||
  |
|||||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №326
|
||||||
Зарегистрирован: 23 мар 2012, 10:13 |
№14 Подробности: №16 Подробности: №18 Подробности: |
||||||
  |
|||||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
|
Вы не можете начинать темы |
|
|
Решение и ответы заданий № 1–12 варианта №326 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
Тимофей на день рождения Ангелине купил флеш карту объемом 64 Гб за 850 рублей, после чего увидел флеш карту объемом 128 Гб. И хотя она стоила на 90% дороже уже купленной, Тимофей взял в подарок ее, решив флеш карту меньшей емкости оставить себе. Не меньше какой суммы в рублях было у Тимофея с собой изначально?
Задание 2.
На графике жирными точками показана цена барреля нефти в течение восьми дней 2011 года на международных рынках. По оси абсцисс отмечена дата, по оси ординат – цена барреля нефти в долларах на данный период. Для наглядности жирные точки соединены линиями. Определите по графику разницу (в долларах) между наибольшей и наименьшей ценами барреля нефти за указанный период.
Задание 3.
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1см х 1см (см. рис.). В ответе запишите .
Задание 4.
Вероятность того, что Гриша сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найдите вероятность того, что Гришей будут сданы по крайней мере два экзамена.
Задание 5.
Решить уравнение
Задание 6.
Точки A(-3;1), B(2;-1), C(4;4) являются вершинами треугольника АВС с биссектрисой ВК. Найдите 16AK2.
Задание 7.
В точке А графика функции y = x3 + 4x +2 проведена касательная к нему, параллельная прямой y = 4x + 5. Найдите сумму координат точки А.
Задание 8.
Цилиндрическая кастрюля, диаметр дна которой равен 36 см, наполнена водой. Какое минимальное число кастрюль той же высоты и с диаметром дна, равным 12 см, потребуется для того, чтобы перелить в них эту воду?
Задание 9.
Найдите sin α, если
Задание 10.
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных соосных цилиндров: центрального массой m = 2 кг и радиуса R = 8 см и двух боковых с массами M = 2 кг и с радиусами R + h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг∙см2, дается формулой
При каком максимальном значении h момент инерции катушки не превышает предельного значения 402 кг∙см2? Ответ выразите в сантиметрах.
Задание 11.
Два садовника вместе стригут кусты за 5 часов. Если бы первый садовник подстригал кусты один 3 часа, то второму понадобилось бы 7,5 часов, чтобы доделать работу до конца. За сколько часов второй садовник может один подстричь все кусты?
Задание 12.
Найдите наибольшее значение функции на отрезке [
;3]
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Канал видеоролика: Математикс
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #учиться #e_math #егэматематика
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
Разбор Задачи №19 из Варианта Ларина №276
Математикс

Разбор Задачи №13 из Варианта Ларина №277
Математикс

Разбор Задачи №15 из Варианта Ларина №277
Математикс

Разбор Задачи №18 из Варианта Ларина №277
Математикс
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
ЕГЭ 2008, Математика, 11 класс, Вариант 326.
Укажите рисунок, на котором изображен график функции, принимающей на промежутке (- 3; 3) только отрицательные значения.
Примеры.
Две машинистки, работая вместе, могут напечатать 30 страниц текста за 1 ч. Работая отдельно, первая машинистка печатает 140 страниц такого же текста на 5 ч дольше, чем вторая машинистка печатает 80 страниц. За сколько часов первая машинистка сможет напечатать 280 страниц?
Дан конус с вершиной М, радиус основания которого равен 2/6. На окружности его основания выбраны точки A, В, С так, что углы
ВМА, АМС, СМВ равны 90° каждый. Точка F выбрана на дуге ВС окружности основания конуса, не содержащей точки А, так, что объем пирамиды MABFC наибольший. Найдите расстояние от точки F до плоскости МАВ.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ 2008, Математика, 11 класс, Вариант 326 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ 2008, Математика, 11 класс, Вариант 326
— pdf — Яндекс.Диск.
Дата публикации: 05.08.2014 10:25 UTC
Теги:
ЕГЭ по математике :: математика :: 11 класс
Следующие учебники и книги:
- ЕГЭ по математике, варианты № 101-190, 11 класс, 2010
- ЕГЭ по математике, вариант № 001, 11 класс, 2007
- ЕГЭ 2008, Математика, 11 класс, Критерии оценивания, Вариант 91
- ЕГЭ 2008, Математика, 11 класс, Варианты 8, 51, 60
Предыдущие статьи:
- ЕГЭ 2008, Математика, 11 класс, Варианты 1-2
- ЕГЭ 2008, Математика, 11 класс
- ЕГЭ 2009, Математика, 11 класс, Тренировочная работа №4, Варианты 1-2
- ЕГЭ 2009, Математика, 11 класс, Тренировочная работа №3, Варианты 1-2
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Ниже Вы можете бесплатно скачать электронные книги и учебники и читать статьи и уроки к разделу ЕГЭ по математике 2023, 2022, 2021, 2020:
У нас Вы можете скачать реальные задания ЕГЭ по математике 2023, 2022, 2021, 2020, 2019, 2018, 2017, 2016, 2015, 2014, 2013, демоверсию ЕГЭ, реальные и демонстрационные варианты, официальные варианты.
Специально для всех абитуриентов в данной категории собраны все необходимые материалы для подготовки к Единому Государственному Экзамену по математике следующих авторов: Колесникова С.И., Семёнов А.Л., Ященко И.В., Кочагин В.В., Кочагина М.Н., Лысенко Ф.Ф., Кулабухова С.Ю., И.В, Шестаков С.А, Захаров П.И., Сергеев И.Н., Дорофеев Г.В., Титаренко А.М., Третьяк Т.М, Виноградова Т.М., Рязановский А.Р., Попов М.А., Клово А.Г., Мальцев Д.А., Абзелилова Л.И., Глазков Ю.А., Корешкова Т.А., Мирошин В.В., Шевелева Н.В., Гордин Р.К., Смирнов В.А., Гущин Д.Д., Высоцкий И.Р. и др.
По опросу всех учащихся математика — один из самых сложных предметов, изучаемых в школе. Тем более, что он подразделяется на алгебру и геометрию. Следовательно, сдать ЕГЭ по математике на отлично невероятно трудно. Нужно готовиться, решать экзаменационные варианты, проходить интенсивный курс подготовки, решать сборник тренировочных работ и заданий, тематические тесты, искать репетиторов.
Не забудьте просмотреть задания открытого бланка, почитать методические указания, практикум по выполнению типовых тестовых заданий ЕГЭ, ознакомиться с решением сложных задач, скачать справочник, учебно-методическое пособие для подготовки к экзамену, рабочую тетрадь, диагностические работы по математике в формате ЕГЭ 2023, 2022, 2021, 2020, 2019, 2018, 2017, 2016, 2015, 2014, 2013, 2012, 2011, 2010, 2009.
Готовьтесь по книгам, вариантам и сборникам тестов, решайте реальные задания, используйте КИМ — контрольно измерительные материалы, смотрите демонстрационные варианты ниже к подготовке к сдаче экзамена Единый государственный экзамен по математике, и у Вас получится успешно сдать его, ответить на все вопросы и тесты к экзамену по математике.
В 2011 и 2010 тест ЕГЭ по математике состоял из 18 заданий.
С 2010 года группа заданий А отсутствует в ЕГЭ по математике.
В 2012 и 2013 году тест ЕГЭ по математике состоял из 20 заданий.
В 2014 году тест ЕГЭ по математике состоит из 20 заданий, которые по уровню сложности и типу ответов на задачи можно разделить следующим образом: