Единый государственный экзамен по математике тренировочный вариант 358 - Помощь в подготовке к экзаменам и поступлению

Задание 1

Решите уравнение $$cos(frac{pi x}{2}-frac{27pi}{16})=0$$

В ответе запишите наибольший отрицательный корень уравнения

Ответ: -1,625

Скрыть

$$frac{pi x}{2}-frac{27pi}{16}=frac{pi}{2}+pi n$$

$$frac{x}{2}-frac{27}{16}=frac{1}{2}+n$$

$$x=frac{35}{8}+2n$$

$$n=-3$$

$$x=4frac{3}{8}-6=-1,625$$

Задание 2

В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что «орел» выпадет не менее 2 раз.

Ответ: 0,5

Скрыть

Вероятность $$P$$ события $$A$$ равна:

$$P(A)=frac{m}{n}$$, где $$m$$ — числа благоприятных исходов, а $$n$$ — число всех равновозможных исходов испытания

ООО ООР ОРО ОРР

РРР РРО РОР РОО

$$m=4, n=8$$

$$P=frac{4}{8}=0,5$$

Задание 3

Найдите площадь равнобедренной трапеции, диагональ которой равна $$3sqrt{2}$$ и составляет с основанием угол $$45^{circ}$$.

Ответ: 9

Скрыть

Диагонали равнобедренной трапеции равны.

Диагонали трапеции пересекаются и образуют два подобных треугольника, опирающихся на основания трапеции; в случае равнобедренной трапеции эти треугольники тоже равнобедренные и (по условию) прямоугольные (т.к. углы при основании по 45°); следовательно, диагонали данной трапеции перпендикулярны.

Площадь четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей (это верно не только для ромба)

$$S=3cdotsqrt{2}cdot3cdotfrac{sqrt{2}}{2}=9$$

Задание 4

Найдите $$tg^6t$$, если $$5sin^2 t+8cos^2 t=6$$.

Ответ: 8

Скрыть

$$5sin^2 t+5cos^2 t+3cos^2 t=6$$

$$3cos^2 t=1$$

$$cos^2 t=frac{1}{3}$$

$$frac{1}{cos^2 t}=3$$

$$1+tg^2 t=3$$

$$tg^2 t=2$$

$$tg^6 t=8$$

Задание 5

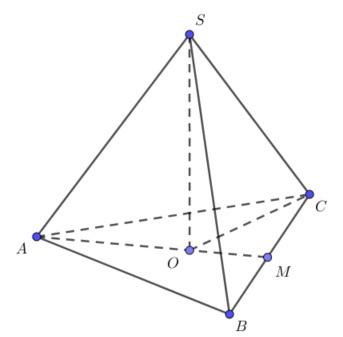
В основании пирамиды лежит треугольник со сторонами $$3sqrt{3}$$, $$11$$ и углом $$30^{circ}$$ между ними. Все боковые ребра пирамиды равны $$8$$. Найдите объем пирамиды $$(V)$$. В ответе запишите $$Vsqrt{5}$$.

Ответ: 41,25

Скрыть

$$T_{cos}: x^2=(3sqrt{3})^2+11^2-2cdot3sqrt{3}cdot11cdotfrac{sqrt{3}}{2}$$

$$x^2=49$$

$$x=7$$

$$11^2>(3sqrt{3})^2+7^2<A>90^{circ}$$

$$Delta ABC$$ — тупоугольный.

Данная пирамида — «особая». Её все боковые рёбра равны между собой $$Rightarrow$$ её вершина S проецируется в центр окружности, описанной около её основания. Радиус основания $$R$$.

$$R=frac{ABcdot BCcdot AC}{4S_{осн}}$$

$$S_{осн}=frac{1}{2}cdot3sqrt{3}cdot11cdotsin30^{circ}=frac{33sqrt{3}}{4}$$

$$OC=R=frac{3sqrt{3}cdot7cdot11}{33sqrt{3}}=7$$

$$SO=sqrt{8^2-7^2}=sqrt{15}$$

$$V_{пир}=frac{1}{3}cdotfrac{33sqrt{3}}{4}cdotsqrt{15}=frac{11sqrt{3}cdotsqrt{15}}{4}=frac{11sqrt{45}}{4}$$

$$frac{11sqrt{45}cdotsqrt{5}}{4}=41,25$$

Задание 6

На рисунке изображён график функции $$y=f'(x)$$, где $$f'(x)$$ — производная функции $$y=f(x)$$, определённой на интервале $$(-5;6)$$. В какой из точек -2, -1, 0, 1 значение функции $$y=f(x)$$ будет наименьшим? В ответе укажите эту точку.

Ответ: -2

Скрыть

При $$x=-2;-1;0$$ и $$1$$: $$f'(x)geq0$$ на всём $$D(x)$$.

Тогда функция всегда возрастает $$Rightarrow$$ наименьшее при $$x=-2$$.

Задание 7

При нормальном падении света с длиной волны $$lambda=650$$ нм на дифракционную решётку с периодом $$d$$ нм наблюдают серию дифракционных максимумов. При этом угол $$varphi$$ (отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума $$k$$ связаны соотношением $$dsinvarphi=klambda$$. Под каким минимальным углом $$varphi$$ (в градусах) можно наблюдать третий максимум на решётке с периодом, не превосходящим 1950 нм?

Ответ: 90

Скрыть

$$1950cdotsinvarphi=3cdot650$$

$$varphi=90^{circ}$$

Задание 8

Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Ответ: 16

Скрыть

Расстояние между пристанями А и В равно: $$S = 126$$ км

Скорость течения реки равна: $$V_р = 2$$ км/час

Расстояние, которое проплыл плот: $$S_п = 34$$ км

Скорость яхты в неподвижной воде: $$V_я$$ км/час

Яхта отправилась в путь через время после плота: $$Т_о = 1$$ час

Так как скорость плота равна скорости течения реки: $$V_п = V_р$$ км/час,

то время плавания плота: $$Т_п =frac{S_п}{V_р} = frac{34}{2} = 17$$ час

Время плавания яхты:

$$Т_я = Т_п — Т_о = 17 — 1 = 16$$ час;

Рассчитаем время $$Т_я$$:

$$Т_я = frac{S}{V_я + V_р} + frac{S}{V_я — V_р} = Scdotfrac{2cdot V_я}{V_я^2-4} = 16$$

$$252cdot V_я = 16cdot V_я — 64$$

$$4cdot V_я^2 — 63cdot V_я — 16 = 0$$

$$V_{я1,2} = frac{63pmsqrt{63^2 + 4cdot4cdot16}}{4cdot2}=frac{63pm65}{8}$$

Отрицательный корень не имеет смысла

$$V_я = frac{63 + 65}{8} = 16$$ км/час

Задание 9

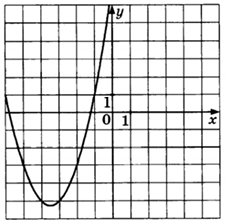
На рисунке изображен график функции вида $$f(x)=ax^2+bx+c$$. Найдите значение $$a$$ по этому графику.

Ответ: 1

Скрыть

График проходит через (-3;-5), (-4;-5) и (-1;1).

$$left{begin{matrix} -5=(-3)^2a-3b+c\ -5=(-4)^2a-4b+c\ 1=(-1)^2a-b+c end{matrix}right.Leftrightarrowleft{begin{matrix} 0=-7a+b\ -6=15a-3b\ c=1-a+b end{matrix}right.Leftrightarrowleft{begin{matrix} b=7a\ -6=15a-21a\ c=1-a+b end{matrix}right.Leftrightarrowleft{begin{matrix} b=7\ a=1\ c=7 end{matrix}right.$$

Задание 10

Баскетболист на тренировке бросает мяч в корзину с дистанции 6 м. При каждом броске он попадает в корзину с вероятностью 0,7. Найдите математическое ожидание числа попаданий при 40 бросках.

Ответ: 28

Скрыть

Повторные испытания с двумя исходами.

$$n=40$$

$$p=0,7$$

$$M(X)=np=40cdot0,7=28$$

Задание 11

Найдите наибольшее значение функции $$y=x^3+2x^2+x+3$$ на отрезке $$[-13;-0,5]$$

Ответ: 3

Скрыть

Найдем критические точки функции:

$$y(x) = x^3 + 2x^2 + x + 3$$

$$y'(x) = 3x^2 + 4x + 1$$

$$3x^2 + 4x + 1 = 0$$

$$frac{D}{4} = 2^2 — 3 = 1$$

$$x = frac{-2pmsqrt{1}}{3} = frac{-2pm1}{3}$$

$$x_1 = frac{-2 — 1}{3} = frac{-3}{3} = -1$$

$$x_2 = frac{-2 + 1}{3} = frac{-1}{3}$$

Значения функции в точках $$-3, -1$$ и $$-0,5$$:

$$y(x) = x^3 + 2x^2 + x + 3$$

$$y(-3) = (-3)^3 + 2cdot(-3)^2 + (-3) + 3 = -27 + 18 = -9$$

$$y(-1) = (-1)^3 + 2cdot(-1)^2 + (-1) + 3 = -1 + 2 — 1 + 3 = 3$$

$$y(-0,5) = (-0,5)^3 + 2cdot(-0,5)^2 + (-0,5) + 3 = -0,125 + 0,5 — 0,5 + 3 = 2,875$$

Задание 12

А) Решите уравнение

$$cosfrac{x}{2}sinfrac{3x}{2}=4sin^2(pi+x)cos^2(pi-x)-sinfrac{x}{2}cosfrac{3x}{2}$$

Б) Найдите все корни уравнения, принадлежащие отрезку $$[pi;3pi]$$

Ответ: А)$$frac{pi}{4}+pi n;frac{pi n}{2}, nin Z$$ Б)$$pi;frac{5pi}{4};frac{3pi}{2};2pi;frac{9pi}{4};frac{5pi}{2};3pi$$

Задание 13

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ проведена секущая плоскость, содержащая диагональ АС1 и пересекающая ребра ВВ₁ и DD₁ в точках F и Е соответственно.

а) Докажите, что сечение AFC₁E — параллелограмм.

б) Найдите площадь сечения, если известно, что AFC₁E — ромб и АВ = 3, ВС = 2, АА₁ = 5.

Ответ: $$sqrt{133}$$

Задание 14

Решите неравенство:

$$log_2(4-x)^2+2log_2(2x-1)leq4log_2 3$$

Ответ: $$(0,5;4)cup(4;5]$$

Задание 15

15 декабря планируется взять кредит в банке на 480 тысяч рублей на 27 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;

— со 2-го по 14 число каждого месяца необходимо выплатить часть долга;

— 15-го числа первые два месяца и последний долг должен уменьшиться на m тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на n тысяч рублей.

Найдите отношение $$frac{m}{n}$$, если всего было выплачено банку 656,4 тысяч рублей?

Ответ: 8

Задание 16

В равнобедренной трапеции ABCD длины оснований AD и BC соответственно равны 4 и 3. Точки M и N лежат на диагонали BD, причем точка М расположена между точками В и N, а отрезки АМ и CN перпендикулярны диагонали BD.

a) Докажите, что BN : DM = 3 : 4.

б) Найдите длину отрезка CN, если известно, что BM : DN = 2:3.

Ответ: $$frac{sqrt{15}}{2}$$

Задание 17

Найдите все положительные значения параметра $$a$$, при каждом из которых система уравнений

$$left{begin{matrix}
(|x|+|y|-10)cdot(9-|xy|)=0\
x^2+y^2=a^2
end{matrix}right.$$

имеет не менее 12 решений

Ответ: $$[5sqrt{2};sqrt{82})cup(sqrt{82};10]$$

Задание 18

В океанариуме каждой акуле дают 2,5 кг рыбы, мурене — 0,2 кг, скату — 1,5 кг ежедневно. Известно, что в среднем у каждой акулы бывает ежедневно 260 посетителей, у каждой мурены — 21, у каждого ската — 150. Все эти животные есть в океанариуме.

а) Какое число посещений будет у этих животных, если ежедневно в океанариуме им дают 6,5 кг рыбы?

б) Может ли ежедневно распределяться 18,4 кг рыбы, если известно, что за 1 день у этих животных было больше 2000 посещений?

в) Каким может быть наибольшее ежедневное число посещений, если океанариум ежедневно распределяет между ними 7 кг рыбы?

Ответ: А) 665, Б) нет, В) 725

Источник


2955	Найдите все положительные значения параметра а, при каждом из которых система уравнений { ((abs(x)+abs(y)-10)(9-abs(xy))=0), (x^2+y^2=a^2) :} имеет не менее 12 решений Решение График	Найдите все положительные значения параметра а ! Тренировочный вариант 358 от Ларина Задание 17 (18) # Решение Антонова Михаила Николаевича (Москва)

2946	В равнобедренной трапеции ABCD длины оснований АD и BC соответственно равны 4 и 3. Точки M и N лежат на диагонали BD, причем точка М расположена между точками В и N, а отрезки АМ и CN перпендикулярны диагонали BD. a) Докажите, что BN : DM = 3 : 4. б) Найдите длину отрезка CN, если известно, что BM : DN = 2 : 3 Решение	В равнобедренной трапеции ABCD длины оснований АD и BC соответственно равны 4 и 3 ! Тренировочный вариант 358 от Ларина Задание 16

2943	Найдите площадь равнобедренной трапеции, диагональ которой равна 3sqrt2 и составляет с основанием угол 45 градусов Решение	Найдите площадь равнобедренной трапеции, диагональ которой равна 3 корня из 2 ! Тренировочный вариант 358 от Ларина Задание 3 (6)

2942	Найдите tg^6t, если 5sin^2t+8cos^2t=6 Решение	Найдите tg6 t, если 5sin2 t +8cos2 t =6 ! Тренировочный вариант 358 от Ларина Задание 4 (9)

2941	Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч Решение	Расстояние между пристанями А и В равно 126 км ! Тренировочный вариант 358 от Ларина Задание 8 (11) ЕГЭ

2940	Найдите наибольшее значение функции y=x^3+2x^2+x+3 на отрезке [-13; -0,5] Решение График	Найдите наибольшее значение функции y=x3+2×2+x+3 на отрезке [-13; -0,5] ! Тренировочный вариант 358 от Ларина Задание 11 (12) ЕГЭ

2939	В основании пирамиды лежит треугольник со сторонами 3sqrt3, 11 и углом 30^@ между ними. Все боковые ребра пирамиды равны 8. Найдите объем пирамиды (V). В ответе запишите Vsqrt5 Решение	В основании пирамиды лежит треугольник со сторонами 3 корня из 3, 11 и углом 30 градусов между ними ! Тренировочный вариант 358 от Ларина Задание 5 (8) ЕГЭ

2938	В прямоугольном параллелепипеде ABCDA1B1C1D1 проведена секущая плоскость, содержащая диагональ АC1 и пересекающая ребра BB1 и DD1 в точках F и E соответственно. а) Докажите, что сечение AFC1E — параллелограмм. б) Найдите площадь сечения, если известно, что AFC1E – ромб и AB=3, BC=2, AA1=5 Решение	В прямоугольном параллелепипеде ABCDA1B1C1D1 проведена секущая плоскость ! Тренировочный вариант 358 от Ларина Задание 13 (14) ЕГЭ

2937	Решите уравнение cos((pix)/2-(27pi)/16)=0 В ответ запишите наибольший отрицательный корень уравнения Решение График	В ответ запишите наибольший отрицательный корень уравнения ! Тренировочный вариант 358 от Ларина Задание 1

2936	а) Решите уравнение cos(x/2)sin(3/2x)= 4sin^2(pi+x)cos^2(pi-x)-sin(x/2)cos(3/2x) б) Найдите все корни уравнения, принадлежащие отрезку [pi; 3pi]. Решение График	Тренировочный вариант 358 от Ларина Задание 12 (13) ЕГЭ

Источник

На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023

Тренировочный вариант Ларина №358 ЕГЭ 2022 по математике с ответами Решение и ответы на задачи на официальном сайте источника онлайн.

Новый тренировочный вариант №358 Алекса Ларина с ответами и решением по новой демоверсии ЕГЭ 2022 года по математике профильный уровень

Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%82%d1%80%d0%b5%d0%bd%d0%b8%d1%80%d0%be%d0%b2%d0%be%d1%87%d0%bd%d1%8b%d0%b9-%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-%d0%bb%d0%b0%d1%80%d0%b8%d0%bd%d0%b0-%e2%84%96358-%d0%b5%d0%b3%d1%8d-2022/

Ответы и решение задачи онлайн

Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.

Источник

Тренировочный вариант Ларина №358 ЕГЭ 2022 по математике с ответами

Новый тренировочный вариант №358 Алекса Ларина с ответами и решением по новой демоверсии ЕГЭ 2022 года по математике профильный уровень для подготовки к экзамену, дата выхода варианта: 04.09.2021 (4 сентября 2021 года)

Тренировочный вариант №358: задания | ответы

Решать тренировочный вариант Ларина №358 ЕГЭ 2022 по математике:

Сложные и интересные задания с варианта:

2)В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что «орел» выпадет не менее 2 раз.

Ответ: 0,5

3)Найдите площадь равнобедренной трапеции, диагональ которой равна 3 корень из 2 и составляет с основанием угол 45 градусов

Ответ: 9

8)Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Ответ: 16

10)Баскетболист на тренировке бросает мяч в корзину с дистанции 6 м. При каждом броске он попадает в корзину с вероятностью 0,7. Найдите математическое ожидание числа попаданий при 40 бросках.

Ответ: 28

13)В прямоугольном параллелепипеде АВСDA1B1C1D1 проведена секущая плоскость, содержащая диагональ АС1 и пересекающая ребра ВВ1 и DD1 в точках F и Е соответственно. а) Докажите, что сечение АFC1E ‐ параллелограмм. б) Найдите площадь сечения, если известно, что АFC1E – ромб и АВ = 3, ВС = 2, АА1 = 5.

15)15 декабря планируется взять кредит в банке на 480 тысяч рублей на 27 месяцев. Условия его возврата таковы: – 1‐го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца; – со 2‐го по 14 число каждого месяца необходимо выплатить часть долга; – 15‐го числа первые два месяца и последний долг должен уменьшиться на m тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15‐е число предыдущего месяца на n тысяч рублей. Найдите отношение m n , если всего было выплачено банку 656,4 тысяч рублей?

Ответ: 8

16)В равнобедренной трапеции ABCD длины оснований АD и BC соответственно равны 4 и 3. Точки M и N лежат на диагонали BD, причем точка М расположена между точками В и N, а отрезки АМ и CN перпендикулярны диагонали BD. a) Докажите, что BN : DM = 3 : 4. б) Найдите длину отрезка CN, если известно, что BM DN : 2 :3.

18)В океанариуме каждой акуле дают 2,5 кг рыбы, мурене – 0,2 кг, скату – 1,5 кг ежедневно. Известно, что в среднем у каждой акулы бывает ежедневно 260 посетителей, у каждой мурены – 21, у каждого ската – 150. Все эти животные есть в океанариуме.

Решение варианта №195 ОГЭ по математике Ларин

Задание №2. Решение варианта №195 ОГЭ по математике Ларин

Номер дорожки	1	2	3	4
Время (с)	7,3	6,7	6,9	7,0

Решение

Зачет получит только девочка со второй дорожки исходя из таблицы.

Задание №3

4 — a > 0,
5 — a < 0.
а – 4 < 0.
a – 8 > 0.

Решение

4 − a = 4 − 5 , 8 > 0 — неверно.

5 − a = 5 − 5 , 8 = − 0 , 8 < 0 — верно.

a − 4 = 5 , 8 − 4 < 0 — неверно.

a − 8 = 5 , 8 − 8 > 0 — неверно.

Задание №4

Решение

Задание №5. Решение варианта №195 ОГЭ по математике. Ларин

Решение

Как видно из графика 15 числа выпало 6 мм осадков.

Задание №6. Решение варианта №195 ОГЭ по математике Ларин

Решение

(x+15)² = (x-11)² ⇔ (x+15)² = (x-11)² = 0 ⇒

(x+15-x+11)(x+15+x-11)=0 ⇔ 26(2x+4) = 0

2x = 4 = 0 ⇔ x = − 2.

Задание №7. Решение варианта №195 ОГЭ по математике. Ларин

Решение

Пусть стоимость брюк -100% ⇒

x = ( 3185 ∗ 100 )/ 2450 = 1 3 0 % составляет стоимость пиджака относительно стоимости брюк.

Задание №8

Решение

В Австрии количество католиков и протестантов составляет более 75%.

Задание №9. Решение варианта №195 ОГЭ по математике Ларин

Решение

Вероятность того, что пишет хорошо:

P = 1 − 0 , 0 9 = 0 , 9 1.

Задание №10

Найдите значение с по графику функции y = ax²+bx+c , изображенному на рисунке.
Варианты ответа:

Решение

Коэффициент c равен значению ординаты точки пересечения графика функции и оси Oy ⇒ c = 3 , ⇒ 4 вариант ответа.

Задание №11. Решение варианта №195 ОГЭ по математике Ларин

Решение

Найдем разность данной прогрессии:

d = a n + 1 − a n = 2 3 − 3 0 = − 7.

⇒ a n = a 1 + d(n-1) = 30 — 7(n-1) = 37 — 7n < 0 ⇔

-7n < -3,7 ⇔ n > 37 /7 .

С учетом n ∈ N , n = 6 , ⇒ a 6 = 3 0 − 7 ( 6 − 1 ) = − 5.

Задание №12. Решение варианта №195 ОГЭ по математике Ларин

Решение

2 0 a b − 5 ( − 2 a − b )² = 2 0 a b − 5 ( 4 a² + 4 a b + b² ) =

− 5 ( 4√ ( 5 )² + √ ( 5 )² ) = -5(20 + 6) = -130.

Задание №13. Решение варианта №195 ОГЭ по математике Ларин

Решение

t = Q/I²R = 328/3²*7 = 6 секунд.

Задание №14. Решение варианта №195 ОГЭ по математике Ларин

a > 40.
a < 40.
a < − 40.
a > − 40.

Решение

a < 4 0 ⇒ 2 вариант ответа.

Задание №15

Решение

x – высота меньшей ⇒ ( x + 2 , 5)/2 = 2 , 2 ⇔

Задание №16. Решение варианта №195 ОГЭ по математике Ларин

Решение

∠ O K M = ∠ O M K ( Δ O M K — равнобедренный).
∠ O K M = 9 0° − 3 5° = 5 5°.
∠ M O K = 1 8 0° − 2 ∗ 5 5° = 7 0°.

Задание №17. Решение варианта №195 ОГЭ по математике Ларин

Решение

По теореме Пифагора — c-гипотенуза, h-высота:

c = 24² + 7² = 2 5 .
h = ( 24 ∗ 7 )/2 = 6 , 7 2.

Задание №18

Решение

S = ( ( 3 + 7 )/2) ∗ 4 = 2 0 клеток.
Площадь клетки:

5 ∗ 5 = 2 5.
Итоговая площадь:

2 0 ∗ 2 5 = 5 0 0.

Задание №19

Решение

Задание №20. Решение варианта №195 ОГЭ по математике Ларин

Площадь трапеции равна произведению средней линии на высоту.
Площадь параллелограмма равна произведению его сторон.
Площадь квадрата равна произведению его диагоналей.

Решение

Да.
Нет — Площадь параллелограмма равна произведению на синус угла между ними.
Нет — Площадь квадрата равна половине произведения.

Правильным ответом будет вариант под номером 1

Задание №21

Решение

Выделим полные квадраты под корнем (чтобы воспользоваться формулой a² = ∣ a ∣ :

Задание №22

Решение

Задание №23

Решение

Кроме того, наличие модуля отображает ту часть графика, которая находится под осью Ох (показана на рисунке), симметрично относительно Ох:

Итоговый график функции будет выглядеть:

Необходимо найти такое значение а, при котором будет ровно два решения. В таком случае график прямой должен касаться графика исходной функции (точка B):

Задания 1-11 вариант 358 Ларин ЕГЭ математика профиль

Вам не понравилось видео. Спасибо за то что поделились своим мнением!

Разбор заданий 1-11 варианта ЕГЭ № 358 Александр Ларин. Математика, профильный уровень. Пользуемся таймингом по задачам ниже.

00:00 1) Решите уравнение cos(pix/2-27pi/16)=0. В ответе напишите наибольший отрицательный корень уравнения.

04:51 2) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что «орел» выпадет не менее 2 раз.

06:24 3) Найдите площадь равнобедренной трапеции, диагональ которой равна 3sqrt(2) и составляет с основанием угол 45 градусов.

10:28 4) Найдите tg^(6)t, если 5sin^(2)t+8cos^(2)t=6

13:13 5) В основании пирамиды лежит треугольник со сторонами 3sqrt(3), 11 и углом 30 градусов между ними. Все боковые ребра пирамиды равны 8. Найдите объем пирамиды (V). В ответе запишите Vsqrt(5).

22:17 6) На рисунке изображён график функции f(x), где f (x) — производная функции y=f(x), определён-ной на интервале (-5;6). В какой из точек ‐2, ‐1, 0, 1 значение функции y =f (x) будет наименьшим? В ответе укажите эту точку.

25:53 7) При нормальном падении света с длиной волны 650 нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол (отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума k связаны соотношением. Под каким минимальным углом (в градусах) можно наблюдать третий максимум на решётке с периодом, не превосходящим 1950нм?

30:27 Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

38:52 9) На рисунке изображен график функции вида y=ax^2+bx+c. Найдите значение а по этому графику.

44:55 10) Баскетболист на тренировке бросает мяч в корзину с дистанции 6 м. При каждом броске он попадает в корзину с вероятностью 0,7. Найдите математическое ожидание числа попаданий при 40 бросках.

45:50 11) Найдите наибольшее значение функции y=x^3+2x^2+x+3 на отрезке от -13 до -0,5.

Источник