Задание 1
Решите уравнение $$log_{2022^{-2}}x+log_{2022}(2022^2cdot x)=3$$
Ответ: 4088484
Скрыть
$$log_{2022^{-2}}x+log_{2022}(2022^2cdot x)=3Leftrightarrow -frac{1}{2}log_{2022}x+log_{2022}2022^2+log_{2022}x=3Leftrightarrow$$
$$Leftrightarrow frac{1}{2}log_{2022}x+2=3Leftrightarrow log_{2022}x=2Leftrightarrow x=2022^2=4088484$$
Задание 2
В кошельке Деда Мороза лежит четыре пятирублевые монеты и шесть десятирублевых. Какова вероятность того, что, взяв случайным образом две монеты, обе они окажутся десятирублевыми? Ответ округлите до сотых
Ответ: 0,33
Скрыть
$$P(A)=frac{6}{10}cdotfrac{5}{9}approx0,33$$
Задание 3
Для сторон четырехугольника ABCD, описанного около окружности, выполнены соотношения: АВ : ВС = 3 : 7, AD : CD = 5 : 9. Периметр четырехугольника ABCD равен 2022. Найдите меньшую из сторон этого четырехугольника.
Ответ: 252,75
Скрыть
Окружность можно вписать в четырехугольник, если суммы его противолежащих сторон равны.
В нашем случае $$AB : BC = 3 : 7, AD : CD = 5 : 9$$ это отношение частей сторон и выполняется равенство $$AB+CD=3+9=12$$ и$$ BC+AD=7+5=12.$$
На сумму двух сторон приходится $$frac{1}{2}cdot2022=1011$$
Пусть одна часть $$x,$$ тогда $$12х=1011Rightarrow х=84,25.$$
Самая маленькая сторона состоит из трёх частей и равна $$3cdot84,25=252,75$$
Задание 4
Вычислите: $$sin^2 1752^{circ}+sin^2 2022^{circ}$$
Ответ: 1
Скрыть
$$sin^2 1752^{circ}=sin^2(1800^{circ}-48^{circ})=sin^2 48^{circ}$$
$$sin^2 2022^{circ}=sin^2(1980^{circ}+42^{circ})=sin^2 42^{circ}=sin^2(90^{circ}-48^{circ})=cos^2 48^{circ}$$
Получим: $$sin^2 48^{circ}+cos^2 48^{circ}=1$$
Задание 5
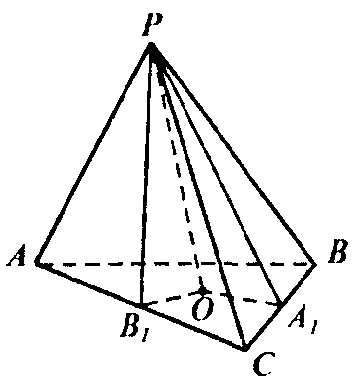
Высота треугольной пирамиды равна 15, а все высоты боковых граней, проведенные из вершины пирамиды равны 17. Найдите площадь основания пирамиды, если его периметр равен 2022.
Ответ: 8088
Скрыть
ОА1 — проекция РА1, поэтому ОА1 ⊥ ВС. Значит OA1 — расстояние от точки О до BC. Аналогично ОВ1 и ОС1 — расстояние от точки О до АС и AB соответственно. Но по теореме Пифагора:
$$OB_1=sqrt{PB_1^2-PO^2}=sqrt{17^2-15^2}=sqrt{64}=8,$$
аналогично ОА1 и ОС1 равны 9 см. Но это и означает, что О — центр вписанной окружности.
Площадь треугольника S вычисляется через радиус r вписанной окружности и полупериметр p по следующей формуле:
$$S=pr=8cdot1011=8088$$
Задание 6
Прямая $$y=10x+b$$ является касательной к графику функции $$y=x^4-22x+2022.$$ Найдите значение коэффициента $$b.$$
Ответ: 1974
Скрыть
$$(10x+b)’=(x^4-22x+2022)’Leftrightarrow 10=4x^3-22Leftrightarrow 4x^3=32Rightarrow x^3=8Rightarrow x=2$$
Получим: $$10cdot2+b=2^4-22cdot2+2022Rightarrow b=1974$$
Задание 7
Компания «Нарру New Year» продает свою продукцию по цене $$p = 400$$ руб. за единицу, переменные затраты на производство одной единицы продукции составляют $$v = 200$$ руб., постоянные расходы компании $$f = 500000$$ руб. в месяц. Месячная операционная прибыль компании, выраженная в рублях, вычисляется по формуле $$А = q(p — v) — f.$$ Определите наименьший месячный объем производства $$q$$ (единиц продукции), при котором месячная операционная прибыль компании будет не меньше $$202200$$ руб.
Ответ: 3511
Скрыть
$$A=202200Leftrightarrow q(p-v)-f=202200Leftrightarrow q(400-200)-500000=202200Leftrightarrow$$
$$Leftrightarrow q=3511$$
Задание 8
Снеговик на скоростных электросанях отправился из деревни Морозилкино в село Зимнее, находящееся в 120 км от Морозилкино. Обратно он выехал с той же скоростью, но через час после выезда остановился на 10 мин. После этой остановки он продолжил путь до Морозилкино, увеличив скорость электросаней на 6 км/ч. Какова была первоначальная скорость (км/ч) Снеговика, если известно, что на обратный путь он затратил столько же времени, сколько на путь от Морозилкино до Зимнего?
Ответ: 48
Скрыть
За $$x$$ принимаем скорость туда. За $$x+6$$ принимаем скорость обратно. 10 минут — это $$frac{1}{6}$$ часа. Составляем уравнение времени:
$$frac{120}{x}=frac{120-x}{x+6}+frac{1}{6}+1.$$
$$120cdot(x+6)=xcdot(120-x)+7cdotfrac{x^2+6x}{6}.$$
$$120x+720-120x+x^2-frac{7cdot(x^2+6x)}{6}=0.$$
$$720cdot6+6x^2-7x^2-42x=0.$$
$$4320-x^2-42x=0.$$
$$x^2+42x–4320=0.$$
$$x = 48$$ км/час.
Задание 9
На рисунке изображен график функции $$f(x)=frac{kx+a}{x+b}.$$ Найдите $$a.$$
Ответ: 9
Скрыть
График проходит через $$(1;2), (-3;6), (-5;-4).$$ Получим:
$$left{begin{matrix} 2=frac{k+a}{1+b}\ 6=frac{-3k+a}{-3+b}\ -4=frac{-5k+a}{-5+b} end{matrix}right.Leftrightarrowleft{begin{matrix} 2+2b=k+a\ -18+6b=-3k+a\ 20-4b=-5k+a end{matrix}right.$$
Вычтем второе из первого и третьего:
$$left{begin{matrix} 20-4b=4k\ 38-10b=-2k end{matrix}right.Leftrightarrowleft{begin{matrix} 5-b=k\ -19+5b=k end{matrix}right.Leftrightarrowleft{begin{matrix} 24-6b=0\ 5-b=k end{matrix}right.Leftrightarrowleft{begin{matrix} b=4\ k=1 end{matrix}right.$$
Тогда:
$$2+2cdot4=1+aRightarrow a=9$$
Задание 10
Из ящика, содержащего 5 новогодних подарков, из которых три подарка для мальчиков, а два подарка для девочек, перекладывают наудачу 2 подарка в другой ящик, содержащий одинаковое количество подарков для мальчиков и девочек. Найдите вероятность того, что во втором ящике после этого окажется одинаковое количество подарков для мальчиков и девочек.
Ответ: 0,6
Скрыть
Во втором изначально одинаковое количество. Чтобы это сохранить, надо взять 1 для мальчиков (3 из 5) и 1 для девочек (2 из оставшихся после забора подарка 4). Получим:
$$frac{3}{5}cdotfrac{2}{4}=frac{3}{10}.$$
Можно взять сначала для девочки (2 из 5), потом для мальчика (3 из 4):
$$frac{2}{5}cdotfrac{3}{4}=frac{3}{10}.$$
Оба исхода удовлетворяют: $$frac{3}{10}+frac{3}{10}=0,6.$$
Задание 11
Найдите наибольшее значение функции: $$y=(sqrt{2022})^{12x^2-x^3-254}$$ на отрезке $$[-3;14]$$
Ответ: 2022
Скрыть
$$y’=(sqrt{2022}^{12x^2-x^3-254})’=(2022^{6x^2-frac{x^3}{2}-127})’=$$
$$=2022^{6x^2-frac{x^3}{2}-127}cdotln2022cdot(6x^2-frac{x^3}{2}-127)’=0$$
$$Rightarrow (6x^2-frac{x^3}{2}-127)=0$$
$$f(x)=12x-frac{3}{2}x^2=0Leftrightarrow frac{3}{2}x(8-x)=0Rightarrow x=0;8$$
$$f(1)=frac{3}{2}cdot7>0$$
$$f(-1)=frac{3}{2}cdot(-1)cdot9<0Rightarrow x=0$$ — min
$$f(9)=frac{3}{2}cdot9cdot(-1)<0Rightarrow x=8$$ — max
$$y(8)=(sqrt{2022})^{12cdot64-512-254}=(sqrt{2022})^2=2022$$
Задание 12
А) Решите уравнение $$frac{2022^{cos 2x}-2022^{cos x}}{sqrt{-2021sin x}}=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{11pi}{2};-frac{9pi}{2}]$$
Ответ: А)$$-frac{2pi}{3}+2pi n,nin Z$$ Б)$$-frac{14pi}{3}$$
Задание 13
Точка Q симметрична вершине S правильной четырехугольной пирамиды SABCD относительно плоскости основания АВС.
А) Докажите, что плоскости SBC И QDA параллельны.
Б) Найдите расстояние между плоскостями SBC и QDA, если сторона основания пирамиды SABCD равна 2, а ее боковое ребро равно $$sqrt{2022}.$$
Ответ: $$2sqrt{frac{2020}{2021}}$$
Задание 14
Решите неравенство: $$log_2^2(x-2022)^2-log_{0,5}frac{(x-2022)^4}{(x-2021)^3}+3log_2(x-2021)leq24$$
Ответ: $$(2021;frac{16175}{8}],[frac{16177}{8};2026]$$
Задание 15
В августе 2022-го года Казбек Эльбрусович для строительства резиденции Деда Мороза в Кисловодске собирается взять кредит на 5 лет в размере 210 млн. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего месяца;
— c февраля по июль каждого года необходимо выплатить одним платежом часть долга;
— в августе 2023, 2024 и 2025-го года долг остается равным 210 млн рублей;
— выплаты в 2026 и 2027-м году равны;
— к августу 2027-го года кредит должен быть полностью погашен.
Найдите r, если известно, что общий размер выплат по погашению долга Казбека Эльбрусовича составит 305 млн рублей.
Ответ: 10
Задание 16
В четырехугольнике ELKA диагонали ЕК и AL перпендикулярны сторонам АК и EL соответственно. Прямые АК и EL пересекаются в точке М, а угол LMK равен 60o.
А) Докажите, что угол АОЕ, где О — точка пересечения диагоналей четырёхугольника ELKA, равен 120o.
Б) Найдите длину отрезка МО, если $$EL = 2022sqrt{3}, АК = 3EL.$$
Ответ: $$1348sqrt{39}$$
Задание 17
Найдите все значения параметра $$a,$$ при которых уравнение
$$frac{a^2-3x^2+2ax+2a+8x+1}{(sqrt{2x+1})^2}=log_p p,$$ где $$p=frac{5}{3}-frac{x^2}{6}-frac{a^2}{6},$$
имеет ровно 1 корень.
Ответ: $$(-3;-2,5],left{-2;-3sqrt{0,4};-1,5;0right},[1;1,5)$$
Задание 18
Гипермаркет, реализующий новогодние товары, состоит их 3 отделов. В первом отделе представлены новогодние товары, цена каждого из которых меньше 100 рублей. Средняя цена товаров в этом отделе равна 90 рублей. Во втором отделе представлены новогодние товары, цена каждого из которых больше 100 рублей. Средняя цена товаров в этом отделе равна 120 рублей. Цена каждого товара в третьем отделе равна 100 рублей. Средняя цена всех товаров в гипермаркете равна 110 рублей, а общее число товаров равно 200. Все цены выражаются целым числом рублей.
А) Может ли в первом отделе быть столько же товаров, сколько и во втором?
Б) Может ли в третьем отделе быть на 14 товаров больше, чем во втором?
В) Чему может равняться наибольшая возможная при этих условиях цена товара в этом гипермаркете?
Ответ: А) нет, Б) нет, В) 2628
Автор: admin ·
Опубликовано 30 марта, 2019 · Обновлено 30 марта, 2019
Вариант с досрочного этапа ЕГЭ по математике профильный уровень. Экзамен прошел 29 марта 2019 года. В предложенном реальном варианте задания и ответы. Автор этого варианта А. Ларин.
Ответы
1 – 918 2 – 8 3 – 18 4 – 0,375 5 – 6 6 – 98 7 – 4 8 – 10 9 – -1 10 – 8 11 – 36 12 – 8
Видеоразбор вторая часть
Сайт заблокирован за не оплату услуг хостинга или нарушения правил.
Бесплатный конструктор сайтов
Создайте сайт без технических знаний!
Большой выбор готовых шаблонов для создания сайта
Подробнее
Хостинг сайтов SSD от 55 рублей
У нас можно купить хостинг и получить бесплатно домен и SSL сертификат
Бесплатное тестирование хостинга
Подробнее
Регистрация доменов от 99 рублей
Мы гарантируем самые низкие цены на регистрацию доменов в популярных зонах
Подробнее
SSL сертификаты для сата от 399 рублей
Купите SSL сертификат для сайта и получите месяц хостинга бесплатно
Подробнее
VPS сервера от 209 рублей
Виртуальные серверы VPS с быстрой активацией услуг
Подробнее
Выделенный сервера от 3499 рублей
Огромный выбор выделенных серверов по всему миру
Подробнее
ПОДЕЛИТЬСЯ
Тренировочный вариант №375 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 01.01.2022 (1 января 2022 года)
Скачать вариант Ларина
Ответы для варианта
Решать вариант Алекса Ларина №375 ЕГЭ 2022 по математике 11 класс:
2)В кошельке Деда Мороза лежит четыре пятирублевые монеты и шесть десятирублевых. Какова вероятность того, что, взяв случайным образом две монеты, обе они окажутся десятирублевыми? Ответ округлите до сотых.
Ответ: 0,33
3)Для сторон четырехугольника ABCD, описанного около окружности, выполнены соотношения: АВ : ВС = 3 : 7, AD : CD = 5 : 9. Периметр четырехугольника АВСD равен 2022. Найдите меньшую из сторон этого четырехугольника.
Ответ: 252,75
5)Высота треугольной пирамиды равна 15, а все высоты боковых граней, проведенные из вершины пирамиды равны 17. Найдите площадь основания пирамиды, если его периметр равен 2022.
Ответ: 8088
8)Снеговик на скоростных электросанях отправился из деревни Морозилкино в село Зимнее, находящееся в 120 км от Морозилкино. Обратно он выехал с той же скоростью, но через час после выезда остановился на 10 мин. После этой остановки он продолжил путь до Морозилкино, увеличив скорость электросаней на 6 км/ч. Какова была первоначальная скорость (км/ч) Снеговика, если известно, что на обратный путь он затратил столько же времени, сколько на путь от Морозилкино до Зимнего?
Ответ: 48
10)Из ящика, содержащего 5 новогодних подарков, из которых три подарка для мальчиков, а два подарка для девочек, перекладывают наудачу 2 подарка в другой ящик, содержащий одинаковое количество подарков для мальчиков и девочек. Найдите вероятность того, что во втором ящике после этого окажется одинаковое количество подарков для мальчиков и девочек.
Ответ: 0,6
15)В августе 2022‐го года Казбек Эльбрусович для строительства резиденции Деда Мороза в Кисловодске собирается взять кредит на 5 лет в размере 210 млн. рублей. Условия его возврата таковы: —каждый январь долг возрастает на r % по сравнению с концом предыдущего месяца; — c февраля по июль каждого года необходимо выплатить одним платежом часть долга; — в августе 2023, 2024 и 2025‐го года долг остается равным 210 млн рублей; — выплаты в 2026 и 2027‐м году равны; — к августу 2027‐го года кредит должен быть полностью погашен. Найдите r, если известно, что общий размер выплат по погашению долга Казбека Эльбрусовича составит 305 млн рублей.
Ответ: 10
18)Гипермаркет, реализующий новогодние товары, состоит их 3 отделов. В первом отделе представлены новогодние товары, цена каждого из которых меньше 100 рублей. Средняя цена товаров в этом отделе равна 90 рублей. Во втором отделе представлены новогодние товары, цена каждого из которых больше 100 рублей. Средняя цена товаров в этом отделе равна 120 рублей. Цена каждого товара в третьем отделе равна 100 рублей. Средняя цена всех товаров в гипермаркете равна 110 рублей, а общее число товаров равно 200. Все цены выражаются целым числом рублей. А) Может ли в первом отделе быть столько же товаров, сколько и во втором? Б) Может ли в третьем отделе быть на 14 товаров больше, чем во втором? В) Чему может равняться наибольшая возможная при этих условиях цена товара в этом гипермаркете?
Смотрите также другие варианты Ларина ЕГЭ 2022 по математике:
-
Вариант Ларина №373 ЕГЭ 2022 по математике профиль с ответами
-
Вариант Ларина №374 ЕГЭ 2022 по математике профиль с ответами
Решаем ЕГЭ 265 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №265 (alexlarin.com)
Решаем ЕГЭ 265 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №265 (alexlarin.com)
Задание 1
Необходимо перевезти 50 скутеров весом 300 килограмм каждый. Сколько рейсов понадобится сделать для этого, используя машину грузоподъемностью 5 тонн?
Ответ: 4
Скрыть
В одну машину заходит максимум 16 скутеров: 4,8 тоны $$Rightarrow$$ $$frac{50}{16}approx$$ 4 рейса
Задание 2
На графике показано изменение удельной теплоёмкости водного раствора некоторого вещества в зависимости от температуры. По горизонтали указывается температура в градусах Цельсия, по вертикали – удельная теплоёмкость в Дж/Кг*0С . Определите по рисунку, на сколько изменится удельная теплоемкость при нагревании раствора с 20° до 100°. Ответ дайте в Дж/Кг*0С .
Ответ: 10
Скрыть
При 20 градусах: 4200 ; при 100 градусах : 4210 ; Изменение :4210-4200-=10
Задание 3
Площадь маленького круга равна 4. Найдите площадь закрашенной фигуры
Ответ: 10,5
Скрыть
Радиус большого круга R=2 клетки, малого $$r=frac{R}{2}Rightarrow$$ $$S_{1} =pi (frac{R}{2})^{2}=frac{pi R^{2}}{4}=frac{S}{4}=4$$, где $$S$$ и $$S_{1}$$ площади большого и малого кругов соответственно , тогда S=4*4=16
Тогда площадь кольца: $$S-S_{1}=12$$. При этом уберем сегмент (его площадь $$frac{1}{8}$$ от кольца) $$Rightarrow$$ итоговая площадь $$12*frac{7}{8} =10,5$$.
Задание 4
В классе учится 16 человек: 6 мальчиков и 10 девочек. Перед началом уроков классный руководитель случайным образом выбирает двух учащихся класса для дежурства в столовой. Какова вероятность, что дежурить в столовую отправятся мальчик с девочкой?
Ответ: 0,5
Скрыть
Вероятность выбрать сначала мальчика, потом девочку: $$frac{6}{16}*frac{10}{15}=frac{1}{4}$$
Девочку, потом мальчика: $$frac{10}{16}*frac{6}{15}=frac{1}{4}$$
Следовательно, вероятность, что попадут мальчик и девочка: $$frac{1}{4}+frac{1}{4}=0,5$$
Задание 5
Найдите корень уравнения $$sqrt{3-x}=1-x$$ . Если корней несколько, то в ответе укажите больший из них.
Ответ: -1
Скрыть
$$sqrt{3-x}=1-xLeftrightarrow$$ $$left{begin{matrix}3-x=(1-x)^{2}1-xgeq 0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}3-x=1-2x+x^{2}xleq 1end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x^{2}-x-2=0xleq 1end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}left[begin{matrix}x=2x=-1end{matrix}right.xleq 1 end{matrix}right.Leftrightarrow$$ $$x=-1$$
Задание 6
Радиус окружности, описанной около правильного шестиугольника, равен $$sqrt{3}$$ . Найдите радиус вписанной окружности
Ответ: 1,5
Скрыть
$$R=frac{r}{sin 60}$$, где R-описанной; r –вписанной $$Rightarrow$$ $$r=R sin 60 =sqrt{3} *frac{sqrt{3}}{2}=1,5$$
Задание 7
По графику функции у = f(x) определите количество точек на интервале (‐3; 4), в которых касательная к графику параллельна прямой у = 0,3х – 4 или совпадает с ней.
Ответ: 5
Скрыть
Если параллельна или совпадает , то $$f^{‘}=(0,3x-4)^{‘}=0,3$$. Тогда точки (отмечены на рисунке) находятся на промежутке возрастания , и их количество 5. (Можно построить схематичный график производной)
Задание 8
Объем правильной шестиугольной призмы равен 180. Сначала каждое ее боковое ребро увеличили в два раза, а затем каждую сторону каждого основания уменьшили в три раза. Найдите объем полученной призмы.
Ответ: 40
Скрыть
Пусть h –начальная высота $$Rightarrow$$ $$h_{1}=2h$$, a –сторона основания $$Rightarrow$$ $$a_{1} =frac{a}{3}Rightarrow$$ $$frac{S}{S_{1}}=(frac{3}{1})^{2}=frac{9}{1}$$, где $$a_{1},h$$ и $$S_{1}$$ –сторона , высота и площадь основания новой призмы . $$Rightarrow$$ $$frac{V}{V_{1}}=frac{Sh}{S_{1}h_{1}}=frac{9}{2}=4,5$$$$Rightarrow$$ $$V_{1}=frac{V}{4,5}=40$$
Задание 9
Найдите значение выражения $$log_{frac{4}{25}} (log_{4} 32)$$
Ответ: -0,5
Скрыть
$$log_{frac{4}{25}}log_{4}32=$$$$log_{(frac{2}{5})^{2}} log_{2^{2 }}2^{5}=$$$$frac{1}{2} log_{frac{2}{5}}frac{5}{2} log_{2} 2=$$$$frac{1}{2}log_{frac{2}{5}}frac{5}{2}=-0,5$$
Задание 10
Максимальная высота подъёма тела, брошенного под углом к горизонту, вычисляется по формуле $$h=frac{(v*sin^{2} alpha)^{2}}{2g}$$ , где v (м/c) – начальная скорость тела, α – угол, под которым тело брошено к горизонту, g – ускорение свободного падения (считать, что g=10 м/с2). С какой скоростью необходимо бросить мяч под углом 30º к горизонту, чтобы он поднялся на высоту 5 м?
Ответ: 20
Скрыть
Выразим из формулы скорость: $$h=frac{(v sin alpha )^{2}}{2g}Leftrightarrow$$ $$2gh=v^{2} sin ^{2}alpha Leftrightarrow$$ $$frac{2 gh}{sin ^{2}alpha }=v^{2}Leftrightarrow$$ $$v=frac{sqrt{2gh}}{sin alpha }$$
Найдем скорость : $$v=frac{sqrt{2*10*5}}{sin 30}=frac{10}{frac{1}{2}}=20$$
Задание 11
Сцепленные зубчатые колеса вместе в сумме делают 240 оборотов в минуту. Найдите количество зубьев у второго колеса, если у первого их 100, и делает оно на 80 оборотов в минуту больше, чем второе колесо.
Ответ: 200
Скрыть
Пусть x-количество оборотов второго колеса, тогда $$x+80$$ — первого и $$x+x+80=240Leftrightarrow$$ $$2x=160$$$$Leftrightarrow$$ $$x=80$$ — второе колесо, 160-первое.
Первое колесо за 160 оборотов пройдет $$160*100=16000$$ зубьев. Второе пройдет столько же, но за 80 оборотов, следовательно , у него $$frac{16000}{80}=200$$ зубьев.
Задание 12
Найдите наибольшее значение функции $$y=(x-1)*2^{x}$$ на отрезке [2; 6]
Ответ: 320
Скрыть
1) Найдем производную функции и приравняем к 0 : $$y^{‘}=(x-1)^{‘}2^{x}+(x-1)(2^{x})^{‘}=2^{x}+(x-1)2^{x}ln 2=0Leftrightarrow$$$$2^{x}(1+(x-1)ln 2)=0Leftrightarrow$$ $$1+(x-1)ln 2=0Leftrightarrow$$ $$x-1=frac{-1}{ln 2}Leftrightarrow$$ $$x=-frac{1}{ln 2}-1=-log_{2}e-1=$$$$log_{2}frac{1}{e}-1=$$$$log_{2}frac{1}{2e}<0Rightarrow$$ на промежутке [2 ;6] $$y_{max}=y(6)=(6-1)2^{6}=320$$
2) Можно решить рассуждением:
На промежутке [2; 6] : y=(x-1) и возрастает $$y=2^{x} Rightarrow$$ $$y=(x-1)2^{x}Rightarrow$$ $$y_{max}=y(6)$$
Задание 13
а) Решите уравнение $$3*2^{cos x+3sqrt{1-sin^{2} x}}+11*2^{2cos x}-34=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{pi}{2};frac{5pi}{2}]$$
Ответ: А) $$pm frac{pi}{3}+2 pi n , n in Z$$ Б) $$pm frac{pi}{3};frac{5pi}{3};frac{7pi}{3}$$
Скрыть
A) $$3*2^{cos x+3sqrt{1-sin ^{2}x}}+11 *2^{2 cos x}-34=0Leftrightarrow$$ $$3*2^{cos x+3sqrt{cos ^{2}x}}+11*2^{2 cos x}-34=0Leftrightarrow$$ $$3*2^{cos x+3left | cos ^{2}x right |}+11*2^{2 cos x}-34=0$$
1) при $$cos xgeq 0$$$$Leftrightarrow$$ $$x in [-frac{pi}{2}+2 pi n, frac{pi}{2}+2 pi n], n in Z$$: $$3*2^{4 cos x}+11*2^{2 cos x}-34=0$$
Пусть $$2^{2 cos x}=y>0$$, тогда $$3y^{2}+11y-34=0$$: $$D=121+408=529$$
$$left[begin{matrix}y_{1}=frac{-11+23}{6}=2y_{2}=frac{-11-23}{6}<0end{matrix}right.Leftrightarrow$$ $$2 ^{2 cos x}=2Leftrightarrow$$ $$2 cos x=1Leftrightarrow$$ $$cos x=frac{1}{2}Leftrightarrow$$ $$x=pm frac{pi}{3}+2 pi n , n in Z$$
2) при $$cos x<0$$: $$3*2^{cos x-3 cos x}+11*2^{2 cos x}-34=0Leftrightarrow$$$$3*2^{-2cos x}+11*2^{2 cos x}-34=0$$
Пусть $$2^{2 cos x}=y>0$$ , тогда $$frac{3}{y}+11*y-34=0Leftrightarrow$$ $$frac{11y^{2}-34y+3}{y}=0Leftrightarrow$$ $$11y^{2}-34y+3=0$$
$$D=1156-132=1024$$
$$left[begin{matrix}y_{1}=frac{34+32}{22}=3y_{2}=frac{34-32}{22}=frac{1}{11}end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}2^{2 cos x}=32 ^{2 cos x}=frac{1}{11}end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}4^{cos x}=34^{cos x}=frac{1}{11}end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}cos x=log_{4}3>0Rightarrow varnothingcos x=log_{4}frac{1}{11}<-1Rightarrow varnothing & &end{matrix}right.$$
Б) На промежутке $$[-frac{pi}{2};frac{5pi}{2}]$$:
$$frac{pi}{3}+2 pi n$$: $$frac{pi}{3};frac{7pi}{3}$$
$$-frac{pi}{3}+2 pi n$$: $$frac{pi}{3};frac{5pi}{3}$$
Задание 14
В основании пирамиды с вершиной S лежит прямоугольник, центр которого находится на высоте пирамиды. Плоскость пересекает боковые ребра пирамиды в точках P, Q, M и N так, что Р и М – противоположные вершины четырехугольника PQMN. Известно, что $$SP=7$$, $$SM=frac{7}{6}$$, $$SQ+SN=frac{25}{6}$$, $$SQ>SN$$
А) Найдите SQ и SN
Б) Найдите, в каком отношении плоскость делит высоту пирамиды, если дополнительно известно, что боковое ребро пирамиды равно 10.
Ответ: А)$$frac{5}{2};frac{5}{3}$$ Б)$$frac{1}{4}$$
Скрыть
A) 1)Через P проведем плоскость параллельную (ABC): $$PQ_{1}M_{1}N{1})$$$$Rightarrow$$ $$SP=SQ=SM_{1}=SN_{1}=7$$. Пусть H –центр ABCD $$Rightarrow$$ SH –высота пирамиды; $$SHcap (PQMN)=O$$, $$SHcap (PQ_{1}M_{1}N_{1})=O_{1}$$ ; $$MM_{1}=SM_{1}-SM=frac{35}{6}$$
2) Из $$Delta SM_{1}P$$: $$M_{1}Q_{1}=O_{1}PRightarrow$$ по т. Менелая для $$Delta MPM_{1}$$ : $$frac{SO}{OO_{1}}*frac{O_{1}P}{PM_{1}}*frac{M_{1}M}{MS}=1Leftrightarrow$$ $$frac{SO}{OO_{1}}*frac{1}{2}*frac{35}{6}:frac{7}{6}=1Leftrightarrow$$ $$frac{SO}{OO_{1}}=frac{2}{5}$$
3) Рассмотрим $$Delta SQ_{1}N_{1}$$: пусть $$SQ=xRightarrow$$ $$SN=frac{25-x}{6}$$; Построим $$N_{2}Q_{2}left | right |N_{1}Q_{1}Rightarrow$$ $$Delta SON_{2}sim Delta SO_{1}N_{1}Rightarrow$$ $$frac{SN_{2}}{N_{2}N_{1}}=frac{SO}{OO_{1}}=frac{2}{5}$$. Т.е. $$SN_{1}=7$$, то $$SN_{2}=2=SQ_{2}$$, тогда $$N_{2}N=SN_{2}-SN=2-(frac{25}{6}-x)=x-frac{13}{6}$$; $$Q_{2}Q=SQ-SQ_{2}=x-2$$
По т. Менелая для $$Delta NSQ$$: $$frac{N_{2}O}{OQ_{2}}*frac{Q_{2}Q}{QS}*frac{SN}{NN_{2}}=1$$$$Leftrightarrow$$ $$frac{1}{1}*frac{x-2}{x}*frac{frac{25}{6}-x}{x-frac{13}{6}}=1$$$$Leftrightarrow$$ $$(x-2)(frac{25}{6}-x)=x(x-frac{13}{6})|*6$$$$Leftrightarrow$$ $$12x^{2}-50x+50=0Leftrightarrow$$ $$6x^{2}-25x+25=0Leftrightarrow$$ $$left[begin{matrix}x_{1}=frac{5}{2}x_{2}=frac{5}{3}end{matrix}right.$$
$$frac{5}{3}$$ не подходит, т.к. $$frac{25}{6}-frac{5}{3}=frac{5}{2}$$ и $$frac{5}{3}<frac{5}{2}$$, а по условию $$SQ>SNRightarrow$$ $$SQ=frac{5}{2}$$; $$SN=frac{5}{3}$$
Б) 1) Рассмотрим $$Delta SHD$$: $$SQ_{2}=2$$; $$Q_{2}Q_{1}=5$$; $$Q_{1}D=SD-SQ_{1}=10-7=3Rightarrow$$ $$Q_{2}D=5+3=8$$
2) $$Delta SOQ_{2}sim Delta SHDRightarrow$$ $$frac{SO}{OH}=frac{SQ_{2}}{Q_{2}D}=frac{2}{8}=frac{1}{4}$$
Задание 15
Решите неравенство $$(log_{3+x} (1-2x))(log_{1-2x} x^{2})leq (log_{3+x} (1-3x))(log_{1-3x} (2-x))$$
Ответ: $$(-3; -2) cup (-2; 0)cup (0; frac{1}{3})$$
Скрыть
$$(log_{3+x}(1-2x))(log_{1-2x}x^{2})leq (log_{3+x}(1-3x))(log_{1-3x}(2-x))$$
ОДЗ: $$left{begin{matrix}1-2x>03+x>03+xneq 11-2xneq 1x^{2}>01-3x>02-x>01-3xneq 1end{matrix}right.$$$$Leftrightarrow$$ $$left{begin{matrix}x<0,5x>-3xneq -2xneq 0x<frac{1}{3}x<2end{matrix}right.$$$$Leftrightarrow$$ $$x in (-3; -2)cup (-2; 0)cup (0; frac{1}{3})$$
Решение: $$frac{1}{log_{1-2x}(3+x)}*log_{1-2x}x^{2}leq frac{1}{log_{1-3x}(3+x)}*log_{1-3x}(2-x)Leftrightarrow$$ $$log_{3+x}x^{2}leq log_{3+x}(2-x)Leftrightarrow$$ $$(3+x-1)(x^{2}-2+x)leq 0Leftrightarrow$$ $$(x+2)(x+2)(x-1)leq 0Leftrightarrow$$ $$left[begin{matrix}x+2=0xleq 1end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x=-2xleq 1end{matrix}right.$$
С учетом ОДЗ: $$x in (-3; -2) cup (-2; 0)cup (0; frac{1}{3})$$
Задание 16
На основаниях AD и ВС трапеции ABCD построены квадраты ADMN и BCRS, расположенные вне трапеции. Диагонали трапеции пересекаются в точке Т.
А) Докажите, что центры квадратов и точка Т лежат на одной прямой.
Б) Найдите длину отрезка RN, если AD=8, BC=3, а TN=20.
Ответ: 27,5
Скрыть
A) 1) $$angle KBL=angle ADL=45$$ (угол между диагональю и стороной квадрата);
$$angle HBT=angle TDA$$ (накрест лежащие )$$Rightarrow$$ $$angle KBT=angle TDL$$;
$$angle BTK=angle LTD$$ (вертикальные )$$Rightarrow$$ $$Delta KBTsim Delta TDL$$$$Rightarrow$$ $$angle BKT=angle TLD$$
2) из $$angle KBT=angle NDLRightarrow$$ $$BKleft | right |LD$$ $$Rightarrow$$ $$angle BKT=angle TLD$$, то они накрест лежащие $$Rightarrow$$ $$KTleft | right |TL$$ или $$K,T,L in KL$$, но параллельны быть не могут (так как имеют общую точку) $$Rightarrow$$ KL-секущая
Б) 1) Аналогично п. A $$Delta RCT sim TAN$$ ($$angle C=90$$; $$angle BCD=angle TAD$$ — накрест лежащие )$$Rightarrow$$ $$ANleft | right |RC$$; $$angle TNA=angle TRC$$$$Rightarrow$$ $$R,T,N in RN$$
2) из подобия : $$frac{AN}{RC}=frac{NT}{TR}Leftrightarrow$$ $$frac{8}{3}=frac{20}{x}Rightarrow$$ $$x=frac{3*20}{8}=7,5Rightarrow$$ $$RN=27,5$$
Задание 17
В июле планируется взять кредит в банке на сумму 12 млн. рублей на 15 лет. Условия его возврата таковы:
‐ пока долг больше половины исходной суммы, каждый январь он возрастает на 12% по сравнению с концом предыдущего года;
‐ если долг меньше половины исходной суммы, то каждый январь он в по сравнению с концом предыдущего года;
‐ с февраля по июнь каждого года необходимо выплатить часть долга;
‐ в июле каждого последующего года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года
Какую сумму нужно вернуть банку?
Ответ: 21728000
Скрыть
Пусть $$S=12*10^{6}$$ руб. –первоначальная сумма кредита, $$n=15$$ лет-срок кредита, $$a=12$$ % , $$b=4$$ % . Составим таблицу платежей (каждый платеж состоит из суммы по основному долгу $$frac{S}{15}$$ (за 15 лет надо отдать S) и начисленные за год процентов) :
| № года | Долг на начало года | Сумма по начисленному проценту | Итоговый платеж (по основному долгу и проценту) |
| 1 | $$S$$ | $$frac{Sa}{100}$$ | $$frac{S}{15}$$+$$frac{Sa}{100}$$ |
| 2 | $$frac{14S}{15}$$ | $$frac{14S}{15}*frac{a}{100}$$ | $$frac{S}{15}$$+$$frac{14Sa}{1500}$$ |
| … | … | … | … |
| 8 | $$frac{8S}{15}$$ | $$frac{8S}{15}*frac{a}{100}$$ | $$frac{S}{15}$$+$$frac{8Sa}{1500}$$ |
| 9 | $$frac{7S}{15}$$ | $$frac{7S}{15}*frac{b}{100}$$ | $$frac{S}{15}$$+$$frac{7Sb}{1500}$$ |
| … | … | … | … |
| 15 | $$frac{S}{15}$$ | $$frac{S}{15}*frac{b}{100}$$ | $$frac{S}{15}$$+$$frac{Sb}{1500}$$ |
Итого будет выплачено : $$frac{S}{15}*15+frac{Sa}{100}(1+frac{14}{15}+..+frac{8}{15})+frac{8b}{100}(frac{7}{15}+frac{6}{15}+..+frac{1}{15})$$
Подставим известные значения: $$S+Sa*frac{92}{15}+8b*frac{28}{15}=$$$$S(1+frac{92a}{15}+frac{28b}{15})=$$$$12*10^{6}(1+frac{91*12}{15*100}+frac{28*4}{15*100})=21728000$$
Задание 18
Найдите все значения параметра а, при которых уравнение $$(cos x -1)^{2}=a(cos x+4sin^{2} x-8)$$ имеет на промежутке $$(0;frac{pi}{2}]$$ единственный корень.
Ответ: $$[-frac{1}{4};0)$$
Скрыть
$$(cos x-1)^{2}=a(3 cos x+4 sin ^{2}x-8)Leftrightarrow$$ $$(cos x-1)^{2}=a(3 cos x+4-4cos^{2}x-8)Leftrightarrow$$ $$(cos x-1)^{2}=a(3cos x-4 cos ^{2}x-4)$$
Рассмотрим правую часть : -$$4 cos^{2}x-4 in [-8 ;-4]$$ $$(cos ^{2}x in [0 ;1] )Rightarrow$$ $$3 cos x-4 cos ^{2}x-4leq -1$$ при любом x) , при этом $$(cos x-1)^{2}geq 0Rightarrow$$ чтобы выполнялось решение должно быть $$a<0$$ (при a=0 получим, что $$cos x-1=0 Rightarrow$$ $$cos x=1Rightarrow$$ $$x=2 pi n notin (0 frac{pi}{2}]$$)
При этом, чтобы было решение на $$(0 ;frac{pi}{2}]$$, то $$cos x in [0; 1)$$
Сделаем замену $$cos x=t in [-1; 1]$$: $$(t-1)^{2}=a(3t-4t^{2}-4)Leftrightarrow$$ $$frac{(t-1)^{2}}{a}=-4t^{2}+3t-4$$
Рассмотрим функции : $$f_{1}(t)=frac{(t-1)^{2}}{a}$$ и $$f_{2}(t)=4t^{2}+3t-4p$$
- $$f_{2}(t): t_{0}=-frac{3}{-8}=frac{3}{8}Rightarrow$$ $$f_{2}(t_{0})=-frac{55}{16}$$ — парабола, ветви вниз, вершина $$(frac{3}{8};-frac{55}{16})$$, сужение к оси симметрии
- $$f_{1}(t)$$: парабола, вершина (1; 0) , ветви в зависимости от a ($$a<0 Rightarrow$$ вниз )
При этом необходимо единственное решение на $$x in (0 ;frac{pi}{2}]Rightarrow$$ $$cos x in [0; 1) Rightarrow$$ $$t in [0; 1)$$ -единственное решение на данном промежутке.
Решение такое будет при $$f_{1}(0)leq -4$$ $$Rightarrow$$ $$frac{(01)^{2}}{a}leq -4Rightarrow$$ $$frac{1}{a}leq -4Leftrightarrow$$ $$frac{1+4a}{a}leq 0Rightarrow$$ $$ain [-frac{1}{4};0)$$
Задание 19
Пусть n ‐ трехзначное число, а f (n) ‐ сумма квадратов его цифр
А) Существует ли такое, что $$frac{f(n)}{n}>1$$ ?
Б) Существует ли такое n, что $$frac{f(n)}{n}>frac{1}{2}$$?
В) Найдите наибольшее возможное значение отношения $$frac{f(n)}{n}$$.
Ответ: нет, да, $$frac{163}{199}$$
Скрыть
Пусть $$n=100a+10b+c$$, где $$a in [1; 9]in N, b,c in [0; 9]in Z$$
A) $$frac{a^{2}+b^{2}+c^{2}}{100a+10b+c}>1Rightarrow$$ $$a^{2}+b^{2}+c^{2}>100a+10b+cRightarrow$$ $$a^{2}-100a+b^{2}-10b+c^{2}-c>0Leftrightarrow$$ $$(a-50)^{2}-2500+(b-5)^{2}-25+(c-frac{1}{2})^{2}-0,25>0Leftrightarrow$$ $$(a-50)^{2}+(b-5)^{2}+(c-frac{1}{2})^{2}>2525,25$$
$$(a-50)^{2}=(1-50)^{2}=49^{2}=2401$$. При этом $$max(b-5)^{2}=max(0-5)^{2}=25$$; $$max(c-frac{1}{2})^{2}=72,25$$. При этом сумма этих максимальных значений : $$2401+25+72,25=2498,25$$, что меньше , чем $$2525,25$$ $$Rightarrow$$ не может
Б) Аналогично п.А : может , например 199: $$frac{1^{2}+9^{2}+9^{2}}{199}>frac{1}{2}Leftrightarrow$$ $$frac{163}{199}>frac{1}{2}$$
B) Рассмотрим $$frac{a^{2}+b^{2}+c^{2}}{100a+10b+c}rightarrow max$$. Очевидно , что a=1 (иначе в знаменателе прибавится сотня),а c=9 $$Rightarrow$$ $$frac{^{2}+b^{2}+9^{2}}{100+10b+9}=frac{82+b^{2}}{109+10b}rightarrow max$$
Найдем производную: $$frac{(82+b^{2})^{‘}(109+10b)-(109+10b)^{‘}(82+b^{2})}{(109+10b)^{2}}=$$$$frac{2b(109+10b)-10(82+b^{2})}{(109+10b)^{2}}=$$$$frac{10b^{2}+218b-820}{(109+10b)^{2}}=0Leftrightarrow$$ $$5b^{2}+114b-410=0$$: $$D=20081approx 141Rightarrow$$ $$b_{1}=frac{-114+141}{2*5}=2,7$$; $$b_{2}=frac{-114-141}{10}=-25,5rightarrow$$ 2,7-точка минимума $$Rightarrow$$ $$frac{82+b^{2}}{109+10b}rightarrow$$ $$max$$ при $$b=0$$ или при $$b=9$$:
- $$b=0$$: $$frac{82+0^{2}}{109+10*0}=frac{82}{109}$$;
- $$b=9$$ :$$frac{82+9^{2}}{109+10*9}=frac{163}{199}$$;
$$frac{163}{199}>frac{82}{109}Rightarrow$$ максимальное значение $$frac{163}{199}$$
На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023
Вариант Ларина №375 ЕГЭ 2022 по математике профиль с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Тренировочный вариант №375 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-%d0%bb%d0%b0%d1%80%d0%b8%d0%bd%d0%b0-%e2%84%96375-%d0%b5%d0%b3%d1%8d-2022-%d0%bf%d0%be-%d0%bc%d0%b0%d1%82%d0%b5%d0%bc%d0%b0%d1%82%d0%b8%d0%ba%d0%b5-%d0%bf/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
| 3471 | а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. |
а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12 | |
| 3470 | В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней |
В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13 | |
| 3469 | Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x). |
Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14 |
|
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN |
На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ |
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3466 | Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) |
Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6 | |
| 3465 | Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? |
Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9 | |
| 3464 | а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. |
а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12 | |
| 3463 | SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 |
SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13 | |
| 3462 | Решите неравенство 2^(x/(x+1))-2^((5x+3)/(x+1))+8<=2^((2x)/(x+1)) |
Решите неравенство 2 x/x+1 -2 5x+3 / x+1 +8 <= 2 2x/x+1 ! Тренировочный вариант 398 от Ларина Задание 14 |
|

Показана страница 1 из 89